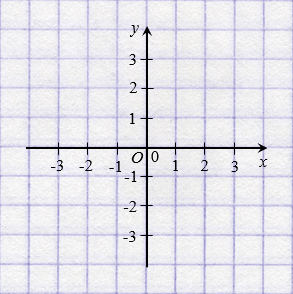- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Координатная плоскость
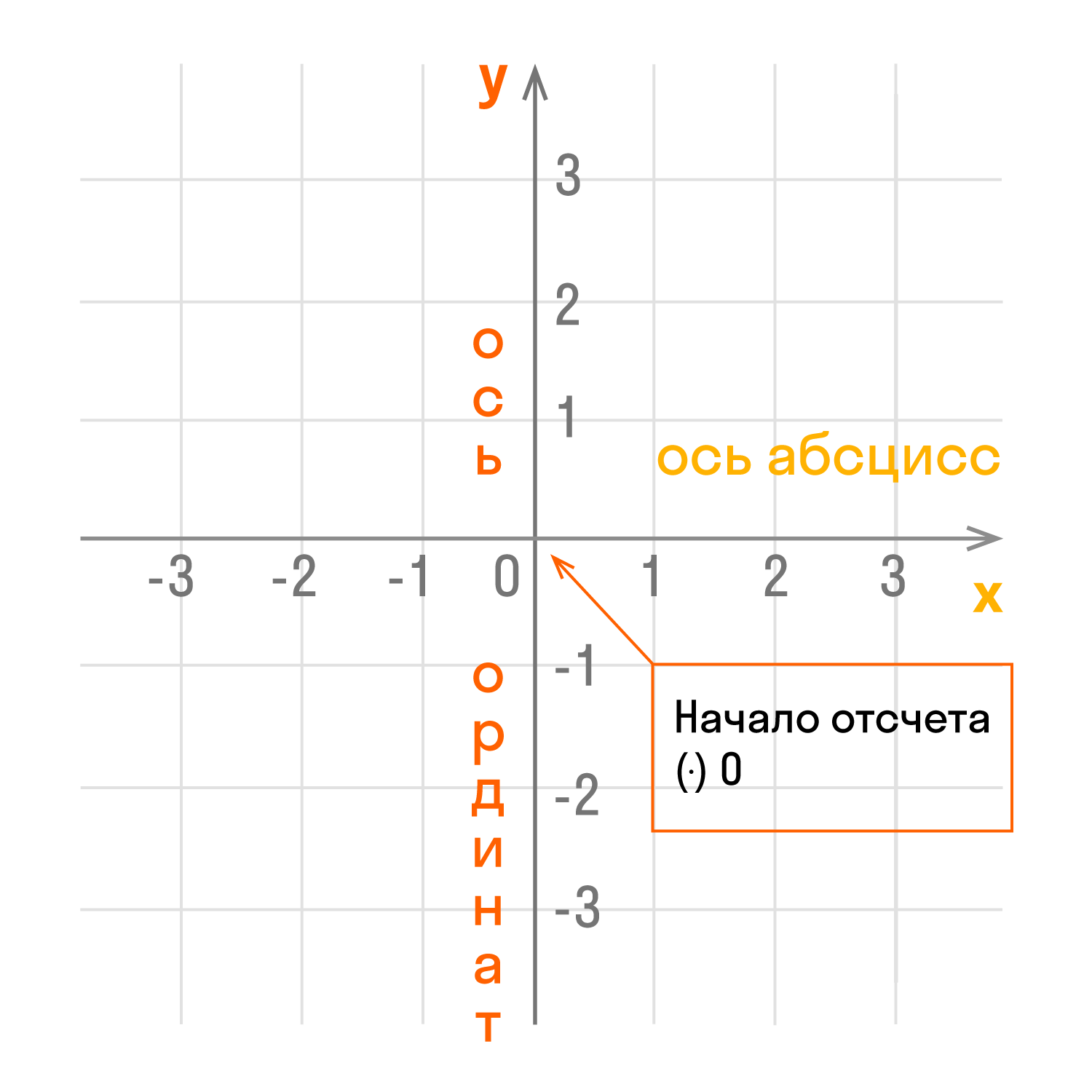
Указать положение точки на плоскости можно с помощью координат. Для этого проведем на плоскости две перпендикулярные координатные прямые так, чтобы их начала отсчета совпадали.
Эти прямые называют осями координат, точку их пересечения О — начало отсчета.
Горизонтальная ось — ось абсцисс, обозначают буквой 

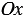
Вертикальная ось — ось ординат, обозначают буквой 

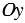
Оси 

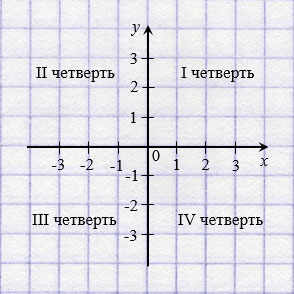
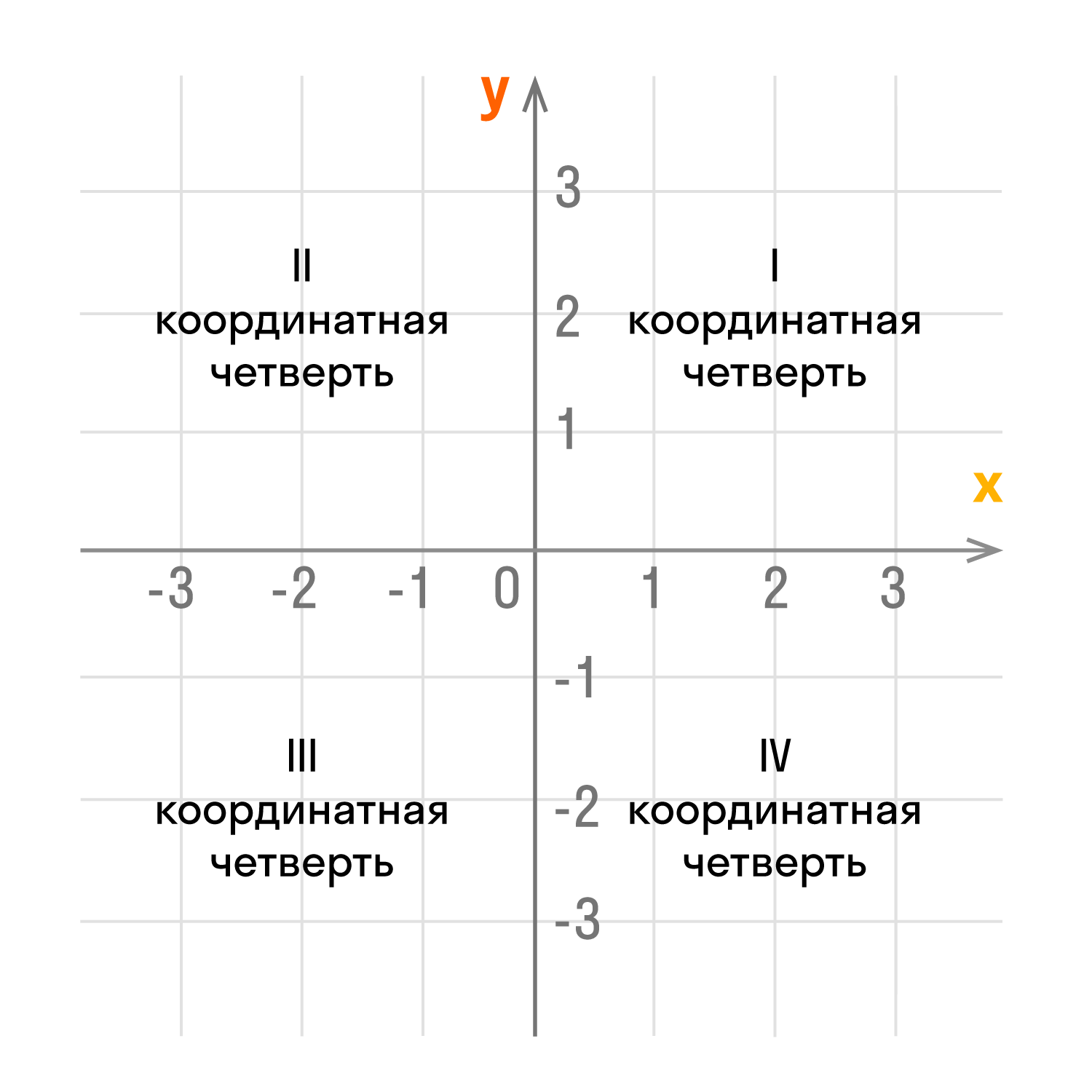
Координатные оси разбивают плоскость на четыре части, которые называют координатными четвертями и нумеруют так, как показано на рисунке ниже.
Отметим на координатной плоскости точку А. Проведем через нее прямую АВ, перпендикулярную оси абсцисс (АВ 
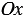
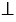
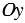
Точка В на оси 





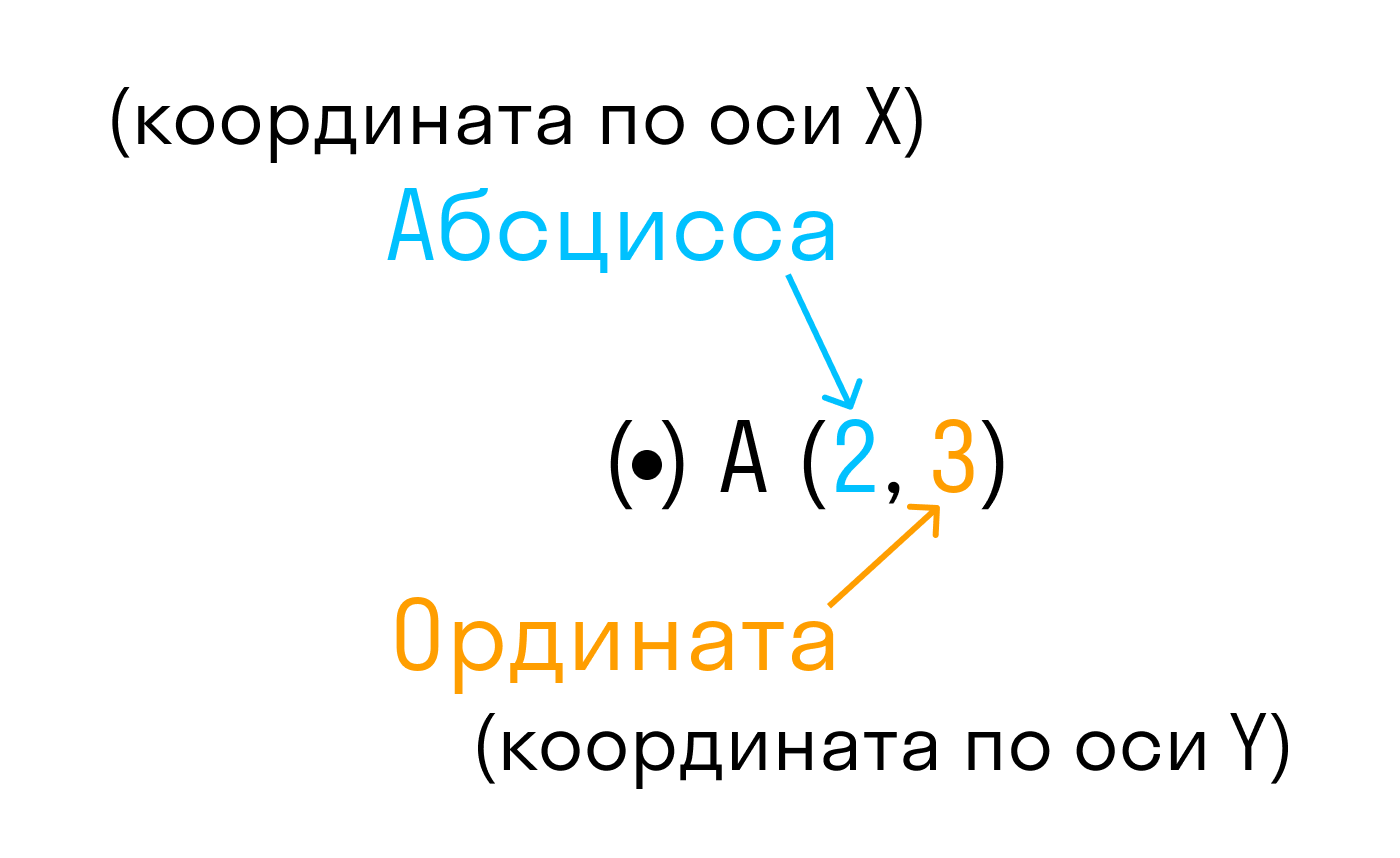
Обратите внимание, записывая координаты точки, абсциссу всегда ставят на первое место, а ординату — на второе. Если числа 5 и 

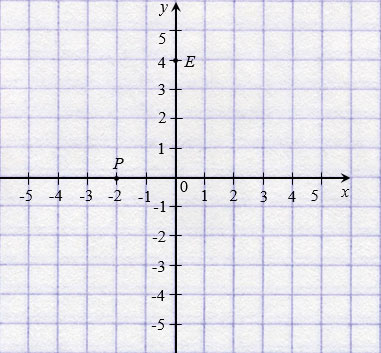
У начала координат абсцисса и ордината равны нулю, записывают так: О(0; 0). Если точка лежит на оси абсцисс, то ее ордината равна нулю, а если на оси ординат, то нулю равна ее абсцисса. На рисунке ниже: Р(
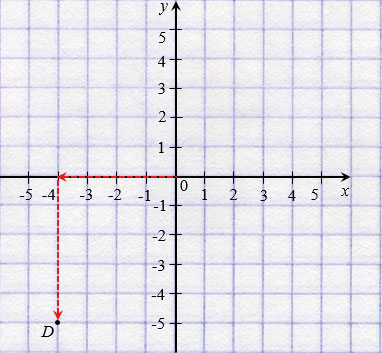
Чтобы попасть в точку D с координатами (


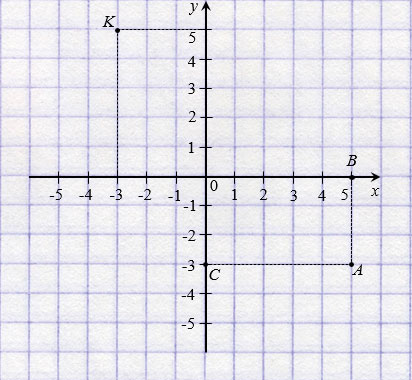
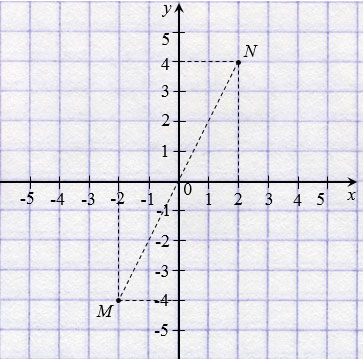
Две точки с противоположными абсциссами и ординатами симметричны относительно начала координат.
На рисунке ниже точки N(2; 4) и М(

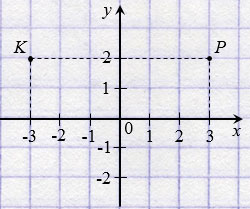
Две точки, имеющие равные ординаты и противоположные абсциссы, симметричны относительно оси ординат.
На рисунке ниже точки Р(3; 2) и К(
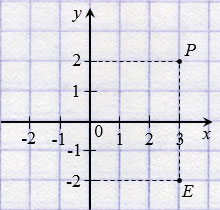
Две точки, имеющие равные абсциссы и противоположные ординаты, симметричны относительно оси абсцисс.
На рисунке ниже точки Р(3; 2) и Е(3; 
Советуем посмотреть:
Перпендикулярные прямые
Осевая и центральная симметрии
Параллельные прямые
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1302,
Мерзляк, Полонский, Якир, Учебник
Номер 1307,
Мерзляк, Полонский, Якир, Учебник
Номер 1317,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Номер 7,
Мерзляк, Полонский, Якир, Учебник
Задание 1399,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1417,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1444,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1534,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1538,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 751,
Мерзляк, Полонский, Якир, Учебник
Номер 775,
Мерзляк, Полонский, Якир, Учебник
Номер 828,
Мерзляк, Полонский, Якир, Учебник
Номер 831,
Мерзляк, Полонский, Якир, Учебник
Номер 879,
Мерзляк, Полонский, Якир, Учебник
Номер 880,
Мерзляк, Полонский, Якир, Учебник
Номер 1011,
Мерзляк, Полонский, Якир, Учебник
Номер 1213,
Мерзляк, Полонский, Якир, Учебник
Номер 1216,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 63,
Мерзляк, Полонский, Якир, Учебник
Номер 333,
Мерзляк, Полонский, Якир, Учебник
Номер 334,
Мерзляк, Полонский, Якир, Учебник
Номер 336,
Мерзляк, Полонский, Якир, Учебник
Номер 337,
Мерзляк, Полонский, Якир, Учебник
Номер 353,
Мерзляк, Полонский, Якир, Учебник
Номер 359,
Мерзляк, Полонский, Якир, Учебник
Номер 361,
Мерзляк, Полонский, Якир, Учебник
Номер 362,
Мерзляк, Полонский, Якир, Учебник
Номер 366,
Мерзляк, Полонский, Якир, Учебник
Как найти координату?
как найти абсциссу и ординату точки на координатной плоскости? Чтобы найти абсциссу, нужно по оси x выбрать то число, которое указано в координатах на первом месте. Чтобы найти ординату, нужно по оси y выбрать то число, которое указано в координатах на втором месте.
Что такое ось ординат в математике?
Если точка A лежит на оси Y, то её абсцисса равна нулю. Если точка A лежит на оси X, то её ордината равна нулю. В прямоугольной системе координат ось X называется «осью абсцисс». В прямоугольной системе координат ось Y называется «осью ординат».
Как запомнить оси абсцисс или ординат?
Итак, есть ось абсцисс и ось ординат — ось x и ось y. Абсцисса начинается на букву «а», ордината — на букву «о». Что у нас в русском алфавите? Сначала идет буква «а», затем — буква «о».
Как расположены точки в координатной плоскости если их ордината равна?
Любая точка, лежащая на этой прямой, имеет ординату 2. … Значит, все точки в координатной плоскости, если их ордината равна 2, расположены на прямой,параллельной оси x и пересекающей ось в точке с ординатой 2.
Что такое абсцисса в алгебре?
Абсциссой (лат. abscissa — отрезок) точки A называется координата этой точки на оси X’X в прямоугольной системе координат. Величина абсциссы точки A равна длине отрезка OB (см.
Кто впервые ввел термины координата абсцисса ордината?
Лейбниц
Как располагается ось абсцисс?
Положительные абсциссы обычно располагаются на оси XX’ справа от начала координат; положительные ординаты – вверх по оси YY’ от начала координат. На рис.
Чему равны абсциссы точек лежащих на оси координат?
ординаты точек,лежащих на оси абсцисс равны нулю.
Какие координаты имеет начало координат?
В декартовой системе координат, начало координат — это точка, в которой пересекаются все оси координат. Это означает, что все координаты этой точки равны нулю.
Что такое система координат?
Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. … Географические координаты.
Как построить прямоугольную систему координат на плоскости?
Прямоугольная система координат на плоскости
- Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат и . …
- Положение точки на плоскости определяется двумя координатами и . …
- При этом координате приписывается знак минус, если точка лежит на луче (а не на луче , как на рисунке).
Как называются оси XYZ?
Оси координат Ox, Oy и Oz называются соответственно: Ox — ось абсцисс, Oy — ось ординат, Oz — ось аппликат. Через две пересекающиеся прямые можно провести плоскость. Получаем три координатные плоскости: (Oxy), (Oyz) и (Oxz). Положение точки A в пространстве определяется тремя координатами: x, y и z.
Как называют координатную ось направленную вертикально вверх?
Одну из осей называют осью абсцисс (осью Ох), другую — осью ординат (осью Оу) (рис. 23). На рисунках ось абсцисс обычно располагают горизонтально и направленной слева направо, а ось ординат — вертикально и направленной снизу вверх.
Как называются координатные оси?
Когда говорят про двухмерную систему коодинат, горизонтальную ось называют осью абсцисс (осью Ox), вертикальную ось — осью ординат (осью Оy). Положительные направления выбирают на оси Ox — вправо, на оси Oy — вверх. Координаты x и y называются соответственно абсциссой и ординатой точки.
Как найти координаты точки зная координаты вектора?
Определеие. Чтобы найти координаты вектора AB, зная координаты его начальной точки А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки. Смотрите также справочник: координаты вектора по двум точкам.
Как найти координаты вектора а?
Основное соотношение. Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Как найти координаты конца вектора?
Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала….Поскольку плоскость проходит через точки A1 и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.
- Подставим вместо x, y и z координаты точки A1 = (0; 0; 1).
- Имеем: A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;
Как искать ординату центра окружности
Декартовы координаты точек плоскости. Уравнение окружности
Числовая ось
Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .
Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Прямоугольная декартова система координат на плоскости
Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy .
Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).
Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .
Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Формула для расстояния между двумя точками координатной плоскости
Утверждение 1 . Расстояние между двумя точками координатной плоскости
вычисляется по формуле
Доказательство . Рассмотрим рисунок 6.
| | A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 . |
(1) |
что и требовалось доказать.
Уравнение окружности на координатной плоскости
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:
Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) .
Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид
Как искать ординату центра окружности
Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно
Это задание ещё не решено, приводим решение прототипа.
Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Диагональ прямоугольника образует два прямоугольных треугольника. Диагональ равна диаметру окружности, описанной около треугольника, следовательно, центр окружности лежит на середине диагонали прямоугольника. Тогда можно легко найти координаты центра окружности.
Материалы к занятию по теме «Параметр в уравнении окружности»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Материалы для занятия по теме
«Параметр в уравнении окружности»
1. Уравнение окружности.
(х ‒ х 0 )² + (у ‒ у 0 )² = R ², где А(х 0 ; у 0 ) ‒ центр окружности, R ‒ радиус.
х² + у² = R ² ‒ уравнение окружности с центром в начале координат.
2. Параметр – радиус.
Если а = 0, то (х ‒ х 0 )² + (у‒ у 0 )² = 0, то есть А(х 0 ; у 0 ) – точка.
Если а ˂ 0, то ни окружность, ни точка не существуют.
Если а > 0, то R =, на плоскости – концентрические окружности с центром (х 0 ; у 0 ).
Пример. (х ‒ 2)² + (у + 2)² = а (а > 0)
3. Параметр в одной из координат центра.
Одна координата с параметром: (х ‒ 2а)² + (у + 3)² = 9. У центра окружности меняется абсцисса, ордината постоянна. Значит, центры окружностей зафиксированы на прямой у = ‒3.
Задание : подставляя разные значения параметра а, определите координаты центров нескольких окружностей и выполните построение.
Аналогично: (х‒3)² +(у ‒ 2а)² = 9. У центра окружности меняется ордината, абсцисса постоянна. Центры окружностей зафиксированы на прямой х=3.
Задание: построить несколько окружностей, удовлетворяющих последнему уравнению.
4. Параметр в обеих координатах центра.
(х ‒ а)² + (у ‒ а)² = 1. Обе координаты с параметром.
Центр окружности ‒ точка А (а ; а). Так как абсцисса и ордината равны, то все точки такие находятся на прямой у = х. Тогда данное уравнение задает множество окружностей , центры которых лежат на прямой у = х , а радиус равен 1.
Задание : построить несколько окружностей, удовлетворяющих следующему уравнению (х ‒ а)² + (у + 2а)² = 4.
Подсказка. Найдем координаты центра окружности: (х ‒ а)² + (у ‒ (‒2а))² = 4
А(а;-2а), значит центры окружностей лежат на прямой у = ‒2х, радиус равен 2.
5. Параметр в координатах центра и в радиусе.
( х ‒ а)² + (у‒ 2а ‒1 )² = а². Это окружности с центрами на прямой у = 2а + 1, радиус равен а. При а=0 – точка.
Задания для самостоятельной работы.
№ 1. Указать центр, радиус и построить каждую окружность , заданную уравнением:
а) (х ‒ 3)² + (у + 2)² = 16; б) (х + 1)² + (у ‒ 4)² = 10.
№ 2. Выяснить, какие из данных уравнений являются уравнениями окружности. Найти координаты центра и радиус каждой окружности:
а) х² + у² + 8х ‒ 4у + 40 = 0;
б) х² + у² ‒ 2х + 4у ‒ 20 = 0;
в) х² + у² ‒ 4х ‒ 2у + 1 = 0.
№ 3. Выделить уравнение окружности, указать ее центр и радиус в задачах с параметром. Описать расположение графика уравнения на координатной плоскости. Выполнить построение:
а) х² + у² + 2ах ‒ 4у + а² ‒ 1 = 0;
б) х² + у² ‒ 6х + 4ау + 4а² = 0;
в) х² + у² ‒ 2а( х ‒ у ) = 4 ‒ 2а².
1.Геометрия. 7-9 классы : учебник для общеобразовательных организаций с приложением на электронном носителе / [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.]. – 3-е изд.-М. : Просвещение, 2014.-383 с.
2.Шестаков С.А. ЕГЭ 2014. Математика. Задача С5. Задачи с параметром / Под ред. А.Л.Семенова и И.В.Ященко. – М.:МЦМНО. 2014.-240 с.
Дистанционные курсы для педагогов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 927 человек из 80 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 321 человек из 71 региона
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 700 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
- Сергеева Татьяна ВладиславовнаНаписать 525 15.02.2020
Номер материала: ДБ-1001835
-
15.02.2020 34
-
15.02.2020 7
-
15.02.2020 39
-
15.02.2020 35
-
15.02.2020 83
-
15.02.2020 33
-
15.02.2020 11
-
15.02.2020 125
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
530 курсов от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
Стартовал региональный этап Всероссийской олимпиады школьников
Время чтения: 2 минуты
Проходной балл ЕГЭ для поступления на бюджет снизился впервые за 10 лет
Время чтения: 3 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
В Китае приняли закон о сокращении нагрузки на школьников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Синус это х или у в окружности
Математика – это очень просто, даже проще, чем мы можем себе представить. Сложной математику делают сами математики.
Страницы
среда, 7 ноября 2012 г.
Тригонометрический круг синус и косинус
Тригонометрический круг представляет значения тригонометрических функций синус (sin) и косинус (cos) в виде координат точек единичной окружности при различных значениях угла альфа в градусах и радианах.
Поскольку я сам вечно путаюсь при переводе координат точек окружности в синусы и косинусы, для простоты все значения косинусов (cos) для углов от 0 до 360 градусов (от 0 пи до 2 пи) подчеркнуты зеленой черточкой. Даже при распечатке этого рисунка тригонометрического круга на черно-белом принтере все значения косинуса будут подчеркнуты, а значения синуса будут без подчеркивания. Если вам интересно, то можете посмотреть отдельные тригонометрические круги для синуса и косинуса.
Напротив указанных углов на окружности расположены точки, а в круглых скобках указаны координаты этих точек. Первой записана координата Х (косинус)
Давайте проведем обзорную экскурсию по этому уголку математического зоопарка. Прежде всего, нужно отметить, что здесь присутствует декартова система координат – одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая – вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы – cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы – sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы – на диване перед телевизором по горизонтали.
В этой системе координат нарисована окружность радиусом, равным единице. Центр окружности находится в начале системы координат – там, где в центе рисунка пересекаются оси абсцисс (ось Х) и ординат (ось У).
Из центра окружности проведены тоненькие черточки, которые показывают углы 30, 45, 60, 120, 135, 150, 210, 225, 240, 300, 315, 330 градусов. В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.
Линии углов заканчиваются точками на единичной окружности. Возле каждой точки, в круглых скобках, записаны координаты этой точки. Первой записана координата Х, которая соответствует косинусу угла, образовавшего эту точку. Второй записана координата У этой точки, что соответствует значению синуса угла. По картинке довольно легко находить синус и косинус заданного угла и наоборот, по заданному значению синуса или косинуса, можно легко найти значение угла. Главное, не перепутать синус с косинусом.
Обращаю особое внимание на тот факт, что если вы по значению синуса или косинуса ищите угол, обязательно нужно дописывать период угла. Математики очень трепетно относятся к этому аппендициту тригонометрических функций и при его отсутствии могут влепить двойку за, казалось бы, правильный ответ. Что такое период при нахождении угла по значению тригонометрической функции? Это такая штучка, которая придумана математиками специально для того, чтобы запутываться самим и запутывать других. Особенно блондинок. Но об этом мы поговорим как-нибудь в другой раз.
Всё, что собрано в кучку на рисунке тригонометрического круга синуса и косинуса, можно внимательно рассмотреть на отдельных картинках с портретами синуса 0, 30, 45 градусов (ссылки на отдельные странички я буду добавлять по мере увеличения фотогалереи синусов и косинусов).
Синусы и косинусы круг – здесь картинка во всей своей тригонометрической красе.
Угол 120 градусов в радианах – равен 2/3 пи или 2 пи деленное на 3, на картинке очень красиво нарисовано.
Значения синусов косинусов углов в радианах – на картинке есть такие, надеюсь, именно те углы, которые вы ищете.
Значение косинуса угла в 45 градусов – равно корню из двух деленному на два, можете проверить по рисунку.
Тригонометрическая окружность – я не совсем уверен, что представленная на картинке окружность является тригонометрической, но что-то от тригонометрии в этой окружности определенно есть, например, синусы и косинусы на окружности – вылитая тригонометрия.
Тригонометрический круг рисунок – есть здесь такой. Правда, не самый красивый рисунок, можно нарисовать гораздо красивее и понятнее. Мне минус в репутацию – почему я до сих пор не нарисовал его для блондинок? Представляете ситуацию в картинной галерее будущего: экскурсовод объясняет группе школьников «Перед вами всемирно известное полотно «Тригонометрическая мадонна с единичным отрезком на руках» – картина гениального художника эпохи Раннего Математического Возрождения . » Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!
Круг синусов и косинусов – именно такой круг совершенно случайно оказался здесь на картинке.
Угол 9 градусов сколько это в пи – в пи это 1/20 или пи/20.
Решение: для перевода градусов в пи радиан, нужно имеющиеся у нас градусы разделить на 180 градусов (это 1 пи радиан). У нас получается 9/180 = 1/20
Ответ: 9 градусов = 1/20 пи.
Синус это вверх или в сторону – синус – это вверх, в сторону – это косинус.
Комментарии к этой статье запрещены. Из-за огромного их количества мои ответы на ваши вопросы о тригонометрическом круге уже не публикуются. Вопросы можете задавать в комментариях к другим страницам. Постараюсь решить проблему за счет удаления части комментариев, тем самым освобожу место для новых.
Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от – ∞ до + ∞ .
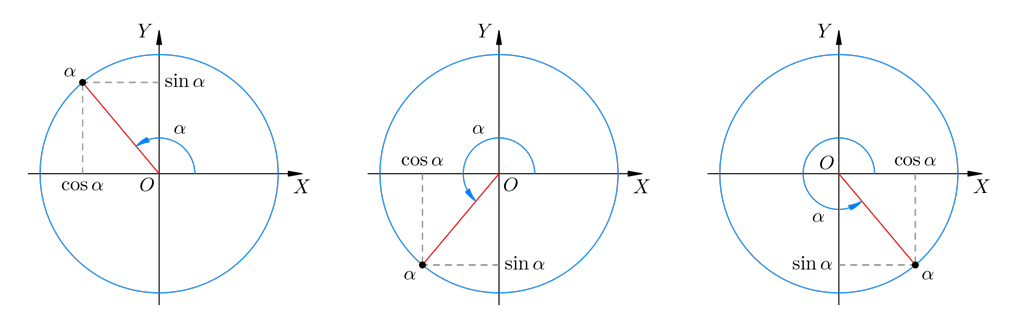
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α – это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α – это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α – это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α – это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , – 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности – точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Геометрическое определение синуса и косинуса
α – угол, выраженный в радианах.
Свойства синуса и косинуса
Принятые обозначения
( sin^2 x equiv (sin x)^2; ) ( quad sin^3 x equiv (sin x)^3; ) ( quad sin^n x equiv (sin x)^n ) ( sin^ x equiv arcsin x ) ( (sin x )^ equiv dfrac1 equiv cosec x ) .
( cos^2 x equiv (cos x)^2; ) ( quad cos^3 x equiv (cos x)^3; ) ( quad cos^n x equiv (cos x)^n ) ( cos^ x equiv arccos x ) ( (cos x )^ equiv dfrac1 equiv sec x ) .
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2π.
( sin(x + 2pi) = sin x; quad ) ( cos(x + 2pi) = cos x )
Четность
Функция синус – нечетная. Функция косинус – четная.
( sin( -x ) = – sin x; quad ) ( cos( -x ) = cos x )
Области определения и значений, экстремумы, возрастание, убывание
Основные свойства синуса и косинуса представлены в таблице (n – целое).
| ( small -dfrac
2 + 2pi n ) ( small ( small dfrac 2 + 2pi n ) |
( small -pi + 2pi n ) ( small ( small 2pi n ) | |
| Убывание | ( small dfrac
2 + 2pi n ) ( small ( small dfrac 2 + 2pi n ) |
( small 2pi n ) ( small ( pi + small 2pi n ) |
| Максимумы, ( small x = ) ( small dfrac
2 + 2pi n ) |
( small x = 2pi n ) | |
| Минимумы, ( small x = ) ( small -dfrac
2 + 2pi n ) |
( small x = ) ( small pi + 2pi n ) | |
| Нули, ( small x = pi n ) | ( small x = dfrac
2 + pi n ) |
|
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы, содержащие синус и косинус
Сумма квадратов
( sin^2 x + cos^2 x = 1 )
Формулы синуса и косинуса суммы и разности
( sin(x + y) = sin x cos y + cos x sin y )
( sin(x – y) = sin x cos y – cos x sin y )
( cos(x + y) = cos x cos y – sin x sin y )
( cos(x – y) = cos x cos y + sin x sin y )
( sin( 2x ) = 2 sin x cos x )
( cos( 2x ) = cos^2 x – sin^2 x = ) ( 2 cos^2 x – 1 = 1 – 2 sin^2 x )
( cosleft( dfrac
2 – x
ight) = sin x ) ; ( sinleft( dfrac
2 – x
ight) = cos x )
( cos( x + pi ) = – cos x ) ; ( sin( x + pi ) = – sin x )
Формулы произведения синусов и косинусов
( sin x cos y = ) ( dfrac12 sin( x – y ) + sin( x + y ) )
( sin x sin y = ) ( dfrac12 cos( x – y ) – cos( x + y ) )
( cos x cos y = ) ( dfrac12 cos( x – y ) + cos( x + y ) )
( sin x cos y = dfrac12 sin 2x )
( sin^2 x = dfrac12 1 – cos 2x )
( cos^2 x = dfrac12 1 + cos 2x )
Формулы суммы и разности
( sin x + sin y = 2 , sin dfrac2 , cos dfrac2 )
( sin x – sin y = 2 , sin dfrac2 , cos dfrac2 )
( cos x + cos y = 2 , cos dfrac2 , cos dfrac2 )
( cos x – cos y = 2 , sin dfrac2 , sin dfrac2 )
Выражение синуса через косинус
Далее мы полагаем, что ( n ) – целое число.
Выражение косинуса через синус
Выражение через тангенс
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
[ img style=»max-w ]
Выражения через комплексные переменные
Формула Эйлера
( e^ = cos z + i sin z )
Выражения через гиперболические функции
( sin iz = i sh z ) ( cos iz = ch z )
( sh iz = i sin z ) ( ch iz = cos z )
Производные
( ( sin x )’ = cos x ) ( ( cos x )’ = – sin x ) . Вывод формул > > >
Производные n-го порядка:
( left( sin x
ight)^ = sinleft( x + ndfrac
2
ight) ) ( left( cos x
ight)^ = cosleft( x + ndfrac
Интегралы
( int sin x , dx = – cos x + C ) ( int cos x , dx = sin x + C )
См. также раздел Таблица неопределенных интегралов >>>
Разложения в ряды
Секанс, косеканс
( sec x = dfrac1 ; ) ( cosec x = dfrac1 )
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Арксинус, arcsin
( y = arcsin x ) ( left )
( sin( arcsin x ) = x ) ( )
( arcsin( sin x ) = x ) ( left )
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Тригонометрическое определение
С помощью формул, указанных выше, можно найти синус и косинус острого угла. Но нужно научиться вычислять синус и косинус угла произвольной величины. Прямоугольный треугольник не даёт такой возможности (тупого угла, например, в нём быть не может); следовательно, нужно более общее определение синуса и косинуса, содержащее указанные формулы как частный случай.
На помощь приходит тригонометрическая окружность. Пусть дан некоторый угол; ему отвечает одноимённая точка на тригонометрической окружности.
Рис. 2. Тригонометрическое определение синуса и косинуса
Косинус угла – это абсцисса точки. Синус угла – это ордината точки.
На рис. 2 угол взят острым, и легко понять, что данное определение совпадает с общим геометрическим определением. В самом деле, мы видим прямоугольный треугольник с единичной гипотенузой O и острым углом. Прилежащий катет этого треугольника есть cos (сравните с рис. 1) и одновременно абсцисса точки ; противолежащий катет есть sin (как на рис. 1) и одновременно ордината точки.
Но теперь мы уже не стеснены первой четвертью и получаем возможность распространить данное определение на любой угол . На рис. 3 показано, что такое синус и косинус угла во второй, третьей и четвёртой четвертях.
Рис. 3. Синус и косинус во II, III и IV четвертях
Табличные значения синуса и косинуса
Абсцисса точки 0 равна 1 , ордината точки 0 равна 0 . Следовательно,
Как найти координаты точки?
О чем эта статья:
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
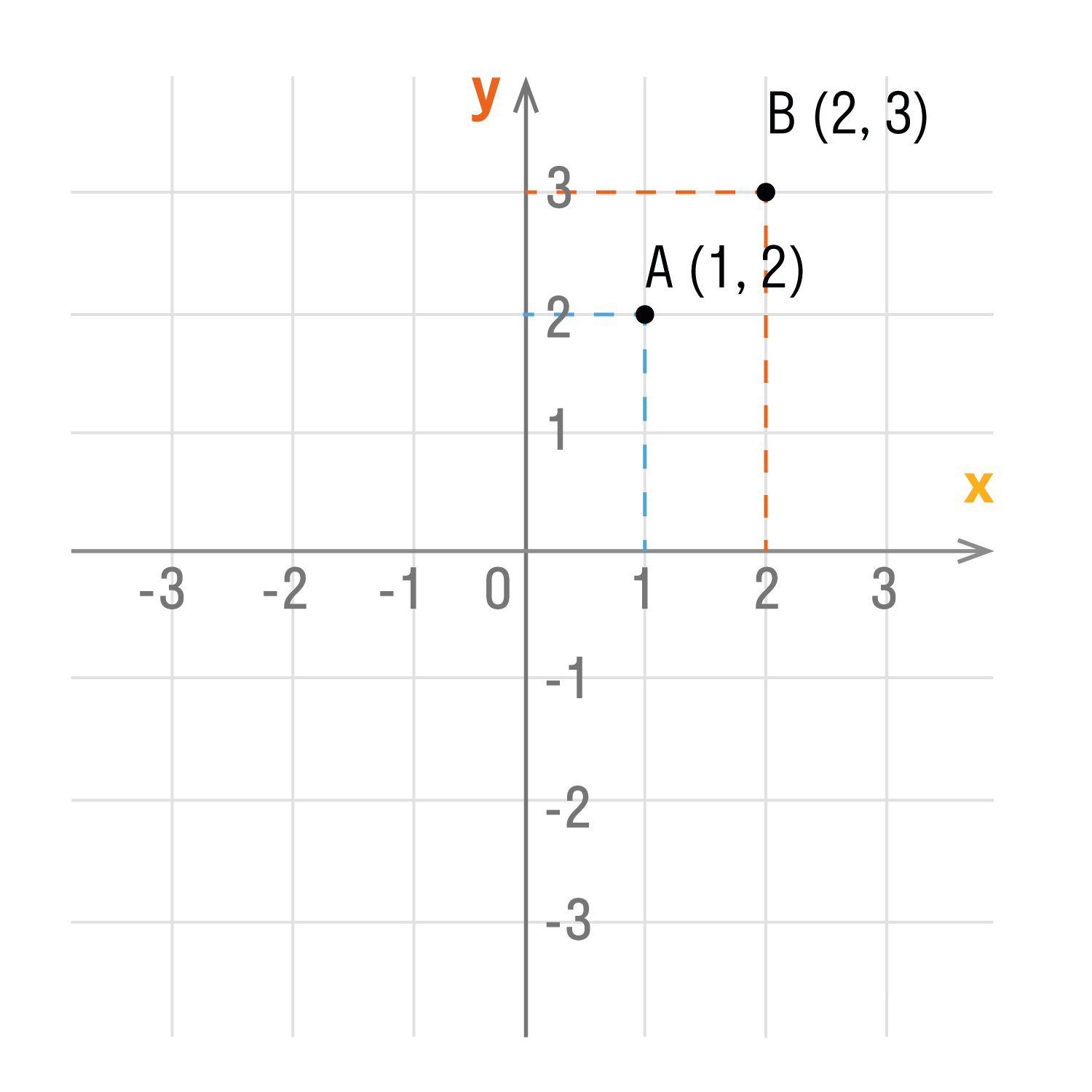
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
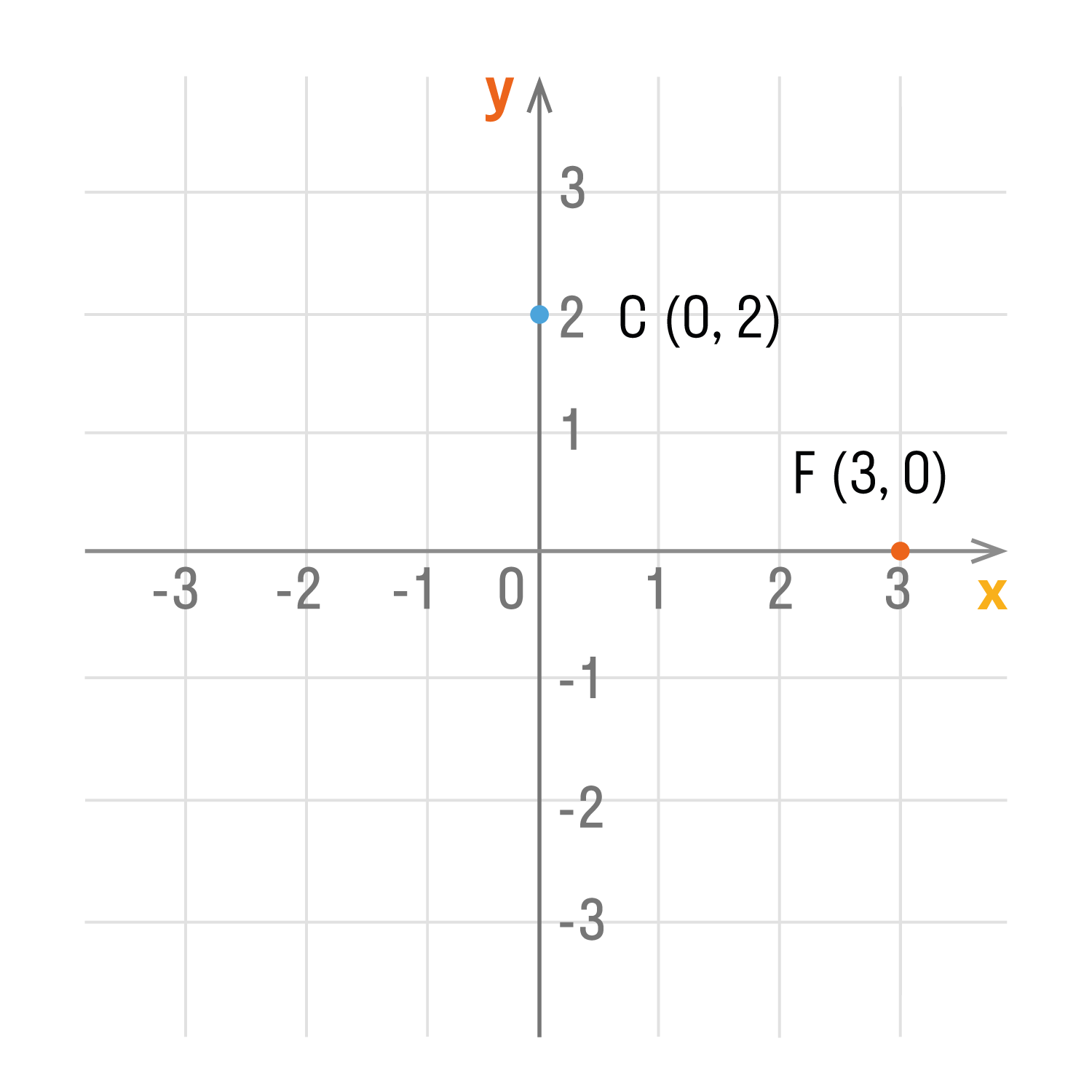
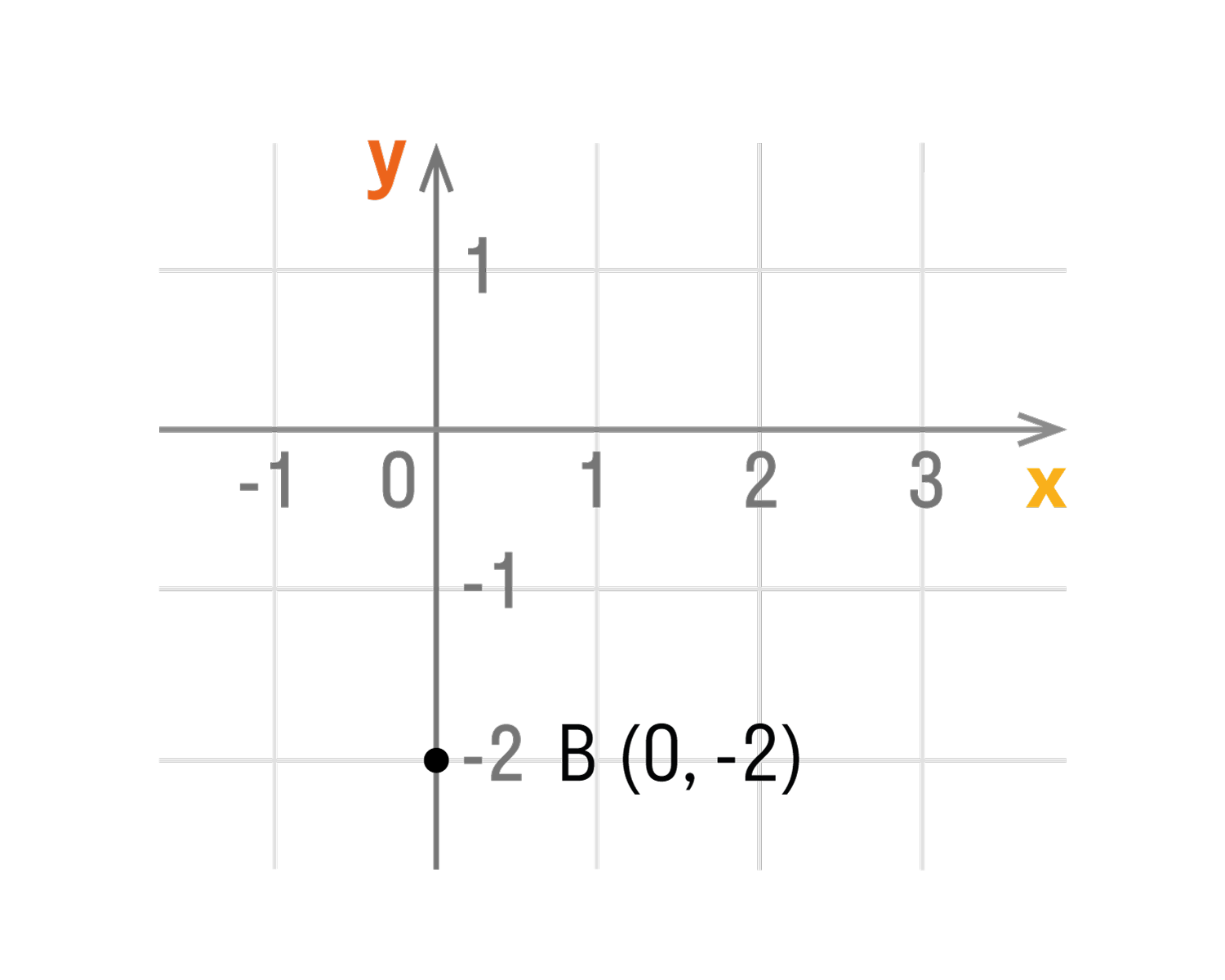
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
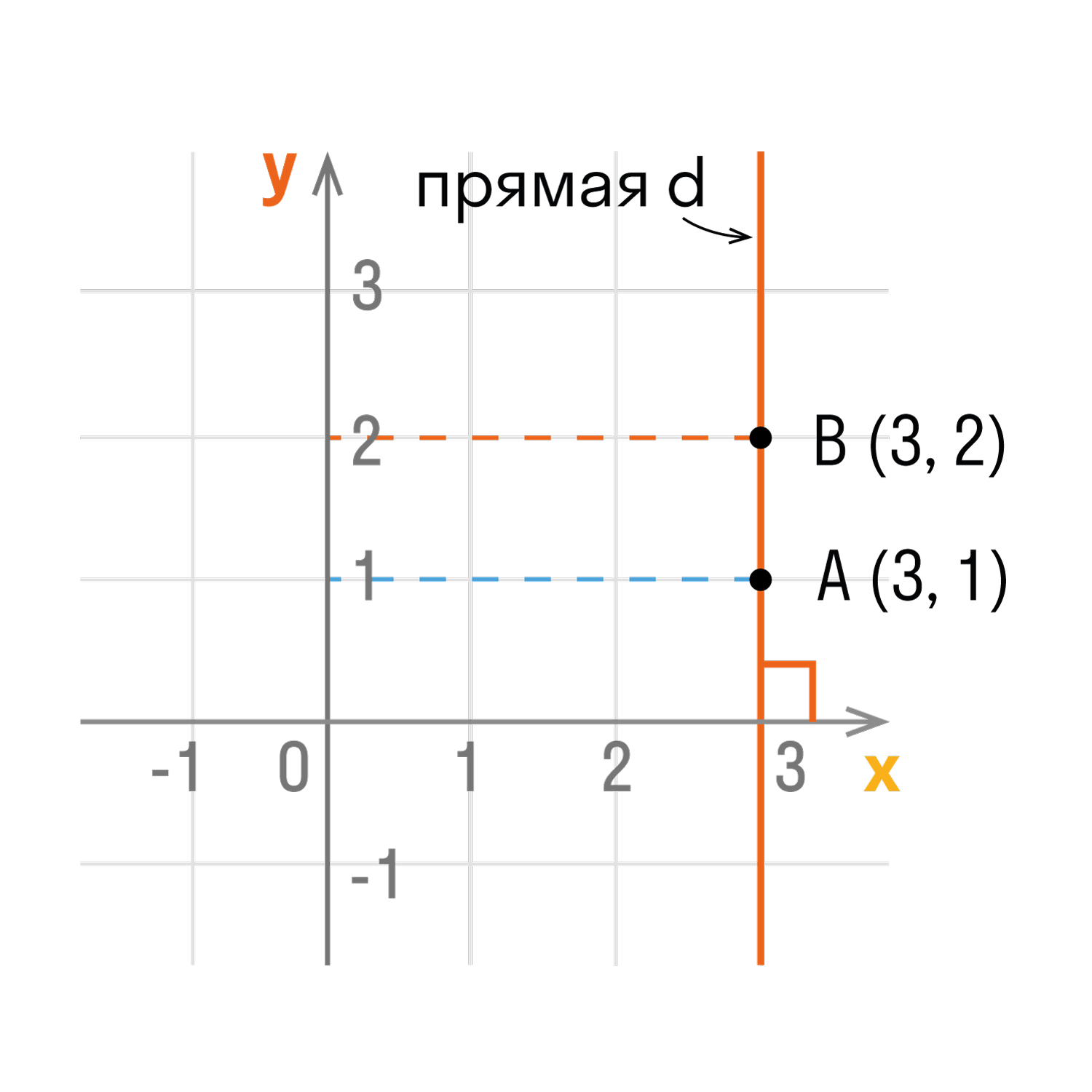
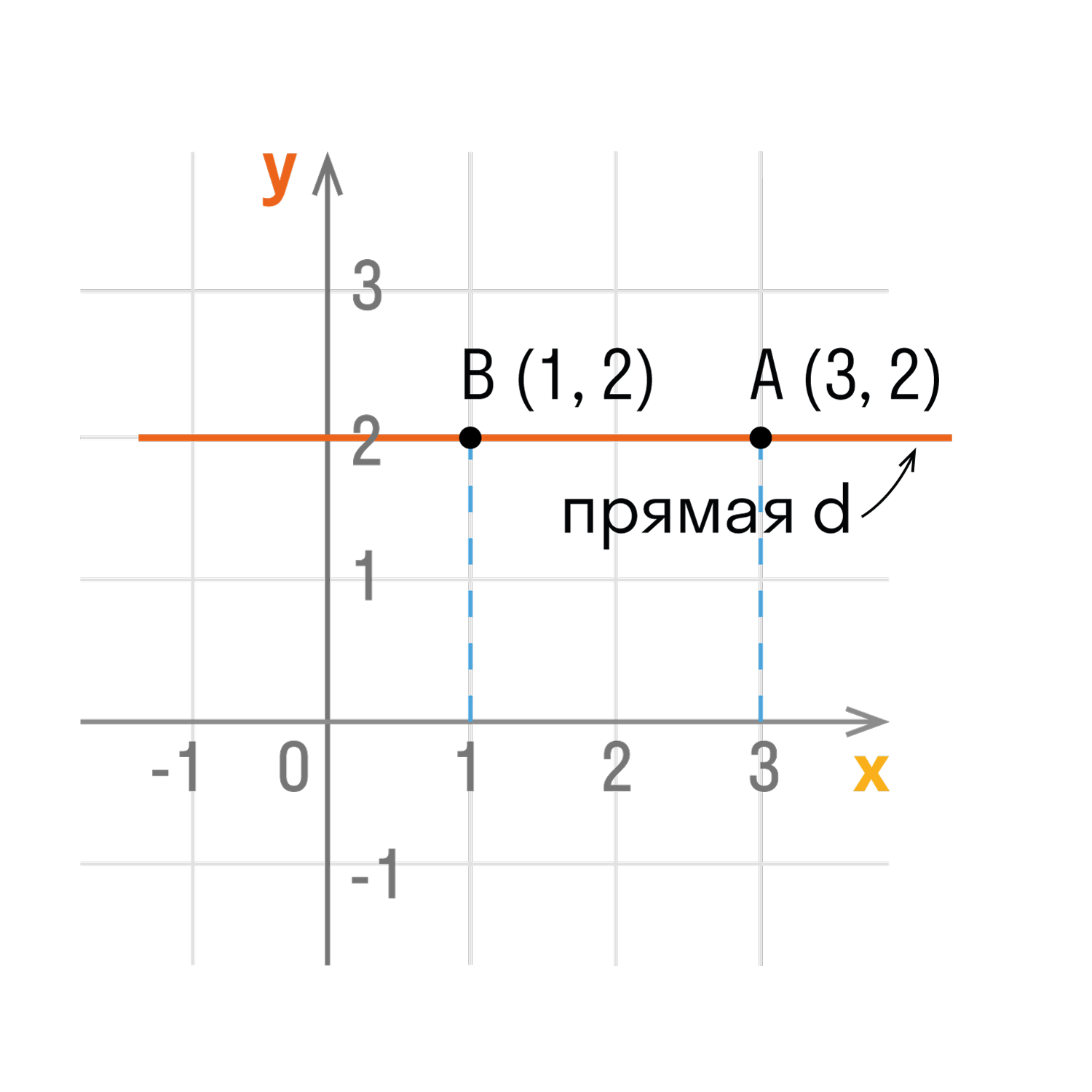
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
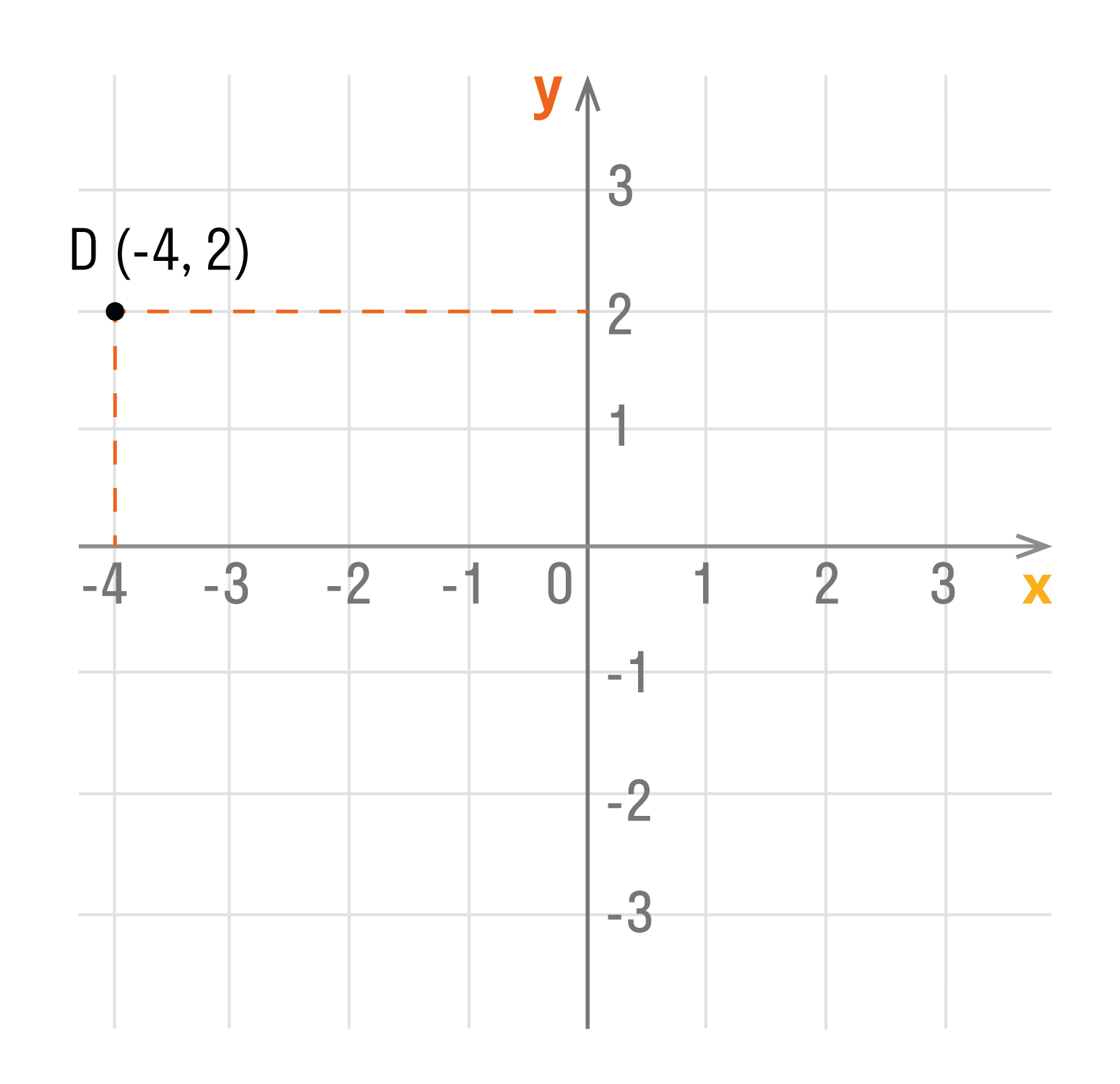
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
http://pcznatok.ru/kompjutery/sinus-jeto-h-ili-u-v-okruzhnosti.html
http://skysmart.ru/articles/mathematic/kak-najti-koordinaty-tochki
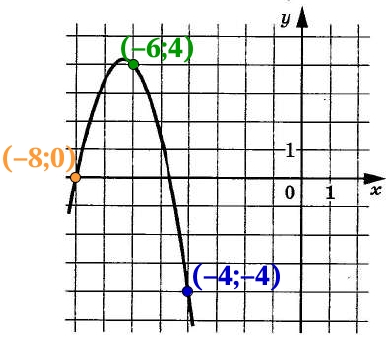
Решение:
Возьмём 3 точки принадлежащие графику функции и составим систему из трёх уравнений:
begin{cases} 0=acdot (-8)^{2}+bcdot (-8)+c \ 4=acdot (-6)^{2}+bcdot (-6)+c \ -4=acdot (-4)^{2}+bcdot (-4)+cend{cases}\begin{cases} 0=acdot 64-bcdot 8+c \ 4=acdot 36-bcdot 6+c : \ -4=acdot 16-bcdot 4+cend{cases}\вычтем :3е :уравнение :из: 1го :и: 2го :уравнения:\begin{cases}0-(-4)=acdot 64-acdot 16-bcdot 8-(-bcdot 4)+c-c : \ 4-(-4)=acdot 36-acdot 16-bcdot 6-(-bcdot 4)+c-cend{cases}\begin{cases}4=acdot 48-bcdot 4 : \ 8=acdot 20-bcdot 2:{color{Blue} |cdot 2} end{cases}\begin{cases}4=acdot 48-bcdot 4 : \ 16=acdot 40-bcdot 4end{cases}\вычтем: 2е: уравнение: из :1го: уравнения:\4-16=acdot 48-acdot 40-bcdot 4-(-bcdot 4)\-12=acdot 8\a=frac{-12}{8}=-1,5
Найдём b, подставив значение а = –1,5 в любое из уравнений после вычитания из них 3-го уравнения:
8 = a·20 – b·2
8 = –1,5·20 – b·2
8 = –30 – b·2
8 + 30 = –2·b
38 = –2·b
b=frac{38}{-2}=-19
Подставим значения а и b в любое из уравнений, найдём с:
0=acdot (-8)^2+bcdot (-8)+c \0=(-1,5)cdot (-8)^2+ (-19)cdot (-8)+c \0=-96+152+c \0=56+с\-56=с
Ордината (y) точки пересечения графика функции c осью ординат (Оу) – это значение коэффициента c = –56.
Ответ: –56.
Как найти координаты точки?
О чем эта статья:
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Как найти ординату вершины параболы
Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.
Нахождение вершины параболы: способы, примеры, советы
График функции y = ax 2 + bx + c, где a — первый коэффициент, b – второй коэффициент, c – свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.
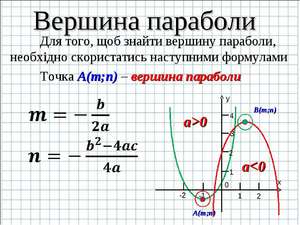
У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.
Первый способ
Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.
Например, y =x 2 –8 x +15;
находим первый, второй коэффициенты и свободный член;
подставляем значения a и b в формулу;
вычисляем значения y;
Значит, вершина находится в точке (4;-1).
Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n – корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.
Рассмотрим на примере y =x 2 –6x+5
1) Приравниваем к нулю:
2) Находим дискриминант, используя формулу: D = b 2 –4 ac:
3) Находим корни уравнения по формуле (-b±√ D)/2a:
- 1 – первый корень;
- 5 – второй корень.
Второй способ
Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.
1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.
2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.
У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:
3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.
4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).
Третий способ
Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:
1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.
Рассмотрим этот способ подробнее.
Дана функция y = 4x²+16x-17;
- Записываем производную и приравниваем к нулю.
f'(x) = (4x²+16x-17)’ = 8x+16 =0
Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).
1) Строим таблицу
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Советы
Правильно находите коэффициенты.
Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.
Делайте всё поэтапно. Следуйте алгоритму.
Обратите ваше внимание на то, что:
- Нужно проверять правильно ли ваше решение.
- Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.
Видео
Это видео поможет вам научиться находить вершину параболы
Парабола – это геометрическое множество точек, равноудалённых от точки F, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$.
Что значит вершина параболы
Вершина параболы – это точка, ближайшая к директрисе параболы. Она является центром отрезка, ограниченного точкой фокуса параболы $F$ и директрисой $d$.
Производная в вершине квадратичной параболы равна нулю.
Каноническое уравнение параболы $y^2 = 2px$ справедливо для параболы, вершина которой находится в центре осей.
Для того, чтобы определить, принадлежит ли точка графику заданной параболы, необходимо подставить её координаты в формулу $y = ax^2 + bx + c$.
Если равенство выполняется — точка принадлежит графику.
Как найти вершины параболы, задающейся квадратичной функцией
Рисунок 1. Пример уравнения и графика квадратичной параболы
Довольно часто парабола задаётся квадратичной функцией вида $y = ax^2 + bx + c$, вершина такой параболы находится в произвольной точке.
Какой-то единой формулы для нахождения сразу обеих координат вершины параболы нет, но при этом определить координаты вершины параболы по уравнению довольно просто.
Попробуй обратиться за помощью к преподавателям
Алгоритм для нахождения вершины параболы такой:
- Запишите коэффициенты $a, b, c$ из уравнения. Если коэффициент $a$ при $y$ положительный, то ветви параболы будут смотреть вверх, а если отрицательный, то вниз.
- Найдите абсциссу вершины параболы ($x$ вершины) по формуле $x = – frac $, для этого воспользуйтесь коэффициентами $a, b, c$ из уравнения.
- Подставьте найденный $x$ в уравнение параболы и вычислите ординату вершины параболы $y$.
- Запишите полученные координаты x и y вершины параболы в форме точки $(x; y)$.
Рассмотрим уравнение параболы $y = x^2 – 5x + 7$
- Коэффициенты этой параболы $a = 1$, $b = -5$, $c = 7$.
- Для вычисления x вершины параболы подставьте $a = 1$ и $b = -5$ в формулу $x = – frac = frac =2.5$
- Подставьте найденный $x$ в исходное уравнение:
- $y = 2,5^2 – 5 cdot 2.5 + 7$
- $y = 0,75$
- Координаты вершины этой параболы $(2.5;0.75)$.
Вершина кубической параболы
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Чтобы найти вершины (точки локальных минимумов и максимумов) кубической параболы, необходимо найти её производную, приравнять её к нулю и затем вычислить $x$ и $y$.
Если же необходимо найти точку перегиба кубической параболы, необходимо найти вторую производную и также приравнять её к нулю.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
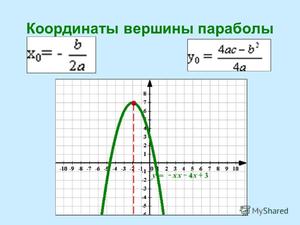
Как найти координаты вершины параболы? Для этого достаточно запомнить всего одну короткую формулу (она же — корень квадратного уравнения для случая, если дискриминант равен нулю).
I. Абсциссу координаты вершины параболы — графика квадратичной функции y=ax²+bx+c, где a, b, c — числа, причем a≠0, находят по формуле
Для нахождения ординаты достаточно подставить в формулу функции xₒ вместо каждого x:
Можно также найти ординату вершины параболы, воспользовавшись формулой
(минус дискриминант, деленный на 4a).
Найти координаты вершины параболы:
Вершина параболы y=x²-7x+3 — точка (3,5; -9,25).
Вершиной параболы y= -x²+8x+2 является точка (4; 18).
(-2; 
Следовательно, (-2,5; 3,75) — вершина параболы y=0,2x²+x+5 .
II. Абсциссу вершины параболы можно также найти как среднее арифметическое между нулями функции (в том случае, если функция имеет нули):
Этим способом удобно находить вершину параболы, когда квадратичная функция задана в виде y=a(x-x1)(x-x2).
Найдём координаты вершины параболы y=5(x-1)(x+7). Ищем нули функции:
Точка (-3; -80) — вершина параболы y=5(x-1)(x+7).
III. Если функция задана в виде
то её вершина — точка ( xₒ; y ₒ ). Например, вершиной параболы
является точка (-3; -1).
2 комментария
При исследовании квадратичной функции, графиком которой является парабола, в одном из пунктов необходимо найти координаты вершины параболы. Как это сделать аналитически, используя заданное для параболы уравнение?
Надежда, в статье выше как раз описывается, как найти координаты вершины параболы. Абсциссу находят по формуле x0=-b/2a. Чтобы найти ординату, достаточно в формулу функции вместо каждого x подставить найденное значение x0 и вычислить.
Как найти ординату точек на окружности
Как искать ординату центра окружности
Декартовы координаты точек плоскости. Уравнение окружности
Числовая ось
Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .
Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Прямоугольная декартова система координат на плоскости
Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy .
Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).
Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .
Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Формула для расстояния между двумя точками координатной плоскости
Утверждение 1 . Расстояние между двумя точками координатной плоскости
вычисляется по формуле
Доказательство . Рассмотрим рисунок 6.
| | A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 . |
(1) |
что и требовалось доказать.
Уравнение окружности на координатной плоскости
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:
Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) .
Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид
Как искать ординату центра окружности
Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно
Это задание ещё не решено, приводим решение прототипа.
Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Диагональ прямоугольника образует два прямоугольных треугольника. Диагональ равна диаметру окружности, описанной около треугольника, следовательно, центр окружности лежит на середине диагонали прямоугольника. Тогда можно легко найти координаты центра окружности.
Материалы к занятию по теме «Параметр в уравнении окружности»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Материалы для занятия по теме
«Параметр в уравнении окружности»
1. Уравнение окружности.
(х ‒ х 0 )² + (у ‒ у 0 )² = R ², где А(х 0 ; у 0 ) ‒ центр окружности, R ‒ радиус.
х² + у² = R ² ‒ уравнение окружности с центром в начале координат.
2. Параметр – радиус.
Если а = 0, то (х ‒ х 0 )² + (у‒ у 0 )² = 0, то есть А(х 0 ; у 0 ) – точка.
Если а ˂ 0, то ни окружность, ни точка не существуют.
Если а > 0, то R =, на плоскости – концентрические окружности с центром (х 0 ; у 0 ).
Пример. (х ‒ 2)² + (у + 2)² = а (а > 0)
3. Параметр в одной из координат центра.
Одна координата с параметром: (х ‒ 2а)² + (у + 3)² = 9. У центра окружности меняется абсцисса, ордината постоянна. Значит, центры окружностей зафиксированы на прямой у = ‒3.
Задание : подставляя разные значения параметра а, определите координаты центров нескольких окружностей и выполните построение.
Аналогично: (х‒3)² +(у ‒ 2а)² = 9. У центра окружности меняется ордината, абсцисса постоянна. Центры окружностей зафиксированы на прямой х=3.
Задание: построить несколько окружностей, удовлетворяющих последнему уравнению.
4. Параметр в обеих координатах центра.
(х ‒ а)² + (у ‒ а)² = 1. Обе координаты с параметром.
Центр окружности ‒ точка А (а ; а). Так как абсцисса и ордината равны, то все точки такие находятся на прямой у = х. Тогда данное уравнение задает множество окружностей , центры которых лежат на прямой у = х , а радиус равен 1.
Задание : построить несколько окружностей, удовлетворяющих следующему уравнению (х ‒ а)² + (у + 2а)² = 4.
Подсказка. Найдем координаты центра окружности: (х ‒ а)² + (у ‒ (‒2а))² = 4
А(а;-2а), значит центры окружностей лежат на прямой у = ‒2х, радиус равен 2.
5. Параметр в координатах центра и в радиусе.
( х ‒ а)² + (у‒ 2а ‒1 )² = а². Это окружности с центрами на прямой у = 2а + 1, радиус равен а. При а=0 – точка.
Задания для самостоятельной работы.
№ 1. Указать центр, радиус и построить каждую окружность , заданную уравнением:
а) (х ‒ 3)² + (у + 2)² = 16; б) (х + 1)² + (у ‒ 4)² = 10.
№ 2. Выяснить, какие из данных уравнений являются уравнениями окружности. Найти координаты центра и радиус каждой окружности:
а) х² + у² + 8х ‒ 4у + 40 = 0;
б) х² + у² ‒ 2х + 4у ‒ 20 = 0;
в) х² + у² ‒ 4х ‒ 2у + 1 = 0.
№ 3. Выделить уравнение окружности, указать ее центр и радиус в задачах с параметром. Описать расположение графика уравнения на координатной плоскости. Выполнить построение:
а) х² + у² + 2ах ‒ 4у + а² ‒ 1 = 0;
б) х² + у² ‒ 6х + 4ау + 4а² = 0;
в) х² + у² ‒ 2а( х ‒ у ) = 4 ‒ 2а².
1.Геометрия. 7-9 классы : учебник для общеобразовательных организаций с приложением на электронном носителе / [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.]. – 3-е изд.-М. : Просвещение, 2014.-383 с.
2.Шестаков С.А. ЕГЭ 2014. Математика. Задача С5. Задачи с параметром / Под ред. А.Л.Семенова и И.В.Ященко. – М.:МЦМНО. 2014.-240 с.
Дистанционные курсы для педагогов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 927 человек из 80 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 321 человек из 71 региона
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 700 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
- Сергеева Татьяна ВладиславовнаНаписать 525 15.02.2020
Номер материала: ДБ-1001835
- 15.02.2020 34
- 15.02.2020 7
- 15.02.2020 39
- 15.02.2020 35
- 15.02.2020 83
- 15.02.2020 33
- 15.02.2020 11
- 15.02.2020 125
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
530 курсов от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
Стартовал региональный этап Всероссийской олимпиады школьников
Время чтения: 2 минуты
Проходной балл ЕГЭ для поступления на бюджет снизился впервые за 10 лет
Время чтения: 3 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
В Китае приняли закон о сокращении нагрузки на школьников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Синус это х или у в окружности
Математика – это очень просто, даже проще, чем мы можем себе представить. Сложной математику делают сами математики.
Страницы
среда, 7 ноября 2012 г.
Тригонометрический круг синус и косинус
Тригонометрический круг представляет значения тригонометрических функций синус (sin) и косинус (cos) в виде координат точек единичной окружности при различных значениях угла альфа в градусах и радианах.
Поскольку я сам вечно путаюсь при переводе координат точек окружности в синусы и косинусы, для простоты все значения косинусов (cos) для углов от 0 до 360 градусов (от 0 пи до 2 пи) подчеркнуты зеленой черточкой. Даже при распечатке этого рисунка тригонометрического круга на черно-белом принтере все значения косинуса будут подчеркнуты, а значения синуса будут без подчеркивания. Если вам интересно, то можете посмотреть отдельные тригонометрические круги для синуса и косинуса.
Напротив указанных углов на окружности расположены точки, а в круглых скобках указаны координаты этих точек. Первой записана координата Х (косинус)
Давайте проведем обзорную экскурсию по этому уголку математического зоопарка. Прежде всего, нужно отметить, что здесь присутствует декартова система координат – одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая – вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы – cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы – sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы – на диване перед телевизором по горизонтали.
В этой системе координат нарисована окружность радиусом, равным единице. Центр окружности находится в начале системы координат – там, где в центе рисунка пересекаются оси абсцисс (ось Х) и ординат (ось У).
Из центра окружности проведены тоненькие черточки, которые показывают углы 30, 45, 60, 120, 135, 150, 210, 225, 240, 300, 315, 330 градусов. В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.
Линии углов заканчиваются точками на единичной окружности. Возле каждой точки, в круглых скобках, записаны координаты этой точки. Первой записана координата Х, которая соответствует косинусу угла, образовавшего эту точку. Второй записана координата У этой точки, что соответствует значению синуса угла. По картинке довольно легко находить синус и косинус заданного угла и наоборот, по заданному значению синуса или косинуса, можно легко найти значение угла. Главное, не перепутать синус с косинусом.
Обращаю особое внимание на тот факт, что если вы по значению синуса или косинуса ищите угол, обязательно нужно дописывать период угла. Математики очень трепетно относятся к этому аппендициту тригонометрических функций и при его отсутствии могут влепить двойку за, казалось бы, правильный ответ. Что такое период при нахождении угла по значению тригонометрической функции? Это такая штучка, которая придумана математиками специально для того, чтобы запутываться самим и запутывать других. Особенно блондинок. Но об этом мы поговорим как-нибудь в другой раз.
Всё, что собрано в кучку на рисунке тригонометрического круга синуса и косинуса, можно внимательно рассмотреть на отдельных картинках с портретами синуса 0, 30, 45 градусов (ссылки на отдельные странички я буду добавлять по мере увеличения фотогалереи синусов и косинусов).
Синусы и косинусы круг – здесь картинка во всей своей тригонометрической красе.
Угол 120 градусов в радианах – равен 2/3 пи или 2 пи деленное на 3, на картинке очень красиво нарисовано.
Значения синусов косинусов углов в радианах – на картинке есть такие, надеюсь, именно те углы, которые вы ищете.
Значение косинуса угла в 45 градусов – равно корню из двух деленному на два, можете проверить по рисунку.
Тригонометрическая окружность – я не совсем уверен, что представленная на картинке окружность является тригонометрической, но что-то от тригонометрии в этой окружности определенно есть, например, синусы и косинусы на окружности – вылитая тригонометрия.
Тригонометрический круг рисунок – есть здесь такой. Правда, не самый красивый рисунок, можно нарисовать гораздо красивее и понятнее. Мне минус в репутацию – почему я до сих пор не нарисовал его для блондинок? Представляете ситуацию в картинной галерее будущего: экскурсовод объясняет группе школьников «Перед вами всемирно известное полотно «Тригонометрическая мадонна с единичным отрезком на руках» – картина гениального художника эпохи Раннего Математического Возрождения . » Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!
Круг синусов и косинусов – именно такой круг совершенно случайно оказался здесь на картинке.
Угол 9 градусов сколько это в пи – в пи это 1/20 или пи/20.
Решение: для перевода градусов в пи радиан, нужно имеющиеся у нас градусы разделить на 180 градусов (это 1 пи радиан). У нас получается 9/180 = 1/20
Ответ: 9 градусов = 1/20 пи.
Синус это вверх или в сторону – синус – это вверх, в сторону – это косинус.
Комментарии к этой статье запрещены. Из-за огромного их количества мои ответы на ваши вопросы о тригонометрическом круге уже не публикуются. Вопросы можете задавать в комментариях к другим страницам. Постараюсь решить проблему за счет удаления части комментариев, тем самым освобожу место для новых.
Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от – ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α – это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α – это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α – это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α – это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , – 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности – точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Геометрическое определение синуса и косинуса
α – угол, выраженный в радианах.
Свойства синуса и косинуса
Принятые обозначения
( sin^2 x equiv (sin x)^2; ) ( quad sin^3 x equiv (sin x)^3; ) ( quad sin^n x equiv (sin x)^n ) ( sin^ x equiv arcsin x ) ( (sin x )^ equiv dfrac1 equiv cosec x ) .
( cos^2 x equiv (cos x)^2; ) ( quad cos^3 x equiv (cos x)^3; ) ( quad cos^n x equiv (cos x)^n ) ( cos^ x equiv arccos x ) ( (cos x )^ equiv dfrac1 equiv sec x ) .
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2π.
( sin(x + 2pi) = sin x; quad ) ( cos(x + 2pi) = cos x )
Четность
Функция синус – нечетная. Функция косинус – четная.
( sin( -x ) = – sin x; quad ) ( cos( -x ) = cos x )
Области определения и значений, экстремумы, возрастание, убывание
Основные свойства синуса и косинуса представлены в таблице (n – целое).
| ( small -dfrac
2 + 2pi n ) ( small ( small dfrac 2 + 2pi n ) |
( small -pi + 2pi n ) ( small ( small 2pi n ) | |
| Убывание | ( small dfrac
2 + 2pi n ) ( small ( small dfrac 2 + 2pi n ) |
( small 2pi n ) ( small ( pi + small 2pi n ) |
| Максимумы, ( small x = ) ( small dfrac
2 + 2pi n ) |
( small x = 2pi n ) | |
| Минимумы, ( small x = ) ( small -dfrac
2 + 2pi n ) |
( small x = ) ( small pi + 2pi n ) | |
| Нули, ( small x = pi n ) | ( small x = dfrac
2 + pi n ) |
|
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы, содержащие синус и косинус
Сумма квадратов
( sin^2 x + cos^2 x = 1 )
Формулы синуса и косинуса суммы и разности
( sin(x + y) = sin x cos y + cos x sin y )
( sin(x – y) = sin x cos y – cos x sin y )
( cos(x + y) = cos x cos y – sin x sin y )
( cos(x – y) = cos x cos y + sin x sin y )
( sin( 2x ) = 2 sin x cos x )
( cos( 2x ) = cos^2 x – sin^2 x = ) ( 2 cos^2 x – 1 = 1 – 2 sin^2 x )
( cosleft( dfrac
2 – x
ight) = sin x ) ; ( sinleft( dfrac
2 – x
ight) = cos x )
( cos( x + pi ) = – cos x ) ; ( sin( x + pi ) = – sin x )
Формулы произведения синусов и косинусов
( sin x cos y = ) ( dfrac12 sin( x – y ) + sin( x + y ) )
( sin x sin y = ) ( dfrac12 cos( x – y ) – cos( x + y ) )
( cos x cos y = ) ( dfrac12 cos( x – y ) + cos( x + y ) )
( sin x cos y = dfrac12 sin 2x )
( sin^2 x = dfrac12 1 – cos 2x )
( cos^2 x = dfrac12 1 + cos 2x )
Формулы суммы и разности
( sin x + sin y = 2 , sin dfrac2 , cos dfrac2 )
( sin x – sin y = 2 , sin dfrac2 , cos dfrac2 )
( cos x + cos y = 2 , cos dfrac2 , cos dfrac2 )
( cos x – cos y = 2 , sin dfrac2 , sin dfrac2 )
Выражение синуса через косинус
Далее мы полагаем, что ( n ) – целое число.
Выражение косинуса через синус
Выражение через тангенс
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
[ img style=»max-w ]
Выражения через комплексные переменные
Формула Эйлера
( e^ = cos z + i sin z )
Выражения через гиперболические функции
( sin iz = i sh z ) ( cos iz = ch z )
( sh iz = i sin z ) ( ch iz = cos z )
Производные
( ( sin x )’ = cos x ) ( ( cos x )’ = – sin x ) . Вывод формул > > >
Производные n-го порядка:
( left( sin x
ight)^ = sinleft( x + ndfrac
2
ight) ) ( left( cos x
ight)^ = cosleft( x + ndfrac
Интегралы
( int sin x , dx = – cos x + C ) ( int cos x , dx = sin x + C )
См. также раздел Таблица неопределенных интегралов >>>
Разложения в ряды
Секанс, косеканс
( sec x = dfrac1 ; ) ( cosec x = dfrac1 )
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Арксинус, arcsin
( y = arcsin x ) ( left )
( sin( arcsin x ) = x ) ( )
( arcsin( sin x ) = x ) ( left )
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Тригонометрическое определение
С помощью формул, указанных выше, можно найти синус и косинус острого угла. Но нужно научиться вычислять синус и косинус угла произвольной величины. Прямоугольный треугольник не даёт такой возможности (тупого угла, например, в нём быть не может); следовательно, нужно более общее определение синуса и косинуса, содержащее указанные формулы как частный случай.
На помощь приходит тригонометрическая окружность. Пусть дан некоторый угол; ему отвечает одноимённая точка на тригонометрической окружности.
Рис. 2. Тригонометрическое определение синуса и косинуса
Косинус угла – это абсцисса точки. Синус угла – это ордината точки.
На рис. 2 угол взят острым, и легко понять, что данное определение совпадает с общим геометрическим определением. В самом деле, мы видим прямоугольный треугольник с единичной гипотенузой O и острым углом. Прилежащий катет этого треугольника есть cos (сравните с рис. 1) и одновременно абсцисса точки ; противолежащий катет есть sin (как на рис. 1) и одновременно ордината точки.
Но теперь мы уже не стеснены первой четвертью и получаем возможность распространить данное определение на любой угол . На рис. 3 показано, что такое синус и косинус угла во второй, третьей и четвёртой четвертях.
Рис. 3. Синус и косинус во II, III и IV четвертях
Табличные значения синуса и косинуса
Абсцисса точки 0 равна 1 , ордината точки 0 равна 0 . Следовательно,
Как найти координаты точки?
О чем эта статья:
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
источники:
http://dudom.ru/kompjutery/kak-najti-ordinatu-vershiny-paraboly/
http://b4.cooksy.ru/articles/kak-nayti-ordinatu-tochek-na-okruzhnosti