Алексей . Малеев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
При расчетах, связанных с циклическими явлениями (например, при описании колебаний математического маятника) важно уметь находить состояние системы, с которого начался отсчет процесса — начальную фазу.
Фаза представляет собой угловую координату, описываемую формулой
$varphi = ω_0 cdot t$,
где $ω_0$ — угловая скорость, $t$ — прошедшее время.
Выбрав в качестве единицы измерения углов радианы, формулу можно переписать как
$varphi = 2 cdot pi cdot frac{t}{T}$,
где $2 cdot pi$ — количество радиан в полном цикле, $T$ — период одного колебания. Отношение $frac{t}{T}$ показывает, сколько колебаний (полных и неполных) выполнила система.
Фазы циклических процессов с одинаковыми угловыми скоростями и длящиеся одинаковое время, могут отличаться в связи с тем, что они в момент начала наблюдений находились в разных состояниях. Такая разница называется сдвигом фаз. Например, углы отклонения от вертикали двух идентичных маятников, колеблющиеся с одинаковой частотой, могут различаться. Это зависит от того, на какой начальный угол каждый из них был отклонен в момент начала отсчета времени. Сдвиг фаз может быть обусловлен тем, что маятники были запущены в разное время (до начала отсчета), или одному из них при меньшем начальном отклонении от вертикали было придано дополнительное угловое ускорение за счет удара и т.п.
Циклический процесс, в отличие от движения по незамкнутой траектории, характеризуется повторяемостью некоторой характеристики (например, напряжения в сети переменного тока), что можно описать с помощью функций синуса или косинуса:
$x = A cdot cos(ω_0 cdot t + varphi)$,
$x = A cdot sin(ω_0 cdot t + varphi)$.
где $A$ — амплитуда (максимальный размах) колебаний, $varphi$ — начальная фаза.
Функцией синуса удобнее пользоваться, когда угловая координата тела в момент начала наблюдений равна нулю, функцией косинуса — когда имеет место сдвиг фаз. Так, «косинус фи» — устойчивое понятие, применяемое в электротехнике при описании переменного тока.
Пример 1
Найти начальную фазу колебаний с амплитудой $A = 0,2 м$, если в момент начала измерений $t_0$ смещение циклического параметра $x$ составляло $-0,2 м$.
Подставим в уравнение числовые значения:
$x = A cdot sin(omega_0 cdot t + varphi)$
$-0,2 = 0,2 cdot sin(omega_0 cdot 0 + varphi) implies -0,2 = 0,2 cdot sin(varphi)$
$sin(varphi) = frac{-0,2}{0,2}$
$varphi = arcsin(frac{-0,2}{0,2}) = frac{3 pi}{2}$
Ответ: колебания начались с фазы $1frac{1}{2} pi$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Начальная фаза в физике, теория и онлайн калькуляторы
Начальная фаза
Рассмотрим гармонические колебания некоторого параметра $xi $. Гармонические колебания описываются уравнением:
[xi =A{cos ({omega }_0t+varphi ) } left(1right),]
где $A={xi }_{max}$ — амплитуда колебаний; ${omega }_0$ — циклическая (круговая) частота колебаний. Параметр $xi $ лежит в пределах $-Ale xi le $+A.
Определение начальной фазы колебаний
Определение
Весь аргумент периодической функции (в данном случае косинуса:$ ({omega }_0t+varphi )$),
описывающей колебательный процесс, называют фазой колебаний.
Весь аргумент периодической функции (в данном случае косинуса:$ ({omega }_0t+varphi )$), описывающей колебательный процесс, называют фазой колебаний. Величина фазы колебаний в начальный момент времени, то есть при $t=0$, ($varphi $)- носит название начальной фазы. Устоявшегося обозначения фазы нет, у нас начальная фаза обозначена $varphi $. Иногда, чтобы подчеркнуть, что начальная фаза относится к моменту времени $t=0$ к букве, обозначающей начальную фазу, добавляют индекс 0, пишут, например, ${varphi }_0.$
Единицей измерения начальной фазы является единица измерения угла — радиан (рад) или градус.
Зная амплитуду колебаний и фазу, используя уравнение (1), определяют механическое состояние системы. В начальный момент времени состояние системы определяют амплитуда колебаний и начальная фаза.
Значения амплитуды и начальной фазы задаются в начальных условиях, это означает, что они зависят от способа возбуждения колебаний.
Фазы колеблющейся величины, ее скорости и ускорения
Возьмем первую производную от параметра $xi $, совершающего гармонические колебания:
[frac{dxi }{dt}=frac{d}{dt}left[A{cos left({omega }_0t+varphi right) }right]=-A{omega }_0{sin left({omega }_0t+varphi right)= }A{omega }_0{cos left({omega }_0t+varphi +frac{pi }{2}right)left(2right). }]
Тогда вторая производная от $xi $ задается функцией:
[frac{d^2xi }{dt^2}=-A{{omega }_0}^2{cos left({omega }_0t+varphi right)=-{{omega }_0}^2xi =A{{omega }_0}^2cosleft({omega }_0t+varphi +pi right)left(3right). }]
Уравнения (2) и (3) показывают, что скорость и ускорение $xi $ совершают гармонические колебания с циклической частотой ${omega }_0$. Амплитуды данных колебаний равны:
[{left(frac{dxi }{dt}right)}_{max}=A{omega }_0;; {left(frac{d^2xi }{dt^2}right)}_{max}=A{{omega }_0}^2left(4right).]
Фаза скорости (${omega }_0t+varphi +frac{pi }{2}$) отличается от фазы ускорения (${omega }_0t+varphi +pi $) на величину равную $frac{pi }{2}$. Фаза ускорения отлична от фазы колеблющейся величины на $pi $. Это значит, что в тот момент времени, когда $xi =0$ скорость ее изменения ($frac{dxi }{dt}$) становится максимальной. При $xi $ равной наибольшему значению меньшему нуля, ее ускорение превращается в максимальное положительное.
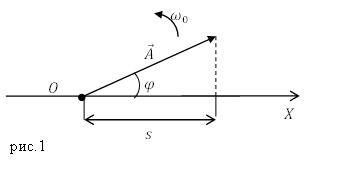
Метод векторных диаграмм
Гармонические колебания можно изобразить при помощи графического ( метод векторных диаграмм). Для этого из произвольно избранной точки О на оси X под углом, равным начальной фазе ($varphi )$, откладывается вектор $overline{A}$. Модуль которого равен амплитуде ($A$) колебаний. Если этот вектор приводить во вращение с угловой скоростью ${omega }_0$, то проекция конца этого вектора перемещается по оси X и принимает значения от $-A$ до $A$. Законом колебаний, будет уравнение (1).
И так, гармонические колебания можно изобразить с помощью проекции на некоторую ось вектора амплитуды $overline{A}$, который отложен из произвольной точки этой оси под углом $varphi $, вращающимся с угловой скоростью ${omega }_0$ вокруг избранной точки.
Сложение колебаний и начальная фаза
Тело, совершающее колебания, может участвовать в нескольких колебательных процессах. В таком случае возникает необходимость выяснить, каким будет результирующее колебание.
Допустим, что два колебания с одинаковыми частотами происходят по одной прямой. Уравнением результирующих колебаний будет выражение:
[xi ={xi }_1+{xi }_2=A{cos left({omega }_0t+varphi right), }]
тогда амплитуда результирующего колебания равна:
[A=sqrt{A^2_1+A^2_2+2A_1A_2{cos left({varphi }_2-{varphi }_1right) }left(5right),}]
где $A_1$; $A_2$ — амплитуды складывающихся колебаний; ${varphi }_2;;{varphi }_1$ — начальные фазы суммирующихся колебаний. При этом начальную фазу полученного колебания ($varphi $) вычисляют, применяя формулу:
[tg varphi =frac{A_1{sin {varphi }_1+A_2{sin {varphi }_2 } }}{A_1{cos {varphi }_1+A_2{cos {varphi }_2 } }}left(6right).]
Уравнение траектории точки, которая принимает участие в двух взаимно перпендикулярных колебаниях с амплитудами $A_1$и $A_2$ и начальными фазами ${varphi }_2и{varphi }_1$ имеет вид:
[frac{x^2}{A^2_1}+frac{y^2}{A^2_2}-frac{2xy}{A_1A_2}{cos left({varphi }_2-{varphi }_1right) }={sin}^2left({varphi }_2-{varphi }_1right)left(7right).]
В случае равенства начальных фаз составляющих колебаний уравнение траектории имеет вид:
[y=frac{A_2}{A_1}x или y=-frac{A_2}{A_1}x left(8right),]
что говорит о движении точки по прямой линии.
Если разность начальных фаз складываемых колебаний составляет $Delta varphi ={varphi }_2-{varphi }_1=frac{pi }{2},$ уравнением траектории становится формула:
[frac{x^2}{A^2_1}+frac{y^2}{A^2_2}=1left(9right),]
что означает, траектория движения эллипс.
Примеры задач с решением
Пример 1
Задание. Материальная точка движется по закону: $x=A{cos left[omega (t+tau )right] }$, где $omega =pi frac{1}{с}$, $tau =0,1 с.$ Какова начальная фаза колебаний?
Решение. Для того чтобы найти начальную фазу вспомним форму записи закона, по которому происходят гармонические колебания, если гармонически изменяется параметр $x$, то запишем:
[x=A{cos ({omega }_0t+varphi ) } left(1.1right),]
где $varphi $ — искомая начальная фаза колебаний. Сравним выражение (1.1) с законом колебаний, который приведен в условии задачи:
[x=A{cos left[omega (t+tau )right] } left(1.2right).]
Используем известные параметры колебаний: $omega =pi frac{1}{с}$, $tau =0,1 с$, выражение (1.2) преобразуем к виду:
[x=A{cos left[pi left(t+0,1right)right]=A{cos left(180{}^circ t+0,1cdot 180right)= } }A{cos left(180{}^circ t+18{}^circ right)left(1.3right). }]
Из выражения (1.3), следует, что начальная фаза равна $varphi =18{}^circ $.
Ответ. $varphi =18{}^circ $
Пример 2
Задание. Каково уравнение траектории движения точки, если она участвует в двух взаимно перпендикулярных колебаниях, которые заданы уравнениями:
[left{ begin{array}{c}
x=2{sin pi t (см);; } \
y={cos left[pi left(t+0,5right)right]left(смright). } end{array}
right.]
Траекторию изобразите.
Решение. Рассмотрим заданные уравнения колебаний:
[left{ begin{array}{c}
x=2{sin pi t left(смright);; } \
y={cos left[pi left(t+0,5right)right]left(смright) } end{array}
left(2.1right).right.]
Из первого уравнения системы мы видим, что начальная фаза первого колебания равна нулю (${varphi }_1=0$)
Второе уравнение системы преобразуем к виду:
[y={cos left[pi left(t+0,5right)right]= }{cos left(pi t+pi cdot 0,5right)={cos left(pi t+frac{pi }{2}right)=-{sin left(pi tright)=-frac{1}{2} } }xleft(2.2right). }]
Начальная фаза колебаний ${varphi }_2=pi $.
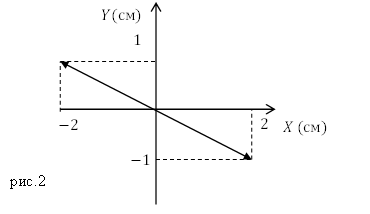
Из уравнения (2.2) видим, что уравнение:
[y=-frac{1}{2}x]
это уравнение прямой, проходящей через начало координат (рис.2):
Ответ. $y=-frac{1}{2}x$. При разности начальных фаз перпендикулярных
колебаний ${varphi }_2-{varphi }_1=pm pi $ результирующее движение представляет собой
гармоническое колебания вдоль прямой $y=-frac{A_2}{A_1}x$
Читать дальше: определение работы в физике.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
§
6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Основные
формулы
• Уравнение
гармонических колебаний
где х
— смещение
колеблющейся точки от положения
равновесия;
t
— время; А,
ω,
φ—
соответственно амплитуда, угловая
частота,
начальная фаза колебаний;
—
фаза колебаний в момент t.
• Угловая частота
колебаний
, или
,
где ν
и
Т — частота и период колебаний.
• Скорость точки,
совершающей гармонические колебания,
• Ускорение при
гармоническом колебании
• Амплитуда
А
результирующего
колебания, полученного при сложении
двух колебаний с одинаковыми частотами,
происходящих по одной прямой, определяется
по формуле
где
a1
и
А2—
амплитуды
составляющих колебаний; φ1
и
φ2—
их
начальные фазы.
•
Начальная фаза φ
результирующего колебания может быть
найдена
из формулы
•
Частота биений,
возникающих при сложении двух колебаний,
происходящих
по одной прямой с различными, но близкими
по значению
частотами ν1
и
ν2,
•
Уравнение траектории
точки, участвующей в двух взаимно
перпендикулярных
колебаниях с амплитудами A1
и A2
и начальными
фазами φ1
и φ2,
Если
начальные фазы φ1
и
φ2
составляющих колебаний одинаковы,
то уравнение траектории принимает вид
т. е. точка движется
по прямой.
В том
случае, если разность фаз
,
уравнение
принимает вид
т. е. точка движется
по эллипсу.
• Дифференциальное
уравнение гармонических колебаний
материальной точки
, или
,
где
m
—
масса точки; k
—
коэффициент
квазиупругой силы (k=тω2).
•
Полная энергия
материальной точки, совершающей
гармонические
колебания,
• Период
колебаний тела, подвешенного на пружине
(пружинный
маятник),
где
m
—
масса тела; k
—
жесткость
пружины.
Формула справедлива для упругих
колебаний в пределах, в которых
выполняется закон Гука (при малой массе
пружины в сравнении
с массой тела).
Период колебаний
математического маятника
где
l
— длина маятника; g
—
ускорение
свободного падения. Период
колебаний физического маятника
где J
— момент инерции колеблющегося тела
относительно оси
колебаний;
а
— расстояние центра масс маятника от
оси колебаний;
— приведенная
длина физического маятника.
Приведенные
формулы являются точными для случая
бесконечно малых амплитуд. При
конечных амплитудах эти формулы дают
лишь приближенные результаты. При
амплитудах не более
ошибка в значении периода не превышает
1 %.
Период
крутильных колебаний тела, подвешенного
на упругой нити,
где J
—
момент
инерции тела относительно оси, совпадающей
с упругой нитью; k
—
жесткость
упругой нити, равная отношению упругого
момента, возникающего при закручивании
нити, к углу, на который нить закручивается.
• Дифференциальное
уравнение затухающих колебаний
, или
,
где r
— коэффициент сопротивления; δ
— коэффициент
затухания:
; ω0—
собственная угловая частота колебаний
*
• Уравнение
затухающих колебаний
где A
(t) —
амплитуда
затухающих колебаний в момент t;
ω
— их угловая частота.
• Угловая частота
затухающих колебаний
О Зависимость
амплитуды затухающих колебаний от
времени
I
где
А0
— амплитуда
колебаний в момент t=0.
• Логарифмический
декремент колебаний
где
A
(t) и
A
(t+T) —
амплитуды
двух последовательных колебаний,
отстоящих по времени друг от друга на
период.
• Дифференциальное
уравнение вынужденных колебаний
, или
,
где
—
внешняя периодическая сила, действующая
на
колеблющуюся
материальную точку и вызывающая
вынужденные
колебания;
F0
—
ее
амплитудное значение;
•
Амплитуда вынужденных
колебаний
•
Резонансная частота
и резонансная амплитуда
и
Примеры решения
задач
Пример
1. Точка
совершает колебания по закону
x(t)= ,
где
А=2
см.
Определить начальную фазу φ,
если
x(0)= см
и х,(0)<0.
Построить векторную диаграмму для
мо-
мента t=0.
Решение.
Воспользуемся уравнением движения и
выразим смещение в момент t=0
через начальную фазу:
О
найдем начальную фазу:
*
В приведенных ранее формулах
гармонических колебаний та же
величина
обозначалась просто ω
(без индекса 0).
Подставим
в это выражение заданные значения x(0)
и А:
φ=
= .
Значению аргумента
удовлетворяют
два
значения угла:
Для
того чтобы решить, какое из этих значений
угла φ
удовлет-
воряет
еще и условию
,
найдем сначала
:
Подставив
в это выражение значение t=0
и поочередно значения
начальных
фаз
и
,
найдем
Т
как всегда A>0
и ω>0,
то условию удовлетворяет
толь
ко
первое значение начальной фазы.
Таким
образом, искомая начальная
фаза
По
найденному значению φ
постро-
им
векторную диаграмму (рис. 6.1).
Пример
2. Материальная
точка
массой т=5
г совершает гармоничес-
кие колебания
с частотой ν
=0,5 Гц.
Амплитуда
колебаний A=3
см. Оп-
ределить: 1) скорость υ
точки
в мо-
мент времени, когда смещение
х=
=
1,5 см; 2) максимальную силу
Fmax,
действующую
на точку; 3)
Рис.
6.1 полную
энергию Е
колеблющейся
точ
ки.
Решение.
1. Уравнение гармонического колебания
имеет вид
(1)
а
формулу скорости получим, взяв первую
производную по времени от смещения:
(2)
Чтобы
выразить скорость через смещение, надо
исключить из формул (1) и (2) время. Для
этого возведем оба уравнения в квадрат,
разделим первое на А2,
второе
на A2
ω
2
и сложим:
, или
Решив
последнее уравнение относительно υ,
найдем
Выполнив вычисления
по этой формуле, получим
см/с.
Знак
плюс соответствует случаю, когда
направление скорости совпадает
с положительным направлением оси х,
знак
минус — когда
направление скорости совпадает с
отрицательным направлением оси
х.
Смещение при
гармоническом колебании кроме уравнения
(1) может быть определено также уравнением
Повторив
с этим уравнением такое же решение,
получим тот же ответ.
2.
Силу действующую на точку, найдем по
второму закону Ньютона:
(3)
где а
— ускорение
точки, которое получим, взяв производную
по времени
от скорости:
, или
Подставив выражение
ускорения в формулу (3), получим
Отсюда максимальное
значение силы
Подставив
в это уравнение значения величин π,
ν,
т
и
A,
найдем
3.
Полная энергия колеблющейся точки есть
сумма кинетической и
потенциальной энергий, вычисленных для
любого момента времени.
Проще
всего вычислить полную энергию в момент,
когда кинетическая
энергия достигает максимального
значения. В этот момент потенциальная
энергия равна нулю. Поэтому полная
энергия E
колеблющейся точки равна максимальной
кинетической энергии
Tmax:
(4)
Максимальную
скорость определим из формулы (2),
положив
:
.
Подставив выражение скорости в фор-
мулу
(4), найдем
Подставив
значения величин в эту формулу и произведя
вычисления, получим
или
мкДж.
Пример
3.
На концах тонкого стержня длиной l
=
1 м и массой m3=400
г
укреплены шарики малых размеров массами
m1=200
г
и
m2=300г.
Стержень
колеблется около горизонтальной оси,
перпен-
дикулярной
стержню и проходящей через его середину
(точка О на рис. 6.2). Определить период Т
колебаний,
совершаемых стержнем.
Решение.
Период колебаний физического маятника,
каким является стержень с шариками,
определяется соотношением
(1)
г
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; lС
— расстояние
от центра масс маятника
до оси.
Момент
инерции данного маятника равен сумме
моментов
инерции шариков J1
и
J2
и
стержня J3:
(2)
Принимая
шарики за материальные точки, выразим
моменты их инерции:
Так
как ось проходит через середину стержня,
то
его
момент инерции относительно этой оси
J3=
= .
Подставив
полученные выражения
J1
,
J2
и
J3
в формулу (2), найдем общий момент инерции
фи-
зического маятника:
Произведя
вычисления по этой формуле, найдем
Рис.
6.2 Масса маятника состоит из масс шариков
и массы
стержня:
Расстояние
lС
центра
масс маятника от оси колебаний найдем,
исходя
из следующих соображений. Если ось х
направить
вдоль стержня
и начало координат совместить с точкой
О,
то
искомое расстояние
l
равно координате центра масс маятника,
т. е.
, или
Подставив
значения величин m1,
m2,
m,
l
и произведя вычисления,
найдем
см.
Произведя
расчеты по формуле (1), получим период
колебаний физического
маятника:
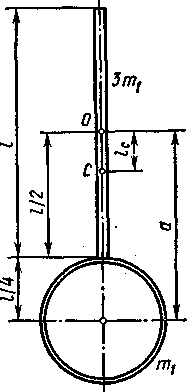
Пример
4. Физический
маятник представляет собой стержень
длиной
l=
1 м и массой 3т1
с прикрепленным
к одному из его концов
обручем
диаметром
и
массой т1.
Горизонтальная
ось Oz
маятника
проходит через середину стержня
перпендикулярно ему (рис. 6.3). Определить
период Т
колебаний
такого маятника.
Решение.
Период
колебаний физического маятника
определяется
по формуле
(1)
где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; lC
— расстояние
от центра масс
маятника до оси колебаний.
Момент
инерции маятника равен сумме моментов
инерции стержня J1
и
обруча J2:
(2).
Момент
инерции стержня относительно
оси,
перпендикулярной
стержню и проходящей
через
его центр масс, определяется по форму-
ле
.
В данном случае т=3т1
и
Момент
инерции обруча найдем, восполь-
зовавшись
теоремой Штейнера
,
где
J
—
момент
инерции относительно про-
извольной
оси;
J0
—
момент
инерции отно-
сительно
оси, проходящей через центр масс
параллельно
заданной оси; а
— расстояние
между
указанными осями. Применив эту фор-
мулу
к обручу, получим
Рис. 6.3
Подставив
выражения J1
и
J2
в формулу
(2), найдем момент инерции маятника
относительно оси вращения:
Расстояние
lС
от
оси маятника до его центра масс равно
Подставив
в формулу (1) выражения J,
lс
и массы маятника
, найдем период его колебаний:
После
вычисления по этой формуле получим
T=2,17
с.
Пример
5. Складываются
два колебания одинакового направле-
ния,
выражаемых уравнениями
;
х2=
=,
где А1=1
см,
A2=2
см,
с,
с, ω
=
=.
1. Определить начальные фазы φ1
и φ
2
составляющих коле-
баний.
2. Найти амплитуду А
и
начальную фазу φ
результирующего колебания.
Написать уравнение результирующего
колебания.
Решение.
1. Уравнение гармонического колебания
имеет вид
(1)
Преобразуем
уравнения, заданные в условии задачи,
к такому же
виду:
(2)
Из
сравнения выражений (2) с равенством (1)
находим начальные фазы
первого и второго колебаний:
рад и
рад.
2.
Для определения амплитуды А
результирующего
колебания удобно воспользоваться
векторной диаграммой,
представленной на рис.
6.4.
Согласно теореме косинусов, получим
(3)
где
— разность фаз составляющих колебаний.
Так
как
,
то, подставляя найденные
значения
φ2
и φ1
получим
рад.
Рис. 6.4
Подставим
значения А1
,
А2
и
в формулу (3)
и
произведем вычисления:
A=2,65
см.
Тангенс
начальной фазы φ
результирующего колебания опреде-
лим
непосредственно из рис. 6.4:
, отку-
да
начальная фаза
Подставим
значения А1,
А2,
φ
1,
φ
2
и произведем вычисления:
= рад.
Так
как угловые частоты складываемых
колебаний одинаковы,
то
результирующее колебание будет иметь
ту же частоту ω.
Это
позволяет
написать уравнение результирующего
колебания в виде
, где A=2,65
см,
,
рад.
Пример
6. Материальная
точка участвует одновременно в двух
взаимно перпендикулярных гармонических
колебаниях, уравнения
которых
(1).
(2)
где
a1=1
см,
A2=2
см,
.
Найти уравнение траектории точ-
ки.
Построить траекторию с соблюдением
масштаба и указать
направление
движения точки.
Решение.
Чтобы
найти уравнение траектории точки,
исключим
время t
из
заданных уравнений (1) и (2). Для этого
восполь-
зуемся
формулой
.
В данном случае
, поэтому
Так
как согласно формуле (1)
,
то уравнение траекто-
рии
(3)
Полученное
выражение представляет собой уравнение
параболы, ось которой совпадает с осью
Ох.
Из
уравнений (1) и (2) следует, что смещение
точки по осям координат ограничено и
заключено в пределах от —1 до +1 см по
оси Ох
и
от —2 до +2 см по оси Оу.
Для
построения траектории найдем по уравнению
(3) значения у,
соответствующие
ряду значений х,
удовлетворяющих
условию
см, и составим таблицу:
|
X |
-1 |
—0,75 |
—0,5 |
0 |
+0,5 |
+ 1 |
|
у, |
0 |
±0,707 |
±1 |
±1,41 |
±1,73 |
±2 |
Начертив
координатные оси и выбрав масштаб,
нанесем на плоскость
хОу
найденные
точки. Соединив их плавной кривой,
получим траекторию точки, совершающей
колебания
в соответствии с уравнениями движения
(1) и (2) (рис. 6.5).
Рис. 6.5
Для
того чтобы указать направление движения
точки, проследим за тем, как изменяется
ее положение с течением времени. В
начальный момент t=0
координаты точки
равны x(0)=1
см и y(0)=2
см. В последующий
момент времени, например при t1=l
с,
координаты точек изменятся и станут
равными х
(1)=
—1
см, y(t)=0.
Зная
положения
точек в начальный и последующий
(близкий) моменты времени, можно указать
направление движения точки по траектории.
На рис. 6.5 это направление движения
указано стрелкой (от точки А
к
началу
координат). После того как в момент
t2
= 2 с колеблющаяся точка достигнет
точки D,
она
будет двигаться в обратном направлении.
Задачи
Кинематика
гармонических колебаний
6.1.
Уравнение колебаний точки имеет вид
,
где
ω=π
с-1,
τ=0,2
с. Определить период Т
и
начальную фазу φ
колебаний.
6.2.
Определить
период Т,
частоту
v
и
начальную фазу φ
колебаний,
заданных уравнением
,
где ω=2,5π
с-1,
τ=0,4
с.
6.3.
Точка
совершает колебания по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и
;
2)
х(0)
=см
и
;
3) х(0)=2см
и
;
4)
х(0)=
и
.
Построить векторную диаграмму
для
момента
t=0.
6.4.
Точка
совершает колебания .по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и
; 2) x(0)=
см и
;
3) х(0)=
см и
;
4)
x(0)=см
и
.
Построить векторную диаграмму для
момента
t=0.
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
КОЛЕБАНИЯ И ВОЛНЫ
Колебания
Механические колебания — периодически повторяющиеся изменения положения тела (материальной точки) относительно положения равновесия.
Амплитуда — максимальное отклонение тела от положения равновесия.
Период — время за которое совершается одно полное колебание. Единица измерения секунда (с).
Частота — количество колебаний
в единицу времени
. Измеряется частота в герцах (Гц) показывающих количество колебаний за секунду. К примеру величина 50 Гц говорит нам о том, что система за одну секунду совершила 50 колебаний.
Так как период это время за которое совершается одно полное колебание, можно выразить частоту следующим образом:
Гармонические колебания — колебания происходящие по законам синуса или косинуса (гармоническому закону).
Фаза колебания () — аргумент периодической функции, описывающей колебательный или волновой процесс.
Начальная фаза колебания — значение фазы колебаний в начальный момент времени, т.е. при t = 0.
Циклическая частота — скалярная физическая величина, мера частоты вращательного или колебательного движения. Единица измерения радиан в секунду (рад/с).
Исходя из этого можно записать
Свободные колебания — колебания возникающие за счет внутренних сил системы, после того как она была выведена из состояния равновесия.
Собственные частота колебаний — частота свободных колебаний колебательной системы.
Затухающие колебания — колебания в которых происходит постепенное уменьшение амплитуды в результате действия сил сопротивления движению (силы трения, силы сопротивления воздуха..).
Вынужденные колебания — колебания, происходящие под действием внешних периодически изменяющейся сил.
Резонанс — резкое увеличение амплитуды колебания при совпадении собственной частоты колебательной системы, с частотой вынуждающей силы.
Математический маятник
Математический маятник — механическая колебательная система представляющая из себя материальную точку подвешенную на нерастяжимой невесомой нити в поле силы тяжести.
Формула Гюгенса для определения периода колебаний математического маятника. l — длинна маятника.
Циклическая частота колебаний математического маятника.
Пружинный маятник
Пружинный маятник — механическая колебательная система представляющая из себя пружину жесткостью , с материальной точкой массой
на одном конце этой пружины.
Колебательный контур
Электромагнитные колебания — периодические изменения напряжённости и магнитной индукции.
Колебательный контур — электрическая цепь, состоящая из конденсатора ёмкостью и катушки индуктивностью
. В этой цепи происходят свободные электромагнитные колебания.
Циклическая частота и период собственных колебаний контура определяются по формуле Томсона:
Связь между амплитудными (максимальными) значениями тока в контуре и заряда на конденсаторе:
Энергия контура:
Связь между амплитудными (максимальными) значениями тока и напряжения в контуре (закон сохранения энергии в колебательном контуре):
Переменный ток
Переменный ток — электрический ток периодически меняющий свое направление.
Действующее значение силы переменного тока равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
Действующее значение напряжения в цепи переменного тока равно напряжению постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
Средняя по времени тепловая мощность переменного тока:
Емкостное сопротивление — сопротивление конденсатора в цепи переменного тока. Емкостное сопротивление зависит от частоты переменного тока, чем частота выше, тем сопротивление ниже. Для постоянного тока конденсатор по сути представляет разрыв цепи, по этому для постоянного тока емкостное сопротивление стремиться к бесконечности.
Где циклическая частота переменного тока.
Закон Ома для участков цепи, содержащих емкость:
Индуктивное сопротивление — сопротивление катушки индуктивности в цепи переменного тока. Так как изменение тока в цепи приводит к появлению токов самоиндукции противодействующих этому изменению, то увеличение частоты переменного тока приводит к увеличению индукционного сопротивления.
Закон Ома для участков цепи, содержащих индуктивность:
Трансформатор
Трансформатор — электромагнитное устройство, которое используется для передачи и преобразования электрической энергии из одной катушки индуктивности на сердечнике в другую. Частота переменного тока при этом не меняется.
Идеальный трансформатор — трансформатор в котором энергетические потери пренебрежимо малы.
Отношение напряжений на вторичной и первичной
обмотках идеального трансформатора равно отношению количеств их витков. (
на вторичной и
первичной). Само это соотношение называют коэффициентом трансформации
.
Если коэффициент трансформации больше единицы, то трансформатор называется понижающим, если меньше, то повышающим.
Закон сохранения энергии для идеального трансформатора:
КПД неидеального трансформатора:
Волны
Волны — колебания распространяющийся в упругих средах. Если направление распространения волн и направление колеблющихся частиц среды совпадают то такие волны называются продольными. А если эти направления перпендикулярны друг другу, то такие волны называют поперечными.
Так как волновые процессы являются часным случаем колебательного движения, они так же будут характеризоваться своими частотой и периодом. Но помимо этого у волн есть еще свои дополнительные характеристики, отличающие их от обычного колебательного движения.
Длина волны — расстояние, на которое успевает распространиться волна за один период;
Скорость распространения волны — отношение длинны волны к периоду ее колебания.
Звуковые волны — разновидность механических волн в слышимом для человека диапазоне ( от 16 Гц до 20 кГц).
















![Rendered by QuickLaTeX.com [T=2pi sqrt{frac{l}{g}}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-29425af3eec4256686ccf44fde46b3ca_l3.png)