Как определить скорость по графику?
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Как определить скорость тела при равномерном движении?
Скорость при прямолинейном движении — величина постоянная. Для того, чтобы найти скорость, необходимо пройденный путь разделить на время, за которое он был пройден.
Как составить уравнение скорости по графику?
График скорости График скорости — графическое представление уравнения скорости тела v = v(t). График v(t) служит для описания движение тела. На этом графике представлено равноУскоренное движение.
Что называется скоростью тела при равномерном движении?
Скорость при равномерном прямолинейном движении. Скорость и (м/с) — векторная физическая величина, которая показывает, какое перемещение совершает тело за единицу времени.
Как изменяется скорость тела при равномерном движении?
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0). Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.
Как составить уравнение движения тела?
х=х +vхt. Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х .
Как записать уравнение проекции скорости?
Зависимость проекции скорости движущегося тела от времени имеет вид: vx = 2 + 3t (м/с).
Как написать уравнение зависимости?
Уравнение зависимости скорости от времени при движении с ускорением имеет вид:
- v(t) = vo + at = 20 + 1.5t. Производная функции зависимости координаты от времени равна функции зависимости скорости от времени:
- x’ (t) = v (t). …
- x(t) = 0.75t 2 + 20t.
Как написать уравнение скорости по графику
Графическое представление равномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V (t) — изменение скорости со временем
S(t) — изменение перемещения (пути) со временем
a(t) — изменение ускорения со временем

За висимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно ( v = const ), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) — прямая линия, параллельная оси времени.
Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.
Зависимость перемещения от времени. График s(t) — наклонная линия :
Из графика видно, что проекция скорости равна:
Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Неравномерное прямолинейное движение.
Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.
Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.
Для характеристики неравномерного движения вводится понятие средней скорости.
Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:
Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.
Различие между средней и мгновенной скоростями показано на рисунке.
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.
Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:
Vx — Скорость тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
ax — Ускорение тела
t — Время движения тела
Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.
Единица измерения ускорения в СИ [м/с 2 ].
Ускорение измеряют акселерометром
Уравнение скорости для равноускоренного движения: vx = vxo + axt
Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):
Sx — Перемещение тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
Vx — Скорость тела при равноускоренном движении по прямой
ax — Ускорение тела
t — Время движения тела
Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:
— если известны начальная, конечная скорости движения и ускорение.
— если известны начальная, конечная скорости движения и время всего движения
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V(t) — изменение скорости со временем
S(t) — изменение перемещения (пути) со временем
a(t) — изменение ускорения со временем
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости vx = vxo + axt . Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:
В координатах зависимость имеет вид:
Уравнение движения, графики равномерного прямолинейного движения
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.
Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin x=x_0+s=x_0+vt\ x=20+10t end
Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin x=x_0-st=x_0-vt\ x=20-10t end Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
 |
Построим графики зависимости координаты от времени для нашего примера: |
x=20+10t — машина движется вправо (в направлении оси OX)
x=20-10t — машина движется влево (в направлении, противоположном оси OX)
x=20 — машина стоит
п.5. Как найти уравнение движения по графику движения?
п.6. График скорости vx=vx(t)
Для рассмотренного примера:
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости:
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:
По графику находим: begin x_1=x(5)=8cdot 5=40 text<(м)>\ x_2=x(10)=8cdot 10=80 text <(м)>end
б) Скорость (v_x=8) м/с — постоянная величина, её график:
$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text <(м)>$$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).
Найдем скорость корабля (v_x): $$ v_x=frac=frac<56-38><2-1>=18 (text<тыс.км/ч>) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text<тыс.км/ч>) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text<тыс.км>) $$
г) Переведем скорость в км/с: $$ 18000frac<text<км>><text<ч>>=frac<18000 text<км>><1 text<ч>>=frac<18000 text<км>><3600 text>=5 text <км/c>$$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
http://www.sites.google.com/site/opatpofizike/teoria/teoria-10-klass/graficeskoe-predstavlenie-dvizenia
http://reshator.com/sprav/fizika/7-klass/uravnenie-dvizheniya-grafiki-ravnomernogo-pryamolinejnogo-dvizheniya/
Загрузить PDF
Загрузить PDF
Скорость является функцией времени и определяется как абсолютной величиной, так и направлением.[1]
Часто в задачах по физике требуется найти начальную скорость (ее величину и направление), которой изучаемый объект обладал в нулевой момент времени. Для вычисления начальной скорости можно использовать различные уравнения. Основываясь на данных, приведенных в условии задачи, вы можете выбрать наиболее подходящую формулу, которая позволит легко получить искомый ответ.
-
1
Используйте подходящее уравнение. При решении физической задачи необходимо знать, какая формула вам понадобится. Для этого первым делом следует записать все данные, приведенные в условии задачи. Если известны конечная скорость, ускорение и время, для определения начальной скорости удобно использовать следующее соотношение:
- Vi = Vf — (a * t)
- В эту формулу входят следующие величины:
- Vi — начальная скорость
- Vf — конечная скорость
- a — ускорение
- t — время
- Обратите внимание, что это стандартная формула, используемая для вычисления начальной скорости.
-
2
Подставьте в формулу известные величины. Выписав все исходные данные и записав необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.
- Если вы где-либо допустили ошибку, то легко сможете найти ее, просмотрев свои записи.
-
3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь стандартными преобразованиями для получения искомого результата. Если можно, используйте калькулятор, чтобы снизить вероятность просчетов при вычислениях.
- Предположим, что объект, двигаясь на восток с ускорением 10 метров в секунду в квадрате в течение 12 секунд, разогнался до конечной скорости 200 метров в секунду. Необходимо найти начальную скорость объекта.
- Запишем исходные данные:
- Vi = ?, Vf = 200 м/с, a = 10 м/с2, t = 12 с
- Умножим ускорение на время: a * t = 10 * 12 =120
- Вычтем полученное значение из конечной скорости: Vi = Vf – (a * t) = 200 – 120 = 80 Vi = 80 м/с на восток
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, в нашем случае метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Предположим, что объект, двигаясь на восток с ускорением 10 метров в секунду в квадрате в течение 12 секунд, разогнался до конечной скорости 200 метров в секунду. Необходимо найти начальную скорость объекта.
-
1
Используйте подходящую формулу. При решении какой-либо физической задачи необходимо выбрать соответствующее уравнение. Для этого первым делом следует записать все данные, приведенные в условии задачи. Если известны пройденное расстояние, время и ускорение, для определения начальной скорости можно использовать следующее соотношение:
- Vi = (d / t) — [(a * t) / 2]
- В эту формулу входят следующие величины:
- Vi — начальная скорость
- d — пройденное расстояние
- a — ускорение
- t — время
-
2
Подставьте в формулу известные величины. После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.
- Допустив ошибку в решении, вы сможете без труда найти ее, просмотрев свои записи.
-
3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь стандартными преобразованиями для нахождения ответа. Если возможно, используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.
- Допустим, объект движется в западном направлении с ускорением 7 метров в секунду в квадрате в течение 30 секунд, пройдя при этом 150 метров. Необходимо вычислить его начальную скорость.
- Запишем исходные данные:
- Vi = ?, d = 150 м, a = 7 м/с2, t = 30 с
- Умножим ускорение на время: a * t = 7 * 30 = 210
- Поделим произведение на два: (a * t) / 2 = 210 / 2 = 105
- Поделим расстояние на время: d / t = 150 / 30 = 5
- Вычтем первую величину из второй: Vi = (d / t) — [(a * t) / 2] = 5 – 105 = -100 Vi = -100 м/с в западном направлении
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, в нашем случае метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Допустим, объект движется в западном направлении с ускорением 7 метров в секунду в квадрате в течение 30 секунд, пройдя при этом 150 метров. Необходимо вычислить его начальную скорость.
-
1
Используйте подходящее уравнение. Для решения физической задачи необходимо выбрать соответствующую формулу. Первым делом следует записать все начальные данные, указанные в условии задачи. Если известны конечная скорость, ускорение и пройденное расстояние, для определения начальной скорости удобно использовать следующее соотношение:
- Vi = √ [Vf2 — (2 * a * d)]
- Эта формула содержит следующие величины:
- Vi — начальная скорость
- Vf — конечная скорость
- a — ускорение
- d — пройденное расстояние
-
2
Подставьте в формулу известные величины. После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.
- Допустив где-либо ошибку, вы сможете без труда найти ее, просмотрев ход решения.
-
3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь необходимыми преобразованиями для получения ответа. По возможности используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.
- Предположим, объект движется в северном направлении с ускорением 5 метров в секунду в квадрате и, преодолев 10 метров, имеет конечную скорость 12 метров в секунду. Необходимо найти его начальную скорость.
- Запишем исходные данные:
- Vi = ?, Vf = 12 м/с, a = 5 м/с2, d = 10 м
- Возведем в квадрат конечную скорость: Vf2= 122 = 144
- Умножим ускорение на пройденное расстояние и на 2: 2 * a * d = 2 * 5 * 10 = 100
- Вычтем результат умножения из квадрата конечной скорости: Vf2 — (2 * a * d) = 144 – 100 = 44
- Извлечем квадратный корень из полученного значения: = √ [Vf2 — (2 * a * d)] = √44 = 6,633 Vi = 6,633 м/с в северном направлении
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, то есть метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Предположим, объект движется в северном направлении с ускорением 5 метров в секунду в квадрате и, преодолев 10 метров, имеет конечную скорость 12 метров в секунду. Необходимо найти его начальную скорость.
-
1
Выберите подходящую формулу. При решении физической задачи необходимо использовать соответствующее уравнение. Прежде всего следует записать все данные, приведенные в условии задачи. Если известны конечная скорость, время и пройденное расстояние, для определения начальной скорости можно использовать следующее соотношение:
- Vi = Vf + 2 (t — d)
- В данную формулу входят следующие величины:
- Vi — начальная скорость
- Vf — конечная скорость
- t — время
- d — пройденное расстояние
-
2
Подставьте в формулу известные значения. После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Внимательно изучите условие задачи и аккуратно записывайте каждый шаг при ее решении.
- Допустив ошибку, вы сможете без труда найти ее, просмотрев решение.
-
3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь необходимыми преобразованиями для получения ответа. Если можно, используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.
- Допустим, объект преодолел расстояние 15 метров (49,2 фута) в течение 45 секунд, и его конечная скорость составляет 17 метров (55,8 фута) в секунду. Найдем начальную скорость объекта.
- Запишем исходные данные:
- Vi = ?, Vf = 17 м/с, t = 45 с, d = 15 м
- Вычтем расстояние из времени: (t – d) = (45 – 15) = 30
- Умножим полученное значение на 2: 2 ( t – d) = 2 (45 – 15) = 60
- Прибавим к этой величине конечную скорость: Vf + 2 (t – d) = 17 + 60 = 77 Vi = 77 м/с в южном направлении
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, то есть метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Допустим, объект преодолел расстояние 15 метров (49,2 фута) в течение 45 секунд, и его конечная скорость составляет 17 метров (55,8 фута) в секунду. Найдем начальную скорость объекта.
Что вам понадобится
- Карандаш
- Бумага
- Калькулятор (необязательно)
Об этой статье
Эту страницу просматривали 150 001 раз.
Была ли эта статья полезной?
Как найти начальную скорость тела
Кинематика рассматривает изменение пространственного положения тел независимо от причин, вызвавших движение. Тело перемещается благодаря действующим на него силам, и этот вопрос является предметом изучения в динамике. Кинематика и динамика – два основных раздела механики.

Инструкция
Если в задаче сказано, что тело движется равномерно, это означает, что скорость остается постоянной на протяжении всего пути. Начальная скорость тела совпадает со скоростью тела вообще, а уравнение движения имеет вид: x=x0+v∙t, где x – координата, x0 – начальная координата, v – скорость, t – время.
Естественно, движение не всегда является равномерным. Удобным случаем, часто рассматриваемым в механике, является равнопеременное движение тела. Такие условия предполагают постоянное ускорение, как по модулю, так и по знаку (положительное или отрицательное). Положительное ускорение говорит о том, что скорость тела растет. При отрицательном ускорении тело постепенно замедляется.
При движении материальной точки с постоянным ускорением скорость определяется кинематическим уравнением v=v0+v0∙t, где v0 – начальная скорость. Таким образом, зависимость скорости от времени здесь будет линейной. А вот координата меняется с течением времени квадратически: x=x0+v0∙t+a∙t²/2. Кстати, перемещением является разность конечной и начальной координат.
В физической задаче может быть задано произвольное уравнение движения. В любом случае, чтобы из функции координат найти функцию скорости, надо продифференцировать имеющееся уравнения, ведь, по определению, скорость – это первая производная координаты по времени: v(t)=x’(t). Чтобы из функции скорости найти начальную скорость, подставьте в уравнение t=0.
Иногда можно найти ускорение тела, применяя законы динамики. Расставьте все силы, действующие на тело. Введите пару прямоугольных координатных осей, относительно которых будете рассматривать вектора сил. Согласно второму закону Ньютона, ускорение прямо пропорционально приложенной силе и обратно пропорционально массе тела: a=F/m. По-другому это записывается как F=ma.
Собственно, именно сила определяет, как будет ускоряться тело. Так, сила тяги заставит тело перемещаться быстрее, а сила трения затормозит его. Важно понимать, что при отсутствии каких-либо внешних сил тело способно не только быть неподвижным, но и равномерно перемещаться в пространстве. Это обусловлено инерционными свойствами массы. Другой вопрос в том, что редко удается достичь условий, приближенных к полному отсутствию сил.
Видео по теме
Источники:
- «Механика»
- начальная скорость
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Download Article
Download Article
Velocity is a function of time and defined by both a magnitude and a direction. [1]
Often in physics problems, you will need to calculate the initial velocity (speed and direction) at which an object in question began to travel. There are multiple equations that can be used to determine initial velocity. Using the information given in a problem, you can determine the proper equation to use and easily answer your question.
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you have values for the final velocity, acceleration, and time involved, you can use the following equation:[3]
- Initial velocity: Vi = Vf — (a * t)
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- a stands for “acceleration”
- t stands for “time”
- Note that this equation is the standard equation used when finding initial velocity.
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
Advertisement
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.[4]
- For example: An object accelerating east at 10 meters (32.8 ft) per second squared traveled for 12 seconds reaching a final velocity of 200 meters (656.2 ft) per second. Find the initial velocity of that object.
- Write the known information:
- Vi = ?, Vf = 200 m/s, a = 10 m/s2, t = 12 s
- Multiply the acceleration and time. a * t = 10 * 12 =120
- Subtract the product from the final velocity. Vi = Vf – (a * t) = 200 – 120 = 80 Vi = 80 m/s east
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating east at 10 meters (32.8 ft) per second squared traveled for 12 seconds reaching a final velocity of 200 meters (656.2 ft) per second. Find the initial velocity of that object.
Advertisement
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation.[5]
If you know values for the distance, time, and acceleration, you can use the following equation:- Initial velocity: Vi = (d / t) — [(a * t) / 2]
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- d stands for “distance”
- a stands for “acceleration”
- t stands for “time”
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object accelerating west at 7 meters (23.0 ft) per second squared traveled a distance of 150 meters (492.1 ft) within 30 seconds. Calculate the initial velocity of that object.
- Write the known information:
- Vi = ?, d = 150 m, a = 7 m/s2, t = 30 s
- Multiply the acceleration and time. a * t = 7 * 30 = 210
- Divide the product by two. (a * t) / 2 = 210 / 2 = 105
- Divide the distance by the time. d / t = 150 / 30 = 5
- Subtract your first quotient from the second quotient. Vi = (d / t) — [(a * t) / 2] = 5 – 105 = -100 Vi = -100 m/s west
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating west at 7 meters (23.0 ft) per second squared traveled a distance of 150 meters (492.1 ft) within 30 seconds. Calculate the initial velocity of that object.
Advertisement
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you are given the final velocity, acceleration, and distance, you can use the following equation:[7]
- Initial velocity: Vi = √ [Vf2 — (2 * a * d)]
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- a stands for “acceleration”
- d stands for “distance”
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object accelerating north at 5 meters (16.4 ft) per second squared traveled 10 meters (32.8 ft), ending up at a final velocity of 12 meters (39.4 ft) per second. Calculate the object’s initial velocity.
- Write the known information:
- Vi = ?, Vf = 12 m/s, a = 5 m/s2, d = 10 m
- Square the final velocity. Vf2= 122 = 144
- Multiply the acceleration by the distance and the number two. 2 * a * d = 2 * 5 * 10 = 100
- Subtract this product from your previous one. Vf2 — (2 * a * d) = 144 – 100 = 44
- Take the square root of your answer. = √ [Vf2 — (2 * a * d)] = √44 = 6.633 Vi = 6.633 m/s north
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating north at 5 meters (16.4 ft) per second squared traveled 10 meters (32.8 ft), ending up at a final velocity of 12 meters (39.4 ft) per second. Calculate the object’s initial velocity.
Advertisement
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you are given the final velocity, time, and distance, you can use the following equation:[9]
- Initial velocity: Vi = 2(d/t) — Vf
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- t stands for “time”
- d stands for “distance”
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object with a final velocity of 3 meters (9.8 ft) traveled south for 15 seconds and covered a distance of 45 meters (147.6 ft). Calculate the object’s initial velocity.
- Write the known information:
- Vi = ?, Vf = 3 m/s, t = 15 s, d = 45 m
- Divide distance by time. (d/t) = (45/15) = 3
- Multiply that value by 2. 2 (d/t) = 2 (45/15) = 6
- Subtract final velocity from the product. 2(d/t) — Vf = 6 — 3 = 3 Vi = 3 m/s south
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object with a final velocity of 3 meters (9.8 ft) traveled south for 15 seconds and covered a distance of 45 meters (147.6 ft). Calculate the object’s initial velocity.
Advertisement
Add New Question
-
Question
What are the difficulties some people have in understanding acceleration?
Sean Alexander is an Academic Tutor specializing in teaching mathematics and physics. Sean is the Owner of Alexander Tutoring, an academic tutoring business that provides personalized studying sessions focused on mathematics and physics. With over 15 years of experience, Sean has worked as a physics and math instructor and tutor for Stanford University, San Francisco State University, and Stanbridge Academy. He holds a BS in Physics from the University of California, Santa Barbara and an MS in Theoretical Physics from San Francisco State University.
Academic Tutor
Expert Answer
One of the difficulties people face is the unit for acceleration, which is meters per second squared. To understand this with a real-world example, think about a rock being dropped off a cliff. Acceleration due to Earth’s gravity is 9.8 meters per second squared, so we can round up to 10 for this example. Neglecting friction, when you first let go of the rock, its velocity is zero. After one second of falling, the speed of the stone will be 10 meters a second. After two seconds of falling, the speed of the stone will be 20 meters a second. After three seconds of falling, the speed of this will be 30 meters per second. It gains 10 meters a second of speed for each second that it is falling.
-
Question
A bullet of 60 gm is fired using a rifle of mass 12kg. Rifle recoils with a velocity of 2.5m/s. What is the initial velocity?
Kinetic energy -> Kinetic energy
0.5mv^2 -> 0.5mv^2
0.5 x 12 x 2,5^2 = 0.5 x 0.06 x v^2
6 x 6.25 = 0.03 x v^2
37.5 = 0.03 x v^2
sqrt(37.5/0.03) = v
sqrt(1250) = v
v = 35.3 m/s -
Question
If displacement and time are related as s = 3.5t + 5t2, what is the initial velocity?
Initial velocity is 3.5. The equation is s = ut + 1/2at^2, where s — distance, u — inititial velocity, and a — acceleration.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Things You’ll Need
- Pencil
- Paper
- Calculator (optional)
About This Article
Article SummaryX
To find initial velocity, start by multiplying the acceleration by the time. Then, divide that number by 2 and write down the quotient you get. Next, divide the distance by the time and write down that quotient as well. Finally, subtract your first quotient from your second quotient to find the initial velocity. To learn how to find initial velocity using the final velocity, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 836,804 times.
Did this article help you?
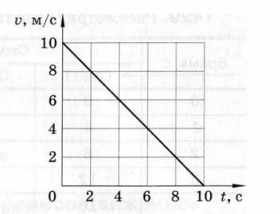
По графику скорости (рис. 232) определите:
а) начальную скорость тела;
б) скорость тела через 5 с;
в) ускорение тела;
г) путь, пройденный телом за 10 с.
рис. 232
reshalka.com
ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Прямолинейное равноускоренное движение. Ускорение. Перемещение при прямолинейном равноускоренном движении. Номер №1443
Решение а
v
0
=
10
м/с.
Решение б
t = 5 c;
v
5
=
5
м/с.
Решение в
Уравнение скорости:
v
=
v
0
+
a
t
;
a
=
v
−
v
0
t
;
a
=
5
−
10
5
=
−
1
м
/
с
2
.
Ответ: − 1
м
/
с
2
.
Решение г
t = 10 c;
S
=
v
0
+
v
2
∗
t
;
S
=
10
+
0
2
∗
10
=
50
м.
Ответ: 50 м.