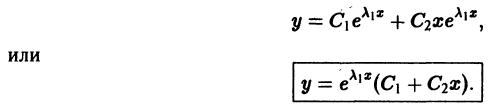
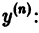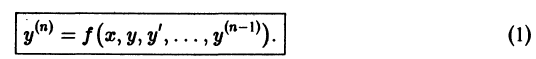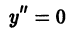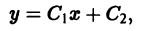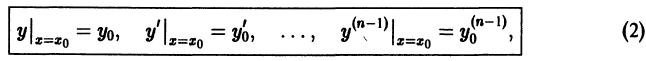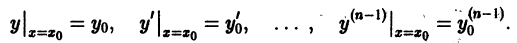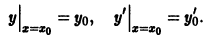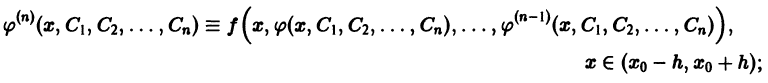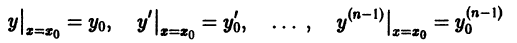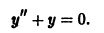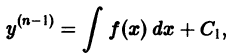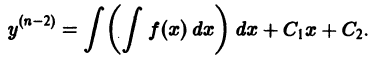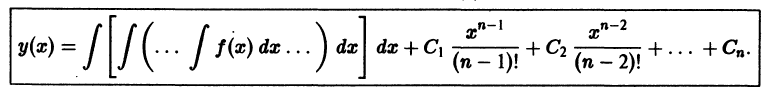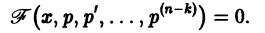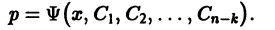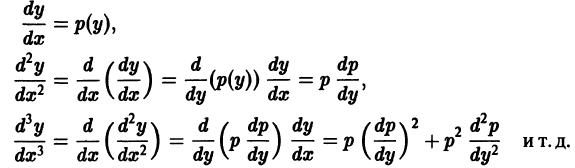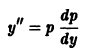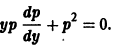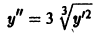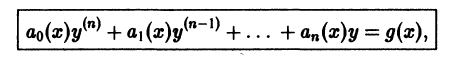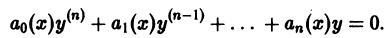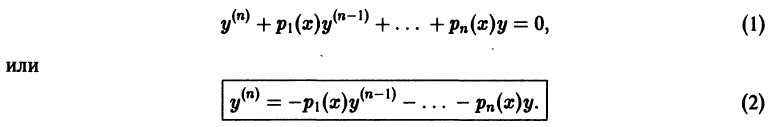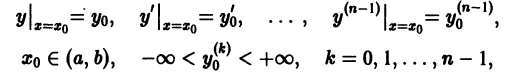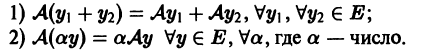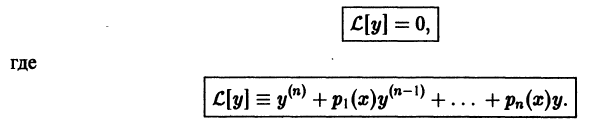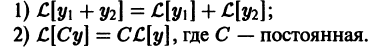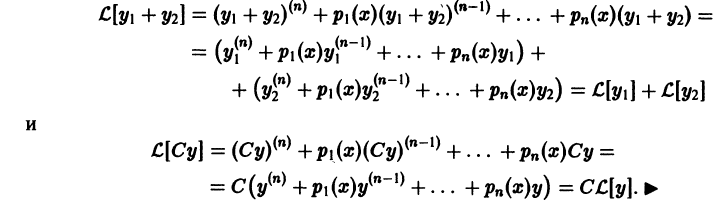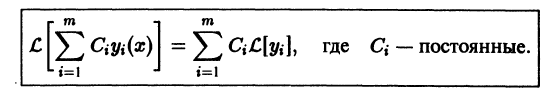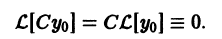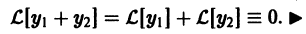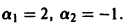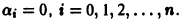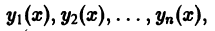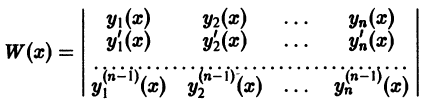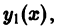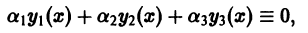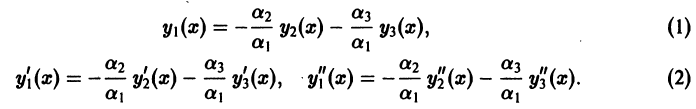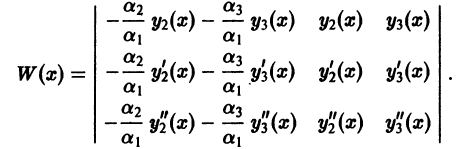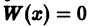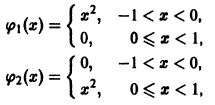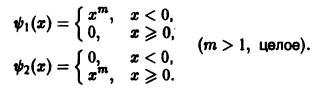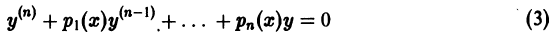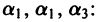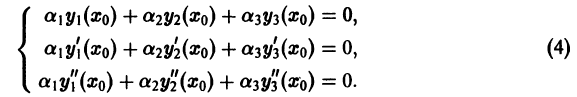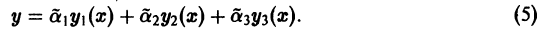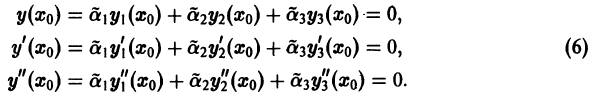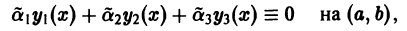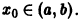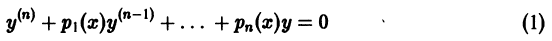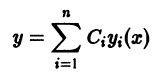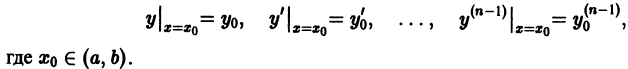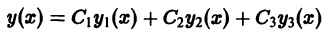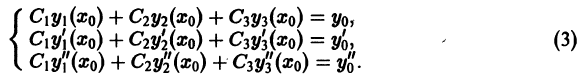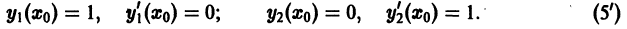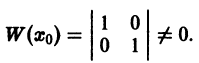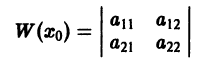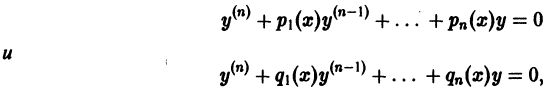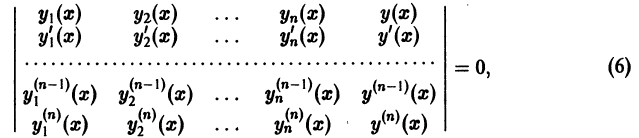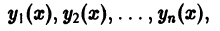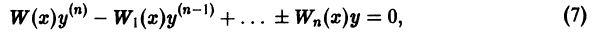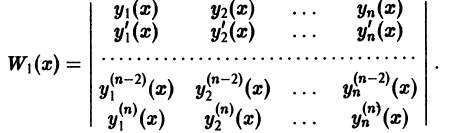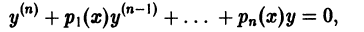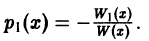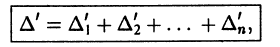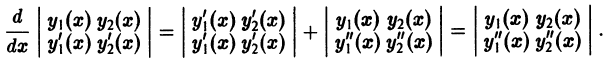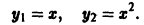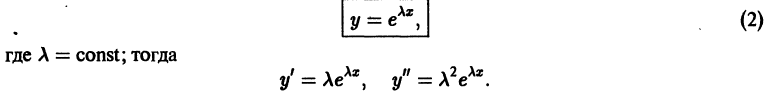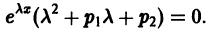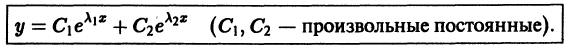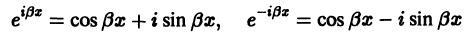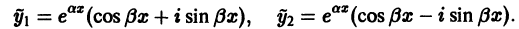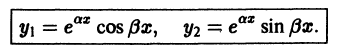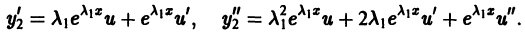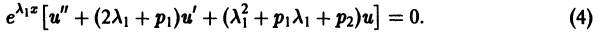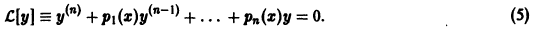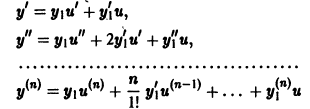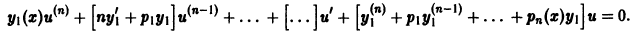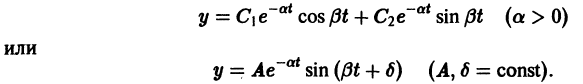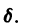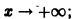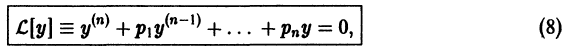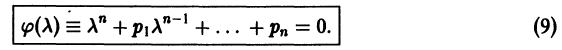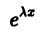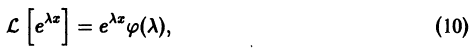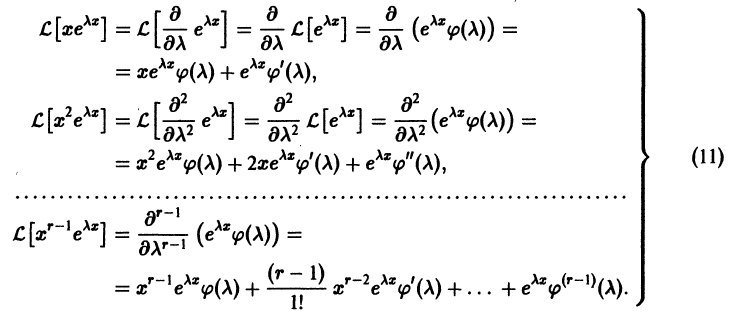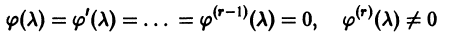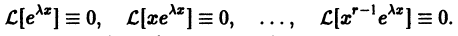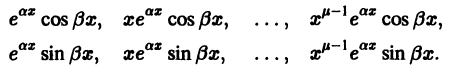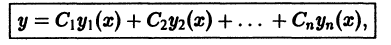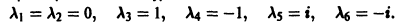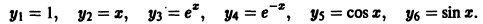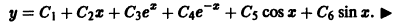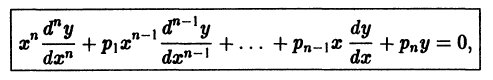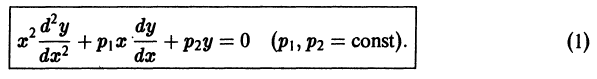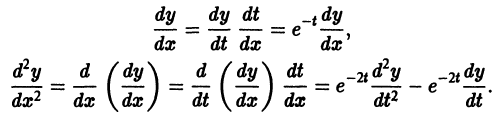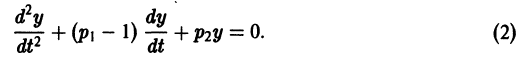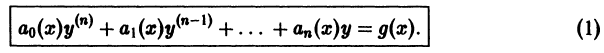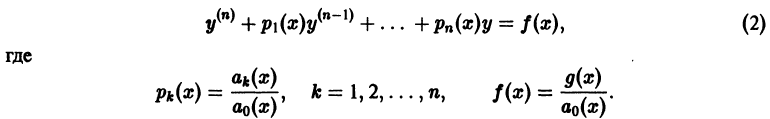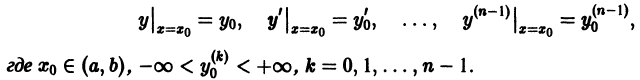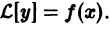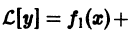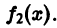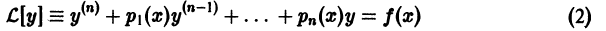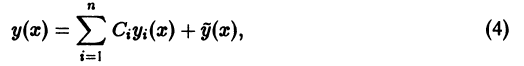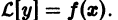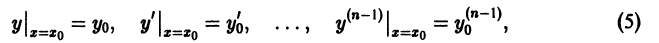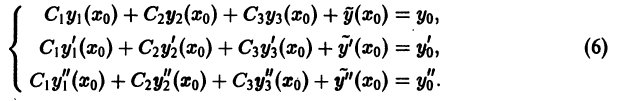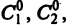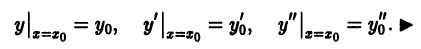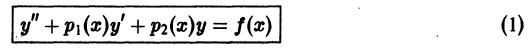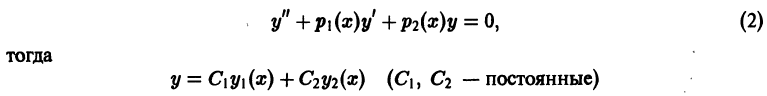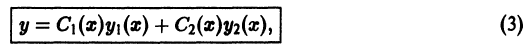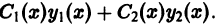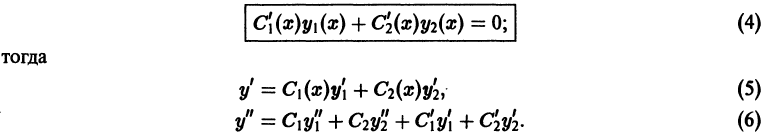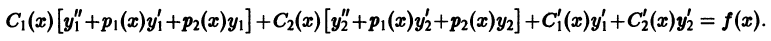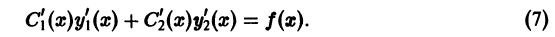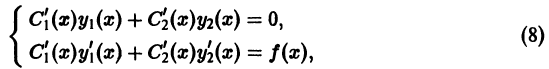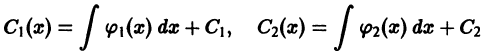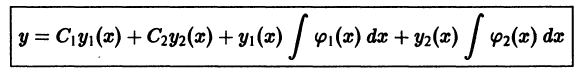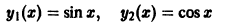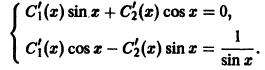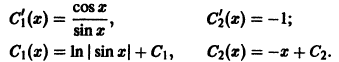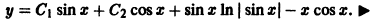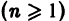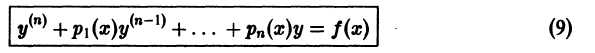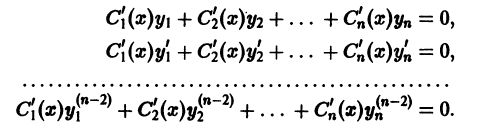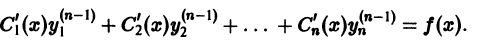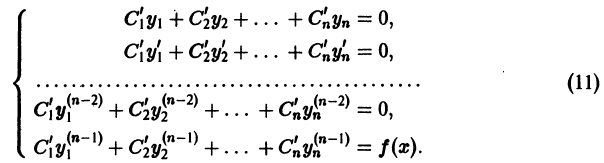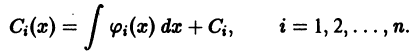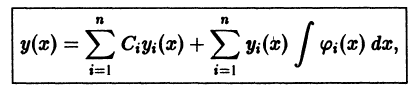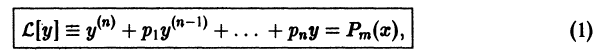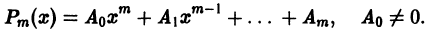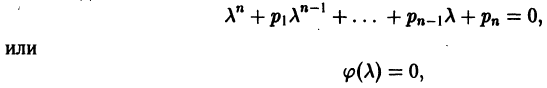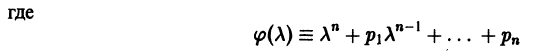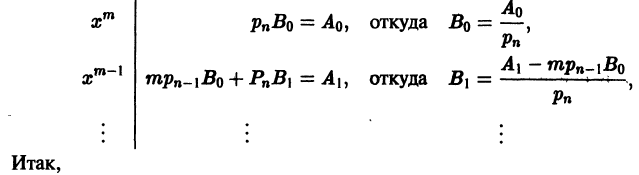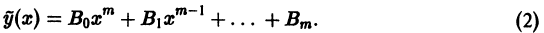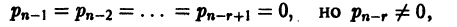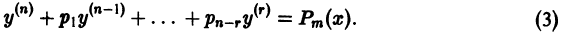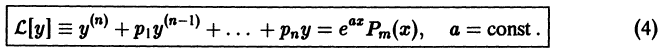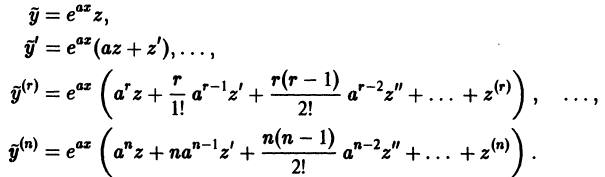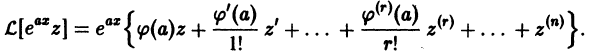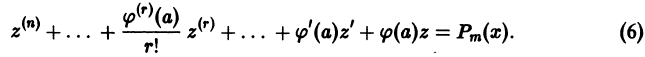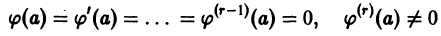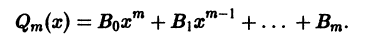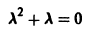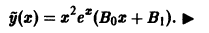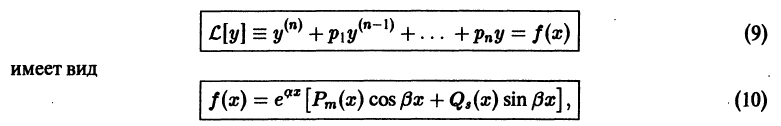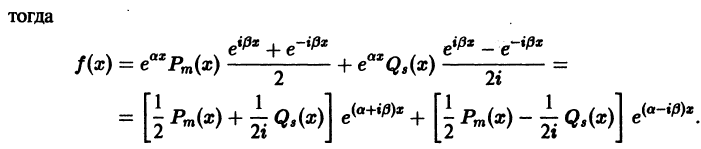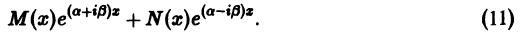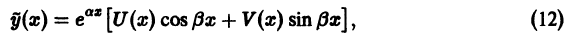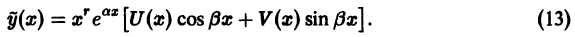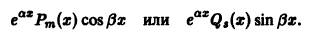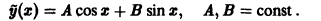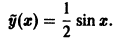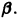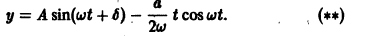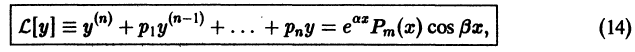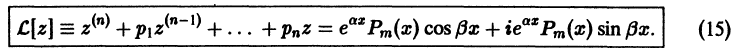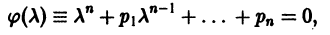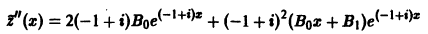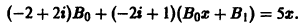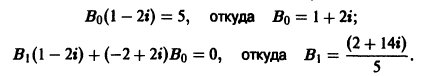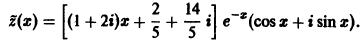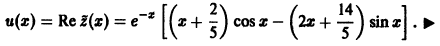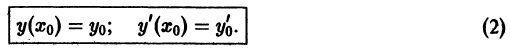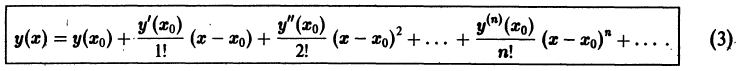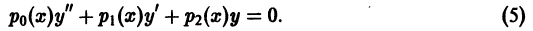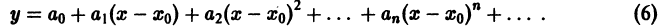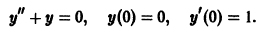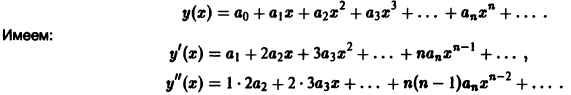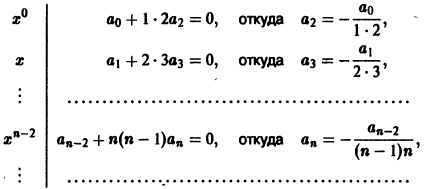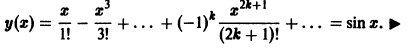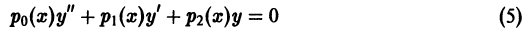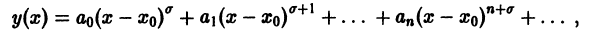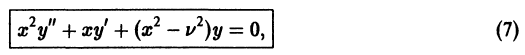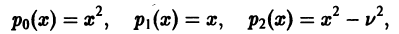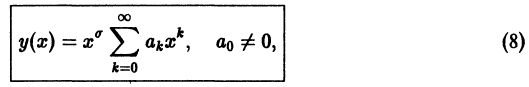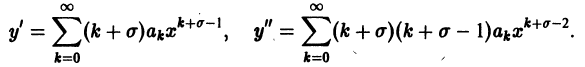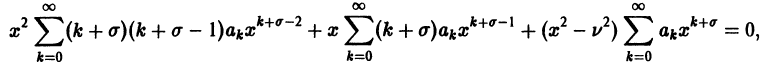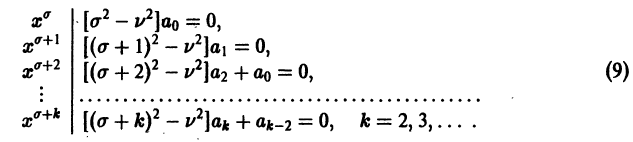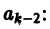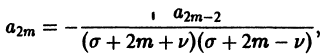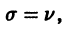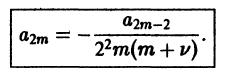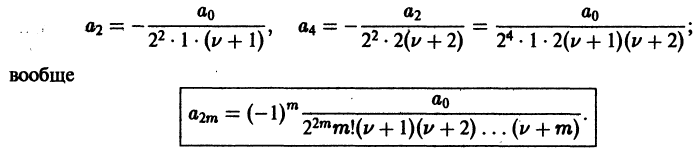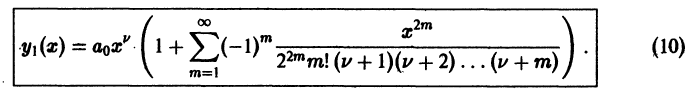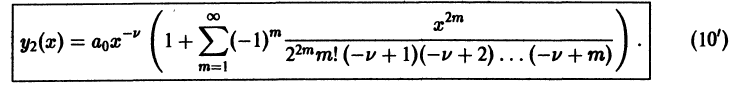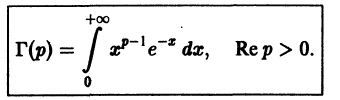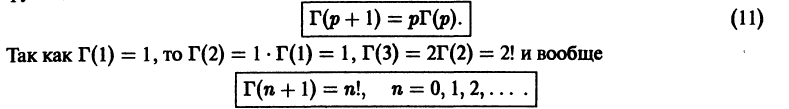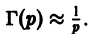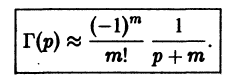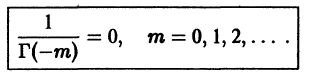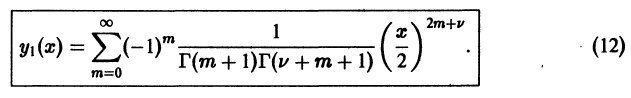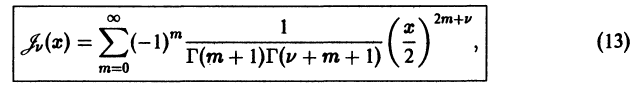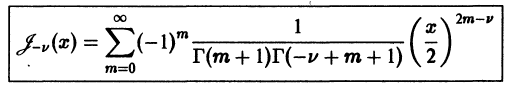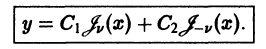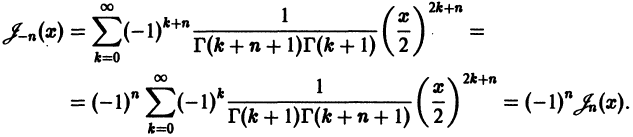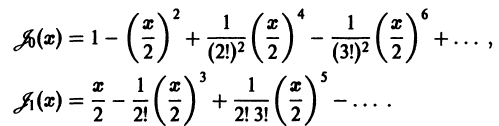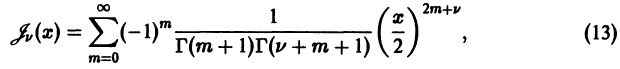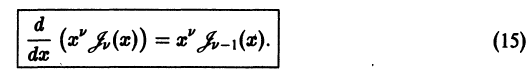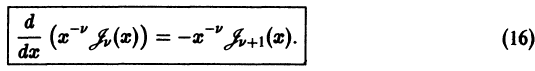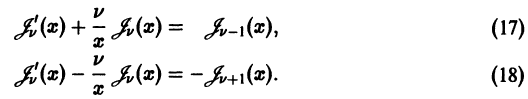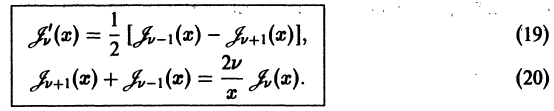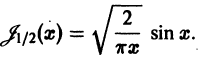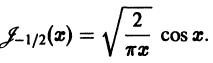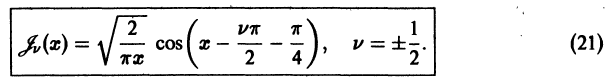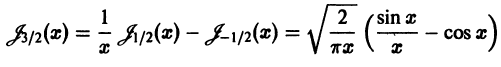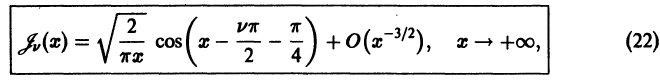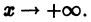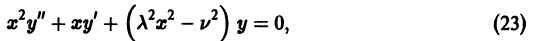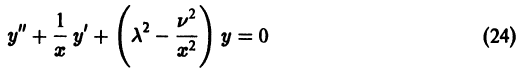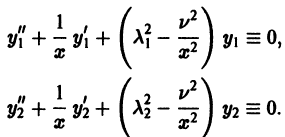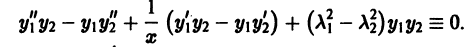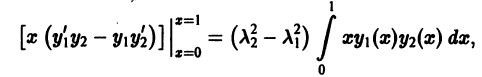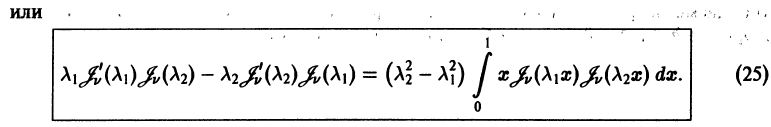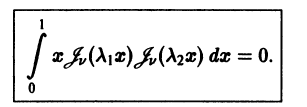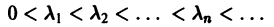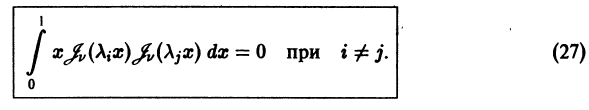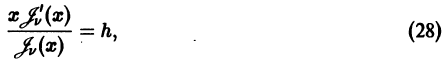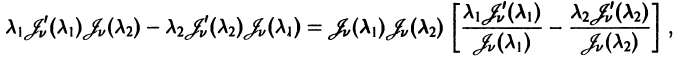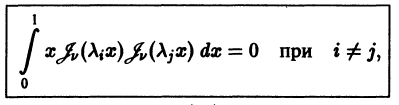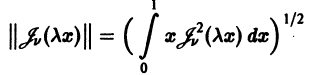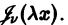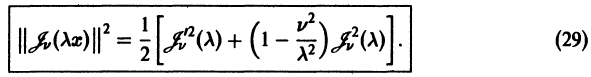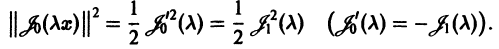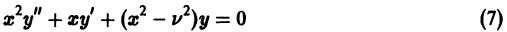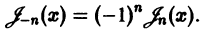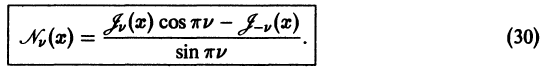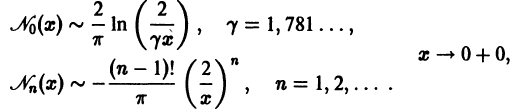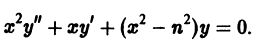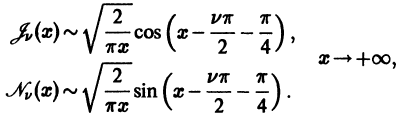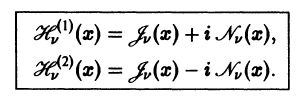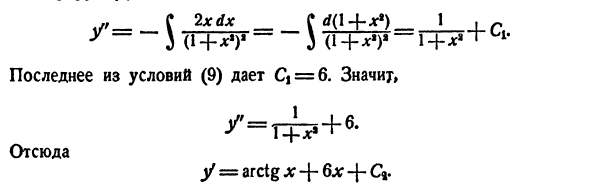Определение.
Начальные
условия
для дифференциального уравнения
-го
порядка — это набор чисел
,
(2)
задающий
для фиксированного значения независимой
переменной
значения неизвестной функции
и ее производных вплоть до порядка, на
единицу меньшего порядка уравнения:
.
Определение.
Задачей
Коши
для дифференциального уравнения
называется задача отыскания решения
,
отвечающего заданным начальным условиям.
Геометрический
смысл задачи Коши для дифференциального
уравнения 1-го порядка
Для
дифференциального уравнения 1-го порядка
(при
)
начальные условия (2) имеют вид пары
чисел.
Тем самым ставится задача отыскания
решения,
для которого.
Геометрически это означает выбор из
совокупности интегральных кривых той,
которая проходит через заданную точку
плоскости(рис. 1).
Рис. 1
Геометрический
смысл задачи Коши для дифференциального
уравнения 2-го порядка
Для
дифференциального уравнения 2-го порядка
(при
)
начальные условия (2) имеют вид тройки
чисел,
и ставится задача отыскания решения,
для которогои
.
Геометрически это означает выбор из
совокупности интегральных кривых той,
которая, во-первых, проходит через
заданную точку плоскости,
и, во-вторых, имеет в этой точке заданный
угловой коэффициент касательной(рис. 2).
М0
Рис. 2
3. Общее решение и общий интеграл
Начальные
условия
,
будучи набором из
чисел, задают точку пространства
.
Множество всех рассматриваемых вариантов
начальных условий образует некоторую
область.
Для
различных видов ограничений на функцию
и на область
имеет место существование и единственность
решения задачи Коши для начальных
условий из.
Приведем примеры соответствующих
теорем.
I.
Пусть уравнение 1-го порядка является
разрешённым относительно производной
:
.
Теорема 1. Если
функция
и ее частная производная
непрерывны в области
плоскости
,
то решение задачи Коши для любых начальных
условийсуществует и единственно в некоторой
окрестности точки.
II.
Пусть
уравнение -го
порядка является разрешённым относительно
старшей производной
:
.
Теорема 2. Если
функция
и ее частные производные
непрерывны в области
-мерного
пространства,
то решение задачи Коши для любых начальных
условийсуществует и единственно в некоторой
окрестности точки.
В дальнейшем будем
предполагать, что дифференциальные
уравнения рассматриваются в области
существования и единственности решения.
Определение.
Общим решением
дифференциального уравнения -го
порядка называется функция
,
зависящая от аргументаи от
произвольных постоянных
,
которая удовлетворяет двум условиям:
1) при любых значениях
произвольных постоянных эта функция
является решением;
2) за счет выбора
значений произвольных постоянных можно
получить решение задачи Коши для любых
начальных условий из области существования
и единственности решения.
Заметим, что
количество
произвольных постоянных равно порядку
уравнения.
Определение.
Частным
решением
дифференциального уравнения называется
функция, которая получается из общего
решения, если произвольным постоянным
придать определенные значения.
Напомним определение
неявной функции: функция
в окрестности
точки
,задана неявно
уравнением
,
если при всехиз этой окрестности справедливо равенство
.
Обычное, «явное»
задание функции можно рассматривать
как частный случай неявного:
;
здесь.
Определение.
Общим
интегралом
дифференциального уравнения -го
порядка называется уравнение
,
(3)
зависящее от
произвольных постоянных
,
которое задает общее решениекак неявную функцию.
Определение.
Частным
интегралом
называется уравнение, которое получается
из общего интеграла (3), если произвольным
постоянным придать определенные
значения.
Замечание.
В тех случаях, когда удается найти
решение дифференциального уравнения,
оно имеет, как правило, вид общего
интеграла (3). Если при этом можно
явно выразить через
(«разрешить уравнение относительно
»),
то приходим к общему решению.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Принцип и понятие
Под задачей Коши для дифференциального уравнения понимают выражение вида: y’ = f (x, y) с начальным условием, соответствующим равенству: y (x0) = y0. По сути, это обозначает, что необходимо найти такое решение уравнения, которое проходит через заданную точку игрек и икс нулевое. Решением задачи называется функция, заданная на указанном интервале в окрестности точки икс нулевое, то есть: x Є (x0 — q, x0 + q).
Для проведения анализа функции должны выполняться следующие критерии:
- y (x0) = y0;
- y’ = f (x, y (x));
- V x Є (x0 — q, x0 + q).
Следует отметить, что решение Коши включает в себя и сам интервал икс нулевое плюс минус кью, фактически q-окрестность. Это обозначает, что одна и та же функция, задаваемая одной формулой, но рассматриваемая на разных интервалах, представляет два разных нахождения задачи Коши. Отсюда возникает вопрос, при каких же ответах существует решение Коши, а также когда оно будет единственным.
Существует теорема, гарантирующая единственность какого-то решения задачи. На самом деле возможность аналитического подхода Коши требует лишь главного условия, при котором функция f будет непрерывной в какой-то окрестности точки x0, y0. Но для доказательства единственности этого недостаточно. Для нормального случая необходимо следующее:
- Функция f (x, y) непрерывна в некоторой окрестности точки (x0, y0).
- Существует такая константа C, что для любых точек икс и игрек выполняется неравенство: |f (x, y) — f (x2, y2)| ⩽ C |y1 — y2|.
По игреку функция должна иметь обыкновенный рост, то есть не убыстряющийся (локальный подъём не превышать линейный). Если эти два условия выполняются, то решение Коши существует и оно будет единственным. Это значит, что тогда у точки икс нулевое найдётся такая окрестность, в которой существует решение и к тому же оно будет единственным.
А это обозначает, что любая другая функция в этой окрестности, удовлетворяющая уравнениям начальных условий, совпадает с той, существование которой утверждается. При этом на практике проверка условия на самом деле вещь не очень сложная, особенно если функция f (y) имеет в окрестности ограниченную производную.
Алгоритм нахождения
Пусть имеется функция у’ = 2 * √ |y| и условие что y (0) = 0. Необходимо её исследовать. Тут можно заметить, что в этом случае функция зависит только от игрека и условию не удовлетворяет. В окрестностях точки с координатами (0, 0) она не удовлетворяет условию, так как любая окрестность захватывает ноль, а у корня квадратного по игреку будет бесконечная производная.
Это приводит не к единственности получения результатов. Так, у уравнения есть два решения: y1 тождественный нулю; y2 равняется x2. Согласно условию, игрек стоит по модулю, точнее, можно сказать, что для отрицательных значений икс будет меньше ноля, а положительных — больше.
Главный же вопрос заключается в продолжаемости анализа. Доказывается возможность простым построением решения с использованием специальных условий. В итоге должна быть найдена окрестность в точке x0. То есть берётся уравнение и точка с начальными координатами, затем выясняется, что в окрестности выполнены условия теоремы и строится решение.
Затем исследуется другая точка и изучается структура её окрестности. Например, обнаруживается, что условия существования единственности выполняются. Согласно теореме, тогда можно будет строить решение, где в качестве начальной точки будет взята любая координата. Другими словами, получается более широкое решение. Поэтому возникает вопрос, насколько можно приблизить точность ответа. Практические примеры показывают, что иногда можно двигаться до бесконечности, а в некоторых случаях сделать не более трёх шагов.
Если есть два уравнения y’ = f (x, y); y (x0) = y0 имеющие два решения: y1 (x), x Є I1 (эX), y2 (x), x єI2 (єX0). Тогда можно утверждать, что игрек два будет продолжением решения y1 (x) если в I2 входит I1, а y2 (x) равняется y1 (x) для любого икс из интервала I1. Следует учесть, что в этом определении в качестве областей функции всегда рассматривается интервал.
В изучении исследуются и матричные функциональные системы, состоящие из нескольких переменных A (z 1, z 2, …, zn). При этом z являются вещественными, а элементы матрицы могут быть как вещественными, так и комплексными. Исходя из этого даётся определение того, что функция, описываемая матрицей, непрерывна тогда, когда все элементы непрерывны в точке или на некотором множестве.
При определении используют численные и векторные функции от аргумента: y = (x), где y — это столбец от набора игреков, а икс со штрихом — от набора иксов. Таким образом, обобщённым решением будет такое действие, которое не будет иметь нетривиального продолжения, то есть вторые интервалы содержать первые.
Примеры задач
На практических занятиях по высшей математике студентам предлагается для понимания курса выполнить ряд практических заданий. Существует типовой набор задач, научившись решать которые учащийся досконально разберётся в теме. Вот некоторые из них.
Первый пример. Имеется уравнение y’ = (2y / x lnx) + 1/x, для которого установлено начальное условие y (e) = 0. Необходимо найти решение, проходящее через точку e. Перед тем как приступить непосредственно к решению, необходимо отметить, что функция f (x, y) определённа всюду, за исключением прямых x = 0 и x = 1. Отсюда следует, что краевое решение не может быть вычислено на интервале от нуля до единицы.
В этом примере должен содержаться интервал, имеющий координату точки e по иксу. Он не может включать значения меньше единицы, так как необходимо, чтобы выполнялось заданное условием уравнение, которое в точке x = 1 теряет смысл, ведь в ней функция неопределённа. Установив это, можно переходить к анализу уравнения.
Заданное равенство является линейным — неоднородным уравнением первого порядка. Для решения нужно сначала рассмотреть левое соотношение: y’ = 2y / x * lnx. Добавив константу, уравнение можно переписать как y = c * e. Теперь необходимо взять интеграл исходя из первообразной формулы: ∫ 2 dx / (x *lnx).
После того как будет найдена постоянная, через общий интегральный метод с учётом условия определения функции, уравнение в окрестности точки e будет иметь решение вида: y = ln2x — lnx. Из полученного выражения можно сделать вывод, что функция будет определена для всех положительных иксов, но рассматривать её необходимо от единицы до плюс бесконечности. Это и будет максимальное непродолжаемое решение задачи: xЄ (1, + ∞).
Второй пример. Пусть имеется функция y’ = y / (1+x2) с начальным условием: y = y (0). В задании нужно будет рассмотреть дифференциальную кривую уравнения, проходящего через точку y0. Нужно заметить, что функция f (x, y) в любой ограниченной области двумерной плоскости удовлетворяет условию регулярности для теоремы существования единственности. В задаче спрашивается, каким должен быть y0, если предел максимального решения при иксе, стремящемся к плюс бесконечности, равняется единице.
Учитывая, что в этой постановке заложено, чтобы решение было определённо до плюс бесконечности и то, что уравнение является однородно линейным, по общей формуле особое решение будет иметь вид: y = c * earctgx. Игрек нулевое не может равняться нулю, ведь в ином случае решением уравнения будет тождественный ноль и заданное условие выполняться не будет. В итоге получится, что y = y0 * earctgx. Это решение и является подходящей функцией для любого интервала.
Операционный метод
Решение задачи Коши (примеров) целесообразно выполнять экономичным методом интегрирования линейных выражений, содержащих постоянные коэффициенты. Суть способа сводится к решению алгебраических равенств или неравенств. Алгоритм исследования заключается в следующих действиях:
- Функции Y (p) и F (p) обозначают как изображения для y (x) и f (x).
- Используя главные преобразования Лапласа, обрабатывая изображения, получают (pn (Yp) — pn -1 y 0 — …- yn -1) + a 1 (pn -1 y (p) — pn -2 y 0 — … — yn -2) + … + anY (p) = F (p) или, A (p)Y (p)+B (p) = F (p), причём A (p) и B (p) являются многочленами.
- Найденное решение y (p) = (F (p) — B (p)) / A (p) и будет искомым y (x) для искомого y (p).
Например, пусть необходимо решить уравнение вида: x» + 4x = sin (2t), при x (0) = 1, x'(0) = -2. Классическим методом находить ответ довольно трудоёмко, поэтому имеет смысл для заданного уравнения использовать операционное исчисление. Для начала следует ввести замену Lx = x. Затем к обеим частям равенства применить преобразование Лапласа: Lx » + L 4 x = L * sin (2 t). Отсюда: Lx = x, Lx » = p 2 x — px (0) — x'(0). Функция Лапласа используется для преобразования вещественной переменной в выражение с комплексной переменной и наоборот. Это и позволяет использовать её при решениях дифференциальных уравнений и систем.
На следующем этапе нужно подставить исходные данные в равенство: Lx» = p2x — p + 2. Далее, следует выполнить преобразование и выразить неизвестную функцию. В итоге должно получиться выражение: X = (p 3 — 2 p 2 — 4 p — 6) / (p 2 + 4)2. Теперь можно найти оригинал изображений: x = L-1 {(p3 — 2p2 + 4p — 6) / (p2+4)2)} = cos (2t) — sin (2t) + (sin (2t) — 2tcos (2t))/8.
Использование онлайн-калькулятора
Часто решение задач по рассматриваемой теме связано с большими трудозатратами. Это касается времени и повышенного внимания. На практике не всегда получается правильно применить алгоритм и избежать ошибок. Поэтому имеет смысл для сложных заданий использовать онлайн-калькулятор. Решения на задачу Коши с его помощью доступны любому заинтересованному, имеющему доступ к интернету и устройство, поддерживающее работу веб-обозревателя.
В интернете существует довольно большое количество различных математических онлайн-решителей. В своём большинстве они бесплатны и ориентированы на работу даже с людьми, совершенно не разбирающимися в тематике. Поэтому они привлекательны не только как инструмент, предоставляющий быстрый и правильный ответ на поставленную задачу, но и как обучающие программы.
Всё дело в том, что на страницах сервисов, предлагающих такого рода услуги, содержится вся необходимая теоретическая информация. Кроме этого, они предлагают к рассмотрению типовые примеры с подробным объяснением решения. Из онлайн-калькуляторов, предоставляющих бесплатный доступ к своим услугам в русском сегменте интернета, можно отметить следующие:
- Math.semestr.
- Allcalc.
- Kontrolnaya-rabota.
- Matematikam.
- Primat.
Приведённые сервисы помогают без труда найти студентам решение дифференциального уравнения с заданными начальными условиями. Для этого в предлагаемую форму необходимо записать дифуравнение и через запятую начальные данные. Затем просто нажать интерактивную кнопку «Решить» и через некоторое время на экране дисплея отобразится ответ.
Для правильной записи уравнения существуют подсказки, так что разобраться, как работает сайт, сможет пользователь даже со слабой компьютерной подготовкой. Кроме этого, некоторые сервисы предлагают не просто ответ, а и пошаговое решение, к которому даётся комментарий. Решив несколько заданий, учащийся сможет разобраться в алгоритме и вычислять уравнения уже самостоятельно.
Следует отметить, что предложенные сервисы могут находить ответ для любой сложности математической задачи, например, вычисляя устойчивость математических моделей. Они также востребованы в инженерии и научных исследованиях, связанных с анализом функций. Для таких расчётов важны точность и время, что вполне могут обеспечить математические онлайн-сервисы.
Начальные условия для дифференциального уравнения задача коши теорема коши
Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах…
Часть II. Глава IV. Обыкновенные дифференциальные уравнения
§ 1. Дифференциальные уравнения первого порядка
1. Основные понятия. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции. Если независимая переменная одна, то уравнение называется обыкновенным; если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.
Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Например:
1) х²у’ + 5xy = у² – обыкновенное дифференциальное уравнение первого порядка;
2) – обыкновенное дифференциальное уравнение второго порядка;
3) y’³ + y»y»’ = х – обыкновенное дифференциальное уравнение третьего порядка;
4) F (х, у, у’, у») = 0 – общий вид обыкновенного дифференциального уравнения второго порядка;
5) – уравнение в частных производных первого порядка.
В этом параграфе рассматриваются обыкновенные дифференциальные уравнения первого порядка, т. е. уравнения вида F (х, у, у’) = 0 или (в разрешенном относительно у’ виде) y’ = f(х, у).
Решением дифференциального уравнения называется такая дифференцируемая функция у = φ (x), которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.
Общим решением дифференциального уравнения первого порядка у’ = f(x, у) в области D называется функция у = φ(x, C), обладающая следующими свойствами: 1) она является решением данного уравнения при любых значениях произвольной постоянной С, принадлежащих некоторому множеству; 2) для любого начального условия у(х0) = у0 такого, что (x0; y0) ∈ 0, существует единственное значение С = С0, при котором решение у = φ(x, C0) удовлетворяет заданному начальному условию.
Всякое решение у = φ(x, C0), получающееся из общего решения у = φ (x, C) при конкретном значении С = С0, называется частным решением.
Задача, в которой требуется найти частное решение уравнения y’ = f(х, у) удовлетворяющее начальному условию у(х0) = y0, называется задачей Коши.
Построенный на плоскости хОу график всякого решения у = φ(х) дифференциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению у = φ(х, С) на плоскости хОу соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной С, а частному решению, удовлетворяющему начальному условию y(x0) = y0, – кривая этого семейства, проходящая через заданную точку М0(x0; у0).
Если функция f(х, у) непрерывна и имеет непрерывную производную в области D, то решение дифференциального уравнения у’= f (х, у) при начальном условии у(х0) = у0 существует и единственно, т. е. через точку (x0; y0) проходит единственная интегральная кривая данного уравнения (теорема Коши).
Особым решением называется такое решение, во всех точках которого условие единственности не выполняется, т. е. в любой окрестности каждой точки (х; у) особого решения существуют по крайней мере две интегральные кривые, проходящие через эту точку.
Особые решения не получаются из общего решения дифференциального управления ни при каких значениях произвольной постоянной С (в том числе и при С = ± ∞).
Особым решением является огибающая семейства интегральных кривых (если она существует), т. е. линия, которая в каждой своей точке касается по меньшей мере одной интегральной кривой.
Например, общее решение уравнения записывается в виде у = sin (х + С). Это семейство интегральных кривых имеет две огибающие: у = 1 и у = -1, которые и будут особыми решениями.
2. Дифференциальные уравнения с разделяющимися переменными. Дифференциальное уравнение вида
относится к типу уравнений с разделяющимися переменными. Если ни одна из функций f1(x), f2(y), φ1(x), φ2(y) не равна тождественно нулю, то в результате деления исходного уравнения на f2 (x) φ1 (y) оно приводится к виду
Почленное интегрирование последнего уравнения приводит к соотношению
которое и определяет (в неявной форме) решение исходного уравнения. (Решение дифференциального уравнения, выраженное в неявной форме, называют интегралом этого уравнения.)
507. Решить уравнение х(у²-4)dx + y dy = 0.
△ Разделив обе части уравнения на у² – 4 ≠ 0, имеем
x² + ln|у² – 4| = ln|C|, или у² – 4 = Сe -λ²
Это общее решение данного дифференциального уравнения.
Пусть теперь у² – 4 = 0, т. е. у = ± 2. Непосредственной подстановкой убеждаемся, что у = ±2 – решение исходного уравнения. Но оно не будет особым решением, так как его можно получить из общего решения при С = 0. ▲
508. Найти частный интеграл уравнения у’ cos х = у / ln у, удовлетворяющий начальному условию y(0) = l.
△ Полагая , перепишем данное уравнение в виде
Проинтегрируем обе части уравнения:
, или
Используя начальное условие у = 1 при х = 0, находим С = 0. Окончательно получаем
▲
509. Найти общий интеграл уравнения у’ = tg x tg y.
△ Полагая и разделяя переменные, приходим к уравнению ctg у dy = tg х dx. Интегрируя, имеем
, или ln|sin у| = -ln|cos x| + ln С.
Отсюда находим sin y = C/cos x, или sin y / cos x = С (общий интеграл). ▲
510. Найти частное решение дифференциального уравнения (l + x²)dy + y dx = 0 при начальном условии у(1) = 1.
△ Преобразуем данное уравнение к виду . Интегрируя, получим
, или ln |y| = – arctg x + С
Это и есть общий интеграл данного уравнения.
Теперь, используя начальное условие, найдем произвольную постоянную С; имеем ln 1 = — arctg 1 + С, т. е. С = π/4. Следовательно,
ln у = – arctg х + π/4,
откуда получаем искомое частное решение y = e π/4 – arctg x . ▲
Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах… Ч. II. Стр. 117-119.
Задача Коши онлайн
Данная задача возникает при поиске частного решения дифференциального уравнения. Наш онлайн калькулятор, построенные на основе системы Wolfram Alpha, позволяет найти решение задачи Коши для различных типов дифференциальных уравнений. Чтобы начать работу, необходимо ввести данные своей задачи (дифференциальное уравнение и начальные условия) в калькулятор.
Найти решение задачи Коши для дифференциального уравнения:
при заданных начальных условиях:
При постановке задачи Коши, указываются так называемые начальные условия, позволяющие однозначно выделить искомое частное решение из общего. Эти условия включают в себя значения функции и всех её производных до включительно (где -порядок дифференциального уравнения), заданные в одной и той же точке .
Поясним вышесказанное на конкретном примере. Пусть нам требуется найти частное решение дифференциального уравнения:
удовлетворяющее начальным условиям:
Первым делом, используя различные методы (Бернули, вариации произвольной постоянной Лагранжа), сначала находим общее решение данного дифференциального уравнения:
Теперь, для поиска частного решения, нам необходимо использовать заданные начальные условия. Для этого, находим производную функции полученной ранее:
Далее, поставляем начальные условия в функцию и её производную :
Решая полученную систему уравнений получаем значения произвольных постоянных и :
Подставляем полученные результаты в общее решение дифференциального уравнения, в результате получаем искомое частное решение:
Другие полезные разделы:
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
Решение задачи Коши
Содержание:
Задача Коши. Одной из важнейших задач в теории дифференциальных уравнений является так называемая задача Коши. Для уравнения (2),

в котором функция у(х) принимает заданное числовое значение Уо при заданное числовом значении х0 независимой переменной х, т. е.








По этой ссылке вы найдёте полный курс лекций по высшей математике:
Задачу Коши геометрически можно сформулировать так: среди всех интегральных кривых уравнения (2)’найти tj (рис. 6), которая проходит через заданную точку
Будем говорить, что задача Коши с начальными условиями (38) имеет единственное решение, если существует та кое число 




отличной от точки 

Возможно вам будут полезны данные страницы:
Вопрос о единственности решения задачи Коши представляет исключительный интерес как для самой теории дифференциальных уравнений, так и для ее многочисленных приложений, ибо, зная, что решение задачи Коши единственно, мы, найдя решение, удовлетворяющее заданным начальным условиям, уверены, что других решений, удовлетворяющих тем же начальным условиям, нет.
В вопросах естествознания эго приводит к тому, что мы получаем вполне определенный, единственный закон явления, определяемый только дифференциальным уравнением и начальным условием. Иллюстрацией сказанного может служить хотя бы пример 1, рассмотренный во введении.
Заметим, что в простейшем случае задача Коши встречается нам уже в интегральном исчислении, именно там, по существу, доказывается, что если функция f(x) непрерывна в интервале (а, Ь),то единственным решением уравнения




Из формулы (40) легко усмотреть характер зависимости решения рассматриваемой задачи Коши как от независимой переменной, так и от начальных данных.
Прежде всего из курса анализа известно, что решение (40) является непрерывно дифференцируемой** функцией от независимой переменной х. Геометрически это означает, что через точку 
Из формулы (40) видно также, что решение задачи К о ш и дл я простейшего дифференциального уравнения (39) я в-ляется непрерывной и даже непрерывно дифференцируемой функцией начальных данных
Особые случаи задачи Коши. При постановке задачи Коши с начальными данными 








Совсем другое положение мы будем иметь, если в точке 



В этом случае задача Коши ставится так:
найти решение вида 


Здесь, так же как и в основном случае задачи Коши, возникают вопросы существования и единственности решения.
Кроме того, здесь возникают и дополнительные вопросы:
1) имеют ли решения, примыкающие к точке 

2) если интегральные кривые примыкают к точке 


В некоторых случаях возникает необходимость искать решения 
Указанные выше особые случаи задачи Коши исследуются в аналитической теории дифференциальных уравнений и в качественной теории дифференциальных уравнений. Во всех случаях задачи Коши наряду с вопросами существования и единственности возникают /вопросы о свойствах решения задачи Коши как функции независимой переменной (аналитический вид, дифференциальные и геометрические свойства и особенности «поведения во всей области существования) и как функции начальных данных. Рассмотрение этих вопросов составляет одну из основных задач теории дифференциальных уравнений.
Достаточное условие существования решения задачи Коши
Предположим, что правая часть уравнения (2) определена и непрерывна в некоторой области G изменения х и у. Тогда, как уже отмечалось раньше (п. 4), уравнение (2) определяет некоторое поле направлений, причем в силу только что сделанного предположения о непрерывности правой части уравнения (2) это ноле направлений непрерывно, так что направления в двух достаточно близких точках разнятся сколь угодно мало. Заметим, что из сделанного предположения о непрерывности
правой части уравнения (2) следует, что всякое решение этого уравнения (если оно существует) будет непрерывно дифференцируемым, так что всякая интегральная кривая будет гладкой. Всякая интегральная кривая, как уже было сказано в п. 4., обладает чем свойством, что в каждой ее точке направление карательной совпадает с направлением поля, определяемым дифференциальным уравнением в этой точке. Попытаемся, пользуясь этим свойством интегральной кривой, найти решение задачи Коши для уравнения (2) с начальными данными 
Возьмем п области G некоторую точку 



На этой прямой возьмем любую точку 




Ясно, что можно построить бесчисленное множество ломаных Эйлера, проходящих через точку 

Можно доказать*, что при сделанном предположении относительно f(x, у) это действительно имеет место, так что для существования непрерывно дифференцируемого решения задачи Коши для уравнения (2) достаточно предположить, что его правая часть непрерывна в окрестности начальных данных (теорема Пеано).
Заметим, однако, что нс исключена возможность существования нескольких последовательностей ломаных Эйлера, проходящих через точку 

Таким образом, теорема Пеано есть только теорема существования решения задачи Коши. Единственности решения она не гарантирует.
Достаточные условия существования и единственности решения задачи Коши
Поставим вопрос: каким условиям достаточно подчинить правую часть уравнения (2) в окрестности начальных данных 

Теорема. Пусть дано уравнение (2),

Предположим, что функция 
с точкой 
У 1. Функция 

II. Функция f(x, у) имеет ограничейную частную производную по аргументу у, т. е.:
где К — постоянное положительное число, а (х, у)—любая точка области R.
При этих предположениях уравнение (2) имеет единственное решение (36),
удовлетворяющее начальному условию (38). Это решение определено и непрерывно дифференцируемо в некоторой окрестности начального значения х0 независимой переменной х, а именно оно заведомо определено в интервале
где h есть наименьшее из чисел


Примеры с решением
Пример 1.
Пусть дано уравнение
и поставлено начальное условие:
Так как правая часть уравнения (45) есть полином относительно х и у, то решение с любыми начальными условиями, в том числе и с начальным условием (46), существует и единственно.
Оценим область определения решения с начальным условием (46).
С этой целью построим прямоугольник R с центром в точке (0, 0),
причем в качестве а и b можно взять любые положительные числа. Будем иметь:
Отсюда видно, что h зависит от выбора чисел а к &*. В частности, при а = b — 1, получим:
Поэтому уравнение (45) имеет единственное решение, заведомо определенное в интервале 
С геометрической точки зрения полученный результат означает, что уравнение (45) имеет только одну интегральную кривую, проходящую через начало координат, причем эта интегральная кривая гладкая.
Этот результат приобретает особое значение, если принять во внимание, что уравнение (45) не интегрируется пи в элементарных функциях, пи в квадратурах от элементарных функций, в чем мы убедимся в п. 51. Установленный факт существования и единственноеги решения дает нам основание пытаться искать его другими методами и в том числе находить это решение приближенно.
Пример 2.
Найти решение уравнения
удовлетворяющее начальному условию:
Так как правая часть уравнения (50) вместе с ее частной производной по 
* Наибольшим значением h будет
Вообще, если в уравнении (2) функция f(x, у) удовлетворяет обоим условиям теоремы Пикара в некоторой окрестности заданной точки (х0, у0) и такова, что 

Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://mathforyou.net/online/calculus/cauchy/
http://natalibrilenova.ru/reshenie-zadachi-koshi/
Дано неоднородное ДУ второго порядка с постоянными коэффициентами. Общее решение которого будет иметь вид $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$. Для начала находим общее решение однородного уравнения $y_{o.o.}$, затем частное решение неоднородного уравнения $y_text{ч.н.}$ с помощью метода подбора правой части уравнения.
На первом этапе решаем уравнение в качестве однородного без правой части, то есть меняем её на ноль. Заменяем все $y$ на новую переменную $lambda$, показатель степени которой будет равен порядку производной. $$y»-y=0,$$ $$lambda^2 — 1 = 0,$$ $$(lambda-1)(lambda+1)=0,$$ $$lambda_1 = -1, lambda_2 = 1.$$ Теперь можно записать общее решение однородного ДУ. $$y_text{о.о.} = C_1e^{lambda x}+C_2e^{-lambda x} = C_1e^{x}+C_2e^{-x}$$
Переходим к получению $y_text{ч.н.}$. Смотрим на правую часть уравнения, данного в условии задачи. В неё входят синус и косинус, умноженные на многочлены нулевой степени. Значит, частное решение ищем в виде $y_text{ч.н.} = Asin x — Bcos x$. Находим вторую производную данного выражения. $$y’ = Acos x + Bsin x,$$ $$y»=-Asin x + Bcos x.$$ Подставляем $y$ и $y»$ в исходное уравнение из условия задачи, чтобы найти неизвестные коэффициенты $A$ и $B$. $$-Asin x + Bcos x — Asin x + Bcos x = 2sin x — 4cos x$$ После приведения подобных получаем $$-2Asin x + 2Bcos x = 2sin x — 4cos x.$$ Далее составляем систему из двух уравнений благодаря коэффициентам перед синусом и косинусом левой и правой части уравнения. $$begin{cases} -2A = 2 \ 2B = -4 end{cases} Leftrightarrow begin{cases} A = -1 \ B = -2 end{cases}$$ Благодаря полученным коэффициентам $A$ и $B$ записываем $$y_text{ч.н.} = -sin x + 2cos x$$
Итак, общее решение неоднородного дифференциального уравнения в итоге будет иметь вид $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.} = C_1e^{x}+C_2e^{-x} -sin x + 2cos x.$$
Так как требуется найти решение задачи Коши, то ход действий на этом не закончен. Переходим к вычислению коэффициентов $C_1$ и $C_2$.
Берём первую производную $y’ = C_1e^x — C_2e^{-x} — cos x — 2sin x$.
Теперь можно составить систему уравнений $$begin{cases} y'(0)=0 \ y(0) = 0 end{cases} Leftrightarrow begin{cases} C_1 — C_2 — 1 = 0 \ C_1 + C_2 + 2 = 0 end{cases}.$$ Решаем систему уравнений. $$begin{cases} C_1 = C_2 + 1 \ C_2 + 1 + C_2 + 2 = 0 end{cases} Leftrightarrow begin{cases} C_1 = C_2 + 1 \ C_2 = -frac{3}{2} end{cases} Leftrightarrow begin{cases} C_1 = -frac{1}{2} \ C_2 = -frac{3}{2} end{cases}.$$
Теперь подставляя полученные константы в общее решение дифференциального уравнения записываем решение задачи Коши в окончательном виде $$y = -frac{1}{2}e^x — frac{3}{2}e^{-x} -sin x + 2cos x.$$
Дифференциальным уравнением порядка n называется уравнение вида 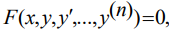
Задача Коши
Пусть имеем дифференциальное уравнение n-го порядка, разрешенное относительно старшей производной
Возникает вопрос: какие надо задать условия, чтобы выделить определенное, частное решение уравнения (1)? Для дифференциального уравнения первого порядка
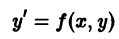
достаточно задать значение у0 частного решения при каком-то значении х0 независимой переменной х, т.е. задать точку 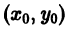
имеет решениями функции
где 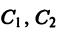
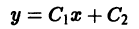
определяет двухпараметрическое семейство прямых на плоскости хОу, и, чтобы выделить определенную прямую, мало задать точку 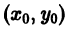
В общем случае дифференциального уравнения n-го порядка (1) для выделения частного решения надо задать n условий:
где 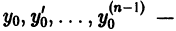
Сформулируем теорему существования и единственности решения задачи Коши.
Теорема:
Существования и единственности решения задачи Коши.
Пусть имеем дифференциальное уравнение n-го порядка, разрешенное относительно старшей производной,
Если правая часть этого уравнения непрерывна как функция n + 1 аргументов 
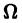
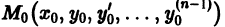
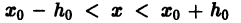
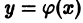
Если, кроме того, функция 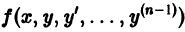
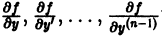
Так, для уравнения
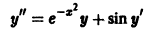
правая часть
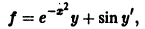
рассматриваемая как функция трех независимых переменных х, у, у’, непрерывна всюду и имеет ограниченные всюду производные
Поэтому, какова бы ни была тройка чисел 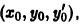
Определение:
Общим решением дифференциального уравнения n-го порядка
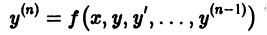
в некоторой области 
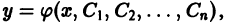
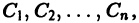
1) при любых допустимых значениях постоянных 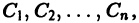
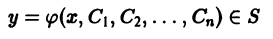
является решением дифференциального уравнения (1), т.е.
2) каковы бы ни были начальные условия
(лишь бы точка 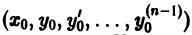
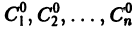
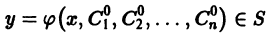
удовлетворяло заданным начальным условиям.
Решение, получаемое из общего при конкретных значениях постоянных 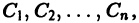
Соотношение 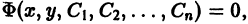
Задача:
Показать, что функция
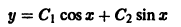
является общим решением уравнения
Уравнения высших порядков, допускающие понижение порядка
- Уравнение вида
где f(x) — известная непрерывная функция, интегрируется в квадратурах. Учитывая, что 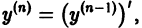
т. е. приходим к уравнению такого же вида, что и исходное; далее находим
Через n шагов получим общее решение уравнения (1):
Пример:
Найти общее решение уравнения
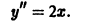
Последовательно интегрируя дважды, получаем искомое общее решение
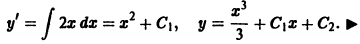
Бели уравнение не содержит искомой функции и ее производных до порядка к — 1 включительно, т. е. имеет вид
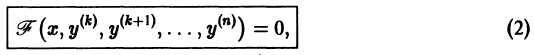
то порядок уравнения может быть снижен до порядка n — к заменой 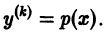
Пусть удалось проинтегрировать полученное уравнение:
Замечая, что 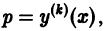
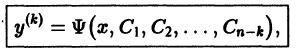
из которого у(х) находится k-кратным интегрированием.
Пример:
Найти общее решение уравнения
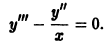
Положим 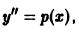
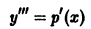
и данное уравнение примет вид
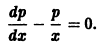
Разделяя переменные в последнем уравнении, найдем 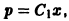
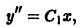
откуда легко получаем общее решение исходного уравнения:
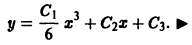
Пусть дифференциальное уравнение не содержит явно независимой переменной х, т. е. имеет вид
Порядок этого уравнения можно понизить на единицу подстановкой у’ = р(у), где р = р(у) рассматривается как новая неизвестная функция, а у принимается за независимую переменную. В этом случае все производные 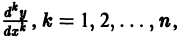
Мы видим, что любая производная 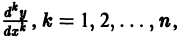
Пример:
Проинтегрировать уравнение
Положим у’ = р(у), тогда
и данное уравнение принимает вид
Сокращая на 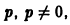
откуда
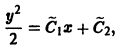
или
Случай р=0 дает решение
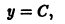
содержащееся в (**).
Всегда следует посмотреть, не является ли левая часть данного уравнения полным дифференциалом некоторого выражения. Так, уравнение (*) можно переписать в виде
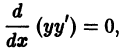
откуда находим:
Часто встречающееся уравнение
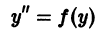
можно легко проинтефировать в квадратурах, если умножить обе его части на у’ (проделайте это!).
Замечание:
Рассмотрим уравнение второго порядка
линейное относительно искомой функции у(х) и ее производных у’ и у». Положим
где u(х), v(x) — новые функции, из которых одну мы можем выбирать произвольно. Подставляя у(х) в форме (5) в исходное уравнение (4), для функции u(х) получаем уравнение
Если известно одно решение 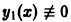
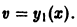
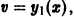
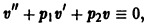
так как, по предположению, 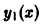
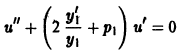
и легко интегрируется. В результате мы найдем общее решение исходного уравнения (4). Если положить
то в уравнении (6) исчезнет слагаемое с первой производной, и уравнение примет вид
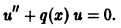
Такое преобразование полезно для качественного анализа уравнения и при использовании приближенных методов решения.
Рассмотрим, например, дифференциальное уравнение Бесселя
(его решения — функции Бесселя — играют важную роль во многих задачах физики); представим его в виде
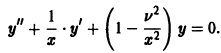
Здесь 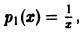
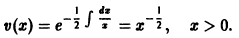
Полагая 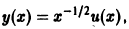
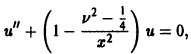
весьма удобное для изучения поведения функций Бесселя при больших значениях х.
Замечание:
При решении задачи Коши для уравнений высших порядков бывает целесообразно определять значения постоянных 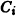
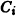
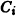
Рассмотрим, например, следующую задачу Коши:
Полагая у’ = р(у), получаем
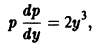
откуда 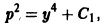
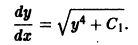
Разделяя переменные, найдем
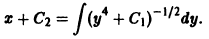
В правой части последнего равенства имеем интеграл от дифференциального бинома. Здесь m = 0, n = 4, 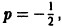
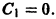
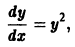
откуда, учитывая начальные условия, находим
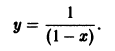
Задача:
Найти два решения задачи Коши для уравнения
с начальными условиями у(0) = у'(0) = 0. Не противоречит ли этот факт теореме существования и единственности решения задачи Коши?
Линейные однородные дифференциальные уравнения n-го порядка
Линейным дифференциальным уравнением п-го порядка называется уравнение, линейное относительно неизвестной функции и всех ее производных. Оно имеет вид
где 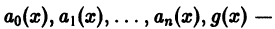
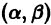
Пусть имеем линейное однородное дифференциальное уравнение
Если 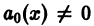
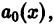
Если коэффициенты 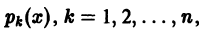
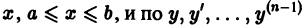
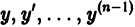
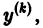
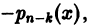
если коэффициенты 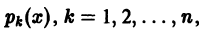
существует единственное решение уравнения (1), удовлетворяющее этим начальным условиям.
Напомним следующее понятие. Говорят, что на множестве Е задан оператор A со значениями в множестве F, если каждому элементу 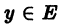
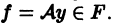
Пусть Е — линейное пространство. Оператор A, заданный на Е, называется линейным, если он аддитивен и однороден, т. е.
Представим линейное однородное уравнение (1) в виде
Нетрудно видеть, что 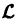
Имеем
Как следствие получаем
Установим некоторые свойства решений линейного однородного уравнения.
Теорема:
Если функция 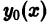
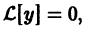
то функция 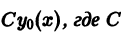
По условию,
Надо доказать, что
Пользуясь свойством однородности оператора 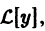
Это означает, что функция 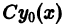
Теорема:
Если функции 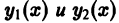
то сумма функций 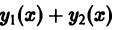
По условию, 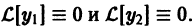
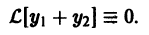
Последнее сразу вытекает из свойства аддитивности оператора
Следствие:
Линейная комбинация с произвольными постоянными коэффициентами
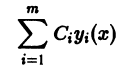
решений 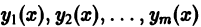
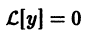
является решением того же уравнения.
Линейное однородное дифференциальное уравнение 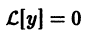
Теорема:
Если линейное однородное уравнение
с действительными коэффициентами 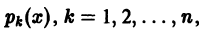
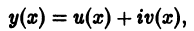
то действительная часть этого решения u(х) и его мнимая часть v(x) в отдельности являются решениями того же однородного уравнения.
Дано, что
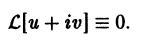
Надо доказать, что
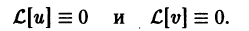
Пользуясь свойствами линейности оператора 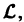
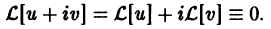
Отсюда следует, что 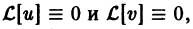
Линейно зависимые и линейно независимые системы функций
Пусть имеем систему функций 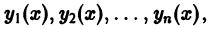
Определение:
Будем говорить, что система функций 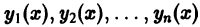
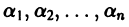
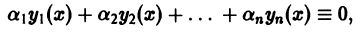
причем хотя бы одно из чисел 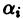
Если это тождество имеет место только при 
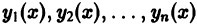
Рассмотрим примеры линейно зависимых и линейно независимых систем функций.
- Функции
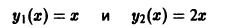
линейно зависимы на любом интервале (a, b), так как имеет место, например, тождество
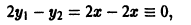
где
2. Функции
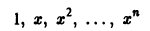
линейно независимы на любом интервале (а, b), так как тождество
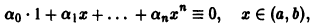
возможно лишь в случае, если
Если хоть одно из чисел 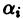
3. Функции
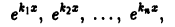
где 
Для простоты ограничимся случаем n = 3. Допустим, что функции 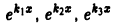
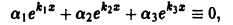
причем хотя бы одно из 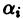
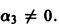
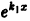
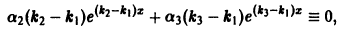
деля которое на 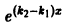
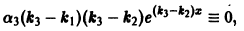
что невозможно, так как 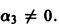

Замечание:
Линейная зависимость пары функций означает, что одна из функций получается из другой умножением на постоянную:
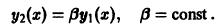
Вообще, если функции 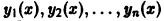
Задача:
Показать, что если система функций
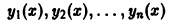
линейно независима на интервале (a, b), то и любая подсистема этой системы функций также линейно независима на (a, b).
Теорема:
Необходимое условие линейной зависимости функций. Если функции
имеющие производные до порядка n — 1 включительно, Линейно зависимы на интервале (а, b), то на этом интервале определитель
называемый определителем Вронского системы функций 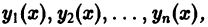
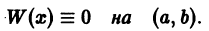
Ограничимся случаем n = 3. Пусть дважды дифференцируемые функции 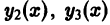
причем не все числа 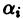
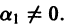
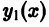
Составим определитель Вронского системы функций
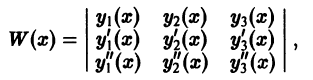
или, с учетом формул (1) и (2),
Первый столбец определителя является линейной комбинацией двух других при любом 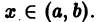
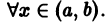
Рассуждением от противного легко доказывается следующая теорема.
Теорема:
Если определитель Вронского W(x) системы n функций не равен тождественно нулю в некотором интервале (а, b), то эти функции линейно независимы в этом интервале.
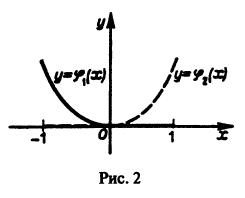
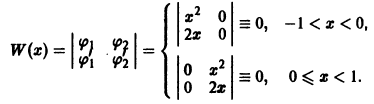
Для произвольной системы n — 1 раз дифференцируемых на (а,b) функций теорема, обратная теореме 5, неверна. Чтобы убедиться в этом, рассмотрим пример.
Для функций (рис. 2)
определитель Вронского на интервале (-1,1) тождественно равен нулю:
Однако, как легко видеть, функции 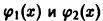
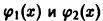
Эти функции линейно независимы в любом интервале, содержащем внутри себя точку х = 0, а вместе с тем их определитель Вронского тождественно равен нулю. При этом, скажем, функция 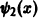
Задача:
Что можно сказать об определителе Вронского системы функций
если только известно, что эти функции а) линейно зависимы; б) линейно независимы?
Теорема:
Необходимое условие линейной независимости решений. Если линейно независимые на интервале (а, b) функции 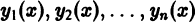
с непрерывными на [а, b] коэффициентами 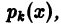
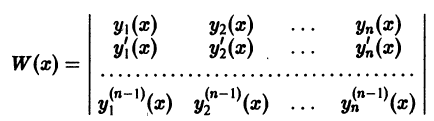
не может обратиться в нуль ни в одной точке интервала (а, b).
Ограничимся рассмотрением случая n = 3. Допустим, что в некоторой точке 
Составим систему трех линейных однородных алгебраических уравнений относительно
Определитель этой системы 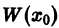
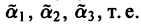
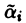
Рассмотрим функцию
Она является линейной комбинацией решений 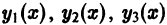
Таким начальным условиям, очевидно, удовлетворяет тривиальное решение 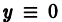
причем хотя бы одно из 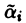
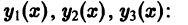
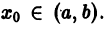
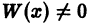
Из теорем 5 и 7 как следствие получаем следующую важную теорему.
Теорема:
Для того, чтобы частные решения 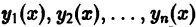
Необходимость условия прямо следует из теоремы 7.
Достаточность условия вытекает из того, что при линейной зависимости функций 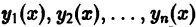
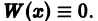
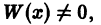
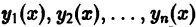
Задача:
Доказать, что два решения уравнения
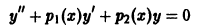
с непрерывными коэффициентами, имеющие максимум при одном и том же значении х, линейно зависимы.
Задача:
Доказать, что отношение двух любых линейно независимых решений уравнения
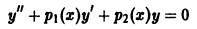
с непрерывными коэффициентами не может иметь точек максимума.
Задача:
Показать, что два линейно независимых решения 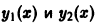
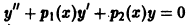
с непрерывными на отрезке [а, b] коэффициентами не могут обращаться в нуль при одном и том же значении
Структура общего решения линейного однородного дифференциального уравнения
Теорема:
О структуре общего решения линейного однородного дифференциального уравнения. Общим решением в области 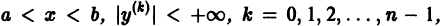
с непрерывными на отрезке [а, b] коэффициентами 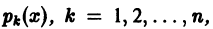

п линейно независимых на интервале (а, b) частных решений 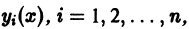
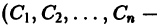
Будем исходить из определения общего решения и просто проверим, что семейство функций
удовлетворяет условиям 1), 2) этого определения.
Функция у(х), определенная формулой (2), является решением дифференциального уравнения (1) при любых значениях постоянных 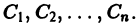
Для уравнения (1) при 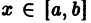
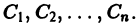
Ограничимся случаем, когда n = 3. Потребовав, чтобы решение
удовлетворяло поставленным начальным условиям, получим систему трех линейных алгебраических уравнений относительно
Определитель этой системы есть определитель Вронского 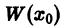
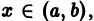
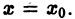
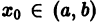
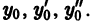
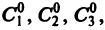
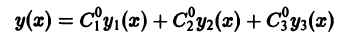
удовлетворяло поставленным начальным условиям, каковы бы они ни были.
Из теоремы 9 следует, что если известно п линейно независимых частных решений линейного однородного дифференциального уравнения n-го порядка, то всякое другое решение этого уравнения представляется в виде линейной комбинации этих частных решений и, значит, линейно зависимо с ними. Отсюда вытекает, что максимальное число линейно независимых решений однородного линейного дифференциального уравнения равно его порядку. Таким образом,
совокупность решений линейного однородного дифференциального уравнения образует линейное пространство, размерность которого равна порядку дифференциального уравнения.
Введем понятие фундаментальной системы решений.
Определение:
Совокупность любых п линейно независимых частных решений линейного однородного дифференциального уравнения n-го порядка называется его фундаментальной системой решений.
Теорема:
У каждого линейного однородного уравнения (1) с непрерывными коэффициентами 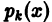
В самом деле, рассмотрим, например, однородное уравнение второго порядка
с непрерывными на отрезке {а, b] коэффициентами. Пусть 
удовлетворяющие при 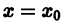
Определитель Вронского в точке 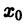
Следовательно, система решений (5) для уравнения (4) фундаментальна. Выбор начальных условий (5′) обеспечил построение одной фундаментальной системы. За начальные данные в точке 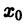
лишь бы определитель Вронского
был отличен от нуля. Очевидно, таких систем чисел можно подобрать бесконечно много и построить бесконечно много фундаментальных систем решений для уравнения (4).
Задача:
Составить общее решение уравнения
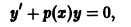
если известно ненулевое частное решение 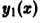
Теорема:
Если два уравнения вида
где функции 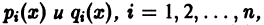
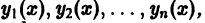
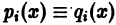
Таким образом, фундаментальная система решений вполне определяет линейное однородное уравнение (1), т.е. полностью определяет коэффициенты 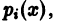
где у(х) — искомая функция, a 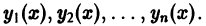
так как при подстановке вместо у(х) каждой из этих п функций два столбца определителя становятся тождественно равными и определитель обращается в нуль тождественно по 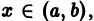
где W{х) — определитель Вронского системы функций 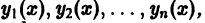
Определитель Вронского W(x) фундаментальной системы решений
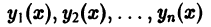
отличен от нуля во всем интервале (а, b). Разделив все члены уравнения (7) на 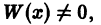
где, в частности,
Можно показать, что если элементы 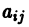

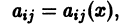
то производная определителя 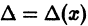
где 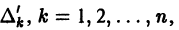
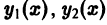
Нетрудно проверить, что 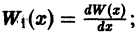
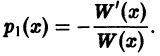
Интегрируя последнее равенство по х от X0 до х, получим формулу Остроградского— Лиувилля:
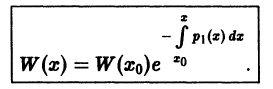
Задача:
Составить линейное дифференциальное уравнение второго порядка, имеющее решения
Показать, что функции 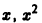
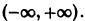
Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Частный случай: уравнение второго порядка
Пусть имеем линейное однородное дифференциальное уравнение второго порядка
где р1, p2 — действительные числа. Чтобы найти общее решение этого уравнения, надо найти два его линейно независимых частных решения. Следуя Эйлеру, будем искать их в виде
Подставляя эти выражения для у и ее производных в уравнение (1), получаем
Так как 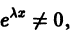
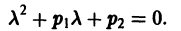
Следовательно, функция 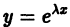
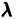
Уравнение (3) называется характеристическим уравнением по отношению к уравнению (1), а его левая часть 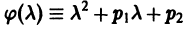
Уравнение (3) есть квадратное уравнение. Обозначим его корни через 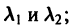
1) действительными и разными;
2) комплексными;
3) действительными и равными.
Рассмотрим каждый случай в отдельности.
- Если корни
характеристического уравнения действительные и разные, то частными решениями уравнения (1) будут функции
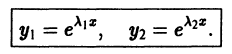
Эти решения линейно независимы 
Пример:
Найти общее решение уравнения
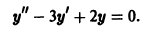
Составляем характеристическое уравнение:
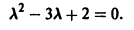
Оно имеет корни
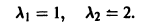
Отсюда получаем искомое общее решение
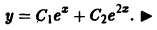
2. Пусть корни характеристического уравнения комплексные. Так как коэффициенты 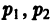
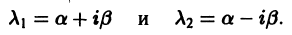
Частные решения дифференциального уравнения (1) можно записать в виде
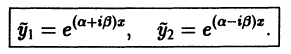
Это комплекснозначные функции действительного аргумента х, а мы будем заниматься лишь действительными решениями. С помощью формул Эйлера
частные решения 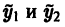
Воспользовавшись теоремой 4, получим, что частными решениями уравнения (1) будут также функции
Эти решения линейно независимы, так как
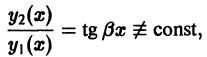
и, значит, составляют фундаментальную систему решений. Общее решение уравнения (1) в рассматриваемом случае имеет вид
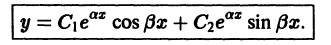
Пример:
Найти общее решение уравнения
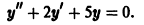
Составляем характеристическое уравнение:
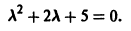
Оно имеет корни
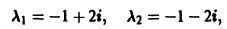
поэтому 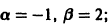
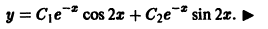
3. Пусть теперь корни характеристического уравнения действительные и равные. Одно частное решение
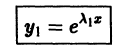
получаем сразу. Второе частное решение, линейно независимое с первым, будем искать в виде
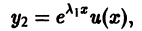
где u(х) — новая неизвестная функция. Дифференцируя, находим:
Подставляя полученные выражения в (1), получаем
Так как 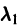
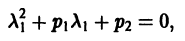
а так как 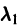
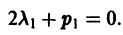
Следовательно, соотношение (4) примет вид
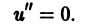
Отсюда
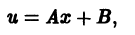
где А и В — постоянные. Можно, в частности, положить А = 1, В = 0; тогда
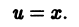
Таким образом, в качестве второго частного решения уравнения можно взять
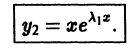
Это решение линейно независимо с первым, так как
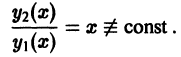
Решения 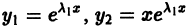
Пример:
Найти общее решение уравнения
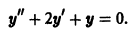
Характеристическое уравнение
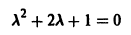
имеет кратные корни
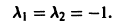
Поэтому общее решение исходного дифференциального уравнения:
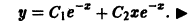
Замечание:
Пусть имеем линейное однородное дифференциальное уравнение (вообще, с переменными коэффициентами)
Пусть 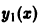
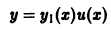
(разрешимым относительно u(х) в тех интервалах, где 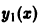
и подставим их в уравнение (5):
Для функции u(x) получаем опять уравнение порядка n, но коэффициент при u(х) есть 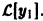
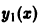
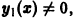
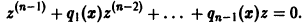
Итак, если известно частное решение уравнения (5), то задача интегрирования этого уравнения приводится к интегрированию линейного однородного уравнения порядка n — 1. Можно показать, что если известны два частных линейно независимых решения, то порядок уравнения может быть понижен на две единицы. Вообще, если известно r частных линейно независимых решений линейного однородного дифференциального уравнения, то порядок этого уравнения может быть понижен на r единиц.
Физические приложения: уравнение колебаний
Линейные дифференциальные уравнения с постоянными коэффициентами возникают в задачах о механических и электрических колебаниях. Рассмотрим уравнение свободных механических колебаний, причем независимой переменной будем считать время t:
где у — отклонение колеблющейся точки от положения равновесия, m — масса точки, h — коэффициент трения (считаем, что сила трения пропорциональна скорости), к > 0 — коэффициент упругости восстанавливающей силы (считаем, что эта сила пропорциональна отклонению). Характеристическое уравнение для (6)
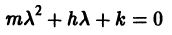
имеет корни
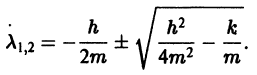
Если трение достаточно велико, 
Так как 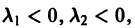
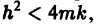
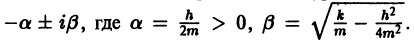
Отсюда видно, что в случае малого трения происходят затухающие колебания.
Пусть теперь трение отсутствует, т. е. h = 0. В этом случае характеристическое уравнение 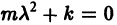
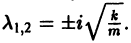
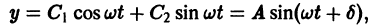
где 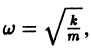
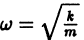
Задача:
При каких
1) все решения уравнения
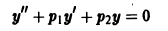
стремятся к нулю при
2) каждое решение уравнения
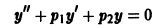
обращается в нуль на бесконечном множестве точек х?
Общий случай: уравнение произвольного порядка
Рассмотрим теперь линейное однородное дифференциальное уравнение произвольного порядка 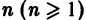
где 
- Ищем решение в виде
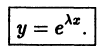
Подставляя вместо у величину 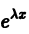
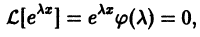
что приводит к характеристическому уравнению
2, Находим корни
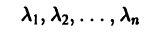
характеристического уравнения.
3. По характеру корней выписываем частные линейно независимые решения уравнения (8), руководствуясь тем, что:
а) Каждому действительному однократному корню 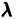
уравнения (8).
б) Каждой паре однократных комплексно сопряженных корней
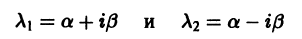
соответствуют два линейно независимых частных решения
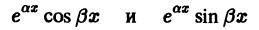
уравнения (8).
в) Каждому действительному корню 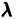
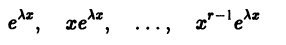
уравнения (8).
Рассмотрим случай в) подробнее. Пусть число 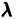
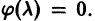
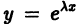
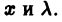
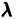
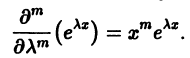
Поэтому частные производные функции 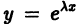
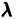
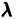
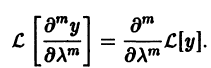
Воспользовавшись этой перестановочностью, а также тем, что
получим
Если 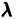
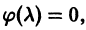
и, стало быть, правые части (10) и (11) тождественно по х равны нулю:
Это означает, что функции 
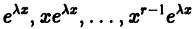
г) Приведенные в пункте в) рассуждения сохраняют силу и для комплексных корней. Поэтому каждой паре комплексно сопряженных корней 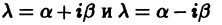
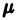
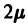
4. Число построенных таким образом частных решений уравнения (8) равно порядку п этого уравнения. Можно показать, что все эти решения линейно независимы в совокупности. Имея n линейно независимых частных решений 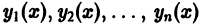
где 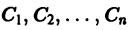
Пример:
Найти общее решение уравнения
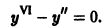
1. Составляем характеристическое уравнение:

2. Находим корни характеристического уравнения:
3. По характеру корней выписываем частные линейно независимые решения дифференциального уравнения:
4. Общее решение дифференциального уравнения имеет вид
Схема решения линейного дифференциального уравнения с постоянными коэффициентами
Уравнения, приводящие к уравнениям с постоянными коэффициентами
Существуют линейные дифференциальные уравнения с переменными коэффициентами, которые с помощью замены переменных преобразуются в уравнения с постоянными коэффициентами. К их числу принадлежит уравнение Эйлера
где 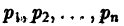
Положим 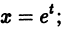
Подставляя выражения для 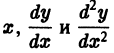
Последнее интегрируется обычным приемом: составляем характеристическое уравнение
находим его корни и по характеру корней выписываем общее решение уравнения (2), после чего возвращаемся к старой переменной х.
Пример:
Найти общее решение уравнения
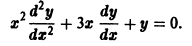
Замена переменной 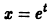
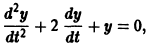
характеристическое уравнение которого
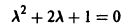
имеет корни 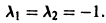
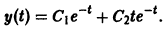
Учитывая, что 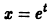
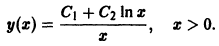
Замечание:
Для преобразованного уравнения (2) в случае действительных и различных корней характеристического уравнения (3) частные решения имеют вид
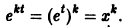
Поэтому можно сразу задаться этим видом частного решения. Подставляя 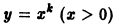
совпадающее с (3). Каждому простому действительному корню уравнения (4) отвечает частное решение
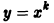
уравнения (1); двукратному корню отвечают два решения
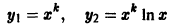
уравнения (1). Паре комплексных сопряженных корней 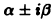
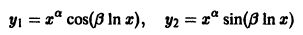
уравнения (1).
Замечание:
Уравнение
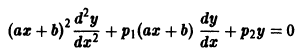
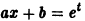
Линейные неоднородные дифференциальные уравнения
Линейное неоднородное дифференциальное уравнение n-го порядка имеет вид
Здесь 
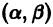
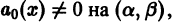
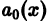
Из теоремы 1 существования и единственности решения задачи Коши получаем:
если на отрезке [а, b] коэффициенты 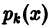
Уравнение (2) можно записать в виде
где, как и выше,
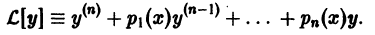
Теорема:
Если 
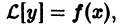
а 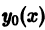
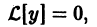
то сумма 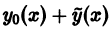
По условию, 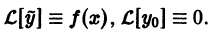
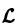
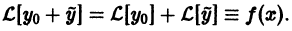
Это означает, что функция 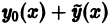
Теорема:
Если 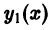
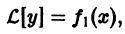
а 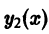
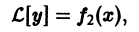
та функция 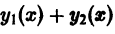
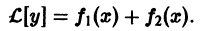
По условию, 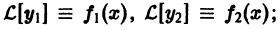
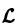
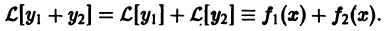
Последнее означает, что функция 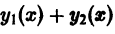
Теорема выражает так называемый принцип суперпозиции (наложения).
Теорема:
Если уравнение
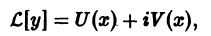
где все коэффициенты 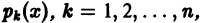
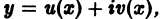
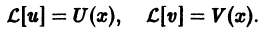
По условию имеем
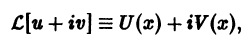
или
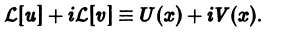
Отсюда получаем:
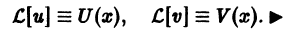
Теорема:
О структуре общего решения линейного неоднородного дифференциального уравнения.
Общее решение в области 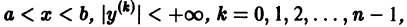
с непрерывными на отрезке [а, b] коэффициентами 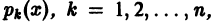
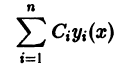
соответствующего однородного уравнения и какого-нибудь частного решения 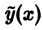
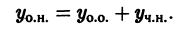
Надо доказать, что
где 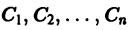
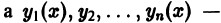
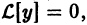
Будем исходить из определения общего решения и просто проверим, что семейство функций у(х), определяемое формулой (4), удовлетворяет условиям 1) и 2), содержащимся в этом определении.
В самом деле, функция у(х), определяемая формулой (4), является решением уравнения (2) при любых значениях постоянных, поскольку сумма какого-либо решения неоднородного уравнения и любого решения соответствующего однородного уравнения есть решение неоднородного уравнения
Так как для уравнения (2) при 
где 
Эта линейная по отношению к 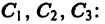
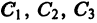
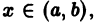
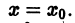
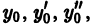
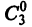
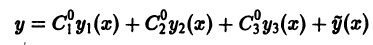
будет решением дифференциального уравнения (2), удовлетворяющим начальным условиям
Из этой теоремы следует, что задача нахождения общего решения линейного неоднородного уравнения сводится к отысканию какого-либо частного решения этого неоднородного уравнения и общего решения соответствующего однородного уравнения.
Пример:
Найти общее решение уравнения
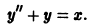
Нетрудно заметить, что функция
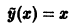
является частным решением данного неоднородного уравнения. Чтобы найти общее решение этого уравнения, остается отыскать общее решение соответствующего однородного уравнения
Это уравнение есть линейное однородное уравнение с постоянными коэффициентами. Характеристическое уравнение, соответствующее уравнению (*), есть
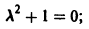
корни его 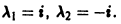
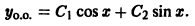
Общее решение исходного неоднородного уравнения:
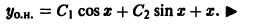
Интегрирование линейного неоднородного дифференциального уравнения методом вариации постоянных
Частный случай: уравнение второго порядка
Начнем для простоты со случая уравнения второго порядка. Пусть имеем дифференциальное уравнение
(функции 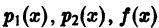
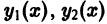
общее решение уравнения (2).
Заметим, что это предположение является весьма стеснительным, так как общего метода отыскания решений линейных однородных уравнений порядка 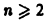
Для интегрирования неоднородного уравнения (1) применим метод вариации постоянных (метод Лагранжа), который состоит в следующем. Будем искать решение неоднородного уравнения (1) в виде
где 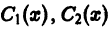
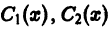
Наложим на функции 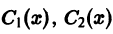
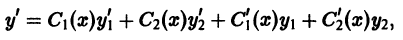
и в качестве дополнительного условия, налагаемого на С1, С2, возьмем следующее (целесообразность этого будет видна из дальнейшего):
Подставляя выражения для 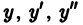
Выражения в квадратных скобках тождественно равны нулю, поскольку 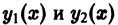
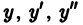
Значит, функция 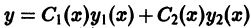
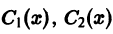
определитель которой есть определитель Вронского линейно независимых решений 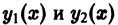
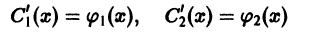
(здесь 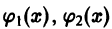
(здесь С1, С2 — постоянные интегрирования). Подставляя эти выражения для 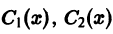
(C1, C2 — произвольные постоянные). Итак,
если известна фундаментальная система решений соответствующего однородного уравнения, то общее решение неоднородного уравнения может быть найдено с помощью квадратур.
Пример:
Найти общее решение уравнения
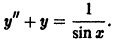
Рассмотрим однородное уравнение, соответствующее данному неоднородному:
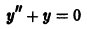
— это есть линейное уравнение с постоянными коэффициентами. Функции
образуют его фундаментальную систему решений. Будем искать решение исходного уравнения в виде
Система (8) для определения 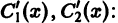
Решая эту систему относительно 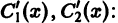
Подставляя найденные выражения для 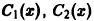
Общий случай: уравнение произвольного порядка
Для интегрирования линейного неоднородного дифференциального уравнения n-го порядка
поступаем аналогично.
Пусть 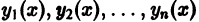
где 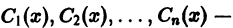
Чтобы найти п функций 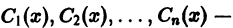
Тогда, чтобы функция у(х), определенная формулой (10), удовлетворяла уравнению (9), надо на функции 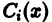
Для определения 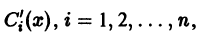
Определитель этой системы есть определитель Вронского фундаментальной системы решений однородного уравнения и, следовательно, отличен от нуля всюду в интервале (а, 6). Поэтому система (11) однозначно разрешима относительно 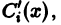
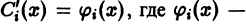
Подставляя найденные выражения для 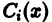
где 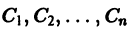
Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами
В предыдущем параграфе был рассмотрен общий метод решения неоднородного линейного дифференциального уравнения — метод вариации постоянных. В случае дифференциального уравнения с постоянными коэффициентами частное решение неоднородного уравнения иногда бывает возможно найти проще — методом подбора. Рассмотрим некоторые виды уравнений, допускающие применение этого метода:
- Уравнение вида
где 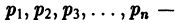
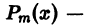
Характеристическое уравнение для соответствующего (1) однородного уравнения имеет вид
-характеристический многочлен.
Если коэффициент 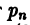
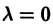
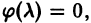
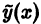
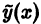
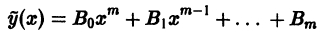

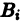
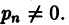
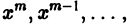
если 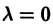
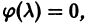
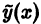
Предположим теперь, что 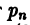
т.е. 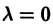
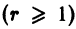
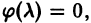
Полагая 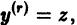
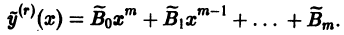
Отсюда получаем, что 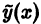
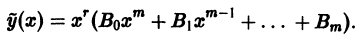
Итак,
если 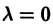
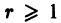
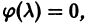
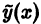
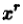
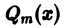
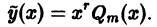
Пример:
Найти частное решение уравнения
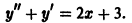
Характеристическое уравнение
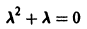
имеет корни 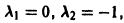
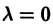
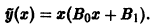
Подставляя 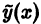
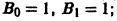
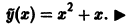
2. Уравнение вида
Частное решение 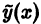
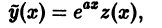
где z = z(x) — функция от х, которая должна быть определена из условия
Тогда имеем:
Умножим функции 
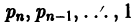
Здесь 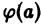
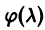
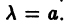
Это линейное неоднородное уравнение с постоянными коэффициентами, его правая часть — многочлен. Поэтому частное решение уравнения (6) надо искать в виде многочлена 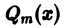
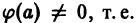
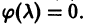
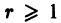
и решение уравнения (6) надо искать в виде 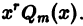
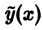
если число а не есть корень характеристического уравнения 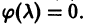
если число а есть корень характеристического уравнения кратности 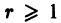
Здесь 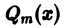
Пример:
Найти частное решение уравнения
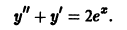
Характеристическое уравнение
имеет корни 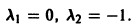
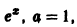
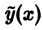
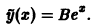
Подставляя 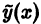
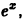
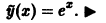
Пример:
Указать вид частного решения уравнения
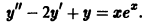
Характеристическое уравнениe
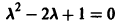
имеет корни 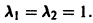
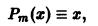
т.е. m = 1 и число а, равное единице, является двукратным корнем (r = 2) характеристического уравнения. Поэтому частное решение 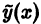
3. Приведенные выше рассуждения остаются справедливыми и при комплексном а. Поэтому, если правая часть линейного дифференциального уравнения
где 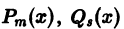
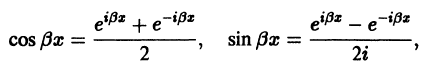
В квадратных скобках стоят многочлены, имеющие степень, равную наивысшей степени многочленов 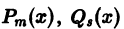
Для каждого слагаемого правой части можно применить указанное правило: если 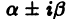
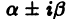
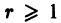
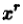
Если опять вернуться к тригонометрическим функциям, то это правило можно сформулировать так:
а) если числа 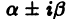
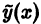
где U(х), V(x) — многочлены с неопределенными коэффициентами, степень каждого из которых равна наивысшей из степеней многочленов 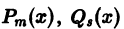
Чтобы найти коэффициенты этих многочленов, надо подставить функцию 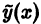
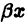
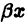
б) если 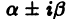
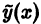
Замечание:
Указанные виды частных решений (12) и (13) сохраняются и в том случае, когда в правой части уравнения один из многочленов 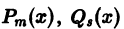
Пример:
Найти частное решение уравнения
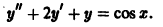
Характеристическое уравнение
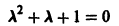
имеет корни 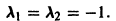
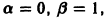
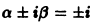
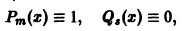
значит, частное решение уравнения следует искать в виде
Подставляя функцию 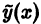
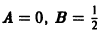
Пример:
Рассмотрим уравнение упругих колебаний без сопротивления при наличии периодической внешней силы
(независимой переменной считаем время t).
Общим решением однородного уравнения является функция
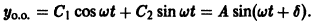
Если 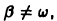
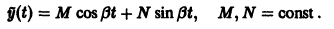
Подставляя это выражение в уравнение (*), найдем, что 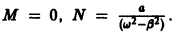
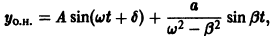
т. е. результирующее движение слагается из собственных колебаний с частотой w и вынужденных колебаний с частотой
Если 
Подставляя 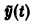
Общее решение уравнения (*) будет иметь вид
Второе слагаемое в правой части (**) показывает, что в этом случае амплитуда колебаний неограниченно возрастает при неограниченном возрастании времени t (рис. 3). Это явление, возникающее при совпадении частоты внешней силы с частотой собственных колебаний системы, называется резонансом.
Удобным для отыскания частных решений является следующий прием. Пусть имеем линейное неоднородное дифференциальное уравнение с действительными постоянными коэффициентами
где 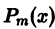
Правая часть уравнения (14) есть действительная часть правой части уравнения (15), и поэтому в силу теоремы 14 действительная часть u(x) решения 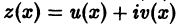
Из приведенных выше рассмотрений следует:
1) если число 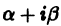
то частное решение уравнения (16) следует искать в виде
где Qm(x) — многочлен степени т с неопределенными коэффициентами,
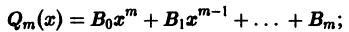
2) если 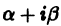
Замена тригонометрических функций показательной упрощает вычисления, так как после подстановки 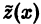
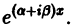
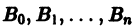

поступаем аналогично: 1) переходим к вспомогательному уравнению (16); 2) находим частное решение 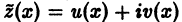
Пример 6. Найти частное решение уравнения
Составляем вспомогательное уравнение
Поскольку число 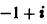
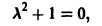
частное решение уравнения (**) ищем в виде
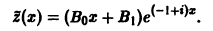
Подставляя 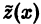
в уравнение (**) и сокращая на 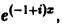
Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях последнего равенства, найдем:
Поэтому для 
Отсюда получаем частное решение данного уравнения:
Применение степенных и обобщенных степенных рядов к интегрированию дифференциальных уравнений
Пусть имеем дифференциальное уравнение
и требуется найти решение этого уравнения, удовлетворяющее начальным условиям
Предположим, что функция f аналитична в окрестности точки 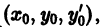
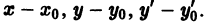
В самом деле, зная 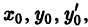
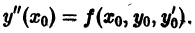
Подставляя в правую часть (4) значения 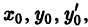
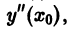
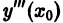
Если ряд (3) сходится в некотором интервале 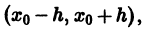
Пример:
Найти решение задачи Коши
В силу (*), (**) имеем
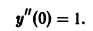
Дифференцируя (*), найдем
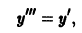
откуда у»‘(0) = у'(0) = 1, и вообще
Рассмотрим линейное дифференциальное уравнение
Теорема:
Об аналитичности решения. Если 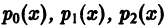
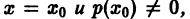
Пример:
Найти решение задачи
Решение будем искать в виде ряда
Подставим у(х) и у»(х) в данное уравнение и приравняем нулю коэффициенты при степенях х:
В силу начальных условий имеем 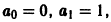
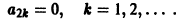
Далее имеем 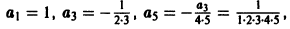
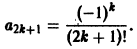
Окончательно получаем
Пусть теперь коэффициент 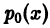
Определение:
Точка х0 называется нулем порядка (кратности) m (m — целое положительное число) функции f(x), если f(х) представима в виде 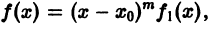
Теорема:
О разложимости решения в обобщенный стеленной ряд. Если в уравнении
коэффициенты 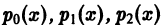
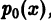
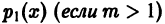
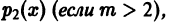
где 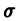
Уравнение Бесселя. Функции Бесселя
Дифференциальное уравнение Бесселя
Дифференциальным уравнением Бесселя называется уравнение вида
где v — действительное число. Это уравнение имеет особую точку х = 0 (коэффициент при старшей производной в (7) обращается в нуль при х = 0). Сравнивая (5) и (7), заключаем, что для уравнения Бесселя
так что х = 0 является нулем второго порядка (m = 2) функции 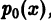
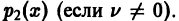
где 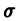
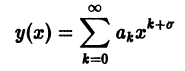
и найдем производные:
Подставим эти выражения в уравнение (7),
и приравнивая нулю коэффициенты при х в степени 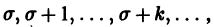
Так как 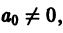
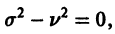
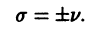
Теперь из второго уравнения (9) будем иметь
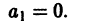
Рассмотрим сначала случай 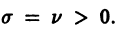
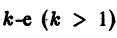
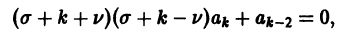
откуда получаем рекуррентную формулу для определения 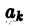
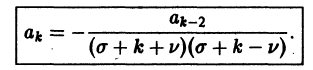
Учитывая, что a1 = 0, получаем отсюда а3 = 0 и вообще 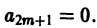
или, с учетом
Последовательное применение этой формулы позволяет найти выражение 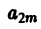
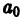
Подставим найденные значения коэффициентов в формулу (8),
Нетрудно проверить, что ряд в правой части (10) сходится на полуоси х > 0 и определяет там функцию у1(х) — частное решение уравнения Бесселя.
Рассмотрим теперь второй случай, когда 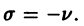
(Если v равно целому положительному числу, то решение (10′) теряет силу, так как начиная с некоторого числа один из множителей в знаменателе членов разложения (10′) будет равен нулю.) Ряд в правой части (10′) также сходится при всех значениях х > 0. Решения 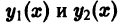
не является постоянным.
Г-функция Эйлера и ее свойства
Для дальнейшего нам понадобятся некоторые свойства Г -функции Эйлера. Она определяется следующим образом:
Интегрированием по частям получаем основное функциональное уравнение для Г-функции:
Можно показать еще, что
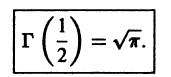
С помощью функционального уравнения (11) можно определить гамма-функцию для отрицательных значений аргумента. Записав уравнение (11) в виде 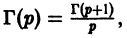
Аналогично, если m — положительное целое число, то для значений р, близких к числу -m, имеем
Можно показать, что 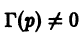
Возвратимся к решению уравнения Бесселя (7). Коэффициент 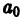
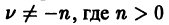
Подставляя это выражение для коэффициентов в (9), получаем
Ряд (12) определяет функцию
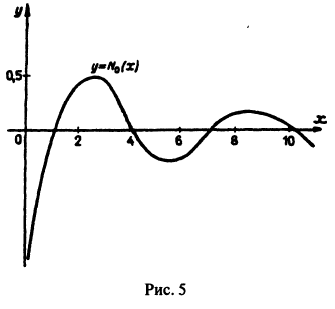
которая является решением уравнения Бесселя и называется функцией Бесселя первого рода v-го порядка.
Ряд
отвечает случаю 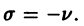
Итак, если v не равно целому числу 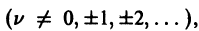
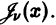
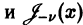
При v целом выполняется линейная зависимость
В самом деле, имеем
Первые n членов ряда исчезают, так как 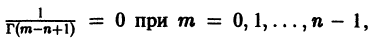
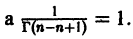
Выпишем ряды для функций Бесселя первого рода нулевого (n = 0) и первого (n = 1) порядков:
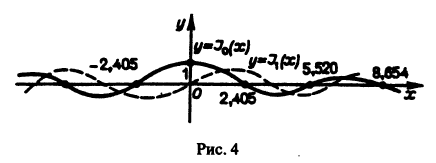
Функции 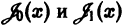
Рекуррентные формулы для функций Бесселя
Используя формулу
непосредственно проверкой убеждаемся в том, что
Точно таким же вычислением находим
Раскрывая в левых частях формул (15) и (16) производные произведений, получаем соответственно равенства
Складывая и вычитая (17) и (18), получим две важные рекуррентные формулы:
Формула (19) показывает, что производные функций Бесселя выражаются через бесселевы же функции. Из формулы (20) вытекает, что, зная 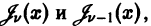
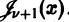
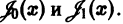
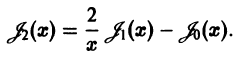
Функции Бесселя полуцелого индекса
Рассмотрим специальный класс бесселевых функций с индексом, равным половине нечетного целого числа. Этот класс встречается в приложениях и замечателен тем, что в рассматриваемом случае бесселевы функции могут быть выражены через элементарные. Так, при 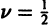
Аналогично, при 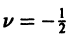
Обе эти формулы можно записать в виде
По рекуррентной формуле (20) подсчитываем, например,
и т. д.
Нули бесселевых функций
При решении многих прикладных вопросов необходимо иметь представление о распределении нулей функций Бесселя. Нули функций 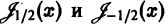
Символ 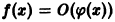
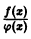
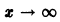
справедливое как для целых, так и для дробных v. Формула (22) показывает, как ведет себя функция Бесселя при возрастании аргумента. Это колеблющаяся функция, бесчисленное множество раз обращающаяся в нуль, причем амплитуда колебаний стремится к нулю при
Распределение нулей функции Бесселя с целым положительным индексом, т. е. корней уравнения
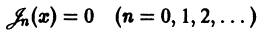
устанавливается следующей теоремой.
Теорема:
Функция 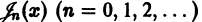
Ортогональность и норма функций Бесселя
Ортогональность функций Бесселя:
Рассмотрим дифференциальное уравнение
где 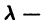
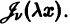
и обозначим 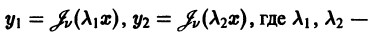
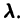
Умножая первое тождество на 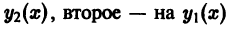
Умножив все члены последнего тождества на x, замечаем, что его можно записать в виде
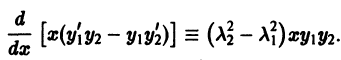
Интегрируя последнее тождество по ж в пределах от 0 до 1, будем иметь
1. Пусть 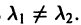
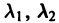
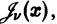
Это означает, согласно определению, что функции 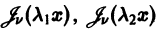
Бесселева функция 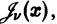
и, следовательно, система функций
есть ортогональная на отрезке [0,1] система с весом р(х) = х,
2. Если 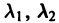
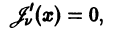
то в этом случае при 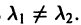
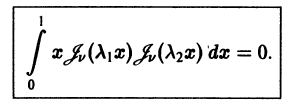
Следовательно, система функций 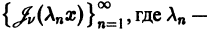
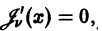
3. Пусть 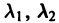
где h — некоторое фиксированное число. Уравнение (28) встречается в математической физике и при v > -1 имеет бесконечное множество положительных корней, но не имеет комплексных корней (исключая случай 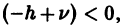
убеждаемся в ортогональности бесселевых функций по нулям линейной комбинации 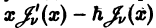
где 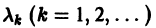
Норма функций Бесселя
Величина
называется нормой функции Бесселя
Пользуясь равенством (25), можно показать, что
В частности, для 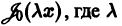
Функции Неймана (Вебера)
Всякое нетривиальное решение уравнения Бесселя
называют цилиндрической функцией. При v нецелом функции 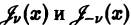
Чтобы к решению 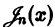
Она является линейной комбинацией решений линейного однородного уравнения (7) и, следовательно, сама есть решение этого уравнения. Переходя в (30) к пределу при 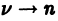
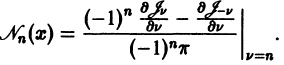
Характерное свойство функций 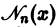
Найденное решение 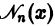
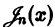
Функцию 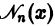
Таким образом, на больших расстояниях от начала координат цилиндрические функции 1 -го и 2-го рода относятся друг к другу как косинус и синус, но затухают с ростом ж благодаря множителю 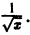
По аналогии с показательными функциями (формулы Эйлера) можно построить линейную комбинацию функций 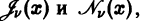
Дополнение к дифференциальным уравнениям высших порядков
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат