Как найти начало круговой кривой - Исправление недочетов и поиск решений вместе с Examum.ru

Рис. 82. Пикетажный журнал

По середине страницы пикетажного журнала проводят прямую, изо— бражающую ось трассы, на ней в масштабе 1:2000 штрихами отмечают положение пикетов и плюсовых точек, подписывая рядом с ними их зна— чения. Каждую новую страницу начинают с пикета, которым закончена предыдущая. В местах поворота трассы от оси стрелкой указывают на—

правление поворота и вблизи на свободном месте в столбик записывают величину угла поворота и элементы кривой. На оси трассы отмечают главные точки кривых (начало, середину и конец), подписывают их пике— таж. Напротив прямых участков трассы выписывают их румбы и длины. Ситуацию в журнале зарисовывают схематично, указывая расстояния от оси трассы до предметов и габариты строений.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

111

1.Какие работы включает в себя трассирование?

2.Что представляет собой план трассы?

3.Что представляет собой продольный профиль трассы?

4.Что является углом поворота трассы и как его определяют?

5.Как разбивают пикетаж, плюсовые точки и поперечники?

6.Как определяют дирекционные углы сторон трассы по углам пово—

рота?

7.Что представляет собой пикетажный журнал и каково его содержа—

ние?

Лекция 12 ДОРОЖНЫЕ ЗАКРУГЛЕНИЯ

План лекции

12.1.Круговые кривые.

12.2.Вычисление пикетажа главных точек круговой кривой.

12.3.Разбивка кривой в главных точках на местности.

12.4.Детальная разбивка круговой кривой.

12.5.Вынос пикетов на кривую.

12.1. Круговые кривые

На всех линейных сооружениях, предназначенных для движения транспорта, в местах изменения направления трассы для сопряжения прямых участков с целью плавного и постепенного поворота движущего— ся транспортного средства устраивают закругления или кривые. Закруг— ления могут быть любыми. Простейшим является дуга окружности опре— деленного радиуса, т. е. круговая кривая.

На железных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 400 и 300 м. Конкретное решение о применении радиусов железнодорожных кривых принимают в соответствии с конкретными условиями и строи— тельно—техническими нормами СТН Ц-01-95 [6].

Круговая кривая характеризуется четырьмя главными точками и ше— стью основными элементами (рис. 83).

112

Рис. 83. Схема круговой кривой

Главными точками кривой, которые определяют положение кривой на местности, являются: вершина угла ВУ; начало круговой кривой НКК; се— редина круговой кривой СКК; конец круговой кривой ККК.

Основными элементами кривой являются:

1.Угол поворота трассы У.

2.Радиус закругления R.

Во время изысканий угол У вычисляют, а радиус R назначают. Ос— тальные элементы находят по формулам, вытекающим из прямоугольно— го треугольника с вершинами ВУ, НКК, О (рис. 83).

3.Тангенс кривой (касательная) Т – расстояние по прямой от верши—

ны угла до начала или конца кривой

Т= R × tg У2 .

4.Длина кривой К от начала кривой до её конца

K= 3602πR° ×У = 180πR° ×У .

5.Биссектриса кривой Б – отрезок от вершины угла до середины кривой

Б =	R		— R =	R		(1- cos	У	) = R(sec	У	-1) .
cos	У	2	cos	У	2	2	2

6.Домер Д – разность между длиной двух тангенсов и кривой

Д= 2Т − K .

113

Все элементы кривой можно вычислить по вышеприведенным фор— мулам. Но так как Т, K, Б и Д находятся в прямой зависимости от угла по— ворота и радиуса, то для их определения составлены специальные таб— лицы для разбивки кривых.

12.2.Вычисление пикетажа главных точек круговой кривой

Вычислить пикетажные значения главных точек кривой – значит узнать, на каких пикетах и плюсовых точках они находятся.

Сначала определяют пикетаж вершины угла поворота ВУ, а затем на— ходят пикетажное значение начала, конца и середины кривой

НКК = ВУ − Т ,

ККК = НКК + K, СКК = НКК + 12K.

Для контроля вторично вычисляют пикетажное значение конца кривой

ККК = ВУ + Т − Д .

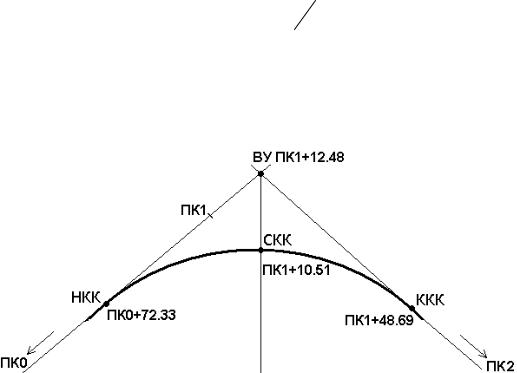
Пример (рис. 84)

Рис. 84. Разбивка пикетажа с учетом кривой

Определены: пикетаж ВУ ПК1+12.48 и основные элементы круговой кривой:

У = 43°45′ ;

R= 100 м;

Т= 40.15 м;

K= 76.36 м;

Б = 7.76 м;

114

Д = 3.94 м.

Найти пикетажные значения НКК, ККК, СКК.

Расчет пикетажа главных точек кривой выполняется в следующей форме:

_ВУ	ПК1+12.48		Контроль
+	ВУ	ПК1+12.48
	Т	ПК0+40.15	Т	ПК0+40.15
	НКК	ПК0+72.33	–Д	ПК1+52.63
+K	ПК0+76.36	ПК0+03,94
	ККК ПК1+48.69		ККК ПК1+48.69
+	НКК ПК0+72.33
12 K ПК0+38.18

СКК ПК1+10,51

12.3. Разбивка кривой в главных точках на местности

Разбить кривую в главных точках на местности – значит найти поло— жение её главных точек на оси линейного сооружения и закрепить их. Положение начала кривой НКК определяют, отложив вычисленное рас— стояние от ближайшего пикета.

В нашем примере (см. рис. 84) ближайшим пикетом является ПК1. От него к ПК0 откладывают расстояние 27,67. В этой точке забивают колы— шек, а на расстоянии 15 – 20 см по направлению трассы забивают сто— рожок и на нем записывают НКК ПК0 + 72.33.

Середину кривой СКК закрепляют, отложив от ВУ по направлению биссектрисы угла, образованного направлениями трассы, отрезок, рав— ный Б.

На следующем, после вершины угла, направлении трассы отклады— вают величину домера (см. рис. 83), после чего продолжают разбивку пи— кетажа. При этом в месте отложения домера две точки – начало домера и его конец получают одно и тоже пикетажное наименование, благодаря чему в конце кривой пикетаж совпадает с пикетажем прямой. Положение

ККК получают, отложив от конца домера расстояние Т − Д , в примере оно равно 36.21 м. Найденное положение ККК закрепляют колышком и сторожком.

12.4. Детальная разбивка круговой кривой

По трем главным точкам точно построить кривую на местности не— возможно, поэтому при строительстве трассы её обозначают рядом до—

115

полнительных точек. Данные работы называются детальной разбивкой кривой.

Расстояние между соседними точками на кривой K при детальной разбивке зависит от её радиуса R и характера сооружения, однако чем меньше R кривой, тем меньше значение K. При R > 500 м разбивку про— изводят через промежутки k = 20 м, при 500 > R > 100 м k = 10 м, при

R < 100 м k = 5 м.

Из всех существующих способов детальной разбивки, различающихся между собой по виду измерений и условиям использования, рассмотрим два способа.

Способ прямоугольных координат от тангенсов

Пусть М – начало кривой радиуса R (рис. 85). Примем тангенс МА за ось абсцисс, а радиус МО за ось ординат. Положение точки кривой 1 в принятой системе координат определяется абсциссой X1 и ординатой Y1.

Рис. 85. Способ прямоугольных координат от тангенсов

116

Из прямоугольного треугольника ОN1 находим

X1 = R sin ϕ и Y1 = R − R cos ϕ = 2R sin2 ϕ2 .

Если условимся производить разбивку через промежутки с длиной ду— ги k , то получим

ϕ = 360°k = 180° k . 2πR πR

Тогда для точек 2, 3 и т. д. координаты вычисляют, подставляя в вы— шеприведенные формулы углы 2ϕ, 3ϕ и т. д.

X2 = R sin 2ϕ , Y2 = 2R sin2 ϕ,

X3 = R sin 3ϕ , Y3 = 2R sin2 3ϕ . 2

По указанным формулам составлены таблицы, из которых по аргу— ментам R и k можно выбрать значение Х и У.

В виду того, что значения k и Х близки между собой, в таблицах часто вместо графы Х дают значения (k – Х), называемые «кривая без абсцис— сы». Разбивку кривой производят с двух сторон – от начала и конца к се— редине кривой. По тангенсам отмеряют значение k и от полученной точки в обратном направлении откладывают значение (k – Х). Из данной точки восстанавливают перпендикуляр и откладывают на нём ординату Y.

Достоинство способа прямоугольных координат состоит в том, что каждая точка кривой выносится независимо от других с примерно одина— ковой точностью.

Детальную разбивку кривой способом прямоугольных координат удобно проводить в открытой и непересеченной местности.

Детальная разбивка кривой способом углов и хорд

Данный способ основывается на том, что углы с вершиной в какой— либо точке круговой кривой, образованные касательной и секущей и за— ключающие равные дуги, равны половине соответствующего централь— ного угла (рис. 86).

Для разбивки кривой при помощи углов и хорд вычисляют цен—

тральный угол ϕ, опирающийся на хорду s sin ϕ2 = 2sR .

Рассчитывают углы ϕi между касательной и направлением на опреде—

ляемые точки

117

ji = i × ϕ2 , (i = 1,2,3,….,n ) .

Рис. 86. Способ углов и хорд

Сначала выполняют разбивку кривой от её начала НКК до середины СКК. Для этого теодолит устанавливают в начале кривой НКК, совмеща— ют нуль алидады с нулем лимба и вращением лимба направляют визир— ную ось по тангенсу. Затем, освободив алидаду, в сторону кривой откла—

дывают от тангенса угол j1 = j2 и по направлению луча визирования

отмеряют лентой заданное расстояние s. Так находят точку 1. После это— го откладывают угол ϕ2 = ϕ , а ленту переносят и совмещают её нуль с

точкой 1. Взявшись пальцем у деления, равного s, вращают ленту вокруг точки 1 в сторону кривой до тех пор, пока деление не попадет на луч ви— зирования. В данном месте отмечают точку 2. Продолжают действовать в той же последовательности, откладывая точку 3 и т. д.

Аналогичным образом выполняют разбивку кривой от её конца ККК до середины СКК.

В рассмотренном способе линейные измерения выполняют вблизи кривой, что выгодно при разбивке точек в стесненных условиях, напри—

118

мер, на насыпи. Но так как положение последующей точки получают от— носительно предыдущей, то с возрастанием длины кривой точность её детальной разбивки быстро падает. В этом главный недостаток способа

углов и хорд.

12.5. Вынос пикетов на кривую

Так как при разбивке пикетажа на трассе мерщики перемещаются по тангенсам кривых, то возникает необходимость выноса пикетов, распо— ложенных на тангенсах, на кривые. Вынос пикетов на кривые выполняет— ся способом прямоугольных координат и в принципе не отличается от де— тальной разбивки кривой с помощью данного способа. Разница лишь в том, что при детальной разбивке кривой необходимые данные берут из таблиц, в которых они даются через определенные расстояния по кривой (20, 10, 5 или 1м). При выносе пикетов с касательной (тангенса) на кри— вую такие данные находят также из таблиц, но при этом используют ме— тод интерполирования.

Например, ПК1 лежит на тангенсе (рис. 87). Для того, чтобы его выне— сти на кривую, вычисляют расстояние K от ПК1 до НКК. Оно равно 27,67 м.

Рис. 87. Вынос пикетажной точки с тангенса на кривую.

Из таблиц при R = 100 м для K = 27,67 м путем интерполяции опреде— ляют X = 27,32 м и Y = 3,80 м. Затем рулеткой от НКК в сторону ПК1 по тангенсу отмеряют X = 27,32 м и из точки М по перпендикуляру отклады— вают ординату Y = 3,80 м.

Основание перпендикуляра М можно определить, отложив от ПК1 в направлении НКК отрезок (k – X) = 0.35 м.

119

В конце ординаты забивают кол и с тангенса в данное место на кри— вой переносят сторожок. Подобным образом выносят на кривую и другие пикеты до СКК.

Вынос пикета на кривую, когда она находится на втором тангенсе, производят аналогично, только за начало координат в данном случае принимают конец кривой.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1.Что такое круговая кривая и для чего она устраивается на трассе?

2.Как называются основные элементы кривой и как они определяются?

3.Какие точки кривой называются главными и как находят их пике— тажное значение?

4.Как находят положение главных точек кривой на местности?

5.Для чего выполняется детальная разбивка кривой?

6.Как выполняют детальную разбивку кривой способом прямоуголь— ных координат от тангенсов?

7.Как выполняют детальную разбивку кривой способом углов и хорд?

8.Как производят вынос пикетов на кривую?

Лекция 13 ЖЕЛЕЗНОДОРОЖНЫЕ КРИВЫЕ

План лекции

13.1.Переходная кривая

13.2.Железнодорожная кривая, её элементы и главные точки

13.3.Вычисление пикетажа главных точек железнодорожной кривой и разбивка кривой в главных точках на местности

13.1. Переходная кривая

Непосредственное сопряжение прямого участка пути с круговой кри— вой приводит к тому, что во время движения поезда в местах сопряжения внезапно возникает центробежная сила F (рис. 88), прямо пропорцио— нальная квадрату скорости движения v и обратно пропорциональная радиусу кривой R

(F = mvR 2 ).

120

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Круговые кривые. Железнодорожные линии (также и автомобильные дороги) в плане состоят из прямолинейных участков, сопряжённых между собой кривыми. Наиболее простой и распространённой формой кривой является дуга окружности. Такие кривые носят название круговых кривых. На железных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 500, 400 и 300 м. Радиус кривой выбирают при проектировании дороги, руководствуясь конкретными техническими условиями.

Главными точками кривой, определяющими её положение на местности, являются вершина угла ВУ, начало кривой НК, середина кривой СК и конец кривой КК (рис. 15.3).

[image]

Рис. 15.3 Схема круговой кривой

Основные элементы кривой – её радиус R и угол поворота a. К основным элементам относятся также:

– тангенс кривой Т (или касательная) — отрезок прямой между вершиной угла и началом или концом кривой;

– кривая К — длина кривой от начала кривой до её конца;

– биссектриса кривой Б — отрезок от вершины угла до середины кривой;

– домер Д — разность между длиной двух тангенсов и кривой.

Во время изысканий угол a измеряют, а радиус R назначают. Остальные элементы вычисляют по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (центр окружности):

Т = R×tg(a/2); К = R×a = p R a°¤180°; Б = R [sec(a/2) — 1], (15.1)

где a° — угол поворота в градусах.

Домер вычисляют по формуле

. (15.2)

Вместо вычислений по формулам можно воспользоваться таблицами для разбивки кривых на железных дорогах, где по заданным радиусу и углу поворота сразу находят значения Т, К, Б и Д.

В месте поворота трассы пикетаж ведётся по кривой. Пикетажное положение главных точек кривой определяют по формулам:

ПК НК = ПК ВУ — Т; ПК КК = ПК НК + К; ПК СК = ПК НК + К/2. (15.3)

Правильность вычислений контролируют по формулам:

ПК КК = ПК ВУ + Т — Д; ПК СК = ПК ВУ + Д/2. (15.4)

Пример.

Измерено a = 18°19¢ и задан радиус R = 600 м. Вершина угла расположена на пикете 6 + 36,00.

По формулам (15.1) и (15.2) или по таблицам находим элементы кривой: Т = 96,73 м; К = 191,81 м; Д = 1,65 м; Б = 7,75 м.

Вычислим пикетажное положение главных точек:

Контроль:

ПК ВУ 6 + 36,00 ПК ВУ 6 + 36,00

— Т 96,73 + Т 96,73

ПК НК 5 + 39,27 7 + 32,73

+ К 1 + 91,81 — Д 1,65

ПК КК 7 + 31,08 ПК КК 7 + 31,08

ПК НК 5 + 39,27 ПК ВУ 6 + 36,00

+ К/2 95,90 — Д/2 0,82

ПК СК 6 + 35,17 ПК СК 6 + 35,18

Переходные кривые. Непосредственное сопряжение прямого участка пути с круговой кривой приводит к тому, что во время движения поезда в месте сопряжения внезапно возникает центробежная сила F, прямо пропорциональная квадрату скорости движения v и обратно пропорциональная радиусу кривой . Чтобы обеспечить постепенное нарастание центробежной силы, между прямой и круговой кривой вставляют переходную кривую, радиус кривизны r которой плавно изменяется от ¥ до R. Если положить, чтобы центробежная сила менялась пропорционально расстоянию s от начала кривой, то получим

где s и r — текущие значения расстояния от начала переходной кривой и ее радиуса кривизны;

R – радиус кривизны в конце переходной кривой.

Индексом k отмечены значения переменных в конце переходной кривой.

Для радиуса кривизны переходной кривой в текущей точке i найдём:

r = lR/s, (15.5)

где через l обозначена длина переходной кривой s_k. Кривая, описываемая уравнением (15.5), в математике называется клотоидой, или радиоидальной спиралью.

Угол поворота трассы на переходной кривой. На бесконечно малом отрезке кривой ds (рис. 15.4, а) происходит поворот трассы на угол

Подставляя выражение радиуса кривизны r из (15.5), получим

Выполним интегрирование от начала кривой НК, где j = 0 и s = 0, до текущей точки i:

откуда

Rlj = s²/2.

б)

а)

[image]

Рис. 15.4 Схема переходной кривой:

а – углы поворота трассы: φ – в текущей точке i, β – в конце

переходной кривой (точка КПК); б — приращения координат

Из полученного уравнения вытекают формулы:

; ; l = 2Rb, (15.6)

где b — угол поворота трассы в конце переходной кривой;

l — длина переходной кривой;

R — радиус кривизны в конце переходной кривой, равный радиусу следующей за нею круговой кривой.

Координаты точки переходной кривой. Совместим начало координат с началом переходной кривой и направим ось x по касательной к ней (см. рис. 15.4, а). Бесконечно малому приращению дуги кривой соответствуют бесконечно малые приращения координат (рис. 15.4, б):

dx = cosj×ds; dy = sinj×ds. (15.7)

Разложим синус и косинус в ряд и, удержав в разложениях по два члена, подставим в них выражения для j из (15.6):

cosj = 1-j²/2 = 1 — s⁴/(8R²l²);

sinj = j — j³/6 = s²/(2Rl) — s⁶/(48R³l³).

Подставляя полученные выражения в (15.7) и выполняя интегрирование, найдём:

; (15.8)

. (15.9)

Смещение начала кривой (сдвижка). На рис. 15.5 дуга НК-КПК представляет собой переходную кривую, переходящую после точки КПК в круговую. Продолжим круговую кривую до точки Q, где её направление, параллельно оси x. Обозначим через m смещение, параллельное оси x, начала переходной кривой относительно точки Q, в которой начиналась бы круговая кривая при отсутствии переходной. Через p обозначим смещение в перпендикулярном направлении. Из рис. 15.5 видно:

где x_КПК и y_КПК — координаты конца переходной кривой, вычисляемые по формулам (15.8) и (15.9) с аргументом s = l .

Сочетание круговой кривой с переходными. На рис. 15.6 показана кривая, поворачивающая трассу на угол a и состоящая из круговой части с радиусом R и двух переходных кривых одинаковой длины l.

[image]

Рис. 15. 5 Смещение начала переходной кривой

Рис. 15.6 Сопряжение круговой кривой

с переходными

Если бы не было переходных кривых, в образованный прямыми линиями трассы угол была бы вписана дуга окружности радиуса R, равная Q-СК-Q₁ и имеющая длину K = Ra.

При наличии переходных кривых на каждой из них происходит поворот трассы на угол b, отчего на долю круговой кривой приходится поворот на угол a-2b. Поэтому суммарная длина кривой равна

K_c = R (a-2b) + 2l = Ra — 2Rb + 2l = K — l + 2l = K + l.

Тангенс и биссектриса определяются по формулам:

Т_с = T + m + T_p; Б_c= Б + Б_p,

где Т_p = ptg(a/2); Б_p = psec(a/2).

Домер в этом случае равен

В полевых условиях значения m, Т_pи Б_p вычисляют на микрокалькуляторе или выбирают из таблиц для разбивки кривых на железных дорогах. Пикетажное положение главных точек кривой вычисляют по формулам, аналогичным (15.3) и (15.4).

Источник

Инфоурок

›

Другое

›Презентации›Определение элементов кривых и пикетажных значений их главных точек

Определение элементов кривых и пикетажных значений их главных точек

Скачать материал

Сейчас обучается 267 человек из 65 регионов

Описание презентации по отдельным слайдам:

1 слайд

Филиал федерального государственного бюджетного общеобразовательного учреждения высшего образования
«Самарский государственный университет путей сообщения»
в г.Ртищево
Открытое занятие на тему:
«Определение элементов кривых и пикетажных значений их главных точек»
2 слайд

Цель открытого занятия: расширение знаний о геодезических съемках. А также познакомить с порядком выполнения разбивки кривой.
Задачи:
Образовательные:
— обеспечить в ходе занятия повторение ранее изученной темы;
— расширить знания обучающихся по геодезическим съемкам;
— закрепить знания и научить определению элементов и главных точек кривой.
Развивающие:
— развивать интерес к учению;
— развивать умение применять формулы и таблицы для решения задач.
Воспитательные:
— содействовать воспитанию аккуратности, сосредоточенности, ответственности за поставленные задачи;
— содействовать воспитанию инициативности и самостоятельности;
— воспитывать интерес к дисциплине, к учению.
3 слайд

АКТУАЛИЗАЦИЯ ПОЛУЧЕННЫХ РАНЕЕ ЗНАНИЙ:

Заполните пропуски в определениях:

Одним из основных документов для разработки проекта является ……, который вычерчивается на основании геодезических съемок.
(топографический план местности);
2. После того, как проект разработан, перед началом строительных работ, проект сооружения необходимо ….
(вынести/ главные точки разбить и закрепить н местности);
3. Разбивка проектных точек на местности производится методами ……
(прямоугольные и полярные координаты, угловые и линейные засечки);
4 слайд

Соедините стрелками понятие с определением
5 слайд

Тема: «Определение элементов кривых и пикетажных значений их главных точек»

Круговая кривая – это участок трассы, представляющий собой в плане дугу окружности.

Переходная кривая – кривая, которая служит для плавного перехода из прямого участка пути в кривую.
7 слайд

Разбивка круговой кривой.

Разбивка кривой – процесс, при котором определяют местоположение всех главных точек кривой

ЭТАПЫ:
8 слайд

Исходные данные.

Разбивку кривой начинают с определением исходных данных:

радиуса кривой (R),
вершина угла (ВУ),
угол поворота трассы (a).
9 слайд

Главными точками круговой кривой являются:
— начало круговой кривой (НКК); -вершина угла (ВУ)
— середина круговой кривой (СКК);
— конец круговой кривой (ККК);

НК
КК
СК
ВУ
10 слайд

Определение главных элементов круговой кривой

Т – тангенс кривой — расстояние от начала кривой (НК) до вершины угла поворота (ВУ) или от ВУ до конца кривой (КК).

К – длина круговой кривой, длина от НК до КК.

Б — биссектриса — расстояние от ВУ до середины кривой СК (длина отрезка биссектрисы угла Q по ее длине до кривой К).

Д – домер — разность длин двух тангенсов 2Т и кривой К.
11 слайд

Схема круговой кривой
Т
Т
Б
К
R
a
НК
ВУ
КК
СК
12 слайд

Как найти главные элементы?

Способы нахождения элементов кривой
13 слайд

Первый способ – определить элементы по формулам:

𝑇=𝑅𝑡𝑔 𝑎 2 (м)

𝐾=П𝑅 𝑎 180° (М)

Б=𝑅 1 𝑐𝑜𝑠 𝑎 2 −1 (м)

Д=2𝑇−К (м)
14 слайд

Второй способ – определить элементы по таблицам Ганьшина:
16 слайд

Пикетаж главных точек можно определить по формулам:

Учитывая, что элементы кривой записываются в пикетажном исчислении!
17 слайд

Для контроля вычислений положение конца круговой кривой получают ККК, если к пикетажному значению вершины угла поворота ВУ прибавить длину тангенса Т и из полученной суммы вычесть домер Д
КОНТРОЛЬ:
ВУ +Т −Д ККК
Если ответ сошелся с вычисленным ранее значением конца кривой, то контроль выполнен правильно, верно

В конце так и пишем: Контроль выполнен, верно!
18 слайд

Определение элементов кривых и пикетажных значений их главных точек первым методом (по формулам)

Задание № 1. Определить главные элементы и точки круговой кривой.
Исходные данные: ВУ 75+38, а=34°, R=1000 м.

Задание решается на доске
19 слайд

Схема круговой кривой
ККК 78+28,87
НКК 72+32,27
СКК 75+27,17
ВУ 75+38
20 слайд

4. Определение элементов кривых и пикетажных значений их главных точек первым методом (по таблицам Ганьшина)

Задание №2. Определить главные элементы и главные точки круговой кривой по таблицам Ганьшина.
Исходные данные: ВУ 55+20 , а= 12°; R=1000 м.
Решение: 1) По таблицам находим заданный угол 12°. На странице 26, мы видим главные элементы данного радиуса и данного угла. Переписываем их в решение.
Т=105,10 м; К= 209,44 м; Д=0,77 м; Б=5,51 м.
2)Как и в первом методе, определяем значение главных точек круговой кривой:
21 слайд

Задание № 1. Определить главные элементы и главные точки круговой кривой, начертить схему круговой кривой.

Исходные данные : ВУ 103+25, а= 63°, R= 800 м.
22 слайд

Задание № 2.
На слайде перечислены определения некоторых понятий, решение элементов, главных точек круговой кривой. Необходимо найти ошибки.

Буквой «К» обозначается расстояние от ВУ до середины кривой СК
(неправильно! обозначается длина кривой);
Чтобы найти начало круговой кривой, необходимо от значения вершины угла отнять длину кривой
(правильно! необходимо от значения вершины угла отнять длину тангенса кривой);
Число, получившееся при вычислении тангенса 1023 м в пикетажном исчислении будет 10+23
(верно!)
23 слайд

Р А З Б И В К А
Д О Р О Г А
Г Р А Д У С Ы
П И К Е Т А Ж
Ж У Р Н А Л
М Е Т Р Ы
Р А Д И У С
К Р И В А Я
К О Н Т Р О Л Ь
Д О М Е Р
Р
24 слайд

Рефлексия

Что сегодня было самым важным на занятии?
Какова цель занятия?
Что для тебя было трудно?
За что ты хочешь похвалить себя или кого-либо из одногруппников?
25 слайд

Вам необходимо продолжить фразу:

Мне было интересно….

Я сегодня понял, что…..

Мне было трудно….

На следующем занятии я хочу узнать…
26 слайд

Домашнее задание:
Электронный учебник. УМЦ ЖДТ. Громов А.Д., Бондаренко А.А. Инженерная геодезия и геоинформатика, страницы 484-491.

— Пройти тест на гугл форме

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 266 078 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

09.04.2022
69
0

09.04.2022
199
3

09.04.2022
156
2

09.04.2022
193
0

09.04.2022
268
3

09.04.2022
1351
6

09.04.2022
808
5

09.04.2022
68
0

Вам будут интересны эти курсы:

Курс повышения квалификации «Правовое обеспечение деятельности коммерческой организации и индивидуальных предпринимателей»
Курс профессиональной переподготовки «Клиническая психология: организация реабилитационной работы в социальной сфере»
Курс повышения квалификации «Основы построения коммуникаций в организации»
Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
Курс повышения квалификации «Правовое регулирование рекламной и PR-деятельности»
Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»
Курс повышения квалификации «Финансы: управление структурой капитала»
Курс профессиональной переподготовки «Организация деятельности секретаря руководителя со знанием английского языка»
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»
Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»
Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
Курс профессиональной переподготовки «Осуществление и координация продаж»
Курс профессиональной переподготовки «Организация маркетинговой деятельности»
Курс профессиональной переподготовки «Стандартизация и метрология»

Настоящий материал опубликован пользователем Шлючкова Татьяна Игоревна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 3 года и 7 месяцев
- Подписчики: 4
- Всего просмотров: 5068
- Всего материалов:
  
  8

Источник

На углах поворота трасс автомобильных дорог производим вставки кривых и пересчет по ним пикетажа. В качестве таких кривых применяем дуги окружностей больших радиусов. Главные точки кривой: начало, середина и конец кривой, далее НК, СК и КК соответственно (рис. 1.5).

Рис. 1.5 Элементы и главные точки горизонтальной круговой кривой

Элементы круговых кривых: угол поворота б, радиус кривой R, дорожный тангенс Т, длина кривой К, биссектриса Б, домер Д. При трассировании на кривых линейные измерения ведут по тангенсам, а длину трассы считают по кривой, домер показывает, насколько расстояние по двум тангенсам длиннее кривой.

Вычисление элементов горизонтальных кривых

Элементы кривых вычисляются по данным б, R и по формулам

, , , .

Вычисление пикетажных значений главных точек круговых кривых

Пикетажные значения главных точек кривых находят по формулам

ПК НК = ПК ВУ — Т, ПК К = ПК НК + К, ПК СК = ПК НК + К/2.

Контроль ПК КК = ПК ВУ + Т — Д, ПК СК = ПК КК — К/2 .

Составление ведомости прямых и кривых

По заданному азимуту начального направления трассы и углам поворота вычисляют азимуты последующих направлений

Вычисленные азимуты переводят в румбы.

Таблица 1.8 Перевод азимутов в румбы.

Азимут	Определение румба по азимуту	№ четверти, название румба
I CB
II ЮВ
III ЮЗ
IV СЗ

Расстояние между вершинами углов:

Длина отрезка от ПК0 до первой вершины угла поворота ВУ1 равна пикетажному значению первой вершины угла.

Вычисляют длины прямых вставок

: .

Длина первой прямой вставки равна ПК НК первой кривой, последней разности ПК конца трассы и ПК КК последней кривой.

Переходные кривые

План трассы следует проектировать из условия наименьшего ограничения и изменения скорости движения автомобилей, обеспечения безопасности и удобства движения, а также возможной реконструкции дороги за пределами перспективного периода. При проектировании элементов плана, равно как и продольного и поперечного профилей, перспективный период следует принимать 20 лет. Начальным годом расчетного перспективного периода является год завершения разработки проекта дороги (или самостоятельного участка дороги).

Для обеспечения плавного въезда в круговую кривую малого радиуса и выезда из кривой последние сопрягают с прямыми участками трассы посредством переходных кривых.

В практике проектирования автомобильных дорог наибольшее распространение получили переходные кривые типа клотоиды, которые характеризуются линейным законом нарастания кривизны по длине и более, чем другие математические кривые, соответствуют фактической траектории движения автомобиля.

Клотоида (или радиоидальная спираль) как математическая кривая представляет собой спираль, радиус кривизны которой непрерывно изменяется от р = ? в начальной точке до р = 0 в бесконечном удалении от начала кривой (рис 1.9)

В качестве переходной кривой, как самостоятельного элемента трассы, применяется только начальный участок клотоиды от точки отхода от прямого участка, где р = ?, до точки на кривой, где р = R.

Уравнение клотоиды имеет вид:

где — радиус кривизны,

— расстояние от начала клотоиды до точки М на ней.

Параметр клотоиды — величина постоянная и выражается как произведение:

где R — радиус кривизны в конце клотоиды в конце отрезка клотоиды длиной L,

L — длина отрезка клотоиды от ее начала до точки на кривой, где радиус кривизны .

Рис. 1.9.1 Клотоида (переходная кривая)

Параметр А характеризует степень изменения кривизны клотоиды.

Наименьшая длина переходной кривой определяется по условию равномерного нарастания центробежной силы в пределах переходной кривой:

где V_p — расчетная скорость движения, принимаемая по СНиП- 2.05.02-85 для дороги соответствующей категории, км/ч;

I — допускаемая скорость нарастания центробежного ускорения, м/с³.

Для дорог 1- V категорий предельное значение 1= 0,3-0,1 м/с³. Чем выше расчетная скорость, тем меньшее значение I следует принимать.

Согласно СНиП [4] сопряжение прямых участков с круговыми кривыми посредством переходной кривой обязательно, если радиус круговой кривой R<3000 м — на дорогах / категории и R<2000 м — на дорогах прочих категорий. Наименьшая длина переходной кривой нормируется в зависимости от радиуса круговой кривой. Нормативную длину переходной кривой рекомендуется увеличить в 1,5 — 2 раза, если это позволяет расстояние между углами поворота трассы. Чем больше длина клотоиды, тем более плавно изменяется ее кривизна, а следовательно, условия движения для пассажиров и водителя более комфортны.

Источник