Как найти надежность выборки

Объем выборки и надежность

Под
объемом выборки понимается число
наблюдений за поведением одного варианта
системы (если проводится факторный
эксперимент, то каждый набор значений
факторов определяет один вариант
системы).

Под
надежностью понимается статистическая
точность выборочной оценки. Она
выражается, например, длиной доверительного
интервала и доверительной вероятностью
(1-).

При
проведении имитированных экспериментов
нам приходится решать две задачи:

1.
Для заранее установленного объема
выборки (числа повторения опытов) найти
надежность оценки.

2.
При фиксированной желаемой надежности
определить требуемый объем выборки.

При
определении надежности первой задачей
является оценивание дисперсий. На основе
этого вычисляется доверительный
интервал.

Стандартные
методы построения доверительного
интервала основаны на предположении
независимости и нормальности наблюдений.
В имитационной модели предположение о
нормальности можно удовлетворить, если
откликом одного опыта сделать среднее
значение интересующей нас величины в
течение одного опыта.

Соответствующая
предельная теорема показывает, что
среднее даже зависимых наблюдений
распределено примерно нормально. Более
существенным является предположение
о независимости результатов различных
имитационных опытов. Проще всего
независимые опыты могут быть получены
повторениями с помощью различных
последовательностей случайных чисел.
Но при этом возможно получение смещенных
результатов из-за наличия неустановившихся
режимов работы модели.

Другой
подход — это деление удлиненного опыта
на подопыты. Средние значения откликов
в каждом подопыте дают нам требуемые
данные. В любом случае доверительный
интервал для интересующей нас величины
строится с помощью распределения
Стьюдента со степенями свободы (n
-1),
где n
число наблюдений, или объем выборки:

–
квантиль
распределения Стьюдента

Кроме
оценки среднего (*) можно применять для
проверки гипотез о среднем. Если мы
хотим проверить гипотезу о том, что Е(х)
= _о,
то мы смотрим, содержится ли _o
в найденном доверительном интервале.
Если нет, то гипотезу отвергаем.

При
проверке различных средних значений
двух моделей мы имеем две нормально
распределенные совокупности:

.

Мы
имеем независимые наблюдения за моделями:

Существует
несколько способов сравнить среднее:

Первый
способ

Наблюдения
х₁
и х₂
можно спарить, применяя общие случайные
числа, тогда х_1i
и
х_2i
будут
зависимыми, а сами пары (х_1i,х_2i)
останутся независимыми. Тогда мы можем
рассматривать величины

.

В
этом случае мы возвращаемся к задаче
проверки гипотезы о равенстве
математического ожидания Е(d)=
0.
Эта задача решается с помощью критерия
Стьюдента.

Второй
способ

Если
обе совокупности имеют одинаковую
дисперсию:

,

то
можно воспользоваться стандартным
критерием Стьюдента. Доверительный
интервал здесь будет:

где
-оценка.

Третий
способ

.

В
этом случае можно воспользоваться
следующим подходом.

Пусть
.

В
этом случае доверительный интервал:

,

Причем,
здесь при вычислении х₂
использованы все n₂
значений опытов со второй моделью, а
при определении U_i
только n₁
первых значений опытов со второй моделью.

Определение
необходимого количества имитационных
опытов при заданной надежности происходит
следующим образом.

Пусть
известно, что закон распределения
переменной отклика нормальный с
дисперсией ².
Если мы хотим, чтобы с вероятностью
(1-)
оценка среднего

отличалась от истинного значения не
более чем на С
единиц, мы используем уравнение:

,
— истинное ср. значение

Поскольку
x
—
среднее n
независимых нормально распределенных
случайных величин, то можем записать:

,

²(x)
– значение дисперсии отклика x при одном
имитационном опыте.

Z^/2
– квантиль нормального распределения.

Т.о.,
можно записать, что:

Это
есть искомое число опытов, которые надо
провести, чтобы получить оценку с
требуемой надежностью. Однако в
имитационном моделировании величина
²(x)
неизвестна, поэтому вместо нее мы
поставим ее оценку S²(x)
и используем критерий Стьюдента с (n -1)
степенями свободы. Т.е. получим:

Как
видно из этого выражения значение n
зависит от результатов экспериментов
S²
(x) и от самого себя
.

Лекция
13

Поэтому
более подходящей является итеративная
процедура определения числа имитационных
опытов n по следующей совокупности
неравенств:

здесь
S_i²
(x), i=2,3,…, n
— последовательная оценка дисперсии
²(x)
по результатам i
наблюдений.

Эти
оценки не являются независимыми и,
следовательно, вероятность интересующего
события подсчитать трудно. Она
необязательно окажется равной (1-).

Подобная
процедура определения количества опытов
называется процедурой автоматического
останова.

Другой
способ – это схема двойной выборки.
Первоначально проводится n₀
имитационных опытов, по которым
оцениваются ²
с (n_o-1)
степенями свободы. Полученная оценка
S²_no
дает
количество требуемых опытов:

.

После
этого проводятся n-n_o

опытов.

Проблемой
при таком подходе является выбор значения
n_o.
Большое
значение n_o
дает уменьшение квантиля
,
но может привести к лишним опытам, когда
n_o
> n.
Т.к. в имитационном моделировании опыты
обычно дороги, то чаще применяют более
эффективную последовательную процедуру.

Рассмотрим
теперь ситуацию в сравнении двух моделей.
Для известных дисперсий ₁²
и ₂²
, исследуемых значений первой и второй
модели мы имеем, что

.

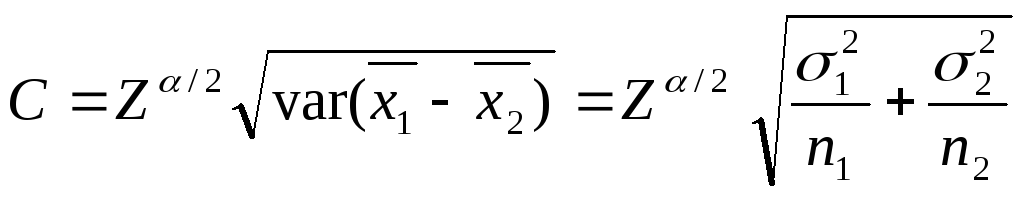
Дисперсия
()
минимальна для фиксированного общего
объема выборки n
= n₁+n₂
при выполнении соотношения:

,

Поэтому

.

Следовательно,

.

Отсюда

А
общее число опытов:

что
позволяет получить доверительный
интервал с размахом С
и вероятностью (1-).

Для
неизвестных дисперсий предлагается
следующий последовательный подход:

а).
Пусть на очередном шаге произведено n₁

и n₂

опытов над соответствующими моделями.
Вычисляются оценки для дисперсий

и
:

Если
,
то следующий опыт будет проводиться
над первой моделью, в противном случае
— над второй.

б).
Для n
= n₁+
n₂
вычисляется величина

.

Дальнейшее
проведение опытов прекращается, как
только осуществляется одно из следующих
условий:

1..

2..

3.
или
.

Организационные
аспекты имитационного моделирования

Согласно
исследованиям, построение модели объекта
в среднем занимает 10.1 месяца. Средняя
группа работающих над моделью — 2.5
человека. Для разработки одной машинной
модели-имитатора сложной системы
требуются специалисты различных
профилей:

• в
  области исследования операций;

• статистики;

• программирования;

• системного
  анализа;

Также
требуются специалисты конкретной
предметной области. Но не все специалисты
нужны одновременно.

На
ранних стадиях разработки необходимы
лишь специалисты по исследованию
операций и специалисты-отраслевики.
Экспертные оценки могут потребоваться
на различных стадиях выполнения проекта.

Программисты
и аналитики включаются в число
разработчиков лишь после завершения
создания программного обеспечения для
первых грубых моделей системы.

Главная
цель создаваемой модели — помочь
руководителю повысить качество
управления. Поэтому перед созданием
модели необходимо вникнуть как в сам
процесс принятия решения, так и в
функции лица, принимающего решения
(ЛПР).

Необходимые
и достаточные условия существования
ситуации принятия решения предполагают
наличие:

• цели,
  которую хочет достичь ЛПР;

• по
  крайней мере, двух альтернативных
  вариантов решения;

• сомнения
  ЛПР о том, какую из альтернатив
  предпочесть.

Необходимо
обратить внимание на следующий аспект
принятия решения: каждое решение содержит
элементы двух типов — фактографические,
ценностные.

Фактографические
элементы представляют собой данные о
наблюдении мира и его закономерностей;
их можно и нужно проверять на истинность
и ложность.

Ценностные
элементы содержат этические и моральные
характеристики принимаемого решения.
Правомерность их проверить невозможно.

Такое
же разделение характерно и для целей,
стоящих перед руководителем при принятии
решения. Поэтому большинство проблем,
связанных с принятием решения, содержат
как объективные, так и субъективные
элементы. Поэтому весьма полезным
оказывается тесное сотрудничество с
ЛПР при разработке модели. В результате
этого ценностные элементы могут найти
свое отражение в моделях.

В
других случаях необходимо, чтобы модель
как можно точнее воспроизводила реальный
объект по всем его фактическим или
объективным характеристикам. ЛПР,
используя результаты моделирования,
накладывает на них свои ценностные
предпочтения для вынесения окончательного
решения.

Модели
используются в двух различных целях:

1.
В научном плане — это один из этапов в
цепи формирования гипотез, построения
моделей, предсказания будущего поведения
системы и оценки результатов. Здесь
обычно судят о модели по ее качеству.
Хорошей моделью считается нетривиальная,
мощная и изящная модель. Нетривиальная
модель вскрывает детали, невидимые при
непосредственном наблюдении. Мощная
модель позволяет получить много таких
нетривиальных деталей. Изящная модель
имеет простую структуру и легко
рассчитывается на компьютере.

2.
Руководители используют модель для
выявления ценностных альтернатив
решения проблемы. С их точки зрения
хорошая модель — это релевантная, точная,
результативная и экономичная. Модель
считается релевантной, если она
предназначена для решения важных для
руководителя проблем. Модель точная,
если результаты обладают высокой
степенью достоверности. Результативная
модель, если получаемые результаты
могут найти успешное применение. Модель
экономичная, если эффект от внедрения
превышает расходы на ее создание и
использование.

При
создании групп по разработке модели
желательно вводить в группу следующих
специалистов:

• одного
  или нескольких специалистов по системному
  анализу; они должны иметь опыт по
  применению используемых методов к
  решению конкретных задач по принятию
  управленческих решений;

• одного
  или нескольких специалистов по
  вычислительной технике; такой специалист
  должен быть не просто программистом,
  но и аналитиком, он должен сам уметь
  строить модель, но его основные усилия
  должны быть направлены на использование
  компьютера для обработки данных и
  получения результатов на основе
  применения математических методов;

• одного
  или нескольких эрудированных лиц,
  хорошо знающих организацию, ее людей
  и особенно ее проблемы;

• одного
  или нескольких сотрудников организаций,
  представляющих отдел, который
  заинтересован в решении проблемы.

Важным
фактором в разработке, программировании
и применении модели является способ
построения машинной программы.

Наиболее
применимым способом здесь является
модульное программирование. Его можно
определить, как систему построения
программы из набора отдельных
взаимосвязанных блоков (модулей), с
помощью различных сочетаний которых
можно получить отдельную программу.

При
противоположном подходе (построение
монолитных программ) возникают следующие
проблемы:

1.
Практически невозможна полная проверка
программы; это объясняется большим
числом общих логических построений,
сложными взаимосвязями и невозможностью
выделить ключевые участки программы
для испытаний;

2.
В алгоритм невозможно внести изменения
без серьезной переделки программы;

3.
Работа всей группы зависит от постоянного
участия в ней программиста — разработчика
такой программы.

При
модульном программировании каждым
модулем реализуется определенная
логическая функция (или несколько
логических функций). Для того, чтобы
определить какие подсистемы и логические
функции понадобятся в программе,
проводится предварительный анализ
проблем. После того, как они выявлены,
каждый модуль кодируется и отлаживается
отдельно. Руководителю разработки
желательно придерживаться следующих
правил при программировании:

• модульный
  подход;

• использование
  коротких (до 50 строк) основных программ
  и подпрограмм;

• начинать
  каждую основную программу и подпрограмму
  комментарием;

• составление
  полной документации программы.

Полное
документирование предполагает наличие
блок-схемы, алгоритмов каждого модуля
и всей программы, описание входных
данных, необходимых для работы программы,
т.е. место расположения входных данных
и требуемое поле записи, описание
переменных программы, не используемых
в качестве входных, словесное описание
задач и функций всех модулей, пусковые
характеристики, необходимые для
выполнения программы на требуемом
компьютере, тестовые примеры.

Так
как имитационная модель создается для
пользователя, то и информация, полученная
с ее помощью, должна быть приемлема для
него же. Критерии приемлемости включают
надежность и полезность информации.

Выходные
данные модели должны быть разумными,
т.е. модель не должна давать абсурдных
ответов, даже если на вход подаются
абсурдные данные.

Второй
аспект применимости состоит в том, что
заказчик-пользователь должен понимать,
как можно использовать результаты
моделирования.

С
достижением конечной цели тесно связано
требование реалистичности данных,
необходимых для использования модели.
Реалистичные данные должны быть
достаточно надежными, доступными и
получаемыми за разумную плату.

Кроме
того, ИМ должна позволять администратору
оценивать и те решения, которые
удовлетворяют его собственным понятиям
рациональности, а также возможные
результаты применения сформулированных
им стратегий.

Подготавливая
результаты исследования для предоставления
их заказчику, рекомендуется придерживаться
следующих правил:

1.
Письменным отчетам следует предпочесть
устные сообщения с одновременным
использованием хорошо продуманных
демонстрационных средств;

2.
Одному большому формальному изложению
результатов следует предпочесть серию
небольших неформальных обсуждений;

3.
Необходимо делать упор на логику вашего
подхода к решению задач;

4.
В первом докладе необходимо четко
описать принятые допущения и ограничения;

5.
Необходимо тщательно описать целевую
функцию и выходные переменные модели;

6.
Тщательно описать концептуальный
подход, основные взаимосвязи, переменные
и обоснования выбранного способа
интерпретации результатов;

7.
Дать общую оценку, а также перечислить
все достоинства и недостатки рассмотренных
альтернатив и результатов, полученных
с помощью модели.

Соседние файлы в папке Лекции

• #
• #
• #
• #
• #
• #

Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.

Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.

Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.

Определение доверительного интервала.

Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 — alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.

Этот интервал часто упоминается как (100 (1 — alpha)% ) доверительный интервал для параметра.

Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).

В этом чтении, мы имеем дело только с двусторонними доверительными интервалами — доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.

Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.

При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.

При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.

Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.

Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.

На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.

Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.

Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.

Построение доверительных интервалов.

Доверительный интервал (100 (1 — alpha)% ) для параметра имеет следующую структуру.

Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.

Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.

Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.

Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).

Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).

Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.

Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.

В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.

---

Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 — alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.

Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:

( sigma_{overline X} = 20 Big / sqrt{100} = 2 )

Доверительный интервал, таким образом, имеет нижний предел:

( overline X — 1.96 sigma_{overline X} ) = 25 — 1.96(2) = 25 — 3.92 = 21.08.

Верхний предел доверительного интервала равен:

( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92

95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.

Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).

Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:

( Large dst overline X pm z_{alpha /2}{sigma over sqrt n}  ) (Формула 4)

Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.

Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.

Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:

Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.

«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»

см. Freund и Williams (1977), стр. 266.

На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.

Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.

---

Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).

Распределение статистики (t) называется t-распределением Стьюдента (англ. «Student’s t-distribution») из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.

В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.

Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, — это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).

В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).

Доверительные интервалы для среднего по совокупности — z-альтернатива (большая выборка, дисперсия совокупности неизвестна).

Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:

( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)

Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.

Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.

Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.

[см. также: CFA — Коэффициент Шарпа]

Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.

Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.

---

Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).

Доверительный интервал будет равен:

( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } \ &= 0.45 pm 1.65{0.30 over sqrt {100}} \ &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495   end{aligned} )

Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.

В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.

Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.

Концепция степеней свободы.

Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.

Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.

Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.

t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.

Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.

Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n — 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.

Мы также используем ( n — 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.

---

Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?

При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.

Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n — 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.

Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.

t-распределение Стьюдента.

Предположим, что мы делаем выборку из нормального распределения.

Коэффициент (z = (overline X — mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X — mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n — 1) степеней свободы.

Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.

Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.

На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.

Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.

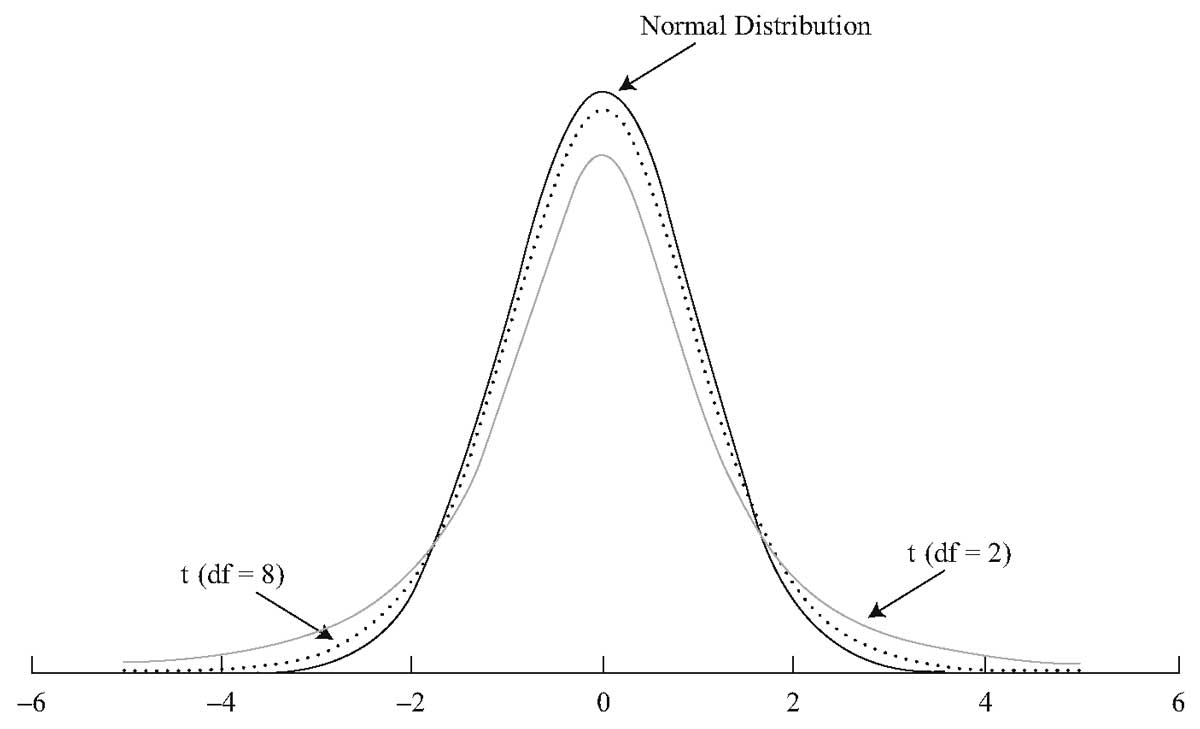
Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.

По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.

Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.

t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.

Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.

Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.

Например,

Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.

Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) — t-распределение.

Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:

• выборка является большой, или
• выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,

то доверительный интервал (100 (1 — alpha)% ) для среднего совокупности ( mu ) задается формулой:

Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.

Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.

Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.

Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение — 0.30.

Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.

Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.

Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.

Доверительный интервал будет:

( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } \  &= 0.45 pm 1.66{0.30 over sqrt {100}} \ &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498   end{aligned} )

Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.

В Таблице 3 приведены различные факторы надежности, которые мы использовали.

Таблица 3. Основы для расчета факторов надежности.

Выборка из:	Статистика для выборки малого размера	Статистика для выборки большого размера
Нормальное распределение с известной дисперсией	(z)	(z)
Нормальное распределение с неизвестной дисперсией	(t)	(t)*
Ненормальное распределение с известной дисперсией	недоступно	(z)
Ненормальное распределение с неизвестной дисперсией	недоступно	(t)*

* Использование (z) также приемлемо.

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних

1. Формула (даже две)

Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).

Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.

На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).

В таких случаях для расчета объема выборки используется следующая формула:

где 

n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.

Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.

Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.

Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.

Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне

Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.

ШПАРГАЛКА (скопируйте  ссылку или текст)

Подходы к решению проблемы:

Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где 
n – объем выборки,

N – объем генеральной совокупности, 

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,

p – доля респондентов с наличием исследуемого признака,

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования) 

∆ – предельная ошибка выборки.

Например,

рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки: 

Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%

При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.

2. Причины «раздувать» выборку

Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).

Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок

Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра

При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).

Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:

• увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
• добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).

Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).

---

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ

Доверительный уровень:

Ошибка выборки (?):
%

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

РЕЗУЛЬТАТ

Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам. 

Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.

Объем выборки рассчитывается по следующим формулам

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.

Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.

ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:

Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:

n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек

Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек. 

---

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Доля признака (p):
%

РЕЗУЛЬТАТ

Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).

Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.

Ошибка выборки для доли признака рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

 (в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.

p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.

Δ– предельная ошибка выборки.

Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:

Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%

Рассчитаем доверительный интервал:

(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)

Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).

Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.

---

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Среднее значение (x̄):

Стандартное отклонение (s):

РЕЗУЛЬТАТ

Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).

Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.

Ошибка выборки для среднего значения рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.

s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Δ– предельная ошибка выборки.

Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:

Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44

Рассчитаем доверительный интервал:

(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)

Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.

---

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ

Доверительный уровень:

	Измерение 1	Измерение 2
Доля признака (p):	%	%
Объём выборки (n):

РЕЗУЛЬТАТ

Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.

Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.

Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.

В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:

• Обе выборки – простые случайные 
• Выборки независимы (между значениями двух выборок нет закономерной связи) 
• Генеральные совокупности значительно больше выборок 
• Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.

В калькуляторе используются следующие вводные данные:

Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.

Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

---

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ

Доверительный уровень:

	Измерение 1	Измерение 2
Среднее значение (x̄):
Стандартное отклонение (s):
Объём выборки (n):

РЕЗУЛЬТАТ

 

Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?

Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.

Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.

В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:

• Обе выборки – простые случайные 
• Выборки независимы (между значениями двух выборок нет закономерной связи)
• Генеральные совокупности значительно больше выборок 
• Распределения значений в выборках близки к нормальному распределению.

В калькуляторе используются следующие вводные данные:

Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.

Среднее значение ( ̅x) – среднее арифметическое показателя.

Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

Что делает данные выборки надежными?

На чтение 2 мин Просмотров 97 Опубликовано 01.01.2023

Данные — это набор измерений и фактов, а также инструмент, который помогает человеку или группе людей прийти к правильному выводу, предоставляя им некоторую информацию. Это помогает аналитику понять, проанализировать и интерпретировать различные социально-экономические проблемы, такие как безработица, бедность, инфляция и т. д. Помимо понимания проблем, это также помогает в определении причин проблемы, чтобы найти возможные решения для них. Данные включают не только теоретическую информацию, но и некоторые числовые факты, которые могут подтвердить эту информацию. Сбор данных является первым этапом статистического исследования и может быть получен из двух разных источников, а именно из первичных и вторичных источников.

Содержание

1. Что такое выборка?
2. Надежность данных выборки
3. 1. Размер образца:
4. 2. Метод отбора проб:
5. 3. Предвзятость корреспондентов и счетчиков:
6. 4. Обучение счетчиков:

Что такое выборка?

Процесс статистического анализа, с помощью которого исследователи из большей совокупности проводят заранее определенное количество наблюдений, известен как выборка. Метод отбора проб зависит от типа анализа, проводимого для исследования; однако он может включать систематическую выборку или простую случайную выборку.

Надежность данных выборки

Если характеристики вселенной полностью представлены выборкой, это означает, что данные выборки надежны. Основными факторами, от которых зависит достоверность данных выборки, являются следующие:

1. Размер образца:

Надежность выборочных данных зависит от размера выборки. Если размер выборки очень мал, он не сможет представить генеральную совокупность. А из-за небольшого размера выводы, сделанные по выборке, будут недостаточно достоверными.

2. Метод отбора проб:

Если используемый метод выборки не является простым и исчерпывающим, он не будет адекватно отражать данную совокупность. И из-за этого полученные результаты не будут надежными.

3. Предвзятость корреспондентов и счетчиков:

Со стороны корреспондентов и счетчиков должно быть как можно меньше предубеждений; в противном случае данные выборки не будут надежными.

4. Обучение счетчиков:

Надежность выборки также зависит от подготовки исследователей. Если следователи или счетчики не обучены тому, чтобы стать экспертами в своей области исследований, то выборка будет недостаточно надежной.