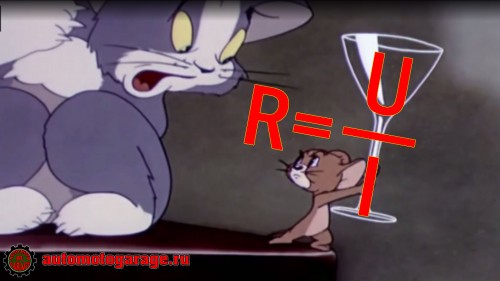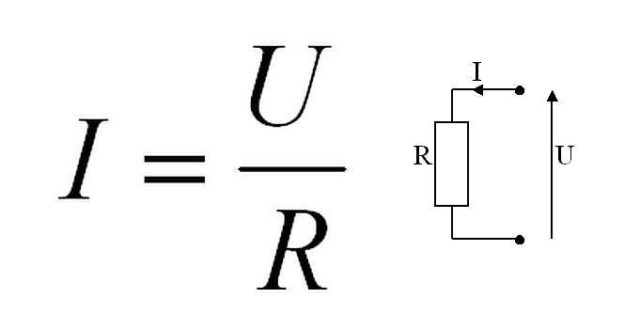Большинство бытовых приборов, подключаемых к сети, характеризуются таким параметром, как электрическая мощность устройства. С физической точки зрения мощность представляет собой количественное выражение совершаемой работы. Поэтому для оценки эффективности того или иного устройства вам необходимо знать нагрузку, которую он будет создавать в цепи. Далее мы рассмотрим особенности самого понятия и как найти мощность тока, обладая различными характеристиками самого устройства и электрической сети.
Понятие электрической мощности и способы ее расчета
С электротехнической точки зрения она представляет собой количественное выражение взаимодействия энергии с материалом проводников и элементами при протекании тока в электрической цепи. Из-за наличия электрического сопротивления во всех деталях, задействованных в проведения электротока, направленное движение заряженных частиц встречает препятствие на пути следования. Это и обуславливает столкновение носителей заряда, электроэнергия переходит в другие виды и выделяется в виде излучения, тепла или механической энергии в окружающее пространство. Преобразование одного вида в другой и есть потребляемая мощность прибора или участка электрической цепи.
В зависимости от параметров источника тока и напряжения мощность также имеет отличительные характеристики. В электротехнике обозначается S, P и Q, единица измерения согласно международной системы СИ – ватты. Вычислить мощность можно через различные параметры приборов и электрических приборов. Рассмотрим каждый из них более детально.
Через напряжение и ток
Наиболее актуальный способ, чтобы рассчитать мощность в цепях постоянного тока – это использование данных о силе тока и приложенного напряжения. Для этого вам необходимо использовать формулу расчета: P = U*I
Где:
- P – активная мощность;
- U – напряжение приложенное к участку цепи;
- I — сила тока, протекающего через соответствующий участок.
Этот вариант подходит только для активной нагрузки, где постоянный ток не обеспечивает взаимодействия с реактивной составляющей цепи. Чтобы найти мощность вам нужно выполнить произведение силы тока на напряжение. Обе величины должны находиться в одних единицах измерения – Вольты и Амперы, тогда результат также получится в Ваттах. Можно использовать и другие способы кВ, кА, мВ, мА, мкВ, мкА и т.д., но и параметр мощности пропорционально изменит свой десятичный показатель.
Через напряжение и сопротивление
Для большинства электрических устройств известен такой параметр, как внутреннее сопротивление, которое принимается за константу на весь период их эксплуатации. Так как бытовые или промышленные единицы подключаются к источнику с известным номиналом напряжения, определять мощность достаточно просто. Активная мощность находится из предыдущего соотношения и закона Ома для участка цепи, согласно которого ток на участке прямо пропорционален величине приложенного напряжения и имеет обратную пропорциональность к сопротивлению:
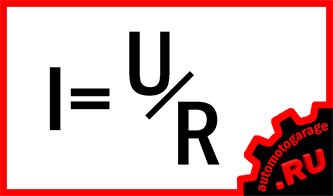
I = U/R
Если выражение для вычисления токовой нагрузки подставить в предыдущую формулу, то получится такое выражение для определения мощности:
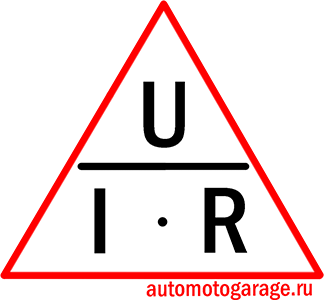
P = U*(U/R)=U2/R
Где,
- P – величина нагрузки;
- U – приложенная разность потенциалов;
- R – сопротивление нагрузки.
Через ток и сопротивление
Бывает ситуация, когда разность потенциалов, приложенная к электрическому прибору, неизвестна или требует трудоемких вычислений, что не всегда удобно. Особенно актуален данный вопрос, если несколько устройств подключены последовательно и вам неизвестно, каким образом потребляемая электроэнергия распределяется между ними. Подход в определении здесь ничем не отличается от предыдущего способа, за основу берется базовое утверждение, что электрическая нагрузка рассчитывается как P = U×I, с той разницей, что напряжение нам не известно.
Поэтому ее мы также выведем из закона Ома, согласно которого нам известно, что падение напряжения на каком-либо отрезке линии или электроустановки прямо пропорционально току, протекающему по этому участку и сопротивлению отрезка цепи:
U=I*R
после того как выражение подставить в формулу мощности, получим:
P = (I*R)*I =I2*R
Как видите, мощность будет равна квадрату силы тока умноженной на сопротивление.
Полная мощность в цепи переменного тока
Сети переменного тока кардинально отличаются от постоянного тем, что изменение электрических величин, приводит к появлению не только активной, но и реактивной составляющей. В итоге суммарная мощность будет также состоять активной и реактивной энергии:

Где,
- S – полная мощность
- P – активная составляющая – возникает при взаимодействии электротока с активным сопротивлением;
- Q – реактивная составляющая – возникает при взаимодействии электротока с реактивным сопротивлением.
Также составляющие вычисляются через тригонометрические функции, так:
P = U*I*cosφ
Q = U*I*sinφ
что активно используется в расчете электрических машин.
Пример расчета полной мощности для электродвигателя
Отдельный интерес представляет собой нагрузка, подключенная к трехфазной сети, так как электрические величины, протекающие в ней, напрямую зависят от номинальной нагрузки каждой из фаз. Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.
Особенность питания и асинхронной и синхронной электрической машины заключается в том, что на обмотки может подаваться и фазное и линейное напряжение. Тот или иной вариант, как правило, обуславливается способом соединения обмоток электродвигателя. Тогда мощность будет вычисляться по формуле:
S = 3*Uф*Iф
В случае выполнения расчетов с линейным напряжением, чтобы найти мощность формула примет вид:
Активная и реактивная мощности будут вычисляться по аналогии с сетями переменного тока, как было рассмотрено ранее.
Теперь рассмотрим вычисления на примере конкретной электрической машины асинхронного типа. Следует отметить, что официальная производительность, указываемая в паспортных данных электродвигателя – это полезная мощность, которую двигатель может выдать при совершении оборотов вала. Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.
Как видите, для вычислений с шильда мы возьмем следующую информацию об электродвигателе:
- полезная производительность – 3 кВт, а в переводе на систему измерения – 3000 Вт;
- коэффициент полезного действия – 80%, а в пересчете для вычислений будем пользоваться показателем 0,8;
- тригонометрическая функция соотношения активных и реактивных составляющих – 0,74%;
- напряжение, при соединении обмоток треугольником составит 220 В;
- сила тока при том же способе соединения – 13,3 А.
С таким перечнем характеристик можно воспользоваться несколькими способами:
S = 1,732*220*13,3 = 5067 Вт
Чтобы найти искомую величину, сначала определяем активную составляющую:
P = Pполезная / КПД = 3000/0.8 = 3750 Вт
Далее полную по способу деления активной на коэффициент cos φ:
S = P/cos φ = 3750/0.74 = 5067 Вт
Как видите, и в первом, и во втором случае искомая величина получилась одинакового значения.
Примеры задач
Для примера рассмотрим вычисление на участках электрической цепи с последовательным и параллельным соединением элементов. Первый вариант предусматривает ситуацию, когда все детали соединяются друг за другом от одного полюса источника питания до другого.
Как видите на рисунке, в качестве источника мы используем батарейку с номинальным напряжением 9 В и три резистора по 10, 20 и 30 Ом соответственно. Так как номинальный ток нам не известен, расчет произведем через напряжение и сопротивление:
P = U2/R = 81 / (10+20+30) = 1.35 Вт
Для параллельной схемы подключения возьмем в качестве примера участок цепи с двумя резисторами и одним источником тока:
Как видите, для удобства расчетов нам нужно привести параллельно подключенные резисторы к схеме замещения, из чего получится:
Rобщ = (R1*R2) / (R1+R2) = (10*15) / (10+15) = 6 Ом
Тогда искомый номинал нагрузки мы можем узнать через значение тока и сопротивления:
P = I2*R = 25*6 = 150 Вт
Видео по теме
Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.
В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.
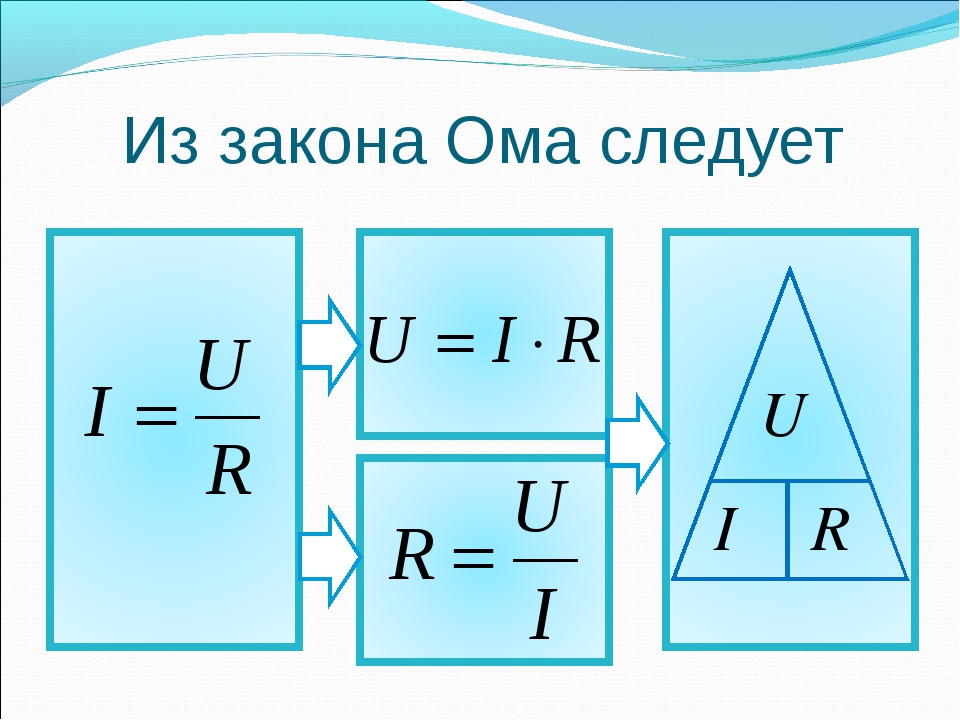
Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению
Так записывается основная формула:
Путем преобразования основной формулы можно найти и другие две величины:
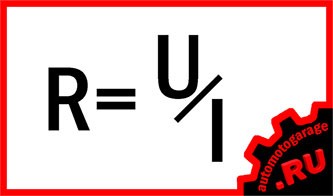
Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Формула мгновенной электрической мощности:
Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.
Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.
Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.
Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.
Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.
Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.
Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.
Этот круг также, как и треугольник можно назвать магическим.
-
Александр (Гость)15 ноября 2020 / 07:52
-
Привет. У меня есть нерабочий строительный фен. Я нашёл, скажем так, новый нагреватель на замену нерабочего, но у него 3 вывода, т.е. на 2 рабочих положения. Но ещё одного вывода для запитки двигателя нет. Сопротивление обоих спиралей большое. Нагреватель я уже установил в корпус и вытаскивать его назад чревато поломкой. Вот я и подумал: возможно запитать двигатель автономным, не зависящим от спиралей, питанием. Двигатель, я думаю, на 12-18 вольт.
-
Павл (Гость)21 марта 2023 / 00:24
-
Удивляюсь. Люди не выставляют размерность, а потом предъяляют претензии автору.
Расчет кто-то в комментариях делал на 3кВ и 1МОм. Дело в том что калькулятор считает сначала верхнюю строку (I). Если силу тока выставить до расчёта в мкА или в мА, то и расчёт будет верный — 3000 мкА или 3 мА.
С 5В и 1000 Ом ещё проще. 5 вольт — это напряжение, например, выходное блока питания ЗУ (у телефона и т.д.). Его никто не меряет чисто в амперах, даже производитель ЗУ ставит маркировку в мА. Итого, вычисляем: 5В на 1кОм — это 5мА и 0.03Вт
Размерность, господа, размерность важна!
-
Матвей (Гость)6 апреля 2023 / 15:28
-
Калькулятор странный, например мне надо узнать какой будет ток, через резистор 2 вт 15 ом и 28 в
Выставляю эти значения, остается пустым сила тока, нажимаю рассчитать, а он сам меняет мощность на 52 вт, и уже от этого рисует мне 1.87А -
Вася (Гость)29 апреля 2023 / 10:37
-
Матвей. 1,87ампер потечет через резистор, а значит мощность нужна будет 52вт , для того, чтобы резистор выдержал на себе такое напряжение.
Содержание
- 1 Как рассчитать сопротивление зная мощность и напряжение?
- 2 Как узнать амперы зная мощность?
- 3 Как сопротивление зависит от мощности?
- 4 Как найти сопротивление Ом?
- 5 Как рассчитать ток по мощности?
- 6 Как найти сопротивление из формулы мощности?
- 7 Сколько идет ампер на 1 квт?
- 8 Сколько ватт в 1 ампере 12 вольт?
- 9 Чему равен 1 ампер?
- 10 Как сила тока зависит от мощности?
- 11 Как рассчитать мощность?
- 12 Какая буква обозначает мощность?
- 13 Как найти сопротивление при параллельном соединении?
- 14 Как найти общее сопротивление в электрической цепи?
Как рассчитать сопротивление зная мощность и напряжение?
Узнать мощность, если известны напряжение и сопротивление. W = 220 в * 220 в / 500 ом = 96.8 вт.
Как узнать амперы зная мощность?
Таким образом, чтобы получить амперы, нужно ватты разделить на вольты питания — мощность разделить на напряжение I = P/U (вольт в бытовой сети 220-230). Бывает часто, что на сетевом электроприборе мощность указана в киловаттах (кВт), тогда может потребоваться перевести киловатты в амперы.
Как сопротивление зависит от мощности?
Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление. … В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.
Как найти сопротивление Ом?
Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I. Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: RO = 9 В / 3 А = 3 Ом.
Как рассчитать ток по мощности?
Формула расчета мощности электрического тока
Согласно закону Ома, сила тока(I) пропорциональна напряжению(U) и обратно пропорциональна сопротивлению(R), а мощность(P) рассчитывается как произведение напряжения и силы тока. Исходя из этого, ток в участке сети рассчитывается: I = P/U.
Как найти сопротивление из формулы мощности?
U = (P*R)
…
Электрическое сопротивление:
- R = U / I.
- R = U 2/ P.
- R = P / I.
Сколько идет ампер на 1 квт?
Сколько ампер в киловатте и сколько киловатт в ампере
Поскольку в одном киловатте 1000 ватт, то для сетевого напряжения в 220 вольт можно принять, что в одном киловатте 4,54 ампера, потому что I = P/U = 1000/220 = 4,54 ампер.
Сколько ватт в 1 ампере 12 вольт?
А значит, если имеем дело с автомобильной сетью на 12 вольт, то 1 ампер — это 12 Ватт, а в бытовой электросети 220 V такая сила тока будет в электроприборе мощностью 220 Вт (0,22 кВт). В промышленном оборудовании, питающемся от 380 Вольт, целых 657 Ватт.
Чему равен 1 ампер?
Ампе́р (обозначение: А) — единица измерения силы электрического тока в системе СИ, а также единица магнитодвижущей силы и разности магнитных потенциалов (устаревшее наименование — ампер-виток). 1 Ампер это сила тока, при которой через проводник проходит заряд 1 Кл за 1 сек.
Как сила тока зависит от мощности?
Количество электричества, проходящего через поперечное сечение цепи в течение одной секунды, есть не что иное, как сила тока в цепи. Следовательно, мощность электрического тока будет прямо пропорциональна разности потенциалов (напряжению) и силе тока в цепи.
Как рассчитать мощность?
Определите мощность источника питания.
Напряжение – это величина, характеризующая электрическое поле, создаваемое током. Мощность равна произведению силы тока на напряжение, то есть 1 Вт = 1 А х 1 В. Формула: Р = I х V. Например, если сила тока равна 3 А, а напряжение равно 110 В, то мощность равна: 3 х 110 = 330 Вт.
Какая буква обозначает мощность?
Обычно в формулах механики обозначается символом N. В электротехнике обычно обозначается символом P — от лат. potestas (сила, мощь, действенность); Иногда используется символ W (от англ.
Как найти сопротивление при параллельном соединении?
Общее сопротивление цепи при параллельном соединении проводников определяется по формуле: 1 R = 1 R 1 + 1 R 2 . Обратное значение общего сопротивления равно сумме обратных значений сопротивлений отдельных проводников. Для проверки формулы можно использовать омметр.
Как найти общее сопротивление в электрической цепи?
Формула для вычисления общего сопротивления последовательной цепи: Req = R1 + R2 + …. Rn где n — общее количество резисторов в цепи, соединенных последовательно. Таким образом, сопротивления всех резисторов просто суммируются. Например, найдем сопротивление цепи, показанной на рисунке.
Закон Ома для участка цепи
Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома:
Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.
I = U/R
Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.
Отсюда следуют ещё два полезных соотношения:
Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).
U = IR
Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.
R = U/I
Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R. Кроме того, следует помнить, что Закон Ома справедлив только для линейных элементов цепи.
Как звучит закон Ома для участка цепи
Есть говорить об официальной формулировке, то закон Ома можно озвучить так:
Сила тока имеет прямую зависимость от напряжения и обратную от сопротивления. Это высказывание справедливо для участка цепи с каким-то определенным и стабильным сопротивлением.
Формула этой зависимости на рисунке. Тут I — это сила тока, U — напряжение, R — сопротивление.
Формула закона Ома
- Чем больше напряжение, тем больше ток.
- Чем больше сопротивление, тем ток меньше.
Не так легко представить себе смысл этого выражения. Ведь электричество нельзя увидеть. Мы только приблизительно знаем что это такое. Попытаемся уяснить себе смысл этого закона при помощи аналогий.
Закон Ома для замкнутой цепи
Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:
I — Сила тока в цепи.
— Электродвижущая сила (ЭДС) — величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника. r — Внутреннее сопротивление источника питания. Для электродвижущей силы внешнеее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I = /(R+r) .
Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR. Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания. С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы.
По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = — I*r. Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U. Если ток в цепи равен нулю, следовательно,
= U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.
В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС (≈ U ) независимо от сопротивления внешней цепи R. Такой источник питания называют источником напряжения.
Закон Ома для переменного тока
При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.
В таком случае запись Закона Ома будет иметь вид:
I = U/Z
Здесь Z — полное (комплексное) сопротивление цепи — импеданс. В него входит активная R и реактивная X составляющие. Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи. Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.
С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:
— комплексная амплитуда тока. = Iampe jφ
— комплексная амплитуда напряжения. = Uampe jφ
— комплексное сопротивление. Импеданс.
φ — угол сдвига фаз между током и напряжением.
e — константа, основание натурального логарифма.
j — мнимая единица.
Iamp , Uamp — амплитудные значения синусоидального тока и напряжения.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Нелинейные элементы и цепи
Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников.
Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы.
Такие элементы и цепи, в которых они используются, называют нелинейными.
Напряжение, ток и сопротивление
Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.
Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.
Единицы измерения: вольт, ампер и ом
Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любые другие физические величины. Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:
| Ток | I | Ампер | А |
| Напряжение | V | Вольт | В |
| Сопротивление | R | Ом | Ом |
«Символ», присвоенный каждой величине, представляет собой стандартную букву латинского алфавита, используемую для представления этой величины в формулах. Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.
Каждая единица измерения названа в честь известного экспериментатора в области электричества: ампер в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта, а ом в честь немца Георга Симона Ома.
Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя («Resistance» и «Voltage», соответственно), тогда как «I» для тока кажется немного странным. Предполагается, что буква «I» должна представлять «интенсивность» («Intensity»)(потока заряда). Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «I».
Другой символ напряжения, «E», означает «электродвижущую силу» («Electromotive force»). Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.
Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (так называемые «мгновенные» значения). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени.
Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.
Кулон и электрический заряд
Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.
Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении).
В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Формула Закона Ома
В 1827 году Георг Симон Ом открыл закон силы электрического тока. Его именем назвали Закон и единицу измерения величины сопротивления. Смысл закона в следующем.
Чем толще труба и больше давление воды в водопроводе (с увеличением диаметра трубы уменьшается сопротивление воде) – тем больше потечет воды. Если представить, что вода это электроны (электрический ток), то, чем толще провод и больше напряжение (с увеличением сечения провода уменьшается сопротивление току) – тем больший ток будет протекать по участку цепи.
Сила тока, протекающая по электрической цепи, прямо пропорциональна приложенному напряжению и обратно пропорциональна величине сопротивления цепи.
где I – сила тока, измеряется в амперах и обозначается буквой А;U – напряжение, измеряется в вольтах и обозначается буквой В;R – сопротивление, измеряется в омах и обозначается Oм.
Если известны напряжение питания U и сопротивление электроприбора R, то с помощью вышеприведенной формулы, воспользовавшись онлайн калькулятором, легко определить силу протекающего по цепи тока I.
С помощью закона Ома рассчитываются электрические параметры электропроводки, нагревательных элементов, всех радиоэлементов современной электронной аппаратуры, будь то компьютер, телевизор или сотовый телефон.
Анализ простых схем с помощью закона Ома
Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:
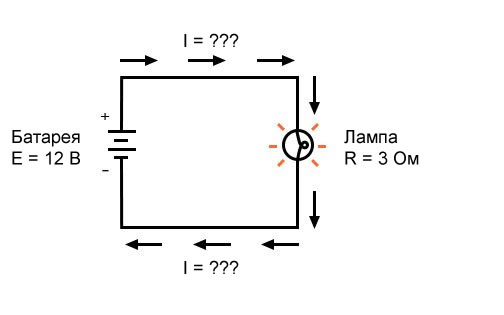
Рисунок 1 – Пример простой схемы
В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):
Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампы
Какая величина тока (I) в этой цепи?
[I = frac{E}{R} = frac{12 В}{3 Ом} = 4 А]
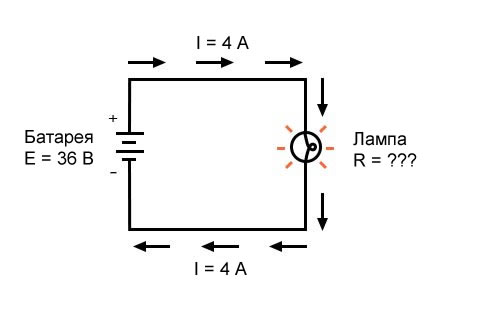
Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):
Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепи
Какое сопротивление (R) оказывает лампа?
[R = frac{E}{I} = frac{36 В}{4 А} = 9 Ом]
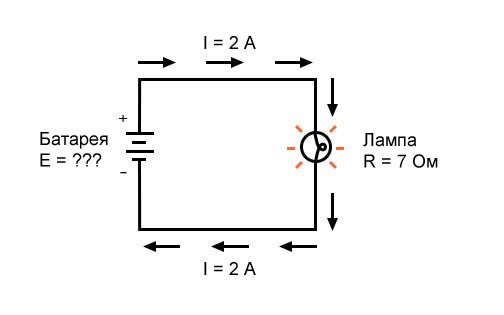
В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):
Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампы
Какое напряжение обеспечивает батарея?
[E = IR = (2 А)(7 Ом) = 14 В]
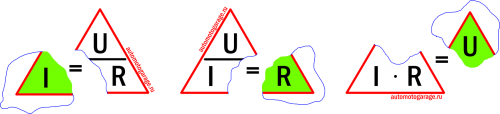
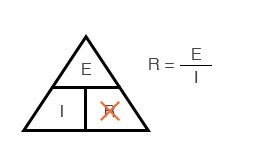
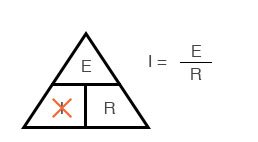
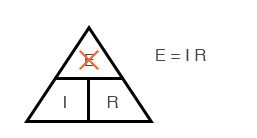
Метода треугольника закона Ома
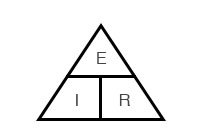
Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Рисунок 5 – Треугольник закона Ома
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Рисунок 6 – Закон Ома для определения R
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Рисунок 7 – Закон Ома для определения I
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
Рисунок 8 – Закон Ома для определения E
В конце концов, вам придется научиться работать с формуми, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!
Формула Закона Джоуля-Ленца
Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца.
Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.
где P – мощность, измеряется в ваттах и обозначается Вт;U – напряжение, измеряется в вольтах и обозначается буквой В;I – сила ток, измеряется в амперах и обозначается буквой А.
Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.
Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания. Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала.
Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.
Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В. Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.
Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.
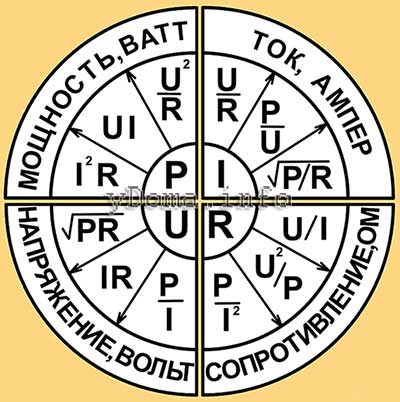
Преобразованные формулы Закона Ома и Джоуля-Ленца
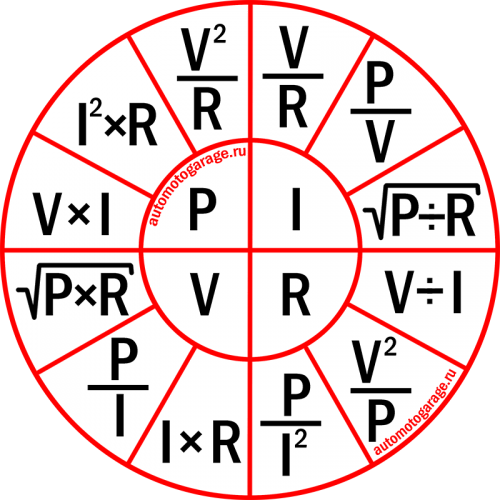
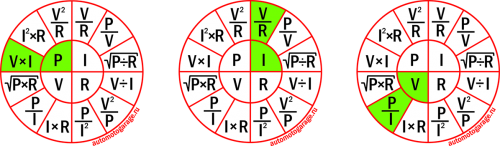
Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой не связанные между собой четыре сектора и очень удобна для практического применения
По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.
А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.
Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.
Применение закона Ома на практике
На практике часто приходится определять не силу тока I, а величину сопротивления R. Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R, зная протекающий ток I и величину напряжения U.
Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению. Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения. Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Задача 1.1
Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.
Задачка простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.
Параллельное и последовательное соединение
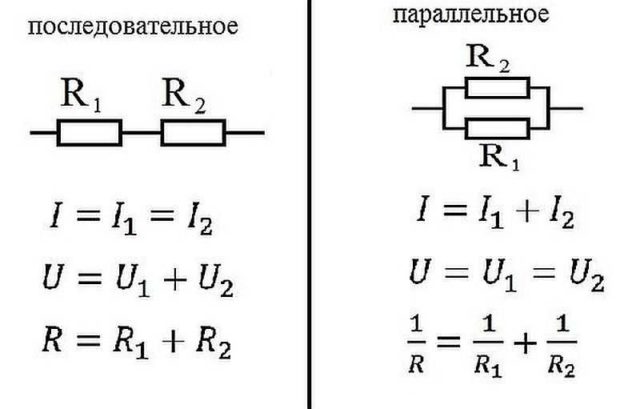
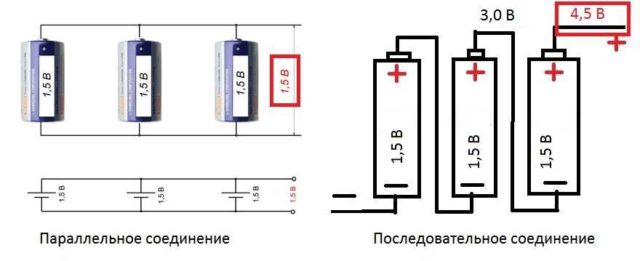
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
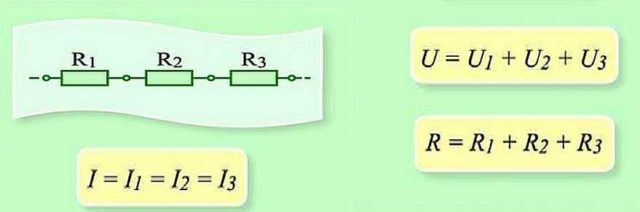
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Последовательное соединение и параметры этого участка цепи.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
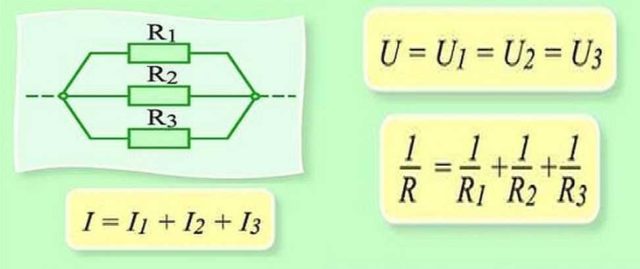
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
- Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
- Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.
Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока
В общем, это наиболее распространенные варианты использования этих соединений.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Видеоурок: Закон Ома простыми словами
Онлайн калькулятор закона Ома позволяет определять связь между силой тока, электрическим напряжением и сопротивлением проводника в электрических цепях.
Для расчета, вам понадобится воспользоваться отдельными графами:
— сила тока вычисляется в Ампер, исходя из данных напряжения (Вольт) и сопротивления (Ом);
— напряжение вычисляется в Вольт, исходя из данных силы тока (Ампер) и электрического сопротивления (Ом);
— электрическое сопротивление вычисляется в Ом, исходя из данных силы тока (Ампер) и напряжения (Вольт);
— мощность вычисляется в Ватт, исходя из данных силы тока (Ампер) и напряжения (Вольт).
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»