Если известно сколько составляет часть от целого, то по известной части можно «восстановить»
целое.
Для этого пользуемся правилом нахождения целого (числа)
по его дроби (части).
Запомните!
Чтобы найти число по его части, выраженной дробью, нужно данное число
разделить на дробь.
Пример. Рассмотрим задачу.
Поезд прошёл 240 км, что составило
всего пути.
Какой путь должен пройти поезд?
Решение. 240 км — часть всего пути. Эти же километры
выражены дробью 15/23
от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части,
и 15 таких частей составляют 240 км
(числитель дроби равен 15).
Значит, можно найти, сколько составляет
часть пути.
240 : 15 = 16 (км)
Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью
.
Значит, чтобы найти весь путь (23 части, каждая из которых по
16 км) нужно:
16 · 23 = 368 (км)
Кратко запись решения такой задачи можно сделать следующим образом.
Ответ: поезд должен пройти 368 км.
Сложные задачи на нахождение числа по его части
Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.
Рассмотрим задачу.
При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?
Решение. Как обычно подчеркнём в условии задачи все важные данные.
Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.
Такую часть всех слов составляют 4 слова.
Итак, 4 слова — это
от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь
.
Ответ: всего 48 слов надо было выучить к диктанту.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Мы уже научились находить часть от числа (см. здесь).
А сегодня мы поговорим о том, как найти число по его части (число по его дроби). Эти умения необходимы при решении задач.
Обратимся опять же к пицце.
1. Пиццу разрезали на 8 кусков. Один кусок весит 60 г. Надо узнать вес пиццы. Мы знаем, что пиццу разрезали на 8 частей, т.е. 1 кусок – это 1/8 от целого.
Изобразим это на схеме:
Если 1 кусок весит – 60 г, значит, вся пицца весит в 8 раз больше и надо 60 г умножить на 8.
В дроби 1/8 – знаменатель 8. Итак, чтобы найти целое – надо вес 1 части умножить на знаменатель.
2. Рассмотрим другой пример:
2 куска пиццы весят 120 г. Надо узнать вес целой пиццы.
Как поступим в этом случае?
Вес целой пиццы мы узнавали в предыдущем случае: вес одного куска умножали на число кусков. Значит, надо узнать вес одного куска. Для этого 120 : 2 = 60 (г)
А потом 60 умножим на 8 (как в примере 1).
Итак: 2/8 = 120
данное число 120 разделили на 2 (это числитель дроби), а потом умножили на 8 (это знаменатель дроби):
120 : 2 х 8
Заменим деление на дробь:
Итак, для того чтобы было легко найти целое по его дроби и дробь от целого, используйте памятку.
Похожие статьи
Правило нахождения числа по его дроби:
Чтобы найти число по данному значению его дроби, нужно это значение разделить на дробь.
Рассмотрим, как найти число по его дроби, на конкретных примерах.
Примеры.
1) Найти число, 3/4 которого равны 12.
Решение:
Чтобы найти число по его дроби, это число делим на эту дробь. Чтобы разделить число на дробь, надо данное число умножить на число, обратное к дроби (то есть на перевернутую дробь). Чтобы умножить дробь на число, надо числитель умножить на это число, а знаменатель оставить без изменения. Сокращаем 12 и 3 на 3. Так как в знаменателе получили единицу, ответ — целое число.
2) Найти число, если 9/10 его равняются 3/5.
Решение:
Чтобы найти число по данному значению его дроби, это значение делим на эту дробь. Чтобы разделить дробь на дробь, первую дробь умножаем на обратную ко второй (перевернутую). Чтобы умножить дробь на дробь, числитель умножаем на числитель, знаменатель — на знаменатель. Сокращаем 10 и 5 на 5, 3 и 9 — на 3. В результате получили правильную несократимую дробь, значит это — окончательный результат.
3) Найти число, 9/7 которого равны
Решение:
Чтобы найти число по значению его дроби, это значение делим на эту дробь. Смешанное число переводим в неправильную дробь и умножаем его на число, обратное ко второму (перевернутую дробь). Сокращаем 99 и 9 на 9, 7 и 14 — на 7. Поскольку получили неправильную дробь, необходимо выделить из нее целую часть.
Для примера возьмём случай из школьной жизни:
На творческом вечере актовый зал заполнен на 3/4, что составляет 216 кресел. Сколько всего кресел установлено в актовом зале?
Получается, нам необходимо найти число по его дроби. А чтобы найти число по заданному значению его дроби, надо это значение разделить на дробь.
Вычислим:

Или вот пример с десятичными дробями:
На хлебозавод привезли 210,5 т пшеницы. Это количество составляет 0,25 от всего количества пшеницы, переработанной за один рабочий день. Сколько всего пшеницы переработали за рабочий день?
Алгоритм такой же: делим заданное число — 210,5 — на значение его дроби — 0,25.
210,5 : 0,25 = 2105 : 2,5 = 842 (т) — столько пшеницы переработали за один рабочий день.
Ответ: всего было переработано 842 тонны пшеницы.
Мы надеемся, что Вы разобрались, как производится нахождение числа по заданной дроби. И без труда
решите следующую задачу:
В конкурсе талантов приняли участие 57отдыхающих, а это 120 ребят. Сколько всего детей отдыхает в лагере?
Мы желаем Вам лёгкого решения задачи и напоминаем о том, что Ваш ребёнок может изучить любую математическую тему вместе с квалифицированным педагогом абсолютно бесплатно! Да, первое занятие в World of Math, на котором Вы подробно разбираете материал, закрепляете его, а после получаете рекомендации по дальнейшему образованию чада, идёт без оплаты.
Команда WoM стремится к тому, чтобы как можно больше современных школьников поняли и полюбили как математику, так и учёбу в целом. Наши счастливые ученики, которых уже более 1400, и благодарные отзывы их родителей свидетельствуют о том, что мы на правильном пути.
Мы приглашаем Вашего ребёнка отправиться в увлекательное путешествие по Миру Математики! Учиться с нами — легко и увлекательно! Осталось только записаться на бесплатный урок.
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Нахождение числа по его дроби
Замечание 1
Чтобы найти число по данному значению его дроби нужно это значение разделить на дробь.
Пример 1
Антон за неделю учебы заработал три четверти отличных отметок. Сколько всего отметок получил Антон, если отличных отметок было 6.
Решение.
По условию задачи $6$ отметок – это $frac{3}{4}$.
Найдем количество всех отметок:
$6div frac{3}{4}=6 cdot frac{4}{3}=frac{6 cdot 4}{3}=frac{2 cdot 3 cdot 4}{3}=2 cdot 4=8$.
Ответ: всего $8$ отметок.
Пример 2
Выкосили $frac{4}{9}$ пшеницы на поле. Найти площадь поля, если было скошено $36$ га.
Решение.
По условию задачи $36$ га – это $frac{4}{9}$.
Найдем площадь всего поля:
$36div frac{4}{9}=36 cdot frac{9}{4}=frac{36 cdot 9}{4}=frac{4 cdot 9 cdot 9}{4}=81$.
Ответ: площадь всего поля $81$ га.
Пример 3
За один день автобус проехал $frac{2}{3}$ маршрута. Найти продолжительность намеченного маршрута, если за день автобус проехал $350$ км?
Решение.
По условию задачи $350$ км – это $frac{2}{3}$.
Найдем продолжительность всего маршрута автобуса:
$350div frac{2}{3}=350 cdot frac{3}{2}=frac{350 cdot 3}{2}=175 cdot 3=525$.
Ответ: продолжительность намеченного маршрута $525$ км.
Пример 4
Рабочий поднял производительность своего труда на $% $и сделал за такой же срок на $24$ детали больше, чем было запланировано. Найти количество деталей, запланированных для выполнения рабочим.
Решение.
По условию задачи $24$ детали = $8%$, а $8% = 0,08$.
Найдем количество деталей, запланированных для выполнения рабочим:
$24div 0,08=24div frac{8}{100}=24 cdot frac{100}{8}=frac{24 cdot 100}{8}=frac{3 cdot 8 cdot 100}{8}=300$.
Ответ: запланировано $300$ деталей для выполнения рабочим.
«Нахождение числа по его дроби, дробные выражения» 👇
Пример 5
В цехе отремонтировали $9$ станков, что составляет $18%$ всех станков цеха. Сколько станков находится в цехе?
Решение.
По условию задачи $9$ станков = $18%$, а $18% = 0,18.$
Найдем количество станков в цехе:
$9div 0,18=9div frac{18}{100}=9 cdot frac{100}{18}=frac{9 cdot 100}{18}=frac{9 cdot 100}{2 cdot 9}=frac{100}{2}=50$.
Ответ: в цехе $50$ станков.
Дробные выражения
Рассмотрим дробь $frac{a}{b}$, которая равна частному $adiv b$. В таком случае частное от деления одного выражения на другое удобно записывать также с помощью черты.
Пример 6
Например, выражение $(13,5–8,1)div (20,2+29,8)$ можно записать следующим образом:
$frac{13,5-8,1}{20,2+29,8}$.
После выполнение расчетов получим значение данного выражения:
$frac{13,5-8,1}{20,2+29,8}=frac{5,4}{50}=frac{10,8}{100}=0,108$.
Определение 1
Дробным выражением называется частное двух чисел или числовых выражений, в котором знак $«:»$ заменен дробной чертой.
Пример 7
$frac{2,4}{1,3 cdot 7,5}$, $frac{frac{5}{8}+frac{3}{11}}{2,7-1,5}$, $frac{2a-3b}{3a+2b}$, $frac{5,7}{ab}$ – дробные выражения.
Определение 2
Числовое выражение, которое записывается выше дробной черты, называется числителем, а числовое выражение, которое записывается ниже дробной черты, – знаменателем дробного выражения.
В числителе и знаменателе дробного выражения могут стоять числа, числовые или буквенные выражения.
Для дробных выражений могут применяться правила, которые справедливы для обыкновенных дробей.
Пример 8
Найти значение выражения $frac{5 frac{3}{11}}{3 frac{2}{7}}$.
Решение.
Умножим числитель и знаменатель данного дробного выражения на число $77$:
$frac{5 frac{3}{11}}{3 frac{2}{7}}=frac{5 frac{3}{11} cdot 77}{3 frac{2}{7} cdot 77}=frac{406}{253}=1,6047…$
Ответ: $frac{5 frac{3}{11}}{3 frac{2}{7}}=1,6047…$
Пример 9
Найти произведение двух дробных чисел $frac{16,4}{1,4}$ и $1 frac{3}{4}$.
Решение.
$frac{16,4}{1,4} cdot 1 frac{3}{4}=frac{16,4}{1,4} cdot frac{7}{4}=frac{4,1}{0,2}=frac{41}{2}=20,5$.
Ответ: $frac{16,4}{1,4} cdot 1 frac{3}{4}=20,5$.
Пример 10
Найти сумму двух дробей $frac{2}{0,7}+frac{3}{1,4}$.
Решение.
$frac{2}{0,7}+frac{3}{1,4}=frac{4+3}{1,4}=frac{7}{1,4}=frac{70}{14}=5$.
Ответ: $frac{2}{0,7}+frac{3}{1,4}=5$.
Для выполнения сложения дробных выражений удобно сразу их преобразовать к виду обыкновенных дробей, а затем выполнить сложение:
$frac{2}{0,7}+frac{3}{1,4}=frac{20}{7}+frac{30}{14}=frac{20}{7}+frac{15}{7}=frac{35}{7}=5$.
Пример 11
Найти значение выражения: $frac{frac{7}{11} cdot frac{33}{21}+1,23}{5,1-2,8}$.
Решение.
$frac{frac{7}{11} cdot frac{33}{21}+1,23}{5,1-2,8}=frac{frac{7 cdot 33}{11 cdot 21}+1,23}{2,3}=frac{1+1,23}{2,3}=frac{2,23}{2,3}=frac{9,79}{2,3}=0,96956…$
Ответ: $frac{frac{7}{11} cdot frac{33}{21}+1,23}{5,1-2,8}=0,96956…$
Пример 12
Найти значение выражения $frac{2,48+3 frac{5}{9} cdot 1 frac{1}{8}}{6,1-3,7}$.
Решение.
В числителе смешанные числа преобразуем к виду неправильных дробей и выполним вычисления:
$frac{2,48+3 frac{5}{9} cdot 1 frac{1}{8}}{6,1-3,7}=frac{2,48+frac{32}{9} cdot frac{9}{8}}{2,4}=frac{2,48+4}{2,4}=frac{6,48}{2,4}=2,7$.
Ответ: $2,7$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

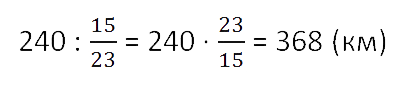
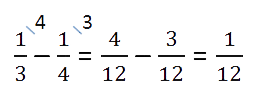
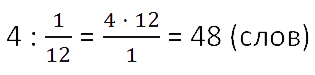


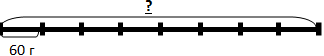
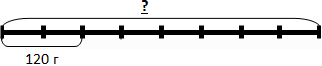
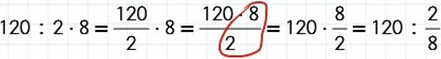
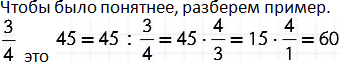

![Rendered by QuickLaTeX.com [12:frac{3}{4} = 12 cdot frac{4}{3} = frac{{mathop {12}limits^4 cdot 4}}{{mathop 3limits_1 }} = frac{{4 cdot 4}}{1} = 16.]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-36511d1819111c033089ca3273acc85f_l3.png)
![Rendered by QuickLaTeX.com [frac{3}{5}:frac{9}{{10}} = frac{3}{5} cdot frac{{10}}{9} = frac{{mathop 3limits^1 cdot mathop {10}limits^2 }}{{mathop 5limits_1 cdot mathop 9limits_3 }} = frac{{1 cdot 2}}{{1 cdot 3}} = frac{2}{3}.]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-bf84912aa20ee4de9b744cbdba8d5218_l3.png)
![Rendered by QuickLaTeX.com [7frac{1}{{14}}:frac{9}{7} = frac{{99}}{{14}} cdot frac{7}{9} = frac{{mathop {99}limits^{11} cdot mathop 7limits^1 }}{{mathop {14}limits_2 cdot mathop 9limits_1 }} = ]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-b33fab4d662914875c6a6b923654f611_l3.png)