В этой статье мы разберём нахождение наибольшего и наименьшего значения функции на отрезке, интервале, в
бесконечности, а также повторим основные свойства функции и связанные термины.
Что такое функция
Наш мир — это огромная коллекция взаимосвязей, которые порой явно, а порой невидимо влияют на всех, кто в них
участвует. Ваше настроение может влиять на успеваемость в школе, питание — на спортивные достижения, навыки — на
возможность поступить в университет. В физическом мире температура влияет на скорость протекания процесса,
плотность тела — на его способность к плаванию в воде, угол падения лучей — на то, каким образом они будут преломляться, пройдя
через прозрачную призму.
Некоторые из этих взаимоотношений можно описать математически: обозначить участников буквами латинского алфавита и
описать их взаимосвязь через математические действия и знаки.
Функция — это правило, формула или выражение, которое описывает взаимосвязь двух величин.
Как описать зависимость пройденного пути от времени?
Есть ли правило, которое описывает отношение ускорения тела и силы, приложенной к нему? Да:
А что, если нужно вычислить зависимость остатка денег от количества купленных товаров? Пожалуйста:
, где
— остаток денег,
— исходная сумма,
— количество товара,
— стоимость товара за одну единицу.
В каждом из этих выражений есть зависимая и независимая переменные. Зависимая переменная — это и есть функция, а
независимая — аргумент. Так, в нашем последнем примере стоимость товара за одну его единицу
является независимой переменной (цену назначил продавец, и мы на это повлиять никак не можем). Зато остаток в
кошельке поддаётся изменениям — чем меньше мы купим товара, тем больше останется денег. И так в любой зависимости!
Обратите внимание
Зависимая переменная стоит слева от знака «равно» и определяется через выражение, содержащее аргумент.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
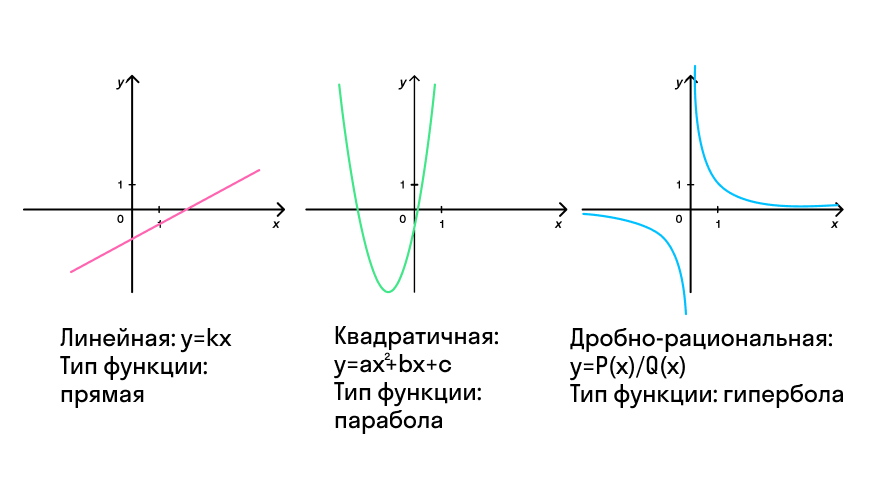
Графическое задание функции
Представьте, что для школьной научной конференции вы готовите доклад о загрязнении окружающей среды. Как вы
думаете, что произведёт больший эффект на аудиторию:
-
перечисление статистических данных об увеличении количества мусора за последний год;
-
наглядная демонстрация роста загрязнений в виде графика?
Верно — иллюстрации, фотографии, графики и диаграммы говорят порой громче любых слов! 📈
Для наглядного отображения зависимости одной переменной от другой мы введём систему координат, в которой построим график.
График — это прямая, кривая или ломаная линия, которая была построена чётко по уравнению
(функции).
Как мы уже говорили, функция состоит из зависимой и независимой переменной. В декартовой системе координат
независимая переменная отображается с помощью оси
зависимая — с помощью оси
В зависимости от типа функции график может выглядеть, например, так:
Наибольшее и наименьшее значение функции
На уроках алгебры учитель просит определить наибольшее и наименьшее значение функции. Что он имеет в виду?
Чтобы найти наименьшее или наибольшее значение функции, необходимо понять, какое наименьшее или наибольшее
численное значение принимает
— зависимая переменная.
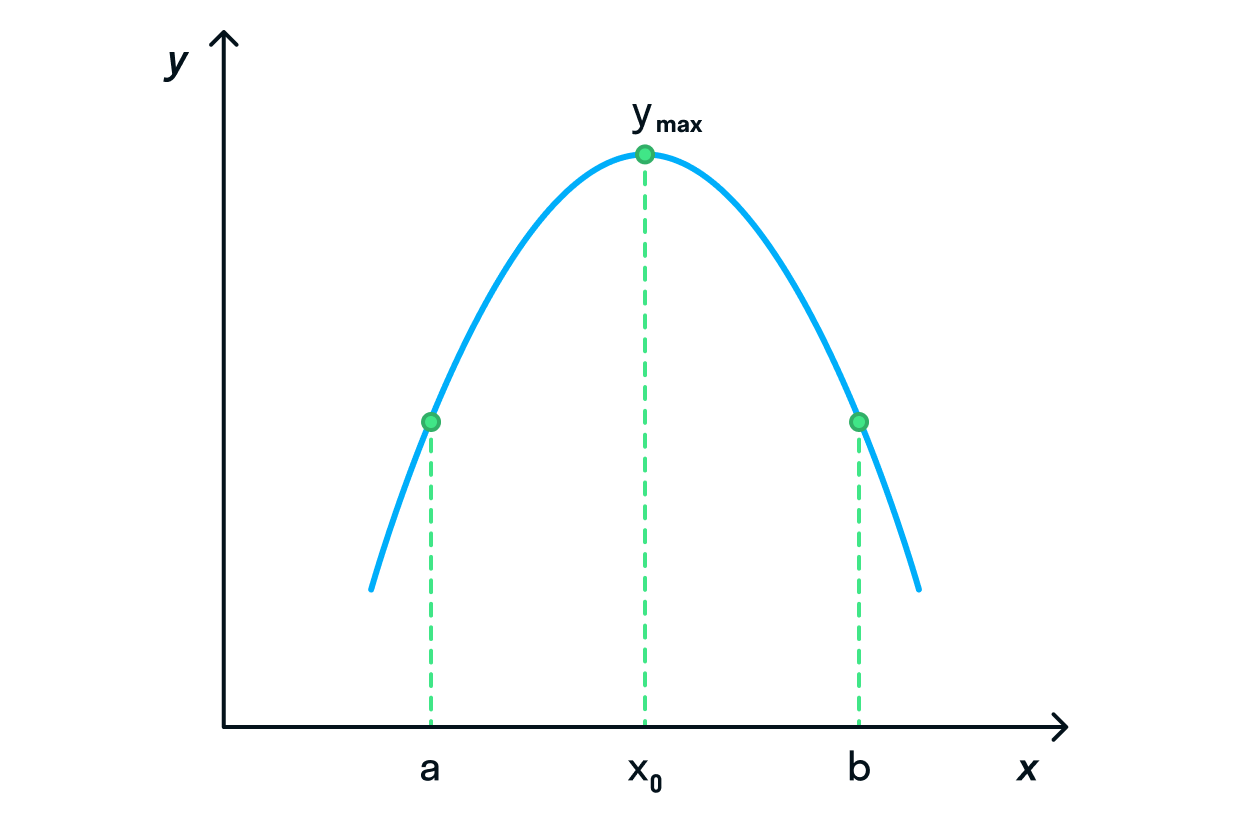
Наибольшее значение функции
на некотором промежутке
— это значение
которое при любом значении
делает справедливым неравенство
Теперь расшифровка! 😅 Если на данном интервале значение
больше, чем значение
в окрестностях точки
то такой
будет считаться наибольшим значением на данном промежутке.
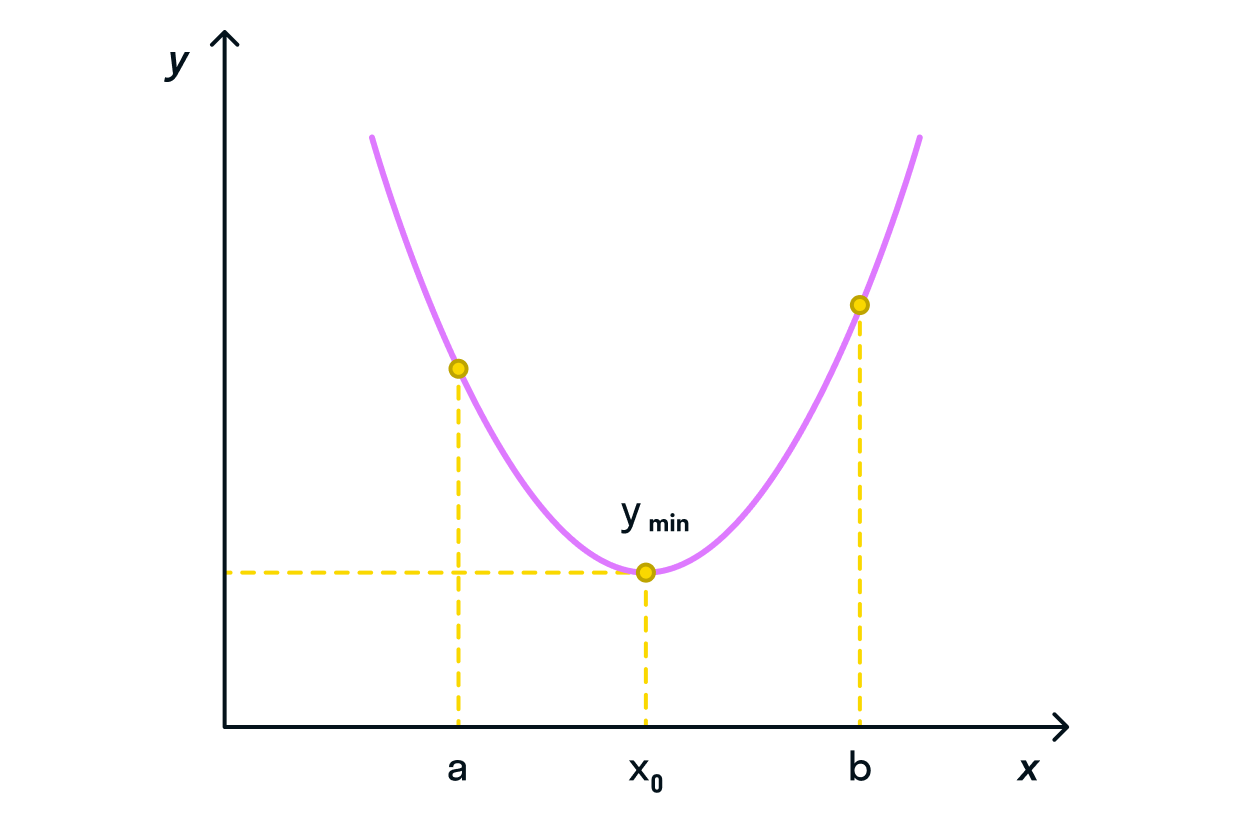
Наименьшее значение функции
на некотором промежутке
— это значение
которое при любом значении
делает справедливым неравенство
Если на данном интервале значение
меньше, чем значение
в окрестностях точки
то такой
будет считаться наименьшим значением на данном промежутке.
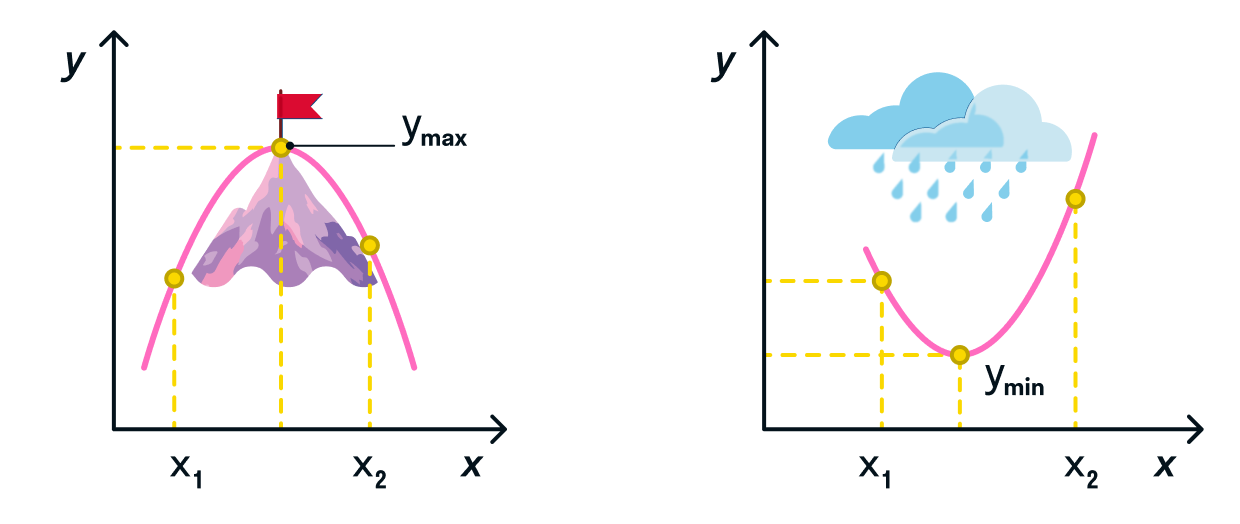
Наибольшее и наименьшее значение функции на графиках
Самый простой способ определить
и
— рассмотреть график.
Если заданный интервал представлен прямой:
-
при возрастающей функции: наименьшее значение функция примет при наименьшем аргументе и наоборот, наибольшее
значение функции будет соответствовать наибольшему значению аргумента; -
при убывающей функции: наименьшее значение функция примет при наибольшем аргументе и наоборот, наибольшее
значение функции будет соответствовать наименьшему значению аргумента.
Если заданный интервал представлен кривой:
-
максимальное значение функции выглядит как вершина горы, возвышенности, тогда как минимальное значение мы
можем определить как самую низкую точку относительно этого пика; -
минимальное значение функции выглядит как дно низины, оврага, тогда как максимальное значение мы можем
определить как самую высокую точку относительно этого пика.
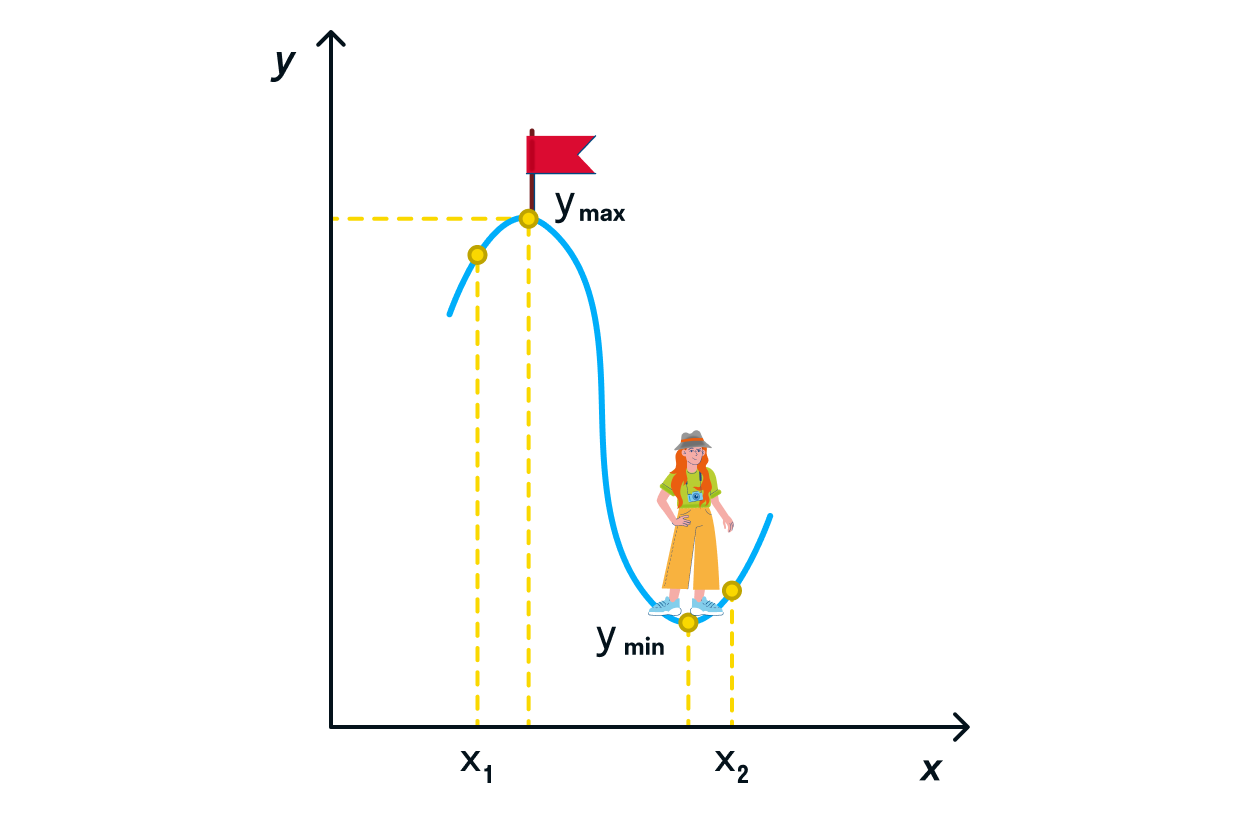
Возможен и такой вариант, когда горы и овраги встречаются на одном промежутке — тогда мы просто объединяем оба
пункта для нахождения
и
Помним главное правило: максимальное значение функции всегда представлено самой
высокой точкой относительно оси
минимальное значение функции — самой низкой точкой.
Определение наименьшего и наибольшего значения через производную
Удобен ли способ нахождения
и
через график? Определённо!
Всегда ли его можно использовать? К сожалению, нет.
Дело в том, что большинство заданий в алгебре на эту тему даются не через график, а через уравнение функции.
Зачастую эти функции сложные, и построение их графиков займёт время. Ошибётесь в построении — допустите ошибку и в
нахождении максимального и минимального значения, а нам это не нужно.
Способ, который не уступает первому в простоте и лаконичности, заключается в определении производной функции и
поиске стационарных точек. Кажется, нам встретились два новых термина — давайте их разберём.
Производная функции — это отношение приращения функции к приращению аргумента при бесконечно
малом приращении аргумента.
Производная функции показывает, как быстро увеличивается функция
при бесконечно малом увеличении
По сути, найти производную означает провести определённые действия с помощью таблицы производных
функций. Обязательно загляните в нашу статью об этом и изучите материал, а мы пока пойдём дальше.
Стационарная точка — точка, в которой значение аргумента производной функции равно нулю.
Дело в том, что по теореме Ферма в стационарных точках определяется экстремум функции, поэтому можно сделать
вывод, что на некотором промежутке в них можно определить и наибольшее/наименьшее значение функции.
Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке
Как определить наибольшее и наименьшее значения функции на отрезке?
-
Найдём область определения данной функции и проверим, входит ли в неё заданный отрезок.
-
Найдём производную данной функции.
-
Приравняем производную к нулю и найдём точки, в которых она обращается в нуль (решим уравнение).
-
Выберем из корней уравнения те точки, которые попадают в заданный промежуток, и вычислим значение функции в
них. -
Возьмём точки начала и конца отрезка и найдём значение функции в них.
-
Сделаем вывод о наибольшем и наименьшем значении функции.
Разберём пару примеров.
Задача 1
Найдите наибольшее и наименьшее значение функции
на отрезке
Решение:
-
ОДЗ:
-
не попадает в промежуток
Найдём значение функции только в крайних точках:
-
Тогда
является наименьшим значением на данном отрезке, а
наибольшим.
Задача 2
Найдите наибольшее и наименьшее значение функции
на отрезке
Решение:
-
ОДЗ:
-
, но в таком случае знаменатель равен нулю, что невозможно. А значит, производная
не обращается в нуль, стационарных точек нет. -
Найдём значение функции в крайних точках отрезка:
— точка максимума на промежутке;
— точка минимума на промежутке.
Наименьшее и наибольшее значение функции на открытом или бесконечном интервале
В чём отличие отрезка от интервала? В отрезке определены крайние точки, в интервале же крайние точки могут не
существовать (например
), или значение функции в них мы рассматривать не будем (на интервале
мы рассмотрим значение функции в окрестностях этих точек, но не в них самих).
Вариантов задания интервала может быть множество, но каждый из них сведёт определение
и
к поиску производной и вычислению пределов в крайних точках, например
и
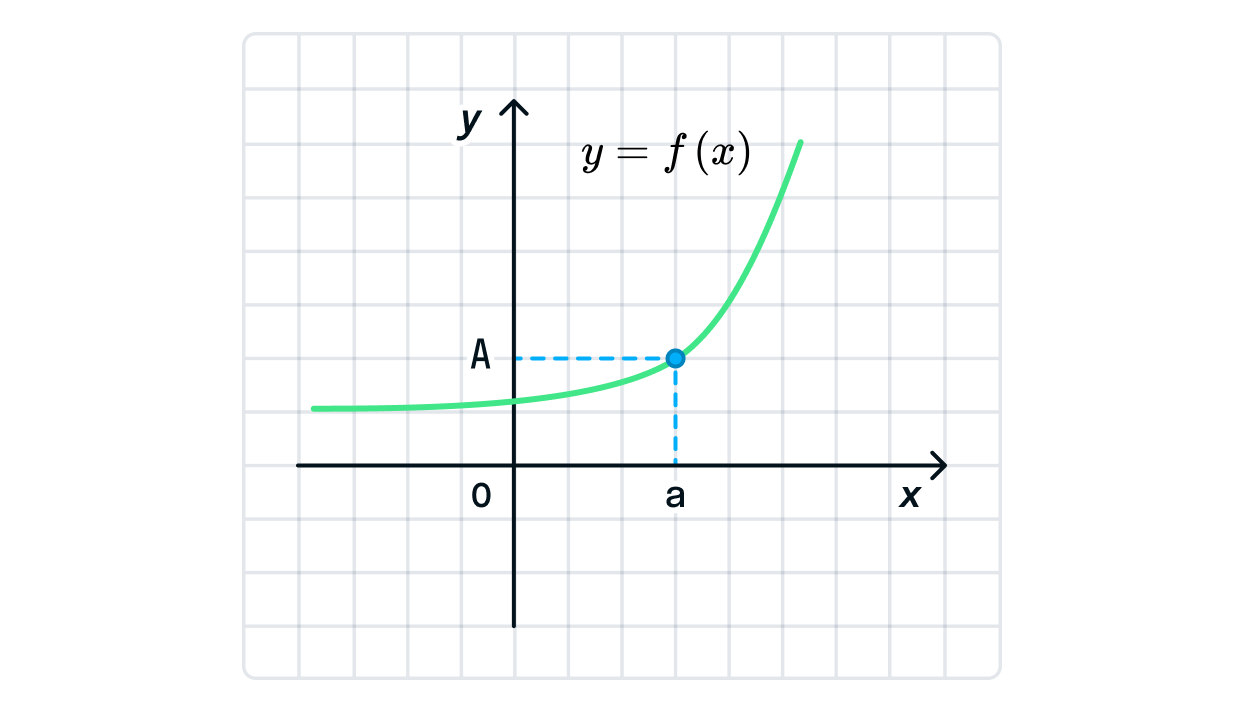
Вернёмся на пару шагов назад. А что такое предел функции?
Если говорить коротко, то предел функции — это такое число
, к которому функция стремится, в то время как аргумент стремится достичь числа
Предположим, наша функция представлена уравнением
Найдём предел функции при
подставив это значение вместо
в уравнение:
Это означает, что функция стремится приблизиться к числу
в то время как аргумент тоже приближается к этому значению. В отрыве от настоящего
уравнения мы могли бы представить это так:
Функция может стремиться не только к рациональному
числу, но также и к бесконечности. В таком случае при подстановке бесконечности в функцию возникает
неопределённость, которую необходимо решить разными методами.
В рамках этой статьи мы не можем посвятить этому много времени, поэтому ждём Вас на курсах математики в онлайн-школе
Skysmart — там ни один предел не останется незамеченным. 😉
Вернёмся к функции! Итак, как же определить наибольшее и наименьшее значение на интервале?
-
Найдём область определения данной функции и проверим, входит ли в неё заданный интервал.
-
Найдём производную данной функции.
-
Приравняем производную к нулю и найдём точки, в которых она обращается в нуль (решим уравнение).
-
Выберем из корней уравнения те точки, которые попадают в заданный промежуток, и вычислим значение функции в
них. -
Возьмём крайние точки интервала и вычислим значение предела в этих точках (согласно типу интервала).
-
Сделаем вывод о наибольшем и наименьшем значении функции.
Для вычисления предела вам поможет сводная таблица, которая учитывает вид интервала:
Если при вычислении одностороннего предела вы получаете бесконечность, то вычислить наибольшее/наименьшее
значение невозможно.
Задача 3
Необходимо найти наибольшее и наименьшее значение функции
на всём промежутке области определения.
Решение:
-
ОДЗ:
-
Найдём стационарные точки:
-
Точка
входит в промежуток области определения и является точкой минимума.
-
Так как
— парабола, ветви которой направлены вверх, мы не можем определить точку
максимума.
Cегодня мы на славу потрудились и разобрали множество важных вопросов:
-
что такое функция, какой она бывает;
-
что такое наименьшее и наибольшее значение функции;
-
как определить
и
на отрезке;
-
как находить наименьшее и наибольшее значение функции на интервале;
-
что такое предел и производная.
Вот и ещё одна тема по математике стала понятнее! А если всё же остались вопросы, спешим ещё раз пригласить вас на уроки математики в Skysmart — мы постараемся ответить на них, закрепить материал и попрактиковаться в решении задач. Обещаем, будет увлекательно и безумно интересно!
Наибольшее и наименьшее значения функции можно найти по графику функции. Иногда это значения удаётся найти, используя свойства функции. В общем случае наибольшее и наименьшее значения функции находятся с помощью производной. Для этого сформулируем некоторые теоремы.
1. Если функция непрерывна на отрезке, то она достигает на нём и своего наибольшего, и своего наименьшего значений (Эта теорема доказывается в курсе высшей математики).
2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
3. Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
Как найти наименьшее и наибольшее значения функции на отрезке?
Пусть функция (f(x)) напрерывна на отрезке ([a; b]), тогда:
1) находим производную функции f′(x);
2) приравниваем производную к нулю, определяем точки экстремума функции, отбираем из них те, которые принадлежат отрезку ([a; b]);
3) находим значения функции y=f(x) в отобранных точках, и в конечных точках отрезка (a) и (b); выбираем среди полученных значений наименьшее (yнаим) и наибольшее (yнаиб).
А что делать, если нужно найти наибольшее или наименьшее значения функции, непрерывной на интервале? Один из вариантов — графический метод, который подразумевает построение графика функции и определение наименьшего или наибольшего значения функции по нему. Однако не всегда этот способ удобен, целесообразнее использовать следующую теорему.
Теорема. Пусть функция y=f(x) непрерывна на промежутке (X) и имеет внутри него единственную стационарную или критическую точку x0. Тогда:
а) если x=x0 — точка максимума, то yнаиб=f(xo);
б) если x=x0 — точка минимума, то yнаим=f(xo).
На рисунках продемонстрированы геометрические иллюстрации данной теоремы.

Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.
Как найти наибольшее и наименьшее значения функции на отрезке?
Для этого мы следуем известному алгоритму:
1. Находим ОДЗ функции.
2. Находим производную функции
3. Приравниваем производную к нулю
4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:
Если на промежутке I производная функции 

Если на промежутке I производная функции 

5. Находим точки максимума и минимума функции.
В точке максимума функции производная меняет знак с «+» на «-«.
В точке минимума функции производная меняет знак с «-» на «+».
6. Находим значение функции в концах отрезка,
- затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
- или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции
Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.
Рассмотрим функцию 

1. Рассмотрим функцию на отрезке
Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: 

2. Рассмотрим функцию на отрезке
Очевидно, что наибольшее значение функция принимает в точке максимума 


3. Если мы рассмотрим функцию на отрезке ![{x}{in}delim{[}{-1;2}{]} {x}{in}delim{[}{-1;2}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_3bae536560f42bd0f0875793dd5a92e2.png)


Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть 

Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:
1. ОДЗ функции 
2.
3. 

Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:
Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике
1. Задание B15 (№ 26695)
Найдите наибольшее значение функции 
![[-{pi}/2;0] [-{pi}/2;0]](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980.5_9a7375f1961203c68e53ad122ab84a77.png)
1. Функция 
2.
3.


y(0)=5
Ответ: 5.
2. Задание B15 (№ 26702)
Найдите наибольшее значение функции 

1. ОДЗ функции 
2.
Производная равна нулю при 





Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:
у(0)=5
Ответ: 5.
3. Задание B15 (№ 26708)
Найдите наименьшее значение функции 

1. ОДЗ функции 
2.
3.

Расположим корни этого уравнения на тригонометрической окружности.
Промежутку ![delim{[}{-{pi}/3;{pi}/3}{]} delim{[}{-{pi}/3;{pi}/3}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_982_e5f186d35c95dd888150972e98bd371a.png)

Расставим знаки. Для этого определим знак производной в точке х=0: 


Изобразим смену знаков производной функции 
Очевидно, что точка 

![delim{[}{-{pi}/3;{pi}/3}{]} delim{[}{-{pi}/3;{pi}/3}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_982_e5f186d35c95dd888150972e98bd371a.png)

Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а 
Ответ: -1
Вероятно, Ваш браузер не поддерживается. Попробуйте скачать
Firefox
И.В. Фельдман, репетитор по математике.
Вопросы
занятия:
·
рассмотреть
применение производных для отыскания наибольшего и наименьшего значений функции
на промежутке.
Материал
урока.
Пусть
у нас есть график некоторой функции f(x) на промежутке [a;
b]. По графику легко найти наибольшее
и наименьшее значения функции на промежутке. Иногда наибольшее и наименьшее
значения можно отыскать и без построения графика.
Например,
А
как же быть в других случаях, когда наличие наибольшего и наименьшего значения
функции на промежутке не так очевидно? Можно, конечно, каждый раз строить
график функции и с помощью него находить игрек наибольшее и наименьшее. Но это
не очень удобно и долго.
Для
того, чтобы избежать построения графика функции воспользуемся следующими утверждениями.
1.
Если функция непрерывна на отрезке, то она достигает на нем и своего
наибольшего, и своего наименьшего значений.
Справедливость
данного утверждения мы не будем доказывать.
2.
Наибольшего и наименьшего значений непрерывная функция может достигать как на
концах отрезка, так и внутри него.
Это
утверждение можно проиллюстрировать графиками функций.
Видно,
что на первом графике наибольшее и наименьшее значения достигаются во
внутренних точках. На втором графике наибольшее значение достигается в конце
промежутка, а наименьшее значение достигается во внутренней точке.
3.
Если наибольшее или наименьшее значение достигается внутри отрезка, то только в
стационарной или критической точке.
Для
доказательства данного утверждения достаточно вспомнить, что в данном случае
идёт речь об экстремумах функции, а экстремум достигается только в стационарной
или критической точке.
Давайте
сформулируем алгоритм нахождения наименьшего и наибольшего значений непрерывной
функции игрек равно f(x) на отрезке [a;
b].
Рассмотрим несколько примеров.
Пример.
Рассмотрим ещё
один пример.
Пример.
Как находить наибольшее и наименьшее
значение функции на отрезке мы разобрались. А что же делать, если надо найти
эти значения на незамкнутом интервале? Там же невозможно найти значения на
концах промежутка. Можно конечно построить график функции, но тогда мы получим
приближенные значения и опять же это долго.
Для решения таких задач удобно пользоваться
следующей теоремой.
Теорема.
Пусть функция y = f(x)
непрерывна на промежутке X
и имеет внутри него единственную стационарную или критическую точку x
= x0.
Тогда:
а) если x
= x0
− точка максимума, то yнаиб
= f(x0);
б) если x
= x0
− точка минимума, то yнаим
= f(x0).
Давайте геометрически проиллюстрируем эту
теорему.
Рассмотрим несколько примеров.
Пример.
Рассмотрим ещё один пример.
Пример.
Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.
Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.
Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].
Решение
Сначала вычисляем производную исходной функции:
y′=3×2−12xy’=3x^2-12x
Затем приравниваем ее к нулевому значению и решаем уравнение:
3×2−12x=03x^2-12x=0
x(3x−12)=0x(3x-12)=0
x1=0x_1=0
x2=4x_2=4
Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.
Находим значение функции в точке x1x_1:
f(0)=9f(0)=9
Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:
f(−1)=−1−6+9=2f(-1)=-1-6+9=2
f(2)=8−24+9=−7f(2)=8-24+9=-7
Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.
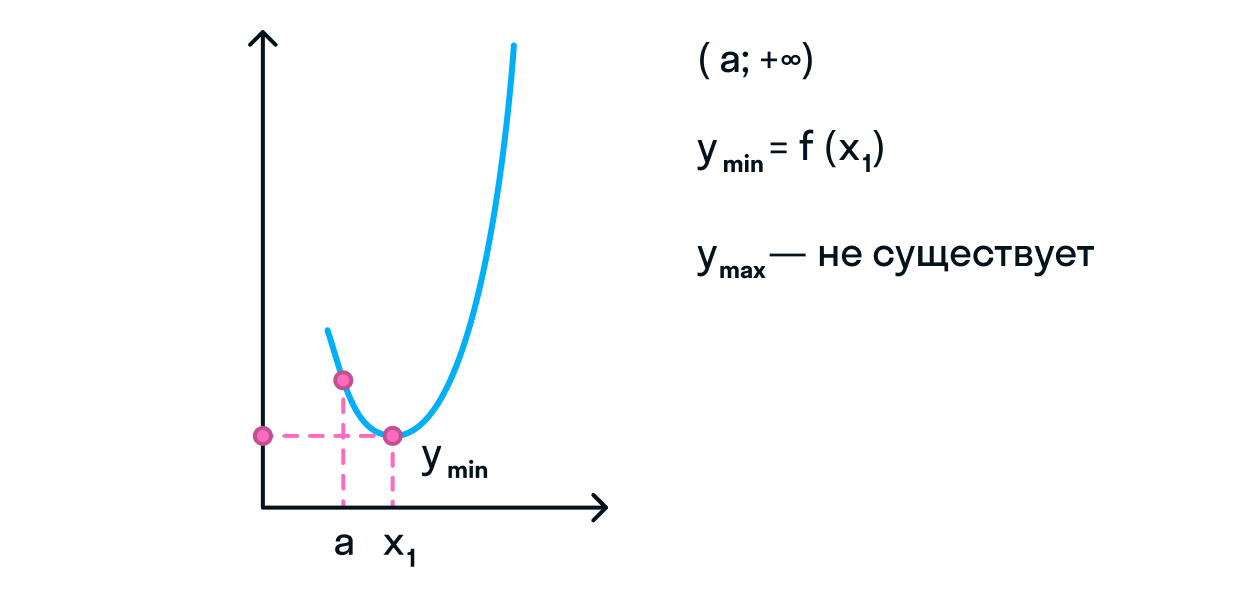
Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.
Решение
Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:
y′=6xy’=6x
Приравниваем производную к нулю:
6x=06x=0
x=0x=0
Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.
Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.
Тест по теме “Наибольшие и наименьшие значения функции”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат


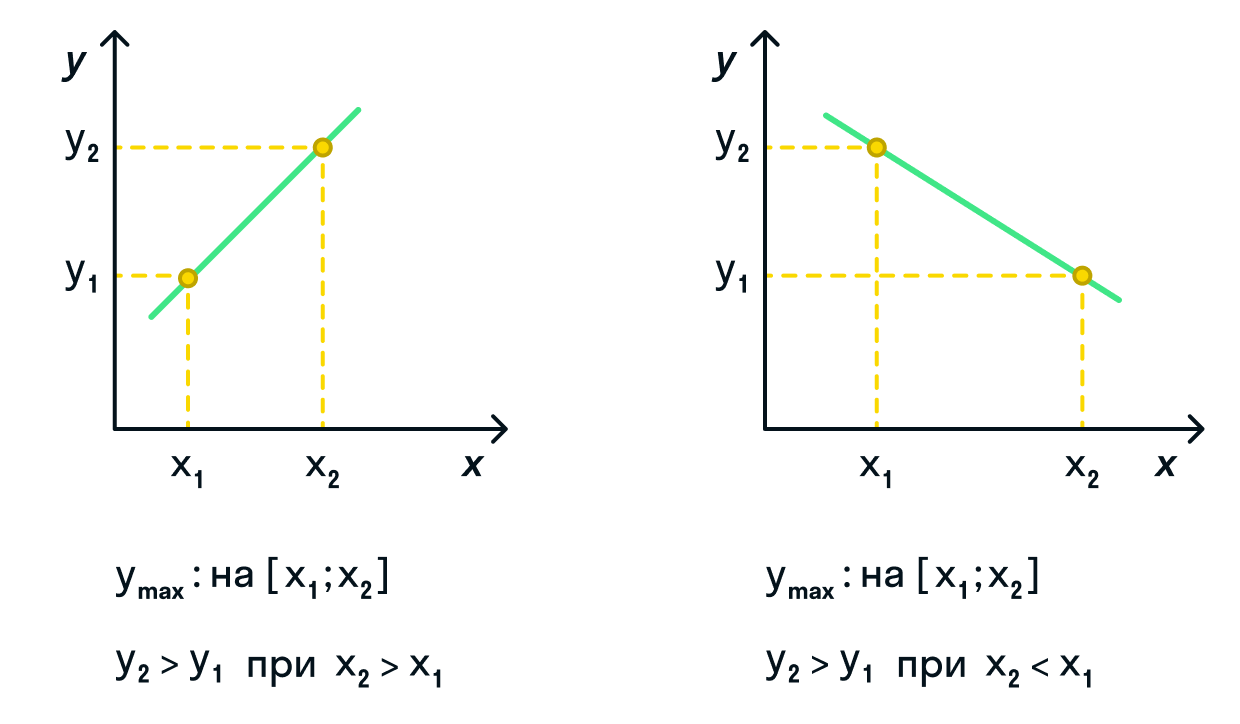



![{x}{in}delim{[}{-1;0}{]} {x}{in}delim{[}{-1;0}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_8d4ac2719ab1423f162f9779293da981.png)
![{x}{in}delim{[}{-1;1}{]} {x}{in}delim{[}{-1;1}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_fbae2bb0d6eaada0859d11280c8d6a23.png)


















