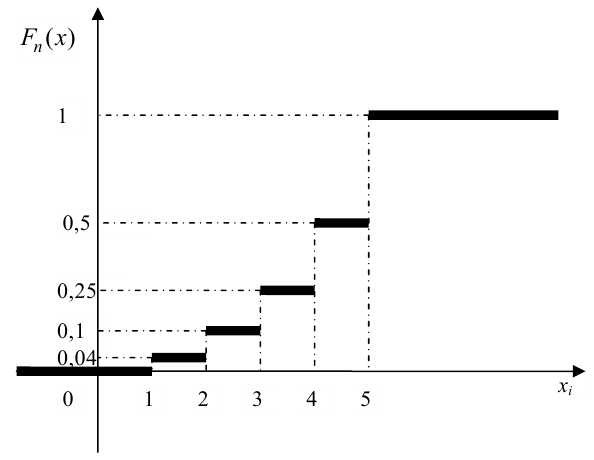
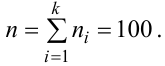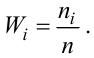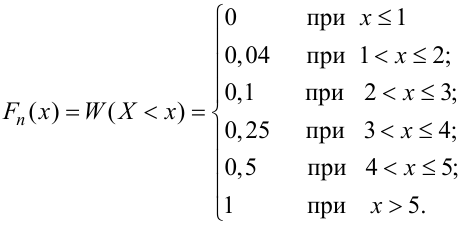Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике — мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
Наряду
с математическим ожиданием, дисперсией
и моментами для описания распределения
случайной величины применяют также
моду и медиану.
Модой
Mo
случайной величины X
называется наиболее вероятное значение
случайной величины.
Термин
«наиболее вероятное значение»,
строго говоря, применим только к ДСВ, в
случае НСВ мода совпадает с таким
значением случайной величины, при
котором плотность распределения имеет
максимум. Различают унимодальные
(имеющие одну моду), бимодальные
(имеющие две моды) и мультимодальные
(имеющие несколько мод) распределения.
Иногда встречаются распределения,
обладающие посередине не максимумом,
а минимумом. Такие распределения
называются антимодальными.
Мода, например,
часто используется при экономических
расчетах, когда нужно дать ответ на
вопрос, каковы преобладающие в данный
момент уровни производительности труда,
себестоимость, какой товар имеет
наибольший спрос и т.д. В связи с этим
вводятся понятия модальная
производительность, модальная
себестоимость и т.д.
Медианой
Me
случайной величины X
называется такое ее значение, для которой
справедливо равенство
P(X<Me)
= P(X>Me)
т.е.
равновероятно, что случайная величина
окажется меньше или больше медианы.
С
геометрической точки зрения, медиана
– это абсцисса точки, в которой площадь,
ограниченная кривой распределения,
делится пополам. Так как вся площадь
должна равняться единице, то функция
распределения в этой точке равна 0,5:
.
Отметим
оптимальное
свойство медианы:
сумма
абсолютных величин отклонений возможных
значений случайной величины от медианы,
умноженных на соответствующие вероятности,
меньше, чем от любой другой величин,
т.е. медианы удовлетворяют условию:
Это
свойство медианы, в частности, используется
в теории оптимального проектирования.
Например, при проектировании остановок,
при условии, чтобы общий путь пассажиров
был минимальным.
Следует отметить,
что если распределение симметрично и
унимодально, то математическое ожидание,
медиана и мода совпадают.
Кроме
моды и медианы иногда используются и
другие числовые характеристики. Например,
—квантилью
Q
(0<<1)
случайной
величины X
называется число, удовлетворяющее
неравенствам
.
Квантили находят
самое широкое применение в математической
статистике при построении доверительных
интервалов и проверке статистических
гипотез. Отметим, ½-квантиль совпадает
с медианой.
Энтропия
H=H(X)
дискретной случайной величины X
определяется по формуле
.
Отметим,
что энтропия не зависит от значений xi
от случайной величины X,
а зависит только от вероятностей pi,
с которыми эти значения принимаются.
Энтропия является мерой априорной
неопределенности случайной величины.
Максимального значения Hmax=logn
энтропия ДСВ достигает тогда, когда все
n
возможных значений случайная величина
принимает с одной и той же вероятностью
pi=1/n,
минимальное Hmin=0
– когда случайная величина принимает
единственное значение с вероятностью,
равной единице.
Энтропия
играет важную роль в теории информации,
она в некотором смысле представляет
собой минимальный объем памяти,
необходимый для записи информации,
содержащейся в случайной величине.
Поскольку информация записывается
обычно в двоичной системе, то основание
логарифма берется число 2.
Энтропия
H=H(X)
непрерывной случайной величины X
определяется по формуле
.
Заметим,
что в отличие, например, от математического
ожидания энтропию НСВ нельзя получить
предельным переходом от дискретного
случая. Отметим также, что при заданной
дисперсии 2
максимальную энтропию
имеет нормально распределенная случайная
величина.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Наивероятнейшее число. Примеры задач и калькулятор
Полезная страница? Сохрани или расскажи друзьям
Напомню, что мы рассматриваем типовые задачи схемы Бернулли (или независимых повторных испытаний). Чаще всего эти задачи связаны с нахождением вероятности того, что событие произойдет сколько-то раз в серии опытов (см. решения задач про выстрелы, билеты лотереи, партии в шахматы или рождения детей). Но еще один часто встречающийся тип задач — тот, где требуется подсчитать наиболее вероятное число наступлений события.
Вычисление этого значения имеет большое практическое значение, что легко видно из постановки задач:
1. С завода отправили 100 ящиков с хрупким товаром. Вероятность того, что ящик повредится в пути, равна 0,01. Какое наиболее вероятное число поврежденных ящиков будет на станции приема груза?
2. Вероятность того, что лампа небракованная, равна 0,97. Для ресторана закупили 124 лампы. Каково наиболее вероятное число рабочих ламп?
Конечно, в реальной жизни эти задачи формулируются более сложно и решаются по иным правилам, но для учебных целей мы разбираем простейшие случаи. Перейдем к формуле, для чего сформулируем общую постановку задачи еще раз:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых одинакова равна $p$. Тогда наивероятнейшее число $m$ наступлений события $A$ в этой серии опытов можно найти по формуле:
$$
np-q le m le np+p, quad q=1-p. qquad (1)
$$
Часто после нахождения наибольшего числа успехов требуется вычислить вероятность наступления именно этого числа, для чего используем обычную формулу Бернулли:
$$
P_n(m)= C_n^m cdot p^m cdot q^{n-m}. qquad (2)
$$
Далее:
- Онлайн калькулятор
- Видеоурок и шаблон Excel
- Примеры решенных задач
- Полезная информация
Видеоурок и шаблон Excel
Посмотрите наш ролик о решении задач о наивероятнейшем значении успехов, узнайте, как использовать Excel для решения типовых задач.
Расчетный файл Эксель из видео можно бесплатно скачать и использовать для решения своих задач.
Примеры решений задач о наиболее вероятном значении
Рассмотрим несколько типовых примеров.
Пример 1. Вероятность изготовления изделия высшего сорта на данном предприятии равна 0,8. Чему равно наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 100 изделий?
Выписываем известные величины $n=100, p=0,8$ и подставляем в формулу (1):
$$
100 cdot 0,8 — 0,2 le m le 100 cdot 0,8 + 0,8, \
79,8 le m le 80,8,\
m=80.
$$
Наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 100 изделий равно 80 изделиям.
Пример 2. Вероятность выигрыша в лотерею на один билет равна 0,2. Куплено 12 билетов. Найти наивероятнейшее число выигравших билетов и соответствующую вероятность.
Всего куплено $n=12$ билетов, вероятность выигрыша по каждому $p=0,2$. Получаем по формуле (1):
$$
12 cdot 0,2 — 0,8 le m le 12 cdot 0,2 + 0,2, \
1,6 le m le 2,6,\
m=2.
$$
Наиболее вероятное число выигрышных билетов равно двум. Найдем вероятность этого события по формуле Бернулли (2):
$$
P_{12}(2)= C_{12}^2 cdot 0,2^{2} cdot 0,8^{10}=66cdot 0,2^{2} cdot 0,8^{10}=0,283.
$$
Пример 3. Для данного баскетболиста вероятность забить мяч при одном броске равна 0,6. Произведено 10 бросков по корзине. Найти наивероятнейшее число попаданий и соответствующую вероятность.
Спортсмен делает $n=10$ независимых бросков, вероятность забить мяч при каждом $p=0,6$. Подставляем все в формулу (1):
$$
10 cdot 0,6 — 0,4 le m le 10 cdot 0,6 + 0,6, \
5,6 le m le 6,6,\
m=6.
$$
Наиболее вероятное число попаданий равно 6. Найдем вероятность этого события по формуле Бернулли (2):
$$
P_{10}(6)= C_{10}^6 cdot 0,6^{6} cdot 0,4^{4}=210 cdot 0,6^{6} cdot 0,4^{4}=0,251.
$$
Пример 4. Сколько раз нужно подбросить игральную кость, чтобы наивероятнейшее число выпадения 6 очков было равно 50?
Это несколько иная постановка задачи, хотя речь в ней тоже идет о наиболее вероятном числе. В отличие от разобранных выше, здесь уже задано $m=50$, $p=1/6$ (вероятность выпадения 6 очков на кости), а вот общее число бросков $n$ необходимо найти.
Начинаем с формулы (1), разбиваем ее на два неравенства и получаем из каждого выражение для $n$:
$$
np-q le m, quad m le np+p,
$$
$$
np le m+q, quad np ge m-p,
$$
$$
n le (m+q)/p, quad n ge (m-p)/p.
$$
Подставляем наши значения
$$
n le (50+5/6)/(1/6), quad n ge (50-1/6)/(1/6),
$$
$$
n le 305, quad n ge 299.
$$
Таким образом, нужно подбросить игральную кость от 299 до 305 раз.
Лучшее спасибо — порекомендовать эту страницу
Полезные ссылки
- Формулы по теории вероятностей
- Выполненные контрольные по теории вероятностей
- Заказать решение задач о вероятностях
Найдите готовые задачи в решебнике:
Наиболее вероятное значение — случайная величина
Cтраница 1
Наиболее вероятное значение случайной величины называется модой.
[1]
Наиболее вероятное значение случайной величины совокупности называется модой. Ей соответствует максимальное значение плотности.
[2]
Отрезок АВ соответствует наиболее вероятным значениям случайной величины.
[4]
Модой теоретического распределения называется наиболее вероятное значение случайной величины, обозначаемое символом № оХ; модой тйХ эмпирического распределения называется значение, имеющее наибольшую частость.
[5]
Это означает, что наиболее вероятным значением случайной величины, распределенной по нормальному закону, является значение, равное математическому ожиданию.
[6]
Модой ( Мо) называется наиболее вероятное значение случайной величины или то значение этой величины, частота которого наибольшая.
[7]
Математическое ожидание часто интерпретируется как среднее или наиболее вероятное значение случайной величины.
[8]
Таким образом, среднее значение в нормальном распределении является наиболее вероятным значением случайной величины.
[9]
На выходе ВУ мы должны получить корреляционное уравнение, дающее возможность вычислять наиболее вероятные значения выходной случайной величины в зависимости от других случайных величин.
[10]
Точка на оси х, соответствующая максимуму кривой плотности распределения, называется модой, то есть мода — это наиболее вероятное значение случайной величины. Однако, мода существует не у всех распределений.
[11]
Для непрерывной случайной величины модой называют точку максимума плотности распределения ее вероятностей. Распределения с одной модой называются одномодальными; они играют наиболее важную роль в приложениях. Иногда и здесь употребляют выражение наиболее вероятное значение случайной величины; это выражение надо понимать не в буквальном смысле ( вероятность любого значения непрерывной случайной величины равна нулю.
[12]
Страницы:
1
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
Для дискретной случайной величины X эта формула принимает вид:
Для непрерывной случайной величины: 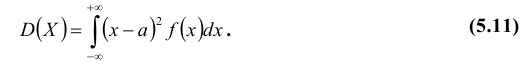
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 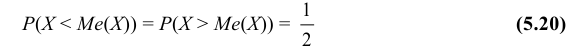
Пример №2
Найти моду, медиану случайной величины Х с плотностью вероятности
Решение:
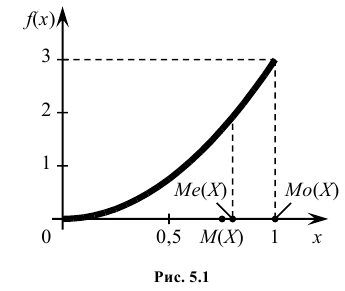
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 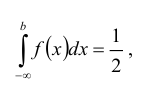
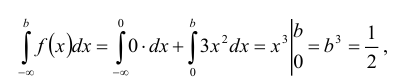
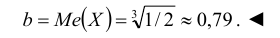
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
Пример №3
По данным примера 5.3 найти квантиль
Решение:
Находим функцию распределения 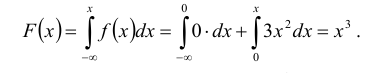
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
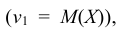
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 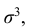
Полученная величина А называется коэффициентом асимметрии случайной величины: 
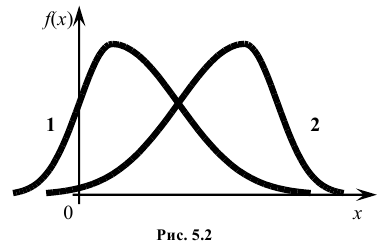
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число 
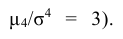
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 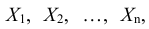
Обозначим среднее арифметическое n взаимно независимых случайных величин через
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 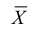
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
раз меньше дисперсии D каждой из величин:
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:
Пример:
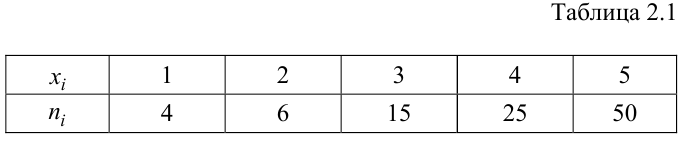
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
Решение. Определяем объем выборки:
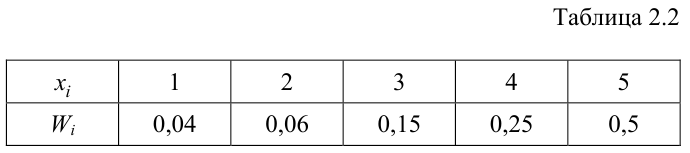
Определяем относительные частоты вариант (табл. 2.2):
Так как значение 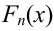
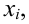
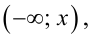
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины

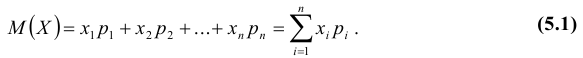
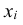
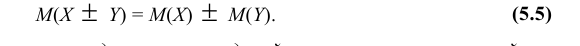


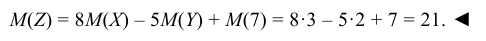







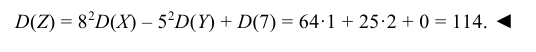
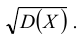

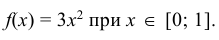

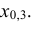
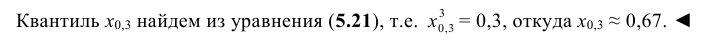



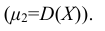
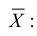
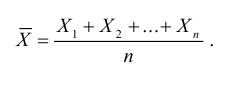

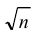 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: