Обновлено: 27.05.2023
Так как функция линейная, то будет возрастать (или убывать) на всем множестве определения, поэтому достаточно найти значение функции на концах отрезка.
Ответ: наибольшее значение 1, наименьшее -5.
- Написать правильный и достоверный ответ;
- Отвечать подробно и ясно, чтобы ответ принес наибольшую пользу;
- Писать грамотно, поскольку ответы без грамматических, орфографических и пунктуационных ошибок лучше воспринимаются.
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Применяя эту формулу, зная конкретное значение (x), можно вычислить соответствующее значение (y).
Чтобы построить график данной функции, нам нужны координаты двух точек, принадлежащих графику функции.
В жизни существует множество ситуаций, которые можно описать математической моделью с помощью линейных функций.
на овощной базе хранится (700) т картофеля. Каждый день запасы пополняют на (30) т. Сколько картофеля станет на овощной базе через (2); (4); (10) дней?
После (x) дней количество (y) картофеля на овощной базе можно записать в виде формулы (y = 700 + 30x).
Если функцию (y = kx + m) надо исследовать только для значений (x) из некоторого множества (X), то записывают y = kx + m , x ∈ X .
b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
b) y = 1 3 x + 1, x ∈ − 6 ; 3 , концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
Наибольшее и наименьшее значения функции на множестве
(основные определения)
Пусть X – некоторое множество, входящее в область определения D ( f ) функции y = f (x) .
Определение 1. Значение f (x0) функции y = f (x) в точкеназывают наибольшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство
Наибольшее значение функции f (x) на множестве X часто обозначают
Определение 2. Значение f (x0) функции y = f (x) в точке называют наименьшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство
Наименьшее значение функции f (x) на множестве X часто обозначают
Определение 3. Наибольшее значение функции на множестве X часто называют максимальным значением функции f (x) на множестве X или максимумом функции f (x) на множестве X . Наименьшее значение функции на множестве X часто называют минимальным значением функции f (x) на множестве X или минимумом функции f (x) на множестве X .
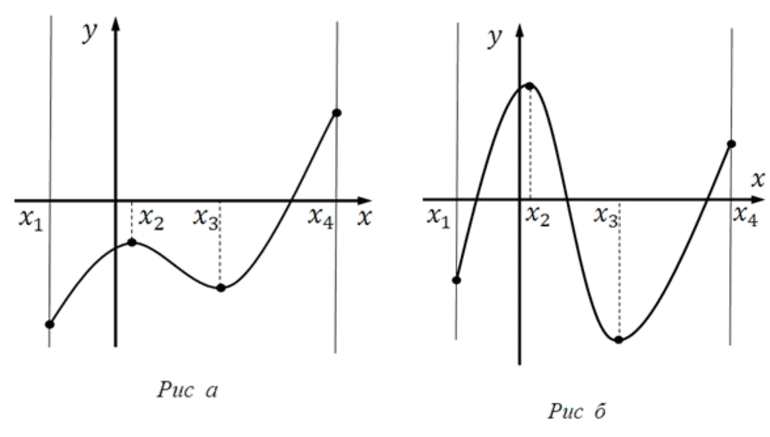
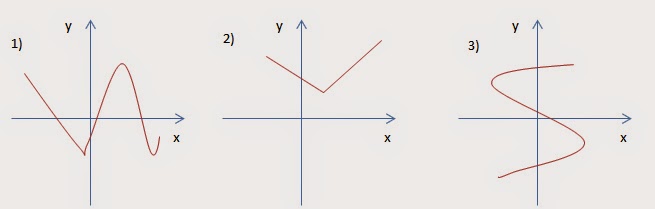
Пример 1. Минимальным значением функции y = x 2 на множестве является число 0 (рис. 1).
Максимального значения функция y = x 2 на множестве не имеет.
Пример 2. Максимальным значением функции y = – x 2 на множестве является число 0 (рис. 2).
Минимального значения функция y = – x 2 на множестве не имеет.
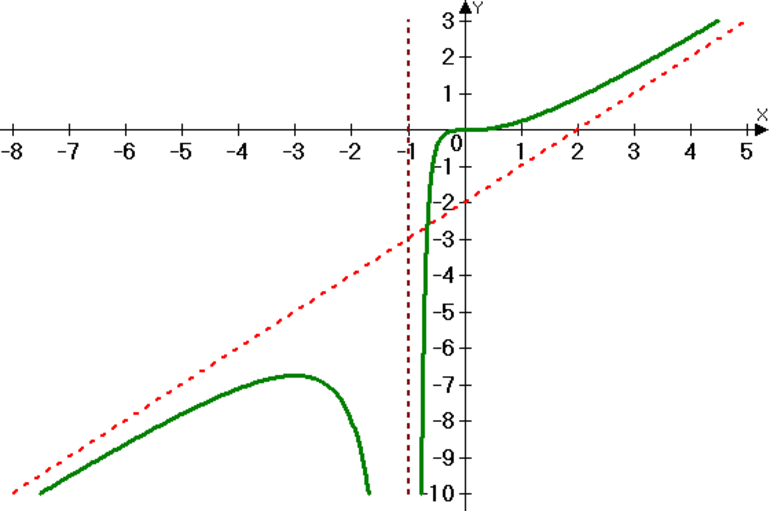
Пример 3. Функция y = x на множестве не имеет ни максимального, ни минимального значений (рис. 3).
Пример 4. Функция y = arctg x на множестве не имеет ни максимального, ни минимального значений (рис. 4).
Существование наибольшего и наименьшего значений функции на отрезке. Теорема Вейерштрасса
Как мы видели в примерах 1 — 4, даже такие хорошо известные функции, как
не имеют наибольших или наименьших значений на множестве. Однако, если бы в качестве множества X мы взяли произвольный отрезок, то ситуация стала бы принципиально иной, что вытекает из следующей теоремы.
Теорема Вейерштрасса. Если функция непрерывна на отрезке, то на этом отрезке существует точка, в которой функция принимает наибольшее значение, а также точка, в которой функция принимает наименьшее значение.
Доказательство теоремы Вейерштрасса выходит за рамки школьного курса математики и здесь не приводится.
Примеры решения задач
| y = 2x 3 + 3x 2 – 36x + 30 | (1) |
Из формулы (2) получаем, что критическими точками функции (1) являются точки x = – 3 , x = 2, причем только точка x = 2 принадлежит отрезку [–2, 4] . Вычисляя значения функции (1) в критической точке x = 2, а также на концах отрезка x = – 2 и x = 4 , получим:
| y (2) = – 14 , |
| y (– 2) = 98 , |
| y (4) = 62 . |
Ответ. Наибольшее значение функции (1) на отрезке [–2, 4] равно 98 , а наменьшее значение функции (1) на отрезке [–2, 4] равно – 14 .
на отрезке [–1, 27] .
Решая уравнение y’ = 0 , получим
Заметим также, что производная (4) функции (3) не существует в точке x = 0 . Следовательно, у функции (3) есть три критические точки: x = 0, и , причем все эти точки лежат на отрезке [–1, 27] . Вычисляя значения функции (3) в критических точках x = 0, и , а также на концах отрезка x = – 1 и x = 27 , получим:
| y (0) = 0 , |
| y (– 1) = – 1 , |
| y (27) = 99 . |
Ответ. Наибольшее значение функции (3) на отрезке [–1, 27] равно 99 , а наменьшее значение функции (3) на отрезке [–1, 27] равно – 1 .
Решение. Для того, чтобы найти критические точки функции (5), перепишем правую часть формулы (5), используя определение модуля:
В точке x = 0 производная функции (5) не существует. Критическими точками являются точки
Все критические точки принадлежат отрезку [–1, 6] . Вычисляя значения функции (5) в критических точках x = 0, x = 3, x = 5, а также на концах отрезка x = – 1 и x = 6 , получим:
| y (0) = – 4 , |
| y (3) = – e 3 , |
| y (5) = e 5 , |
| y (– 1) = – 5e , |
| y (6) = 2e 6 . |
Ответ. Наибольшее значение функции (5) на отрезке [–1, 6] равно 2e 6 , а наменьшее значение функции (5) на отрезке [–1, 6] равно – e 3 .
| y = (x – 27) e 28 – x | (6) |
на отрезке [23, 40] .
В некоторых задачах нужно найти наибольшее и наименьшее значения функции. Если неизвестен алгоритм и основные правила, то простое задание превращается в изнурительный труд, который очень редко приносит положительные результаты. В интернете существует множество информации, но не вся она достоверна. Самое страшное — применение неверных методик нахождения.
Общая информация
Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.
- Нахождение области определения функции (ОДФ).
- Понятие дифференциала и основные методы его нахождения.
- Умение решать уравнения.
- Знание графиков простых функций.
- Основные типы функций, полуинтервал и интервал.
Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.
Область определения
Обозначение интервалов
Результатом решения задач на нахождение ОДЗ является определенный интервал. Важно правильно его обозначать, поскольку это существенно влияет на решение. Нужно руководствоваться следующими правилами:
Очень важно правильно читать интервалы. Например, запись (1;4) читается следующим образом: переменная принимает значения, которые находятся в интервале от 1 не включительно до 4 не включительно. Это числа 2 и 3, поскольку 1 и 4 не входят в промежуток. Запись вида [5;10) читается таким образом: некоторое значение принадлежит интервалу от 5 включительно, до 10 не включительно.
Зависимость от типа
Функции различаются между собой. От этого и зависит нахождение их области определения. Они бывают простыми и сложными. Первые состоят из единичных элементов, а сложные включают в себя несколько типов. Их еще называют составными. Простые классифицируются на три вида:
- Алгебраические: рациональные и иррациональные.
- Тригонометрические: sin, cos, tg и ctg.
- Трансцендентные: степенные, показательные и логарифмические.
Рациональные бывают целыми и дробными. Они не включают в себя выражения, содержащие такие элементы: корень, степень, логарифм и тригонометрические функции. D(f) этих функций — все действительные числа (Z). Если она является дробной, то это означает, что в ее числителе и (или) знаменателе находится аргумент, значение которого не должно обращать ее в пустое множество.
Когда под корнем находится выражение, содержащее независимую переменную, то она называется иррациональной. В этом случае D(f) — множество Z, кроме тех, которые превращают выражение под корнем четной степени в отрицательное значение. Функция, представленная степенными выражениями, имеет D(f) = Z, но только тогда, когда значение аргумента не превращает функцию в пустое множество.
Метод нахождения
Для решения любой задачи нужно применять определенные правила. Они называются алгоритмом. Для каждого типа функций существует конкретный вариант решения. Для дробной он является следующим:
- Найти корни уравнения знаменателя, приравнивая его к 0.
- Определить интервал, значения из которого может принимать аргумент.
В случае, когда выражение является иррациональной функцией, корень которой является четным, следует решать не уравнение, а неравенство. Его значение не должно быть меньше 0. Для логарифмического типа выражение натурального логарифма (ln) должно быть всегда больше 0.
Для sin(x) и cos(x) областью определения является множество значений Z. Однако для tg(x) и ctg(x) следует помнить, что аргумент не должен принимать значение x = (Pi / 2) + Pi * k и x = Pi * k соответственно. Следует отметить, что коэффициент k принадлежит множеству чисел Z.
Для примера нужно разобрать задачу, в которой следует найти D(3x / [(x — 1) * (x + 1) * (10 — x)^(1/2)]). Решать ее необходимо по такому алгоритму:
- Знаменатель является сложным. Он состоит из двух выражений: (x — 1) * (x + 1) и (10 — x)^(1/2).
- Первое выражение (решить уравнение): (x — 1) * (x + 1) = 0. Оно имеет два корня: x1 = -1 и x2 = 1. Числовой промежуток: (-бесконечность;-1) U (1;+бесконечность).
- Второе (неравенство): (10 — x) a). Например, (a;+inf): х = lim [f(x)], где x->a и x->+inf.
Для нахождения минимального и максимального значения функции достаточно материала, изложенного выше. Специалисты рекомендуют разобраться с теорией, а затем переходить к практике.
Примеры решений
Дана квадратичная функция y = x^2 + 6x + 9. Необходимо найти наименьшее значение функции квадратного уравнения на отрезке [1;5]. Для этой цели нужно воспользоваться алгоритмом:
- D(y): все множество Z.
- Отрезок входит в D(y).
- Производная: y’ = [x^2 + 6x + 9]’ = 2x + 6 (существует во всех точках).
- Стационарные точки (y’ = 0): 2x + 6 = 0. Отсюда, x = -3.
- Подставить в исходное выражение: y(-3) = (-3)^2 + 6 * (-3) + 9 = 9 — 18 + 9 = 0, y(1) = (1)^2 + 6 * (1) + 9 = 1 + 6 + 9 = 16 и y(5) = (5)^2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.
- Максимум и минимум (с учетом стационарной точки и интервала): MIN(y) = 0 и MAX(y) = 64.
Одним из простейших типов задач является следующая: найдите наибольшее значение линейной функции z = 5x + 10 на отрезке [-3;3]. Для ее решения можно также воспользоваться алгоритмом:
- D(z) — все значения от бесконечно малого до бесконечно большого чисел.
- Промежуток, на котором нужно найти максимум и минимум, полностью входит в D(f).
- Дифференциал: z’ = 5 (существует во всех точках, а стационарных точек нет вообще).
- Минимум и максимум: MIN(z(-3)) = 5 * (-3) + 10 = -5 и MAX(z(3)) = 5 * (3) + 10 = 25.
Последнюю задачу необязательно решать по алгоритму, поскольку она считается простейшей. Математики рекомендуют тренироваться в нахождении MIN и MAX функции, поскольку только практика позволяет быстро решать задачи.
Таким образом, для нахождения максимального и минимального значений заданной функции необходимо пользоваться специальным универсальным алгоритмом. Кроме того, нужно правильно находить дифференциалы, область определения, а также разбираться в интервалах.
Читайте также:
- Обработка кокеток план урока
- Счастлив ли мечтатель белые ночи кратко
- План урока рог1аллин терахьдешнаш 6 класс
- Почему в русских школах учат немецкий язык
- Проект по вокалу в доу
построить график линейной функции:
a)
y=13x+1,x∈−6;3
; b)
y=13x+1,x∈−6;3
.
Составим таблицу значений функции:
| (x) | (-6) | (3) |
| (y) | (-1) | (2) |
Построим на координатной плоскости (xOy) точки ((-6;-1)) и ((3;2)) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции
y=13x+1,x∈−6;3
.
Точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены тёмными кружочками.
b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.
По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
В случае
a)
y=13x+1,x∈−6;3
, имеем:
yнаиб
(= 2) и
yнаим
(= -1);
b)
y=13x+1,x∈−6;3
, концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
Наибольшее и наименьшее значение функции
Как найти?
Постановка задачи
Найти наибольшее и наименьшее значение функции $ f(x) $ на отрезке $ [a,b] $
План решения
Наибольшее и наименьшее значение непрерывной функции $ f(x) $ на промежутке $ [a,b] $ достигаются в критических точках, то есть в точках в которых производная функции равна нулю $ f'(x) = 0 $, бесконечности $ f'(x) = pm infty $, не существует, либо на концах отрезка $ [a,b] $
- Проверяем на непрерывность функцию $ f(x) $ на заданном отрезке
- Если функция непрерывная, то находим производную $ f'(x) $ и приравниваем её к нулю
- Решая уравнение $ f'(x) = 0 $ получаем корни, являющиеся критическими точками
- Выбираем критические точки, принадлежащие отрезку $ [a,b] $
- Вычисляем значения функции $ f(x) $ в оставшихся критических точках, а так же на концах промежутка $ [a,b] $. Затем выбираем из них наибольшее $ M $ и наименьшее $ m $
Примеры решений
| Пример 1 |
| Найти наибольшее и наименьшее значение функции $ y = 2x^3 — 3x^2 — 4 $ на отрезке $ [0;2] $ |
| Решение |
|
Функция представляет собой кубический многочлен. Точек разрыва нет, значит функция непрерывна на отрезке $ [0;2] $. Находим производную: $$ y’ = (2x^3 — 3x^2 — 4)’ = 6x^2 — 6x $$ Приравниваем производную к нулю. Решаем уравнение и получаем критические точки: $$ 6x^2 — 6x = 0 $$ $$ 6x(x — 1) = 0 $$ $$ x_1 = 0, x_2 = 1 $$ Проверяем принадлежность полученных точек отрезку $ [0;2] $: $$ x_1 in [0;2], x_2 in [0;2] $$ Так как обе точки принадлежат отрезку, то вычисляем в них значение функции $ f(x) $, так же значение этой функции на концах интервала $ [0;2] $: $$ y(x_1) = y(a) = f(0) = 2 cdot 0^3 — 3 cdot 0^2 — 4 = -4 $$ $$ y(x_2) = y(1) = 2 cdot 1^3 — 3 cdot 1^2 — 4 = -5 $$ $$ y(b) = y(2) = 2 cdot 2^3 — 3 cdot 2^2 — 4 = 0 $$ Среди полученных значений наибольшее $ M = 0 $, наименьшее $ m = -5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ M = 0, m = -5 $$ |
| Пример 2 |
| Найти наименьшее и наибольшее значение функции $ y = frac{4x^2}{3+x^2} $ на $ [-1;1] $ |
| Решение |
|
Функция непрерывна на $ x in [-1;1] $ так как знаменатель не обращается в ноль ни при каком $ x $. Выполняем нахождение производной: $$ y’ = (frac{4x^2}{3+x^2})’ = frac{(4x^2)'(3+x^2)-(4x^2)(3+x^2)’}{(3+x^2)^2} = $$ $$ = frac{8x(3+x^2)-(4x^2)(2x)}{(3+x^2)^2} = frac{24x+8x^3-8x^3}{3+x^2)^2} = frac{24x}{(3+x^2)^2} $$ Приравниваем полученную производную к нулю и вычисляем критические точки: $$ frac{24x}{(3+x^2)^2} = 0 $$ $$ 24x = 0, 3+x^2 neq 0 $$ $$ x = 0 $$ Получена единственная критическая точка $ x = 0 $, которая принадлежит $ [-1; 1] $. Вычисляем значение функции $ f(x) $ в критической точке и на концах интервала $ [-1;1] $: $$ y(-1) = frac{4cdot (-1)^2}{3+(-1)^2} = frac{4}{4}=1 $$ $$ y(0) = frac{0}{3} = 0 $$ $$ y(1) = frac{4cdot 1^2}{3+1^2} = frac{4}{4} = 1 $$ Из полученных значений видно, что максимальное значение $ M = 1 $ и минимальное значение $ m = 0 $. |
| Ответ |
| $$ m = 0, M = 1 $$ |
§ 9 ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЁ ГРАФИК
1. Преобразование уравнения ах + by + с = 0 к виду у = kx + m
Алгоритм построения графика уравнения ах + by + с = 0, который мы сформулировали в § 8, при всей его чёткости и определённости математикам не очень нравится. Обычно они выдвигают претензии к первым двум шагам алгоритма. Зачем, говорят они, дважды решать уравнение относительно переменной у: сначала ах1 + by + с = 0, затем ах2 + by + с = 0? Не лучше ли сразу выразить у из уравнения ах + by + с = 0, тогда легче будет проводить вычисления (и, главное, быстрее)? Давайте проверим.
Рассмотрим сначала уравнение Зх — 2у + 6 = 0 (см. пример 2 из § 8), т. е. 2у = Зх + 6.
Умножив обе части уравнения на ½ получим …
Впрочем, тот же результат мы получили бы, если обе части исходного уравнения почленно разделили на 2. Обычно предпочитают в подобных случаях говорить не об умножении, а о почленном делении обеих частей уравнения на одно и то же число.
Придавая х конкретные значения, легко вычислить соответствующие значения у. Например, при х = 0 получаем у = 3; при х = -2 имеем у = 0; при х = 2 имеем у = 6; при х = 4 получаем у = 9. Видите, как легко и быстро найдены точки (0; 3), (-2; 0), (2; 6) и (4; 9), которые были выделены в примере 2 из § 8.
Точно так же уравнение 5х — 2у = 0 (см. пример 4 из § 
Из этого уравнения можно найти решения (0; 
Рассмотрим теперь указанные преобразования в общем виде.
Случаи, когда в уравнении ах + by + с = 0 коэффициенты а и b равны нулю, мы рассмотрели в § 8. Там же мы отметили, что в случае, когда а Ф О, b = 0, графиком уравнения является прямая, параллельная оси у.
Рассмотрим случай, когда b ≠ 0. Имеем ах + by + с = 0; (1) bу = -ах – с;
Введя обозначения … получаем у = kx + m.
Таким образом, линейное уравнение (1) с двумя переменными х и у в случае, когда b ≠ 0, можно преобразовать к виду у = kx + m (2) где k, m — числа (коэффициенты).
Это частный вид линейного уравнения. Зная, чему равен х, по правилу у = kx + m всегда можно найти, чему равен у. Будем называть уравнение (2) линейной функцией.
С помощью уравнения (2) легко, указав конкретное значение х, вычислить соответствующее значение у. Пусть, например, у = 2х + 3. Тогда:
если х = 0, то у = 3;
если х = 1, то у = 5;
если х = -1, то у = 1;
если х = 3, то у = 9 и т. д.
Обычно эти результаты оформляют в виде таблицы:
Значения у из второй строки таблицы называют значениями линейной функции у = 2х + 3 соответственно в точках х = 0, х = 1, х = -1, х = 3.
В уравнении (1) переменные хну равноправны, а в уравнении (2) — нет: конкретные значения мы придаём одной из них — переменной х, тогда как значение переменной у зависит от выбранного значения переменной х. Поэтому обычно говорят, что х — независимая переменная (или аргумент), у — зависимая переменная.
Частным случаем теоремы 1 из § 8 является следующая теорема.
ТЕОРЕМА 2. Графиком линейной функции у = kx + m является прямая.
ПРИМЕР 1. Построить график линейной функции у = 2х + 3.
Решение: Составим таблицу:
х I 0 I 1
У I 3 I 5
Построим на координатной плоскости хОу точки (0; 3) и (1; 5) и проведём через них прямую. Это и есть график линейной функции у = 2х + 3 (рис. 34).
Замечание. В русском языке часто один и тот же объект называют по-разному, например: «дом», «здание», «сооружение», «коттедж», «особняк», «барак», «хибара», «избушка». В математическом языке ситуация примерно та же. Скажем, равенство с двумя переменными у = kx + m, где k, m — конкретные числа, можно назвать линейной функцией, можно назвать линейным уравнением с двумя переменными х и у (или с двумя неизвестными x и у), можно назвать формулой, можно назвать соотношением, связывающим х и у, можно, наконец, назвать зависимостью между хну. Это неважно, главное — понимать, что во всех случаях речь идёт о математической модели у = kx + m.
2. Линейные функции как математические модели реальных ситуаций
Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции. Приведём примеры.
Первая ситуация. На складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Если пройдёт х дней, то количество у угля на складе (в тоннах) выразится формулой у = 500 + ЗОх. Таким образом, линейная функция у = ЗОх + 500 есть математическая модель ситуации.
Теперь нетрудно установить, что:
- при х = 2 имеем у = 560 (в уравнение у = ЗОх + 500 подставили х = 2 и получили у = 560);
- при х = 4 имеем у = 620;
- при х = 10 имеем у = 800.
Вторая ситуация. На складе было 500 т угля. Ежедневно стали увозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Здесь математической моделью ситуации является линейная функция у = 500 — ЗОх. С помощью этой модели нетрудно ответить на вопрос задачи:
- если х = 2, то у = 440 (в уравнение у = 500 — ЗОх подставили х = 2 и получили у = 440);
- если х = 4, то у = 380;
- если х = 10, то у = 200.
Третья ситуация. Турист проехал на автобусе 15 км от пункта А до пункта В, а затем продолжил движение в том же направлении, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от пункта А будет турист через 2 ч, через 4 ч, через 5 ч ходьбы?
Математической моделью ситуации является линейная функция у = 15 + 4х, где х — время ходьбы (в часах), у — расстояние от А (в километрах). С помощью этой модели отвечаем на вопрос задачи:
- если х = 2, то у = 23 (в уравнение у = 15 + 4х подставили х = 2 и получили у = 23);
- если х = 4, то у = 31;
- если х = 6, то у = 39.
Итак, в каждой из рассмотренных ситуаций математической моделью служит линейная функция. Но (внимание!), строго говоря, все три составленные модели не совсем точны, они не учитывают тех ограничений на переменную, которые вытекают из смысла задачи. Ведь ясно, что в первой ситуации независимая переменная х может принимать только значения 1, 2, 3, …, поскольку х — число дней. Следовательно, уточнённая математическая модель первой ситуации выглядит так:
у = 500 + ЗОх, где х — натуральное число.
Вторую ситуацию необходимо уточнить условием у > 0. Это значит, что независимая переменная х, обозначающая, как и в первой ситуации, число дней, может принимать только значения 1, 2, 3, …, 16. Действительно, если х = 16, то по формуле у = 500 — ЗОх находим у = 500 — 30 • 16 = 20. Значит, уже на 17-й день вывезти со склада 30 т угля не удастся, поскольку на складе к этому дню останется всего 20 т и процесс вывоза угля придётся прекратить. Следовательно, уточнённая математическая модель второй ситуации выглядит так:
у = 500 — ЗОх, у > 0 или у = 500 — ЗОх, где х = 1, 2, 3, …, 16.
В третьей ситуации независимая переменная х теоретически может принять любое неотрицательное значение (х = 0, х = 2, х = 3,5 и т. д.), но практически турист не может шагать с постоянной скоростью без сна и отдыха сколько угодно времени. Значит, нам нужно было принять разумные ограничения для х, скажем, 0 < х < 6 (т.е. турист идёт не более 6 ч).
Напомним, что геометрической моделью нестрогого двойного неравенства 0 < х < 6 служит отрезок [0; 6] координатной прямой (рис. 35). Значит, уточнённая модель третьей ситуации выглядит так: у = 15 + 4х, где х принадлежит отрезку [0; 6].
Условимся вместо фразы «х принадлежит множеству X» писать х е X (читают: «элемент х принадлежит множеству X», е — знак принадлежности). Как видите, наше знакомство с математическим языком постоянно продолжается. Множество натуральных чисел обычно обозначают буквой N. Значит, вместо фразы «х — натуральное число» мы можем использовать соотношение х е N.
Если линейную функцию у = kx + m надо рассматривать не при всех значениях х, а лишь для значений х из некоторого числового множества X, то пишут у = kx + m, х ∈ Х.
А теперь запишем более точные математические модели для рассмотренных выше трёх ситуаций.
- Первая ситуация: у = 500 + ЗОх, х е N.
- Вторая ситуация: у = 500 — ЗОх, х е {1, 2, 3, …, 16}.
- Третья ситуация: у = 15 + 4х, х е [0; 6].
3. Построение графика линейной функции на заданном промежутке
Построить график линейной функции:
Решение: а) Составим таблицу для линейной функции у = -2х + 1:
х | -3 | 2
y I 7 I -3
Построим на координатной плоскости хОу точки (-3; 7) и (2; -3) и проведём через них прямую линию. Это график уравнения у = -2х + 1. Далее выделим отрезок, соединяющий построенные точки (рис. 36). Этот отрезок и есть график линейной функции у = -2х + 1, где х е [-3; 2].
Обычно говорят, что мы построили график линейной функции у = -2х + 1 на отрезке [-3; 2].
б) Чем отличается этот пример от предыдущего? Линейная функция та же (у = -2х + 1), значит, и графиком её служит та же прямая. Но — будьте внимательны! — на этот раз х е (-3; 2), т. е. значения х = -3 и х = 2 не рассматриваются, они не принадлежат интервалу (-3; 2). Как мы отмечали концы интервала на координатной прямой? Светлыми кружочками (рис. 39), об этом мы говорили в § 5. Точно так же и точки (-3; 7) и (2; -3) придётся отметить на чертеже светлыми кружочками. Это будет напоминать нам о том, что берутся лишь те точки прямой у = -2х + 1, которые лежат между точками, отмеченными кружочками (рис. 37). Впрочем, иногда в таких случаях используют не светлые кружочки, а стрелки (рис. 38). Это непринципиально: главное — понимать, о чём идёт речь.
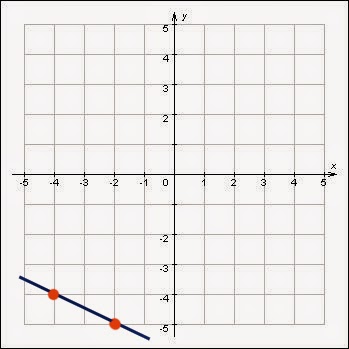
ПРИМЕР 3. На координатной прямой отмечены точки А(-4), В(-3). Найти наибольшее и наименьшее значения линейной функции у = х/2 + 4 на отрезке [0; 6].
Решение: Составим таблицу для линейной функции. Построим на координатной плоскости хОу точки (0; 4) и (6; 7) и проведём через них прямую — график линейной функции
Нам нужно рассмотреть эту линейную функцию не целиком, а на отрезке [0; 6], т. е. для х е [0; 6]. Соответствующий отрезок графика выделен на чертеже. Обратим внимание, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 — это и есть наибольшее значение линейной функции у = х/2 + 4 на отрезке [0; 6]. Обычно используют такую запись:
Замечаем, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке 40 части прямой, равна 4 — это и есть наименьшее значение линейной функции у — iх + 4 на отрезке [0; 6]. Обычно используют такую запись:
Ответ: унаиб = 7, унаим = 4.
ПРИМЕР 4. Найти унаиб и унаим для линейной функции у = -1,5х + 3,5:
- а) на отрезке [1; 5];
- б) на интервале (1; 5);
- в) на полуинтервале [1; 5);
- г) на луче [0; +оо);
- д) на луче (~°°; 3].
Решение
Составим таблицу для линейной функции. Построим на координатной плоскости хОу точки (1; 2) и (5; -4) и проведём через них прямую (рис. 41—45). Выделим на построенной прямой часть, соответствующую значениям х из отрезка [1; 5] (рис. 41), из интервала (1; 5) (рис. 42), из полуинтервала [1; 5) (рис. 43), из луча [0; +°°) (рис. 44), из луча (~°°; 3] (рис. 45).
а) С помощью рисунка 41 нетрудно сделать вывод, что унаиб = 2 (этого значения линейная функция достигает при х = 1), а унаим = -4 (этого значения линейная функция достигает при х = 5).
б) В отличие от предыдущего случая, оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, из рассмотрения исключены (рис. 42). Среди остальных точек графика нет ни точки с наименьшей ординатой, ни точки с наибольшей ординатой. Значит, ни наибольшего, ни наименьшего значений на заданном интервале у данной линейной функции нет.
в) С помощью рисунка 43 заключаем, что унаиб 2 (как и в первом случае), а наименьшего значения у линейной функции нет (как и во втором случае).
г) унаиб = 3,5 (этого значения линейная функция достигает при х = 0), а унаим не существует (рис. 44).
д) унаим = -1 (этого значения линейная функция достигает при х — 3), а унаиб не существует (рис. 45).
4. Свойства линейной функции
ПРИМЕР 5. Построить график линейной функции у = 2х — 6. С помощью графика ответить на следующие вопросы:
а) при каком значении х будет у = 0;
б) при каких значениях х будет у > 0;
в) при каких значениях х будет у < 0?
Решение: Составим таблицу для линейной функции у = 2х — 6:
Через точки (0; -6) и (3; 0) проведём прямую — график линейной функции у = 2х — 6 (рис. 46).
- а) у = 0 при х = 3. График пересекает ось х в точке х = 3, это и есть точка с ординатой у — 0.
- б) у > 0 при х > 3. В самом деле, если х > 3, то соответствующая часть прямой расположена выше оси х, значит, ординаты соответствующих точек прямой положительны.
- в) у < 0 при х < 3. В самом деле, если х < 3, то соответствующая часть прямой расположена ниже оси х, значит, ординаты соответствующих точек прямой отрицательны.
Обратите внимание, что в этом примере мы с помощью графика решили:
- а) уравнение 2х — 6 = 0 (получили х = 3);
- б) неравенство 2х — 6 > 0 (получили х > 3);
- в) неравенство 2х — 6 < 0 (получили х < 3).
Рассмотрим график линейной функции, изображённый на рисунке 47, а. Если двигаться по этому графику слева направо, то ординаты точек графика всё время увеличиваются, мы как бы «поднимаемся в горку». В таких случаях математики употребляют термин возрастание и говорят так: если к > 0, то линейная функция у = kx + m возрастает.
Рассмотрим график линейной функции, изображённый на рисунке 47, б. Если двигаться по этому графику слева направо, то ординаты точек графика всё время уменьшаются, мы как бы «спускаемся с горки». В таких случаях математики употребляют термин убывание и говорят так: если k < 0, то линейная функция у = kx + m убывает.
ПРИМЕР 6. На рисунке 48 изображён график движения автомобиля между пунктами 1 и 2. По оси t отмечено время (в часах), по оси S — расстояние до пункта 1. Требуется охарактеризовать весь процесс движения словами.
Решение: Точка А соответствует началу движения. До пункта 2 автомобиль доехал за 1 1/3 ч — об этом можно судить по абсциссе точки D. Пройденное расстояние равно 50 км — об этом можно судить по ординате точки D. Значит, можно вычислить скорость движения автомобиля: v = 50 : 4/3 = 37,5 км/ч.
На участке графика DE ордината постоянна, т. е. расстояние от пункта 1 не менялось. Это значит, что автомобиль не двигался (стоял в пункте 2). Причём он стоял в промежутке от 1^ ч до 2-| ч (это абсциссы точек D и Е). Остановка длилась, таким образом, 1 ч 20 мин.
На обратный путь после остановки автомобиль потратил столько же времени, сколько на путь от 1 до 2, значит обратно он ехал с той же скоростью.
Вопросы для самопроверки
- Что такое линейная функция?
- Что является графиком линейной функции?
- Сколько точек достаточно взять для построения графика линейной функции?
- Опишите процесс построения графика линейной функции у = 2х + 3, где х е [0; 2]. Что изменится, если х е (0; 2)?
- Дана линейная функция у = kx + m, х е X, где X — некоторый числовой промежуток. Что такое унаим, унаиб?
- Дано: у = 2х + 3, х е [0; +оо). Найдите, если возможно, унаим, унаиб. Что изменится, если х е (0; +оо)? если х е (—оо; 0]? если X € (-оо; 0)?
- Как с помощью графика линейной функции у = kx + m, где k Ф 0, решить: а) уравнение kx + m = 0; б) неравенство kx + m > 0; в) неравенство kx + m < 0?
- В каком случае линейная функция возрастает, а в каком — убывает? Как об этом можно судить по графику линейной функции?
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
Переменную х называют независимой переменной или аргументом, а переменную у — зависимой переменной. Говорят, что у является функцией от х.
Значение у, соответствующее заданному значению х, называют значением функции.
Все значения, которые принимает независимая переменная (x) образуют область определения функции; все значения, которые принимает зависимая переменная (y), образуют множество значений функции.
Обозначают D — область определения, Е — множество значений функции.
Функция может быть задана формулой, таблицей, графиком.
1. Область определения.
Это множество всех допустимых значений аргумента x, при которых выражение f(x) имеет смысл.
2. Область значений функции.
Это множество всех действительных значений y, которые принимает функция.
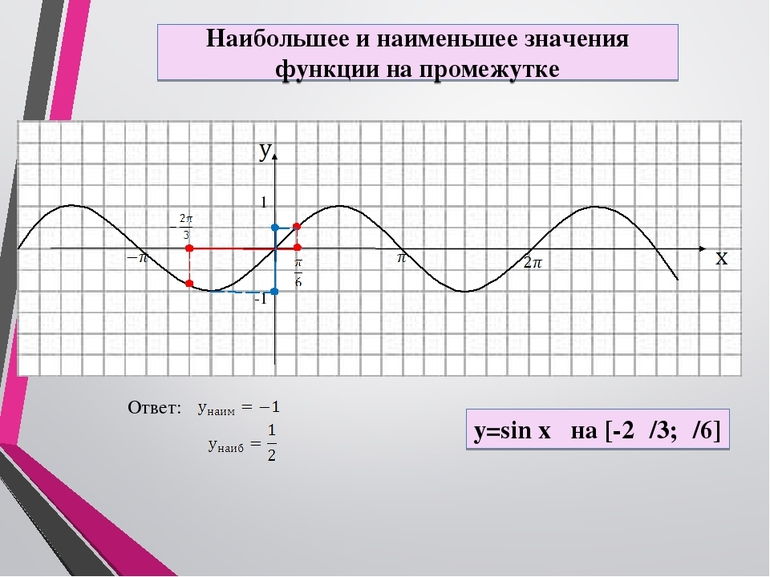
3. Наибольшее и наименьшее значения функции на промежутке.
Наибольшее значение функции — это самое большее значение у из области значений функции. Наименьшее значение функции — это самое маленькое значение у из области значений функции.
4. Нули функции.
Это значения аргумента х, при которых значение функции равно нулю.
Чтобы найти нули функции y=f(x), нужно решить уравнение f(x)=0. Корни этого уравнения и будут нулями функции.
Для нахождения нулей функции y=f(x) по графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции.
5. Промежутки знакопостоянства.
Это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть f(x)>0 или f(x)<0.
Нахождение промежутков знакопостоянства функции y=f(x) по ее графику: найти промежутки значений аргумента х, при которых график функции расположен выше оси ОХ: f(x)>0; найти промежутки значений аргумента х, при которых график функции расположен ниже оси ОХ: f(x)<0.
6. Промежутки монотонности функции.
Промежутки монотонности функции – это такие промежутки значений аргумента х, при которых функция возрастает или убывает.
Функция y=f(x) возрастает на промежутке, если для любых двух значений аргумента принадлежащих промежутку и если x1<x2 выполняется соотношение: f(x1)<f(x2)..
Другими словами, функция возрастает на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция y=f(x) убывает на промежутке, если для любых двух значений аргумента , принадлежащих промежутку и если x1<x2 выполняется соотношение: f(x1)>f(x2).
Другими словами, функция убывает на промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
График линейной функции y=kx+b — прямая линия.
Для построения графика линейной функции достаточно двух точек, например А(0; b) и В(-b/k; 0).
Если b=0 и k≠0, то график функции проходит через начало координат.
Если k=0, то функция у=b — постоянная и ее графиком является прямая, параллельная оси OX.
Например:
Построить график функции y=2x+3.
Если х=0, то у=3. Координаты первой точки (0; 3).
Если у=0, то х=-1,5. Координаты второй точки (-1,5; 0).
Отметим эти точки и проведем через них прямую — график функции у=2х+3.
Свойства линейной функции
1. Область определения линейной функции — множество всех действительных чисел: D=(-∞; +∞).
2. Область значений функции.
Если k≠0, то Е=(-∞; +∞).
Если k=0, то Е={b}.
3. Наибольшее и наименьшее значения функции на промежутке.
Линейная функция не имеет наибольшего и наименьшего значений , если k≠0.
4. Нули функции.
График функции пересекает ось Ох в точке (-b/k; 0), если k≠0.
Если k=0, b≠0, то нулей нет.
Если k=0 и b=0, то у=0 при любых х.
5. Промежутки знакопостоянства.
Если k>0, то y>0 при х ∈ (-b/k; +∞);
y<0 при х ∈ (-∞; -b/k).
Если k<0, то y>0 при х ∈ (-∞; -b/k);
y<0 при х ∈ (-b/k; +∞).
Если k=0 и b>0, то у>0 при х ∈ (-∞; +∞);
b<0, то у<0 при х ∈ (-∞; +∞);
6. Промежутки монотонности функции.
Если k>0, то функция возрастает.
Если k<0, то функция убывает.
Если k=0, то функция ни возрастающая, ни убывающая.
Прямая пропорциональность
Прямой пропорциональностью называется функция, которую можно задать формулой y = kx, где х – независимая переменная, k – не равное нулю число.
Число k называют коэффициентом прямой пропорциональности.
График прямой пропорциональности представляет собой прямую, проходящую через начало координат.
Прямая пропорциональность является частным случаем линейной функции.
Взаимное расположение прямых
Прямые у=k1x+b1 и y=k2x+b2:
пересекаются, если k1 ≠ k2
параллельны, если k1 = k2 и b1 ≠ b2
перпендикулярны, если k1
× k2 =-1.
УПРАЖНЕНИЯ
1. а) Автомобиль проехал 300 км, двигаясь со скоростью V км/ч. Запишите формулу для вычисления времени t, потраченного на весь путь. Является ли t функцией от V?
б) Самолет пролетел 3000 км за t часов. Запишите формулу для вычисления скорости его движения V. Является ли V функцией от t?
Решение:
а) t= 300 : V. t является функцией от V, т.к. значение переменной t зависит от значения переменной V.
2. Выберите рисунки, на которых изображены графики функций:
а)
б)
Решение:
а) На рисунке изображен график функции, если каждому значению х соответствует единственное значение у. Данному определению соответствуют рисунки 1 и 2.
Ответ: 1,2.
3. Из перечисленных функций выберите те, графики которых:
а) параллельны прямой у=4-0,5х:
1) y=-0,5x; 2) у=2+0,5х; 3) у=2-0,5х; 4) у=4-5х.
б) параллельны прямой у=0,2х-3:
1) у=-3; 2) у=-0,2х+3; 3) у=0,2х+3; 4) у=0,2х.
Решение:
а) Прямые параллельны, если k1 = k2 и b1 ≠ b2. k1 = -0,5. Такой же коэффициент k у функций 1) y=-0,5x; 3) у=2-0,5х.
Ответ: 1, 3.
4. Из перечисленных функций выберите те, график которых:
а) пересекает прямую у=-0,6х+1,7:
1) у=0,6х+1,7; 2) у=-0,6х+2; 3) у=3-0,6х; 4) у=-0,6х.
б) пересекает прямую у=0,8х-3,2:
1) у=0,8х+1,5; 2) у=-0,8х+3,6; 3) у=4+0,8х; 4) у=-0,8х.
Решение:
а) Прямые пересекаются, если k1 ≠ k2. k1 = -0,6. Коэффициент, отличный от -0,6 у функции 1) у=0,6х+1,7.
Ответ: 1.
5. а) Из функций у=2х-3; у=-4х; у=0,9х-12; у=-0,1х+43; у=-2 выберите убывающие.
б) Из функций у=4-3х; у=5; у=0,4х+3; у=-0,1х-1; у=0,005х-12 выберите возрастающие.
Решение:
а) Функция у=kx убывает, если k<0. Следовательно, убывающие функции: у=-4х; у=-0,1х+43.
Ответ: у=-4х; у=-0,1х+43.
6. Найдите нуль функции:
а) у=2,5х+4,2; б) у=-1,6х+2,5.
Решение:
а) Для нахождения нуля функции возьмем у=0, получим уравнение 0=2,5х+4,2.
Решим уравнение 0=2,5х+4,2,
2,5х=-4,2,
х= -4,2: 2,5,
х=1,68.
Ответ: 1,68.
7. а) График функции у=kx-5 проходит через точку А(-0,6; 10). Найдите коэффициент k.
б) График функции у=kx+3 проходит через точку А(0,2; -5). Найдите коэффициент k.
Решение:
а) Т.к. график проходит через точку А(-0,6; 10), то х=-0,6 и у=10. Подставив х и у в функцию у=kх-5, получим уравнение 10=-0,6k-5.
Решим уравнение 10=-0,6k-5,
-0,6k=15,
k=15:(-0,6),
k=25.
Ответ: 25.
8. а) Нулем линейной функции y=kx+b является число 3,5, а точка пересечения с осью ОY имеет ординату -2. Найдите коэффициент k.
б) Нулем линейной функции y=kx+b является число -2,5, а точка пересечения с осью ОY имеет ординату 5. Найдите коэффициент k.
Решение:
а) Т.к. нулем функции является число 3,5, то график функции проходит через точку (3,5; 0). Т.к. точка пересечения с осью OY имеет ординату -2, то график функции проходит через точку (0; -2).
Подставим в формулу y=kx+b координаты первой и второй точек:
0=3,5k+b и -2=0k+b. Из второго уравнения найдем b=-2. Подставим b в первое уравнение и найдем k: 0=3,5k-2
3,5k=2,
k=4/7.
Ответ: 4/7.
9. а) Приведите пример линейной функции, график которой пересекает прямую у=3-0,5х в точке, принадлежащей оси ординат.
б) Приведите пример линейной функции, график которой пересекает прямую у=8х-1 в точке, принадлежащей оси ординат.
Решение:
а) График функции у=3-0,5х пересекает ось ординат в точке (0; 3), следовательно и новый график функции пересекает ось ординат в точке (0; 3), это означает, что коэффициент b новой функции равен 3. Т.к. прямые пересекаются, то k1 ≠ k2, и примером заданной линейной функции могут быть: у=5х+3; у=-2х+3; у=0,25х+3.
10. а) Коэффициент k прямой y=kx+b равен 2,5. Постройте эту прямую, если абсцисса точки пересечения ее с осью ОХ равна -3.
б) Коэффициент k прямой y=kx+b равен -1,5. Постройте эту прямую, если абсцисса точки пересечения ее с осью ОХ равна 4.
Решение:
а) Запишем уравнение прямой с коэффициентом 2,5, проходящей через точку (-3; 0). Найдем коэффициент b: 0=-3*2,5+b; b=7,5.
Уравнение прямой: у=2,5х+7,5.
Для построения графика найдем еще одну точку: х=-2, тогда у=2,5*(-2)+7,5=2,5.
Построим график функции, который проходит через точки (-3; 0) и (-2; 2,5).
11. Постройте график функции и укажите ее свойства:
а) у=-6 — 0,5х; б) у=-4х.
Решение:
а) Для построения графика функции у=-6 — 0,5х найдем две точки:
Если х=-4, то у=-4; если х=-2, то у=-6-0,5*(-2)=-5.
Построим график функции, который проходит через точки (-4; -4) и (-2; -5).
Свойства:
1. Область определения функции D=(-∞; +∞);
2. Область значений функции Е=(-∞; +∞);
3. Функция не имеет наибольшего и наименьшего значений.
4. Нули функции.
0=-6-0,5х; -0,5х=6; х = 6 : (-0,5)=-12. Нуль функции х=-12.
5. Промежутки знакопостоянства.
y>0 при х ∈ (-∞; -12);
y<0 при х ∈ (-12; +∞).
6. Промежутки монотонности функции.
Функция убывает на промежутке (-∞; +∞).
12. а) График прямой пропорциональности проходит через точку А(20; 5). Найдите коэффициент прямой пропорциональности. Проходит ли этот график через точку В(8; 2)?
б) График прямой пропорциональности проходит через точку А(3; -15). Найдите коэффициент прямой пропорциональности. Проходит ли этот график через точку В(-1; -5)?
Решение:
а) Формула прямой пропорциональности у=kx. Т.к. график функции проходит через точку А(20; 5), то подставив х=20 и у=5 в формулу найдем k.
5=20k,
k=5:20,
k=0,25 — коэффициент прямой пропорциональности.
Формула заданной прямой пропорциональности у=0,25х.
Проверим, проходит ли график функции через точку В(8; 2):
2=0,25*8, получим 2=2 — истинное равенство, следовательно точка принадлежит графику.
Ответ: 0,25; да.
13. Запишите уравнение прямой, проходящей через точки:
а) А(-2; 3) и В(5; -1); б) А(3; -6); В(-4; 5).
Решение:
а) Уравнение прямой в общем виде у=kx+b. Подставим координаты первой и второй точек в уравнение и решим систему из двух уравнений.
14. а) Прямая y=kx+b проходит через точку пересечения прямых у=-3х+0,5 и у=6х-0,5 и не пересекает прямую у=17х-5. Найдите k и b.
б) Прямая y=kx+b проходит через точку пересечения прямых у=5х-0,7 и у=-4х+0,3 и не пересекает прямую у=-16х+2. Найдите k и b. (№ 4.4.7 [7])
Решение:
а) Найдем точку пересечения прямых у=-3х+0,5 и у=6х-0,5, для этого решим систему из двух уравнений:
Т.к. прямая не пересекает прямую у=17х-5, то k=17. Зная коэффициент и точку, через которую прямая проходит, найдем b:
1/6=17*(1/9)+b, b=1/6 — 17/9 = -31/18.
Ответ: k=17; b= -31/18.
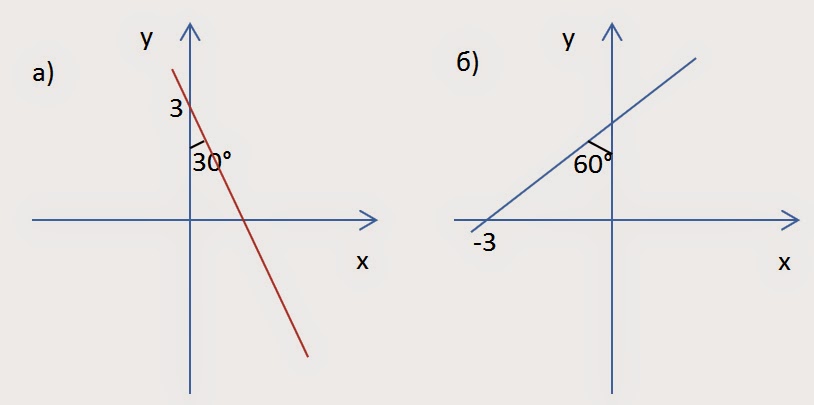
15. а) Задайте формулой линейную функцию по изображению ее графика.
Решение:
а) Рассмотрим прямоугольный треугольник, который образуют прямая с осями координат. В этом треугольнике угол равен 30 градусов и прилежащий катет равен 3. Найдем противолежащий катет:
График функции проходит через точки (0; 3) и
Уравнение прямой в общем виде у=kx+b. Подставим координаты первой и второй точек в уравнение и решим систему из двух уравнений.
16. а) Прямые у=k1x+b1 и y=k2x+b2 параллельны и составляют острый угол с положительным направлением оси абсцисс. Приведите пример значений k1, b1, k2, b2, если расстояние между точками пересечения этих прямых с осью OY равно 5.
б) Прямые у=k1x+b1 и y=k2x+b2 параллельны и составляют тупой угол с положительным направлением оси абсцисс. Приведите пример значений k1, b1, k2, b2, если расстояние между точками пересечения этих прямых с осью OY равно 7.
Решение:
а) Т.к. прямые у=k1x+b1 и y=k2x+b2 параллельны, то k1 = k2. Прямые составляют острый угол с осью абсцисс, следовательно k>0. Коэффициент b первой прямой отличается от коэффициента b второй прямой на 5.
Тогда коэффициенты могут быть следующими: k1=1, b1=-3, k2=1, b2 =2.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Какая из точек А(-2;1), В(0;4), С(-3; 8), К(-1; 4), Н(1;1) принадлежит графику функции у=4-3х?
2. Из перечисленных функций выберите те, график которых проходит через начало координат: у=3-х; у=5х; у=5х-1; у=-4х; у=5.
3. Найдите значения х, при которых функция у=5-3х неотрицательна.
4. Точка А(c,d) принадлежит графику функции у=4х. Найдите c и d, если d больше с на 2.
5. График постоянной функции проходит через точку А(5;-3). Задайте эту функцию формулой. Проходит ли этот график через точку В(-85; -3)?
6. В одной системе координат постройте графики функций у=0,6х; у=0,6; у=-0,6х+2. Укажите среди этих функций постоянную.
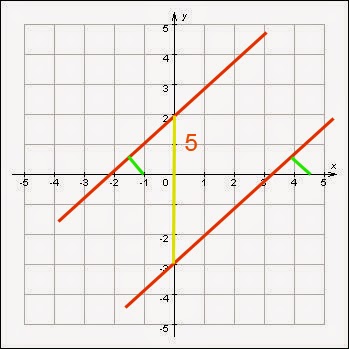
7. Запишите уравнение прямой по ее графику:
8. Прямая пересекает ось ОХ в точке с абсциссой 2,5, а ось OY в точке с ординатой -2,5. Задайте эту прямую формулой.
9. Коэффициент k прямой y=kx+b — наименьшее простое число. Задайте эту прямую уравнением, если нулем функции y=kx+b является число -3.
10. Графиком функции является ломаная ABCD. Изобразите этот график, если А(-6;3), В(-3; -2), С(2;4), D(4; -1). Найдите среднее арифметическое нулей этой функции.