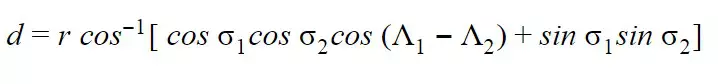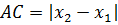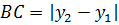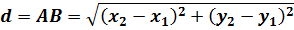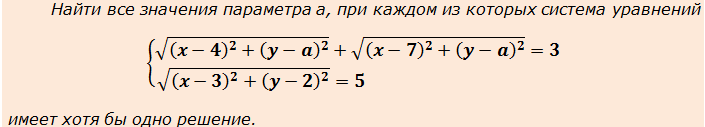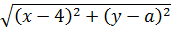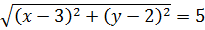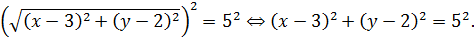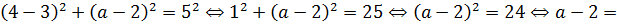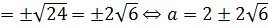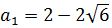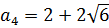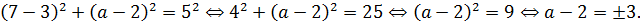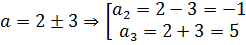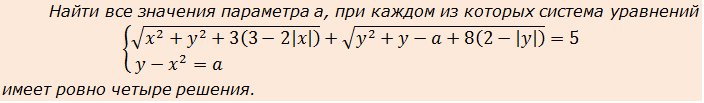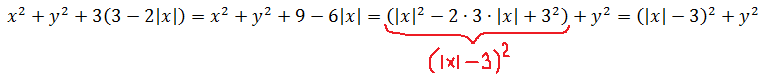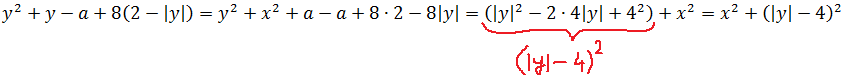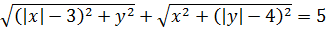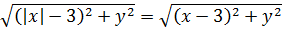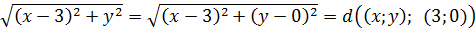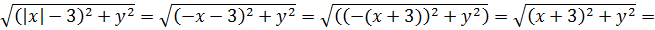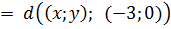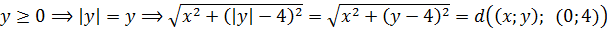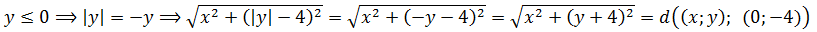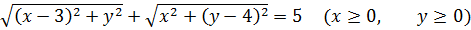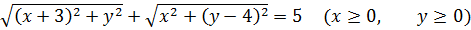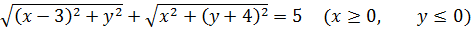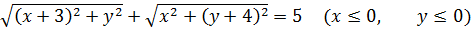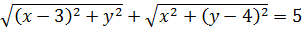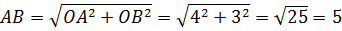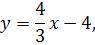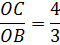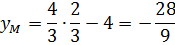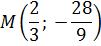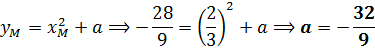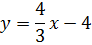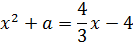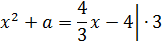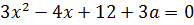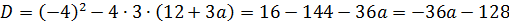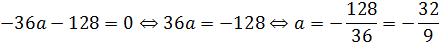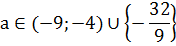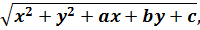Как найти наибольшее расстояние между точками

Решение задач по математике у учащихся часто сопровождается многими трудностями. Помочь учащемуся справиться с этими трудности, а так же научить применять имеющиеся у него теоретические знания при решении конкретных задач по всем разделам курса предмета «Математика» – основное назначение нашего сайта.

Приступая к решению задач по теме «Расстояние между двумя точками на плоскости», учащиеся должны уметь строить точку на плоскости по ее координатам, а так же находить координаты заданной точки.

Вычисление расстояния между взятыми на плоскости двумя точками А(х_А; у_А) и В(х_В; у_В), выполняется по формуле d = √((х_А –  х_В)² + (у_А – у_В)²), где d – длина отрезка, который соединяет эти точки на плоскости.

Если один из концов отрезка совпадает с началом координат, а другой имеет координаты М(х_М; у_М), то формула для вычисления d примет вид ОМ = √(х_М² + у_М²).

1. Вычисление расстояния между двумя точками по данным координатам этих точек

Пример 1.

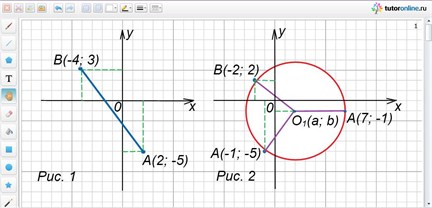
Найти длину отрезка, который соединяет на координатной плоскости точки А(2; -5) и В(-4; 3) (рис. 1).

Решение.

В условии задачи дано: х_А = 2;  х_В = -4; у_А = -5 и у_В = 3. Найти d.

Применив формулу d = √((х_А – х_В)² + (у_А – у_В)²), получим:

d = АВ = √((2 – (-4))² + (-5 – 3)²) = 10.

2. Вычисление координат точки, которая равноудалена от трех заданных точек

Пример 2.

Найти координаты точки О₁, которая равноудалена от трех точек А(7; -1) и В(-2; 2) и С(-1; -5).

Решение.

Из формулировки условия задачи следует, что О₁А = О₁В = О₁С. Пусть искомая точка О₁ имеет координаты (а; b). По формуле d = √((х_А – х_В)² + (у_А – у_В)²) найдем:

О₁А = √((а – 7)² + (b + 1)²);

О₁В = √((а + 2)² + (b – 2)²);

О₁С = √((а + 1)² + (b + 5)²).

Составим систему из двух уравнений:

{√((а – 7)² + (b + 1)²) = √((а + 2)² + (b – 2)²),
{√((а – 7)² + (b + 1)²) = √((а + 1)² + (b + 5)²).

После возведения в квадрат левой и правой частей уравнений запишем:

{(а – 7)² + (b + 1)² = (а + 2)² + (b – 2)²,
{(а – 7)² + (b + 1)² = (а + 1)² + (b + 5)².

Упростив, запишем

{-3а + b + 7 = 0,
{-2а – b + 3 = 0.

Решив систему, получим: а = 2; b = -1.

Точка О₁(2; -1) равноудалена от трех заданных в условии точек, которые не лежат на одной прямой. Эта точка – есть центр окружности, проходящей через три заданные точки (рис. 2).

3. Вычисление абсциссы (ординаты) точки, которая лежит на оси абсцисс (ординат) и находится на заданном расстоянии от данной точки

Пример 3.

Расстояние от точки В(-5; 6) до точки А, лежащей на оси Ох равно 10. Найти точку А.

Решение.

Из формулировки условия задачи следует, что ордината точки А равна нулю и  АВ = 10.

Обозначив абсциссу точки А через а, запишем А(а; 0).

По формуле d = √((х_А –  х_В)² + (у_А – у_В)²) находим:

АВ = √((а + 5)² + (0 – 6)²) = √((а + 5)² + 36).

Получаем уравнение √((а + 5)² + 36) = 10. Упростив его, имеем

а² + 10а – 39 = 0.

Корни этого уравнения а₁ = -13; а₂ = 3.

Получаем две точки А₁(-13; 0) и А₂(3; 0).

Проверка:

А₁В = √((-13 + 5)² + (0 – 6)²) = 10.

А₂В = √((3 + 5)² + (0 – 6)²) = 10.

Обе полученные точки подходят по условию задачи (рис. 3).

4. Вычисление абсциссы (ординаты) точки, которая лежит на оси абсцисс (ординат) и находится на  одинаковом расстоянии от двух заданных точек

Пример 4.

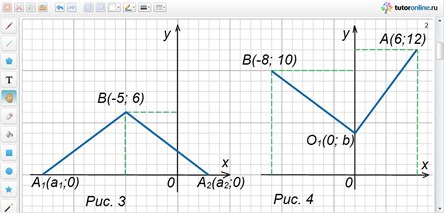
Найти на оси Оу точку, которая находится на одинаковом расстоянии от точек А(6; 12) и В(-8; 10).

Решение.

Пусть координаты нужной по условию задачи точки, лежащей на оси Оу, будут О₁(0; b) (у точки, лежащей на оси Оу, абсцисса равна нулю). Из условия следует, что О₁А = О₁В.

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) находим:

О₁А = √((0 – 6)² + (b – 12)²) = √(36 + (b – 12)²);

О₁В = √((а + ² + (b – 10)²) = √(64 + (b – 10)²).

Имеем уравнение √(36 + (b – 12)²) = √(64 + (b – 10)²) или 36 + (b – 12)² = 64 + (b – 10)².

После упрощения получим: b – 4 = 0, b = 4.

Необходимая по условию задачи точка О₁(0; 4) (рис. 4).

5. Вычисление координат точки, которая находится на одинаковом расстоянии от осей координат и некоторой заданной точки

Пример 5.

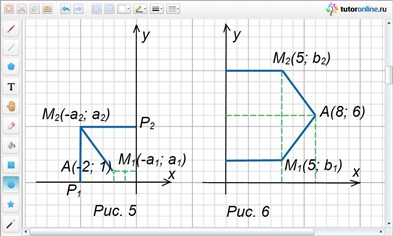
Найти точку М, расположенную на координатной плоскости на одинаковом расстоянии от осей координат и от точки А(-2; 1).

Решение.

Необходимая точка М, как и точка А(-2; 1), располагается во втором координатном углу, так как она равноудалена от точек А, Р₁ и Р₂ (рис. 5). Расстояния точки М от осей координат одинаковые, следовательно, ее координатами будут (-a; a), где а > 0.

Из условия задачи следует, что МА = МР₁ = МР₂, МР₁ = а; МР₂ = |-a|,

т.е. |-a| = а.

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) находим:

МА = √((-а + 2)² + (а – 1)²).

Составим уравнение:

√((-а + 2)² + (а – 1)²) = а.

После возведения в квадрат и упрощения имеем: а² – 6а + 5 = 0. Решим уравнение, найдем а₁ = 1; а₂ = 5.

Получаем две точки М₁(-1; 1) и М₂(-5; 5), удовлетворяющие условию задачи.

6. Вычисление координат точки, которая находится на одинаковом заданном расстоянии от оси абсцисс (ординат) и от данной точки

Пример 6.

Найти точку М такую, что расстояние ее от оси ординат и от точки А(8; 6) будет равно 5.

Решение.

Из условия задачи следует, что МА = 5 и абсцисса точки М равна 5. Пусть ордината точки М равна b, тогда М(5; b) (рис. 6).

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) имеем:

МА = √((5 – ² + (b – 6)²).

Составим уравнение:

√((5 – ² + (b – 6)²) = 5. Упростив его, получим: b² – 12b + 20 = 0. Корни этого уравнения b₁ = 2; b₂ = 10. Следовательно, есть две точки, удовлетворяющие условию задачи: М₁(5; 2) и М₂(5; 10).

Известно, что многие учащиеся при самостоятельном решении задач нуждаются в постоянных консультациях по приемам и методам их решения. Зачастую, найти путь к решению задачи без помощи преподавателя учащемуся не под силу. Необходимые консультации по решению задач учащийся и может получить на нашем сайте.

 Остались вопросы? Не знаете, как найти расстояние между двумя точками на плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Найти наибольшее расстояние между точками

21.01.2012, 06:47. Показов 5079. Ответов 13

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

#include<stdio.h>
#include<iostream.h>
#include<conio.h>
#include<math.h>
 
float maxspacing (int x, int y, int n1, int i1, int j1, int &rT1, int &rT2)
{
      float space=0, d=0;
      for (i1=0; i1<n1-1; i1++)
      {
          for (j1=i1+1; j1<n1-2; j1++)
          {
              d=sqrt((x[i1]-x[j1])*(x[i1]-x[i1]) + (y[i1]-y[j1])*(y[i1]-y[j1]));
              if (d>space)
              {
                 space=d;
                 rT1=i1;
                 rT2=j1;
              }  
              d=0;
          }
      }
      
      return space;
}
                     
int main()
{
    int i, j, n, t1, t2;
    float sp=0, d=0;  
    int koordx[n];
    int koordy[n];
    
    std::cout << "vvedite kolichestvo tochek: ";
    std::cin >> n;
    std::cout << "nn";
    
    for (i=0; i<n; i++)
    {
        j=i+1;
        std::cout << "zadaite koordinatu x " << j << "-i tochki: ";
        std::cin >> koordx[i];
    }
    
    std::cout << "nn";
    
    for (i=0; i<n; i++)
    {
        j=i+1;
        std::cout << "zadaite koordinatu y " << j << "-i tochki: ";
        std::cin >> koordy[i];
    }
    
    sp = maxspacing (koordx, koordy, n, i, j, t1, t2);
    
    std::cout << "max rasstoyanie mezhdu tochkami s koordinatami:n";
    std::cout << "(" << koordx[t1] << "; " << koordy[t1] << ") i (";
    std::cout << koordx[t2] << "; " << koordy[t2] << ")";
    
    system("pause");
}

0

Всегда ли прямая линия — самое короткое расстояние между двумя точками?

Нет, прямая линия не всегда является самым коротким расстоянием между двумя точками. Наименьшее расстояние между двумя точками зависит от геометрии объекта/поверхности. Для плоских поверхностей линия действительно является кратчайшим расстоянием, но для сферических поверхностей, таких как Земля, расстояния по большому кругу на самом деле представляют собой самое короткое расстояние.

В раннем возрасте всех нас учили, что «линия — это наикратчайшее расстояние между двумя точками». Однако, что если бы кто-то сказал вам, что эта почтенная во времени поговорка не совсем верна.

Как оказалось, это утверждение лишь отчасти правдиво. Самое короткое расстояние между двумя точками на самом деле зависит от геометрии рассматриваемого объекта.

Если бы мы жили на плоской земле (чего у нас нет), то да, прямая линия была бы наименьшим расстоянием между точками A и B. Однако, Земля — это приблизительная сфера, а наименьшее расстояние между двумя точками на поверхности сферы — это дуга, известная как «расстояние по большой окружности».

Большое расстояние круга

Большое расстояние круга не новая концепция; на самом деле, многие из вас уже видели это в действии.

Люди, которые путешествовали по воздуху или только проверяли маршруты полета, вероятно, заметили, что рейсы не следуют прямым путем, а вместо этого берут изогнутый маршрут к месту назначения. Изогнутые маршруты не используются для того, чтобы выкопать более глубокую яму в карманах пассажиров, а используются потому, что на самом деле они являются самым коротким расстоянием между любыми двумя заданными точками на нашей планете.

Эти изогнутые маршруты часто сбивают с толку, так как маршруты очерчены на плоской двухмерной карте, где прямая линия может показаться наименьшим расстоянием. Однако ни одна двумерная карта Земли не является точной.

Чтобы дать вам понять суть, наша любимая Земля является трехмерным пространством и лучше всего представлена с помощью модели глобуса. Однако, когда пытаешься сравнять сферу с прямоугольной формой, как это делают большинство карт, на первый план выходит вековая дилемма искажений. Большинство прямоугольных карт торгуют формами страны, размерами, промежуточными расстояниями и даже легитимной информацией для удобства понимания.

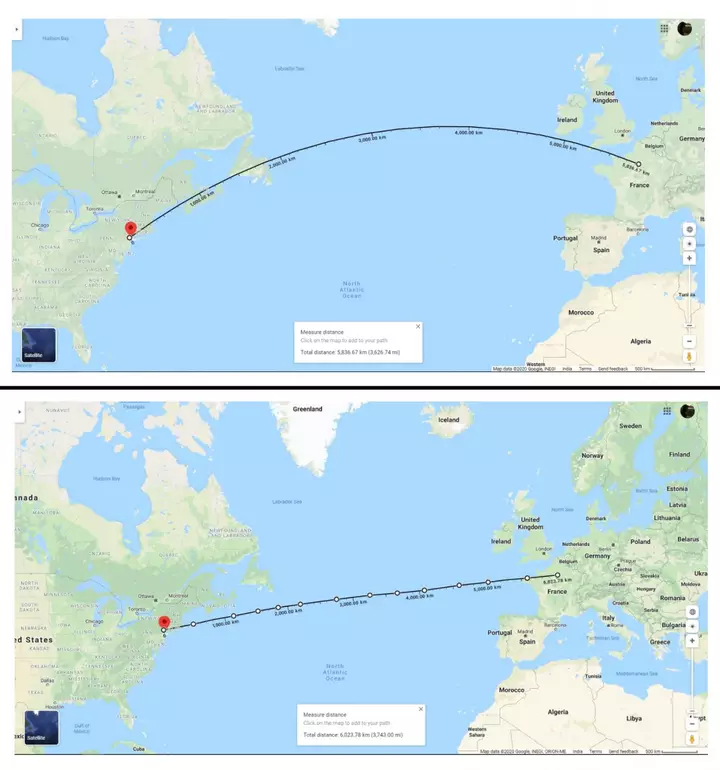
Представьте, что вы хотите улететь из кишащих крысами глубин Нью-Йорка в город любви, Париж. На глобусе кратчайшее расстояние между двумя городами было бы дугой примерно 3630 миль, но та же самая дуга, когда она проецируется на 2D-карту, превращается в прямую линию, измеряющую приблизительно 3750 миль.

Чтобы убедиться в этом самим, откройте Google Maps на соседней вкладке и найдите Нью-Йорк. Найдя его, щелкните правой кнопкой мыши на именном теге и выберите «измерить расстояние». Затем уменьшите масштаб или прокрутите немного вправо, чтобы найти Париж, и нажмите на него. Следующее расстояние будет представлять собой кривую, представляющую собой кратчайшее расстояние между двумя городами. Нажмите в любом месте на этой кривой, чтобы сделать ключевую фигуру, и перетащите её немного на юг, чтобы преобразовать кривую в прямую линию. Вы можете использовать несколько ключевых кадров, чтобы составить прямую линию между двумя точками. После этого сравните размеры кривой и прямой линии (и приготовьтесь к тому, что ваша реальность будет разрушена!).

Разница между двумя числами (3,750 – 3,630 = 120 миль) может показаться несущественной, но, учитывая тот факт, что Boeing 747 потребляет в среднем 5 галлонов топлива на милю полета, самолет потребует дополнительных (5 галлонов/км × 120 миль =) 600 галлонов (2250 литров), чтобы пройти дополнительное расстояние, что является большим делом и добавит к стоимости билетов на самолет.

Расстояние большого круга в математических терминах

Говоря чисто математическим языком, большой круг (также известный как геодезические сферы) — это любой круг, нарисованный на сфере, центр которой совпадает с центром сферы, и таким образом делит сферу на две равные половины. Проще говоря, большой круг — это самый большой круг, который можно вырезать из сферы. Малый круг, с другой стороны, это когда центр круга и сферы не совпадают.

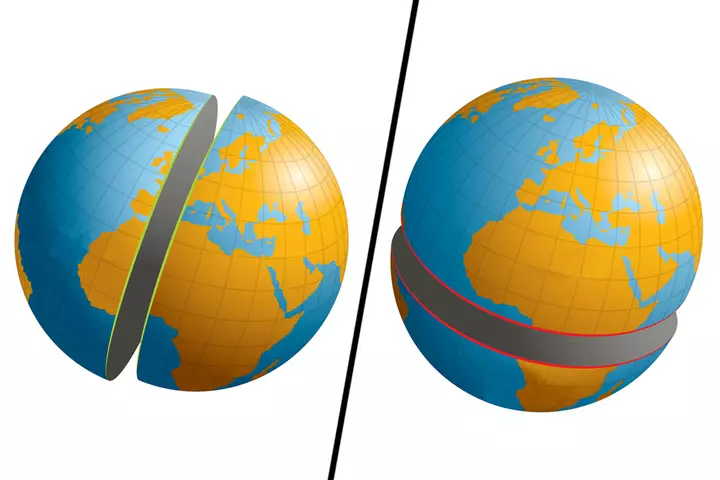
Представьте себе (или просто посмотрите на рисунок ниже), разрезая землю вдоль экватора или полюсов. Результирующие полушария в обоих случаях будут равны, и грани этих полушарий будут иметь тот же диаметр и центр, что и сама сфера (Земля).

Для любых двух не диаметральных точек (положений) на сфере (Земле) существует только один уникальный большой круг, тогда как для диаметральных точек на сфере можно нарисовать бесконечное число больших кругов. Эти точки делят окружность на две дуги; меньшая дуга представляет собой истинное кратчайшее расстояние между двумя точками и называется расстоянием большого круга.

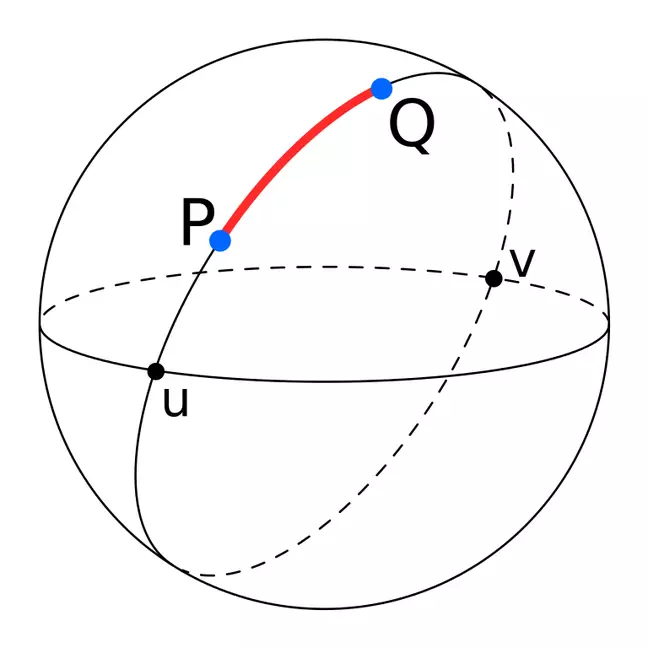
На приведенном ниже изображении точки P и Q являются двумя не диаметральными точками, а дуга PQ представляет собой кратчайшее расстояние между ними (расстояние большого круга). Точки u и v, с другой стороны, известны как противоположные или диаметрально противоположные точки и разделяют большой круг на две идентичные дуги.

Вычисление расстояния большого круга между любыми двумя точками на поверхности сферы требует использования сферической тригонометрии, и хотя мы, возможно, не были знакомы с существованием больших расстояний круга еще в наши школьные годы, всеобщая ненависть к синусам и косинусам хорошо известна.

Здесь d-расстояние большого круга, r-радиус сферы (Земли) и термин cos -1 (cos σ ₁ .cos σ ₂ .cos (λ₁ – λ₂) + sin σ ₁ .sin σ ₂) — центральный угол, под которым расположены две точки с координатами σ ₁, λ ₁ и σ ₂, λ ₂ соответственно.

Как уже говорилось ранее, большие круги находят свое основное применение в дальних путешествиях, в частности в воздушной и морской навигации. Искривленный характер больших окружных расстояний, дополненный вращением нашей планеты, заставляет пилотов и моряков постоянно корректировать свой курс. Поэтому большое расстояние по окружности разбивается на «линии Румба», которые представляют собой постоянное направление.

Сказав все это, даже большие расстояния по кругу не представляют собой истинное кратчайшее расстояние между двумя заданными местоположениями. Расстояния большого круга рассчитываются исходя из предположения, что Земля является идеальной сферой, но планета представляет собой более плоскую сферу с различными значениями радиуса в направлении экватора и полюсов. Значения большого круга, таким образом, имеют допуск около ± 5%.

Тем не менее большие расстояния по окружности сыграли огромную роль в дальних поездках за последние несколько лет и будут продолжать делать это, экономя топливо авиакомпаний и экономя деньги путешественников!

Взаимное расположение окружностей

Выясним, каким может быть взаимное расположение двух окружностей.

Две окружности могут пересекаться, не пересекаться либо касаться друг друга.

I. Пересекающиеся окружности имеют две общие точки.

Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов:

II. Не пересекающиеся окружности не имеет общих точек.

Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:

Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов:

R + r]» title=»Rendered by QuickLaTeX.com»/>

III. Касающиеся окружности имеют одну общую точку — точку касания.

При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:

При внутреннем касании расстояние между центрами равно разности радиусов:

Концентрические окружности разного радиуса не пересекаются. Расстояние между центрами концентрических окружностей равно нулю: O1O2=0.

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Графические способы решения задач с параметрами. Формула расстояния между двумя точками на плоскости.

            В данном материале будет рассмотрен один из очень красивых геометрических методов решения задач с параметрами — метод расстояний. А именно — применение формулы расстояния между двумя точками прямоугольной декартовой системы координат OXY.

        Выводится она довольно просто.

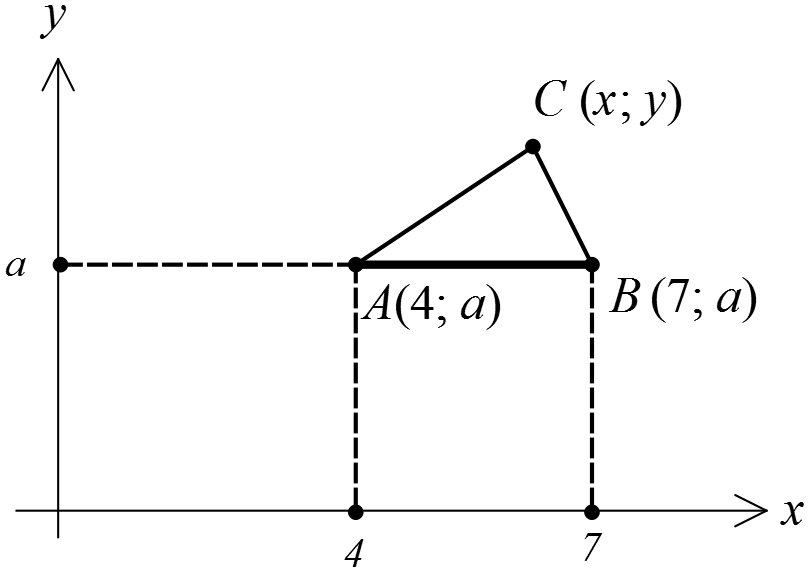
        Пусть на плоскости OXY заданы две точки А(x₁; y₁) и B(x₂; y₂) (см. рисунок). И наша задача — определить расстояние между этими точками. Или длину отрезка АВ.

        Как видно из рисунка, отрезок АВ является гипотенузой прямоугольного треугольника АВС с катетами АС и ВС. Их длины равны разности абсцисс и ординат концов А и В отрезка АВ:

        Модули ставятся для того, чтобы было неважно, как именно ориентирован наш отрезок и какая из координат больше — первая или вторая: модуль просто отсекает возможный минус, если, вдруг, скажем, х₂ окажется меньше, чем х₁. Ведь длина отрезка, очевидно, величина неотрицательная.

        Теперь, призвав на помощь тяжёлую артиллерию великую и могучую теорему Пифагора, получим наше искомое расстояние:

        .

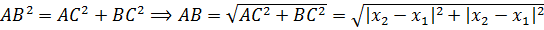
        Поскольку как квадрат, так и модуль обладают одним весьма удобным и замечательным свойством — чётностью, то модули под корнем можно совершенно спокойно и без последствий заменить на обычные скобки. 

        Итого:

        Вот такая полезная формула. Что ж, на этом краткая теоретическая часть закончена. Пора теперь посмотреть, как именно эта формула работает на примере некоторых задач с параметрами из профильного ЕГЭ по математике.

        Пример 1

        Иными словами, от нас требуется найти такие а, при которых система имеет решение в принципе. Хотя бы одно. Ни сами решения, ни их количество находить при этом не нужно.

        Проанализируем наши уравнения.

        Первое уравнение представляет собой сумму квадратных корней из выражений с двумя переменными. Обычно, как только ученик видит уравнение с квадратными корнями, первое что приходит в голову, — срочно возвести обе части в квадрат!) Однако, традиционный «лобовой» способ решения путём возведения в квадрат обеих частей уравнения здесь вряд ли приведёт к чему-либо хорошему. А вы возведите! После первого возведения — да, квадраты обоих корней дадут просто подкоренные выражения, но… согласно бескомпромиссной формуле квадрата суммы (a+b)²=a²+2ab+b², выплывет удвоенное произведение слагаемых, где корни сохранятся! Что потребует возводить в квадрат повторно… И в результате полной ликвидации корней у вас получится уравнение аж четвёртой степени, да ещё и с иксом и игреком… Короче, ужас!

        Нет, надо идти каким-то обходным путём. Каким же?

        В данном примере как раз таки здорово выручает формула расстояния между двумя точками на плоскости. Давайте присмотримся к первому уравнению системы:

        .

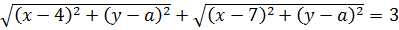
        Каждый из корней, фигурирующих в уравнении, очень похож на формулу расстояния между некими точками. Это намёк.) Займёмся расшифровкой каждого корня.

        Сопоставим первый корень с выведенной только что формулой расстояния:

        .

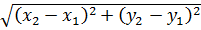
        Просто присматриваемся к этим двум корням и сравниваем. Похожи ведь, правда? Тогда, согласно нашей формуле расстояния, можно принять:

        x₁ = 4; 

        x₂ = x;

        y₁ = a; 

        y₂ = y.

        Значит, первый корень — это на самом деле расстояние от точки  (4; a) до точки (x; y).

        Аналогично сопоставив с формулой второй корень, увидим, что он тоже представляет собой расстояние от точки (7; a) опять же до точки (x; y).

        А теперь переведём первое уравнение с алгебраического языка (языка формул) на геометрический (язык расстояний).

        Алгебра:

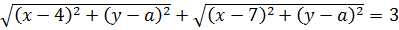
        Геометрия:

        Сумма расстояний от точки (x; y) до точек (4; a) и (7; a) равна трём.

        Для наглядности нарисуем картинку, чтобы представлять, а чего, собственно, от нас хотят.)

        Значит, согласно рисунку, с геометрической точки зрения первое уравнение системы выглядит так:

        AC + BC = 3,

где точки А и В зафиксированы (для конкретного значения параметра), а третья точка С как-то «гуляет» по координатной плоскости.

        Вообще говоря, множество точек плоскости, сумма расстояний от которых до двух фиксированных точек постоянна и равна некому положительному числу, представляет собой замкнутую кривую, которая называется красивым словом эллипс, а данные фиксированные точки являются фокусами эллипса. Но проблема состоит в том, что понятие эллипса не входит в школьную программу (зачастую даже физико-математических классов), а изучается уже в ВУЗе в курсе аналитической геометрии.) Так как же обойти это незнакомое (пока) понятие? Может, в данной (и подобных этой) задаче всё гораздо проще?

        Вынужден признаться. Да, всё гораздо проще!

        Дело всё в том, что понятие эллипса справедливо только в том случае, если эта самая сумма расстояний будет больше расстояния между самими фиксированными точками. Если же сумма расстояний от точки С(x; y)  до двух фиксированных точек (в данном случае A и B) точно равна расстоянию AB между ними, то точка С(x; y) обязательно будет лежать на отрезке AB, и никакого эллипса уже не будет, а будет просто отрезок AB с «гуляющей» по нему третьей точкой.

        Давайте посмотрим, чему же равно расстояние между нашими фиксированными точками:

        .

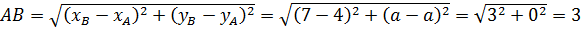
        Итак, длина отрезка АВ в точности получилась равной трём, как и правая часть уравнения. Это не случайно!) Что это означает? Это означает то, что наша точка С(x; y) обязательно лежит на отрезке AB и как-то по нему гуляет.) И только на отрезке! Ведь в противном случае, если бы точка С лежала где-то за его пределами (скажем, где-то выше или где-то ниже), то сумма расстояний от неё до концов отрезка АВ была бы строго больше тройки, что противоречило бы первому уравнению.

        Что ещё важного можно заметить в данном уравнении и на рисунке? А то, что при любом значении параметра «а» игрековые координаты А и В концов нашего отрезка совпадают (обе равны а). Это означает, что в любом случае наш отрезок АВ будет строго горизонтален (то бишь, параллелен оси ОХ), а его концы, в зависимости от значения параметра, будут как бы скользить вдоль направляющих прямых x=4 и x=7 (поскольку абсциссы его концов никак не зависят от «а», оставаясь всё время равными 4 и 7).

        Итак, первое уравнение разложили по полочкам, переходим ко второму.

        Вот тут возведение обеих частей в квадрат вполне прокатит. Возводим:

        Ну как, знакомо? Да, это классическое уравнение окружности с центром в точке (3;2) и радиусом 5.

        Кстати сказать, а как понять, что второе уравнение задаёт именно окружность не через возведение в квадрат, а через расстояние между точками? Снова переводим второе уравнение с алгебры на геометрию, используя нашу формулу расстояния.

        Алгебра:

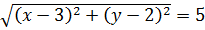
        Геометрия:

        Расстояние от точки (x;y) до точки (3;2) равно пяти.

        А что же это за множество точек, находящихся от фиксированной точки (3;2) на расстоянии 5? Ну, конечно! Окружность радиуса 5 с центром в данной точке.

        Что ж, у нас уже имеется всё необходимое, чтобы нарисовать общий чертёж к задаче. Поехали!

        1) Итак, сначала, как водится, чертим координатные оси X и Y.

        2) Проводим пунктиром вспомогательные вертикальные прямые x=4 и x=7. Вдоль этих прямых, в зависимости от параметра «а», будет скользить наш отрезок АВ, всё время оставаясь горизонтальным. Как вагонная ось катится по рельсам.))

        3) Отмечаем точку (3; 2) — центр нашей окружности.

        4) Собственно, рисуем саму окружность с центром в данной точке и радиусом — пятёрка.

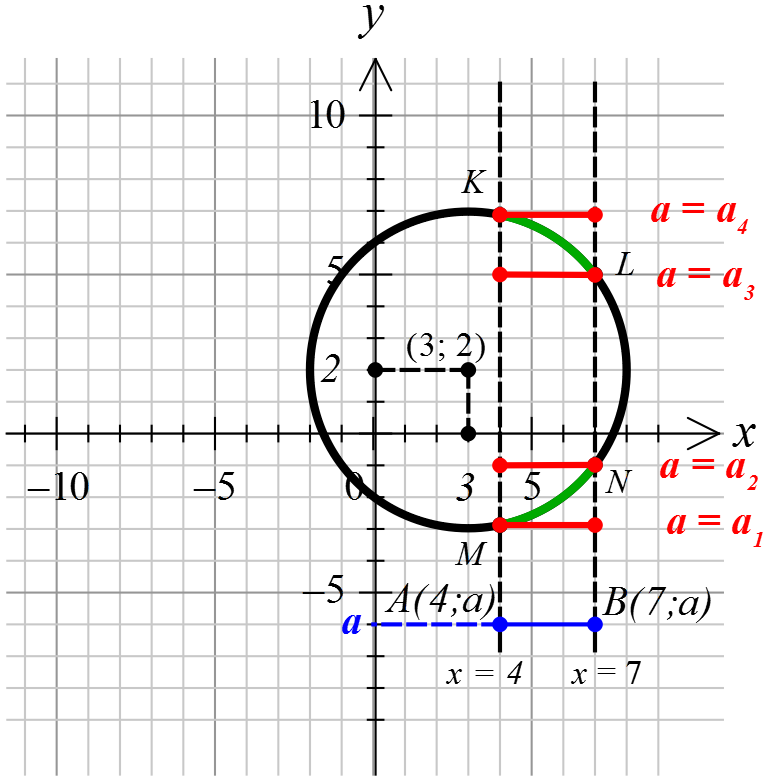
        5) Готово! Что в конечном итоге получилось — смотрим рисунок ниже.

        А теперь пора рассуждать и включать воображение.) В задаче от нас требуется, чтобы система имела хотя бы одно решение. Что это означает с точки зрения нашего рисунка? А то, что наши отрезок (первое уравнение) и окружность (второе уравнение) должны иметь хотя бы одну общую точку. Когда такое возможно?

        Пусть при каком-то конкретном сильно отрицательном (например, -6) значении параметра а наш отрезок АВ (синего цвета) лежит где-то внизу и пока что вообще не пересекает окружность. Теперь мысленно начинаем двигать отрезок вверх по нашим «рельсам».)

        Имеем четыре граничные ситуации.

        Первое граничное положение отрезка, которое нас устроит, — когда его левый конец совпадёт с точкой М окружности (а = а₁). И пересечение отрезка с окружностью будет до того момента, пока его правый конец не совпадёт с точкой N (а = а₂). То есть, хотя бы одно (и единственное!) решение системы будет при таких а, когда отрезок пересекается с дугой MN окружности (показана зелёным цветом).

        Двигаем отрезок вверх дальше. При a > a₂ отрезок оказывается целиком внутри окружности и, следовательно, решений у нашей системы снова нет. И следующие два граничных положения — момент, когда правый конец попадает в точку L (a = a₃) и момент, когда левый конец попадает в точку K (a = a₄). И пересечение будет тогда, когда отрезок находится между этими крайними положениями, пересекая уже верхнюю дугу KL. Все граничные положения отрезка показаны красным цветом. При дальнейшем движении отрезка вверх (то есть росте параметра «а») пересечений (а, следовательно, и решений системы) больше не будет.

        Итак, можно даже составить заготовку для будущего ответа:

.

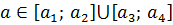
        Причём граничные значения параметра а нас тоже устраивают, посему все скобки квадратные.

        Что ж, остаются сущие пустяки — определить эти самые граничные значения параметра.)

        Начнём с левого конца отрезка. То есть, точки А(4; a). Подставим координаты точки А в уравнение окружности (ведь мы же как раз отлавливаем пересечение отрезка с окружностью!):

        Получили два значения параметра. Очевидно, знак минус соответствует крайнему нижнему положению отрезка при a = a₁, а знак плюс — крайнему верхнему при а = а₄. Таким образом,

        Аналогично расправляемся и с правым концом — с точкой B(7; a):

        То есть,

       Итак, а₂ = -1;  a₃ = 5.

          Всё! Все интересующие нас значения параметра найдены, и теперь можно с чистой совестью записывать окончательный ответ.)

        Ответ:

        .

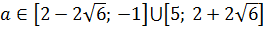
        В рассмотренном примере формула расстояния между точками была подана на блюдечке прослеживалась довольно явно. А вот следующий пример будет гораздо сложнее. Там, во-первых, в нагрузку добавятся модули, а во-вторых, потребуются дополнительные преобразования. Но ничего, мы тоже его распутаем.)

        Итак, приступим!

        Пример 2

        Во, накрутили… Сумма корней, под корнями модули… Кошмар!

        Как здесь можно узнать формулу расстояния между точками? Ясно, что надо как-то преобразовывать и приводить к красивому виду первое уравнение.

        Посмотрим, что получается под первым корнем. Раскроем скобки:

        Здесь мы воспользовались тем фактом, что и квадрат и модуль — функции чётные, а значит, x² и |x|² — одно и то же, поэтому без ущерба для здоровья мы заменили выражение x² на |x|², что позволило свернуть выражение с иксом по формуле квадрата суммы.

        А вот второй корень сразу так красиво преобразовать не выйдет: ведь там у нас совсем нет икса в квадрате, а вместо этого затесался параметр а, да ещё и игрек в первой степени. Чтобы избавиться от а и y, воспользуемся вторым уравнением и подставим в первое уравнение вместо y выражение x²+a:

        Вот так. И теперь первое уравнение системы стало выглядеть гораздо симпатичнее:

        Уже потихоньку вырисовывается нечто знакомое, правда? Что делать дальше? Ясно, что надо раскрывать модули. Лучше, когда их нет.) Давайте начнём с первого корня, то есть с икса.

        Если x≥0, то модуль раскрывается с плюсом (|x| = x), и тогда

        Таким образом, если x≥0, то первый корень представляет собой расстояние между точками (x; y) и (3; 0). С какой такой стати? Элементарно!

        Ведь можно же записать данное выражение вот так:

        Аналогично, если x<0, то наш модуль раскрывается с минусом (|x| = —x), и тогда

        Точно так же, раскрывая модуль игрека во втором радикале, получим:

        Значит, первое уравнение нашей системы разбивается на четыре случая раскрытия модулей:

        Каждое из полученных четырёх уравнений выражает сумму расстояний от неких двух фиксированных точек плоскости ОXY до точки (x; y), «гуляющей» где-то по плоскости. И эта сумма расстояний у нас постоянна и равна пяти.

        Здесь опять таки не будем выпендриваться и сделаем вид, что понятия не имеем про эллипс, а вместо этого снова посчитаем расстояния между точками.)

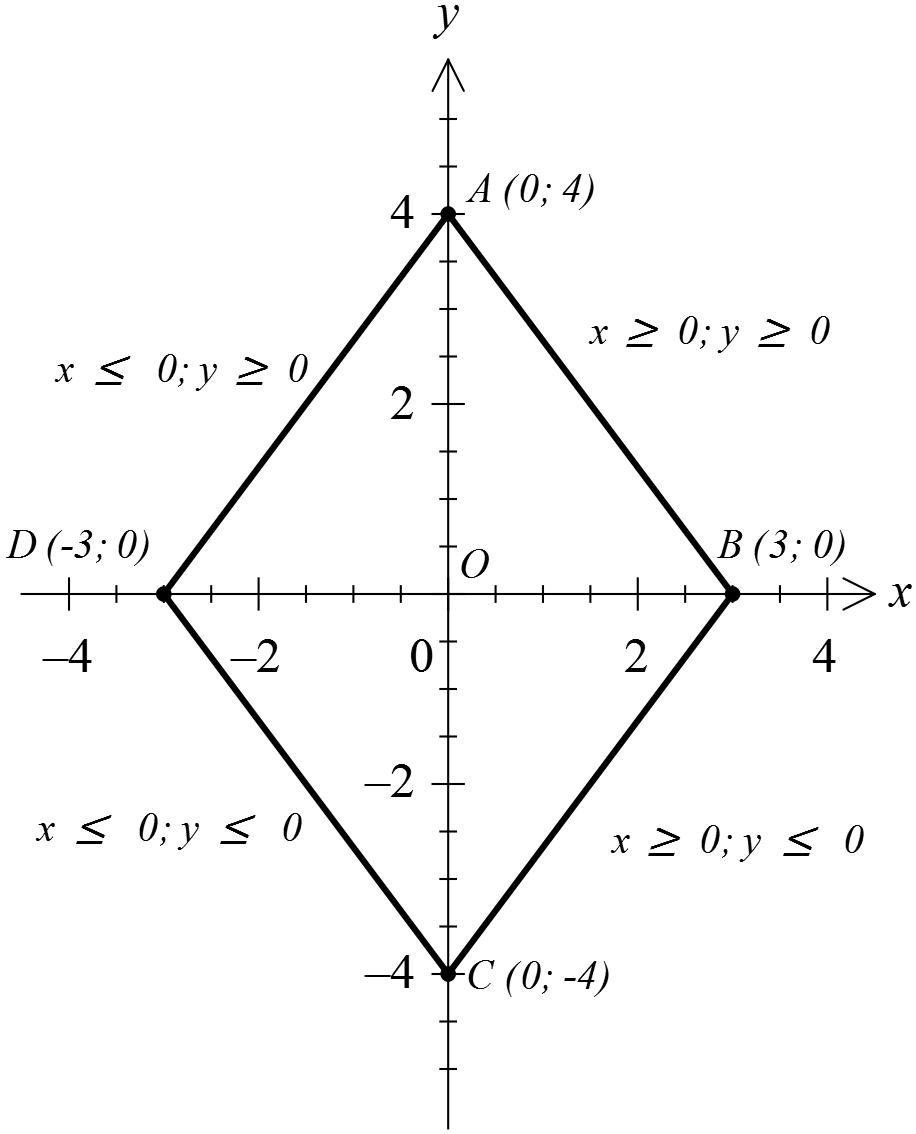
        Для этого изобразим все наши точки на координатой плоскости и соединим их отрезками. Это будут точки A(0; 4), B(3; 0), C(0; -4) и D(-3; 0). Вот наша картинка:

        Теперь подробно рассмотрим, к примеру, первый случай:

        Он представляет собой сумму расстояний от точки (x; y) до точек A и B.

Вычислим длину отрезка АВ из треугольника AOB:

        Получили в точности пятёрку. То есть, длину отрезка AB! Что это означает? Это означает, что наша точка  с координатами (x; y) обязательно лежит на отрезке АВ и как-то по нему гуляет! Таким же образом доказывается, что и в остальных трёх случаях точка (x; y) лежит на соответствующем отрезке. Итак, множество точек, описывающих первое уравнение системы, — ромб ABCD со стороной 5. Каждая сторона ромба отвечает за свой случай раскрытия модулей.

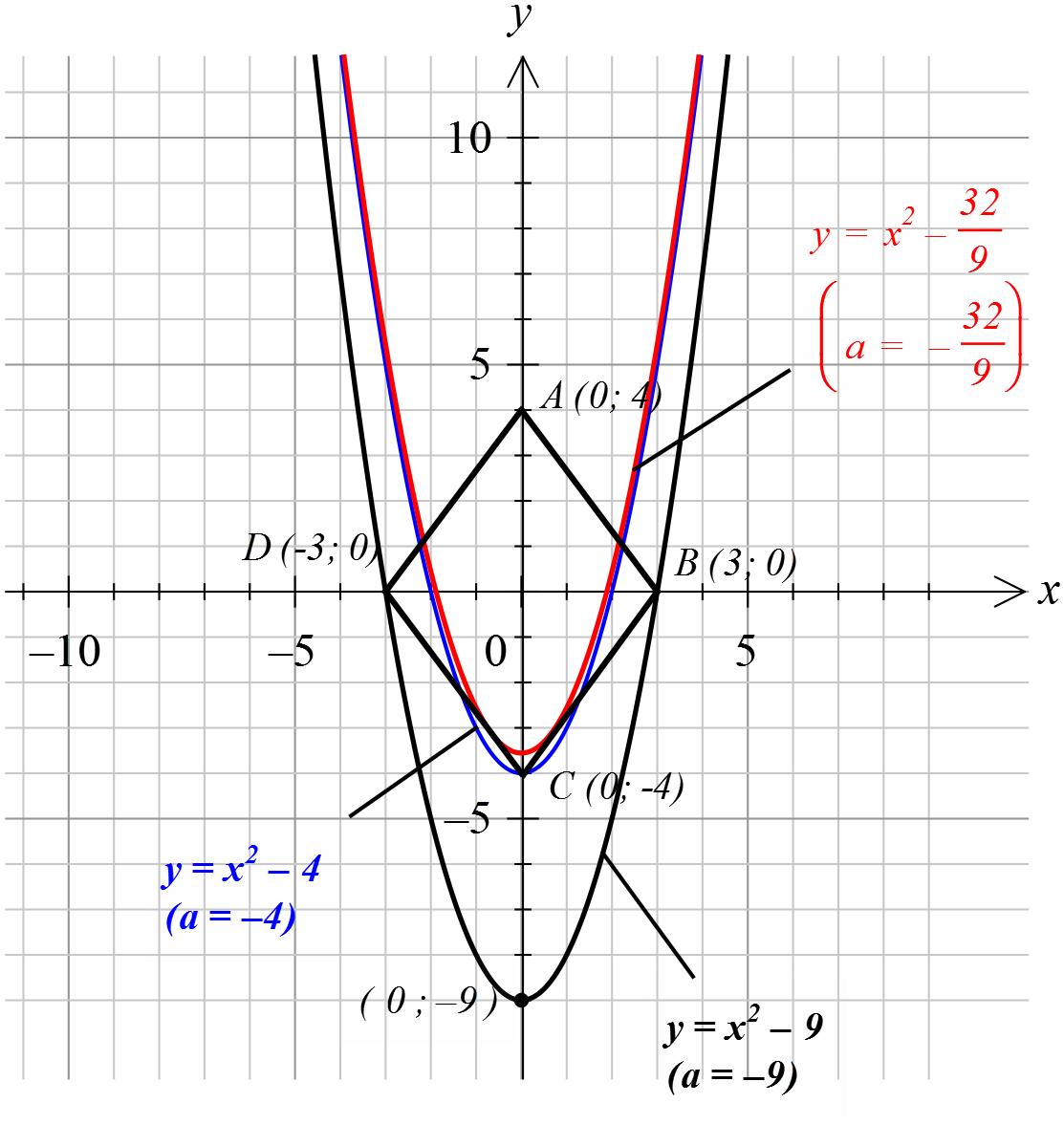
        А вот второе уравнение нашей системы — обычная парабола y = x² с вершиной в точке (0; a), гуляющая вверх-вниз вдоль оси игреков в зависимости от параметра. Вот наша картинка:

        А теперь (внимание!) начинаем двигать нашу параболу снизу вверх вдоль оси OY, меняя тем самым параметр а!

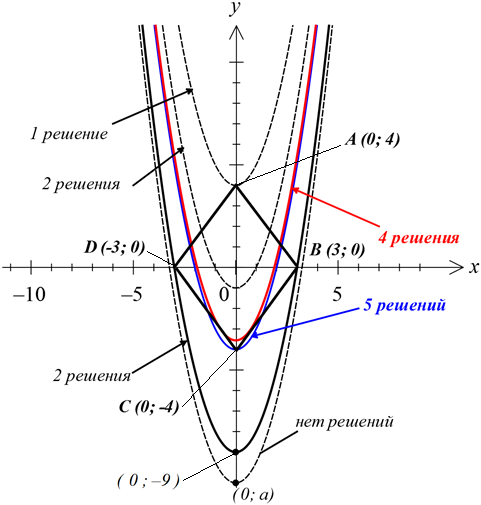
        Тогда видно, что, если вершина находится где-то совсем низко, то пересечений у параболы и ромба вообще не будет. Первый граничный случай соответствует a = -9, когда ветви параболы проходят через точки B и D ромба (показан чёрным цветом). В этом случае решений будет два. Как только вершина параболы сместится чуть выше -9, то каждая её ветвь пересечёт по две стороны ромба, и решений станет уже четыре — как раз то что нам и нужно. И так будет продолжаться до тех пор, пока вершина параболы не окажется в точке С (синий цвет), то есть, а = -4, когда решений станет пять.

        Таким образом, первая часть ответа будет такая:

        .

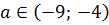
        Сами границы нас не устраивают и в ответ, естественно, не включаются.

        Но… Это ещё не всё!) Продолжим дальше двигать вверх по оси ОY нашу параболу. Когда вершина окажется чуть выше точки С, то пересечений станет уже шесть: по два с нижними сторонами ромба и по одному с верхними. И так будет до тех пор, пока ветви параболы не станут касаться сторон CD и CB ромба (красный цвет). В случае касания решений снова станет четыре, что от нас и требуется. И это значение параметра а, при котором парабола касается нижних сторон ромба, теперь нам и предстоит «отловить».)

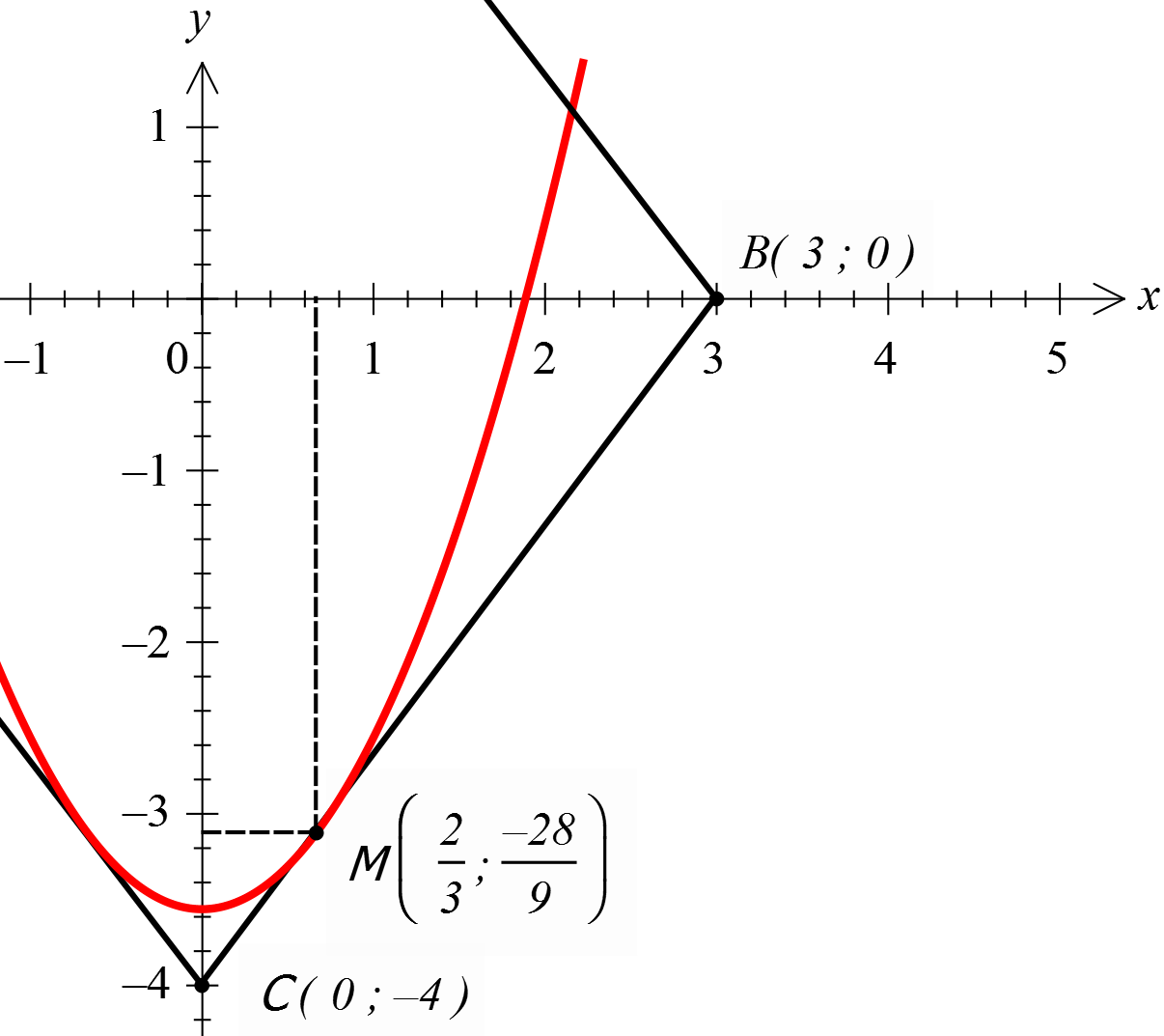
        На помощь придёт такой мощный инструмент, как производная. В силу симметрии картинки, рассматривать будем только правую ветвь параболы. Итак, пусть наша красная парабола касается нижнего отрезка ромба СВ в какой-то точке М.

        Уравнение прямой, задающей отрезок СВ, будет

        поскольку тангенс угла наклона прямой CB к оси ОХ равен:

        Уравнение нашей параболы будет y = x² + a. Мы не знаем пока, чему равно «а», но зато твёрдо знаем, что отрезок CB её касается, а значит, производная нашей параболы в точке касания M должна быть равна 4/3.

        Вычислим эту самую производную:

        (x²+a)’ = (x²)’ + a’ = 2x

        Тогда 2x = 4/3 и тогда x = 2/3 — абсцисса точки касания M.

        Поскольку точка M лежит на отрезке CB, то её координаты обязательно удовлетворяют уравнению этого отрезка:

Значит, координаты нашей точки касания следующие:

        Но! Точка M принадлежит не только отрезку, но ещё и параболе! Поэтому, подставив координаты точки M в уравнение параболы, мы теперь уже без труда найдём интересующее нас значение а:

        Вот теперь всё. Все характерные положения параболы представлены на картинке.

        Легко видеть, что при дальнейшем росте параметра а четырёх решений уже не будет, а будет либо два, либо одно, либо ни одного.

        Кстати сказать, а можно ли в данной ситуации обойтись без производной? Уж больно напряжно с ней возиться, как правило…

        Что ж, специально для разумных халявщиков предлагаю способ-лайт.) Но, следует предупредить, что он срабатывает только в случае каких-нибудь простеньких графиков — в основном для параболы. В случае более сложных функций способ с производной — самый надёжный.)

        Итак, нам требуется отыскать значение параметра, при котором происходит касание прямой

        и параболы

        .

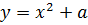
Что означает сей факт с алгебраической точки зрения? Только то, что уравнение

        имеет строго один корень! То есть, дискриминант получившегося квадратного уравнения обязан быть равен нулю!

        Что ж, остаётся только привести наше уравнение к стандартному виду, посчитать дискриминант да приравнять его к нулю.) Действуем:

        Как и следовало ожидать, результат получился тем же самым.)

        Ответ:

        Заключение: если в примере предложено какое-то зверское на вид уравнение или неравенство с корнями, но подкоренные выражения представляют собой какие-то квадратичные конструкции от x и y вида 

то ни в коем случае не возводим обе части в квадрат с целью избавиться от корней и не тратим своё время! Вместо этого пробуем выделить полные квадраты под корнями по каждой из переменных.

        Очень часто в таких конструкциях срабатывает именно формула расстояния между двумя точками, что значительно упрощает дальнейшее решение примера и тем самым открывает дорогу к успеху.

        Заметим, что данный приём работает только тогда, когда наше подкоренное выражение именно такого вида — то есть, переменные под корнем стоят в квадрате и в первой степени (а не в кубе или более высоких степенях) и именно сами по себе, без попарных произведений xy . Если данное требование не выполняется, и под корнем затесалось, скажем, ещё и произведение xy, то либо его надо на что-то заменять (скажем, если оно выражается из второго уравнения), либо данный пример решается как-то по-другому.

        Успехов!

using System;
 
class Program
{
 
    static void Main()
    {
        Console.WriteLine("===== Исходная матрица =====");
        Random r = new Random();
        double[,] mas = new double[100, 2];
        double temp1 = 0, temp2 = 0, sum = 0, maxX = 0, maxY = 0;
        for (int i = 0; i < 100; ++i)
        {
            for(int j = 0; j < 2; ++j)
            {  
                mas[i, j] = r.NextDouble() * 100;
                if (j == 0)
                {
                    Console.Write("{0:f2}", mas[i, j]);
                    temp1 = mas[i, j];
                }
                else
                {
                    Console.Write("t{0:f2}", mas[i, j]);
                    temp2 = mas[i, j];
                }
                if (Math.Abs(temp1 - temp2) > sum)
                {
                    sum = Math.Abs(temp1 - temp2);
                    maxX = temp1;
                    maxY = temp2;
                }
            }
            Console.WriteLine();
        }
 
        Console.WriteLine("Наибольшее расстояние находится между {0:f2} и {1:f2} ", maxX, maxY);
        Console.ReadKey();
 
    }
}