Как найти наибольшее значение числового набора

Изучаем статистику: средние значения

Один из разделов описательной статистики посвящен знакомству
с характеристиками числового набора: минимальное значение, максимальное
значение, размах, среднее арифметическое и медиана. Ученики должны научиться
определять их для набора чисел, заданного списком, таблицей или диаграммой
рассеивания.

Мы изучали этот материал в течение трех уроков. На первых
двух были введены новые понятия и решались задачи из учебного пособия (авт.
Ю.Н. Тюрин, А.А. Макаров, И.Р. Высоцкий, И.В. Ященко). Например. Найдите
наибольшее и наименьшее значение, размах, среднее значение и медиану набора
чисел: 12; 7; 25; 3; 19; 15. (Ответ: 25; 3; 22; 13,5; 13,5).

Однако естественно показать учащимся, зачем мы все это
изучаем. На третьем уроке мы решали задачи, в которых требуется выбрать
такое среднее, которое наилучшим образом отражает особенности данного набора
чисел в соответствии с их природой и требованиями задачи. В одних задачах не
сказано, какую характеристику надо искать, поэтому, чтобы ответить на вопрос
задачи, приходится примерять к поставленной задаче поочередно разные средние и
выяснять, какое подходит больше других. В этом случае ответом к задаче является
не число, а название подходящей характеристики. В других задачах присутствует
необходимость правильно интерпретировать полученные результаты, отнестись к ним
критически, попытаться найти здравое зерно даже там, где, на первый взгляд, «все
сделано неверно». И наконец, предложен и третий вид задач, в которых природа
данных накладывает определенные дополнительные требования на найденное значение
среднего: например, оно должно быть целым.

Тем самым мы не только продолжаем закреплять навык подсчета
среднего, но и демонстрируем возможности применения изученного в реальных
жизненных ситуациях. Ведь для учащихся важным фактором освоения нового является
осознание необходимости знания этого нового, то есть не только как
найти, но и зачем находить.

Данная статья состоит из двух частей. В первой дается описание наиболее
употребительных средних. Во второй части предлагается набор задач для решения в
классе и для самостоятельной работы учащихся.

Знакомимся со средними

Наибольшее и наименьшее значения

Слова «минимальный», «максимальный», «меньший», «больший»
интуитивно понятны учащимся, поэтому первые две характеристики: наибольшее
и наименьшее значения оставим без определения. Скажем, что в наборе,
упорядоченном по возрастанию, наименьшее число стоит на первом месте, а
наибольшее — на последнем.

В пособии имеются задания, в которых требуется найти
наибольшее или наименьшее значения среди чисел, указанных в таблице. К ним
добавим задания с другой формой представления данных — в виде диаграммы
рассеивания.

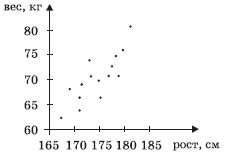
Задание. Имеется диаграмма 1 рассеивания, показывающая
взаимосвязь роста и веса 15 опрошенных юношей. Найти рост самого высокого и рост
самого низкого юноши (т.е. определить минимальное и максимальное значения набора
чисел, заданного диаграммой рассеивания).

Для этого будем использовать следующее: минимальный рост
соответствует абсциссе точки, расположенной левее других, а
максимальный — абсциссе крайней точки справа. Получим:

min ≈ 167 см, max ≈ 181 см.

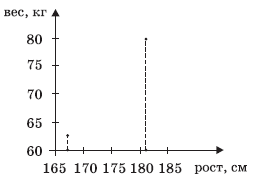
Интересно, что остальные 13 точек участия в «обсуждении»
вообще не принимают. Их можно стереть — результат от этого не изменится (см.
диаграмму 2).

Диаграмма 1

Вторая особенность получаемого результата в том, что, в
отличие от работы с таблицей, данные, получаемые с помощью графиков и диаграмм,
являются не точными, а приближенными, то есть ответы могут отличаться.

Аналогично находим минимальное и максимальное значения веса,
как ординаты самой нижней и самой верхней точек.

Диаграмма 2

С каким же видом представления данных удобнее работать?

Преимущество таблицы заключается в точности получаемых
результатов, но работа с ней требует концентрации внимания на протяжении
длительного времени: нельзя пропустить искомое число, а оно может попасть в
любой исследуемый столбец. И если таблица содержит не 15 чисел, а 5000, то этот
аргумент становится решающим в пользу наглядного представления данных. Оно дает
менее точные результаты, зато обработка такой информации происходит за
считанные секунды. Даже если диаграмма будет содержать 5000 точек, нас будут
интересовать только две крайние, на остальные мы даже не посмотрим.

Размах

В отличие от предыдущих понятий, размах — это
незнакомая учащимся характеристика набора. Он показывает протяженность набора
вдоль числовой оси, меру его разброса.

Определение. Размах набора чисел (R) — это
разность между наибольшим и наименьшим числом набора.

Например, в предыдущем задании размах равен: R = 181 –
167 = 14 см.

Что показывает размах значений?

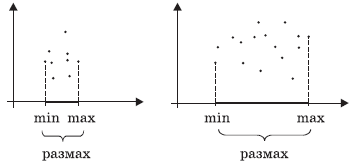
Сравним диаграммы 3 и 4:

Диаграмма 3                 Диаграмма 4

Точки, изображенные на диаграмме 3, расположены ближе друг к
другу, соответственно, и максимальное и минимальное значение отличаются друг от
друга меньше, чем на диаграмме 4. Таким образом, размах показывает, сильно ли
отличаются числа набора друг от друга.

Маленький размах показывает, что исследуемая величина
принимала практически одинаковые значения. Большой размах показывает, что
некоторая величина принимает значительно отличающиеся друг от друга значения, то
есть нестабильность. Иногда большой размах свидетельствует о наличии
грубой ошибки измерений, о том, что какое-то из чисел попало в список случайно.

Если вычислить полусумму наименьшего и наибольшего значений
набора и обозначить ее с, а половину размаха обозначить то можно
утверждать, что все числа набора содержатся в промежутке На бытовом уровне
размах (а точнее, полуразмах) дает информацию о точности информации: расстояние
от дома до дачи (100 ± 5) км, цена на хлеб (14 ± 2) р. и т.д.

Среднее арифметическое

Определение. Средним арифметическим нескольких чисел () называется частное от деления суммы этих чисел на количество чисел.

Например, средним арифметическим чисел 4; 6; 11 является
число

Зачастую среднее арифметическое называют просто «средним» в
силу его наибольшей популярности. Говорят о среднем балле аттестата,
среднегодовом потреблении населением фруктов. «Потребительская корзина» для
определенного слоя граждан рассчитывается исходя из средних показателей.

Рассмотрим следующий пример. На олимпиаде по математике
предлагалось решить пять задач по 4 балла за каждую. В протоколе указана сумма
баллов каждого из восьми участников этой олимпиады:

12; 14; 14; 16; 17; 18; 19; 200.

Для ускорения подсчета имеется автоматизированная система
обработки данных, которая находит среднее арифметическое любых введенных чисел.
Какой средний балл набрали участники олимпиады?

У данного набора среднее равно 38,75. Однако такую сумму
баллов никто из участников набрать не мог. К тому же семь чисел из данных восьми
намного меньше его. Все значения этого набора, кроме крайнего правого,
достаточно кучно попадают в интервал [12; 19], а 38,75 в него не попадает. Все
это говорит о том, что полученное среднее арифметическое не только не передает
особенностей данного набора чисел, но и вообще противоречит здравому смыслу.
Значит, либо в условие, либо в решение вкралась ошибка! Посмотрим еще раз на
данные числа. Теперь, получив явно бессмысленный результат, мы сможем более
критически отнестись к условию: первые семь чисел вполне реальны, а вот
последнее… Откуда оно взялось?! Видимо, оно случайно попало в этот список:
возможно, в результате описки. Однако обнаружение ошибки в условии не избавляет
нас от необходимости довести решение до конца. Можно, конечно, посоветовать
комиссии снова переписать результаты учащихся и ввести числа из нового,
«правильного» протокола. Но где гарантия, что в нем снова не будет опечатки?

Когда все результаты более или менее кучно располагаются на
числовой оси, кроме, быть может, нескольких ненадежных значений, анализировать
результаты можно! Достаточно высокую точность полученных значений будет
гарантировать применение других средних — в частности, урезанного среднего.
Для его нахождения сначала упорядочивают набор по возрастанию, а затем
отбрасывают слева и справа равное небольшое количество чисел. При этом «выбросы»
(или ошибки наблюдений) в дальнейших вычислениях не участвуют. У полученного
«урезанного» набора обычным образом находят среднее арифметическое. Оно и
является урезанным средним исходного набора.

Вернемся к задаче. Если отбросить по одному числу с каждой
стороны, то есть числа 12 и 200, то у оставшегося набора из шести чисел среднее
равно

Это и есть урезанное среднее. Оно неплохо передает реальное
среднее количество баллов, набранных юными математиками.

Некоторая аналогия с нахождением урезанного среднего
просматривается в правилах судейства во многих видах спорта. Например, в
соревнованиях по прыжкам с трамплина технику каждого прыжка оценивают 5 судей.
Чтобы получить объективные оценки, две из них — высшую и низшую — отбрасывают, а
для трех оставшихся находят сумму. Такой подход не дает возможности судьям
повышать баллы своим соотечественникам, а спортсменам затрудняет нечестный путь
к медалям.

Медиана

Медианой числового набора является число, которое
разделяет этот набор на две одинаковые по части.

Если набор упорядочен и в нем имеется нечетное количество
чисел (2n + 1), то медиана стоит посередине этого набора, на (n +
1)-м месте. Если упорядоченный набор состоит из четного количества чисел (2n),
то медианой является любое число, находящееся между двумя числами, которые стоят
в середине (под номерами n и n + 1). Обычно берется их полусумма.

В наборе 12; 14; 14; 16; 17; 18; 19; 200 медианой является
любое число из интервала (16; 17), например, 16,5. Напомним, что урезанное
среднее равнялось 16,3. Похоже!

Перейдем к решению задач.

Вычисляем средние

1. Про отличника. У отличника Коли были отметки по математике
«5», «5», «5», «5».
И вдруг в конце четверти он получил «2». Он знает, что
учитель математики выставляет четвертную отметку как среднее всех отметок,
имеющихся у ученика, и не признает пересдач. Какое среднее было бы
предпочтительнее для Коли, если он, естественно, надеется на пятерку в четверти?

Решение. 1. Попробуем начать с такого очень
распространенного способа выставления четвертных отметок, как нахождение
среднего арифметического:

Естественно, что любой учитель округлит этот результат в
меньшую сторону и выставит итоговую отметку «4». Значит, это среднее Колю не
устраивает.

Мы видим, что один неудачный ответ на балл снизил четвертную
отметку. Ведь до этого среднее арифметическое равнялось 5.

2. Помочь Колиной мечте сбыться может другое среднее, и не
одно! Например, если в качестве среднего учитель Коли возьмет медиану или
урезанное среднее, то в четверти Коле обеспечена пятерка:

— медиана набора 2, 5, 5, 5, 5 равна 5;

— урезанное среднее набора 5, 5, 5, равно

Ответ: медиана или урезанное среднее.

2. Про лодку. Рыбаки собираются порыбачить на озере. Но не
везде им обеспечен хороший улов. Чтобы найти рыбное место, они решили
воспользоваться лодкой с мотором. На лодке установлен мотор, который можно
регулировать по высоте, поднимая или глубже погружая его. Известно, что мотор
работает надежно и не перегревается во время работы, если опустить его как можно
ниже в глубь воды. Но тогда возникает опасность зацепить им за дно водоема.
Мотор устанавливается на желаемую высоту на берегу, в воде менять глубину
погружения нельзя. Какой информацией о глубине воды в озере надо располагать
рыбакам, чтобы не повредить мотор о дно?

Решение. Рыбаки должны узнать глубину озера вдоль
предполагаемого маршрута следования. Затем у полученного набора чисел надо найти
минимальное значение. Оно обеспечит им удачное прохождение и других,
более глубоких участков.

Ответ: минимальное значение.

3. Библиотека. Известно, что детская библиотека выдает в день
в среднем 180 книг. Сколько книг выдает библиотека в среднем за неделю? за
месяц? за год?

Решение. Под средним в данной задаче подразумевается
среднее арифметическое. Так как библиотека работает 6 дней в неделю, значит,
за неделю она выдает около 1806
= 1080 книг. За 26 рабочих дней месяца она выдаст 18026
= 4700 книг. За 12 месяцев выдача составит 468012
= 56 000 книг.

Ответ: 1080 книг, около 4700 книг, около 56 000 книг.

Решая эту задачу, уместно обсудить вопрос точности полученных
результатов. Во-первых, из условия неясно, за какой период было получено
среднедневное значение. Если наблюдения велись лишь одну неделю, то к полученным
вычисленным значениям нужно относиться весьма скептически. Для получения более
точных результатов надо было проводить более длительное наблюдение, сопоставимое
по длительности с запрашиваемым периодом. А во-вторых, возможно, наблюдатели
«попали» на неделю «книжного бума», тогда результаты, распространенные на месяц
и тем более на год получатся явно завышенными. Возможна и обратная картина: нам
сообщили результаты, полученные в период летних каникул, значит, результаты
вычислений будут заниженными. Другими словами, к полученным числам нужно
относиться с большой осторожностью, если нет возможности уточнить, как было
проведено исследование, и за какой период было вычислено среднее значение 180
книг.

Этот пример показывает, что для получения достоверных
результатов исследований нужно соблюдать некоторые условия, следовать
определенным правилам, чтобы полученным выводам можно было доверять.

4. Метание молота. Спортивный клуб должен организовать
соревнования по метанию молота среди спортсменов с разной спортивной подготовкой
и разными достижениями. Для этого он должен пригласить необходимое количество
судей в сектор для метания. Судьи, с которыми сотрудничает клуб, точно отмечают
место падения молота, если находятся не далее четырех метров от него. Спортивный
клуб может запросить любую информацию о прошлых результатах приглашенных
спортсменов. Какой информацией должны располагать организаторы, чтобы пригласить
необходимое количество судей?

Решение. Надо запросить предыдущие результаты метания
молота всех участников и найти максимальный, минимальный результаты и размах.
Зная величину угла сектора для метания и максимальный результат, можно
вычислить длину дуги, вдоль которой через каждые 8 м надо расставить судей.

Количество таких рядов зависит от размаха результатов.
Если он окажется менее 8 м, то судьи могут стоять в один ряд. Если размах
окажется бóльшим, то чтобы успешно фиксировать как более далекие, так и близкие
результаты судей надо расставить в несколько рядов через каждые 8 м.

Ответ: максимальный результат, размах.

5. Отпуск на юге. Для успешной рекламы отдыха на Кипре
туристическая фирма запросила данные о погоде на острове за последние 10 лет.
Выяснилось, что за этот период было лишь 216 пасмурных или дождливых дней,
которые были равномерно распределены по запрашиваемым годам. Сколько дней в году
на острове Кипр светит солнце?

Решение. За 10 лет наблюдалось 3652 – 216 = 3436
солнечных дней. Значит, в среднем за один год — 343,6 дня. Поскольку в ответе
надо писать целое число дней, то можно округлить до целых, а можно и до
десятков: в рекламе круглые числа смотрятся лучше.

Ответ: около 340 дней.

Задачи для самостоятельного решения

1. а) Через речку хотят построить мост. Известно, что уровень
воды в реке меняется в течение года: весной при таянии снега повышается,
засушливым летом понижается. Какую характеристику уровня воды в реке надо
учитывать, чтобы построенный мост был над водой?

б) Периодически в средствах массовой информации нам сообщают
о стихийных бедствиях, в результате которых переполненные водой реки выходят из
своих берегов и даже затопляют улицы городов. Понимая возможность подобного
стихийного бедствия, не будет ли разумнее построить мост (а заодно и высокую
дамбу) как можно выше, насколько это будет технически возможно? Ведь гибель
людей несравнима ни с какими материальными затратами, позволяющими предупредить
беду.

2. За урок учительница вызывает в среднем 5 человек из класса
и каждому ставит отметку за устный ответ. Сколько отметок за устные ответы
выставит эта учительница за неделю, если она проводит в этом классе 5 уроков в
неделю? За четверть?

3. В забеге на 800 м принимали участие 19 спортсменов,
разделенных на группы, стартующие в разное время. Как судьи определили
победителя забега?

4. На зимние каникулы в одной из школ города Мурманска
учительница дала детям задание: следить за погодой и найти среднюю температуру.
Ежедневно в течение десяти дней в 15 часов Наташа записывала показания
термометра:

–13, –10, –15, 11, –9, –9, –11, –12, –10, –11.

А затем вычислила среднее арифметическое и получила –8,9.

а) Действительно ли в период наблюдений температура
колебалась вблизи этого числа?
б) Почему большинство значений (9 из 10) меньше найденного
среднего?
в) Как исправить ответ, если он неверный (заново повторить
наблюдение, естественно, нельзя)?

5.  Имеются данные об успеваемости по химии 8 «А» и 8 «Б» : о
количестве учащихся, получивших ту или иную четвертную отметку. Данные занесены
в таблице:

Отметка	8 «А»	8 «Б»
5	6 чел.	4 чел.
4	12 чел.	10 чел.
3	6 чел.	5 чел.

Какой класс в среднем имеет лучшие результаты?

6. Лучший нападающий баскетбольной команды «Луч» за восемь
прошедших матчей принес своей команде 61 очко. Сколько в среднем очков добавлял
своей команде этот игрок за каждую игру?

Подводя итог сказанному, хочется отметить, что решение задач,
приведенных в этой статье, было встречено учениками с большим интересом. В их
глазах просматривалось и удивление: оказывается школьные знания имеют прямое
отношение к реальной жизни. Длинные формулировки задач не только не мешали
воспринимать задачу, а напротив, учащиеся успевали глубже погрузиться в
ситуацию, пропустить ее через себя. Сюжеты не были надуманными, они
согласовывались с имеющимся у детей жизненным опытом, поэтому даже слабо
подготовленные ученики на этих уроках проявляли необычную для них активность.
Решение некоторых задач проходило в форме жаркой, но доброжелательной дискуссии,
и доказать свою правоту могла только та сторона, которая аргументированно
отстаивала свою позицию, опираясь на строгие математические факты и здравый
смысл!

Решения и ответы

1. а) Максимальное значение уровня воды в реке.
б) Все зависит от массы обстоятельств: географического
положения реки, «поведения» реки в прошлом и др. Конечно, раз в 100–150 лет даже
на самой «мирной» реке может быть катастрофический паводок. Однако стоит ли
строить очень высокий мост через каждую речку, ожидая ужасного, но
маловероятного катаклизма?

2. Около 25 отметок; около 200 отметок.

3. Победитель затратил на преодоление дистанции минимальное
время.

4. а) Нет, в период наблюдений температура колебалась в
промежутке [–15; –9], которому найденное среднее не принадлежит;
б) потому что имеется число 11, которое существенно
отличается от всех остальных и поэтому меняет среднее в большую сторону;
в) найти урезанное среднее данного набора:

–9, –9, –10, –10, –11, –11, –12, –13, –15,
11. Оно приближенно равно 11,4.

5. 8 «А».

6. Около 8 очков.

Багишова О.

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Наибольшее и наименьшее значение, размах числового набора.
  7 класс Урок 13
  07.01.2023
  Описательная статистика

• 

  2 слайд

  07.01.2023
  2
  Повторение
  1. Среднее арифметическое числового массива равно 5,1. Найдите новое среднее арифметическое, если все числа массива:
  а) увеличить в 10 раз;
  б) уменьшить в 3 раза;
  в) увеличить на 1,9.
  2. В числовом массиве 10 чисел, а их среднее равно 99. Найдите новое среднее арифметическое, если:
  а) какое-то одно число массива увеличить на 1;
  б) какое-то одно число массива увеличить на 5;
  в) два каких-то числа уменьшить на 20;
  г) первое число увеличить на 3, а второе число уменьшить на 5. д) к массиву добавить число 121;
  е) из массива удалить число 27.
  Ответы: 1. а) 51; б) 1,7; в) 7.
  2. а) 99,1; б) 99,5; в) 95; г) 98,8; д) 101; е) 107.

• 

  3 слайд

  3
  Наименьшее и наибольшее значения.
  Отрезок (интервал) значений, размах числового набора
  В любом конечном наборе чисел всегда есть наименьшее и наибольшее значения. Иногда их называют минимальным и максимальным значениями или даже короче – минимум и максимум. Иногда для удобства пользуются обозначениями min и max .
  Разность между наибольшим и наименьшим значением называется размахом числового набора.
  Размах равен длине отрезка, на котором располагаются все значения. Такой отрезок называют интервалом значений.

• 

  4 слайд

  Пример 1. Дан набор чисел. Найти наибольшее и наименьшее значения и размах.
  1 3 2 1 45 3 2 7 5 4 3 2 2.

  4
  Даже не упорядочивая числа, мы видим, что min =1, а max = 7 . Значит, размах равен 7 -1 = 6 .
  Пример 2. В наборе данных наименьшее значение равно 6, а наибольшее равно 13. Найдите длину интервала значений.
  Решение: 13 — 6 = 7 .

• 

  5 слайд

  Пример 3 Рассмотрите пример из учебника. Ответьте на вопросы
  5

• 

  6 слайд

  Пример 4. Дан набор из 5 чисел, которые все равны между собой:
  4 4 4 4 4.
  Наименьшее значение равно 4, наибольшее значение тоже равно 4. Более того, все средние (арифметическое, геометрическое, гармоническое3, меди ана и т.п.) равны между собой и равны числу 4. Размах равен 0.

  6

• 

  7 слайд

  7
  Пример 5.
  При определении фарватера судоходной реки производится промер глубин. Затем на основе промеров находят показатель, который называется гарантированная глубина судового хода. Если судно имеет осадку меньше гарантированной глубины, то оно может пройти по фарватеру.
  В таблице 1 дан массив результатов промеров глубин на некотором участке фарватера реки.

  Табл. 1. Глубины на фарватере реки
  .
  а) Какую меру следует использовать для определения гарантированной глубины?
  б) Предложите способ, как определить гарантированную глубину на основе этих данных

• 

  8 слайд

  8
  Пример 6. При проектировании зданий нужно учитывать ветровую нагрузку, которая характерна для данной местности. Ветровая нагрузка – это давление воздуха на вертикальную стену сооружения при ветре. Чем скорость ветра выше, тем больше ветровая нагрузка. Приблизительное соответствие между скоростью ветра в м/с и давлением ветра в паскалях6 (Па) показано в табл. 2.
  Табл. 2. Давление ветра в зависимости от скорости ветра
  В таблице 3 показаны результаты измерения максимальных скоростей ветра в Великом Новгороде за период с 1949 по 1963 годы по месяцам. Рассмотрите таблицы 2 и 3 и ответьте на вопросы.
  а) Какую меру ветрового давления следует использовать для определения прочности сооружения при проектировании?
  б) Определите, на какое ветровое давление нужно рассчитывать сооружения в Великом Новгороде, опираясь на данные наблюдений 1949 – 1963 г.

• 

  9 слайд

  9
  в) Можно ли использовать данные таблицы 3 в наше время или Т требуется регулярное обновление наблюдений над скоростью ветра?

• 

  10 слайд

  Пример 7. В фигурном катании применяется специальная система оценивания элементов (прыжков, вращений). Каждый элемент имеет базовую стоимость в баллах. Чем труднее элемент, тем выше его базовая стоимость. После выступления фигуриста 9 судей ставят ему оценки за каждый элемент. Оценки ставятся по 11-балльной шкале (от –5 до +5 баллов). Затем итоговая оценка фигуриста за элементы вычисляется по следующему алгоритму:
  из массива, в котором девять оценок, удаляется одна наименьшая и одна наибольшая оценка за каждый элемент, остается семь оценок за элемент;
  семь оставшихся оценок усредняются: вычисляется их среднее арифметическое;
  получившееся среднее прибавляется к базовой стоимости. Получается оценка за элемент.
  оценки за все отдельные элементы складываются. Результат является итоговой оценкой выступления фигуриста за элементы катания.
  На соревнованиях выступал фигурист Петров и в ходе своего выступления выполнил несколько элементов. В таблице показаны базовые стоимости этих элементов и оценки судей.
  10
  Нетипичность (ненадежность) наибольших и наименьших значений

• 

  11 слайд

  Табл.4. Базовые стоимости элементов и оценки судей

  11
  а) Пользуясь описанным алгоритмом, вычислите оценку за четверной тулуп.
  б) Как вы думаете, почему было введено правило об удалении наибольшей и наименьшей оценок?
  6,7 + -1-1-1-1-1-1-1 = 6,7 -1 = 5,7 .
  7

• 

  12 слайд

  Выводы и итоги урока.
  Существуют важные виды данных, где нужно знать наибольшее и наименьшее значение.
  Такие показатели важны не только в спорте. Мы видели примеры с глубинами реки и с ветровым давлением на стены сооружений.
  Размах – простейшая мера рассеивания данных – равен разности между наибольшим и наименьшим значением.
  Он показывает длину интервала значений.
  Наименьшее и наибольшее значение в числовом массиве часто являются наименее надежными, нетипичными или даже ошибочными значениями.
  Поэтому нужно с осторожностью включать их в расчеты, а иногда вовсе удалять, как это делают судьи в фигурном катании.

  12

• 

  13 слайд

  Домашнее задание
  Изучить §15 с.64-67,
  ответить на вопросы1-3,
  Выполнить № 106, 107, 108.
  07.01.2023
  13

• 

  14 слайд

  Спасибо за урок!
  До встречи на следующем!
  07.01.2023
  14

Краткое описание документа:

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СТАТИСТИКА. 7 КЛАССУрок 13. Наибольшее и наименьшее значение, размах числового набора Цель урока. Сформировать представление об отрезке, на котором сосредоточены числа данного массива; о случаях, когда наименьшее или наибольшее значение являются естественной мерой. Учащиеся должны понять, что во многих случаях минимум и максимум являются наименее надежными показателями, подверженными сильной случайной изменчивости.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 265 155 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»

• Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»

• Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Наибольшее и наименьшее значение. Размах.

Цель урока : ввести новые понятия, характеризующие набор величин ; показать  что в некоторых ситуациях полезнее оценить их значения и разброс.

Актуализация знаний учащихся: 

1. Анализ практической работы

1.1.Дайте определение среднего значения, медианы. Расскажите, как их вычислить?

1.2.Устно ответьте на вопросы:

  -Дан набор, в котором число 3 встречается один раз, число 7-десять раз, число 8-сто раз. Других чисел в наборе нет. Укажите медиану данного набора.

-Изменится ли медиана, если к набору добавить число 100? ( Это задание не требует вычислений, только понимание смысла и способа вычисления медианы).

Повторение

Задача 1.Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:

№ ученика	1	2	3	4	5	6	7	8	9	10
Количество Правильный ответов	12	19	19	14	17	16	18	20	15	25
№ ученика	11	12	13	14	15	16	17	18	19	20
Количество Правильный ответов	13	20	25	16	17	12	24	13	21	13

Найдите среднее число правильных ответов, медиану ряда.

Решение. Средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20= = 349:20 = 17,45.
Расположим число ответов в порядке возрастания:

12,12,13,13,13,14,15,16,16,17,17,18,19,19,20,20,21,24,25,25.

Медиана ряда 17

Задача 2. Первые 5 часов автомобиль ехал со скоростью 60км/ч, следующие 3 часа— со скоростью 100км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение:

Средняя скорость, это отношение пройденного пути ко времени, за который пройден этот путь.

За первые 5 часов автомобиль проехал 5·60=300км, за следующие три часа— 3·100=300км и за последние 4 часа— 4·75=300км. Весь путь составил 300+300+300=900км, а суммарное время движения— 5+3+4=12часов, откуда средняя скорость автомобиля на протяжении всего пути 900/12 = 75 км/ч.

Задача 3. Девочки на уроке физической культуры прыгали в высоту и показали  результаты: 90, 125, 125, 130, 130, 135, 135, 135, 140, 140, 140  см. Какое значение наилучшим образом характеризует спортивную подготовку класса?  

Решение. Медиана – 135 см, Среднее арифметическое – 1425: 11= 129,5 см.

(Задание направлено на то, чтобы ещё раз вспомнить, что на данном этапе известны две величины, характеризующие набор. Учащиеся должны сделать вывод, что за счет всего одного низкого результата, среднее значение будет ниже медианы. В данном примере лучшей характеристикой будет медиана.)

Изучение и отработка нового материала:

Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.

В некоторых жизненных ситуациях нас интересуют не только среднее значение и медиана, но и другие характеристики, связанные с набором чисел. — Как определяются победители в соревнованиях по бегу, плаванию , велогонкам.

— Разумно ли сравнить средние результаты таких спортсменов?

Определение наибольшего и наименьшего значения величин важно в различных областях жизни. Поговорить о книге рекордов Гиннеса, подчеркнув бесполезность некоторых рекордов.

Выполняя следующее задание, обратить внимание на местоположение наименьшего значения на числовой прямой. Проанализируйте с помощью координатной прямой правильно ли найдено наименьшее значение:

-для набора  чисел 0, 3, 4, 5, 6, 7, 8 наименьшее значение равно 0;

-для набора чисел 6, 1, 9 наименьшее значение равно 1;

-для набора 3, 3, 4, 5, 6 наименьшее значение не существует.

Часто бывает важно знать не только «среднее» «типичное» значение в наборе чисел, но и иметь представление, насколько числа в наборе отличаются друг от друга или от среднего. Рассмотрим таблицу:

Таблица 46. Результаты прыжков в длину с места, см

Номер прыжка	Пётр	Иван	Алексей	Сергей
1	215	197	203	205
2	228	205	212	234
3	208	212	227	240
4	236	241	205	212
5	205	233	215	203
Среднее значение	218,4	217,6	212,4	219,4
Наибольшее значение	238	241	227	240
Наименьшее значение	205	197	203	203

Рассмотрите результаты и ответьте на вопросы:

— как вы думаете, почему результаты в разных попытках у ребят различаются?

— какие из перечисленных обстоятельств (факторов) могут влиять на результат: удача; техника прыжка; рост; вес; тренированность; настроение; плотный обед; усталость; обувь?

— какие еще факторы могут повлиять на дальность прыжка?

Самое большое среднее значение прыжка у Сергея, По этому показателю Иван только третий. Но рекордсменом стал Иван: в одной из попыток он прыгнул дальше всех.

В спорте не разумно использовать средние показатели для оценки результатов: нужно учитывать лучший. Тем не менее тренеру есть над чем задуматься.

Дать определение размаха набора чисел .

Выполнить задания на закрепление материала.

1. Даны два набора чисел: 5, 6, 21 и 1001, 1002, 1003. У какого набора размах больше?

Проанализируйте результат. ( Учащиеся должны понимать, что размах- разность между наибольшим и наименьшим значением; он больше у первого набора, хотя сами числа в нем меньше ).

2. В тетрадях № 106 ( 2022)

Найдите наибольшее и наименьшее значения, размах , среднее арифметическое и медиану набора чисел: б)17,19,5,41,13,19.

3. К набору 4, 4, 4 добавьте ещё одно число так, так чтобы размах стал равен 10. ( Как правило, после выполнения предыдущего упражнения учащиеся сами дают два  ответа, но в некоторых классах нужен наводящий вопрос о том, сколькими способами это можно сделать).

Добавьте к этому набору ещё одно число, чтобы наименьшее значение стало равно 0.

Заключение

На этом уроке мы рассмотрели некоторые элементы математической статистики.

Ссыл­ки на уроки Ин­тер­не­ту­ро­ка по рас­смот­рен­ным темам:

1. Ста­ти­сти­че­ская об­ра­бот­ка дан­ных (Ал­геб­ра, 11 класс, раз­дел «Эле­мен­ты ма­те­ма­ти­че­ской ста­ти­сти­ки-ком­би­на­то­ри­ки и тео­рии ве­ро­ят­но­сти»)

2.  Эле­мен­ты ма­те­ма­ти­че­ской ста­ти­сти­ки (Ал­геб­ра, 9 класс, раз­дел «Эле­мен­ты ма­те­ма­ти­че­ской ста­ти­сти­ки-ком­би­на­то­ри­ки и тео­рии ве­ро­ят­но­сти»)

Выводы

На данном уроке мы ознакомились с основными понятиями математической статистики и научились решать простые задачи по математической статистике.

 Список рекомендованной литературы

1. Башмаков М.И. Алгебра 8 класс. М.: Просвещение. 2004 г.

2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. М.: Просвещение. 2010 г.

3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. М.: Просвещение. 2006 г.

Рефлексия

1. Что нового узнали на уроке?

2. Разумно ли в спортивных соревнованиях использовать средние показатели для оценки результатов?

3. Что показывает размах числового набора?

4. Реально оцените.

Ваш одноклассник тратит на дорогу до школы 10-15 минут. Успеет ли он к первому уроку, если выйдет из дома в 8-10? Успеет ли он на первый урок математики на 3 этаж, если он выйдет в 8-29?

Домашнее задание п.10, № 93 а,96 ( учебник 2020 г)

Была ли эта статья полезной?