Как найти наибольшее значение функции cosx - Исправление недочетов и поиск решений вместе с Examum.ru

Развертка абсциссы движения точки по числовой окружности в функцию от угла
Свойства функции y=cos⁡x
Примеры

п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла

Развертка абсциссы движения точки по числовой окружности в функцию от угла (см. §2 данного справочника).

Рассмотрим, как изменяется косинус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=cosx на этом отрезке.

В результате получаем график y=cosx для любого (xinmathbb{R}).

График y=cosx называют косинусоидой.
Часть косинусоиды для –π≤x≤π называют волной косинусоиды.
Часть косинусоиды для (-fracpi2leq xleqfracpi2) называют полуволной или аркой косинусоиды.

Заметим, что термин «косинусоида» используется достаточно редко. Обычно, и в случае косинуса, говорят о «синусоиде».

п.2. Свойства функции y=cosx⁡

1. Область определения (xinmathbb{R}) — множество действительных чисел.

2. Функция ограничена сверху и снизу $$ -1leq cosxleq 1 $$ Область значений (yin[-1;1])

3. Функция чётная $$ cos(-x)=cosx $$

4. Функция периодическая с периодом 2π $$ cos(x+2pi k)=cosx $$

5. Максимальные значения (y_{max}=1) достигаются в точках $$ x=2pi k $$ Минимальные значения (y_{min}=-1) достигаются в точках $$ x=pi+2pi k $$ Нули функции (y_{0}=cosx_0=0) достигаются в точках (x=fracpi2 +pi k)

6. Функция возрастает на отрезках $$ -pi+2pi kleq xleq 2pi k $$ Функция убывает на отрезках $$ 2pi kleq xleqpi+2pi k $$

7. Функция непрерывна.

п.3. Примеры

Пример 1.Найдите наименьшее и наибольшее значение функции y=cosx на отрезке:

a) (left[fracpi6; frac{3pi}{4}right]) $$ y_{min}=cosleft(frac{3pi}{4}right)=-frac{sqrt{2}}{2}, y_{max}=cosleft(fracpi6right)=frac{sqrt{3}}{2} $$ б) (left[frac{5pi}{6}; frac{5pi}{3}right]) $$ y_{min}=cos(pi)=-1, y_{max}=cosleft(frac{5pi}{3}right)=frac12 $$

Пример 2. Решите уравнение графически:
a) (cosx=fracpi2-x)

Один корень: (x=fracpi2)

б) (cosx-x=1)
(cosx=x+1)

Один корень: x = 0

в) (cosx-x^2=1)
(cosx=x^2+1)

Один корень: x = 0

г*) (cosx-x^2+frac{pi^2}{4}=0)
(cosx=x^2-frac{pi^2}{4})
(y=x^2-frac{pi^2}{4}) – парабола ветками вверх, с осью симметрии (x_0=0) (ось OY) и вершиной (left(0; -frac{pi^2}{4}right)) (см. §29 справочника для 8 класса)

Два корня: (x_{1,2}=pmfracpi2)

Пример 3. Постройте в одной системе координат графики функций $$ y=cosx, y=-cosx, y=2cosx, y=cosx-2 $$

(y=-cosx) – отражение исходной функции (y=cosx) относительно оси OX. Область значений (yin[-1;1]).
(y=2cosx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=cosx-2) — исходная функция опускается вниз на 2. Область значений (yin[-3;-1]).

Пример 4. Постройте в одной системе координат графики функций $$ y=cosx, y=cos2x, y=cosfrac{x}{2} $$

Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под косинусом изменяет период колебаний.
(y=cosx) – главная арка косинуса соответствует отрезку (-fracpi2leq xleqfracpi2)
(y=cos2x) — период уменьшается в 2 раза, главная арка укладывается в отрезок (-fracpi4leq xleqfracpi4).
(y=cosfrac{x}{2}) — период увеличивается в 2 раза, главная арка растягивается в отрезок (-pi leq xleq pi).

Источник

Функция

y=cosx

определена на всей числовой прямой, и множеством её значений является отрезок

−1;1

Поэтому её график не выходит за границы полосы между прямыми

y=−1

y=1

Используя свойство периодичности функции

y=cosx

, можно построить её график на промежутке

−π≤x≤π

длиной

2π

и повторить несколько периодов с такими же значениями.

Функция

y=cosx

— чётная. Её график симметричен относительно оси (Oy).

Построим график функции на промежутке

−π≤x≤π

. Так как функция

y=cosx

является чётной, можно построить график на промежутке

0≤x≤π

, а потом симметрично отобразить относительно оси (Oy).

Значения функции в удобных точках на этом отрезке

0≤x≤π

равны:

cos0=1;cosπ6=32;cosπ4=22;cosπ3=12;cosπ2=0;cosπ=−1

Учитывая периодичность функции

y=cosx

, нарисуем её график.

1. Область определения — все действительные числа (множество

ℝ

2. Множество значений — промежуток

−1;1

3. Функция

y=cosx

имеет период

2π

4. Функция

y=cosx

является чётной.

5. Нули функции:

x=π2+πn,n∈ℤ;

наибольшее значение равно (1) при

x=2πn,n∈ℤ

;

наименьшее значение равно (-1) при

x=π+2πn,n∈ℤ

;

значения функции положительны на интервале

−π2;π2

, с учётом периодичности функции на интервалах

−π2+2πn;π2+2πn,n∈ℤ

;

значения функции отрицательны на интервале

π2;3π2

, с учётом периодичности функции на интервалах

π2+2πn;3π2+2πn,n∈ℤ

— возрастает на отрезке

π;2π

, с учётом периодичности функции на отрезках

π+2πn;2π+2πn,n∈ℤ

;

— убывает на отрезке

0;π

, с учётом периодичности функции на отрезках

2πn;π+2πn,n∈ℤ

Источник

hote
4 года назад

Светило науки — 2975 ответов — 40394 помощи

Для нахождения max или min нужно воспользоваться производной

y= cos x

y`= — sin x

y`=0; -sin x=0; x=πn; n∈Z

точки, в которых производная равна 0, являются точками экстремума функции. (т.е. точками или max или min)

определим знаки производной учитывая наш отрезок

______ 0 ____ (п/4) ______ п_______(5п/3) ______ 2п

y`<0 y`>0

функция убывает функция возрастает

Значит х=п, точка минимума функции

cos (п) = -1

Определим точки максимума на отрезке

т.к. максимумы функции бубт точки х=0 и х= 2п

то проверим значение функции вточках х=п/4 и х=5п/3 и сравним

cos (п/4)=√2/2; cos (5п/3)=1/2

Значит наименьшее значение функции в точке х=п и равно -1

наибольшее значение функции в точке х= п/4 и равно √2/2

Источник

14. Свойства функций синуса, косинуса, тангенса

и котангенса и их графики

14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК

Т а б л и ц а 21

График функции y = sin x (синусоида)

Свойства функции y = sin x

Объяснение и обоснование

Описывая свойства функций, мы будем чаще всего выделять такие их характеристики:

1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями

координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания * ;8) наибольшее и наименьшее

З а м е ч а н и е. Абсциссы точек пересечения графика функции с осью Ох

(то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.

Напомним, что значение синуса — это ордина-

та соответствующей точки единичной окружности

(рис. 79). Поскольку ординату можно найти для

любой точки единичной окружности (в силу того,

что через любую точку окружности всегда можно

провести единственную прямую, перпендикуляр-

ную оси ординат), то область определения функции

y = sin x — все действительные числа. Это можно за-

писать так: D (sin x) = R.

Для точек единичной окружности ординаты нахо-

дятся в промежутке [–1; 1] и принимают все значения

от –1 до 1, поскольку через любую точку отрезка [–1; 1]

оси ординат (который является диаметром единичной

окружности) всегда можно провести прямую, перпендикулярную оси орди-

нат, и получить точку окружности, которая имеет рассматриваемую орди-

нату. Таким образом, для функции y = sin x область значений: y ∈ [–1; 1].

Это можно записать так: E (sin x) = [–1; 1].

Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда

соответствующей точкой единичной окружности является точка A, то есть при

Наименьшее значение функции sin x равно минус единице. Это значение

достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть

при

Как было показано в § 13, синус — нечетная функция: sin(-x)= — sin x,

поэтому ее график симметричен относительно начала координат.

В § 13 было обосновано также, что синус — периодическая функция с наименьшим положительным периодом

T = 2π: sin (x + 2π) = sin x , таким образом, через промежутки длиной 2π вид графика функции sin x повторя-

ется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной 2 π , а

потом полученную линию парал лельно перенести вправо и влево вдоль оси Ox на расстояние kT = 2πk , где

k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат,

напомним, что на оси Oy значение x = 0. Тогда соответствующее значение

y = sin 0 = 0, то есть график функции y = sin x проходит через начало координат.

На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при

которых sin x, то есть ордината соответствующей точки единичной окруж

ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж-

ности будут выбраны точки C или D, то есть при x = πk, k ∈ Z (см. рис. 79).

Промежутки знакопостоянства . Как было обосновано в § 13, значения

функции синус положительны (то есть ордината соответствующей точки

единичной окружности положительна) в I и II четвертях (рис. 80). Таким

образом, sin x > 0 при всех x ∈ (0; π), а также, учитывая период, при всех

x ∈ (2πk; π + 2πk), k ∈ Z.

Значения функции синус отрицательны (то есть ордината соответствую-

щей точки единичной окружности отрицательна) в III и IV четвертях, поэто-

Промежутки возрастания и убывания

Учитывая периодичность функции sin x с периодом T = 2π, достаточно

исследовать ее на возрастание и убывание на любом промежутке длиной

2π, например на промежутке

то при увеличении аргумента x (x ₂ > x ₁ ) ордината соответствующей точки единичной окружности увеличивается (то есть

sin x ₂ > sin x ₁ ), следовательно, на этом промежутке функция sin x возрастает. Учитывая периодичность функции sin x,

делаем вывод, что она такж е возрастает на каждом из промежутков

Если x ∈ (рис. 81, б), то при увеличении аргумента x (x ₂ > x ₁ ) ордината соответствующей точки единичной

окружности уменьшается (то есть sin x ₂ ₁ ), таким образом, на этом промежутке функция sin x убывает. Учитывая

периодичность функции sin x, делаем вывод, что она также убывает на каждом из промежутков

Проведенное исследование позволяет обоснованно построить график функции y = sin x. Учитывая периодичность этой

функции (с периодом 2π), д о статочно сначала построить график на любом промежутке длиной 2π, на пример на

промежутке [–π; π]. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината

соответствующей точки единичной окружности. На рисунке 82 показано построение графика функции y = sin x на

промежутке [0; π]. Учитывая нечетность функции sin x (ее график симметричен относительно начала координат), для

построения графика на промежутке [–π; 0] отображаем полученную кривую симметрич но относительно начала координат

Поскольку мы построили график на

промежутке длиной 2π, то, учитывая

периодичность синуса (с периодом 2π),

повторяем вид графика на каждом про-

межутке длиной 2π (то есть переносим па-

раллельно график вдоль оси Ох на 2πk,

где k — целое число).

Получаем график, который называется

З а м е ч а н и е. Тригонометрические функции широко применяются в ма тематике, физике и технике. Например,

множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п.,

описываются функцией, которая задается формулой y = A sin (ωх + φ). Та кие процессы называют гармоническими

колебаниями. График функции y = A sin (ωx + φ) можно получить из синусоиды y = sin х сжатием или растяжением ее вдоль

координатных осей и параллельным пере носом вдоль оси Ох. Чаще всего гармоническое колебание является функцией

времени t. Тогда оно задается формулой y = A sin (ωt + φ), где А — амплитуда колебания, ω — частота, φ — начальная

фаза,

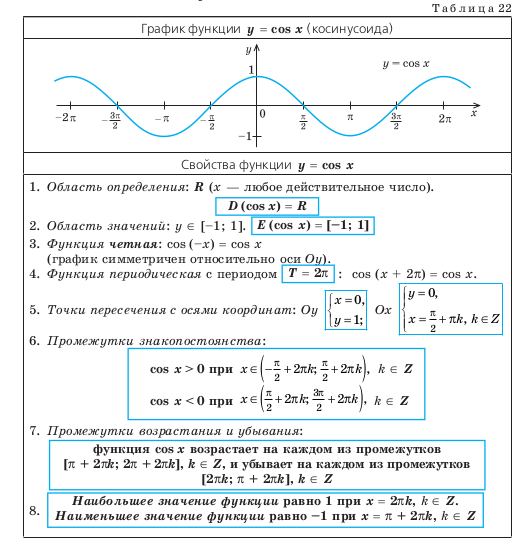
14.2. СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК

Объяснение и обоснование

Напомним, что значение косинуса — это абсцис-

са соответствующей точки единичной окружности

(рис. 85). Поскольку абсциссу можно найти для лю-

бой точки единичной окружности (в силу того, что

через любую точку окружности, всегда можно про-

вести единственную прямую, перпендикулярную оси

абсцисс), то область определения функции y = cos x —

все действительные числа. Это можно записать так:

D (cos x) = R.

Для точек единичной окружности абсциссы нахо-

дятся в промежутке [–1; 1] и принимают все значе-

ния от –1 до 1, поскольку через любую точку отрезка [–1; 1] оси абсцисс (который является диаметром единичной

всегда можно провести прямую, перпендикулярную оси абсцисс, и получить

точку окружности, которая имеет рассматриваемую абсциссу. Следователь но, область значений функции y = cos x:

y ∈ [–1; 1]. Это можно записать так: E (cos x) = [–1; 1]. Как видим, наибольшее значение функции cos x равно единице. Это

зна чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при

x = 2πk, k ∈ Z. Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда

соответствующей точкой единичной окруж ности является точка B, то есть при x = π + 2πk, k ∈ Z.

Как было показано в § 13, косинус — четная функция : cos (–x) = cos x, поэтому ее график симметричен относительно оси

Оу. В § 13 было обосновано также, что косинус — периодическая функция с наименьшим положительным периодом

T = 2π: cos (x + 2π) = cos x. Таким об разом, через промежутки длиной 2π вид графика функции cos x повторяется.

Чтобы найти точки пересечения графика функции с осями координат , напомним, что на оси Oy значение x = 0. Тогда

соответствующее значение y = cos 0 = 1. На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при

которых cos x, то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только

тогда, когда на единичной окружности будут выбраны точки C или D, то есть при

Промежутки знакопостоянства. Как было обосновано в § 13, значения

функции косинус положительны (то есть абсцисса соответствующей точки

единичной окружности положительна) в I и IV четвертях (рис. 86). Следова-

тельно, cos x > 0 при x ∈ (-П/2; П/2) а также, учитывая период, при всех

Значения функции косинус отрицательны (то есть абсцисса соответству-

ющей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях,

поэтому cos x

Промежутки возрастания и убывания

Учитывая периодичность функции cos x (T = 2π), достаточно исследовать

ее на возрастание и убывание на любом промежутке длиной 2π, например

на промежутке [0; 2π].

Если x ∈ [0; π] (рис. 87, а), то при увеличении аргумента x (x ₂ > x ₁ ) абсцисса соответствующей точки единичной

окружности уменьшается (то есть cos x ₂ ₁ ), следовательно, на этом промежутке функция cos x убывает. Учитывая

периодичность функции cos x, делаем вывод, что она также убывает на каждом из промежутков [2πk; π + 2πk], k ∈ Z.

Если x ∈ [π; 2π] (рис. 87, б), то при увеличении аргумента x (x ₂ > x ₁ ) аб-

сцисса соответствующей точки единичной окружности увеличивается (то

есть cos x ₂ >cos x ₁ ), таким образом, на этом промежутке функция cos x

возрастает. Учитывая периодичность функции cos x, делаем вывод, что

она возрастает также на каждом из промежутков [π + 2πk; 2π + 2πk], k ∈ Z.

Проведенное исследование позволяет построить график функции y = cos x

аналогично тому, как был построен график функ-

ции y = sin x. Но график функции у = cos x можно

также получить с помощью геометрических преоб-

разований графика функции у = sin х, используя

Эту формулу можно обосновать, например, так.

Рассмотрим единичную окружность (рис. 88), отметим на ней точки

Функция y = cos x, её свойства и график

п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла

Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x косинусоидой .
Часть косинусоиды для –π≤x≤π называют волной косинусоиды .
Часть косинусоиды для (-fracpi2leq xleqfracpi2) называют полуволной или аркой косинусоиды .

п.2. Свойства функции y=cosx⁡

1. Область определения (xinmathbb) — множество действительных чисел.

2. Функция ограничена сверху и снизу $$ -1leq cosxleq 1 $$ Область значений (yin[-1;1])

3. Функция чётная $$ cos(-x)=cosx $$

4. Функция периодическая с периодом 2π $$ cos(x+2pi k)=cosx $$

5. Максимальные значения (y_=1) достигаются в точках $$ x=2pi k $$ Минимальные значения (y_=-1) достигаются в точках $$ x=pi+2pi k $$ Нули функции (y_<0>=cosx_0=0) достигаются в точках (x=fracpi2 +pi k)

6. Функция возрастает на отрезках $$ -pi+2pi kleq xleq 2pi k $$ Функция убывает на отрезках $$ 2pi kleq xleqpi+2pi k $$

7. Функция непрерывна.

п.3. Примеры

Пример 1. Найдите наименьшее и наибольшее значение функции y=cosx на отрезке:

a) (left[fracpi6; frac<3pi><4>right]) $$ y_=cosleft(frac<3pi><4>right)=-frac<sqrt<2>><2>, y_=cosleft(fracpi6right)=frac<sqrt<3>> <2>$$ б) (left[frac<5pi><6>; frac<5pi><3>right]) $$ y_=cos(pi)=-1, y_=cosleft(frac<5pi><3>right)=frac12 $$

Пример 2. Решите уравнение графически:
a) (cosx=fracpi2-x)

Один корень: (x=fracpi2)

б) (cosx-x=1)
(cosx=x+1)

Один корень: x = 0

в) (cosx-x^2=1)
(cosx=x^2+1)

Один корень: x = 0

г*) (cosx-x^2+frac<pi^2><4>=0)
(cosx=x^2-frac<pi^2><4>)
(y=x^2-frac<pi^2><4>) – парабола ветками вверх, с осью симметрии (x_0=0) (ось OY) и вершиной (left(0; -frac<pi^2><4>right)) (см. §29 справочника для 8 класса)

Два корня: (x_<1,2>=pmfracpi2)

Пример 4. Постройте в одной системе координат графики функций $$ y=cosx, y=cos2x, y=cosfrac <2>$$

Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под косинусом изменяет период колебаний.
(y=cosx) – главная арка косинуса соответствует отрезку (-fracpi2leq xleqfracpi2)
(y=cos2x) — период уменьшается в 2 раза, главная арка укладывается в отрезок (-fracpi4leq xleqfracpi4).
(y=cosfrac<2>) — период увеличивается в 2 раза, главная арка растягивается в отрезок (-pi leq xleq pi).

Синус (sin x) и косинус (cos x) – свойства, графики, формулы

Геометрическое определение синуса и косинуса

α — угол, выраженный в радианах.

Тригонометрическое определение

С помощью формул, указанных выше, можно найти синус и косинус острого угла. Но нужно научиться вычислять синус и косинус угла произвольной величины. Прямоугольный треугольник не даёт такой возможности (тупого угла, например, в нём быть не может); следовательно, нужно более общее определение синуса и косинуса, содержащее указанные формулы как частный случай.

На помощь приходит тригонометрическая окружность. Пусть дан некоторый угол; ему отвечает одноимённая точка на тригонометрической окружности.

Рис. 2. Тригонометрическое определение синуса и косинуса

Косинус угла — это абсцисса точки. Синус угла — это ордината точки.

На рис. 2 угол взят острым, и легко понять, что данное определение совпадает с общим геометрическим определением. В самом деле, мы видим прямоугольный треугольник с единичной гипотенузой O и острым углом. Прилежащий катет этого треугольника есть cos (сравните с рис. 1) и одновременно абсцисса точки ; противолежащий катет есть sin (как на рис. 1) и одновременно ордината точки.

Но теперь мы уже не стеснены первой четвертью и получаем возможность распространить данное определение на любой угол . На рис. 3 показано, что такое синус и косинус угла во второй, третьей и четвёртой четвертях.

Рис. 3. Синус и косинус во II, III и IV четвертях

Табличные значения синуса и косинуса

Абсцисса точки 0 равна 1 , ордината точки 0 равна 0 . Следовательно,

источники:

http://reshator.com/sprav/algebra/10-11-klass/funkciya-y-cosx-svojstva-i-grafik/

http://calcsbox.com/post/sinus-sin-x-i-kosinus-cos-x-svojstva-grafiki-formuly.html

Источник

Тема 11.

Исследование функций с помощью производной

Поиск наибольшего/наименьшего значения у функций с тригонометрией

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

исследование функций с помощью производной

Решаем задачи

Найдите наибольшее значение функции на отрезке [ π]
0;2 .

Показать ответ и решение

Функция y =y(x) определена при всех Определим участки, на которых функция возрастает или убывает. Для этого
найдем ее производную:

Найдем нули производной:

6
y′ = 0 ⇒ cosx= 5 ⇔ x∈ ∅

Следовательно, функция убывает на всем значит, принимает наибольшее значение в начале отрезка, то есть в
точке x = 0:

Найдите наибольшее значение функции

на отрезке [ 3π]
0; 2 .

Показать ответ и решение

Найдем нули производной:

Следовательно, функция убывает на всем значит, принимает наибольшее значение в левом конце отрезка, то
есть в точке x= 0:

Найдите наибольшее значение функции на отрезке [− 3π;0] .
2

Показать ответ и решение

Функция y =y(x) определена при всех . Определим участки, на которых функция возрастает или убывает. Для этого найдем ее
производную:

′
y = −7sinx +16

Найдем нули производной:

′ 16
y =0 ⇒ sinx = 7 ⇔ x∈ ∅

Следовательно, функция возрастает на всем , значит, принимает наибольшее значение в конце отрезка, то есть в x =0 , и
оно равно

Найдите наибольшее значение функции на отрезке [− π;0]
2 .

Показать ответ и решение

′
y= 15− 3cosx =3(5− cosx)

Найдем нули производной:

′
y =0 ⇔ 3(5 − cosx)=0 ⇔ cosx =5 ⇔ x∈ ∅

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Производная не
имеет нулей, следовательно, принимает значения одного знака. Так как , то , следовательно, y′ >0 при всех
. Следовательно, функция возрастает на всей своей области определения, значит, на любом отрезке наибольшее
значение функция принимет в конце этого отрезка. Следовательно, наибольшее значение функции на указанном отрезке
равно

Найдите наименьшее значение функции на отрезке [ π]
0;2 .

Показать ответ и решение

Найдем нули производной:

13
y′ = 0 ⇒ cosx = 9- ⇔ x∈ ∅

Следовательно, функция возрастает на всем значит, принимает наименьшее значение в начале отрезка, то есть
в x= 0, и оно равно

Найдите наибольшее значение функции √ - √-
y = 12 sinx− 6 3x + 3π+ 6 на отрезке [ π]
0;2 .

Показать ответ и решение

√-
y′ = 12cosx− 6 3

Найдем нули производной:

√3- π
y′ = 0 ⇒ cosx= -2- ⇔ x = ±6-+ 2πn,n ∈ ℤ

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на
каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких
промежутков. Из точек, где производная равна нулю или не существует, на отрезок [0; π]
2 попадает только нуль производной
π
x = 6.

PICT

При [ π)
x∈ 0;6 производная положительна (для проверки можно подставить в производную точку из этого промежутка
x = 0 ), при ( ]
x∈ π6; π2 производная отрицательна (подставляем x = π2 ). Следовательно, функция принимает
наибольшее значение в и оно равно

( )
y π- = 6− √3π+ √3π + 6= 12
6

Найдите наибольшее значение функции

на отрезке [ π-π]
− 3;3 .

Показать ответ и решение

Функция определена при всех π
x ⁄= 2 + πk,k ∈ℤ . Определим участки, на которых функция возрастает или убывает.
Для этого найдем ее производную:

2 2cos2x− 1 cos2x
y′ = − cos2x-+ 4= 2⋅-cos2x-- =2 ⋅cos2x-

Найдем нули производной:

Найдем точки, где производная не существует:

π-
cosx⁄= 0 ⇔ x ⁄= 2 + πk,k ∈ ℤ

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на
каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких
промежутков. Тогда из точек, где производная равна нулю или не существует, на отрезок попадают нули производной
x = − π; π
4 4 .

PICT

Тогда функция убывает на , затем возрастает на , затем снова убывает на ,
следовательно, наибольшее значение принимает в одной из точек π
x= − 3 или π
x = 4 . Найдем значение функции в этих точках
и сравним:

( π ) √ - 4π √ - 7π
y −-3 = 2 3− 3-− π − 3 = 2 3− 3−-3
( )
y π- = −2+ π − π − 3= −5
4

Очевидно, что больше.

Найдите наибольшее значение функции на отрезке [ π-π]
− 3;3 .

Показать ответ и решение

Функция определена при всех π
x ⁄= 2 + πk, Определим участки, на которых функция возрастает или убывает.
Для этого найдем ее производную:

7 2cos2x− 1 cos2x
y′ =14 − cos2x-= 7⋅-cos2-x--= 7 ⋅cos2x-

Найдем нули производной:

Найдем точки, где производная не существует:

π-
cosx⁄= 0 ⇔ x ⁄= 2 + πk,k ∈ ℤ

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на
каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких
промежутков. Тогда из точек, где производная равна нулю или не существует, на отрезок попадают нули производной
x = − π; π.
4 4

PICT

Тогда функция убывает на затем возрастает на затем снова убывает на
следовательно, наибольшее значение принимает в одной из точек π
x= − 3 или π
x = 4. Найдем значение функции в этих точках
и сравним:

( π ) 14π √- 7π √- 49π
y −3- = − -3-+ 7 3 −-2 + 11= 11+ 7 3− -6-
( )
y π- = 7π − 7 − 7π-+ 11= 4
4 2 2

Очевидно, что y =4 больше.

Найдите наибольшее значение функции на отрезке [ π]
0;4 .

Показать ответ и решение

Функция определена при всех π
x ⁄= 2 + πk,k ∈ℤ. Определим участки, на которых функция возрастает или убывает.
Для этого найдем ее производную:

3 1− cos2x
y′ = 3− cos2x-= −3⋅-cos2-x--

Найдем нули производной:

Найдем точки, где производная не существует:

cosx⁄= 0 ⇔ x ⁄= π+ πk,k ∈ ℤ
2

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на
каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких
промежутков. Тогда из точек, где производная равна нулю или не существует, на отрезок [ π]
0;4 попадает только нуль
производной x =0.

PICT

При [ ]
x∈ 0; π4 производная отрицательна (подставляем x= π4 ). Следовательно, функция y =y(x) убывает на всем отрезке
[ ]
− π4;0 , значит, наибольшее значение принимает в начале отрезка, и оно равно

Найдите наибольшее значение функции на отрезке [− π;π].
4 4

Показать ответ и решение

Функция y =y(x) определена при всех x⁄= π+ πk,k∈ ℤ
2 . Определим участки, на которых функция возрастает или убывает. Для этого
найдем ее производную:

′ 16 1 − cos2x
y = cos2x-− 16 =16⋅--cos2x-

Найдем нули производной:

Найдем точки, где производная не существует:

π
cosx ⁄=0 ⇔ x⁄= 2 + πk,k∈ ℤ

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Тогда из
точек, где производная равна нулю или не существует, на отрезок [ ]
− π4;π4 попадает только нуль производной x = 0 .

PICT

При [ π )
x∈ −4;0 производная положительна (для проверки можно подставить в производную точку из этого промежутка π
x= −-6 ), при
( π]
x ∈ 0;4 производная также положительна (подставляем π
x= 6 ). Следовательно, функция возрастает на всем отрезке
[ ]
− π4;π4 , значит, наибольшее значение принимает в конце отрезка, и оно равно

( ) ( )
y π = 16tg π − 16⋅ π+ 4π− 5= 16 − 4π+ 4π− 5= 11.
4 4 4

Найдите наибольшее значение функции на отрезке [− π;0].
4

Показать ответ и решение

′ 3 1− cos2 x
y = cos2x-− 3 =3⋅-cos2x--

Найдем нули производной:

Найдем точки, где производная не существует:

π
cosx ⁄=0 ⇔ x⁄= 2 + πk,k∈ ℤ

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Из
точек, где производная равна нулю или не существует, на отрезок [ ]
− π4;0 попадает только нуль производной x= 0 .

PICT

При [ π ]
x∈ −4;0 производная положительна (подставляем π
x= −4 ). Следовательно, функция возрастает на всем отрезке
[ π ]
− 4;0 , значит, наибольшее значение принимает в конце отрезка, и оно равно

Найдите наибольшее значение функции

18
y = 2cosx − π-x+ 4

на отрезке [ 2π ]
− 3-;0 .

Показать ответ и решение

18
y′ = − 2sinx − π

Найдем нули производной:

y′ = 0 ⇒ sin x= − 9- ⇔ x ∈∅
π

Следовательно, функция убывает на всем , значит, принимает наибольшее значение в начале отрезка, то есть в
x = − 2π
3 , и оно равно

( ) ( )
2π 2π- 18 2π
y − 3 = 2cos − 3 + π ⋅3 + 4 =15

Найдите наибольшее значение функции 36
y = 10 sinx− π x + 7 на отрезке [ 5π ]
− 6 ;0 .

Показать ответ и решение

36
y′ =10cosx−-π

Найдем нули производной:

y′ = 0 ⇒ cosx= -36 ⇔ x∈ ∅
10π

Следовательно, функция убывает на всем значит, принимает наибольшее значение в начале отрезка, то есть в
x = − 5π,
6 и оно равно

( ) ( )
5π 5π 36 5π
y − 6 =10 sin − 6 + π ⋅ 6 + 7= 32

Найдите наибольшее значение функции

√ - √ -
y = 12cosx + 6 3⋅x− 2 3π + 6

на отрезке [ π]
0;2 .

Показать ответ и решение

√- ( √3-)
y′ = −12sin x+ 6 3 = −12 sin x−-2-

Найдем нули производной:

( √ -) √-
y′ = 0 ⇔ −12 sinx− --3 =0 ⇔ sinx = -3-
2 2

PICT

На отрезке [ π]
0;2 содержится одна точка π
x = 3 , в которой производная равна нулю. При [ π)
x∈ 0;3 функция
возрастает, так как √-
sinx < 23 , следовательно, , а при ( ]
x∈ π3; π2 функция убывает.

Следовательно, x= π3 — точка максимума функции на отрезке и в ней функция принимает наибольшее значение,
равное

Найдите наименьшее значение функции на отрезке [− π;0].
4

Показать ответ и решение

′ 4 1− cos2x
y= 4− cos2x-= −4⋅--cos2x-

Найдем нули производной:

Найдем точки, где производная не существует:

π
cosx ⁄=0 ⇔ x⁄= 2 + πk,k∈ ℤ

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Тогда из
точек, где производная равна нулю или не существует, на отрезок [ ]
− π4;0 попадает только нуль производной x= 0 .

PICT

При [ π ]
x∈ −4;0 производная отрицательна (подставляем π
x= − 4 ). Следовательно, функция убывает на всем отрезке
[ π ]
− 4;0 , значит, наименьшее значение принимает в конце отрезка, и оно равно

Найдите наименьшее значение функции y = −14x+ 7tgx + 7π +11
2 на отрезке [− π;π].
3 3

Показать ответ и решение

′ 7 1− 2cos2x cos2x
y= −14+ cos2-x = 7⋅-cos2x---=− 7⋅cos2x-

Найдем нули производной:

π π
y′ = 0 ⇒ cos2x= 0 ⇔ x =-4 + 2n,n∈ ℤ

Найдем точки, где производная не существует:

cosx ⁄=0 ⇔ x⁄= π + πk,k∈ ℤ
2

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Тогда из
точек, где производная равна нулю или не существует, на отрезок попадают нули производной .

PICT

Тогда функция возрастает на [ π π)
− 3;− 4 , затем убывает на ( π π)
− 4;4 , затем снова возрастает на (π π]
4;3 ,
следовательно, наименьшее значение принимает в одной из точек π
x= −3 или π
x = 4 . Найдем значение функции в этих точках и
сравним:

( ) ( ) √ -
y − π = 14π-+7 tg − π + 7π+ 11= 49π+ 11− 7 3
3 3 3 2 6
y (π)= − 7π-+ 7tg π+ 7π+ 11= 18
4 2 4 2

Очевидно, что y = 18 меньше.

Найдите наименьшее значение функции на отрезке [− π ;π].
3 3

Показать ответ и решение

′ 2 1− 2cos2x cos2x
y =cos2x − 4= 2⋅-cos2x---=− 2⋅cos2x-

Найдем нули производной:

π π
y′ = 0 ⇒ cos2x= 0 ⇔ x =-4 + 2n,n∈ ℤ

Найдем точки, где производная не существует:

cosx ⁄=0 ⇔ x⁄= π + πk,k∈ ℤ
2

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Тогда из
точек, где производная равна нулю или не существует, на отрезок попадают нули производной .

PICT

( ) √ -
y − π =− 2 3+ 4π+ π− 3
3 3
y (π)= 2− π+ π− 3= −1
4

Очевидно, что меньше.

Найдите наименьшее значение функции на отрезке [0;π].
4

Показать ответ и решение

′ 5 1− cos2 x
y = cos2x-− 5 =5⋅-cos2x--

Найдем нули производной:

Найдем точки, где производная не существует:

π
cosx ⁄=0 ⇔ x⁄= 2 + πk,k∈ ℤ

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков.
Из точек, где производная равна нулю или не существует, на отрезок [ ]
0;π4 попадает только нуль производной x =0 .

PICT

При [ π ]
x∈ 0;-4 производная положительна (подставляем π
x = 4 ). Следовательно, функция возрастает на всем отрезке
[ π]
0;4 , значит, наименьшее значение принимает в начале отрезка, и оно равно