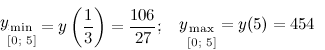Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.
Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.
Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].
Решение
Сначала вычисляем производную исходной функции:
y′=3×2−12xy’=3x^2-12x
Затем приравниваем ее к нулевому значению и решаем уравнение:
3×2−12x=03x^2-12x=0
x(3x−12)=0x(3x-12)=0
x1=0x_1=0
x2=4x_2=4
Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.
Находим значение функции в точке x1x_1:
f(0)=9f(0)=9
Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:
f(−1)=−1−6+9=2f(-1)=-1-6+9=2
f(2)=8−24+9=−7f(2)=8-24+9=-7
Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.
Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.
Решение
Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:
y′=6xy’=6x
Приравниваем производную к нулю:
6x=06x=0
x=0x=0
Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.
Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.
Тест по теме “Наибольшие и наименьшие значения функции”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Заказать задачи по любым предметам можно здесь от 10 минут
Наибольшее и наименьшее значение функции
Как найти?
Постановка задачи
Найти наибольшее и наименьшее значение функции $ f(x) $ на отрезке $ [a,b] $
План решения
Наибольшее и наименьшее значение непрерывной функции $ f(x) $ на промежутке $ [a,b] $ достигаются в критических точках, то есть в точках в которых производная функции равна нулю $ f'(x) = 0 $, бесконечности $ f'(x) = pm infty $, не существует, либо на концах отрезка $ [a,b] $
- Проверяем на непрерывность функцию $ f(x) $ на заданном отрезке
- Если функция непрерывная, то находим производную $ f'(x) $ и приравниваем её к нулю
- Решая уравнение $ f'(x) = 0 $ получаем корни, являющиеся критическими точками
- Выбираем критические точки, принадлежащие отрезку $ [a,b] $
- Вычисляем значения функции $ f(x) $ в оставшихся критических точках, а так же на концах промежутка $ [a,b] $. Затем выбираем из них наибольшее $ M $ и наименьшее $ m $
Примеры решений
| Пример 1 |
| Найти наибольшее и наименьшее значение функции $ y = 2x^3 — 3x^2 — 4 $ на отрезке $ [0;2] $ |
| Решение |
|
Функция представляет собой кубический многочлен. Точек разрыва нет, значит функция непрерывна на отрезке $ [0;2] $. Находим производную: $$ y’ = (2x^3 — 3x^2 — 4)’ = 6x^2 — 6x $$ Приравниваем производную к нулю. Решаем уравнение и получаем критические точки: $$ 6x^2 — 6x = 0 $$ $$ 6x(x — 1) = 0 $$ $$ x_1 = 0, x_2 = 1 $$ Проверяем принадлежность полученных точек отрезку $ [0;2] $: $$ x_1 in [0;2], x_2 in [0;2] $$ Так как обе точки принадлежат отрезку, то вычисляем в них значение функции $ f(x) $, так же значение этой функции на концах интервала $ [0;2] $: $$ y(x_1) = y(a) = f(0) = 2 cdot 0^3 — 3 cdot 0^2 — 4 = -4 $$ $$ y(x_2) = y(1) = 2 cdot 1^3 — 3 cdot 1^2 — 4 = -5 $$ $$ y(b) = y(2) = 2 cdot 2^3 — 3 cdot 2^2 — 4 = 0 $$ Среди полученных значений наибольшее $ M = 0 $, наименьшее $ m = -5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ M = 0, m = -5 $$ |
| Пример 2 |
| Найти наименьшее и наибольшее значение функции $ y = frac{4x^2}{3+x^2} $ на $ [-1;1] $ |
| Решение |
|
Функция непрерывна на $ x in [-1;1] $ так как знаменатель не обращается в ноль ни при каком $ x $. Выполняем нахождение производной: $$ y’ = (frac{4x^2}{3+x^2})’ = frac{(4x^2)'(3+x^2)-(4x^2)(3+x^2)’}{(3+x^2)^2} = $$ $$ = frac{8x(3+x^2)-(4x^2)(2x)}{(3+x^2)^2} = frac{24x+8x^3-8x^3}{3+x^2)^2} = frac{24x}{(3+x^2)^2} $$ Приравниваем полученную производную к нулю и вычисляем критические точки: $$ frac{24x}{(3+x^2)^2} = 0 $$ $$ 24x = 0, 3+x^2 neq 0 $$ $$ x = 0 $$ Получена единственная критическая точка $ x = 0 $, которая принадлежит $ [-1; 1] $. Вычисляем значение функции $ f(x) $ в критической точке и на концах интервала $ [-1;1] $: $$ y(-1) = frac{4cdot (-1)^2}{3+(-1)^2} = frac{4}{4}=1 $$ $$ y(0) = frac{0}{3} = 0 $$ $$ y(1) = frac{4cdot 1^2}{3+1^2} = frac{4}{4} = 1 $$ Из полученных значений видно, что максимальное значение $ M = 1 $ и минимальное значение $ m = 0 $. |
| Ответ |
| $$ m = 0, M = 1 $$ |
Если функция $y=f(x)$ определена и
непрерывна на отрезке
$[a ; b]$ , то она на этом отрезке достигает своих наибольшего
и наименьшего значений. Если свое наибольшее значение $M$
функция $f(x)$ принимает в точке
$x_{0} in[a ; b]$, то
$M=fleft(x_{0}right)$ будет локальным максимумом функции
$f(x)$, так как в этом случае существует окрестность точки
$x_{0}$, такая, что
$f(x) leq fleft(x_{0}right)$ .
Однако свое наибольшее значение $M$ функция
$f(x)$ может принимать и на концах отрезка
$[a ; b]$ . Поэтому, чтобы найти наибольшее значение
$M$ непрерывной на отрезке
$[a ; b]$ функции
$f(x)$, надо найти все максимумы функции на интервале
$(a ; b)$ и значения
$f(x)$ на концах отрезка
$[a ; b]$, то есть
$f(a)$ и
$f(b)$, и выбрать среди них наибольшее. Вместо исследования
на максимум можно ограничиться нахождением значений функции в критических точках.
Наименьшим значением $m$ непрерывной на отрезке
$[a ; b]$ функции
$f(x)$ будет наименьший минимум среди всех минимумов функции
$f(x)$ на интервале
$(a ; b)$ и значений
$f(a)$ и
$f(b)$.
Пример
Задание. Найти наибольшее и наименьшее значение функции
$y(x)=4 x^{3}-2 x^{2}+4$ на отрезке
$[0 ; 5]$ .
Решение. Находим производную функции:
$y^{prime}(x)=left(4 x^{3}-2 x^{2}+4right)^{prime}=12 x^{2}-4 x$
Находим точки, в которых производная равна нулю:
$y^{prime}(x)=0 Rightarrow 12 x^{2}-4 x=0 Rightarrow x_{1}=0, x_{2}=frac{1}{3}$
Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку
$[0 ; 5]$ . Оба значения лежат в этом промежутке.
Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:
$y(0)=4 ; quad yleft(frac{1}{3}right)=frac{106}{27} approx 3,92 ; y(5)=454$
Таким образом,
Ответ.
Читать дальше: выпуклость функции, точки перегиба.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Что такое наибольшее и наименьшее значение функции
Множество значений каждой функции ограничено, и для представления о ее свойствах часто бывает необходимо вычислить границы этого множества. Функция может обладать такими свойствами, как периодичность, четность и нечетность. Иногда это имеет значение при вычислении наибольшего и наименьшего значений, т. к. равенства, определяющие периодичность, четность и нечетность, ограничивают область определения.
Возьмем в качестве примера функцию, описанную уравнением (y = (f)x), являющуюся непрерывной на отрезке ([а; b]). Наибольшим значением функции (f(x)) будет точка (x_{0}), принадлежащая этому отрезку, значение которой больше или равно любой из точек (x), также принадлежащих отрезку ([а; b]). Аналогично определяется наименьшее значение функции — точка, значение которой меньше или равно любой их точек на отрезке ([а; b]).
Точки максимума и минимума функции также называют точной верхней и нижней гранью множества значений функции.
Как записать, каким символом обозначают
Обозначение независимой переменной, или аргумента функции — буква х, зависимой переменной, или значения функции — буква у. Выражение, содержащее х, записывают как (f(x).)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Максимум функции на множестве ([a;b]), входящем в область ее определения, можно записать так: (;underset{lbrack a;brbrack;}{y_{max}}) или ({y_{max}}, y(x_{max})), указав границы множества отдельно.
Минимум — (;underset{lbrack a;brbrack;}{y_{min}}) или ({y_{min}}, y(x_{min}).)
Нахождение наибольшего и наименьшего значения функции на промежутке
Если (x_{0}) — точка экстремума, тогда (f’ (x_{0}) = 0.)
Если в точке (x_{0} f’ (x)) меняет знак с «+» на «-», то (x_{0}) — точка максимума.
Если в этой точке (f’ (x)) меняет знак с «-» на «+», то (x_{0}) — точка минимума.
Как найти через производную на отрезке ([а; b]), формулы
Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке ([а; b]:)
- Вычислить производную( f'(x).)
- Найти критические точки f(х) на отрезке ([а; b]): производная будет равна нулю при х, равном искомым точкам.
- Найти значения функции в критических точках (f (x_{1}),) (f (x_{2})) и т. д.
- Вычислить( f (а)), (f (b).)
- Выбрать наименьшее и наибольшее значение из ряда вычисленных точек, включающем не только критические точки, но и крайние точки отрезка.
Производная — мгновенный частный результат действия функции.
Производная функции (у = f(x)) в точке (x_{0}) — это предел отношения приращения функции к точке (x_{0}) к приращению аргумента, когда приращение аргумента стремится к нулю. Это можно выразить следующей формулой:
(f'(x_{0}) = lim_{triangle x rightarrow 0}frac{triangle f}{triangle x}.)
(triangle f = f(x_{0}triangle x) — f(x_{0}).)
Найти производную можно, воспользовавшись специальными таблицами или вычислив ее по правилам:
- ((u + v)’ = u’ + v’.)
-
((u times v)’ = u’ times v + u times v’.)
-
((frac{u}{v})’ = frac{u’ times v — u times v’}{v^{2}}.)
Примеры задач с решением
Задача № 1
Найти наибольшее и наименьшее целые значения (f(х)=х^{3} -1,5x^{2} — 6х+1) на отрезке ([-2; 0].)
Решение:
(f'(х)= 3x^{2} — 3х — 6.)
Производная равна нулю, если x равен — 1 или 2.
2 не принадлежит отрезку, но — 1 — принадлежит.
Вычисляем значения критических точек:( f(-1) = 4,5, f(-2) = — 1, f(0) = 1.)
Ответ: на отрезке ([-2; 0]) целые ( min f(x) = f(-2) = -1,) (max f(x) = f(-1) = 4.)
Задача № 2
Найти наибольшее и наименьшее значения( f(х)=2х^{3}-12x^{2} + 18х + 3) на отрезке ([-1; 2].)
Решение:
(f'(х)= 6x^{2} — 24х + 18.)
Производная равна нулю, если x равен 1 или 3.
3 не принадлежит отрезку, но 1 — принадлежит.
Вычисляем значения критических точек: (f(1) = 11,) (f(-1) = — 29,) (f(2) = 7.)
Ответ: на отрезке ([-1; 2]) (min f(x) = f(-2) = -29), (max f(x) = f(-1) = 11.)
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Проверить, какие стационарные точки входят в заданный отрезок.
- Вычислить значение функции на концах отрезка и в стационарных точках из п.3
- Выбрать из полученных результатов наибольшее или наименьшее значение.
Чтобы найти точки максимума или минимума необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Разложить производную функции на множители.
- Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
- Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.
Таблица производных некоторых элементарных функций:
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n, n∈N$ | $nx^{n-1}, n∈N$ |
| ${1}/{x}$ | $-{1}/{x^2}$ |
| ${1}/x{^n}, n∈N$ | $-{n}/{x^{n+1}}, n∈N$ |
| $√^n{x}, n∈N$ | ${1}/{n√^n{x^{n-1}}, n∈N$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | ${1}/{cos^2x}$ |
| $ctgx$ | $-{1}/{sin^2x}$ |
| $cos^2x$ | $-sin2x$ |
| $sin^2x$ | $sin2x$ |
| $e^x$ | $e^x$ |
| $a^x$ | $a^xlna$ |
| $lnx$ | ${1}/{x}$ |
| $log_{a}x$ | ${1}/{xlna}$ |
Основные правила дифференцирования
1. Производная суммы и разности равна производной каждого слагаемого
$(f(x) ± g(x))′= f′(x)± g′(x)$
Пример:
Найти производную функции $f(x) = 3x^5 – cosx + {1}/{x}$
Производная суммы и разности равна производной каждого слагаемого
$f′(x)=(3x^5)′–(cosx)′+({1}/{x})’=15x^4+sinx-{1}/{x^2}$
2. Производная произведения.
$(f(x)∙g(x))′=f′(x)∙g(x)+f(x)∙g(x)′$
Пример:
Найти производную $f(x)=4x∙cosx$
$f′(x)=(4x)′∙cosx+4x∙(cosx)′=4∙cosx-4x∙sinx$
3. Производная частного
$({f(x)}/{g(x)})’={f^'(x)∙g(x)-f(x)∙g(x)’}/{g^2(x)}$
Пример:
Найти производную $f(x)={5x^5}/{e^x}$
$f'(x)={(5x^5)’∙e^x-5x^5∙(e^x)’}/{(e^x)^2}={25x^4∙e^x-5x^5∙e^x}/{(e^x)^2}$
4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))′=f′(g(x))∙g′(x)$
Пример:
$f(x)= cos(5x)$
$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$
Пример:
Найдите точку минимума функции $y=2x-ln(x+11)+4$
Решение:
1. Найдем ОДЗ функции: $х+11>0; х>-11$
2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$
3. Найдем стационарные точки, приравняв производную к нулю
${2x+21}/{x+11}=0$
Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю
$2x+21=0; x≠-11$
$2х=-21$
$х=-10,5$
4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.
$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$
5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума.
Ответ: $-10,5$
Пример:
Найдите наибольшее значение функции $y=6x^5-90x^3-5$ на отрезке $[-5;1]$
Решение:
1. Найдем производную функции $y′=30x^4-270x^2$
2. Приравняем производную к нулю и найдем стационарные точки
$30x^4-270x^2=0$
Вынесем общий множитель $30x^2$ за скобки
$30x^2(x^2-9)=0$
$30x^2(х-3)(х+3)=0$
Приравняем каждый множитель к нулю
$x^2=0 ; х-3=0; х+3=0$
$х=0;х=3;х=-3$
3. Выберем стационарные точки, которые принадлежат заданному отрезку $[-5;1]$
Нам подходят стационарные точки $х=0$ и $х=-3$
4. Вычислим значение функции на концах отрезка и в стационарных точках из п.3
$y(-5)= 6∙(-5)^5-90∙(-5)^3-5=6∙(-3125)+90∙125-5= -18750+11250-5=-7505$
$y(-3)= 6∙(-3)^5-90∙(-3)^3-5=-1458+2430-5=967$
$y(0)= -5$
$y(1)= 6∙1^5-90∙1^3-5=6-90-5= -89$
Наибольшее значение равно $967$
Ответ: $967$