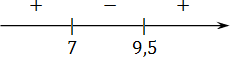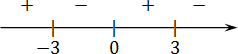Как найти наибольшее значение функции логарифма

Наибольшее и наименьшее значение логарифмической функции. Задание 12

В этой статье мы рассмотрим решение двух примеров, которые на первый взгляд очень похожи, а на второй принципиально отличаются друг от друга.

Итак.

Пример 1

Най­ди­те наи­боль­шее зна­че­ние функ­ции y=ln(x+5)^5-5x на от­рез­ке delim{[}{-4,5;0}{]}.

Чтобы найти наибольшее значение функции, нам надо найти ее производную, затем приравнять производную к нулю, определить ее знаки и выяснить поведение функции на отрезке.

В этом примере под знаком логарифма стоит выражение  x+5 в пятой, то есть в нечетной степени. Если мы возводим отрицательное число в нечетную степень, то в результате получаем отрицательное число. Поскольку выражение по знаком логарифма должно быть больше нуля, следовательно, (x+5)^5>0 и отсюда x+5>0 .

Упростим функцию: вынесем показатель степени за знак логарифма. Получим y=5ln(x+5)-5x.

Найдем производную функции. (Не забываем, что мы, строго говоря, имеем дело со сложной функцией.)

y{prime}=5/{x+5}{(x+5)}{prime}-5=5/{x+5}-5

Найдем нули производной:

5/{x+5}-5=0

{5-5x-25}/{x+5}=0

{-5x-20}/{x+5}=0

-5x-20=0;~~x=-4

Определим знаки производной: (учитываем, что x+5>0)

И, соответственно, поведение функции:

В точке x=-4 производная меняет знак с «+» на «-«, следовательно, это точка максимума функции. Точка -4 принадлежит заданному отрезку:

Следовательно, в точке x=-4 функция y=ln(x+5)^5-5x принимает наибольшее значение на отрезке delim{[}{-4,5;0}{]}.

Найдем значение функции при x=-4: y(-4)=ln(-4+5)^5-5(-4)=ln1+20=20

Ответ: 20.

Замечание. Так как при решений заданий В-части в ответе должно получиться целое число или конечная десятичная дробь, а  натуральный логарифм при рациональном аргументе принимает такие значения только в том случае, если его аргументом является число 1, то мы могли бы сразу сказать, что x=-4, т.к. x+5=1 . Но это для тех, кому трудно освоить алгоритм нахождения наибольшего или наименьшего значения функции на отрезке.

Пример 2.

Най­ди­те точку мак­си­му­ма функ­ции y=ln(x+4)^2+2x+7

В этом примере под знаком логарифма стоит выражение в квадрате. Выражение в четной степени больше нуля, если основание степени не равно нулю, поэтому область допустимых значений этой функции x<>-4. Если бы мы решили вынести показатель степени за знак логарифма, то получили бы такое выражение:

y=2ln{delim{|}{x+4}{|}}+2x+7

При вынесении четной степени не забываем ставить модуль! Если бы мы забыли поставить знак модуля, то сузили бы область определения функции.

Далее, чтобы взять производную, нам пришлось бы раскрыть модуль, а для этого рассмотреть два промежутка: x>-4 и x<-4. Но поскольку в школе практически не рассматривают нахождение производной от функции с модулем, мы не будем выносить показатель степени за знак производной, а найдем производную сложной функции:

y=ln(x^2+8x+16)+2x+7

y{prime}={1/{x^2+8x+16}}*(x^2+8x+16){prime}+2={2x+8}/{x^2+8x+16}+2={2(x+4)}/{(x+4)^2}+2=2/{x+4}+2

Найдем нули производной:

2/{x+4}+2=0

{2+2x+8}/{x+4}=0

2x+10=0

x=-5;

В точке -4 производная не определена, но меняет знак.

Исследуем знаки производной:

В точке x=-5 производная равна нулю и меняет знак с «+» на «-«, следовательно, это точка максимума функции.

Ответ: -5

Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать

Firefox

И.В. Фельдман, репетитор по математике.

Источник

Всего: 28    1–20 | 21–28

Добавить в вариант

Найдите точку максимума функции y= логарифм по основанию 2 левая круглая скобка 2 плюс 2x минус x в квадрате правая круглая скобка минус 2.

Найдите точку минимума функции y= логарифм по основанию 5 левая круглая скобка x в квадрате минус 6x плюс 12 правая круглая скобка плюс 2.

Найдите наименьшее значение функции y= логарифм по основанию 3 левая круглая скобка x в квадрате минус 6x плюс 10 правая круглая скобка плюс 2.

Найдите наибольшее значение функции y= логарифм по основанию 5 левая круглая скобка 4 минус 2x минус x в квадрате правая круглая скобка плюс 3.

Найдите точку максимума функции y= логарифм по основанию 8 левая круглая скобка минус 40 минус 14x минус x в квадрате правая круглая скобка плюс 3.

Найдите точку максимума функции y= логарифм по основанию 2 левая круглая скобка минус 21 минус 14x минус x в квадрате правая круглая скобка минус 2.

Найдите точку минимума функции y= логарифм по основанию 5 левая круглая скобка x в квадрате минус 30x плюс 249 правая круглая скобка плюс 8.

Найдите точку минимума функции y= логарифм по основанию 9 левая круглая скобка x в квадрате минус 30x плюс 230 правая круглая скобка плюс 5.

Найдите наименьшее значение функции y= логарифм по основанию 4 левая круглая скобка x в квадрате плюс 14x плюс 305 правая круглая скобка плюс 9.

Найдите наименьшее значение функции y= логарифм по основанию 3 левая круглая скобка x в квадрате плюс 14x плюс 130 правая круглая скобка плюс 3.

Найдите наибольшее значение функции y= логарифм по основанию 8 левая круглая скобка 4 минус 4x минус x в квадрате правая круглая скобка плюс 8.

Найдите наибольшее значение функции y= логарифм по основанию 5 левая круглая скобка минус 116 плюс 22x минус x в квадрате правая круглая скобка минус 8.

Найдите точку максимума функции y = логарифм по основанию 3 левая круглая скобка 11 плюс 4x минус x в квадрате правая круглая скобка минус 2.

Найдите наибольшее значение функцииy= логарифм по основанию левая круглая скобка дробь: числитель: 1, знаменатель: 4 конец дроби правая круглая скобка левая круглая скобка x в квадрате плюс 4x плюс 8 правая круглая скобка .

Найдите наибольшее значение функции y= логарифм по основанию левая круглая скобка дробь: числитель: 1, знаменатель: 3 конец дроби правая круглая скобка левая круглая скобка x в квадрате плюс 6x плюс 12 правая круглая скобка на отрезке левая квадратная скобка минус 19; минус 1 правая квадратная скобка .

Всего: 28    1–20 | 21–28

Источник

  Функции с логарифмами (наибольшее и наименьшее значение). В этой статье речь пойдёт о задачах на нахождение  наибольшего и наименьшего значения функции. Рассмотрим задачи с логарифмами. Задания связанные с исследованием функции разнообразны. Кроме логарифмических функций рассматриваются: функции с числом е, с тригонометрическими функциями, дробно-рациональные функции и прочие.

В любом случае рекомендую ещё раз просмотреть теорию изложенную в статье «Исследование функций. Это нужно знать». Если вы этот материал поняли и имеете хороший навык нахождения производных, то любую задачу в этой теме решите без труда.

Напомню алгоритм нахождения наибольшего или наименьшего значения функции на заданном отрезке:

1. Вычисляем производную.

2. Приравниваем её к нулю и решаем уравнение.

3. Определяем принадлежат ли полученные корни (нули производной) данному отрезку. Отмечаем те, которые принадлежат.

4. Вычисляем значения функции на границах отрезка и в точках (полученных в предыдущем пункте) принадлежащих данному отрезку.

*В некоторых случаях удобно обойтись без п.4. Достаточно определить убывание (возрастание) функции чтобы найти точку максимума (минимума) и далее вычислить наименьшее (наибольшее) значение.

Найдите наименьшее значение функции у=5х–ln (х+5)5  на отрезке [–4,5;0].

Необходимо вычислить значение функции на концах интервала, и в точках экстремума, если таковые имеются на данном интервале, и выбрать наименьшее из них.

Вычисляем производную, приравниваем её к нулю, решаем уравнение.

Производная функции:Нахождение наибольшего или наименьшего значения на отрезке.

Найдем нули производной:

*Дробь равна нулю тогда, когда числитель равен нулю.

Точка  х= – 4  принадлежит заданному интервалу. 

Таким образом, вычисляем значение функции в точках: – 4,5; – 4; 0.

Значения с логарифмами, которые мы получили, вычислить (или проанализировать) можно. НО! На это уйдет драгоценное время

Вычислять их не обязательно. Почему? Мы знаем, что ответом должно быть либо, целое число, либо конечная десятичная дробь. А значения с логарифмами:  – 22,5 – ln 0,55  и   – ln3125  такого ответа не дадут.

Кроме того, убедится в том, что в точке х=–4 функция приобретает минимальное значение, можно определив знаки производной на интервалах от (– 5:– 4) и (– 4;+∞). 

Теперь информация для тех, у кого с производной и пониманием того, как решать подобные задачи, нет вообще никаких трудностей. Как можно обойтись без вычисления производной и без лишних расчётов?

Итак, если учесть, что ответом должно быть целое число, либо конечная десятичная дробь, то такое значение мы можем получить только тогда, когда х будет являться целым числом, либо целым с конечной десятичной дробью и при этом под знаком логарифма в скобках у нас получится единица или число е. В противном случае, мы не сможем получить оговоренное значение. А это возможно только при  х = – 4.

Значит именно в этой точке значение функции будет наименьшим, вычислим его:

Ответ: – 20

Решить самостоятельно:  

Найдите наименьшее значение функции у=3х– ln (х+3)3 на отрезке [–2,5;0].

Посмотреть решение

Найдите наибольшее значение функции у=ln (х+5)5–5х  на отрезке [–4,5;0].

Посмотреть решение

Найдите наибольшее значение функции у=х2–13х+11∙lnх+12 на отрезке [13/14; 15/14]. 

Чтобы найти наименьшее значение функции на отрезке, необходимо вычислить значение функции на его концах, и в точках экстремума, если таковые имеются на данном интервале.

Вычислим производную, приравниваем её к нулю, решим полученное уравнение:

Решив квадратное уравнение,  получим

Точка  х = 1, принадлежит заданному интервалу.

Точка  х = 22/4 ему не принадлежит.

Таким образом, вычисляем значение функции в точках:

Мы знаем, что ответом является целое число либо конечная десятичная дробь, значит наибольшее значение функции равно 0. В первом и третьем случае такое значение мы не получим, так как натуральный логарифм данных дробей  такого результата не даст.

Кроме того, убедится в том, что в точке х = 1 функция приобретает максимальное значение, можно определив знаки производной на интервалах от (0:1) и (1;+∞). 

Как решить такой тип задач без вычисления производной?

Если учесть, что ответом должно быть целое число, либо конечная десятичная дробь, то это условие обеспечивается только тогда, когда х будет являться целым числом, либо целым с конечной десятичной дробью и при этом под знаком логарифма у нас будет единица или число е.

Это возможно только при  х = 1. Значит в точке х=1 (или 14/14) значение функции будет наибольшим, вычислим его:

Ответ: 0

Решите самостоятельно:

Найдите наибольшее значение функции  у = 2х2–13х+9∙lnх+8 на отрезке [13/14; 15/14]. 

Посмотреть решение

Отмечу, что способ решения таких заданий без нахождения производных, можно использовать только для экономии времени при вычислении задания на самом экзамене. И только в том случае, когда вы отлично понимаете, как решать такие задачи через нахождение производной (по алгоритму) и хорошо умеете это делать. Бесспорно, что при решении без вычисления производной должен быть некоторый опыт в аналитике.

«Хитрых» приёмов, которые порой помогают в конкретных заданиях множество, и все их не запомнить. Важно понимать принципы решения, свойства. Если же вы возложите свои надежды на какой-то приём, то он может просто не сработать по простой причине: вы его забудете или вам попадёт такой тип задания,  который вы видите впервые.

В данной рубрике продолжим рассматривать задачи, не пропустите! 

На этом всё. Успехов Вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

22 февраля 2012

Вообще говоря, для решения задачи B15 с логарифмом надо знать две формулы:

Производная натурального логарифма

Первая формула — классическая производная натурального логарифма, вторая — производная сложной функции. Обратите внимание: в числителе стоит число k, это не опечатка.

Добавьте к этим формулам стандартные правила вычисления производных — и задача B15 решена:

(f ± g) ’ = f ’ ± g ’;
(c · f) ’ = c · f ’, c ∈ R.

В настоящих задачах логарифмы никогда не встречаются сами по себе. Поэтому обязательно приводите всю производную к общему знаменателю. Почему это важно, узнаете из примеров.

Задача. Найдите наименьшее значение функции на отрезке [0,5; 4]:

y = 2x2 − 4 ln x + 5

Находим производную:

Производная логарифмической функции

Выясняем, когда производная равна к нулю. Дробь равна нулю, когда ее числитель равен нулю. Имеем:

4(x2 − 1) = 0;
x2 = 1;
x = ±1.

Корень x = −1 не принадлежит отрезку [0,5; 4], поэтому нас интересует только x = 1. Кроме того, рассмотрим концы отрезка — числа 0,5 и 4. Итого три числа: 0,5; 1; 4. Поскольку требуется найти наименьшее значение функции, подставляем эти числа в исходную функцию:

y (0,5) = 2 · 0,52 − 4 ln 0,5 + 5 = 0,5 − 4 ln 0,5 + 5 = 5,5 − 4 ln 0,5;
y (1) = 2 · 12 − 4 ln 1 + 5 = 2 − 0 + 5 = 7;
y (4) = 2 · 42 − 4 ln 4 + 5 = 32 − 4 ln 4 + 5 = 37 − 4 ln 4.

В общем, выбирать особо не из чего. Ответ: 7. Потому что числа 5,5 − 4ln 0,5 и 37 − 4ln 4 иррациональны, их нельзя записать в виде конечной десятичной дроби.

Задача. Найдите точку минимума функции:

y = 2x − 5 ln (x − 7) + 3

Снова считаем производную:

Производная еще одной логарифмической функции

Под логарифмом стоит линейная функция y = x − 7. Коэффициент при переменной x равен k = 1, поэтому в числителе никаких дополнительных множителей не возникнет — только множитель 5, который стоит перед логарифмом.

Поскольку требуется найти точку минимума, считаем нули числителя и знаменателя:

2x − 19 ⇒ x = 19 : 2 = 9,5;
x − 7 = 0 ⇒ x = 7.

Отмечаем эти точки на прямой, расставляем знаки производной между точками:

Знаки производной на числовой прямой

Итак, в точке x = 9,5 производная меняет знак с минуса на плюс, если считать слева — направо, в направлении стрелки. Это и есть точка минимума.

Задача. Найдите наибольшее значение функции на отрезке [−1,5; 1]:

y = 3 ln (x + 2) − 3x + 10

Считаем производную:

Производная сложной логарифмической функции

Находим нули числителя:

−3x − 3 = 0;
x = −1.

Нули знаменателя нас не интересуют, поскольку требуется найти значение функции. А когда знаменатель равен нулю, значение функции не определено.

Поскольку корень x = −1 ∈ [−1,5; 1], получаем три точки: −1,5; −1; 1. Подставляем их в исходную функцию:

y (−1,5) = 3 ln (−1,5 + 2) − 3 · (−1,5) + 10 = 3 ln 0,5 + 14,5;
y (−1) = 3 ln (−1 + 2) − 3 · (−1) + 10 = 3 ln 1 + 13 = 0 + 13 = 13;
y (1) = 3 ln (1 + 2) − 3 · 1 + 10 = 3 ln 3 + 7.

Понятно, что числа 3 ln 0,5 + 14,5 и 3 ln 3 + 7 нельзя записать в ответ. Остается только число 13 — это и будет наибольшее значение.

Вынесение степени за знак логарифма

Еще одна полезная фишка, которая избавит вас от сложных производных:

ln (f (x))k = k · ln f (x)

Обратите внимание: в первом случае внутри логарифма стоит степень, для которой потребуется производная сложной функции. Во втором случае все намного проще, поскольку чаще всего f (x) — это обычная линейная функция.

Этот прием часто встречается в задачах на вычисление максимального и минимального значения. В задачах на точки экстремума его почти не применяют. Прежде чем решать такую задачу, обязательно найдите ОДЗ логарифма. Если забыли, что это такое, см. «Что такое логарифм».

Задача. Найдите наименьшее значение функции на отрезке [−4; 1]:

y = 5x − ln (x + 5)5

Итак, область допустимых значений логарифма — аргумент должен быть больше нуля. Имеем:

(x + 5)5 > 0;
x + 5 > 0;
x > −5;
x ∈ (−5; +∞).

Теперь решаем задачу. Сначала немного преобразуем исходное выражение:

y = 5x − 5 ln (x + 5)

Это и есть вынесение степени за знак логарифма. Считаем производную:

Снова производная логарифмической функции

Дальше все стандартно. Нас интересует значение функции, поэтому приравниваем числитель к нулю:

5x + 20 = 0;
x = −4.

Полученное число x = −4 ∈ [−4; 1] совпадает с концом отрезка, поэтому кандидатов на наименьшее значение всего два: −4 и 1. Оба числа подходят по ОДЗ. Поскольку требуется найти наименьшее значение, подставляем эти числа в исходную функцию:

y (−4) = 5 · (−4) − 5 · ln (−4 + 5) = −20 − 5 · ln 1 = −20;
y (1) = 5 · 1 − 5 · ln (1 + 5) = 5 − 5 ln 6.

Второе число — точно не ответ, поскольку его нельзя представить в виде десятичного числа. Значит, наименьшее значение функции равно −20.

Задача. Найдите точку максимума функции:

y = 18 ln x − x2 + 5

ОДЗ логарифма: x > 0 ⇒ x ∈ (0; +∞). Считаем производную:

Последняя производная логарифмической функции

Поскольку требуется найти точку максимума, нас интересует и числитель, и знаменатель. Приравниваем их к нулю:

2 · (9 − x2) = 0 ⇒ x2 = 9 ⇒ x = ±3 — числитель;
x = 0 — знаменатель.

Получили три точки. Отмечаем эти точки и знаки производной на числовой прямой:

Знаки производной: 3 корня

Требуется найти точку максимума — там, где плюс меняется на минус. Таких точек две: x = −3 и x = 3. Но вспомним ОДЗ: x ∈ (0; +∞). Значит, точка x = −3 не подходит. Остается точка x = 3 — это и будет ответ.

Смотрите также:

  1. Показательные функции в задаче B15
  2. Задача B15: частный случай при работе с квадратичной функцией
  3. Решение ЕГЭ-2011: вариант 1, часть B
  4. Как решать задачи B15 без производных
  5. Как быстро запомнить таблицу синусов и косинусов
  6. ЕГЭ 2022, задание 6. Касательная к графику функции
Источник

Нахождение
наибольшего значения логарифмической  функции.

Краткая
теоретическая часть

Рассмотрим,
как производная используется для нахождения  наибольшего  и наименьшего
значения функции  на отрезке. Наибольшее и наименьшее значение непрерывной
функции на отрезке может быть как на концах отрезка, так и внутри него. ( в
отличие от  экстремумов функции, которые на концах промежутка не могут быть).
Если наибольшее или наименьшее значение достигается внутри отрезка, то это
только в стационарных точках (где производная равна нулю)  или в
критических ( где производная не существует). Будем их называть
одним словом «Критические».

        Алгоритм нахождения
наибольшего и наименьшего значения функции  y
= f(x)
на отрезке [a;b]

1.  Найти
производную f  ´(x).

2.  Найти
стационарные и критические точки  (приравнять производную к нулю, то есть

найти  f 
´(x)=0).

3.   Из
полученных точек выбрать те, которые попадают в заданный  по  условию отрезок.

4.  Вычислить
значение функции в выбранных точках и на концах промежутка.

5.   Из
полученных чисел выбрать самое наибольшее Унаиб
или самое наименьшее Унаим.

           Самостоятельная
работа.

Вариант
1.

1.    Найдите наибольшее
значение функции y~=~ln {{(x+5)}^{5}}-5x

на отрезке [-4,5;0].

 2.Найдите
наибольшее значение функции y~=~ln {{(x+4)}^{9}}-9x

на
отрезке [-3,5;0].

3. Найдите
наибольшее значение функции y~=~8ln (x+7)-8x+3 на отрезке [-6,5;0].

4.
Найдите наибольшее значение функции y~=~ln (4x)-4x+9  

на
отрезке [frac{1}{8};frac{5}{8}].

5.
Найдите наибольшее значение функции y~=~ln (11x)-11x+9  

на
отрезке [frac{1}{22};frac{5}{22}].

6.
Найдите наибольшее значение функции y~=~2x^2-10x+6ln x+5на отрезке [frac{10}{11};frac{12}{11}].

7.
Найдите наибольшее значение функции y=log_8(4-4x-x^2)+8.

8.
Найдите наибольшее значение функции y=log_2(-17+10x-x^2)+7.

                                                                    Вариант
2.

1.    Найдите наибольшее
значение функции y~=~ln {{(x+5)}^{7}}-7x

   
на отрезке [-4,5;0].

2.    Найдите наибольшее
значение функции y~=~ln {{(x+4)}^{5}}-5x

   
на отрезке [-3,5;0].

   3.
Найдите наибольшее значение функции y~=~6ln (x+6)-6x+5        на
отрезке [-5,5;0].

 
4. Найдите наибольшее значение функции y~=~ln (5x)-5x+11

  
на отрезке [frac{1}{10};frac{1}{2}].

 5.Найдите
наибольшее значение функции y~=~ln (2x)-2x+11

  
на отрезке [frac{1}{4};frac{5}{4}].

 6.
Найдите наибольшее значение функции y~=~x^2-7x+5ln x-12     на отрезке
[frac{7}{8};frac{9}{8}].

 7.
Найдите наибольшее значение функции y=log_3(242-2x-x^2)+3.

8.
Найдите наибольшее значение функции y=log_5(-39+16x-x^2)+2

                            Вариант 3.

 
1.Найдите наибольшее значение функции y~=~ln {{(x+5)}^{3}}-3x

  
на отрезке [-4,5;0].

  
2. Найдите наибольшее значение функции y~=~ln {{(x+3)}^{9}}-9x

  
на отрезке [-2,5;0].

3.    Найдите наибольшее
значение функции y~=~4ln (x+6)-4x+3

на отрезке [-5,5;0].

4.   
Найдите
наибольшее значение функции y~=~ln (10x)-10x+5

на
отрезке [frac{1}{20};frac{1}{4}].

5.   
Найдите
наибольшее значение функции y = ln (7x)-7x+16

на
отрезке [frac{1}{14};frac{5}{14}].

6.   
Найдите
наибольшее значение функции y~=~x^2-5x+3ln x-4   

на
отрезке [frac{5}{6};frac{7}{6}].

7.
Найдите наибольшее значение функции y=log_8(503-6x-x^2)-3.

8.
Найдите наибольшее значение функции y=log_2(-17+10x-x^2)+7

                                Вариант 4

 
1.Найдите наибольшее значение функции y = ln {{(x+15)}^{12}}-12x 

  
на отрезке [-14,5;0].

2.    Найдите наибольшее
значение функции y~=~ln {{(x+7)}^{2}}-2x

на отрезке [-6,5;0].

3.    Найдите наибольшее
значение функцииy~=~8ln (x+7)-8x+10 

 на отрезке [-6,5;0].

4.    Найдите наибольшее
значение функции y = ln (2x)-2x+8

на отрезке [frac{1}{4};frac{5}{4}].

5.    Найдите наибольшее
значение функции y = ln (6x)-6x+18

на отрезке [frac{1}{12};frac{5}{12}].

6.    Найдите наибольшее
значение функции y=log_3(-198-30x-x^2)+2.

7.    Найдите наибольшее
значение функции y~=~x^2-8x+6ln x+5

на
отрезке [frac{8}{9};frac{10}{9}].

 8.Найдите
наибольшее значение функции y=log_7(-74+18x-x^2)-1 

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти корни у неравенств
  • Как найти заказчиков на перевод
  • Как найти посылку по трек номеру казахстан
  • Мышка быстро кликается как исправить
  • Как найти телефон службы поддержки авито