Общая информация
Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.
Для решения такого типа задач необходим определенный «багаж» знаний, поскольку без него вообще не обойтись. В его состав входят следующие элементы:
- Нахождение области определения функции (ОДФ).
- Понятие дифференциала и основные методы его нахождения.
- Умение решать уравнения.
- Знание графиков простых функций.
- Основные типы функций, полуинтервал и интервал.
Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.
Область определения
Область определения какой-либо функции вида y = f(x) — область значений аргумента, при которых она существует. У каждой функции существует два типа неизвестных: зависимые и независимые. К первым следует отнести переменную y, которая зависит от независимой переменной «х». Необходимо отметить, что бывают функции, в которых нет аргумента. Примером их считается функция вида y = const, где const — константа (любое число).
Область определения обозначается в теории литерой «D». Однако обозначение можно менять, когда исследуются несколько функций. Чтобы не путаться, специалисты рекомендуют следующую запись D(f(x)). Например, для y = x^2 — 27x и y = 12sinx ОДФ записывается таким образом: D(x^2 — 27x) и D(12sinx) соответственно.
Обозначение интервалов
Результатом решения задач на нахождение ОДЗ является определенный интервал. Важно правильно его обозначать, поскольку это существенно влияет на решение. Нужно руководствоваться следующими правилами:
- Жесткая граница обозначается квадратной скобкой «[» или «]». Она обозначает, что число входит включительно в этот интервал. Можно использовать не только одну скобку, но и две одновременно.
- Для обозначения числового значения, которое не входит в промежуток, пользуются круглыми скобками «(» и «)». Их можно применять одновременно.
- Типы границ можно комбинировать.
- Если нужно объединить интервалы, то следует использовать символ «U».
Очень важно правильно читать интервалы. Например, запись (1;4) читается следующим образом: переменная принимает значения, которые находятся в интервале от 1 не включительно до 4 не включительно. Это числа 2 и 3, поскольку 1 и 4 не входят в промежуток. Запись вида [5;10) читается таким образом: некоторое значение принадлежит интервалу от 5 включительно, до 10 не включительно.
Зависимость от типа
Функции различаются между собой. От этого и зависит нахождение их области определения. Они бывают простыми и сложными. Первые состоят из единичных элементов, а сложные включают в себя несколько типов. Их еще называют составными. Простые классифицируются на три вида:
- Алгебраические: рациональные и иррациональные.
- Тригонометрические: sin, cos, tg и ctg.
- Трансцендентные: степенные, показательные и логарифмические.
Рациональные бывают целыми и дробными. Они не включают в себя выражения, содержащие такие элементы: корень, степень, логарифм и тригонометрические функции. D(f) этих функций — все действительные числа (Z). Если она является дробной, то это означает, что в ее числителе и (или) знаменателе находится аргумент, значение которого не должно обращать ее в пустое множество.
Когда под корнем находится выражение, содержащее независимую переменную, то она называется иррациональной. В этом случае D(f) — множество Z, кроме тех, которые превращают выражение под корнем четной степени в отрицательное значение. Функция, представленная степенными выражениями, имеет D(f) = Z, но только тогда, когда значение аргумента не превращает функцию в пустое множество.
Метод нахождения
Для решения любой задачи нужно применять определенные правила. Они называются алгоритмом. Для каждого типа функций существует конкретный вариант решения. Для дробной он является следующим:
- Найти корни уравнения знаменателя, приравнивая его к 0.
- Определить интервал, значения из которого может принимать аргумент.
В случае, когда выражение является иррациональной функцией, корень которой является четным, следует решать не уравнение, а неравенство. Его значение не должно быть меньше 0. Для логарифмического типа выражение натурального логарифма (ln) должно быть всегда больше 0.
Для sin(x) и cos(x) областью определения является множество значений Z. Однако для tg(x) и ctg(x) следует помнить, что аргумент не должен принимать значение x = (Pi / 2) + Pi * k и x = Pi * k соответственно. Следует отметить, что коэффициент k принадлежит множеству чисел Z.
Для примера нужно разобрать задачу, в которой следует найти D(3x / [(x — 1) * (x + 1) * (10 — x)^(1/2)]). Решать ее необходимо по такому алгоритму:
- Знаменатель является сложным. Он состоит из двух выражений: (x — 1) * (x + 1) и (10 — x)^(1/2).
- Первое выражение (решить уравнение): (x — 1) * (x + 1) = 0. Оно имеет два корня: x1 = -1 и x2 = 1. Числовой промежуток: (-бесконечность;-1) U (1;+бесконечность).
- Второе (неравенство): (10 — x) < 0. Интервал: (-бесконечность;10].
- Результат (объединение всех интервалов): (-бесконечность;-1) U (1;10].
Данный пример показывает особенность решения задачи, которая заключается в объединении двух алгоритмов. Это довольно часто практикуется. Результат — объединение трех множеств, при объединении которых получается два интервала.
Сведения о производных
Производная — скоростное изменение какой-либо функции. Эта характеристика присуща не всем, поскольку некоторые из них являются постоянными. Если она имеет производную в некоторой точке, то является дифференцируемой. Дифференцирование применяется не только для исследования функций, но и во многих отраслях науки и техники.
Для нахождения дифференциалов необходима таблица производных. Кроме того, следует освоить все основные правила, поскольку не во всех случаях функция соответствует одному из табличных значений. Для этого нужно воспользоваться некоторыми свойствами. Математики-специалисты рекомендуют применять на начальных стадиях обучения алгоритм нахождения производной, который позволяет существенно сократить время выполнения задания, а также количество ошибок.
Таблица дифференциалов
В некоторых простых задачах возникает необходимость определить производную некоторой элементарной функции. Для этих целей применяется специальная таблица, в которой записаны основные простые выражения.
Данные значения были получены практическим методом — нахождением отношения приращения функции к приращению аргумента. Необходимо учитывать, что последний стремится к нулевому значению.
Однако иногда приходится упрощать выражение, а потом находить его производную. Для этого существует специальный простой алгоритм:
- Выполнить математические преобразования (упростить выражение).
- Найти производную по таблице.
Данный алгоритм справедлив только для простых выражений. Для сложных функций нужно руководствоваться некоторыми свойствами.
Основные свойства
Когда выражение не совпадает с табличным значением или состоит из нескольких элементов, то нужно применять специальные правила. Ими являются следствия из доказательств различных теорем. К ним можно отнести следующие:
- Если константа A (в некоторых источниках «С»), то при дифференцировании ее можно выносить за знак производной: (A * f(x))’ = A(f(x))’.
- Дифференциал суммы или разности 2 и более функций эквивалентен дифференциалу каждой из них: (w(x) + z(x))’ = w'(x) + z'(x) и (w(x) — z(x))’ = w'(x) — z'(x).
- Производная произведения 2 функций соответствует сумме, которая является произведением каждой из них на дифференциал другой: (w(x) * z(x))’ = (w'(x) * z(x) + w(x) * z'(x).
- Если нужно взять производную дробной функции вида w(x) / z(x), то результат действия является дробью, числитель которой равен разности произведений дифференциала числителя на знаменатель, и дифференциала знаменателя, умноженного на числитель. Знаменатель результирующей дроби соответствует знаменателю исходной функции, возведенного в квадрат: (w(x) / z(x))’ = [(w'(x) * z(x) — w(x) * z'(x)] / (z(x))^2.
В некоторых случаях функция является сложной. Для нахождения ее дифференциала нужно разбить ее на составные функции. Затем взять отдельно производную каждого из элементов. Результат — произведение дифференциалов всех элементов. Например, нужно найти дифференциал z = (1/8 * sin (4x^4 — 3x^3 + 6). Алгоритм решения следующий:
- По правилу нужно вынести константу, равную 1/8.
- Состоит из 2 частей: sin и (4x^4 — 3x^3 + 6).
- Производная последней — дифференциал разности (2 свойство): [4x^4 — 3x^3 + 6]’ = ((4 * x^3) / 4) — ((3 * x^2) / 3) + 0 = x^3 — x^2.
- Для второй: (sinx)’ = cosx.
- Итоговый результат: z’ = (1/8) * (x^3 — x^2) * sin (4x^4 — 3x^3 + 6).
Очень важно уметь разбивать выражение на части, поскольку от этого зависит результат решения. В некоторых случаях выражение можно упростить.
Наибольшее и наименьшее значения
Задачи на нахождения максимума и минимума применяются не только в математике, но и в бизнесе, науке, производстве и т. д. Например, вычисление наименьшего значения функции на отрезке (за последний промежуток времени) позволяет узнать минимизацию издержек производства. Кроме того, можно определить максимальную прибыль, найти оптимальную загрузку техники и т. д. Данные значения следует искать на каких-либо интервалах. Они классифицируются следующим образом:
- Отрезок: [a;b].
- Открытый тип: (a;b), (a;b] и [a;b).
- Промежуток бесконечности (в некоторой литературе обозначается «inf»): (-бесконечность;а], (-inf;а), [a;+inf), (a;+inf) и (-inf;+inf).
Следует отметить, что наибольшее и наименьшее значение производной по графику функции можно также найти, однако расчетный метод намного проще.
Универсальный алгоритм
Для данной операции, как и для других математических действий, существуют определенные правила или последовательность действий, которые называются алгоритмом. Специалисты для решения различных задач в любых сферах рекомендуют использовать их. Они позволяют не только существенно экономить время, минимизируя количество вычислений, но и с их помощью можно избежать некоторых ошибок. Суть алгоритма очень проста. Он состоит из определенной последовательности таких шагов:
- Найти D(f(x)).
- Проверить вхождение заданного интервала.
- Взять производную и выполнить поиск всех точек, в которых она не существует (их может и не быть).
- Приравнять к нулю результат, полученный в пункте 4, и найти корни уравнения. Это и будут стационарные точки, но они могут не существовать.
- Подставить в исходную функцию значения границ и стационарные точки.
- Выбрать из них MAX(f(x)) и MIN(f(x)).
Выполнение шестого шага зависит от вида интервала. В некоторых случаях можно просто подставить значение, а в других — найти предел. Если указана скобка «[» или «]», то x равен значению возле этой скобки. Когда указаны круглые скобки, нужно брать предел x = lim (f(x)), где x стремится к числовому значению или бесконечности, которые находятся возле скобки (x->a). Например, (a;+inf): х = lim [f(x)], где x->a и x->+inf.
Для нахождения минимального и максимального значения функции достаточно материала, изложенного выше. Специалисты рекомендуют разобраться с теорией, а затем переходить к практике.
Примеры решений
Дана квадратичная функция y = x^2 + 6x + 9. Необходимо найти наименьшее значение функции квадратного уравнения на отрезке [1;5]. Для этой цели нужно воспользоваться алгоритмом:
- D(y): все множество Z.
- Отрезок входит в D(y).
- Производная: y’ = [x^2 + 6x + 9]’ = 2x + 6 (существует во всех точках).
- Стационарные точки (y’ = 0): 2x + 6 = 0. Отсюда, x = -3.
- Подставить в исходное выражение: y(-3) = (-3)^2 + 6 * (-3) + 9 = 9 — 18 + 9 = 0, y(1) = (1)^2 + 6 * (1) + 9 = 1 + 6 + 9 = 16 и y(5) = (5)^2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.
- Максимум и минимум (с учетом стационарной точки и интервала): MIN(y) = 0 и MAX(y) = 64.
Одним из простейших типов задач является следующая: найдите наибольшее значение линейной функции z = 5x + 10 на отрезке [-3;3]. Для ее решения можно также воспользоваться алгоритмом:
- D(z) — все значения от бесконечно малого до бесконечно большого чисел.
- Промежуток, на котором нужно найти максимум и минимум, полностью входит в D(f).
- Дифференциал: z’ = 5 (существует во всех точках, а стационарных точек нет вообще).
- Минимум и максимум: MIN(z(-3)) = 5 * (-3) + 10 = -5 и MAX(z(3)) = 5 * (3) + 10 = 25.
Последнюю задачу необязательно решать по алгоритму, поскольку она считается простейшей. Математики рекомендуют тренироваться в нахождении MIN и MAX функции, поскольку только практика позволяет быстро решать задачи.
Таким образом, для нахождения максимального и минимального значений заданной функции необходимо пользоваться специальным универсальным алгоритмом. Кроме того, нужно правильно находить дифференциалы, область определения, а также разбираться в интервалах.
Дата публикации: 09 апреля 2017.
Что будем изучать:
1. Нахождение наибольшего и наименьшего значения по графику функции.
2. Нахождение наибольшего и наименьшего значения с помощью производной.
3. Алгоритм поиска наибольшего и наименьшего значения непрерывной функции y=f(x) на отрезке [a;b].
4. Наибольшее и наименьшее значение функции на незамкнутом интервале.
5. Примеры.
Нахождение наибольшего и наименьшего значения по графику функции
Ребята, мы с вами находили наибольшее и наименьшее значения функции и раньше. Мы смотрели на график функции и делали вывод, где функция достигает наибольшего значения, а где — наименьшего.
Давайте повторим:
По графику нашей функции видно, что наибольшее значение достигается в точке x= 1, оно равно 2. Наименьшее значение достигается в точке x= -1, и оно равно -2. Данным способом довольно просто находить наибольшие и наименьшие значения, но не всегда существует возможность построить график функции.
Нахождение наибольшего и наименьшего значения с помощью производной
Ребята, а как вы думаете, как с помощью производной можно найти наибольшее и наименьшее значение?
Ответ можно найти в теме экстремумы функции. Там мы с вами находили точки максимума и минимума, не правда ли термины похожи. Однако, путать наибольшее и наименьшее значение с максимум и минимум функции нельзя, это разные понятия.
Итак, давайте введем правила:
а) Если функция непрерывна на отрезке, то она достигает своего наибольшего и наименьшего значения на этом отрезке.
б) Наибольшего и наименьшего значения функция может достигать как на концах отрезках, так и внутри него.
Давайте рассмотрим этот пункт подробнее.
На рисунке а функция достигает своего наибольшего и наименьшего значения на концах отрезках [a;b].
На рисунке б функция достигает своего наибольшего и наименьшего значения внутри отрезка [a;b].
На рисунке в точка минимума находится внутри отрезка, а точка максимума — на конце отрезка, в точке b.
в) Если наибольшее и наименьшее значение достигается внутри отрезка, то только в стационарных или критических точках.
Алгоритм поиска наибольшего и наименьшего значения непрерывной функции y= f(x) на отрезке [a;b]
- Найти производную f'(x).
- Найти стационарные и критические точки внутри отрезка [a;b].
- Вычислить значение функции в стационарных и критических точках, а так же в f(a) и f(b). Выбрать наименьшее и наибольшее значения, это и будут точки наименьшего и наибольшего значения функции.
Наибольшее и наименьшее значение функции на незамкнутом интервале
Ребята, а как же искать наибольшее и наименьшее значение функции на незамкнутом интервале? Для этого воспользуемся важной теоремой, которая доказывается в курсе высшей математики.
Теорема. Пусть функция y= f(x) непрерывна на промежутке x, и имеет внутри этого промежутка единственную стационарную или критическую точку x= x0, тогда:
а) если x= x0 – точка максимума, то yнаиб.= f(x0).
б) если x= x0 – точка минимума, то yнаим.= f(x0).
Пример
Найти наибольшее и наименьшее значение функции y= $frac{x^3}{3}$ + 2x2 + 4x — 5 на отрезке
а) [-9;-1], б) [-3;3], в) [3;9].
Решение: Найдем производную: y’= x2 + 4x + 4.
Производная существует на всей области определения, тогда нам надо найти стационарные точке.
y’= 0, при x= -2.
Дальнейшие расчеты проведем для требуемых отрезков.
а) Найдем значения функции на концах отрезка и в стационарной точки.
Тогда yнаим.= -122, при x= -9; yнаиб.= y = -7$frac{1}{3}$, при x= -1.
б) Найдем значения функции на концах отрезка и в стационарной точке.
Наибольшее и наименьшее значение достигается на концах отрезка.
Тогда yнаим.= -8, при x= -3, yнаиб.= 34, при x= 3.
в) Стационарная точка не попадает на наш отрезок, найдем значения на концах отрезка.
Тогда yнаим.= 34, при x= 3, yнаиб.= 436, при x= 9.
Пример
Найти наибольшее и наименьшее значение функции y= x2 — 3x + 5 + |1-x| на отрезке [0;4].
Решение: Раскроем модуль и преобразуем нашу функцию:
y= x2 — 3x + 5 + 1 — x, при x ≤ 1.
y= x2 — 3x + 5 — 1 + x, при x ≥ 1.
Тогда наша функция примет вид:
begin{equation*}f(x)=
begin{cases}
x^2 — 4x + 6,quad приquad x ≤ 1
\
x^2 — 2x + 4,quad приquad x ≥ 1
end{cases}
end{equation*}
Найдем критические точки:
begin{equation*}f'(x)=
begin{cases}
2x — 4,quad приquad x ≤ 1
\
2x — 2,quad приquad x ≥ 1
end{cases}
end{equation*}
begin{equation*}f'(x)=0,quad приquad x=
begin{cases}
2,quad приquad x ≤ 1
\
1,quad приquad x ≥ 1
end{cases}
end{equation*}
Итак, мы имеем две стационарные точки и не будем забывать, что наша функция состоит как бы из двух функций при разных x.
Найдем наибольшее и наименьшее значения функции, для этого вычислим значения функции в стационарных точках и на концах отрезка:
Ответ: Функция достигает наименьшего значения в стационарной точке x= 1, yнаим.= 3. Функция достигает наибольшего значения на конце отрезка в точке x= 4, yнаиб.= 12.
Пример
Найти наибольшее значение функции y= $frac{3x}{x^2 + 3}$ на луче: [0;+∞).
Решение: Найдем производную нашей функции:
y’= $frac{(3x)'(x^2+3)-(x^2+3)'(3x)}{(x^2+3)^2}$= $frac{3(x^2+3)-(2x)(3x)}{(x^2+3)^2}$= $frac{3x^2+9-6x^2}{(x^2+3)^2}$= $frac{-3x^2+9}{(x^2+3)^2}$
Производная определена всюду.
Найдем стационарные точки:
y’= = $frac{-3x^2+9}{(x^2+3)^2}$ = 0
$frac{-3x^2+9}{(x^2+3)^2}$= 0
-3x2 + 9= 0
-3x2= -9
x2= 3
x= ±√3
Отрезку [0;+∞) принадлежит только точка x= √3.
Определим характер монотонности около этой точки:
Тогда x= √3 – точка максимума. Используя теорему о наибольшем и наименьшем значение функции на незамкнутом интервале, получаем, что в точке x= √3 достигается наибольшее значение.
Найдем наименьшее значение:
y(√3)= $frac{3√3}{√3^2 + 3}$= $frac{3√3}{6}$= $frac{√3}{2}$.
Ответ: yнаиб.= $frac{√3}{2}$.
Задачи для самостоятельного решения
а) Найти наибольшее и наименьшее значение функции y= x4 — 3x3 + 2x2 — 9x + 1
на отрезке а) [-3;1], б) [2;5], в) [-4;7].
б) Найти наибольшее и наименьшее значение функции y= x2 — 6x + 8 + |x — 2| на отрезке [-1;5].
в) Найти наибольшее и наименьшее значение функции y= $-2x-frac{1}{2x}$ на луче (0;+∞).
|
Департамент образования города Москвы |
|
Юго-Восточное окружное управление образования |
|
Государственное бюджетное общеобразовательное учреждение города Москвы |
|
«Школа с углубленным изучением английского языка № 1319 |
|
(ГБОУ Школа № 1319) |
«Методические рекомендации
по решению текстовых задач на нахождение наибольших и наименьших значений функций»
(для учащихся старших классов, и учителей математики средних школ)
Учитель: Рыжкова И.Г.
Квалификационная категория: высшая
Рассмотрено и утверждено на заседании
школьного методического объединения
Москва
2015 год
Учебные пособия по рассматриваемой тематике для средней школы, как правило, обладают одним из двух недостатков: приводимые в них решения задач либо излишне подробны, либо вообще отсутствуют. В данных рекомендациях, помимо подробного разбора иллюстративных примеров, предложен большой набор задач из различных областей науки и техники с краткими методическими указаниями по их решению.
Задачи на нахождение наибольшего и наименьшего значений функции относятся к числу наиболее интересных и содержательных математических задач. В основном это связано с тем, что в процессе своей деятельности люди стремятся наилучшим образом использовать различного рода ресурсы и при заданном объеме производства свести к минимуму различного вида затраты или при заданных ресурсах добиться максимального выпуска продукции. Такого вида задачи носят название оптимизационных. Общие методы решения оптимизационных задач разрабатываются в различных разделах современной математики. Простейшие же из этих задач целесообразно решать (и это предусмотрено действующими программами) как в школьном курсе математики средней школы, так и в курсе математического анализа школ с углубленным и профильным уровнем изучения предмета.
Материалы данного пособия будут полезны как при организации групповой работы в классе, так и для индивидуальной работы при отработке метапредметных понятий.
Предлагаем задачи на нахождение наибольшего и наименьшего значений функции из различных областей науки и техники (геометрии, некоторых разделов физики, биологии, экономики и др.). Для решения каждой из них следует сначала, используя условие задачи, составить функцию с указанием промежутка, на котором она определяется, а затем отыскать наибольшее (наименьшее) значение полученной функции на этом промежутке. (Тем самым мы исключаем здесь задачи на нахождение наибольшего и наименьшего значений функции, решаемые, например, геометрическими методами).
Отметим, что в зависимости от вида промежутка, на котором рассматривается непрерывная функция, методы отыскания ее наибольшего и наименьшего значений на этом промежутке, различны.
Рассмотрим наиболее часто встречаемые случаи.
I. Функция f (x) непрерывна на отрезке [a; b] и имеет на этом отрезке конечное (быть может, равное нулю) число критических точек. В этом случае для нахождения наибольшего (наименьшего) значения функции достаточно вычислить значения функции на концах отрезка и во всех критических точках и из полученных чисел выбрать наибольшее (наименьшее). Таким образом, в рассматриваемом случае для нахождения наибольшего (наименьшего) значения функции не требуется отыскивать промежутки ее монотонности.
П р и м е р: Дальность R=|OA| полета снаряда в пустоте, выпущенного с начальной скоростью 0 из орудия, наклоненного под углом γ к горизонту, вычисляется по формуле
, где g – ускорение силы тяжести. Найти угол γ , при котором дальность R будет наибольшей при данной начальной скорости
0.
Р е ш е н и е.
Найдем наибольшее значение функции R(γ)= на отрезке [0;
]. Для этого отыщем сначала критические точки функции R (γ), принадлежащие (0;
). Имеем: R‘(γ )=
. Поэтому R’(y) = 0 ↔ 2γ=
+k
↔ γ =
+
k (k є z).
Из полученных критических точек лишь одна, а именно γ =, является точкой промежутка (0;
). Осталось сравнить числа R(
), R(0) и R(
). Имеем R(
) =
, R(0) = 0 и R(
) = 0. Таким образом, Rнаиб = R(
)=
.
Ответ: y =.
II. Функция f(x) непрерывна на конечном промежутке [a; b) (или (a; b], или (a; b)), имеет на этом промежутке лишь конечное число критических точек и, наконец, функцию f(x) можно рассматривать как непрерывную и на отрезке [a; b]. Если наибольшее (наименьшее) значения функции f(x) на отрезке [a; b] достигается во внутренней точке отрезка, то наибольшее (наименьшее) значения функции f(x) на отрезке [a; b] и на исходном промежутке совпадают. Таким образом, и в этом случае для нахождения наибольшего (наименьшего) значения функции не требуется отыскивать промежутки ее монотонности.
П р и м е р. Число 26 представить в виде суммы трех положительных слагаемых, сумма квадратов которых наименьшая, если известно, что второе слагаемое втрое больше первого.
Р е ш е н и е. Обозначим неизвестные слагаемые через x, y, z. По условию задачи введенные неизвестные удовлетворяют системе уравнений: . Выразим неизвестное y и z через x. Получим y=3x, z=26-4x.
Таким образом, задача сводится к исследованию функции
S(x)= x2+9x2+(26-4x)2, или S(x)=26x2 — 208x+676.
Промежуток изменения аргумента в данном случае определяем из условия положительности всех слагаемых:
.
Итак, решение задачи сведено к нахождению наименьшего значения функции S(x) на (0;). Так как функция S(x) непрерывна и на отрезке [0;
], то рассмотрим сначала ее на этом отрезке. Имеем: S‘(x)=52x–208; S‘(x)=0
52x–208=0
x=4. Так что единственной критической точкой функции S(x) является x=4
(0;
). Осталось сравнить числа S(0)=676, S(4)=260 и S(
)=422,5.
Таким образом, наименьшее значение на отрезке [0; ] функция S(x) достигает во внутренней точке x=4 этого отрезка. Значит, число S(4)=260 является наименьшим значением функции S(x) и на промежутке (0;
).
З а м е ч а н и е. Число S(0)=676 является наибольшим значением функции S(x) на отрезке [0; ]. Однако, как легко видеть, функция S(x) на промежутке (0;
) не достигает своего наибольшего значения.
Ответ: 26=4+12+10.
III. Функция f(x) непрерывна на конечном или бесконечном промежутке (причем в случае конечного промежутка функция f(x) не может рассматриваться как непрерывная на соответствующем отрезке) и имеет на указанном промежутке конечное число критических точек. В этом случае для отыскания наибольшего (наименьшего) значения функции на указанном промежутке следует исследовать функцию на монотонность.
П р и м е р: Стоимость эксплуатации катера, плывущего со скоростью км/час, составляет 90+0,4
2 руб/час. С какой скоростью должен плыть катер, чтобы стоимость эксплуатации катера на 1 км пути была наименьшей?
Р е ш е н и е. По условию задачи стоимость эксплуатации катера, плывущего со скоростью км/час, равна 90+0,4
2 руб/час. Но за 1 час катер проплывает
км. Значит, стоимость эксплуатации катера за 1 км пути равна
(руб/км).
Таким образом, требуется определить, при каком значении функция S(
)=
принимает свое наименьшее значение на луче (0;+ ∞).
Найдем критические точки этой функции: . Производная существует в каждой точке промежутка (0; + ∞). Далее S’(
) = 0↔
+ 0,4 = 0↔
2 = 225 ↔
=15 или
=
15. Из двух найденных критических точек лишь одна, а именно
=15, принадлежит промежутку (0; + ∞).
Так как (
) < 0 на промежутке (0; 15) и
(
) > 0 на промежутке (15; + ∞), то
=15 является точкой минимума функции S(
). Наконец, так как функция S(
) убывает на (0; 15) и возрастает на (15; + ∞), то эта функция достигает своего наименьшего значения на промежутке (0; + ∞) в точке
=15.
Ответ: =15 км/час.
Часто можно найти наибольшее (наименьшее) значение функции и без использования понятия производной.
П р и м е р. Найти число, которое, в сумме со своим квадратом, дает наименьшую сумму.
Р е ш е н и е. Обозначим искомое число через х и через f(x) сумму x+x2. Таким образом, требуется определить, при каком значении x функция f(x)=x2+x принимает свое наименьшее значение на промежутке (– ∞; + ∞).
Имеем, f(x)=x2+x=(x2+x+) –
=(x+
)2 –
.
Так как (x+)2 ≥ 0 при любом значении х из промежутка (– ∞; + ∞), то f(x) ≥ —
на этом промежутке и свое наименьшее значение, равное –
, функция f(x) принимает при таком значении x, при котором (х+
)2 = 0, т.е. при х= –
. Ответ: –
.
Отметим, что при нахождении наибольшего (наименьшего) значения функции очень часто бывают полезными следующие утверждения:
А. Если функция f(x) неотрицательна на некотором промежутке, то точка, в которой она принимает свое наибольшее (наименьшее) на этом промежутке значение, совпадает с точкой, в которой принимает свое наибольшее (наименьшее) на этом же промежутке значение функция f2n(x). (Сами же наибольшее (наименьшее) значения функций f(x) и f2n(x), вообще говоря, различны).
Б. Если функция f(x) определена на некотором промежутке, то точка, в которой она принимает свое наибольшее (наименьшее) на этом промежутке значение, совпадает с точкой, в которой принимает свое наибольшее (наименьшее) на этом же промежутке значение функция f2n-1(x).
В. Если функция f(x) положительна на некотором промежутке, то точка, в которой она принимает свое наибольшее (наименьшее) на этом промежутке значение, совпадает с точкой, в которой принимает свое наименьшее (наибольшее) на этом промежутке значение функция .
З а м е ч а н и е. В каждом из сформулированных выше трех утверждений предполагается, что хотя бы одна из рассматриваемой пары функций принимает на промежутке свое наибольшее (наименьшее) значение.
В заключение отметим, что все предлагаемые ниже задачи снабжены краткими указаниями, ответами и при необходимости пояснительными рисунками. Все задачи разбиты на разделы. И хотя отнесение некоторых задач к тому или иному разделу довольно условно (например, отдельные геометрические задачи можно трактовать и как задачи экономические), все же такое деление, как нам кажется, должно оказать определенную помощь учителю (в частности, при учете индивидуальных возможностей учащихся) .
ГЕОМЕТРИЯ.
З а д а ч а №1. Найти размеры прямоугольника наибольшей площади с данным периметром Р.
Решение задачи сводится к отысканию такого значения х (и, следовательно, у = ), при котором функция S(x)= x
принимает свое наибольшее значение на промежутке (0;
).
Из равенства S(х)=x следует, что таким значением является x=
.
Ответ: х=у=.
З а д а ч а №2. Найти размеры прямоугольника с наименьшим периметром и с данной площадью S.
Решение задачи сводится к нахождению того значения х (и, следовательно, у =), при котором функция Р(х) = 2(х + у) = 2(х+
) принимает свое наименьшее значение на промежутке ( 0 ; + ∞).
Ответ: х = у =.
З а д а ч а №3. Каковы размеры прямоугольника наибольшей площади, который можно вписать в полукруг радиуса R таким образом, чтобы одна сторона прямоугольника лежала на диаметре полукруга?
Решение задачи сводится к нахождению того значения DC=x и, следовательно, CB=у=, при котором функция S(х)=ху=x
принимает свое наибольшее значение на промежутке (0; 2R). Ясно, что вместо функции S(x) целесообразно исследовать функцию f(x) = S2(x) отрезке [0; 2R].
Ответ: .
З а д а ч а №4. Найти стороны прямоугольника наибольшей площади, который можно вырезать из параболического сегмента, ограниченного осью Ох и параболой ,если известно, что одна сторона прямоугольника лежит на оси Ох (а > 0; Н > 0).
Решение задачи сводится к нахождению того значения х (и, следовательно, ), при котором функция S(x)=2x
=2Hx —
, принимает свое наибольшее значение на промежутке (0; a). Функцию S(х) целесообразно исследовать на отрезке [0; a]
Ответ: 2x=, y=
.
З а д а ч а №5. Найти высоту равнобочной трапеции наибольшей площади, которую можно вырезать из параболического сегмента, ограниченного осью Ох и параболой , если известно, что нижнее основание трапеции совпадает с основанием параболического сегмента (a>0; Н>0).
Решение задачи сводится к нахождению того значения х (и, следовательно, высоты трапеции ), при котором функция
принимает свое наибольшее значение на промежутке (0; a) . Функцию S(x) целесообразно исследовать на отрезке [0; а].
Ответ: .
З а д а ч а №6. Найти трапецию наибольшей площади, которую можно вписать в полукруг радиуса R таким образом, чтобы одно из оснований трапеции лежало на диаметре полукруга.
Решение задачи сводится к нахождению такого значения х (и, следовательно, ), при котором функция
принимает свое наибольшее значение на промежутке (0; R). Вместо исследования функции S(x) на промежутке (0; R) целесообразно исследовать функцию f(х) = S2(х) на отрезке [0; R] .
Ответ: .
З а д а ч а № 7. Сечение туннеля имеет форму прямоугольника, завершенного полукругом.
а) Зная периметр сечения 2р, выяснить, при каком радиусе полукруга площадь сечения будет наибольшей.
Решение задачи сводится к нахождению такого значения х (половина стороны прямоугольника, на которой построена окружность, соответственно, y-другая сторона), при котором функция
S(x)=Sполукр+S□= принимает свое наибольшее значение на промежутке (0;
). Функцию S(x) целесообразно исследовать на отрезке [0;
].
б) Зная площадь сечения S, выяснить, при каких условиях периметр сечения будет наименьшим.
По условию задачи, . Отсюда
.
Решение задачи сведено к нахождению такого значения х (и. следовательно ), при котором функция
принимает свое наименьшее значение на (0;
).
Ответ: а) ; б)
.
3 а д а ч а № 8. Из куска картона размером 32 см * 20 см требуется изготовить открытую сверху коробку наибольшей вместимости, вырезая по углам квадраты и затем загибая выступы для образования боковых стенок коробки. Найти объем такой коробки.
Решение задачи сводится к нахождению наибольшего значения функции V(x) = (20 – 2х)(32–2х) х на (0; 10) (x- сторона вырезаемого квадрата). Функцию V(х) целесообразно исследовать на отрезке [0; 10].
Ответ: Vнаиб=V(4)=1152 см3.
З а д а ч а № 9. Требуется изготовить коническую воронку с образующей, равной 20 см. Какова должна быть высота воронки, чтобы её объём был наибольшим?
По условию задачи, R2=l2-h2=400-h2. Поэтому Vкон=V(h)=πR2h=
(400 – h2)h. Таким образом, решение задачи сводится к нахождению такого значения h, при котором функция V(h) принимает свое наибольшее значение на промежутке (0; 20) . Целесообразно исследовать функцию V(h) на отрезке [0;20].
Ответ: h=см.
З а д а ч а №10. Каковы должны быть размеры закрытой коробки с квадратным основанием, если объем ее равен V и требуется израсходовать наименьшее количество материала?
Пусть а=b=x, с=y.
По условию задачи, х2у= V . Отсюда .
Таким образом, решение задачи сводится к нахождению такого значения х (и, следовательно, у), при котором функция
S(x) =2х2+4ху =2x2+ принимает свое наименьшее значение на бесконечном промежутке (0; + ∞).
Ответ: x=y=.
З а д а ч а №11. Из полосы жести шириной 11 см требуется сделать открытый сверху желоб, поперечное сечение которого имеет форму равнобочной трапеции. Дно желоба должно иметь ширину 7 см. Какова должна быть ширина желоба наверху, чтобы он вмещал наибольшее количество воды?
В принятых обозначениях верхнее основание поперечного сечения желоба c=7+2x, а высота желоба . Таким образом, задача сводится к нахождению такого значения х, (и, следовательно, значения с), при котором функция
принимает свое наибольшее значение на промежутке (0; 2). Целесообразно вместо функции S(x) исследовать функцию f(x)=S2(x) на отрезке [0; 2].
Ответ: c=8 см.
З а д а ч а №12. Из всех правильных треугольных призм, имеющих данный объем V, найти призму с наименьшей суммой всех ее ребер. Чему равна длина стороны основания такой призмы?
Пусть х- сторона основания призмы, H — боковое ребро.
По условию задачи, V = SоснH = . Отсюда
V. Таким образом, решение задачи сводится к отысканию такого значения х (и, следовательно, Н), при котором функция l(х) = 6х+3Н = =6х+
V принимает свое наименьшее значение на промежутке (0; + ∞).
Ответ: ;
.
З а д а ч а №13. В сферу радиуса R вписана правильная четырёхугольная пирамида. Какой должна быть высота пирамиды, чтобы ее объем был наибольшим? Чему равен этот наибольший объем?
Пусть х – сторона основания, а h – высота пирамиды. Тогда , или x2=2h(2R-h).
Таким образом, решение задачи сведено к нахождению наибольшего значения функции ) на промежутке (0; 2R). Целесообразно исследовать функцию V(h) на отрезке [0; 2R].
Ответ: Vнаиб=V.
З а д а ч а №14. а) Среди всех цилиндров данного объема V найти тот, который имеет наименьшую полную поверхность. (Иная формулировка: Консервная банка данного объема V имеет форму цилиндра. Каково должно быть отношение её высоты к диаметру основания, чтобы на изготовление банки ушло наименьшее количество материала?)
а) Пусть радиус цилиндра –r, высота –h. По условию задачи πr2h=V. Отсюда . Таким образом, решение задачи сводится к нахождению такого значения r (и, следовательно, h), при котором функция Sполн=S(r)=2πr2+2πrh=2πr2
принимает свое наименьшее значение на (0; + ∞).
б) Найти цилиндр наибольшего объема с заданной площадью S полной поверхности.
По условию задачи 2πr2+2πrh=S. Отсюда . Отметим, что из условия задачи (S>2πr2 )следует неравенство
. Таким образом, решение задачи сводится к нахождению такого значения r (и, следовательно, h), при котором функция
принимает свое наибольшее значение на промежутке (0;
). Целесообразно исследовать функцию V(r) на отрезке [0;
].
Ответ: а) h=2r, где r=;
б) h=2r, где .
З а д а ч а №15. а) Найти размеры цилиндра наибольшего объема, который можно вписать в данный шар радиуса R. Чему равен этот наибольший объем?
а) По условию задачи, h2+(2r)2=(2R)2 .0тсюда . Таким образом, решение задачи сводится к нахождению наибольшего значения функции V(h)=πr2h =π (R2h —
) на промежутке (0; 2R). Целесообразно исследовать функцию V(h) на отрезке [0; 2R].
б) Найти размеры цилиндра с наибольшей площадью боковой поверхности, который можно вписать в данный шар радиуса R. Чему равна эта наибольшая площадь боковой поверхности?
Как и выше, . Так что решение задачи сводится к нахождению наибольшего значения функции
на промежутке (0;2R). Целесообразно вместо функции S(h) исследовать функцию f(h)=S2(h) на отрезке [0; 2R].
Ответ: а)
б) .
З а д а ч а № 16. а) Найти размеры цилиндра наибольшего объёма, который можно вписать в конус с высотой h и радиусом основания r. Чему равен этот наибольший объем?
а) Так как то,
и поэтому
. Таким образом, решение задачи сводится к нахождению наибольшего значения функции V(h) на промежутке (0; h). Целесообразно исследовать V(h) на отрезке [0; h].
б) Найти размеры конуса наименьшего объема, который можно описать около цилиндра с высотой h и радиусом основания r. Чему равен этот наименьший объем?
Так как , то
и поэтому
. Таким образом, решение задачи сводится к нахождению наименьшего значения функции V(h) на луче (h; + ∞).
Ответ: а)
б) .
З а д а ч а № 17. а) Доказать, что конический шатер данной вместимости V требует наименьшего количества материи, когда его высота в раз больше радиуса основания. (Иная формулировка: найти размеры конуса с данным объёмом V и имеющим наименьшую площадь боковой поверхности).
а) По условию задачи, .Отсюда
. Кроме того,
.Таким образом, задача сведена к нахождению такого значения H, (и, следовательно, значения R), при котором функция
принимает свое наименьшее значение на промежутке (0; + ∞). Целесообразно вместо функции S(H) исследовать функцию f(H)=S2(H) на промежутке (0; + ∞).
б) Найти высоту и радиус основания конуса наибольшего объёма с данной площадью S боковой поверхности. Чему равен этот наибольший объём ?
По условию задачи πRl=S. Отсюда . Тогда
. Отметим, что из неравенства πR2<πRl =S следует неравенство
. Таким образом, решение задачи сведено к отысканию наибольшего значения функции
на промежутке (0;
). Целесообразно вместо функции V(R) исследовать функцию f(R)=V2(R) на отрезке [0;
].
Ответ: а)
б) .
ФИЗИКА.
Механика.
З а д а ч а № 18. Из пункта А, находящегося в лесу в 5 км от прямолинейной дороги, пешеходу нужно попасть в пункт В, расположенный на этой дороге на расстоянии 13 км от пункта А. По дороге пешеход может двигаться со скоростью 5 км/ч, а по лесу – 3 км/ч. За какое минимальное время пешеход сможет добраться из пункта А в пункт В?
Отметим, что |ЕВ| = 12. Решение задачи сводится к нахождению наименьшего значения функции на отрезке на отрезке [0; 12].
Ответ: 3 ч 44 м.
З а д а ч а № 19. Три пункта А, В и С расположены так, что угол ABC = 60°. Из А в В движется автомобиль со скоростью V 1 = 80 км/ч , а из В в С – поезд со скоростью V 2 = 50 км/ч. Через сколько времени расстояние между поездом и автомобилем будет наименьшим, если движение началось одновременно и |АВ|=200 км?
Пусть в момент времени t автомобиль находится в п. М, а поезд — в п. Е. Тогда |AM| = υ1t = 80t (поэтому |MB|=200 – 80t, если 0 ≤ t ≤ 200/80 = 2,5 ч) и |BE|= υ2t = 50t. По теореме косинусов,|ME|2=(200 – 80t)2+(50t)2 – 2(200 –80t)50t cos 60º=12900t2 – 42000t +40000.
Таким образом, решение задачи сведено к нахождению такого значения t, при котором функция f(t)=12900t2 – 42000t + 40000 принимает наименьшее значение на отрезке [0; 2,5].
Ответ: ч.
З а д а ч а № 20. Дождевая капля, начальная масса которой равна m0 г, а начальная скорость равна 0, падает под действием силы тяжести, равномерно испаряясь так, что убыль массы пропорциональна времени (коэффициент пропорциональности равен k г/с). Через сколько секунд после начала падения кинетическая энергия капли будет наибольшей? Чему равна наибольшая кинетическая энергия капли?
Кинетическая энергия тела, обладающего массой m и движущегося со скоростью υ, равна . По условию задачи υ = υ0 + gt = gt и m = m0 – Δm = m0 – kt. Таким образом, решение задачи сводится к нахождению наибольшего значения функции
на отрезке [0; T], где Т – некоторое постоянное число (
).
Ответ: (
).
З а д а ч а № 21. Тело массой m0 = 3000 кг падает с высоты Н = 2000 м, теряя массу (сгорает) пропорционально времени падения. Коэффициент пропорциональности к = 100 кг/с. Считая, что начальная скорость тела равна 0, ускорение свободного падения g=10 м/с2 и, пренебрегая сопротивлением воздуха, найти наибольшую кинетическую энергию тела.
См. указание к предыдущей задаче.
Ответ: Wнаиб=W(20)=108 ().
З а д а ч а № 22. Поперечное сечение бревна есть круг диаметром d. Из бревна вытесывается брус с прямоугольным поперечным сечением. Прочность бруса пропорциональна основанию и квадрату высоты. Найти размеры поперечного сечения, при котором брус имеет наибольшую прочность.
Пусть AD=x, CD=y, AC=d
По условию задачи, прочность бруса J=Kxy2. Так как x2+y2=d2, то y2=d2 – x2 и поэтому J=J(x)=K(xd2 – x3). Таким образом, решение задачи сведено к нахождению такого значения х (и, следовательно, у), при котором функция J(x) принимает свое наибольшее значение на промежутке (0; d). Целесообразно исследовать функцию J(x) на отрезке [0; d].
Ответ: .
З а д а ч а № 23. Груз весом Р, лежащий на горизонтальной поверхности, требуется сдвинуть с места приложенной силой . При каком наклоне этой силы к горизонту ее величина будет наименьшей, если коэффициент трения равен к?
Как принято, будем обозначать ||=F, |
тр|=Fтр.. и т.д. Имеем: Fх=Fтр, Fх=F cos t, Fтр=k(P – Fy)=k(P – F sin t. Поэтому F cos t=k(P – F sin t). Отсюда
. Таким образом, решение задачи сведено к нахождению такого значения t, при котором функция F(t) принимает свое наименьшее значение на промежутке (0;
).
Ответ: t = arctg k.
Электричество.
З а д а ч а № 24. Составляется электрическая цепь из двух параллельно соединенных сопротивлений. При каком соотношении между этими сопротивлениями сопротивление всей цепи максимально, если при последовательном соединении этих сопротивлений оно равно R?
Известно, что при параллельном соединении общее сопротивление цепи Rобщ связано с сопротивлениями R1=x и R2=R – x соотношением или
. Поэтому
. Таким образом, решение задачи сведено к нахождению такого значения х, при котором функция f(x) принимает свое наибольшее значение на промежутке (0; R). Из равенства
следует, что таким значением будет
.
Ответ: R1=R2=.
З а д а ч а № 25. Установлено, что энергия, отдаваемая электрическим элементом, определяется по формуле , где E – э.д.с. элемента, r – его внутреннее сопротивление, a R – внешнее сопротивление. Каким должно быть сопротивление внешней цепи, чтобы отдаваемая элементом энергия была наибольшей ?
Считая Е и r постоянными, рассмотрим как функцию аргумента R. Таким образом, решение задачи сведено к нахождению такого значения R, при котором функция
принимает свое наибольшее значение на промежутке [0; + ∞) .
Ответ:
З а д а ч а № 26. Если в электрической цепи сопротивлением R течет ток I, то количество тепла, выделяющееся в единицу времени, пропорционально I2R. Выяснить, как следует разветвить ток I на токи I1 и I2 с помощью двух проводников с сопротивлениями R1 и R2 и с тем, чтобы выделение тепла было наименьшим?
Обозначим I1=x. Тогда I2=I-x. Количество тепла, выделяющееся на рассматриваемом участке цепи, равно Q=kI12R1 + kI22R2=k(R1x2+R2(I – x)2) = Q(x). Таким образом, задача сведена к нахождению такого значения х, при котором функция Q(x) принимает свое наименьшее значение на отрезке [0; 1].
Ответ:
Оптика.
З а д а ч а № 27. При большом расстоянии от точечного источника света освещенность, получаемая от него, прямо пропорциональна интенсивности источника и обратно пропорциональна квадрату расстояния до него. Освещенность от нескольких источников равна сумме освещенностей от каждого из них. Пусть имеются два маяка на расстоянии 12 км друг от друга, причем интенсивность первого в 8 раз превосходит интенсивность второго. Какая точка отрезка, соединяющего маяки, наименее освещена?
По условию задачи, освещенность в точке М равна , где k – коэффициент пропорциональности, s– интенсивность второго источника (сила света). Таким образом, решение задачи сведено к нахождению такого значения х, при котором функция j(x) принимает свое наименьшее значение на промежутке (0; 12).
Ответ: x=4 км.
Задача № 28. В точках А и В находятся точечные источники света с силой s1 и s2 свечей. Пусть |АВ|=а. На отрезке |АВ| найти наименее освещенную точку М.
См. указания к предыдущей задаче.
Ответ:
З а д а ч а № 29. Лампа висит над центром круглого стола, радиус которого равен r. При какой высоте лампы над столом освещенность предмета, лежащего на краю стола, будет наибольшей? Освещенность прямо пропорциональна косинусу угла падения лучей и обратно пропорциональна квадрату расстояния от источника света.
Пусть х – величина угла падения лучей. По условию зада- чи, освещенность в т. А вычисляется по формуле , где k – коэффициент пропорциональности. Так как
, то j=j(x)=
. Таким образом, решение задачи сведено к нахождению такого значения х, при котором функция j(x) принимает свое наибольшее значение на промежутке (0;
). (Искомая высота лампы над столом может быть найдена, например, по формуле H=rctgx ).
Ответ: .
БИОЛОГИЯ.
З а д а ч а № 30. Реакция организма на введенное лекарство может выражаться в повышении кровяного давления, изменении температуры тела, изменении пульса или других физиологических показателях. Степень реакции зависит от назначенной дозы x лекарств. Предположим, что степень реакции у описывается функцией у = kx2(a – x), где k и a – некоторые постоянные. (Значение постоянной k зависит от индивидуума, а значение постоянной а – от вида лекарства). При каком значении х реакция максимальна?
Решение задачи сводится к нахождению такого значения х, при котором функция у принимает свое наибольшее значение на отрезке [0; a].
Ответ: .
З а д а ч а № 31. Реакция организма на два лекарства как функции от t составляют r1(t)=te-t r2(t)=t2e-t (время t выражается в часах). У какого из лекарств выше максимальная реакция? Какое из лекарств медленнее в своем воздействии?
Решение задачи сводится к нахождению и сравнению наибольших значений функций r1(t) и r2(t) на луче [0; + ∞). Отметим, что, поскольку максимальная реакция организма на 1-е лекарство наступает через час, а на 2-е – через 2 часа, то второе лекарство действует медленнее.
Ответ: r1наиб=r1(1)=e-12наиб=r2(2)=4e-2. У 2-го лекарства максимальная реакция выше, но оно действует медленнее.
З а д а ч а № 32. В питательную среду вносят популяцию из 1000 бактерий. Численность p(t) популяции возрастает следующим образом: , где время t выражается в часах. Каков наибольший размер может достичь эта популяция?
Решение задачи сводится к отысканию наибольшего значения функции p(t) на луче [0; + ∞).
Ответ: pнаиб=p(10)=1050 шт.
Задача № 33. Скорость роста у популяции задана формулой y=0,001t(100 – t), где время t выражается в днях. Через сколько дней скорость роста популяции станет максимальной?
Решение задачи сводится к нахождению такого значения t, при котором функция у принимает свое наибольшее значение на луче [0; + ∞). Из равенства
y=0,001t(100–t)=0,001(502 – (50 – t)2) следует, что функция у принимает свое наибольшее значение при t=50.
Ответ: 50 дней.
Задача № 34. Популяция бактерий изменяется от начального размера в 1000 особей до размера p(t) в момент времени t (t измеряется в днях) в следующей зависимости: . Найти скорость роста p’ (t) популяции. Когда эта скорость максимальна?
Решение задачи сводится к нахождению такого значения t, при котором функция f(t)= p’ (t) принимает свое наибольшее значение на луче [0; + ∞).
Ответ: t=ln 9; p‘наиб=p‘(ln 9) = 2500.
ЭКОНОМИКА.
З а д а ч а № 35. Стоимость бриллианта пропорциональна квадрату его массы. При обработке бриллиант был расколот на две части. Каковы размеры частей, если известно, что при этом произошла максимальная потеря стоимости?
Пусть m –масса исходного бриллианта, а х – масса одной из отколовшихся частей. Решение задачи сводится к нахождению такого значения х, при котором функция
f(x)=km2 – kx2 – k(m – x)2 достигает своего наибольшего значения на отрезке [0; m].
Ответ: x=m-x=m/2.
З а д а ч а № 36. Прямоугольный участок площадью 9000 м2 требуется огородить забором, две противоположные стороны которого каменные, а две другие – деревянные. Один погонный метр каменного забора стоит 2500 руб., а деревянного – 1000 руб. Какое наименьшее количество денег должно быть выделено на строительство этого забора?
Решение задачи сводится к нахождению наименьшего значения функции на луче (0; + ∞).
Ответ: 600000 руб.
Задача № 37. Требуется изготовить открытый цилиндрический бак данного объёма V, причем стоимость 1 кв.м. материала, из которого изготавливается дно бака равна р1 руб., а стоимость 1кв.м. материала, идущего на стенки бака, равна р2 руб. При каком отношении радиуса дна к высоте бака затраты на материал будут наименьшими?
Пусть х – радиус дна бака, а Н – его высота. По условию задачи V=πx2H. Значит , и поэтому стоимость материала, идущего на изготовление всего бака, равна
.
Таким образом, решение задачи сведено к нахождению такого значения х (и, следовательно, Н), при котором функция f(x) принимает свое наименьшее значение на луче (0; + ∞).
Ответ:
З а д а ч а № 38. а) Совхоз хочет расчистить поле в виде прямоугольного участка с присоединенным к одной из его сторон полукруглым участком. Прямоугольный участок планируется отвести под сено, дающее доход в 5 руб. на 1 м2, а полукруглый участок – под рис, дающий доход в 6руб. на 1 м2. Периметр поля должен быть равен 800 м. Как надо спланировать поле, чтобы получить наибольший доход?
б) Предположим, что участок, засеянный рисом, дает доход в 10руб. на 1 м2. Какова будет теперь форма поля?
Пусть х – радиус полукруглого участка. Тогда 2х – ширина прямоугольного участка, а – длина прямоугольного участка.
а) Решение задачи сводится к нахождению такого значения х, при котором функция достигает своего наибольшего значения на отрезке [0;
].
б) То же для функции на том же отрезке.
Ответ: а)
б)
З а д а ч а № 39. Требуется облицевать плиткой стенки и дно открытого бассейна объёмом 81 м3. Стоимость облицовки 1 м2 дна бассейна равна 9 т.руб, а 1 м2 стенки – 12 т руб. При каких размерах бассейна стоимость его облицовки будет минимальной? Чему равна эта минимальная стоимость? Предполагается, что дно бассейна – квадрат.
Пусть х – длина стороны дна бассейна, а Н – его глубина. Тогда .Так что стоимость облицовки бассейна равна:
.
Таким образом, решение задачи сведено к нахождению наименьшего значения функции f(x) на луче (0; + ∞).
Ответ: х = 6 м; H = 2,25 м; fнаим= 972 руб.
З а д а ч а № 40. а) Суточные расходы при плавании корабля состоят из двух частей: постоянной, равной с руб., и переменной, возрастающей пропорционально кубу его скорости. Коэффициент пропорциональности равен k. При какой скорости υ плавание корабля будет наиболее экономичным, т.е. общая сумма расходов на 1км пути будет наименьшей?
б) Расходы на топливо для топки судна пропорциональны кубу его скорости. Известно, что при скорости 10 км/ч они составляют 300 руб/ч; остальные расходы, не зависящие от скорости, составляют 4800 руб/ч. При какой скорости судна общая сумма расходов на 1 км пути будет наименьшей? Какова будет при этом общая сумма расходов в час?
а) Постоянные расходы составляют . Значит, общая сумма расходов за один час пути равна
руб., а общая сумма расходов на 1 км пути равна
руб. Таким образом, решение задачи сведено к нахождению такого значения υ, при котором функция
принимает свое наименьшее значение на луче (0; + ∞).
б) См. указание к п. а). Значение постоянной с определяется из равенства = 4800,а значение коэффициента k – из равенства 300 = k*103
Ответ: а) .
б) 20 км/ч; 432 руб/ч.
З а д а ч а № 41. Завод А отстоит на 60 км, считая по кратчайшему расстоянию, от железной дороги, идущей с юга на север и проходящей через город В. Под каким углом γ к железной дороге следует достроить подъездной путь от завода с тем, чтобы перевозка грузов из A в В была наиболее экономичной, если учесть, что стоимость перевозки одной тонны груза на расстояние в 1 км составляет по подъездному пути 20 руб., а по железной дороге –10 руб. и город В расположен на 120 км севернее завода А?
По условию задачи |AC|=60, |BC|=120. Обозначим |CE|=x. Тогда стоимость перевозки одной тонны груза по ломанной AEB равна . Таким образом, решение задачи сведено к нахождению такого значения х, при котором функция f(x) принимает на отрезке [0; 120] свое наименьшее значение. (Искомое же значение величины угла γ определяется условием
).
Ответ:
З а д а ч а № 42. а) Коксовая печь, работающая при температуре 500 ºС, производит 100 м3 газа в минуту. Это количество увеличивается на 0,2 м3/мин при увеличении температуры Т на 1 ºС вплоть до 750 ºС. Свыше 750 ºС повышение температуры Т на 1ºС вызывает увеличение производительности печи на 0,25 м3/мин. Эксплуатация печи в течение часа при температуре Т ºС, где Т ≥ 500 обходится в 1000+(0,1Т – 100)2 руб. Какова наиболее выгодная температура эксплуатации печи?
б) До введения усовершенствований в методах получения газа при высоких температурах количество газа, производимое описанной выше печью, возрастало лишь на 0,1 м3/мин при повышении температуры на 1 °С свыше 750 ºС. Какова была тогда наиболее выгодная температура эксплуатации печи?
а) В I мин при температуре Т ºС печь производит V(Т) м3 газа, где .
Стоимость эксплуатации печи в течение 1 мин равна: руб. Значит, стоимость производства 1 м3 газа при температуре Т ºC равна:
Таким образом, решение задачи сведено к нахождению наименьшего значения функции f(Т) на луче [500; + ∞).
б) В обозначениях п. а) имеем:
Так что, как и выше, решение задачи сведено к отысканию наименьшего значения функции f(x) на луче [500; +∞).
Ответ: а) fнаим≈f(1080)=0,082; б) fнаим≈f(1000)=0,095.
РАЗНЫЕ ЗАДАЧИ.
З а д а ч а № 43. При каком диаметре круглого отверстия в плотине расход Р воды будет иметь наибольшее значение, если, где у – диаметр отверстия, Н – глубина низшей точки отверстия и с – коэффициент пропорциональности (с и Н – постоянные)?
Решение задачи сводится к нахождению такого значения у, при котором функция
Р (у) = принимает свое наибольшее значение на отрезке [0; H].
Ответ: .
З а д а ч а № 44. Коридор шириной м пересекает второй коридор под прямым углом. По полу первого коридора тянут прямолинейный кусок трубы длиной 8 м (шириной трубы мы пренебрегаем). Какова должна быть ширина второго коридора, чтобы можно было вытащить в него трубу ?
Решение задачи сводится к нахождению наименьшего значения функции на промежутке (0;
).
Ответ:
З а д а ч а № 45. От канала шириной 2,7 м под прямым углом к нему отходит канал шириной 6,4м. Стенки каналов прямолинейны вплоть до вершины угла. Найти наибольшую длину бревна, которое можно сплавить по этим каналам из одного в другой.
Решение задачи сводится к нахождению наименьшего значения функции на промежутке (0;
).
Ответ: 12,5 м.
З а д а ч а № 46. При подготовке к экзамену студент за х дней изучает – ю часть курса и забывает
– ю часть. Сколько дней нужно затратить на подготовку, чтобы была усвоена наибольшая часть курса?
За х дней студент усваивает – ю часть курса. Таким образом, задача сведена к нахождению такого значения х, при котором функция
принимает свое наибольшее значение на луче [0; + ∞).
Ответ: 4 дня.
З а д а ч а № 47. Человек, страдающий сенной лихорадкой, обнаружил, что достигающее его количество пыльцы от данного источника (например, от леса, в котором растут нежелательные для больного деревья) прямо пропорционально интенсивности источника пыльцы (скажем, количеству этих деревьев) и обратно пропорционально расстоянию от источника. К сожалению, больной должен жить где-либо на отрезке, соединяющем два источника пыльцы, отстоящие друг от друга на расстоянии 1км. Один источник в 4 раза интенсивнее другого. Где должен поселиться человек, чтобы испытывать наименьшее неудобство?
Примечание. Сенная лихорадка – заболевание аллергического характера, вызываемое пыльцой определенного вида растений.
По условию задачи |AB| = 1. Обозначаем |AM| = x.
Тогда количество пыльцы, достигающее т. М от обоих источников А и В, равно: .
Таким образом, решение задачи сведено к нахождению такого значения х, при котором функция f(x) принимает свое наименьшее значение на промежутке (0; l) .
Ответ: км.
Как найти наибольшее и наименьшее значение функции алгоритм вычисления и нахождения наименьшего и наибольшего значения функции на отрезке, луче, промежутке, интервале
В некоторых задачах нужно найти наибольшее и наименьшее значения функции. Если неизвестен алгоритм и основные правила, то простое задание превращается в изнурительный труд, который очень редко приносит положительные результаты. В интернете существует множество информации, но не вся она достоверна. Самое страшное — применение неверных методик нахождения.
Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.
Для решения такого типа задач необходим определенный «багаж» знаний, поскольку без него вообще не обойтись. В его состав входят следующие элементы:
Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.
Область определения
Область определения какой-либо функции вида y = f(x) — область значений аргумента, при которых она существует. У каждой функции существует два типа неизвестных: зависимые и независимые. К первым следует отнести переменную y, которая зависит от независимой переменной «х». Необходимо отметить, что бывают функции, в которых нет аргумента. Примером их считается функция вида y = const, где const — константа (любое число).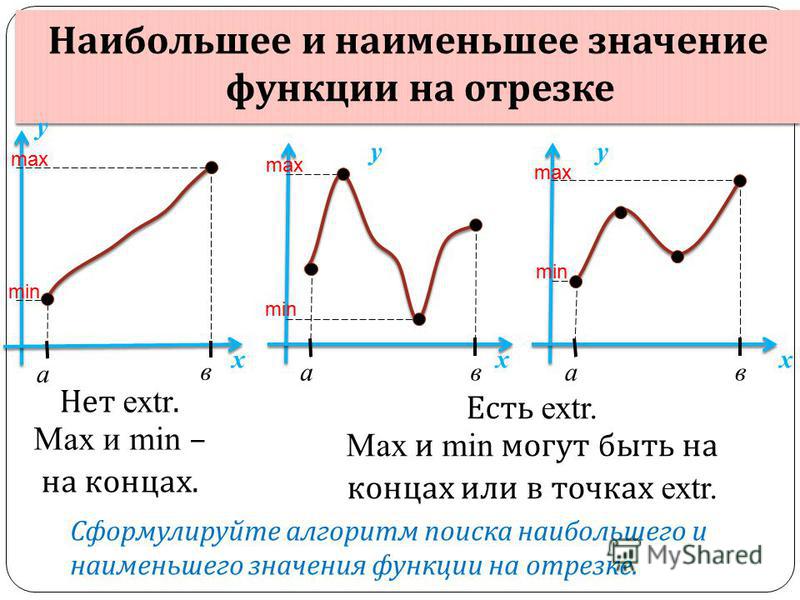
Обозначение интервалов
Результатом решения задач на нахождение ОДЗ является определенный интервал. Важно правильно его обозначать, поскольку это существенно влияет на решение. Нужно руководствоваться следующими правилами:
Очень важно правильно читать интервалы. Например, запись (1;4) читается следующим образом: переменная принимает значения, которые находятся в интервале от 1 не включительно до 4 не включительно. Это числа 2 и 3, поскольку 1 и 4 не входят в промежуток.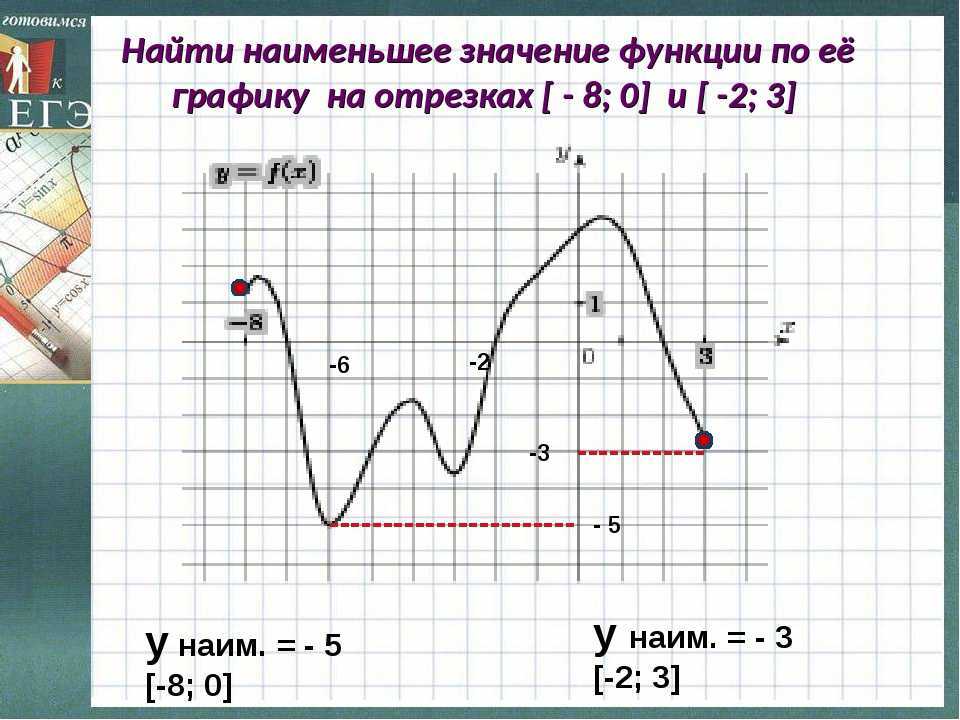
Зависимость от типа
Функции различаются между собой. От этого и зависит нахождение их области определения. Они бывают простыми и сложными. Первые состоят из единичных элементов, а сложные включают в себя несколько типов. Их еще называют составными. Простые классифицируются на три вида:
Рациональные бывают целыми и дробными. Они не включают в себя выражения, содержащие такие элементы: корень, степень, логарифм и тригонометрические функции. D(f) этих функций — все действительные числа (Z). Если она является дробной, то это означает, что в ее числителе и (или) знаменателе находится аргумент, значение которого не должно обращать ее в пустое множество.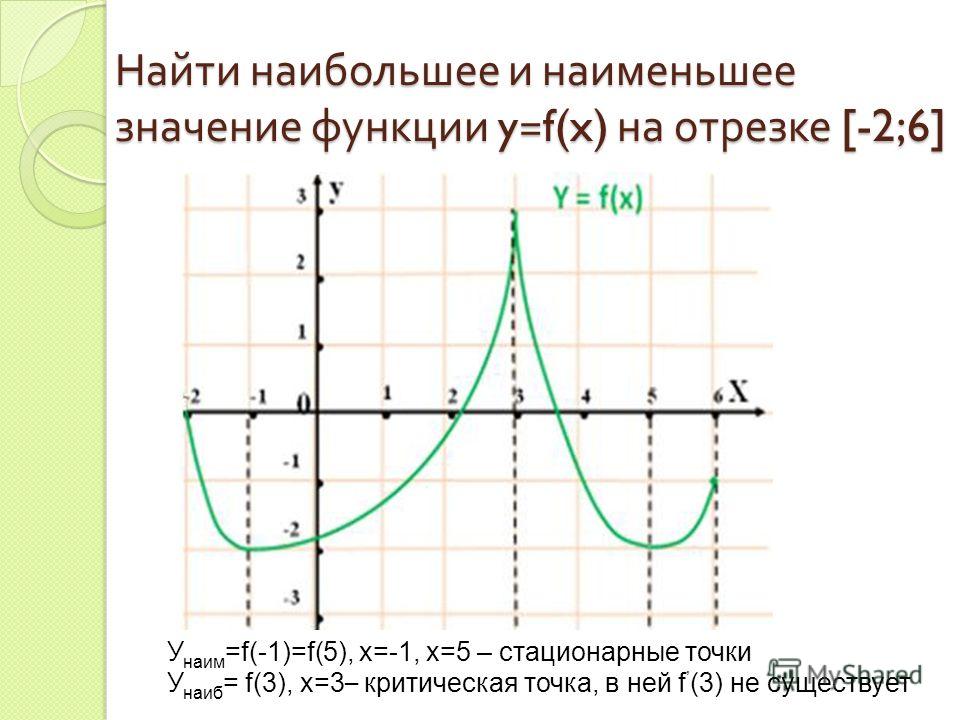
Когда под корнем находится выражение, содержащее независимую переменную, то она называется иррациональной. В этом случае D(f) — множество Z, кроме тех, которые превращают выражение под корнем четной степени в отрицательное значение. Функция, представленная степенными выражениями, имеет D(f) = Z, но только тогда, когда значение аргумента не превращает функцию в пустое множество.
Метод нахождения
Для решения любой задачи нужно применять определенные правила. Они называются алгоритмом. Для каждого типа функций существует конкретный вариант решения. Для дробной он является следующим:
В случае, когда выражение является иррациональной функцией, корень которой является четным, следует решать не уравнение, а неравенство. Его значение не должно быть меньше 0. Для логарифмического типа выражение натурального логарифма (ln) должно быть всегда больше 0.
Данный пример показывает особенность решения задачи, которая заключается в объединении двух алгоритмов. Это довольно часто практикуется. Результат — объединение трех множеств, при объединении которых получается два интервала.
Сведения о производных
Производная — скоростное изменение какой-либо функции. Эта характеристика присуща не всем, поскольку некоторые из них являются постоянными. Если она имеет производную в некоторой точке, то является дифференцируемой. Дифференцирование применяется не только для исследования функций, но и во многих отраслях науки и техники.
Для нахождения дифференциалов необходима таблица производных. Кроме того, следует освоить все основные правила, поскольку не во всех случаях функция соответствует одному из табличных значений. Для этого нужно воспользоваться некоторыми свойствами. Математики-специалисты рекомендуют применять на начальных стадиях обучения алгоритм нахождения производной, который позволяет существенно сократить время выполнения задания, а также количество ошибок.
Таблица дифференциалов
В некоторых простых задачах возникает необходимость определить производную некоторой элементарной функции. Для этих целей применяется специальная таблица, в которой записаны основные простые выражения.
Данные значения были получены практическим методом — нахождением отношения приращения функции к приращению аргумента. Необходимо учитывать, что последний стремится к нулевому значению.
Однако иногда приходится упрощать выражение, а потом находить его производную. Для этого существует специальный простой алгоритм:

Данный алгоритм справедлив только для простых выражений. Для сложных функций нужно руководствоваться некоторыми свойствами.
Основные свойства
Когда выражение не совпадает с табличным значением или состоит из нескольких элементов, то нужно применять специальные правила. Ими являются следствия из доказательств различных теорем. К ним можно отнести следующие:
 3 + 6).
3 + 6).Очень важно уметь разбивать выражение на части, поскольку от этого зависит результат решения. В некоторых случаях выражение можно упростить.
Наибольшее и наименьшее значения
Задачи на нахождения максимума и минимума применяются не только в математике, но и в бизнесе, науке, производстве и т. д. Например, вычисление наименьшего значения функции на отрезке (за последний промежуток времени) позволяет узнать минимизацию издержек производства. Кроме того, можно определить максимальную прибыль, найти оптимальную загрузку техники и т. д. Данные значения следует искать на каких-либо интервалах. Они классифицируются следующим образом:

Следует отметить, что наибольшее и наименьшее значение производной по графику функции можно также найти, однако расчетный метод намного проще.
Универсальный алгоритм
Для данной операции, как и для других математических действий, существуют определенные правила или последовательность действий, которые называются алгоритмом. Специалисты для решения различных задач в любых сферах рекомендуют использовать их. Они позволяют не только существенно экономить время, минимизируя количество вычислений, но и с их помощью можно избежать некоторых ошибок. Суть алгоритма очень проста. Он состоит из определенной последовательности таких шагов:
 2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.
2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.Одним из простейших типов задач является следующая: найдите наибольшее значение линейной функции z = 5x + 10 на отрезке [-3;3]. Для ее решения можно также воспользоваться алгоритмом:
Последнюю задачу необязательно решать по алгоритму, поскольку она считается простейшей. Математики рекомендуют тренироваться в нахождении MIN и MAX функции, поскольку только практика позволяет быстро решать задачи.
Таким образом, для нахождения максимального и минимального значений заданной функции необходимо пользоваться специальным универсальным алгоритмом.
Наибольшее и наименьшее значения функции
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
функция возрастает
Предположим, что функция f
не имеет на отрезке [а; b] критических
точек.
наибольшее
значение
наименьшее
значение
Тогда она возрастает (рис.
убывает (рис. 2) на этом отрезке.
a
b
функция убывает
наибольшее
значение
наименьшее
значение
a
b
Значит,
наибольшее и наименьшее значения
функции f на отрезке [а; b] — это
значения в концах а и b.
Примеры
Пусть теперь функция f имеет на
отрезке [а; b] конечное число
критических точек.
наибольшее
значение
наименьшее
значение
a c
b
наибольшее
значение
наибольшее
значение
наименьшее
значение
наименьшее
значение
a c
n b
Наибольшее и наименьшее
значения функция f может
принимать в критических точках
функции или в точках а и b.
Чтобы найти наибольшее и
наименьшее значения функции,
имеющей на отрезке конечное
число критических точек, нужно
вычислить значения функции во
всех критических точках и на
концах отрезка, а затем из
полученных чисел выбрать
наибольшее и наименьшее.
1.
Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]
Значения функции в
концах отрезка.
1) y(0) = 0
y(4) = 43– 27 4 = – 44
3
-3
Найдем критические
точки, которые
принадлежат
заданному отрезку.
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
y(3) = 33– 27 3 = –54
Выбрать наименьшее из
полученных значений.
x = 3 [0; 4]
x = –3 [0; 4]
Ответ
— 5 4
3
1 0 х
х
Выполнение этапов решения можно изменить, как вам удобно.
Этапы
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее или
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3×2 – 27
3
-3
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
x = 3 [0; 4]
x = –3 [0; 4]
3) y(0) = 0
y(4) = 43– 27 4 = – 44
y(3) = 33– 27 3 = –54
Ответ
— 5 4
3
1 0 х
х
Предположим, что функция f
имеет на отрезке [а; b] одну точку
экстремума.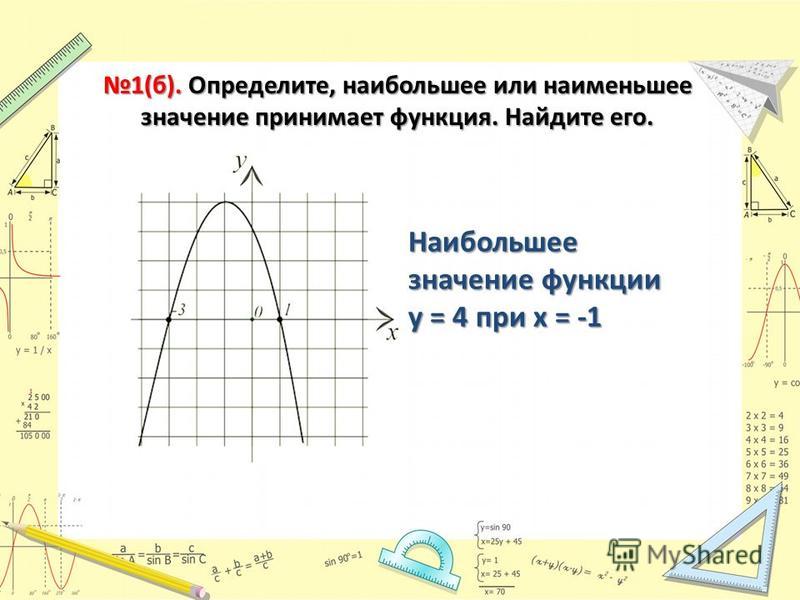
наименьшее
значение
a
b
Если это точка минимума, то в этой
точке функция будет принимать
наименьшее значение.
наибольшее
значение
Если это точка максимума, то в этой
точке функция будет принимать
наибольшее значение.
a
b
Другой способ решения
Этапы
1. Найти f /(x)
2. Найти критические
точки, взять те,
которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее и
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3×2 – 27
3
-3
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
y
y
+
0
-3
–
+
3
min
4
x
3)
y(3) = 33– 27 3 = –54
Ответ
— 5 4
3
1 0
Наименьшее
значение функция
будет принимать в
точке минимума.
Можно сэкономить
на вычислениях
х
х
значений функции в
концах отрезка.
Этот способ будет удобно
вспомнить, когда вычисления значений функции в
концах отрезка будет сложным.
2. Найдите наибольшее значение функции y = x3 – 3x + 4
на отрезке [– 2; 0]
Значения функции в
концах отрезка.
1) y(0) = 4
y(-2) = (-2)3– 3 (-2) +4 = 2
-1
1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
2) y / = 3×2 – 3 = 3(x2 – 1) = 3(x – 1)(x + 1)
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
y(-1) = (-1)3– 3 (-1) + 4 = 6
Выбрать наибольшее из
полученных значений.
x = 1 [-2; 0]
x = –1 [-2; 0]
Ответ
6
3
1 0 х
х
3. Найдите наименьшее значение функции y = x3 – 2×2 + x +3
на отрезке [ 1; 4 ]
Значения функции в
концах отрезка.
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
1) y(1) = 1 – 2 + 1 + 3 = 3
y(4) = 43– 2 42 + 4 + 3 = 39
2) y / = 3×2 – 4x + 1= 3(x – 1)(x – 1 )
3
3×2 – 4x + 1 = 0
D=16–4*3*1=4
4+2
x1=
= 1 [1; 4]
6
4-2
1
= [1; 4]
x2=
6
3
y(1) = 3
Ответ
3
3
1 0 х
х
x3
9x 7
4. Найдите наибольшее значение функции y
3
на отрезке [ -3; 3 ]
3
( 3)
Значения функции в
у ( 3)
9( 3) 7 9 27 7 11
концах отрезка.
3
33
у (3) 9 3 7 9 27 7 25
3
2
Найдем критические
3
х
точки, которые
у/
9 х 2 9 ( х 3)( х 3)
3
принадлежат
заданному отрезку.
x = 3 [-3; 3]
x = –3 [-3; 3]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
y(-3) = 11
y(-3) = -25
В 11
1 1
3
10 х
х
5. Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
Значения функции в
концах отрезка.
3
2
3
2
3
2
y x 3x 1
у(1) 1 3 1 1 1 3 1 1
3
2 2
у (9) 9 3 9 1 (3 ) 27 1
27 27 1 1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
3
х 3 0
3
3
/
у х 3
х 3 2
2
2
3 х 6 0
1
2
х 2
х 4 [1; 9]
3
2
3
2 2
у (4) 4 3 4 1 (2 ) 12 1
8 12 1 3
Выбрать наибольшее из
полученных значений.
Ответ
1
3
1 0 х
х
2
6. Найдите наименьшее значение функции y x х 3 x 1
3
на отрезке [ 1; 9 ]
Значения функции в
концах отрезка.
3
2
3
2
y x 2 31x 1
х 21 3
x 1 1 1
у(1) 1 3y
1 x1
3
2 2
у (9) 9 3 9 13 (3 ) 27 1
y х 2 3x 1
27 27 1 1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
1
Запишем функцию
3 в удобном
х 3 виде
0 2
для дифференцирования
3 2
3
/
у х 3
х 3 2
2
2
3 х 6 0
х 2
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.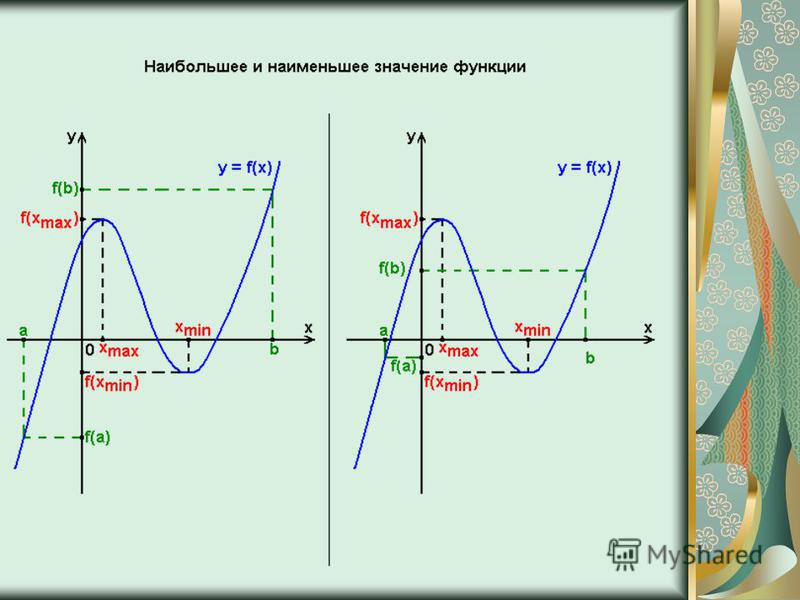
Выбрать наименьшее из
полученных значений.
х 4 [1; 9]
3
2
3
2 2
у (4) 4 3 4 1 (2 ) 12 1
8 12 1 3
Ответ
—
3
3
1 0
х
х
8. Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
1
Значения функции в
концах отрезка.
/
1
1
2
х
х
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
36
y х
х
ООФ: x = 0
y x 36
х
1
у (1) Запишем
1 36 функцию
37
в удобном
1
для дифференцирования
виде
1
у (9) 9 36 9 4 13
9
36 х 2 36
1
/
у 1 36 2 1 2
2
х
х
х
( х 6)( х 6)
x = 6 [ 1; 9]
х2
x = –6 [ 1; 9]
x = 0 D(y)
1
у (6) 6 36 6 6 12
6
Ответ
3 7
3
1 0 х
х
(cosx) – sinx
/
14.
3
; 0
y = 7cosx +16x – 2 на отрезке
2
у 7 sin х 16
/
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
0
7 sin х 16 0
16
sin х
7
т.к. sin х [ 1;1]
Функция на всей области
определения возрастает.
Нетрудно догадаться,
что у / > 0.
Тогда наибольшее
значение функция будет
иметь в правом конце
отрезка, т.е. в точке х=0.
3
3
3
у
7 cos
16
2 24 2
2
2
2
у(0) 7 cos 0 16 0 2 7 2 5
Ответ
5
3
1 0 х
х
Если вы не догадались,
то вычислите значения
функции в каждом конце
отрезка и выберите
наибольшее.
(sinx ) cosx
15. Найдите наибольшее значение функции
/
y = 10sinx –
у 10 cos х
/
1. Найти f
/(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
10 cos х
36
36
36
5
; 0
x + 7 на отрезке
6
Критических точек нет.
Тогда наибольшее
значение функция будет
принимать в одном из
концов отрезка.
36
cos х
10
т.к. cos х [ 1;1]
Можно было и раньше
догадаться, что
наибольшее значение
будет именно в левом
конце отрезка!
Как?
1
5
5 36 5
у
10 sin
7 10 30 7 32
2
6
6 6
Синус –нечетная функция
0
Формула приведения
5
5
1
(
)
у 0 sin
10 sin
7 7 Ответ
0 0
sin
sin sin
3 2
6
6
6
3
1 0 х
х
6
2
(cosx) – sinx
16. Найдите наименьшее значение функции
/
у / 5 sin x 6
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3
у
2
y = 5cosx – 6x + 4 на отрезке
5 sin x 6 0
6
sin х
5
т.к. sin х [ 1;1]
0
3
5 cos
2
3
6
2
у(0) 5 cos 0 0 4 9
Ответ
9
3
1 0 х
Функция на всей области
определения убывает.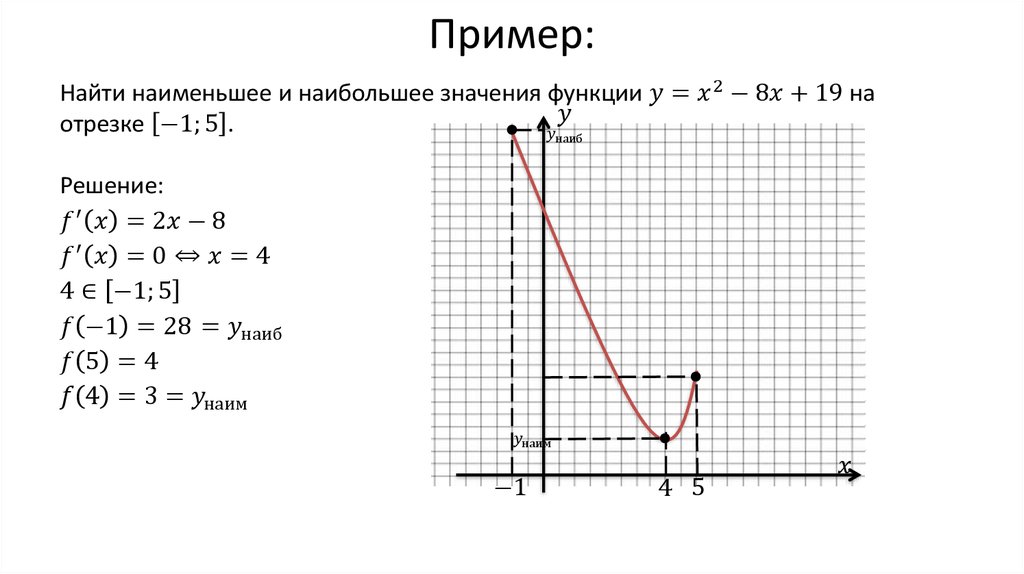
Нетрудно догадаться, что
у / < 0.
Тогда наименьшее
значение функция будет
иметь в правом конце
отрезка, т.е. в точке х=0.
4 9 4
1
х
3
2 ; 0
Если вы не догадались,
то вычислите значения
функции в каждом конце
отрезка и выберите
наименьшее.
17. Найдите наибольшее значение функции
y = 12cosx + 6 3 x – 2 3 + 6 на отрезке 0 ;
2
1. Найти f /(x)
у / 12 sin x 6 3
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
12 sin x 6 3 0
3
sin х
2
х ( 1)
n
3
3
n
Но нам не нужны ВСЕ
у 12 cos 6 3 2 3 6
12
стационарные
точки.
3
3
3
Необходимо сделать выбор тех
значений, которые попадут в
заданный отрезок
у 12 cos 6 3 2 3 6 6 3 0 ;
2
2
2
у (0) 12 cos 0 6 3 0 2 3 6 18 2 3
Ответ
1 2
3
1 0 х
х
2
17. Найдите наибольшее значение функции
y = 12cosx + 6 3 x – 2 3 + 6 на отрезке 0 ;
2
1.
у / 12 sin x 6 3
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
12 sin x 6 3 0
y
y
0
3
sin х
2
+
–
2
x
3
max
3
Убедимся, что данная точка
является точкой максимума на
заданном промежутке.
Значит, наибольшее значение
функция достигает именно в этой
точке.
Тогда значения функции в концах
отрезка можно не считать.
у 12 cos 6 3 2 3 6 12
3
3
3
Ответ
1 2
3
1 0 х
х
18. Найдите наименьшее значение функции
7 3
14 3
7 3
y = 11 +
–
х–
cosx на отрезке 0 ;
2
18
3
3
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
y
y
0
–
7 3 14 3
у
sin x
6
3
3
7 3 14 3
sin x 0
3
3
Можно убедиться, что данная
1
n
точка
является
точкой
х ( 1)
минимума
n
sin x
на заданном промежутке.
6
2
/
+
6 min
2
x
Значит, наименьшее значение
функция
достигает
именно в этой
Но нам не
нужны ВСЕ
точке.
стационарные точки.
Тогда
значения
функции
в концах
Необходимо
сделать
выбор
тех
отрезка
можно
не считать.
значений,
которые
попадут в
заданный отрезок
7 3 7 3 14 3
у 11
cos 11 7 4
18
18
3
6
6
В 11
4
0 ; 2
3
10 х
х
(tgx)
/
19. Найдите наименьшее значение функции
1
cos2x y = 4tgx – 4x – 4 + 5 на отрезке 4 ; 4
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
1
у 4
4
2
cos x
/
4
0
4
4 0
2
cos x
cos 2 x 1
Нам не нужны ВСЕ
у 4 5 1
4
у 4 5 9 2
4
у(0) 0 0 5 5
Ответ
4
стационарные точки.
Необходимо сделать выбор тех
значений, которые попадут в
3.
значения функции
заданный
отрезок
в критических точках
;
и на концах отрезка.
4 4
4. Из вычисленных значений
сделаем выбор наименьшего.
1
3
1 0 х
х
(tgx)
/
20. Найдите наибольшее значение функции
1
2
cos x y = 3tgx – 3x + 5 на отрезке 4 ; 0
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
1
у 3
3
2
cos x
/
0
3
3 0
2
cos x
cos 2 x 1
4
Нам не нужны ВСЕ
3. Вычислим значения функции в критическихстационарные
точках и на концах
точки.отрезка.
Необходимо сделать выбор тех
4. Из вычисленных значений сделаем выбор наибольшего.
значений, которые попадут в
-1
заданный отрезок
3 4 ; 0 3
у 3tg 3 5 3
5 2
4
4
4 0 4 4
у(0) 3tg0 0 5 5
В 11
5
3
10 х
х
English
Русский
Правила
Наибольшее и наименьшее значение функций на промежутке – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Если функция (y=f(x)) определена и непрерывна на отрезке ([a;b]), то она на этом отрезке достигает своих наибольшего и наименьшего значений.
Однако свое наибольшее значение (M) функция (f(x)) может принимать и на концах отрезка ([a;b]). Поэтому, чтобы найти наибольшее значение (M), непрерывной на отрезке ([a;b]), функции (f(x)), надо найти все максимумы функции на интервале ((a;b)) и значения (f(x)) на концах отрезка ([a;b]), то есть (f(a)) и (f(b)), и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.
Наименьшим значением (m) непрерывной на отрезке ([a;b]) функции (f(x)) будет наименьший минимум среди всех минимумов функции (f(x)) на интервале ((a;b)) и значений (f(a)) и (f(b)).
Чтобы найти наибольшее или наименьшее значения функции на отрезке, нужно исследовать поведение функции на данном отрезке с помощью производной.
Для этого мы следуем известному алгоритму:
- Находим ОДЗ функции.
- Находим производную функции.
- Приравниваем производную к нулю.
- Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции: а) если на промежутке I производная функции (f'(x)>0), то функция (y=f(x)) возрастает на этом промежутке; б) если на промежутке I производная функции (f'(x)<0), то функция (y=f(x)) убывает на этом промежутке.
- Находим точки максимума и минимума функции. В точке максимума функции производная меняет знак с «+» на «–». В точке минимума функции производная меняет знак с «–» на «+».
- Находим значение функции в концах отрезка,
- затем сравниваем значение функции на концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции;
- или сравниваем значение функции на концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции.
2+3). График этой функции выглядит так:
В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
1. Рассмотрим функцию на отрезке (xin[-1;0]).
Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: (f(0)), а наименьшее – в левом: (f(-1)).
2. Рассмотрим функцию на отрезке (xin[-1;1]).
Очевидно, что наибольшее значение функция принимает в точке максимума (f(0)), а наименьшее – в одном из концов отрезка, то есть надо найти значения (f(-1)) и (f(1)) и выбрать из них наименьшее.
3. Если мы рассмотрим функцию на отрезке (xin[-1;2]), то, чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и на правом конце отрезка, то есть (f(0)) и (f(2)).
Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и на левом конце отрезка, то есть (f(frac43)) и (f(-1)).
2} — 2 cdot 4 + 5 = 13}.)
Следовательно, наибольшее значение функции равно (f(4)=13), а наименьшее значение составляет (f(1)=4).
Как найти наибольшее и наименьшее значения функции на отрезке.
Как найти наибольшее и наименьшее значения функции на отрезке?
Для этого мы следуем известному алгоритму:
1. Находим ОДЗ функции.
2. Находим производную функции
3. Приравниваем производную к нулю
4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:
Если на промежутке I производная функции , то функция возрастает на этом промежутке.
Если на промежутке I производная функции , то функция убывает на этом промежутке.
5. Находим точки максимума и минимума функции.
В точке максимума функции производная меняет знак с «+» на «-«.
В точке минимума функции производная меняет знак с «-» на «+».
6. Находим значение функции в концах отрезка,
- затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
- или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции
Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.
Рассмотрим функцию . График этой функции выглядит так:
В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
1. Рассмотрим функцию на отрезке
Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: , а наименьшее — в левом: .
2. Рассмотрим функцию на отрезке
Очевидно, что наибольшее значение функция принимает в точке максимума , а наименьшее — в одном из концов отрезка, то есть надо найти значения и и выбрать из них наименьшее.
3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть и .
Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть и .
Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:
1. ОДЗ функции — множество действительных чисел.
2.
3. , если или
Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:
Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике
1.
Задание B15 (№ 26695)
Найдите наибольшее значение функции на отрезке .
1. Функция определена при всех действительных значениях х
2.
3.
Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
y(0)=5
Ответ: 5.
2. Задание B15 (№ 26702)
Найдите наибольшее значение функции на отрезке [].
1. ОДЗ функции
2.
Производная равна нулю при , однако, в этих точках она не меняет знак:
, следовательно, , значит, , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, при .
Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:
у(0)=5
Ответ: 5.
3. Задание B15 (№ 26708)
Найдите наименьшее значение функции на отрезке [].
1. ОДЗ функции :
2.
3.
,
Расположим корни этого уравнения на тригонометрической окружности.
Промежутку принадлежат два числа: и
Расставим знаки. Для этого определим знак производной в точке х=0: . При переходе через точки и производная меняет знак.
Изобразим смену знаков производной функции на координатной прямой:
Очевидно, что точка является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции на отрезке , нужно сравнить значения функции в точке минимума и в левом конце отрезка, .
Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а таковым на является, следовательно подставим в уравнение функции
Ответ: -1
Вероятно, Ваш браузер не поддерживается.
Попробуйте скачать
FirefoxИ.В. Фельдман, репетитор по математике.
Как найти наибольшее и наименьшее значение функции алгоритм вычисления и нахождения наименьшего и наибольшего значения функции на отрезке, луче, промежутке, интервале
В некоторых задачах нужно найти наибольшее и наименьшее значения функции. Если неизвестен алгоритм и основные правила, то простое задание превращается в изнурительный труд, который очень редко приносит положительные результаты. В интернете существует множество информации, но не вся она достоверна. Самое страшное — применение неверных методик нахождения.
Содержание
- Общая информация
- Область определения
- Обозначение интервалов
- Зависимость от типа
- Метод нахождения
- Сведения о производных
- Таблица дифференциалов
- Основные свойства
- Наибольшее и наименьшее значения
- Универсальный алгоритм
- Примеры решений
Исследование функции — распространенная задача, которая показывает ее поведение и свойства.
Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.
Для решения такого типа задач необходим определенный «багаж» знаний, поскольку без него вообще не обойтись. В его состав входят следующие элементы:
- Нахождение области определения функции (ОДФ).
- Понятие дифференциала и основные методы его нахождения.
- Умение решать уравнения.
- Знание графиков простых функций.
- Основные типы функций, полуинтервал и интервал.
- Алгебраические: рациональные и иррациональные.
- Тригонометрические: sin, cos, tg и ctg.
- Трансцендентные: степенные, показательные и логарифмические.
- Найти корни уравнения знаменателя, приравнивая его к 0.
- Определить интервал, значения из которого может принимать аргумент.
- Первое выражение (решить уравнение): (x — 1) * (x + 1) = 0. Оно имеет два корня: x1 = -1 и x2 = 1. Числовой промежуток: (-бесконечность;-1) U (1;+бесконечность).
- Второе (неравенство): (10 — x) < 0. Интервал: (-бесконечность;10].
- Результат (объединение всех интервалов): (-бесконечность;-1) U (1;10].
- Выполнить математические преобразования (упростить выражение).
- Найти производную по таблице.
- Если константа A (в некоторых источниках «С»), то при дифференцировании ее можно выносить за знак производной: (A * f(x))’ = A(f(x))’.
- Дифференциал суммы или разности 2 и более функций эквивалентен дифференциалу каждой из них: (w(x) + z(x))’ = w'(x) + z'(x) и (w(x) — z(x))’ = w'(x) — z'(x).
- Производная произведения 2 функций соответствует сумме, которая является произведением каждой из них на дифференциал другой: (w(x) * z(x))’ = (w'(x) * z(x) + w(x) * z'(x).
3 + 6).
- Отрезок: [a;b].
- Открытый тип: (a;b), (a;b] и [a;b).
- Промежуток бесконечности (в некоторой литературе обозначается «inf»): (-бесконечность;а], (-inf;а), [a;+inf), (a;+inf) и (-inf;+inf).
- Найти D(f(x)).
- Проверить вхождение заданного интервала.
- Взять производную и выполнить поиск всех точек, в которых она не существует (их может и не быть).
- Приравнять к нулю результат, полученный в пункте 4, и найти корни уравнения. Это и будут стационарные точки, но они могут не существовать.
2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.
- Максимум и минимум (с учетом стационарной точки и интервала): MIN(y) = 0 и MAX(y) = 64.
- D(z) — все значения от бесконечно малого до бесконечно большого чисел.
- Промежуток, на котором нужно найти максимум и минимум, полностью входит в D(f).
- Дифференциал: z’ = 5 (существует во всех точках, а стационарных точек нет вообще).
- Минимум и максимум: MIN(z(-3)) = 5 * (-3) + 10 = -5 и MAX(z(3)) = 5 * (3) + 10 = 25.
- Рассмотреть задания на нахождение множества
значений функций; - Рассмотреть задания на отыскание наименьшего и
наибольшего значения функции на промежутке. - Применение нахождения наибольшего и
наименьшего значения функции, и решение
практических задач. -
Выберите ячейку ниже или справа от чисел, для которых вы хотите найти наименьшее число.
-
На вкладке Главная в группе Редактирование щелкните стрелку рядом с Автосумма , щелкните Мин. (вычисляет наименьшее) или Макс. (вычисляет наибольшее значение), а затем нажмите клавишу ВВОД.
- Наклон строка например 2x равно 2, поэтому 14t имеет наклон 14
- Функция квадрата , такая как t 2 , имеет наклон 2t, поэтому 5t 2 имеет наклон 5(2t)
- А потом мы сложили их: 0 + 14 − 5(2t)
Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.
Зависимость от типа
Функции различаются между собой. От этого и зависит нахождение их области определения. Они бывают простыми и сложными. Первые состоят из единичных элементов, а сложные включают в себя несколько типов. Их еще называют составными. Простые классифицируются на три вида:
Рациональные бывают целыми и дробными. Они не включают в себя выражения, содержащие такие элементы: корень, степень, логарифм и тригонометрические функции. D(f) этих функций — все действительные числа (Z). Если она является дробной, то это означает, что в ее числителе и (или) знаменателе находится аргумент, значение которого не должно обращать ее в пустое множество.
Когда под корнем находится выражение, содержащее независимую переменную, то она называется иррациональной. В этом случае D(f) — множество Z, кроме тех, которые превращают выражение под корнем четной степени в отрицательное значение. Функция, представленная степенными выражениями, имеет D(f) = Z, но только тогда, когда значение аргумента не превращает функцию в пустое множество.
Метод нахождения
Для решения любой задачи нужно применять определенные правила. Они называются алгоритмом. Для каждого типа функций существует конкретный вариант решения. Для дробной он является следующим:
В случае, когда выражение является иррациональной функцией, корень которой является четным, следует решать не уравнение, а неравенство. Его значение не должно быть меньше 0. Для логарифмического типа выражение натурального логарифма (ln) должно быть всегда больше 0.
Данный пример показывает особенность решения задачи, которая заключается в объединении двух алгоритмов. Это довольно часто практикуется. Результат — объединение трех множеств, при объединении которых получается два интервала.
Сведения о производных
Производная — скоростное изменение какой-либо функции. Эта характеристика присуща не всем, поскольку некоторые из них являются постоянными. Если она имеет производную в некоторой точке, то является дифференцируемой. Дифференцирование применяется не только для исследования функций, но и во многих отраслях науки и техники.
Для нахождения дифференциалов необходима таблица производных. Кроме того, следует освоить все основные правила, поскольку не во всех случаях функция соответствует одному из табличных значений. Для этого нужно воспользоваться некоторыми свойствами. Математики-специалисты рекомендуют применять на начальных стадиях обучения алгоритм нахождения производной, который позволяет существенно сократить время выполнения задания, а также количество ошибок.
Таблица дифференциалов
В некоторых простых задачах возникает необходимость определить производную некоторой элементарной функции. Для этих целей применяется специальная таблица, в которой записаны основные простые выражения.
Данные значения были получены практическим методом — нахождением отношения приращения функции к приращению аргумента. Необходимо учитывать, что последний стремится к нулевому значению.
Однако иногда приходится упрощать выражение, а потом находить его производную. Для этого существует специальный простой алгоритм:
Данный алгоритм справедлив только для простых выражений. Для сложных функций нужно руководствоваться некоторыми свойствами.
Основные свойства
Когда выражение не совпадает с табличным значением или состоит из нескольких элементов, то нужно применять специальные правила. Ими являются следствия из доказательств различных теорем. К ним можно отнести следующие:
Очень важно уметь разбивать выражение на части, поскольку от этого зависит результат решения. В некоторых случаях выражение можно упростить.
Наибольшее и наименьшее значения
Задачи на нахождения максимума и минимума применяются не только в математике, но и в бизнесе, науке, производстве и т. д. Например, вычисление наименьшего значения функции на отрезке (за последний промежуток времени) позволяет узнать минимизацию издержек производства. Кроме того, можно определить максимальную прибыль, найти оптимальную загрузку техники и т. д. Данные значения следует искать на каких-либо интервалах. Они классифицируются следующим образом:
Следует отметить, что наибольшее и наименьшее значение производной по графику функции можно также найти, однако расчетный метод намного проще.
Универсальный алгоритм
Для данной операции, как и для других математических действий, существуют определенные правила или последовательность действий, которые называются алгоритмом. Специалисты для решения различных задач в любых сферах рекомендуют использовать их. Они позволяют не только существенно экономить время, минимизируя количество вычислений, но и с их помощью можно избежать некоторых ошибок. Суть алгоритма очень проста. Он состоит из определенной последовательности таких шагов:
Одним из простейших типов задач является следующая: найдите наибольшее значение линейной функции z = 5x + 10 на отрезке [-3;3]. Для ее решения можно также воспользоваться алгоритмом:
Последнюю задачу необязательно решать по алгоритму, поскольку она считается простейшей. Математики рекомендуют тренироваться в нахождении MIN и MAX функции, поскольку только практика позволяет быстро решать задачи.
Таким образом, для нахождения максимального и минимального значений заданной функции необходимо пользоваться специальным универсальным алгоритмом.
Предыдущая
АлгебраТригонометрический круг со всеми значениями, круг синусов и косинусов, линия, ось тангенса на окружности, как пользоваться и находить точки
Следующая
АлгебраПравила дифференцирования определение, свойства, формулы, алгоритмы вычислений для функций любой сложности, таблица производных, примеры решений
Урок математики по теме «Наибольшее и наименьшее значения функции»
Цель урока: Систематизация и обобщение
материала по данной теме:
Ход урока
I. Опрос.
1. Что такое множество значений функций?
2. Чем отличаются задания: найти область
определения и найти множество (область) значений
функций?
3.Дайте определение наименьшего, наибольшего
значений функций?
4. Для каждой ли функции можно указать
наибольшее, наименьшее значения?
Приведите пример.
II. Диктант
Для функции найдите множество значений:
А) y=7-x2
Б) y-x2+4x
В) y= lg (x-10)
Г) y=lgx-10
Д) y=5x-3
Е) y=5x-3
Ж) y=|x-5| +9
З) y=arcsin x
2.Укажите функцию, множество значений которой
есть промежуток (-)
A) y= x1/3 ; Б)y=2-x ; B)y=tgx ;Г)y=
3. Какое из следующих чисел входит в множество
значений функции
y=3cosx+2
А)-3; Б)-2; В)6; Г)4
Дополнительно
4.
функции
y=
III. Выполнение упражнений на нахождение
наибольшего и наименьшего значения функций с
последующей проверкой.
1.Найдите наибольшее значение функции
g(x) = 4 cos (x -),
если x ответ
[- 2]
2. Найдите наименьшее значение функции
y(x) = 2 — log 25 5 -х нa [- 3;3]. ответ [0,5]
3. Найдите наименьшее значение функции
y =log 3 (3-x2). ответ [-1].
4. Найдите наибольшее целое значение функции
y= — 32,4 * ( ) 3-cos(2+П).
ответ[-1]
5. Найдите наибольшее значение функции
y=2,7 нa [l;3]
6. Найдите произведение наибольшего и
наименьшего значений функции
y=2sin2x+cos x [-2,125]
IV. Устные упражнения. Найдите ошибки в решении
задачи.
A) Найдите наибольшее значение функции:
y= + 4 = + 4 = sin4x — 2 + 4 = sin4x + 2 .Ответ
3.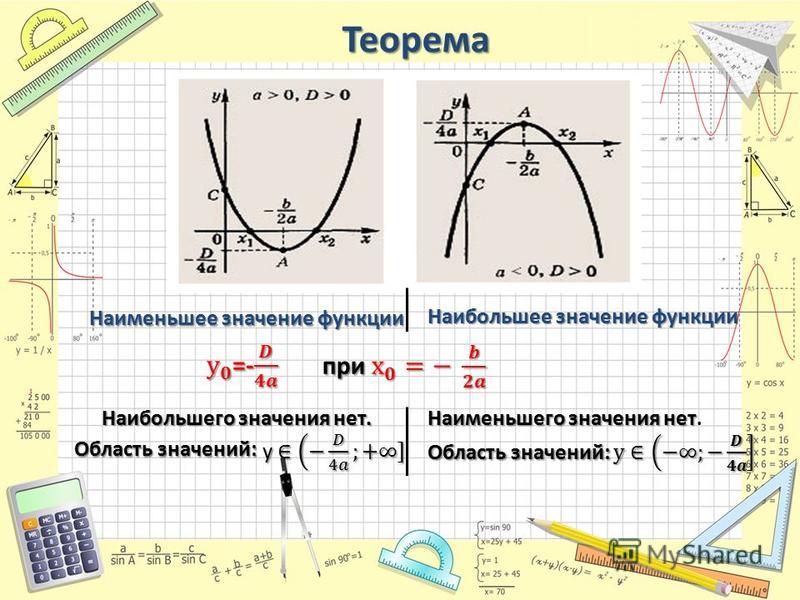
Верный ответ 7, так как
|sin4x – 2|+4 = — (sin4x — 2) + 4 = — sin 4x + 2 +4 = 6 — sin 4x. ответ 7.
Б) Найдите наибольшее значение функции:
У=
-lsin(x+)1
5 sin(x+)67
Ответ:
верный ответ 1, так как наибольшее значение дроби
будет, когда знаменатель принимает наименьшее
значение.
V. Решение практической задачи (работа в
группах)
Задача:
V(см3) – емкость V=S осн.-h =П R2 h=4
Д=х
R=x Vц=Пh h=; h=
S пол=2ПRh+2П=2ПХ
+2П Х2= +2ПХ2=
(x) =
(x) =0 4П-2V=0
Если х0 то, (х)0, если х0 то, (х)0 значит Х= . Функция имеет минимум. Итак, Х= единственная
критическая точка на (0;) и является точкой минимума функции
S (х), следовательно, функция в этой точке
достигает своего наименьшего значения.
h====
Ответ: цилиндр равносторонний.
VI. Множество значений функции (самостоятельная
работа)
Найти множество значений функции y=
Решение: y=
Е(у)=
Найдите наибольшее значение функции: а) у= на промежутке
[2;5]
б) у= – на
промежутке [0;1]
а) решение: функции f(х)=7х-6 и f(х)=определены, непрерывны, возрастают.
Сумма функций имеет те же свойства, значит у= определена,
непрерывна, убывает. Наибольшее значение
принимает на левом конце отрезка у(2)=5.
б) решение: функция f(х)=и g(х)=определены, непрерывны, возрастают,
положительные f(х) и g(х)- обладает теми же свойствами.
f(х)= —
непрерывна, определена, положительная, убывает.
У=– —
определена, непрерывна, отрицательная,
возрастает.
У(0)=—
наименьшее значение.
Решение части III.
1.g(х)=4 cos (х-),
если x — найти
наибольшее.
g()=4cos(= 4cos(= 4cos(= 4cos(=- 4cos=-4=-2
g()=4cos(= 4cos(= 4cos(= 4cos(=- 4cos=-2
g/(х)=-4sin(х-)
g /(х)=0 sin(х-)=0
Опред. знак
g (х)П; ] возрастает g () = –2 –
наибольшее.
2. y(x) = 2 — log 25 5 -х нa [- 3;3]. Наименьшее
значение
y(x) = 2 — log 25 5 –х = 2+ log 5 5=2+ функция возрастает,
значит наименьшее значение y(-3)=0,5
3.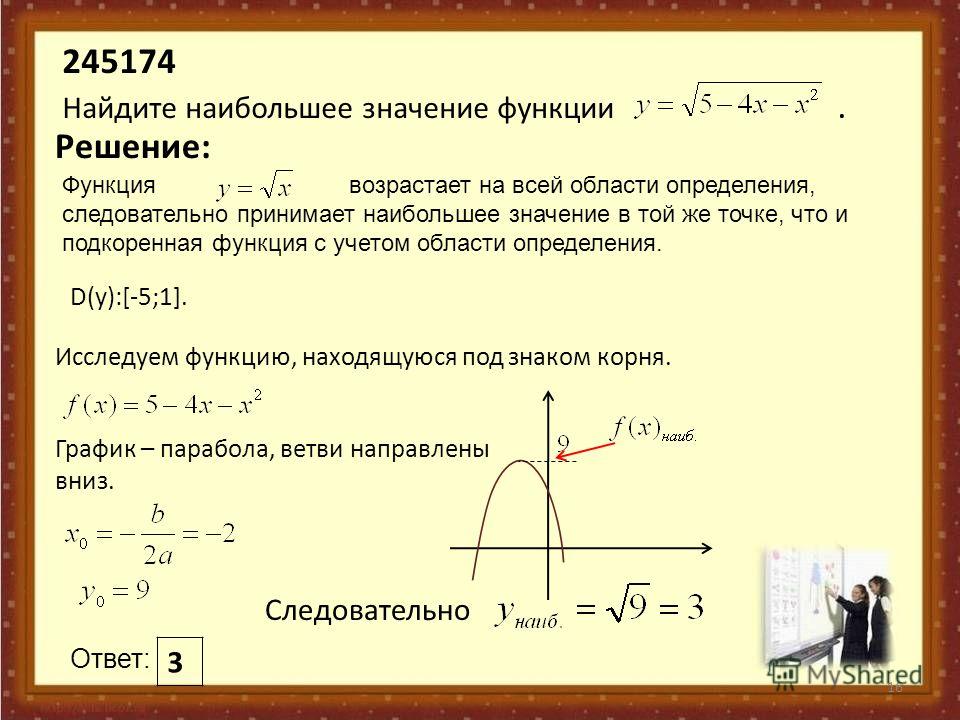
Д (у)= 3-x2
Х (-;)
= =0
х=0
у(0) = =-1
4. y= — 32,4 * ( ) 3-cos(2х+П)
H(х)= ( ) 3-cos(2х+П)=
( ) 3+cos 2х
Наименьшее значение принимает, если g(x)=3+cos2x
-1 cos2x 1
2cos2x4
g(x) = 2
h(x)y = -32,4* = -3,6
— наименьшее.
y=-32,4*()
-1cos(2x+П)1
-1-cos(2x+П)1
23-cos(2x+П)4
32,4*
32,4*
32,4*-
наибольшее.
Ответ: -1
5. y=2,7*e на
[1;3]
y=e —
возрастает наибольшее значение принимает, если t
– наибольшее.
t=3x на [1;3]
t(x)=6x-3x
6x-3x=0
3x(2-x)=0
x=0, x=2/
2 max [1;3].
t=3*2
y=2,7*e=2,7
6. Найдите произведение наибольшего и
наименьшего значений функции
y=2sinx+cosx
y=2(1-cosx)+cos
x=2-2cosx+cos x=-2cosx+cos x+2
cos x=t -1
y=-2t+t+2 –
наибольшее значение в вершине параболы.
T0 = — ==
У= ( ) = -2 + + 2 = +2 = 2 + =2
У (-1) = -2-1+2= -1
У(1)= -2=1=2=1
У ()= 2 — наибольшее значение
У (-1) = -1 – наименьшее
Произведение 2 (-1) = -2
5.1 Максимум и минимум
точка локального максимума на функции является
точка $(x,y)$ на графике функции, координата $y$ которой равна
больше, чем все остальные координаты $y$ на графике в точках «близких
к»$(x,y)$. Точнее, $(x,f(x))$ является локальным максимумом, если существует
интервал $(a,b)$ с $allocal точкой минимума
если он имеет локально наименьшую координату $y$. Опять таки
точнее: $(x,f(x))$ является локальным минимумом, если существует
интервал $(a,b)$ с $локальным экстремумом
является либо локальным минимумом, либо локальным максимумом.
Локальные точки максимума и минимума хорошо различаются на графике
функцию, и поэтому полезны для понимания формы
график. Во многих прикладных задачах мы хотим найти наибольшее или
наименьшее значение, которое достигает функция (например, мы можем захотеть
найти минимальную стоимость, при которой может быть выполнена некоторая задача) и, следовательно,
определение максимальных и минимальных точек будет полезно для прикладных
также проблемы.
показаны на рис. 5.1.1.
Рисунок 5.1.1. Некоторые локальные точки максимума ($A$) и точки минимума ($B$).
Если $(x,f(x))$ — точка, в которой $f(x)$ достигает локального максимума или минимума,
и если производная от $f$ существует в точке $x$, то граф имеет
касательная, а касательная должна быть горизонтальной. Это
достаточно важно, чтобы сформулировать его как теорему, хотя мы не будем его доказывать.
Теорема 5.1.1 (теорема Ферма). Если $f(x)$ имеет локальный экстремум в точке $x=a$ и
$f$ дифференцируема в $a$, тогда $f'(a)=0$.
$qed$
Таким образом, единственный
точки, в которых функция может иметь локальный максимум или минимум
точки, в которых производная равна нулю, как на левом графике в
рисунок 5.1.1,
или производная не определена, как на правом графике. Любое значение
$x$, для которых $f'(x)$ равно нулю или не определено, называется
критическое значение для $f$ и
точка $(x,f(x))$ на кривой называется
критическая точка для $f$.
минимум в $(0,0)$.
Рисунок 5.1.2. Нет ни максимума, ни минимума, хотя производная равна нулю.
Поскольку производная равна нулю или не определена как в локальном максимуме, так и в
точки локального минимума, нам нужен способ определить, какие из них
на самом деле происходит. Большинство
элементарный подход, но часто утомительный или трудный, состоит в том, чтобы
непосредственно проверить, находится ли координата $y$ «близко» к потенциальному
максимум или минимум выше или ниже координаты $y$ в точке
представляет интерес. Конечно, слишком много точек «рядом» с точкой
чтобы проверить, но небольшое размышление показывает, что нам нужно проверить только два, если мы
известно, что $f$ непрерывна (напомним, что это означает, что график
В $f$ нет ни скачков, ни пробелов).
Предположим, например, что мы определили три точки, в которых
$f’$ равно нулю или не существует: $ds (x_1,y_1)$, $ds (x_2,y_2)$, $ds (x_3,y_3)$,
и $ds x_15.
$(a,f(a))$ до $(b,f(b))$, затем вниз до $ds (x_2,f(x_2))$ и где-то в
между ними будет точка локального максимума. (Это не очевидно, это
результат теоремы об экстремальном значении, теорема 6.1.2.)
Но в этом локальном максимуме
производная от $f$ была бы нулевой или не существовала бы, но мы
уже известно, что производная равна нулю или не существует только при $ds x_1$,
$ds x_2$ и $ds x_3$. В результате одно вычисление говорит нам, что
$ds (x_2,f(x_2))$ имеет наибольшую координату $y$ любой точки на
график около $ds x_2$ и левее $ds x_2$. Мы можем выполнить то же самое
тест справа. Если мы обнаружим, что по обе стороны от $ds x_2$ значения
меньше, то должен быть локальный максимум в точке $ds (x_2,f(x_2))$; если
находим, что по обе стороны от $ds x_2$ значения больше, тогда
должен быть локальный минимум в $ds (x_2,f(x_2))$; если мы найдем один из каждого,
то нет ни локального максимума, ни минимума в точке $ds x_2$.
везде и равен нулю в $ds x=pm sqrt{3}/3$. Глядя сначала на
$ds x=sqrt{3}/3$, мы видим, что $ds f(sqrt{3}/3)=-2sqrt{3}/9$. Теперь мы тестируем
две точки по обе стороны
$ds x=sqrt{3}/3$, убедившись, что ни один из них не находится дальше, чем
ближайшее критическое значение; так как $dssqrt{3}-2sqrt{3}/9$
и $ds f(1)=0>-2sqrt{3}/9$, должен быть локальный минимум при
$ds x=sqrt{3}/3$. Для $ds x=-sqrt{3}/3$ мы видим, что
$ds f(-sqrt{3}/3)=2sqrt{3}/9$. На этот раз мы можем использовать $x=0$ и $x=-1$,
и мы находим, что $ds f(-1)=f(0)=0
Конечно, этот пример сделан очень простым благодаря нашему выбору точек для
тест, а именно $x=-1$, $0$, $1$. Мы могли бы использовать другие значения, например
$-5/4$, $1/3$ и $3/4$, но это сделало бы расчеты
значительно утомительнее.
Пример 5.1.3
Найдите все локальные точки максимума и минимума для
$f(x)=sinx+cosx$. Производная равна $f'(x)=cos x-sin x$. Это
всегда определен и равен нулю всякий раз, когда $cos x=sin x$.
$cos x$ и $sin x$ — координаты $x$ и $y$ точек на
единичный круг, мы видим, что $cos x=sin x$, когда $x$ равно $pi/4$,
$pi/4pmpi$, $pi/4pm2pi$, $pi/4pm3pi$ и т. д. Поскольку оба синуса
и косинус имеют период $2pi$, нам нужно только определить состояние
$x=pi/4$ и $x=5pi/4$. Мы можем использовать $0$ и $pi/2$ для проверки
критическое значение $x= pi/4$.
Получаем, что $ds f(pi/4)=sqrt{2}$, $ds f(0)=1
Мы используем $pi$ и $2pi$ для проверки критического значения $x=5pi/4$.
соответствующие значения: $ds f(5pi/4)=-sqrt2$, $ds f(pi)=-1>-sqrt2$,
$ds f(2pi)=1>-sqrt2$, поэтому существует локальный минимум при $x=5pi/4$,
$5pi/4pm2pi$, $5pi/4pm4pi$ и т. д. Более кратко:
локальные минимумы при $5pi/4pm 2kpi$ для
каждое целое число $k$.
$квадрат$
В задачах 1–12 найти все локальные максимумы и минимумы
точек $(x,y)$ методом, описанным в этом разделе.
Пример 5.1.1 92 &$x neq 0$cr}$
(отвечать)
Пример 5.
Для любого действительного числа $x$ существует единственный
целое число $n$ такое, что $n leq x
Пример 5.1.14
Объясните, почему функция $f(x)=1/x$ не имеет локальных
максимумы или минимумы.
Пример 5.1.15
Сколько критических точек может иметь квадратичная полиномиальная функция?
(отвечать)
Пример 5.1.16
Покажите, что кубический многочлен может иметь не более двух критических
точки. Приведите примеры, показывающие, что кубический многочлен может иметь нуль,
одна или две критические точки.
93 + cx +1$, где $c$
является константой. Сколько и каких видов локальных экстремумов существует?
Ваш ответ должен зависеть от значения $c$, т.е.
значения $c$ дадут разные ответы.
Вычислить наименьшее или наибольшее число в диапазоне
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Дополнительно… Меньше
Допустим, вы хотите выяснить, у кого наименьший процент ошибок в производственном цикле на фабрике или у кого самая большая зарплата в вашем отделе.
Если ячейки находятся в непрерывной строке или столбце
Если ячейки не находятся в непрерывной строке или столбце
Для выполнения этой задачи используйте функции MIN, MAX, SMALL или LARGE.
Пример
Скопируйте следующие данные на пустой лист.
|
|
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
См. также
БОЛЬШОЙ
МАКСИМУМ
МИН.
МАЛЕНЬКИЙ
Нахождение максимума и минимума с использованием производных
Где находится функция в верхней или нижней точке? Расчет может помочь!
Максимум — это верхняя точка, а минимум — нижняя точка:
В плавно изменяющейся функции максимум или минимум всегда находится там, где функция сглаживает (за исключением седловой точки ).
Где он выравнивается? Где наклон равен нулю .
Где нулевой наклон? Производная говорит нам!
Перейдем сразу к примеру:
Пример: Мяч подбрасывается в воздух. Его высота в любой момент времени t определяется по формуле:
h = 3 + 14t − 5t 2
Какова его максимальная высота?
Используя производные, мы можем найти наклон этой функции:
d dt h = 0 + 14 − 5(2t)
= 14 − 10t
(см.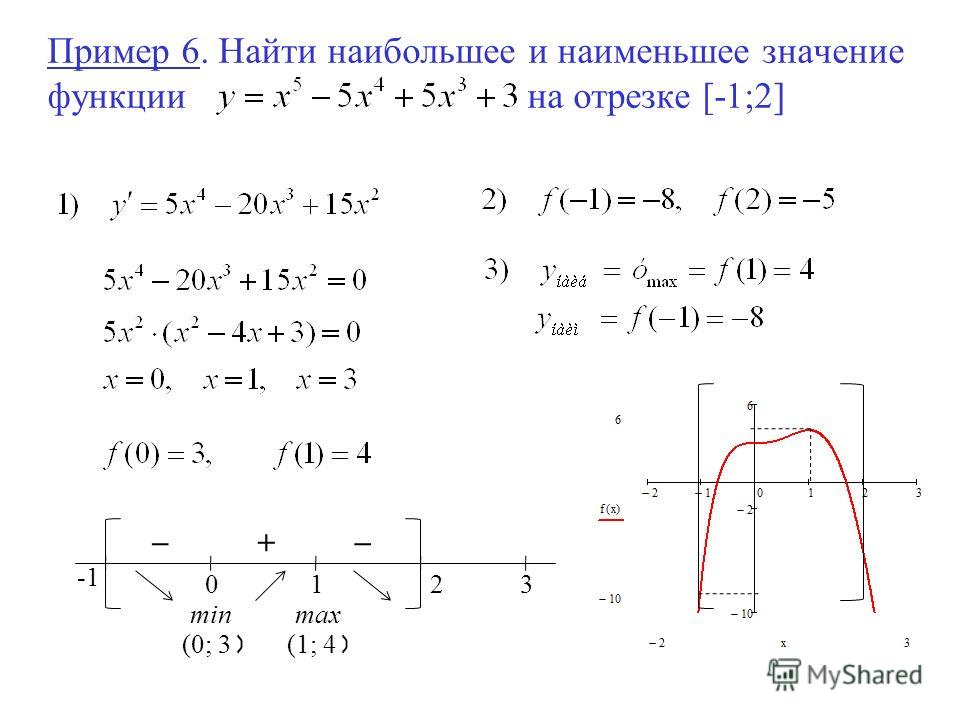
Теперь найдите, когда наклон равен нулю :
14 — 10t = 0
10t = 14
t = 14 /10 = 1,4
Наклон равен нулю при t = 1,4 секунды
, а высота —
h = 3 + 14×1,4 − 5×1,4 2
h = 3 + 19,6 − 9,8 = 12,8
Итак:
Максимальная высота 12,8 м 4t =
Краткий обзор производных
Производная в основном находит наклон функции.
В предыдущем примере мы взяли это:
h = 3 + 14t − 5t 2
и получили следующую производную:
d dt h = 0(5 + 204 − 14) = 14 − 10t
Что говорит нам о наклоне функции в любой момент времени t
Мы использовали следующие производные правила: 0
Откуда мы знаем, что это максимум (или минимум)?
Мы видели это на графике! Но в остальном.
Возьмем производную от наклона (вторая производная исходной функции):
Производная от 14 − 10t равна −10
Это означает, что наклон постоянно уменьшается (-10): при перемещении слева направо наклон начинается с положительного значения (функция возрастает), проходит через ноль (плоская точка), а затем наклон становится отрицательным (функция падает). :
Наклон, который становится меньше (и проходит через 0), означает максимум.
Это называется тестом второй производной
На графике выше я показал наклон до и после, но на практике делаем тест в точке, где наклон равен нулю :
Проверка второй производной
Когда наклон функции равен нулю при x , а вторая производная при x :
- меньше 0, это локальный максимум
- больше 0, это локальный минимум
- равно 0, то тест не пройден (хотя могут быть и другие способы выяснить это)
«Вторая производная: меньше 0 — максимум, больше 0 — минимум»
Example: Find the maxima and minima for:
y = 5x 3 + 2x 2 − 3x
The derivative (slope) is:
d dx y = 15x 2 + 4x − 3
Квадратичное число с нулями:
- x = −3/5
- х = +1/3
Могут ли они быть максимальными или минимальными? (Пока не смотрите на график!)
Вторая производная равна y» = 30x + 4
При x = −3/5:
y» = 30(−3/5) + 4 = −14
меньше 0, поэтому −3/5 является локальным максимумом
При x = +1/3:
y» = 30(+1/3) + 4 = +14
больше 0, поэтому +1/3 является локальным минимумом
(Теперь вы можете посмотреть на график.
слов
Высшая точка называется максимум (множественное число максимум ).
Нижняя точка называется минимум (множественное число минимум ).
Общее слово для обозначения максимума или минимума: экстремум (во множественном числе экстремум ).
Мы говорим местное максимальное (или минимальное), когда могут быть более высокие (или более низкие) точки в другом месте, но не поблизости.
Еще один пример
Пример: Найдите максимум и минимум для:
y = x 3 − 6x 2 + 12x − 5
Производная:
d dx y = 3x 2 − 12x + 12
Какое число является квадратичным с одним нулем в x = 2
Это максимум или минимум?
Вторая производная равна y» = 6x − 12
При x = 2:
y» = 6(2) − 12 = 0
это 0, поэтому тест не пройден 5 2 9000 И вот почему:
Это точка перегиба («седловая точка»)… наклон действительно становится нулевым, но это не максимум и не минимум.
Должен быть дифференцируемым
И есть важный технический момент:
Функция должна быть дифференцируемой (производная должна существовать в каждой точке своей области определения).
Пример: как насчет функции f(x) = |x| (абсолютная величина) ?
При x=0 очень резкое изменение!
На самом деле он там не дифференцируем (как показано на дифференцируемой странице).
Таким образом, мы не можем использовать метод производной для функции абсолютного значения.
Функция также должна быть непрерывной, но любая дифференцируемая функция также непрерывна, так что мы защищены.
max() и min() в Python
В этой статье представлена очень интересная и малоизвестная функция Python, а именно max() и min(). Теперь по сравнению с их аналогом C++, который допускает только два аргумента, которые слишком строго являются числами с плавающей запятой, int или char, эти функции равны 9.
max()
Эта функция используется для вычисления максимального значения, переданного в ее аргументе, и лексикографически наибольшего значения, если в качестве аргументов передаются строки.
Синтаксис: max(a,b,c,..,ключ,по умолчанию) Параметры: a,b,c,.. : аналогичный тип данных. Ключ : функция ключа , в которой передаются итерации и выполняется сравнение. по умолчанию: значение по умолчанию передается, если данная итерация пуста Возвращаемое значение: Возвращает максимум всех аргументов. Исключения : Возвращает TypeError при сравнении конфликтующих типов.
Python3
print ( "Maximum of 4,12,43.3,19 and 100 is : " ,end = "")
print ( max ( 4 , 12 , 43.3 , 19 , 100 ) )
Output :
Maximum of 4,12, 43,3,19 и 100 равно: 100
min()
Эта функция используется для вычисления минимума значений, переданных в ее аргументе, и лексикографически наименьшего значения, если в качестве аргументов передаются строки.
Синтаксис: мин(a,b,c,.., ключ, по умолчанию) Параметры: a,b,c,.. : аналогичный тип данных. ключ : ключевая функция, в которой передаются итерации и выполняется сравнение по умолчанию : значение по умолчанию передается, если данная итерация пуста Возвращаемое значение: Возвращает минимум всех аргументов. Исключения : Возвращает TypeError при сравнении конфликтующих типов.
Python3
8 167 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015
из
Exception
1.
Python3
|
|
| 9015 9015 |
|---|
print ( "Minimum of 4,12,43.3,19 and GeeksforGeeks is : " ,end = "")
print ( min ( 4 , 12 , 43.3 , 19 , "GeeksforGeeks" ) )
Output :
Minimum of 4,12,43.3, 19 и GeeksforGeeks:
Ошибка выполнения:
Обратная трассировка (последний последний вызов): Файл "/home/b5da1d7f834a267f94fbbefe1b31a83c.py", строка 7, в print (мин( 4,12,43.3,19,"GeeksforGeeks") ) TypeError: неупорядоченные типы: str() < int()
Практическое применение
Одним из практических приложений среди многих является нахождение лексикографически самых больших и наименьших строк, т.е. строк, появляющихся первыми в словаре или последними.
Python3
Печать ( ». ( мин ( "Гики" , "Manjeet" , "Algorithm" , 9 "Programithm" .Печать ( «Слово, происходящее в прошлом в DICT. Среди данных:" , конец = "")
Print ( 8 ( 8 ( 8 . 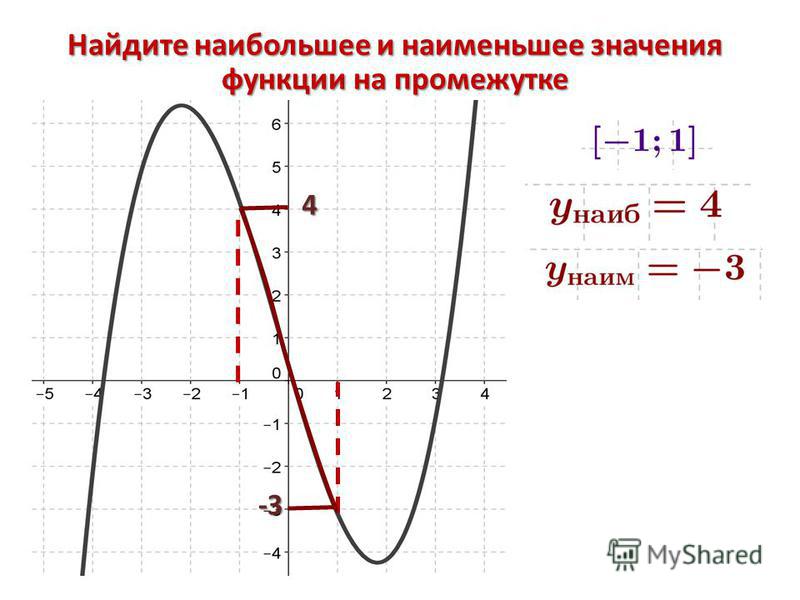
, "Manjeet" , "Алгоритм" , "Программирование" ). среди приведенных: алгоритм
Слово, встречающееся последним в dict. среди приведенных: программирование
Эта статья предоставлена Manjeet Singh . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам.
Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.
Вычисление I - Минимальные и максимальные значения
Онлайн-заметки Пола
Главная
/
Исчисление I
/
Применение производных
/ Минимальные и максимальные значения
Показать мобильное уведомление
Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
Раздел 4-3: Минимальные и максимальные значения
Многие из наших приложений в этой главе будут вращаться вокруг минимальных и максимальных значений функции. Хотя мы все можем визуализировать минимальное и максимальное значения функции, мы хотим быть немного более конкретными в нашей работе здесь. В частности, мы хотим различать два типа минимальных и максимальных значений. Следующее определение дает типы минимальных и/или максимальных значений, которые мы будем рассматривать.
Определение
- Мы говорим, что (fleft( x right)) имеет абсолютный (или глобальный) максимум в (x = c), если(fleft( x right) le fleft( c right)) для каждого (x) в области мы работают над.
- Мы говорим, что (fleft( x right)) имеет относительный (или локальный) максимум в точке (x = c), если (fleft( x right) le fleft ( c right)) для каждого (x) в некотором открытом интервале вокруг (x = c).
- Мы говорим, что (fleft( x right)) имеет абсолютный (или глобальный) минимум в точке (x = c), если (fleft( x right) ge fleft ( c right)) для каждого (x) в домене, над которым мы работаем.
- Мы говорим, что (fleft( x right)) имеет относительный (или локальный) минимум в точке (x = c), если(fleft( x right) ge fleft ( c right)) для каждого (x) в некотором открытом интервале вокруг (x = c).
Обратите внимание: когда мы говорим «открытый интервал вокруг(x = c)», мы имеем в виду, что мы можем найти некоторый интервал (left( {a,b} right)), не включающий конечные точки, например что (а<с
Также мы будем вместе называть точки минимума и максимума функции экстремумами функции. Таким образом, относительные экстремумы будут относиться к относительным минимумам и максимумам, а абсолютные экстремумы — к абсолютным минимумам и максимумам.
Теперь давайте немного поговорим о тонкой разнице между абсолютным и относительным в приведенном выше определении.
У нас будет абсолютный максимум (или минимум) при (x = c) при условии, что (fleft( c right)) является наибольшим (или наименьшим) значением, которое функция когда-либо принимала в области над которым мы работаем. Кроме того, когда мы говорим «область, над которой мы работаем», это просто означает диапазон (x), который мы выбрали для работы с данной проблемой. Могут быть и другие значения (x), которые мы действительно можем подставить в функцию, но по какой-то причине исключили их.
Относительный максимум или минимум немного отличаются. Все, что требуется для того, чтобы точка была относительным максимумом или минимумом, — это чтобы эта точка была максимумом или минимумом в некотором интервале (x) вокруг (x = c).
Также обратите внимание, что для того, чтобы точка была относительным экстремумом, мы должны иметь возможность смотреть на значения функции по обе стороны от (x = c), чтобы увидеть, действительно ли она является максимумом или минимумом в этой точке. Это означает, что относительные экстремумы не возникают в конечных точках области. Они могут возникать только внутри домена.
По предыдущему пункту ведутся споры. Некоторые люди считают, что относительные экстремумы могут возникать на конечных точках домена. Однако в этом классе мы будем использовать определение, в котором говорится, что они не могут встречаться в конечных точках домена. Это будет обсуждаться более подробно в конце раздела, как только мы позаботимся о соответствующем факте.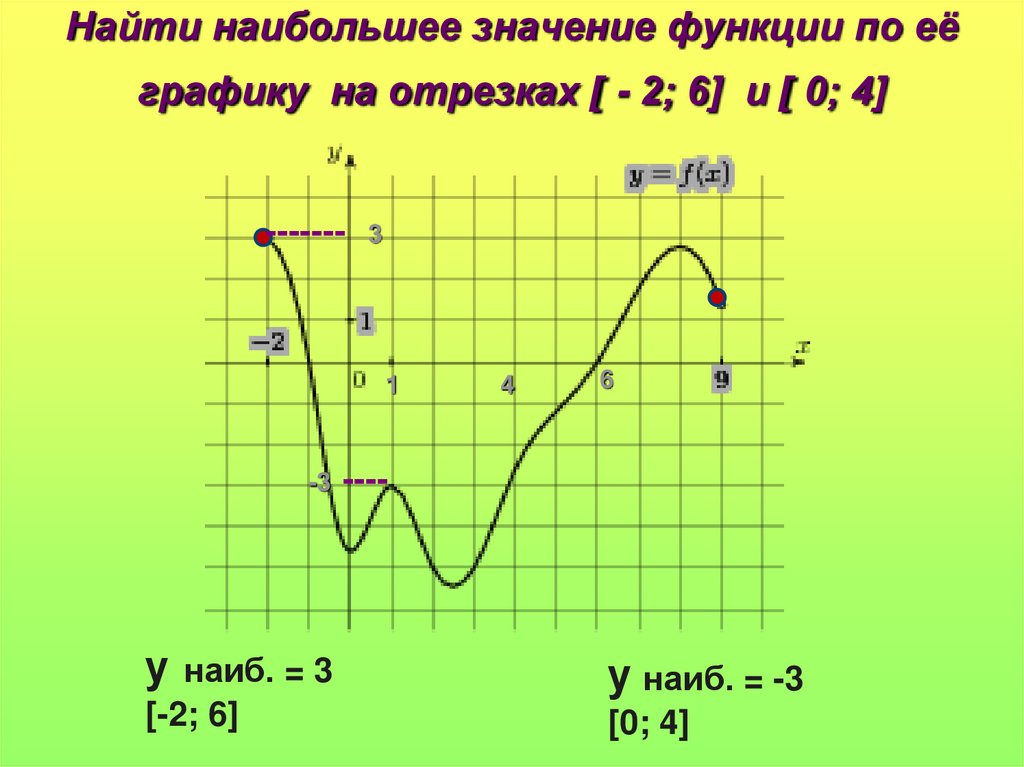
Обычно легче понять определения, взглянув на график.
Для функции, показанной на этом графике, мы имеем относительные максимумы в точках (x = b) и (x = d). Обе эти точки являются относительными максимумами, поскольку они находятся внутри показанной области и являются самой большой точкой на графике в некотором интервале вокруг точки. Мы также имеем относительный минимум в (x = c), так как эта точка находится внутри области и является самой нижней точкой на графике в интервале вокруг нее. Крайняя правая конечная точка (x = e) не будет относительным минимумом, поскольку это конечная точка.
Функция будет иметь абсолютный максимум в точке (x = d) и абсолютный минимум в точке (x = a). Эти две точки являются наибольшей и наименьшей величиной, которой когда-либо будет функция. Мы также можем заметить, что абсолютные экстремумы функции будут возникать либо на концах области, либо на относительных экстремумах. Мы будем использовать эту идею в следующих разделах, так что она важнее, чем может показаться в настоящее время.
Давайте быстро рассмотрим несколько примеров, чтобы убедиться, что у нас есть определения абсолютных экстремумов и относительных экстремумов. 92}hspace{0.25in}{mbox{on}}hspace{0.25in}left[ { - 1,2} right]]
Показать решение
Поскольку эту функцию достаточно легко изобразить в виде графика, давайте сделаем это. Однако нам нужен только график на интервале (left[ { - 1,2} right]). Вот график:
Обратите внимание, что мы использовали точки в конце графика, чтобы напомнить нам, что график заканчивается в этих точках.
Теперь мы можем определить экстремумы на графике. Похоже, у нас есть относительный и абсолютный минимум нуля при (x = 0) и абсолютный максимум четыре при (x = 2). Обратите внимание, что (x = - 1) не является относительным максимумом, поскольку он находится в конечной точке интервала. 92}hspace{0.25in}{mbox{on}}hspace{0.25in}left[ { - 2,2} right]]
Показать решение
Вот график для этой функции.
В этом случае у нас все еще есть относительный и абсолютный минимум нуля в точке (x = 0). У нас также все еще есть абсолютный максимум четыре. Однако, в отличие от первого примера, это произойдет в двух точках: (x = - 2) и (x = 2).
Опять же, функция не имеет относительных максимумов.
Как показано в этом примере, может быть только одно абсолютное максимальное или абсолютное минимальное значение, но они могут встречаться более чем в одном месте домена. 92}]
Показать решение
В этом случае мы не указали домен, поэтому предполагается, что мы возьмем максимально возможный домен. Для этой функции это означает все действительные числа. Вот график.
В этом случае график не перестает расти ни с одной стороны, поэтому для этой функции нет никаких максимумов. Независимо от того, какую точку мы выберем на графике, с обеих сторон будут точки как больше, так и меньше, поэтому у нас не может быть никаких максимумов (любого рода, относительных или абсолютных) на графике.
Показать решение
Опять же, на этот раз мы не ограничиваем домен, поэтому вот график.
В этом случае функция не имеет ни относительных, ни абсолютных экстремумов.
Как мы видели в предыдущем примере, функции не обязательно должны иметь какие-либо экстремумы, относительные или абсолютные.
Пример 6 Определите абсолютный и относительный экстремумы для следующей функции.
[fвлево( x вправо) = cos влево( x вправо)]
Показать решение
Мы не ограничивали домен для этой функции. Вот график.
Косинус имеет экстремумы (относительные и абсолютные), которые встречаются во многих точках. Косинус имеет как относительный, так и абсолютный максимум 1 на
[x = ldots - 4pi ,, - 2pi ,,,0,,,2pi ,,,4pi , ldots ]
Косинус также имеет как относительный, так и абсолютный минимум -1 в точке
[x = ldots - 3pi ,, - pi ,,,pi ,,,3pi , ldots ]
Как показывает этот пример, граф фактически может иметь экстремумы в большом количестве (в данном случае бесконечном) точек.
Теперь мы рассмотрели довольно много примеров и можем использовать эти примеры, чтобы увидеть хороший факт об абсолютных экстремумах. Во-первых, давайте заметим, что все приведенные выше функции были непрерывными функциями. Далее обратите внимание, что каждый раз, когда мы ограничивали домен закрытым интервалом (, т.е. , интервал содержит свои конечные точки), мы получали абсолютные максимумы и абсолютные минимумы. Наконец, только в одном из трех примеров, где мы не ограничивали домен, мы получили и абсолютный максимум, и абсолютный минимум.
Эти наблюдения приводят нас к следующей теореме.
Теорема об экстремальном значении
Предположим, что (fleft( x right)) непрерывно на интервале (left[ {a,b} right]), тогда существуют два числа (a le c,d le b), так что (fleft( c right)) является абсолютным максимумом функции и (fleft( d right)) является абсолютным минимумом функции .
Итак, если у нас есть непрерывная функция на интервале (left[ {a,b} right]), то мы гарантированно имеем как абсолютный максимум, так и абсолютный минимум функции где-то на интервале.
функция теперь будет иметь оба абсолютных экстремума. Мы можем столкнуться с проблемами только в том случае, если интервал содержит точку разрыва. Если нет, то теорема верна.
Следует также отметить, что только потому, что функция не является непрерывной в точке, это не означает, что у нее не будет обоих абсолютных экстремумов на интервале, содержащем эту точку. Ниже приведен график функции, которая не является непрерывной в точке заданного интервала, но имеет оба абсолютных экстремума.
Этот график не является непрерывным в точке (x = c), но имеет как абсолютный максимум ((x = b)) так и абсолютный минимум ((x = c)). Также отметим, что в данном случае один из абсолютных экстремумов пришелся на точку разрыва, но это не обязательно. Абсолютный минимум легко мог быть в другой конечной точке или в какой-то другой точке внутри области. Суть здесь в том, что этот график не непрерывен и все же имеет оба абсолютных экстремума
Суть всего этого в том, что мы должны быть осторожны, чтобы использовать теорему об экстремальном значении только тогда, когда выполняются условия теоремы, и не истолковывать неправильно результат, если условия не соблюдены.
Чтобы использовать теорему об экстремальном значении, у нас должен быть интервал, включающий конечные точки, часто называемый закрытым интервалом, и функция должна быть непрерывной на этом интервале. Если у нас нет замкнутого интервала и/или функция не является непрерывной на интервале, то функция может иметь или не иметь абсолютных экстремумов.
Нам нужно обсудить одну последнюю тему в этом разделе, прежде чем перейти к первому основному применению производной, которое мы собираемся рассмотреть в этой главе.
Теорема Ферма
Если (fleft( x right)) имеет относительный экстремум в точке (x = c) и (f'left( c right)) существует, то (x = c) является критической точкой (fleft( x right)). На самом деле это будет критическая точка такая, что (f'left( c right) = 0).
Доказательство этой теоремы см. в разделе «Доказательства производных приложений» главы «Дополнительно».
Также обратите внимание, что мы можем сказать, что (f'left( c right) = 0), потому что мы также предполагаем, что (f'left( c right)) существует. 92}). Мы видели, что эта функция имеет относительный минимум при (x = 0) в нескольких более ранних примерах. Значит, по теореме Ферма (x = 0) должна быть критической точкой. Производная функции
[f'влево( х вправо) = 2x]
Действительно, (x = 0) является критической точкой.
Не злоупотребляйте этой теоремой. Это не говорит о том, что критическая точка будет относительным экстремумом. Чтобы убедиться в этом, рассмотрим следующий случай.
92}]
Ясно, что (x = 0) является критической точкой. Однако в более раннем примере мы видели, что эта функция не имеет никаких относительных экстремумов. Таким образом, критические точки не обязательно должны быть относительными экстремумами.
Также обратите внимание, что эта теорема ничего не говорит об абсолютных экстремумах. Абсолютный экстремум может быть или не быть критической точкой.
Прежде чем мы покинем этот раздел, нам нужно обсудить пару вопросов.
Во-первых, теорема Ферма работает только для критических точек, в которых (f'left( c right) = 0). Это, однако, не означает, что относительные экстремумы не будут возникать в критических точках, где производная не существует. Чтобы увидеть это, рассмотрим (fleft( x right) = left| x right|). Очевидно, что эта функция имеет относительный минимум при (x = 0), но в предыдущем разделе мы показали на примере, что (f'left( 0 right)) не существует.
Все это означает, что если мы хотим найти относительные экстремумы, все, что нам действительно нужно сделать, это посмотреть на критические точки, поскольку это места, где могут существовать относительные экстремумы.
Наконец, вспомните, что в начале раздела мы заявили, что относительных экстремумов не будет в конечных точках рассматриваемого нами интервала. Причина этого в том, что если мы допустим относительные экстремумы, это вполне может (и фактически в большинстве случаев) нарушить теорему Ферма. Нет оснований ожидать, что конечные точки интервалов будут критическими точками любого вида. Поэтому мы не допускаем существования относительных экстремумов на концах интервалов.
Получение наибольшего, наименьшего и среднего значения элемента массива в JavaScript | Чад Кэмпбелл
Фото Хуанхо Харамильо на Unsplash
Приложениям часто нужно найти наибольшее или наименьшее значение в списке. Фактически, эталонный инструмент, используемый для поиска эффективного способа слияния массивов в JavaScript, должен был получить максимальное и минимальное время выполнения. Аналогичный тестовый инструмент используется в этой статье , чтобы определить способ эффективного получения наибольшего и наименьшего значения в массиве JavaScript в простой способ. Для достижения этой цели необходимо сначала идентифицировать тип элементов массива.
Массив состоит из элементов, которые включают в себя примитивные значения, объекты или и то, и другое. По этой причине в этой статье будет рассмотрена тема для каждого типа элементов. Во-первых, вы увидите, как эффективно находить наибольшее и наименьшее значение в массиве примитивных значений. Затем вы увидите, как получить самое высокое и самое низкое значение в массиве объектов на основе значения свойства. Наконец, в этой статье будет представлен анализ результатов, которые меня удивили. Если у вас мало времени, вот вывод:
Вывод (или TL;DR)
Вам нужно определить, что важнее для вашего сценария: скорость или масштаб. Самый безопасный подход — использовать оператор for. Если скорость критична, вам следует рассмотреть вариант с использованием функций JavaScript Math.[max/min] для небольших массивов. Однако эти функции не будут работать для больших массивов. По этой причине вы должны протестировать свой подход с наибольшим количеством ожидаемых элементов, чтобы избежать непредвиденных последствий.
Вышеприведенный вывод был определен путем реализации 32 для этой статьи. Исходный репозиторий для этой статьи можно найти здесь. Этот репозиторий включает образцы, показанные в следующих разделах, и инструмент для тестирования. Если вы найдете все это полезным, пожалуйста, следуйте за мной сейчас для аналогичного контента. Давайте начнем.
JavaScript позволяет находить самые большие и самые маленькие значения в массиве различными способами. Для этой статьи я реализовал 16 функций, чтобы найти «лучший» способ получить эти значения из массива примитивных значений. В контексте этой статьи «лучший» означает а) быструю и удобочитаемую реализацию, б) надежную и в) в среднем эффективную работу. С учетом этих целей были созданы следующие 8 образцов для поиска наименьшего значения в массиве:
образец 1 образец 2 образец 3 образец 4 образец 5 образец 6 образец 7 образец 8
Образцы 1–8 показывают различные способы получения наименьшего значения в массиве примитивных значений. Как было сказано в начале этой статьи, целью была простота. По этой причине в примерах используются встроенные функции JavaScript. Популярные компьютерные алгоритмы, такие как «разделяй и властвуй» и объединение пар, были включены в этот анализ 90 398, а не 90 399. Эти алгоритмы также не использовались для получения наибольшего и наименьшего значений в массиве объектов на основе значения свойства.
JavaScript позволяет получить самые высокие и самые низкие значения из массива несколькими способами. Используя те же цели, о которых сообщалось ранее, были созданы следующие 8 образцов для поиска наименьшего значения в массиве объектов: объектов. Эти изображения почти идентичны изображениям 1–8 с некоторыми небольшими отличиями. Однако все становится интереснее, когда вы анализируете производительность.
По моему опыту, ничто так не привлекает внимание разработчиков к блоку кода, как некоторые тесты. Тесты и код немедленно проверяются на наличие чего-то неуместного или того, что можно улучшить. Это может быть хорошо. Я готов быть цивилизованным, если вы 😉. Для начала приведу результаты, которые я наблюдал при запуске эталонного инструмента из исходного репозитория этой статьи на 13-дюймовом MacBook Air 2020 года с macOS версии 12.0.1 в Google Chrome 96. 0.4664.55.
изображение 17 — результаты тестов
На изображении 17 показана сводка результатов тестов для ряда сценариев. Эта сводка является результатом четырех других таблиц, представленных здесь. Каждый сценарий запускался 100 раз с 1, 10, 100, 1000, 10 000, 100 000 и 1 000 000 элементов. В результате этих тестовых прогонов и появившихся данных я сделал следующие наблюдения:
- Функции Math.[max/min] в среднем самые быстрые
- Math.[max/min] делают , а не работать с большими массивами.
- Функция Array.map также , а не работает с большими массивами.
- Старомодные операторы for и while кажутся лучшим сочетанием скорости и безопасности.
Для более точного измерения эффективности каждого подхода следует использовать обозначение Big-O. Если вы хотите узнать о нотации Big-O, ознакомьтесь со следующим дочерним курсом нотации Big-O на Educative. Миллисекунды были использованы на изображении 17 для упрощения обсуждения.
Эти наблюдения позволили мне прийти к выводам, изложенным в начале этой статьи. Я рекомендую вам запустить тесты самостоятельно и поэкспериментировать самостоятельно. Лично я надеюсь, что вы запомните эти наблюдения, чтобы создавать лучшие приложения и сервисы. Единственная причина, по которой я написал эту статью, заключалась в том, что я столкнулся с RangeError в приложении. В RangeError было сообщение: Максимальный размер стека вызовов превысил . Код, который я унаследовал, использовал Math.min и Math.max, которые были источником. Хотя реализация выглядела корректно, это был тот случай, когда дьявол прятался в деталях.
В этой статье вы узнали, как получить наибольшее и наименьшее значение элемента массива в JavaScript. Если вы найдете более эффективный подход, надеюсь, вы поделитесь им в комментариях ниже. Если вы нашли эту статью полезной, пожалуйста, поаплодируйте 👏 или похлопайте в ладоши ниже. Это позволяет мне и другим знать, что вы нашли эту статью полезной.
No related posts.
Добавить комментарий
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Email *
Сайт
Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.
Как найти наибольшее и наименьшее значения функции на отрезке?
Для этого мы следуем известному алгоритму:
1 . Находим ОДЗ функции.
2 . Находим производную функции
3 . Приравниваем производную к нулю
4 . Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:
Если на промежутке I производная функции 0″ title=»f^(x)>0″/>, то функция возрастает на этом промежутке.
Если на промежутке I производная функции , то функция убывает на этом промежутке.
5 . Находим точки максимума и минимума функции.
В точке максимума функции производная меняет знак с «+» на «-«.
В точке минимума функции производная меняет знак с «-» на «+».
6 . Находим значение функции в концах отрезка,
- затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
- или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции
Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.
Рассмотрим функцию . График этой функции выглядит так:
В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
1. Рассмотрим функцию на отрезке
Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: , а наименьшее — в левом: .
2. Рассмотрим функцию на отрезке
Очевидно, что наибольшее значение функция принимает в точке максимума , а наименьшее — в одном из концов отрезка, то есть надо найти значения и и выбрать из них наименьшее.
3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть и .
Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть и .
Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:
1. ОДЗ функции — множество действительных чисел.
2.
3. , если или
Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:
Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике
1 . Задание B15 (№ 26695)
Найдите наибольшее значение функции на отрезке .
1. Функция определена при всех действительных значениях х
2.
3.
Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
Ответ: 5.
2 . Задание B15 (№ 26702)
Найдите наибольшее значение функции на отрезке [].
1. ОДЗ функции /2+k, k» title=»x<>/2+k, k»/>
2.
Производная равна нулю при , однако, в этих точках она не меняет знак:
, следовательно, =3″ title=»3/>>=3″/>, значит, =0″ title=»3/>-3>=0″/>, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, при .
Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:
=0″ title=»y^=3/>-3=<3-3cos^2>/>=<3sin^2>/>=3tg^2>=0″/>
Ответ: 5.
3 . Задание B15 (№ 26708)
Найдите наименьшее значение функции на отрезке [].
1. ОДЗ функции : /2+k, k» title=»x<>/2+k, k»/>
2.
3.
,
Расположим корни этого уравнения на тригонометрической окружности.
Промежутку принадлежат два числа: и
Расставим знаки. Для этого определим знак производной в точке х=0: . При переходе через точки и производная меняет знак.
Изобразим смену знаков производной функции на координатной прямой:
Очевидно, что точка является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции на отрезке , нужно сравнить значения функции в точке минимума и в левом конце отрезка, .
Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а таковым на является, следовательно подставим в уравнение функции
Ответ: -1
И.В. Фельдман, репетитор по математике.
Как решать задачи B15 без производных
Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.
В этом случае работают другие приемы, один из которых — монотонность.
Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:
Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:
Другими словами, для возрастающей функции Для убывающей функции все наоборот:
Например, логарифм монотонно возрастает, если основание и монотонно убывает, если Не забывайте про область допустимых значений логарифма:
f ( x ) = log a x ( a > 0; a ≠ 1; x > 0)
Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:
Показательная функция ведет себя аналогично логарифму: растет и убывает Но в отличие от логарифма, показательная функция определена для всех чисел, а не только
f ( x ) = a x (a > 0)
Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.
Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, становится тяжело считать производную. Что при этом происходит — сейчас разберем.
Координаты вершины параболы
Чаще всего аргумент функции заменяется на квадратный трехчлен вида Его график — стандартная парабола, в которой нас интересуют:
- Ветви параболы — могут уходить вверх или вниз Задают направление, в котором функция может принимать бесконечные значения;
- Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее или наибольшее значение.
Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:
Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:
Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно для квадратного трехчлена, а на функцию — забить.
Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:
- Отрезок [ a ; b ] в условии задачи отсутствует. Следовательно, вычислять не требуется. Остается рассмотреть лишь точки экстремума;
- Но таких точек всего одна — это вершина параболы координаты которой вычисляются буквально устно и без всяких производных.
Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:
- Выписать уравнение параболы и найти ее вершину по формуле:
- Найти значение исходной функции в этой точке: Если никаких дополнительных условий нет, это и будет ответом.
На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.
Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.
Задача. Найдите наименьшее значение функции:
Под корнем стоит квадратичная функция График этой функции − парабола ветвями вверх, поскольку коэффициент
x 0 = − b /(2 a ) = −6/(2 · 1) = −6/2 = −3
Поскольку ветви параболы направлены вверх, в точке функция принимает наименьшее значение.
Корень монотонно возрастает, значит точка минимума всей функции. Имеем:
Задача. Найдите наименьшее значение функции:
Под логарифмом снова квадратичная функция: График — парабола ветвями вверх,
x 0 = − b /(2 a ) = −2/(2 · 1) = −2/2 = −1
Итак, в точке квадратичная функция принимает наименьшее значение. Но функция монотонная, поэтому:
y min = y (−1) = log 2 ((−1) 2 + 2 · (−1) + 9) = . = log 2 8 = 3
Задача. Найдите наибольшее значение функции:
В показателе стоит квадратичная функция Перепишем ее в нормальном виде:
Очевидно, что график этой функции — парабола, ветви вниз Поэтому вершина будет точкой максимума:
Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке
Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.
Следствия из области определения функции
Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:
Аргумент логарифма должен быть положительным:
y = log a f ( x ) ⇒ f ( x ) > 0
Арифметический квадратный корень существует только из неотрицательных чисел:
Знаменатель дроби не должен равняться нулю:
Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:
Задача. Найдите наибольшее значение функции:
Под корнем снова квадратичная функция: Ее график — парабола, но ветви вниз, поскольку Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.
Выписываем область допустимых значений (ОДЗ):
3 − 2 x − x 2 ≥ 0 ⇒ x 2 + 2 x − 3 ≤ 0 ⇒
Теперь найдем вершину параболы:
Точка принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции а также на концах ОДЗ:
Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.
Задача. Найдите наименьшее значение функции:
Внутри логарифма стоит квадратичная функция Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:
6 x − x 2 − 5 > 0 ⇒ x 2 − 6 x + 5 x 0 = − b /(2 a ) = −6/(2 · (−1)) = −6/(−2) = 3
Вершина параболы подходит по ОДЗ: Но поскольку концы отрезка нас не интересуют, считаем значение функции только
y min = y (3) = log 0,5 (6 · 3 − 3 2 − 5) =
Наибольшее и наименьшее значение функции
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно мы определяем эти значения в рамках некоторого интервала x , который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [ a ; b ] , так и открытый интервал ( a ; b ) , ( a ; b ] , [ a ; b ) , бесконечный интервал ( a ; b ) , ( a ; b ] , [ a ; b ) либо бесконечный промежуток — ∞ ; a , ( — ∞ ; a ] , [ a ; + ∞ ) , ( — ∞ ; + ∞ ) .
В этом материале мы расскажем, как вычисляется наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x) y = f ( x ) .
Основные определения
Начнем, как всегда, с формулировки основных определений.
Наибольшее значение функции y = f ( x ) на некотором промежутке x – это значение m a x y = f ( x 0 ) x ∈ X , которое при любом значении x x ∈ X , x ≠ x 0 делает справедливым неравенство f ( x ) ≤ f ( x 0 ) .
Наименьшее значение функции y = f ( x ) на некотором промежутке x – это значение m i n x ∈ X y = f ( x 0 ) , которое при любом значении x ∈ X , x ≠ x 0 делает справедливым неравенство f(X f ( x ) ≥ f ( x 0 ) .
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее самое большое значение на известном интервале при абсциссе x 0 , а наименьшее – это самое маленькое принимаемое значение на том же интервале при x 0 .
Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0 .
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения ( m a x y и m i n y ) в стационарных точках, расположенных на отрезке [ — 6 ; 6 ] .
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [ — 3 ; 2 ] . Они соответствуют наибольшему и наименьшему значению заданной функции.
Наибольшее и наименьшее значение функции на открытом интервале
Теперь посмотрим на четвертый рисунок. В нем функция принимает m a x y (наибольшее значение) и m i n y (наименьшее значение) в стационарных точках на открытом интервале ( — 6 ; 6 ) .
Если мы возьмем интервал [ 1 ; 6 ) , то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x , равном 6 , если бы x = 6 принадлежала интервалу. Именно этот случай нарисован на графике 5 .
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала ( — 3 ; 2 ] , а о наибольшем значении мы не можем сделать определенных выводов.
Наибольшее и наименьшее значение функции на бесконечности
На рисунке 7 мы видим, что функция будет иметь m a x y в стационарной точке, имеющей абсциссу, равную 1 . Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y = 3 .
Если мы возьмем интервал x ∈ 2 ; + ∞ , то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2 , то значения функции будут стремиться к минус бесконечности, поскольку прямая x = 2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y = 3 . Именно этот случай изображен на рисунке 8 .
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
- Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x = a и x = b .
- 5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Условие: задана функция y = x 3 + 4 x 2 . Определите ее наибольшее и наименьшее значение на отрезках [ 1 ; 4 ] и [ — 4 ; — 1 ] .
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0 . Иными словами, D ( y ) : x ∈ ( — ∞ ; 0 ) ∪ 0 ; + ∞ . Оба отрезка, заданных в условии, будут находиться внутри области определения.
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y ‘ = x 3 + 4 x 2 ‘ = x 3 + 4 ‘ · x 2 — x 3 + 4 · x 2 ‘ x 4 = = 3 x 2 · x 2 — ( x 3 — 4 ) · 2 x x 4 = x 3 — 8 x 3
Мы узнали, что производная функции будет существовать во всех точках отрезков [ 1 ; 4 ] и [ — 4 ; — 1 ] .
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x 3 — 8 x 3 = 0 . У него есть только один действительный корень, равный 2 . Он будет стационарной точкой функции и попадет в первый отрезок [ 1 ; 4 ] .
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x = 1 , x = 2 и x = 4 :
y ( 1 ) = 1 3 + 4 1 2 = 5 y ( 2 ) = 2 3 + 4 2 2 = 3 y ( 4 ) = 4 3 + 4 4 2 = 4 1 4
Мы получили, что наибольшее значение функции m a x y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 будет достигнуто при x = 1 , а наименьшее m i n y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 – при x = 2 .
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y ( — 1 ) = ( — 1 ) 3 + 4 ( — 1 ) 2 = 3
Значит, m a x y x ∈ [ — 4 ; — 1 ] = y ( — 1 ) = 3 , m i n y x ∈ [ — 4 ; — 1 ] = y ( — 4 ) = — 3 3 4 .
Ответ: Для отрезка [ 1 ; 4 ] — m a x y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 , m i n y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 , для отрезка [ — 4 ; — 1 ] — m a x y x ∈ [ — 4 ; — 1 ] = y ( — 1 ) = 3 , m i n y x ∈ [ — 4 ; — 1 ] = y ( — 4 ) = — 3 3 4 .
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0 , решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.
- Если интервал имеет вид [ a ; b ) , то нам надо вычислить значение функции в точке x = a и односторонний предел lim x → b — 0 f ( x ) .
- Если интервал имеет вид ( a ; b ] , то нам надо вычислить значение функции в точке x = b и односторонний предел lim x → a + 0 f ( x ) .
- Если интервал имеет вид ( a ; b ) , то нам надо вычислить односторонние пределы lim x → b — 0 f ( x ) , lim x → a + 0 f ( x ) .
- Если интервал имеет вид [ a ; + ∞ ) , то надо вычислить значение в точке x = a и предел на плюс бесконечности lim x → + ∞ f ( x ) .
- Если интервал выглядит как ( — ∞ ; b ] , вычисляем значение в точке x = b и предел на минус бесконечности lim x → — ∞ f ( x ) .
- Если — ∞ ; b , то считаем односторонний предел lim x → b — 0 f ( x ) и предел на минус бесконечности lim x → — ∞ f ( x )
- Если же — ∞ ; + ∞ , то считаем пределы на минус и плюс бесконечности lim x → + ∞ f ( x ) , lim x → — ∞ f ( x ) .
- В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.
Пример 2
Условие: дана функция y = 3 e 1 x 2 + x — 6 — 4 . Вычислите ее наибольшее и наименьшее значение в интервалах — ∞ ; — 4 , — ∞ ; — 3 , ( — 3 ; 1 ] , ( — 3 ; 2 ) , [ 1 ; 2 ) , 2 ; + ∞ , [ 4 ; + ∞ ) .
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0 :
x 2 + x — 6 = 0 D = 1 2 — 4 · 1 · ( — 6 ) = 25 x 1 = — 1 — 5 2 = — 3 x 2 = — 1 + 5 2 = 2 ⇒ D ( y ) : x ∈ ( — ∞ ; — 3 ) ∪ ( — 3 ; 2 ) ∪ ( 2 ; + ∞ )
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
y ‘ = 3 e 1 x 2 + x — 6 — 4 ‘ = 3 · e 1 x 2 + x — 6 ‘ = 3 · e 1 x 2 + x — 6 · 1 x 2 + x — 6 ‘ = = 3 · e 1 x 2 + x — 6 · 1 ‘ · x 2 + x — 6 — 1 · x 2 + x — 6 ‘ ( x 2 + x — 6 ) 2 = — 3 · ( 2 x + 1 ) · e 1 x 2 + x — 6 x 2 + x — 6 2
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x = — 1 2 . Это стационарная точка, которая находится в интервалах ( — 3 ; 1 ] и ( — 3 ; 2 ) .
Вычислим значение функции при x = — 4 для промежутка ( — ∞ ; — 4 ] , а также предел на минус бесконечности:
y ( — 4 ) = 3 e 1 ( — 4 ) 2 + ( — 4 ) — 6 — 4 = 3 e 1 6 — 4 ≈ — 0 . 456 lim x → — ∞ 3 e 1 x 2 + x — 6 = 3 e 0 — 4 = — 1
Поскольку 3 e 1 6 — 4 > — 1 , значит, m a x y x ∈ ( — ∞ ; — 4 ] = y ( — 4 ) = 3 e 1 6 — 4 . Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение — 1 , поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к — 3 с левой стороны, мы получим только интервал значений:
lim x → — 3 — 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 — 0 3 e 1 ( x + 3 ) ( x — 3 ) — 4 = 3 e 1 ( — 3 — 0 + 3 ) ( — 3 — 0 — 2 ) — 4 = = 3 e 1 ( + 0 ) — 4 = 3 e + ∞ — 4 = + ∞ lim x → — ∞ 3 e 1 x 2 + x — 6 — 4 = 3 e 0 — 4 = — 1
Значит, значения функции будут расположены в интервале — 1 ; + ∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x = — 1 2 , если x = 1 . Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к — 3 с правой стороны:
y — 1 2 = 3 e 1 — 1 2 2 + — 1 2 — 6 — 4 = 3 e 4 25 — 4 ≈ — 1 . 444 y ( 1 ) = 3 e 1 1 2 + 1 — 6 — 4 ≈ — 1 . 644 lim x → — 3 + 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 ( x + 3 ) ( x — 2 ) — 4 = 3 e 1 — 3 + 0 + 3 ( — 3 + 0 — 2 ) — 4 = = 3 e 1 ( — 0 ) — 4 = 3 e — ∞ — 4 = 3 · 0 — 4 = — 4
У нас получилось, что наибольшее значение функция примет в стационарной точке m a x y x ∈ ( 3 ; 1 ] = y — 1 2 = 3 e — 4 25 — 4 . Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до — 4 .
Для интервала ( — 3 ; 2 ) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y — 1 2 = 3 e 1 — 1 2 2 + — 1 2 — 6 — 4 = 3 e — 4 25 — 4 ≈ — 1 . 444 lim x → — 3 + 0 3 e 1 x 2 + x — 6 — 4 = — 4 lim x → 2 — 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 ( x + 3 ) ( x — 2 ) — 4 = 3 e 1 ( 2 — 0 + 3 ) ( 2 — 0 — 2 ) — 4 = = 3 e 1 — 0 — 4 = 3 e — ∞ — 4 = 3 · 0 — 4 = — 4
Значит, m a x y x ∈ ( — 3 ; 2 ) = y — 1 2 = 3 e — 4 25 — 4 , а наименьшее значение определить невозможно, и значения функции ограничены снизу числом — 4 .
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [ 1 ; 2 ) наибольшее значение функция примет при x = 1 , а найти наименьшее невозможно.
На промежутке ( 2 ; + ∞ ) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка — 1 ; + ∞ .
lim x → 2 + 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 ( x + 3 ) ( x — 2 ) — 4 = 3 e 1 ( 2 + 0 + 3 ) ( 2 + 0 — 2 ) — 4 = = 3 e 1 ( + 0 ) — 4 = 3 e + ∞ — 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x — 6 — 4 = 3 e 0 — 4 = — 1
Вычислив, чему будет равно значение функции при x = 4 , выясним, что m a x y x ∈ [ 4 ; + ∞ ) = y ( 4 ) = 3 e 1 14 — 4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y = — 1 .
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
http://www.berdov.com/ege/extremum/other_way/
http://zaochnik.com/spravochnik/matematika/funktsii/naibolshee-i-naimenshee-znachenie-funktsii/

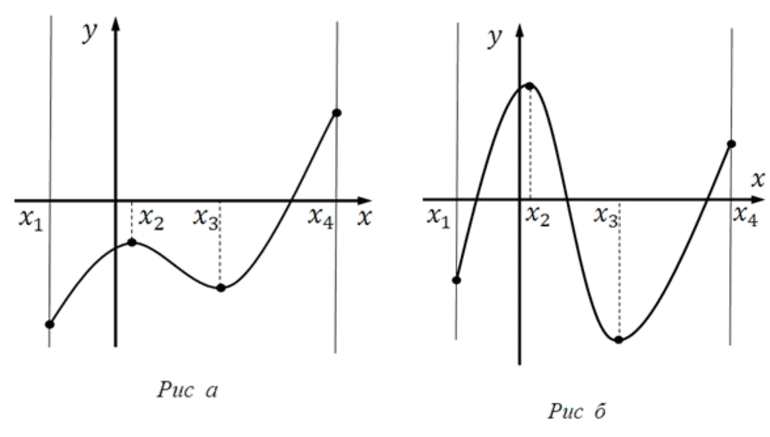
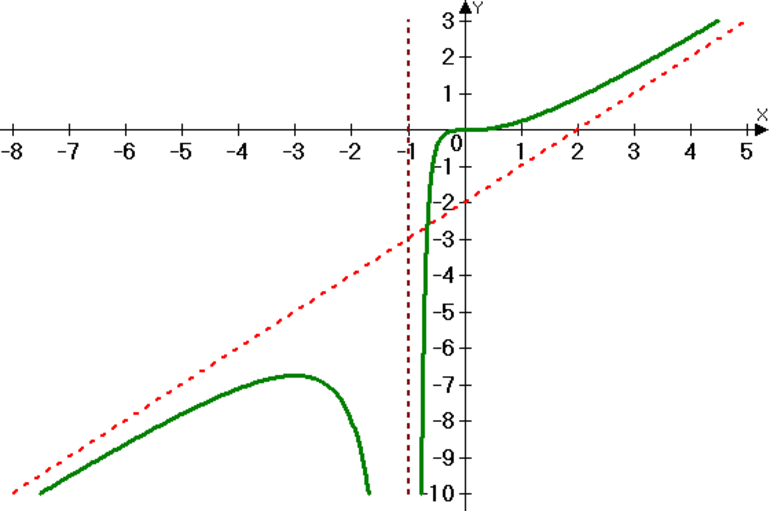

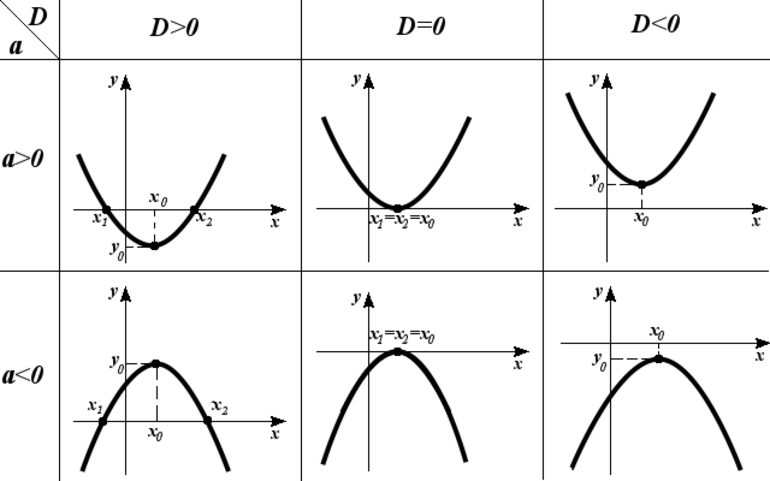



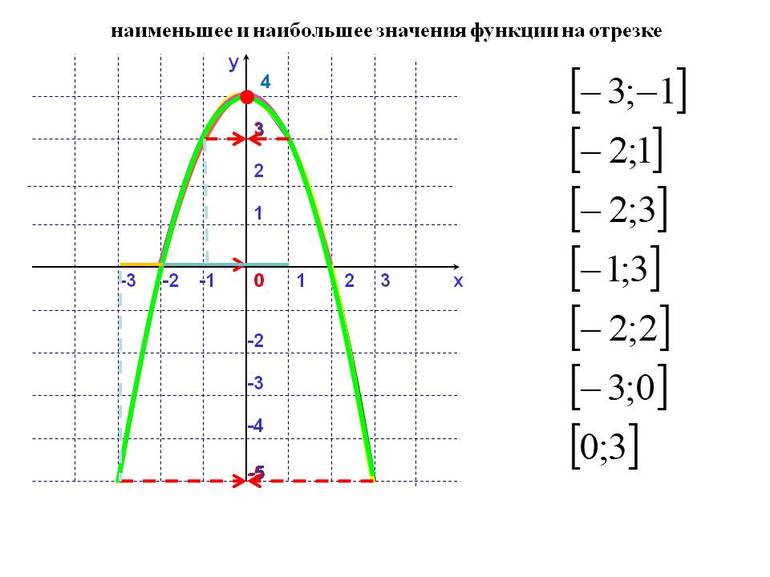
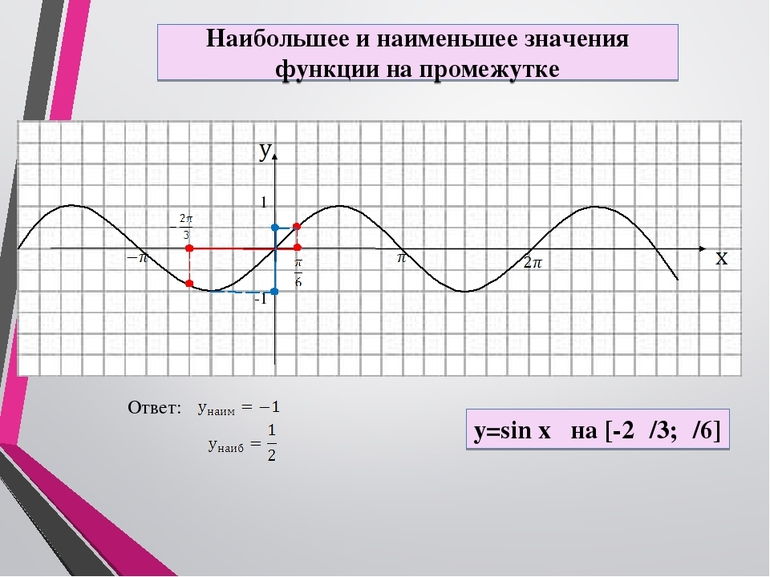







 2+3). График этой функции выглядит так:
2+3). График этой функции выглядит так:
 2} — 2 cdot 4 + 5 = 13}.)
2} — 2 cdot 4 + 5 = 13}.)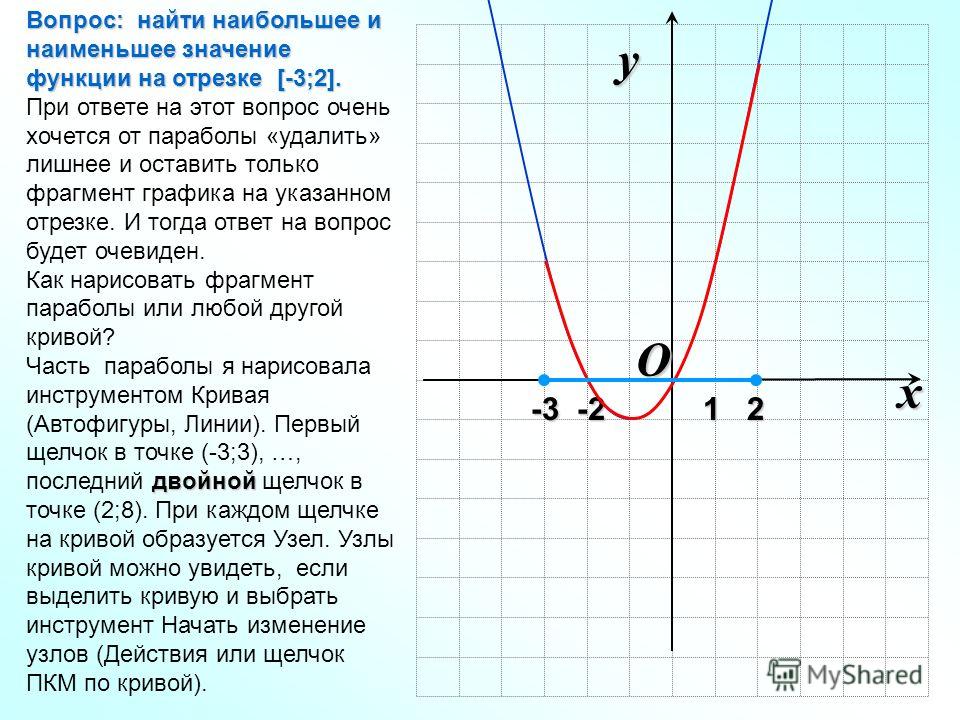

 Задание B15 (№ 26695)
Задание B15 (№ 26695)
 Попробуйте скачать
Попробуйте скачать Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.
Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.
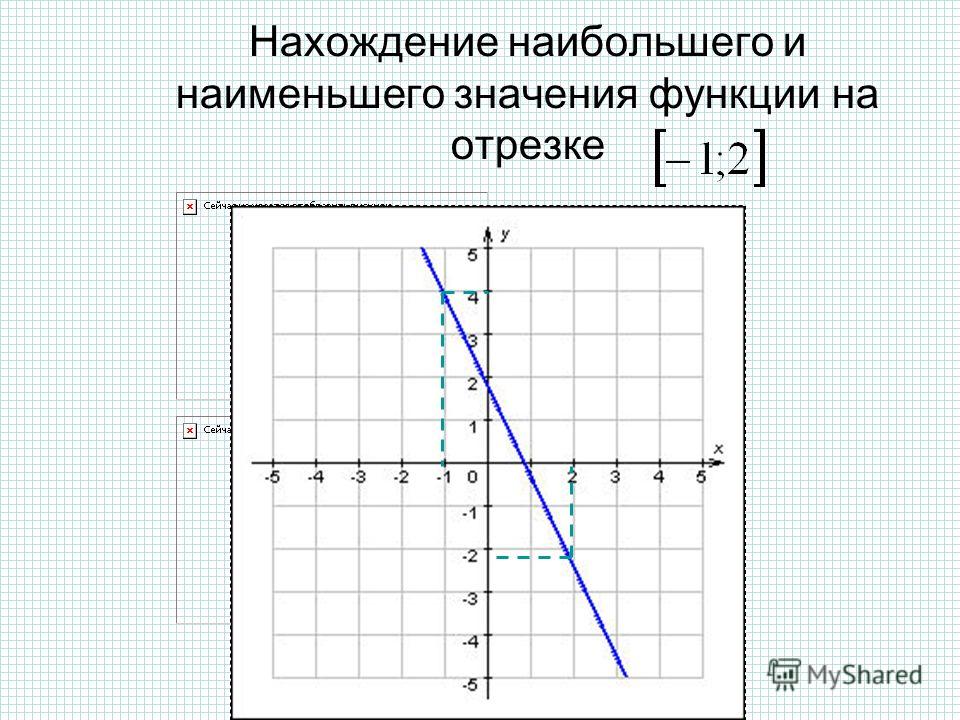 3 + 6).
3 + 6).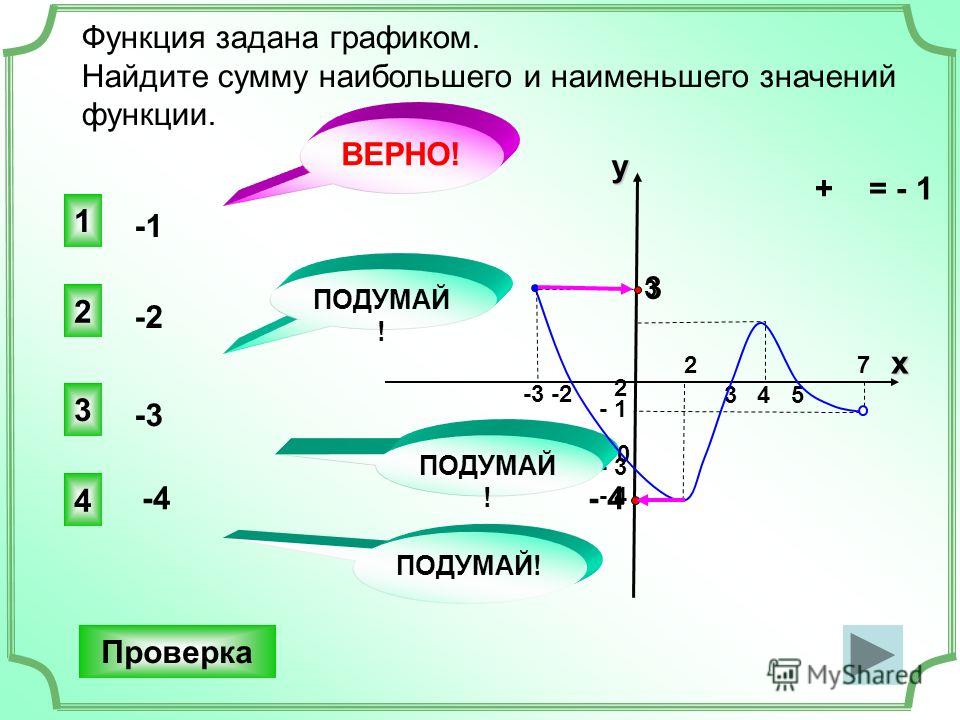
 2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.
2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.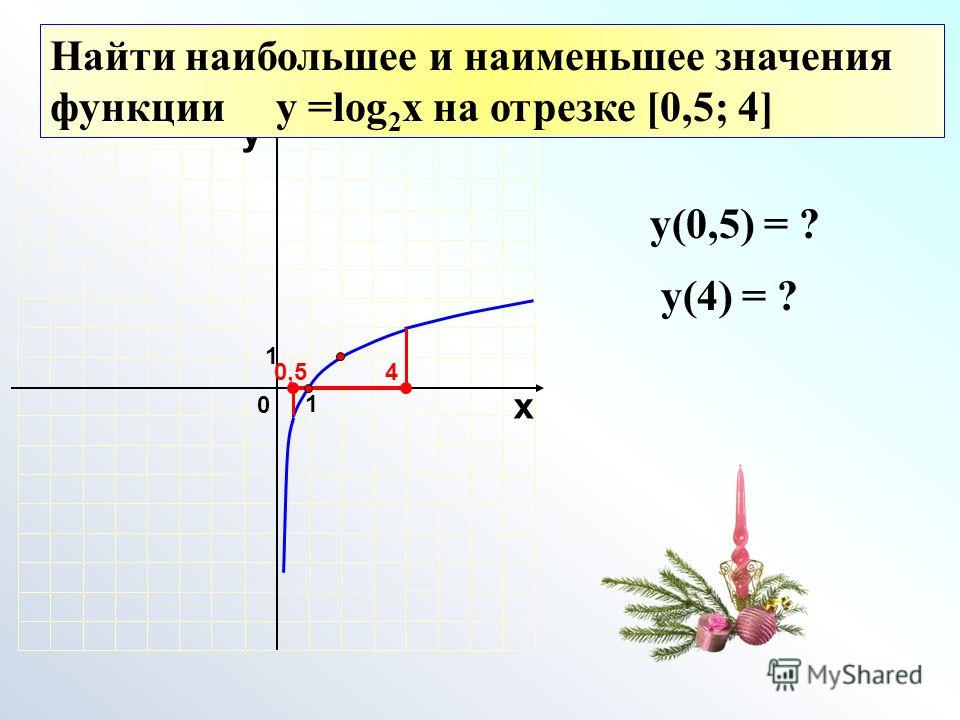
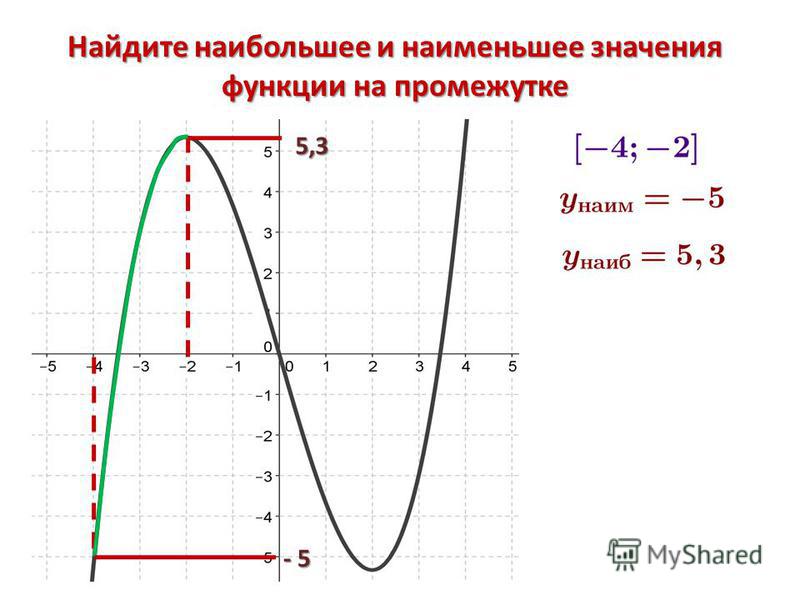 (A2:A7)
(A2:A7) 
 ., ключ, по умолчанию)
Параметры:
a,b,c,.. : аналогичный тип данных.
ключ : ключевая функция, в которой передаются итерации и выполняется сравнение
по умолчанию : значение по умолчанию передается, если данная итерация пуста
Возвращаемое значение:
Возвращает минимум всех аргументов.
Исключения :
Возвращает TypeError при сравнении конфликтующих типов.
., ключ, по умолчанию)
Параметры:
a,b,c,.. : аналогичный тип данных.
ключ : ключевая функция, в которой передаются итерации и выполняется сравнение
по умолчанию : значение по умолчанию передается, если данная итерация пуста
Возвращаемое значение:
Возвращает минимум всех аргументов.
Исключения :
Возвращает TypeError при сравнении конфликтующих типов.  py", строка 7, в
print (мин( 4,12,43.3,19,"GeeksforGeeks") )
TypeError: неупорядоченные типы: str() < int()
py", строка 7, в
print (мин( 4,12,43.3,19,"GeeksforGeeks") )
TypeError: неупорядоченные типы: str() < int() 