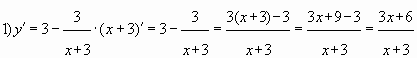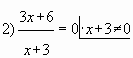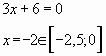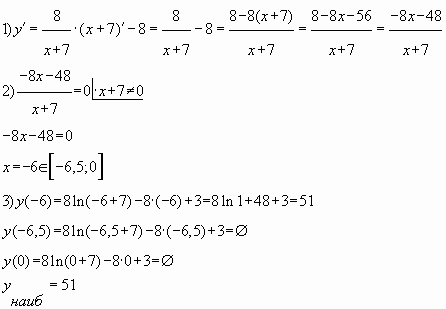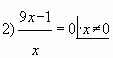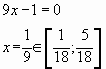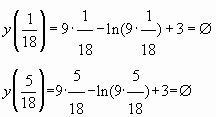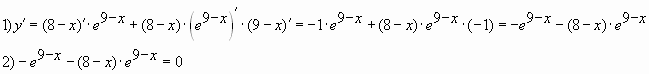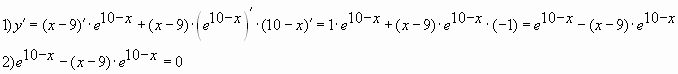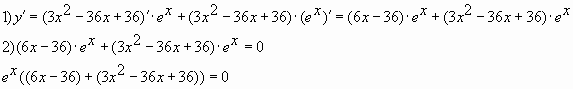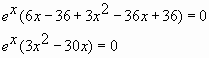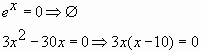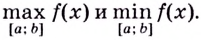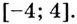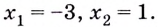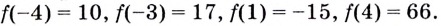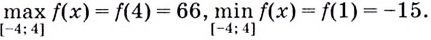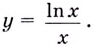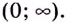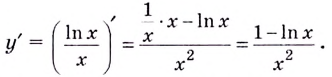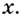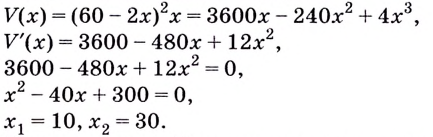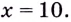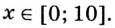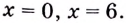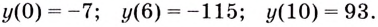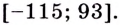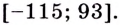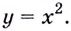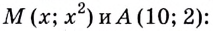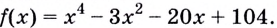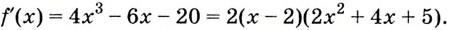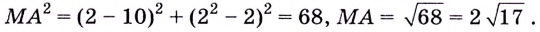Заказать задачи по любым предметам можно здесь от 10 минут
Наибольшее и наименьшее значение функции
Как найти?
Постановка задачи
Найти наибольшее и наименьшее значение функции $ f(x) $ на отрезке $ [a,b] $
План решения
Наибольшее и наименьшее значение непрерывной функции $ f(x) $ на промежутке $ [a,b] $ достигаются в критических точках, то есть в точках в которых производная функции равна нулю $ f'(x) = 0 $, бесконечности $ f'(x) = pm infty $, не существует, либо на концах отрезка $ [a,b] $
- Проверяем на непрерывность функцию $ f(x) $ на заданном отрезке
- Если функция непрерывная, то находим производную $ f'(x) $ и приравниваем её к нулю
- Решая уравнение $ f'(x) = 0 $ получаем корни, являющиеся критическими точками
- Выбираем критические точки, принадлежащие отрезку $ [a,b] $
- Вычисляем значения функции $ f(x) $ в оставшихся критических точках, а так же на концах промежутка $ [a,b] $. Затем выбираем из них наибольшее $ M $ и наименьшее $ m $
Примеры решений
| Пример 1 |
| Найти наибольшее и наименьшее значение функции $ y = 2x^3 — 3x^2 — 4 $ на отрезке $ [0;2] $ |
| Решение |
|
Функция представляет собой кубический многочлен. Точек разрыва нет, значит функция непрерывна на отрезке $ [0;2] $. Находим производную: $$ y’ = (2x^3 — 3x^2 — 4)’ = 6x^2 — 6x $$ Приравниваем производную к нулю. Решаем уравнение и получаем критические точки: $$ 6x^2 — 6x = 0 $$ $$ 6x(x — 1) = 0 $$ $$ x_1 = 0, x_2 = 1 $$ Проверяем принадлежность полученных точек отрезку $ [0;2] $: $$ x_1 in [0;2], x_2 in [0;2] $$ Так как обе точки принадлежат отрезку, то вычисляем в них значение функции $ f(x) $, так же значение этой функции на концах интервала $ [0;2] $: $$ y(x_1) = y(a) = f(0) = 2 cdot 0^3 — 3 cdot 0^2 — 4 = -4 $$ $$ y(x_2) = y(1) = 2 cdot 1^3 — 3 cdot 1^2 — 4 = -5 $$ $$ y(b) = y(2) = 2 cdot 2^3 — 3 cdot 2^2 — 4 = 0 $$ Среди полученных значений наибольшее $ M = 0 $, наименьшее $ m = -5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ M = 0, m = -5 $$ |
| Пример 2 |
| Найти наименьшее и наибольшее значение функции $ y = frac{4x^2}{3+x^2} $ на $ [-1;1] $ |
| Решение |
|
Функция непрерывна на $ x in [-1;1] $ так как знаменатель не обращается в ноль ни при каком $ x $. Выполняем нахождение производной: $$ y’ = (frac{4x^2}{3+x^2})’ = frac{(4x^2)'(3+x^2)-(4x^2)(3+x^2)’}{(3+x^2)^2} = $$ $$ = frac{8x(3+x^2)-(4x^2)(2x)}{(3+x^2)^2} = frac{24x+8x^3-8x^3}{3+x^2)^2} = frac{24x}{(3+x^2)^2} $$ Приравниваем полученную производную к нулю и вычисляем критические точки: $$ frac{24x}{(3+x^2)^2} = 0 $$ $$ 24x = 0, 3+x^2 neq 0 $$ $$ x = 0 $$ Получена единственная критическая точка $ x = 0 $, которая принадлежит $ [-1; 1] $. Вычисляем значение функции $ f(x) $ в критической точке и на концах интервала $ [-1;1] $: $$ y(-1) = frac{4cdot (-1)^2}{3+(-1)^2} = frac{4}{4}=1 $$ $$ y(0) = frac{0}{3} = 0 $$ $$ y(1) = frac{4cdot 1^2}{3+1^2} = frac{4}{4} = 1 $$ Из полученных значений видно, что максимальное значение $ M = 1 $ и минимальное значение $ m = 0 $. |
| Ответ |
| $$ m = 0, M = 1 $$ |
Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.
Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.
Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].
Решение
Сначала вычисляем производную исходной функции:
y′=3×2−12xy’=3x^2-12x
Затем приравниваем ее к нулевому значению и решаем уравнение:
3×2−12x=03x^2-12x=0
x(3x−12)=0x(3x-12)=0
x1=0x_1=0
x2=4x_2=4
Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.
Находим значение функции в точке x1x_1:
f(0)=9f(0)=9
Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:
f(−1)=−1−6+9=2f(-1)=-1-6+9=2
f(2)=8−24+9=−7f(2)=8-24+9=-7
Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.
Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.
Решение
Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:
y′=6xy’=6x
Приравниваем производную к нулю:
6x=06x=0
x=0x=0
Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.
Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.
Тест по теме “Наибольшие и наименьшие значения функции”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Образовательные задачи урока.
- повторить необходимые и достаточные условия
существования точек экстремума, понятия:
стационарные и критические точки; - ввести алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке - сформировать умение решать задачи на
нахождение наибольшего и наименьшего значения
степенной функции на отрезке с помощью
производной. - разобрать прототипы задач № 1 В14
экзаменационной работы в формате ЕГЭ. - Продолжить формирование общеучебных умений и
навыков: навыков самоконтроля, умения писать
необходимом темпе.
Воспитательные задачи:
- cодействовать в ходе урока формированию
основных мировоззренческих идей (материальность
мира, познаваемость мира и его закономерностей,
обусловленность развития науки потребностям
производства); - cодействовать воспитанию у учащихся таких
нравственных качеств, как коллективизм; - cодействовать профилактике утомляемости
школьников, используя разнообразные виды работы
на уроке.
I. Организационный момент. Приветствие.
Проверка готовности класса к уроку. Выявление
отсутствующих.
II. Актуализация знаний учащихся.
Повторить с учащимися основные понятия прошлых
уроков: точки экстремума, каково достаточное
условие точек экстремума, стационарные точки и
критические точки (учащихся отвечают с места)
Повторить таблицу производных основных
функций и основные правила нахождения
III. Изучение нового материала.
Алгоритм нахождения наибольшего и наименьшего
значения функции на отрезке
(учащиеся записывают себе в тетрадь).
Пусть функция непрерывна и дифференцируема на
отрезке , то
для нахождения наибольшего и наименьшего
значения функции на отрезке нужно:
- найти производную функции, найти стационарные
точки (решаем уравнение, приравнивая производную
к нулю) - среди полученных стационарных точек выбрать те,
которые принадлежат отрезку - найти значение в стационарных точках и в концах
отрезка, то естьи
.
- среди полученных значений выбрать наибольшее
или наименьшее.
Записать схему нахождения наибольшего и
наименьшего значения функции на отрезке в
тетради (учитель оформляет схему на доске):
Пусть
непрерывна на
и дифференцируема. Тогда, для нахождения или
:
- Находим
находим
- Проверяем принадлежность
отрезку
- Находим
,
,
.
- Среди полученных значений выбираем
или
.
- Записываем ответ (Акцентировать внимание, что в
ответе должно быть записано либо целое число,
либо конечная десятичная дробь).
Пример № 1. Найти наименьшее значение функции
на отрезке
. (Учитель
совместно с учащимися записывает решение на
доске последовательно проговаривая каждый пункт
алгоритма).
Решение:
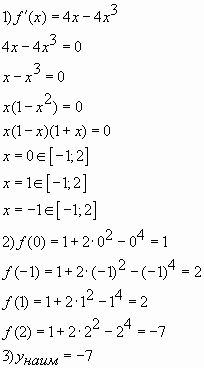
Ответ:
Пример № 2. Найти наибольшее значение
функции на
отрезке
Решение:
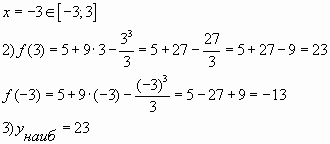
Ответ: 23
Пример № 3. Найдите наименьшее значение
функции на
отрезке .
Решение:
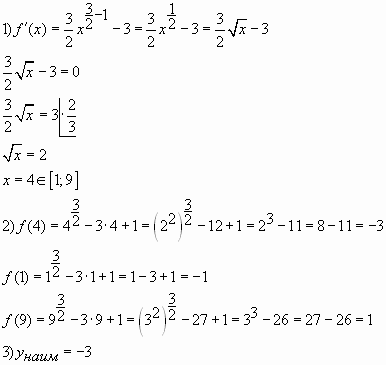
Ответ: -3
Пример № 4. Найдите наибольшее
значение функции на отрезке
.
Решение:
Упростим функцию
Ответ: 1
IV. Закрепление материала.
- Найдите наименьшее значение функции
на отрезке
- Найдите наименьшее значение функции
на отрезке
- Найдите наименьшее значение функции
на отрезке
V. Итоги урока.
- Повторить алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке. - Выставить отметки за урок.
VI. Домашнее задание:
- Найдите наименьшее значение функции
на отрезке
- Найдите наибольшее значение функции
на отрезке
- Найдите наибольшее значение функции
на отрезке
- Найдите наименьшее значение функции
на отрезке
- Найти наибольшее значение функции
на отрезке
Урок № 2. “Нахождение наибольшего и
наименьшего значения функций и
на отрезке
.
Тип урока: комбинированный.
Образовательные задачи:
- обеспечить повторение в ходе урока алгоритма
нахождения наибольшего и наименьшего значения
функции на отрезке; - продолжить формирования навыка применения
этого алгоритма при решении второго типа задач
экзаменационных вариантов ЕГЭ; - продолжить формирование общеучебных умений и
навыков: навыков самоконтроля, умения в
необходимом темпе читать и писать, анализировать
условия задачи.
Воспитательные задачи:
- содействовать в ходе урока формированию
основных мировоззренческих идей (материальность
мира, познаваемость мира и его закономерностей,
обусловленность развития науки потребностям
производства); - содействовать воспитанию у учащихся таких
нравственных качеств, как коллективизм. умение
слушать товарищей; - содействовать профилактике утомляемости
школьников.
I. Организационный момент. Приветствие.
Проверка готовности класса к уроку. Выявление
отсутствующих.
II. Проверка домашнего задания. Фронтальная
проверка домашнего задания. Если у большинства
учащихся возникли вопросы, разобрать на доске
решение конкретного задания, если лишь у
некоторых, объяснить в индивидуальном порядке,
предварительно схематично обговорив решение у
доски.
III. Актуализация знаний. Повторить еще раз
алгоритм нахождения наибольшего и наименьшего
значения функции на отрезке с оформлением схемы
на доске.
Повторить следующие формулы для дальнейшего
изучения материала:
,
,
Решить на повторение примеры (1 учащийся пишет
решение на доске с комментариями по решению,
остальные записывают себе в тетради).
IV. Решение новых прототипов задач (разбирает
решение учитель)
Пример № 1. Найти наименьшее значение
функции на
отрезке
Решение
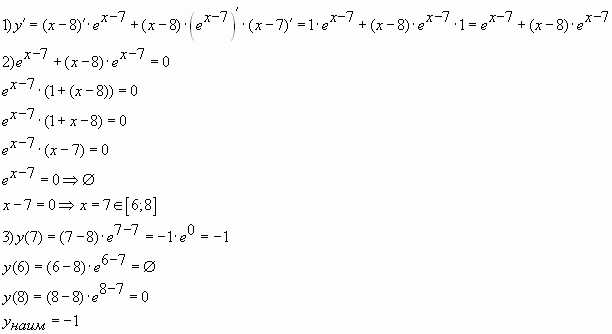
Ответ: —1
Пример № 2. Найти наименьшее значение
функции на
отрезке
Решение. Преобразуем и упростим функцию , используя
свойство логарифмов
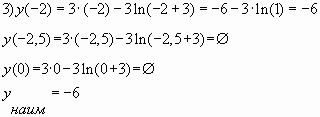
Ответ: -6
V. Закрепление материала (самостоятельное
решение задач учащимися у доски).
Пример № 3. Найти наибольшее значение функции
на отрезке
Решение.
Ответ: 51
Пример № 4. Найти наименьшее значение функции
на отрезке
Решение.
(, так как
)
Ответ: 4
Пример № 5. Найти наименьшее значение функции
на отрезке
Решение
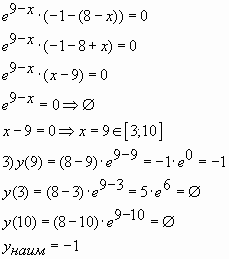
Ответ: -1
Пример № 6. Найти наибольшее значение функции
на отрезке
Решение:
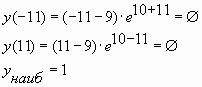
Ответ: 1
Пример № 7: Найдите наибольшее значение
функции на
отрезке
Решение
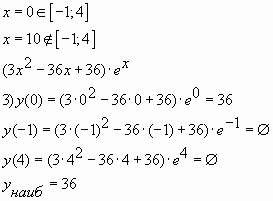
Ответ: 36
VI. Итоги урока.
- Повторить алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке. - Проговорить основные алгоритмы решения тех
примеров, которые изучены на уроке.
VII. Домашнее задание по вариантам.
Преподаватель который помогает студентам и школьникам в учёбе.
Наибольшее и наименьшее значения функции с примерами решения
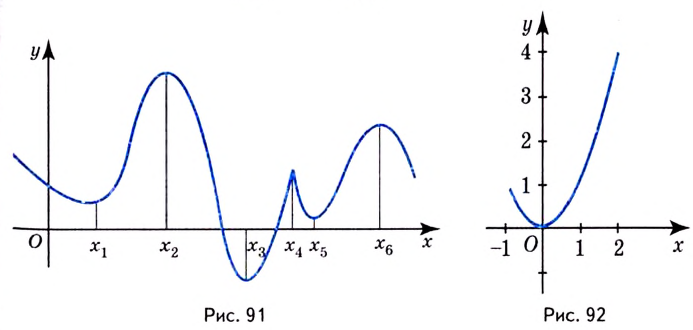
От максимумов и минимумов функции следует отличать её наибольшее и наименьшее значения на промежутке. Функция может иметь несколько максимумов (минимумов) на некотором промежутке (рис. 91), но не более одного наибольшего (наименьшего) значения. Функция может не иметь максимума (минимума) на промежутке, но иметь наибольшее (наименьшее) значение.
Например функция, график которой изображён на рисунке 91, наибольшее значение имеет в точке
Наибольшее и наименьшее значения функции тесно связаны с её областью значений. Если область значений непрерывной функции — промежуток 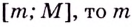
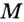
Поскольку непрерывная функция наибольшее и наименьшее значения может иметь только в точках экстремума или на концах отрезка, то для нахождения этих значений пользуются таким правилом.
Чтобы найти наибольшее и наименьшее значения непрерывной функции 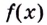
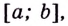
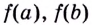
Записывают так:
Пример №1
Найдите наибольшее и наименьшее значения функции 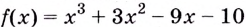
Решение:
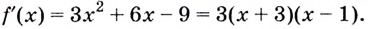
Из этих четырёх значений функции наименьшим является -15, а наибольшим — 66.
Ответ,
Пример №2
Найдите наибольшее и наименьшее значения функции
Решение:
Областью определения функции является промежуток
Если 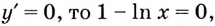
Если 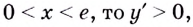
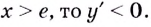

Поскольку на промежутке 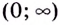
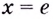
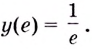
Ответ, 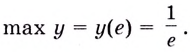
К нахождению наибольшего или наименьшего значений функции сводится решение многих прикладных задач.
Пример №3
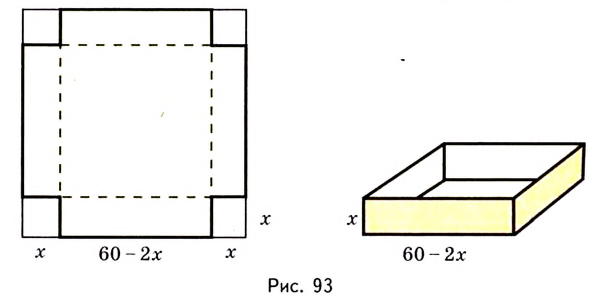
Есть квадратный лист жести со стороной 60 см. Найдите размеры квадратов, которые надо вырезать в углах данного листа, чтобы из полученной заготовки сделать коробку наибольшего объёма {рис. 93).
Решение:
Чтобы получить коробку (в форме прямоугольного параллелепипеда), надо вырезать равные квадраты в углах листа. Пусть 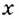
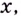
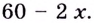
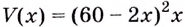
Надо исследовать математическую модель задачи: при каком значении 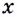
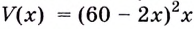
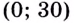
Значение 
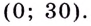
Поскольку при 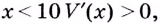
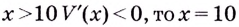
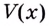
Ответ. Надо вырезать квадраты, стороны которых равны 10 см.
- Заказать решение задач по высшей математике
Пример №4
Найдите область значений функции 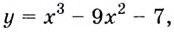
Решение:
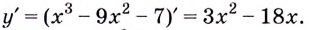
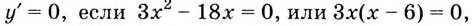
Найдём значение функции на концах промежутка 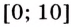
Заданная функция непрерывна, её наибольшее значение 93, а наименьшее -115, значит, область её значений — отрезок
Ответ.
Пример №5
Найдите кратчайшее расстояние от точки 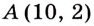
Решение:
Пусть ближайшая к 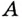
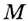
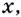
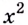
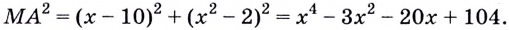
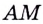
Уравнение 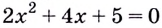
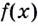
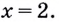
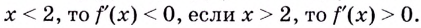
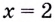
Наименьшее значение квадрата расстояния
Ответ.
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая
- Рациональная дробь
- Функция в математике
- Правило Лопиталя
- Вычисления в Mathematica с примерами
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
В точке производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
Ответ: 17.
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.
В точке производная
меняет знак с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: 1.
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция монотонно возрастает, точка максимума функции
будет при том же
, что и точка максимума функции
А ее найти легко.
при
. В точке
производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
.
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение
достигается в вершине параболы, то есть при
Ответ: — 4.
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции
является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.
В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции
. Поскольку при
функция
убывает,
В этой задаче значение функции на концах отрезка искать не нужно.
Ответ: 12.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
при
Найдем знаки производной.
Точка — точка минимума функции
. Точка
не лежит на отрезке
Поэтому
и
Значит, наименьшее значение функции на отрезке
достигается при
Найдем это значение.
Ответ: -11.
7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если то
Если
, то
Значит, — точка минимума функции
. В этой точке и достигается наименьшее значение функции на отрезке
Ответ: 4.
8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
. Поскольку
если
Найдем знаки производной на отрезке
При знак производной меняется с «плюса» на «минус». Значит,
— точка максимума функции
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Мы нашли, что
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
Ответ: 4.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции
если
Тогда
При
знак производной меняется с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: -7.
10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
По условию, . На этом отрезке условие
выполняется только для
Найдем знаки производной слева и справа от точки
В точке производная функции меняет знак с «плюса» на «минус». Значит, точка
— точка максимума функции
. Других точек экстремума на отрезке
функция не имеет, и наибольшее значение функции
на отрезке
достигается при
Ответ: 12.
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. — нет решений.
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку , получим, что
для всех
, и функция
монотонно возрастает при
Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при
Ответ: 6
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023

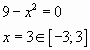
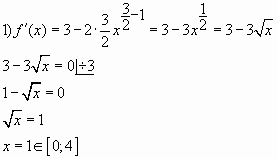
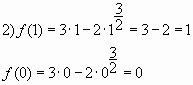
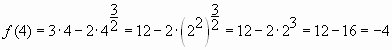
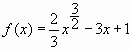 на отрезке
на отрезке