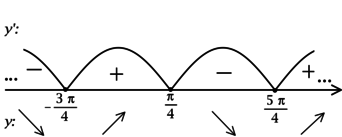
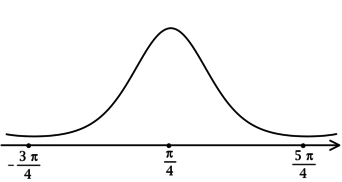
Как найти наибольшее значение функции с параметром - Исправление недочетов и поиск решений вместе с Examum.ru

На этой странице вы узнаете

Можно ли представить прогресс в виде монотонной функции?
Где можно встретить идеальную симметрию?
Как сломать функцию?

В восточных боевых искусствах спортсмены разбивают доски руками. А вот плотники для разрезания досок используют пилу, то есть вспомогательный инструмент. Так стоит ли нам справлять с параметрами голыми руками? Или проще взять специальный инструмент? Такая же дилемма может встать и в решении задач с параметром.

Монотонность функции

В математике пилу, разумеется, не используют. Зато мы можем использовать свойства функции, которые и будут нашей опорой при решении задач с параметром. Давайте попробуем собрать свой “ящик с инструментами”.

Возможно, до детального знакомства с темой, вам захочется вспомнить «Определение и график функции».

Многим из нас знакома монотонная и скучная работа. Например, удалять с телефона ненужные фотографии или стирать пометки из учебника, прежде чем вернуть его в школьную библиотеку. Приходится повторять одно и то же действие на протяжении всего цикла работы — это утомительно и однообразно.

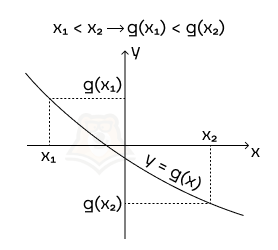
Монотонная функция так же, как и работа, не меняет своих свойств на всем промежутке.

Монотонная функция — функция, строго возрастающая или строго убывающая на промежутке.

Разберемся со “строгостью” функций.

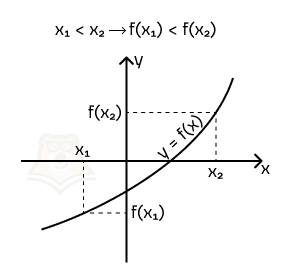
Строго возрастающая функция на промежутке — функция, большему значению аргумента которой из промежутка соответствует большее значение функции.

Иными словами: чем больше х, тем больше у.

Строго убывающая функция на промежутке — функция, большему значению аргумента которой соответствует меньшее значение функции.

Или чем больше х, тем меньше у.

Можно ли представить прогресс в виде монотонной функции?

Идеальная картина: чем больше мы работаем, тем лучше наш результат. С каждым днем мы все растем, становимся лучше и избегаем ошибок. То есть наш прогресс — это монотонная функция.

К сожалению, реальность несколько другая. Прогресс никогда не будет монотонной функцией, всегда будут взлеты и падения. Ошибки — неотъемлемая часть обучения, поэтому нельзя бояться неудач. Если представить прогресс человека в виде функции, то она постоянно будет менять промежутки возрастания на промежутки убывания и обратно.

Что еще можно сказать про возрастание функции? Вспомним «Производную», а именно — ее знаки на промежутках возрастания и убывания функции:

если производная положительна на некотором промежутке, то функция возрастает на этом промежутке;

если производная отрицательна на некотором промежутке, то функция убывает на этом промежутке.

Свойства монотонной функции

Монотонные функции обладают своими свойствами, которые могут пригодиться при решении задач.

Свойство 1. Монотонная функция принимает свое значение единственный раз.

Это можно проследить по графику: для каждого значения у будет единственное значение х.

Свойство 2. Если две функции f(x) и h(x) возрастают на промежутке, то функция y = f(x) + h(x) также будет возрастать.

Это же свойство будет работать и с убыванием функции.

Если две функции f(x) и h(x) убывают на промежутке, то функция

y = f(x) + h(x) также будет убывать.

Свойство 3. Если функции f(x) и h(x) возрастают на промежутке, то функция y = f(x) * h(x) тоже будет возрастать при

Аналогично и с убыванием.

Пример 1. При каких значениях параметра а любое решение уравнения 4x⁷ + 2x + a = 0 принадлежит отрезку [−1;1].

Решение.

Шаг 1. Какой является эта функция: возрастающей или убывающей? Проверим это с помощью производной.

Заметим, что поскольку х стоит в четной степени, то какое бы число мы ни подставили в производную, оно будет положительно. Значит, эта функция строго возрастает.

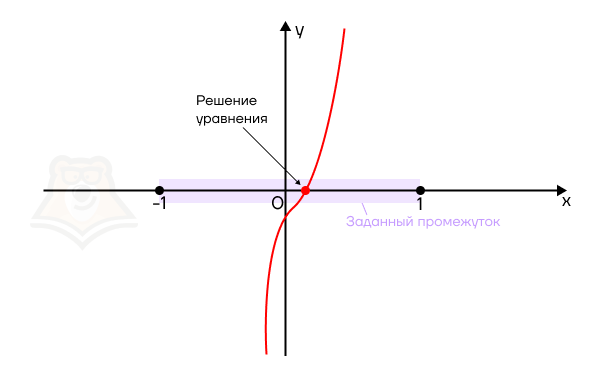
Шаг 2. Как определить, что решение уравнения будет лежать в заданном отрезке? Решением уравнения будет пересечение функции и оси х. То есть точка этого пересечения должна лежать между −1 и 1 включительно.

На графике это будет выглядеть так:

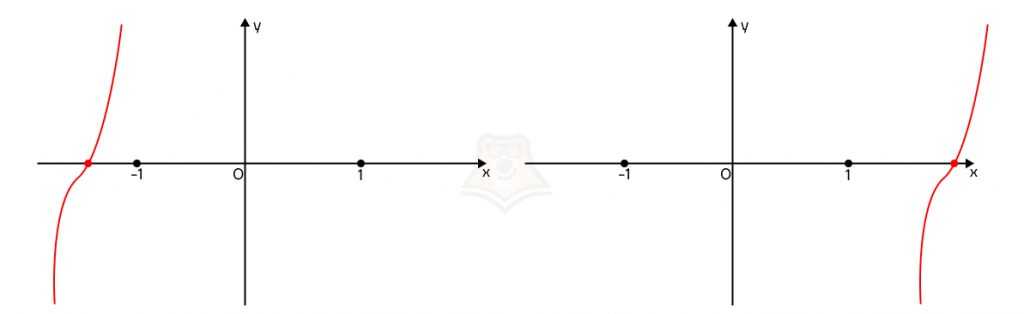
А вот такие случаи нам уже не подходят, поскольку решение уравнения будет лежать за пределами заданного промежутка.

Шаг 3. При x = — 1 функция отрицательна, а при x = 1 функция будет положительна при любом положении в заданном промежутке. Следовательно, мы можем задать ее положение на графике с помощью значения функции при x = — 1 и x = 1.

Шаг 4. Получаем два условия, которые должны выполниться одновременно, то есть систему.

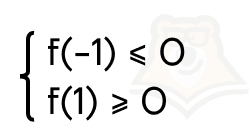
Шаг 5. Решаем первое неравенство системы:

Решаем второе неравенство системы:

Следовательно, условия будут выполняться при

Ответ:

Итак, в наш ящик с инструментами отправляется монотонность функции, ее возрастание и убывание.

Четность функции

Четной функцией называется такая функция, график которой симметричен относительно оси Оу.

Для такой функции будет выполняться условие f(x) = f( — x).

Где можно встретить идеальную симметрию?

В природе идеальная симметрия почти не встречается: даже на миллиметр, но одна сторона животного, растения или человека будет отличаться от другой. Идеальная симметрия встречается в математике, в четной функции. Симметрия часто используется в искусстве и архитектуре для создания гармоничной композиции. Если посмотреть на планы и фасады некоторых храмов и дворцов, созданных много лет назад, то окажется, что части здания располагаются симметрично относительно оси.

Четность функции — это точно не универсальный инструмент, как, например, молоток. Скорее это редкий ключ, который будет большую часть времени просто лежать в ящике, но пригодится в самый ответственный момент.

Алгоритм применения четности функций при решении задач с параметром

Четность можно применить, когда в функции стоят модули, четные степени, четные корни и другие условия, с которыми минус “не дружит”.

Шаг 1. Перенести все слагаемые в одну сторону и ввести f(x).

Шаг 2. Проверить функцию на четность. Для этого нужно удостовериться, что условие f(x) = f( — x) выполняется.
Четная функция имеет четное количество корней, кроме случая
х = 0, когда корень всего один.

Шаг 3. Подставить х = 0.

Шаг 4. Рассмотреть данные значения в зависимости от условия задачи.

Почему функция имеет четное количество корней, кроме случая х = 0? Возьмем зеркало и попробуем подвигать карандаш относительно него. При этом само зеркало будет осью у.

На какое бы расстояние мы не отодвинули карандаш, в зеркале всегда будет его отражение. Следовательно, мы получим два карандаша.

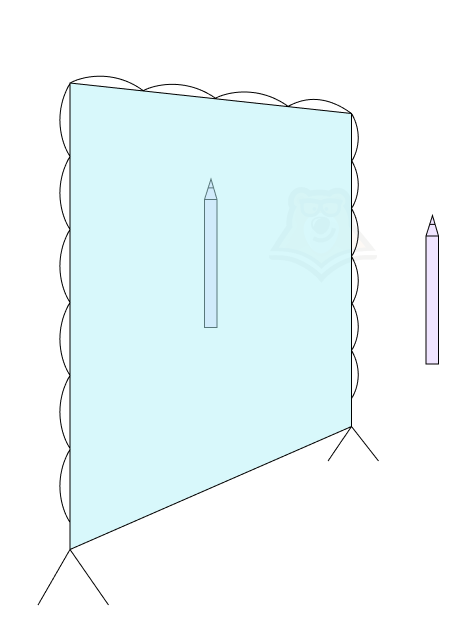
Но если мы приложим карандаш к самому зеркалу, то два карандаша объединятся в один. Условно мы можем сказать, что получили один карандаш.

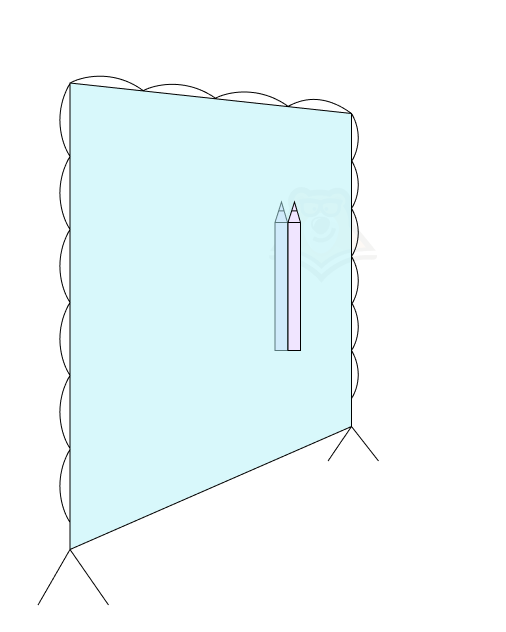
Такая же логика и с корнями четной функции: пока они не будут лежать на зеркале, то есть на оси у, их всегда будет два.

Пример 2. Найдите все значения параметра а, при каждом из которых уравнение

sqrt{a^2+x^2}=a^2-a-14-cos5x

имеет единственное решение.

Решение.

Шаг 1. Введем две функции:

Будем действовать согласно алгоритму. Первый шаг мы уже сделали. Теперь убедимся, что полученные функции четные.

f(-x)=sqrt{a^2+(-x^2)}=sqrt{a^2+x^2}

— функция четная.

g(-x)=a^2-a-14-cos5(-x)=a^2-a-14-cos5x

— функция четная.

Шаг 2. Поскольку функции четные, то при решении уравнения х будет появляться второе решение ( — x). Вспоминаем зеркало: уравнение будет иметь единственное решение только при x = 0.

Шаг 3. Подставим x = 0 в наше уравнение.

sqrt{a^2+0^2} =a^2-a-14-cos5*0

Подробнее про такое преобразование можно прочесть в статье «Модуль».

Шаг 4. Раскроем модуль двумя способами.

— этот корень отрицательный, а значит, он не подходит к условию раскрытия модуля.

— в этом случае нам подходит только корень

Шаг 5. Получаем корни

Проверим, что при них действительно получается решение x = 0.

Шаг 6. a = 5

sqrt{5^2+x^2}=5^2-5-14-cos5x

— решение только при x=0.

sqrt{(-sqrt{15})^2+x^2}=(-sqrt{15})^2+sqrt{15}-14-cos5x

sqrt{-15+x^2}=1+sqrt{15}-cos5x

— решение только при x=0.

Следовательно, корни найдены верно.

Ответ: 5, -√15

В ящик с инструментами отправляется четность функции.

Значение функции

В заданиях с параметрами могут встречаться области определений и значений функции, наибольшее и наименьшее значения. Подробнее про эти свойства в обычных функциях можно прочитать в статье «Исследование функции с помощью производной».

Обычно эти свойства функции применяются в заданиях, где просят исследовать функцию, а не найти количество решений. Как их применять? Рассмотрим на примере.

Пример 1. Найдите все значения параметра а, при каждом из которых функция f(x) = — x² + 4|a² -x|+ 6x имеет хотя бы одну точку минимума.

Решение. Для начала немного упростим функцию и раскроем модуль.

При

f(x)=-x^2+4a^2-4x+6x=-x^2+2x+4a^2

— мы получили квадратное уравнение.

Оно задает параболу с ветвями, направленными вниз. Ее вершина будет в точке

При

f(x)=-x^2-4a^2+4x+6x=-x^2+10x-4a^2

— мы получили квадратное уравнение.

Оно задает параболу с ветвями, направленными вниз. Ее вершина будет в точке

На графике должно получиться две параболы, которые объединятся в одну фигуру, похожую на горы. Как эти горы могут располагаться относительно друг друга?

Первая гора может быть выступом для второй горы. То есть одна гора плавно будет перетекать в другую.

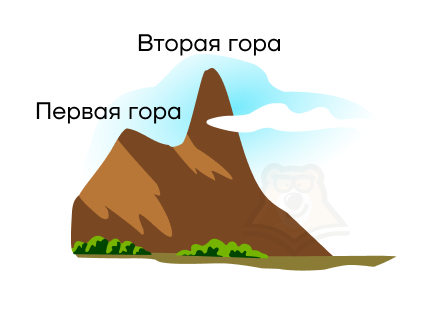
Они могут находиться рядом друг с другом, а между ними будет перевал.

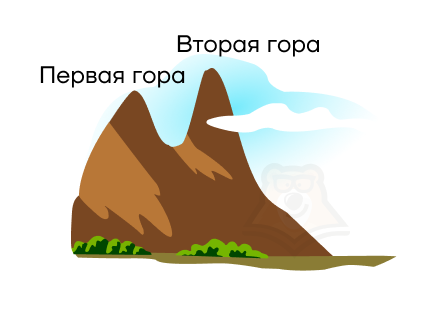
Вторая гора может быть выступом в первой горе.

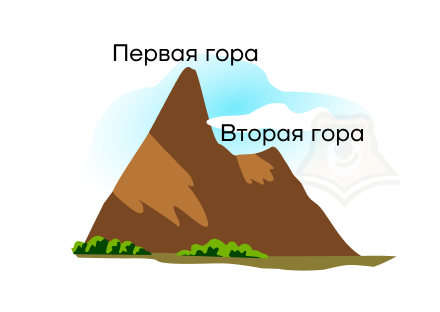
Случай, когда горы находятся на разных материках планеты, мы не рассматриваем, поскольку они обязательно должны быть связаны между собой, иначе бы задавались разными функциями.

Теперь мы можем построить примерные графики функций. При этом в значении a2 будет перелом, поскольку в этой точке происходит переход от первого случая раскрытия модуля ко второму. Эта точка будет называться точкой излома.

Точка излома — точка, в которой одна функция переходит в другую из-за раскрытия модуля.

Как сломать функцию?

Если в функции появляется модуль, ее график будет состоять из нескольких ветвей параболы или прямых. Это связано с тем, что при раскрытии модуля получается две разные функции, соответственно, они имеют разные графики.
Однако при построении графика всей функции, два графика объединяются в один. В точке их соединения, то есть точке излома, функция меняет свое направление.

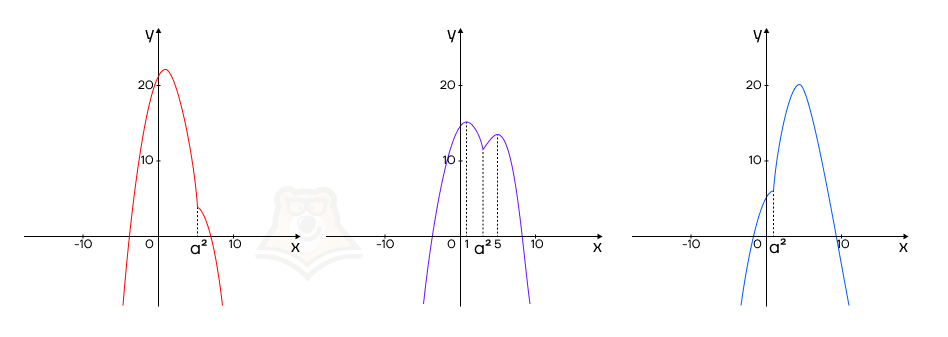
Заметим, что точка минимума — точка, где функция перестает убывать и начинает возрастать — есть только во втором случае, когда каждая “гора” имеет вершину, а точка a² лежит между ними.

Следовательно, получаем неравенство 1 < a² < 5. Разобьем его на системы из двух неравенств:

Решим первое неравенство системы:

(a-sqrt{5})(a+sqrt{5})<0

Решим второе неравенство системы:

ain(-infty;-1)cup(1;+infty)

Осталось найти ответ для системы.

Отсюда

ain(-sqrt{5};-1)cup(1;sqrt{5})

Ответ:

ain(-sqrt{5};-1)cup(1;sqrt{5})

Для удобства решения таких заданий мы можем вывести алгоритм.

Алгоритм решения для задач на значение функции

Шаг 1. Раскрыть модули.

Шаг 2. Рассмотреть полученные функции и проанализировать их. Например, если получаются параболы, то нужно определить направление ветвей и положение ветвей.

Шаг 3. Проанализировать точку излома: найти все случаи, где она может находиться в зависимости от значений параметра.

Шаг 4. Найти значения параметра для каждого подходящего случая.

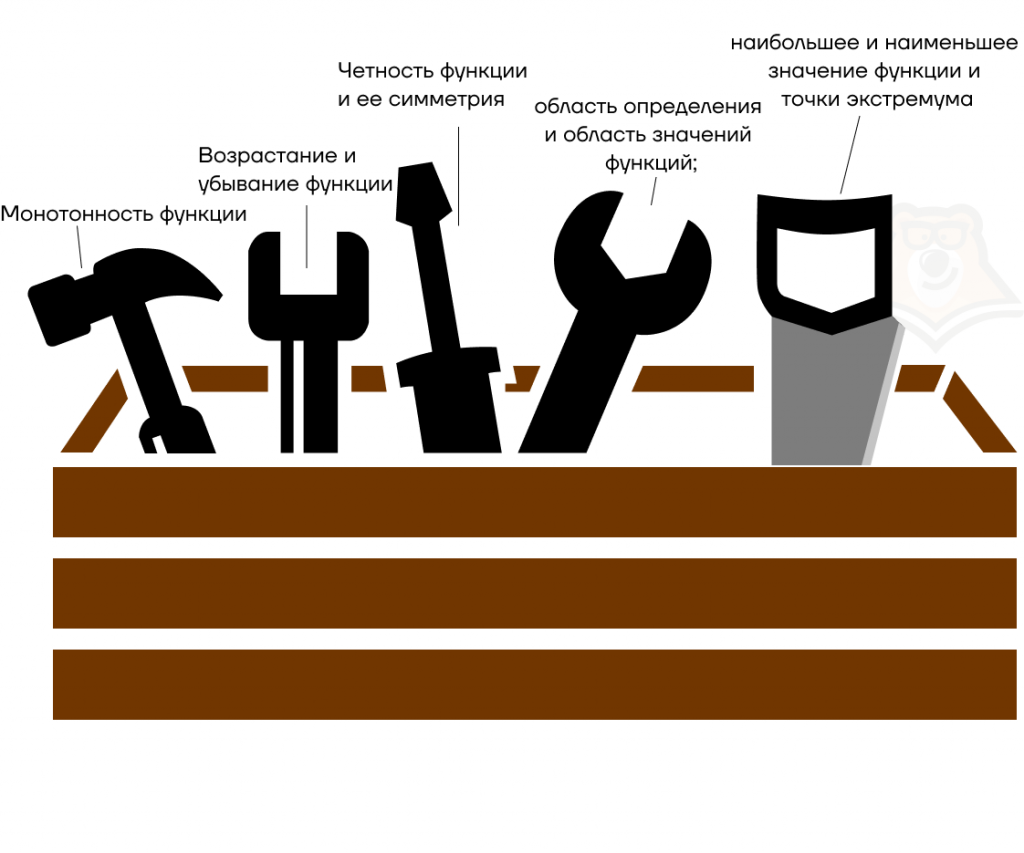
Вот мы и собрали инструменты для решения параметров с помощью свойств функций. В наш ящик вошли:

монотонность функции;
возрастание и убывание функции;
четность функции и ее симметрия;
область определения и область значений функций;
наибольшее и наименьшее значение функции и точки экстремума.

Фактчек

Монотонная функция — функция, строго возрастающая или строго убывающая на промежутке. Если при решении задач с параметром доказать, что функция монотонно возрастает или монотонно убывает, можно применить свойство производных. Это же свойство можно применить и для доказательства монотонности функции.
Производная положительна на промежутках возрастания функции и отрицательна на промежутках убывания.
Четной функцией называется такая функция, график которой симметричен относительно оси Оу. Для такой функции будет выполняться условие f(x)=f(-x). Это же условие можно применять для доказательства четности функции.
В четной функции всегда будет два решения, кроме случая х = 0. При х = 0 у функции будет единственное решение.
Точка излома — точка, в которой одна функция переходит в другую из-за раскрытия модуля. Зная точки излома, можно проанализировать поведение функции.

Проверь себя

Задание 1.

На заданном промежутке функция монотонно возрастает. Чему будет равна производная функции на этом промежутке?

Производная функции будет отрицательна.
Производная функции будет положительна.
Производная функции будет равна 0.
Невозможно определить производную, не зная функцию.

Задание 2.

Выберите верные утверждения для убывающей функции.

Чем больше значение х, тем больше значение у.
Чем больше значение х, тем меньше значение у.
Производная функции положительна.
Производная функции отрицательна.

Задание 3.

Дана четная функция. Сколько будет решений при х = 0?

Четыре решения.
Два решения.
Одно решение.
Решений не будет.

Задание 4.

Что такое точка излома?

Точка, в которой одна функция переходит в другую из-за раскрытия модуля.
Любая точка на функции, в которой график меняет свое направление.
Точки экстремума.
Асимптоты функции.

Ответы: 1. — 2 2. — 24 3. — 3 4. — 1.

Источник

Математики и Data Science-специалисты должны хорошо разбираться в функциях. Предлагаем попрактиковаться в решении задач на обнаружение максимальных и минимальных значений у заданных функций.

Максимум

Задумываясь над тем, как найти максимальное значение функции, нужно четко понимать, с чем предстоит иметь дело. Для этого нужно запомнить такое определение:

Наибольшее значение функции y = f(x) на промежутке x – это max y = f(x₀). Оно будет при любом значении x€ X, x≠x₀ делает справедливым неравенство: f(x)≤f(x₀).

Максимальное значение (максимум) – это точка на функции, в которой значение функции больше, чем в соседних «отметках».

Минимум

Наименьшее значение функции находить так же легко, как и наибольшее. Но сначала нужно понимать, что это такое.

Значение функции на отрезке будет считаться минимумом, если оно меньше, чем в соседних «отметках». Здесь действует такое определение:

Наименьшее значение функции y=f(x) на промежутке x – это miny=f(x₀), которое при любом значении x€ X, x≠x₀ делает справедливым неравенство f(x)≥f(x₀).

Соответствующие определения являются достаточными и очевидными. Если говорить простыми словами, то максимум функции – это ее самое большое значение на заданном промежутке (участке) при абсциссе x₀, а минимум – самое маленькое.

Стационарные точки

При решении вопроса о том, как найти наибольшее или наименьшее значение функции, стоит обратить внимание на так называемые «стационарные точки». Это – значения аргумента функции, при которых ее производная будет равняться нулю.

Стационарная точка – это «отметка», в которой расположен экстремум дифференцируемой функции. А именно – локальный минимум или максимум. В одной из таких «отметок» записанное выражение будет достигать своих предельных параметров.

Здесь рекомендуется запомнить следующее:

Экстремум функции – это минимумы и максимумы.
Если определить производную в точках экстремумов, она будет равно 0.
Когда говорят «экстремумы», подразумевается значение функции. Если же речь идет об «отметках» экстремумов, рассматривать стоит x, в которых достигаются соответствующие пределы.

Этого достаточно для того, чтобы разобраться, как найти наибольшее на заданном отрезке у выражения. Для реализации поставленной задачи вовсе не обязательно составлять график. Поэтому сначала воспользуемся записями формул и вычислений.

План действий

Пример – дана функция f(x) на отрезке [a, b]. Наибольшее и наименьшее значение такой непрерывной функции достигаются в определенных местах. Это – критические точки. Там, где производная записанного выражения будет равно нулю.

Для того, чтобы найти наибольшие значения уравнения, потребуется придерживаться следующего алгоритма:

Узнайте, какая перед вами функция. Для этого нужно проверить ее на непрерывность. В расчет обязательно берется заданный отрезок.
Если запись непрерывная – ищем производную.
После того, как найдем производную, приравниваем ее к нулю. Это поможет найти точки экстремумов. В результате получаются корни.
Образовавшиеся корни – это критические точки. Нужно выбрать те «параметры», что относятся к промежутку [a, b].
Вычислить значения функции на концах отрезка [a, b].
Определить значения имеющегося выражения в критических «отметках».

Теперь понятно, как найти наибольшие функции на заданном отрезке. После произведенных подсчетов остается выбрать из результатов M (максимум) и m (минимум).

На отрезке

Разобравшись в тем, как найти наибольшие «параметры» выражения «на бумаге», стоит рассмотреть соответствующий процесс на графиках. Определять максимумы/минимумы в данном случае будет проще.

Первый график указывает на выражение, у которого точка минимума и максимума находятся в стационарных точках на промежутке [-6;6]. Соответствующие «пределы» обозначены жирным.

Второй график указывает на изменение отрезка. Теперь он будет [1;6]. Минимальное значение останется прежним. А вот максимальное – изменится. Оно образуется в правой части в точке с абсциссой. Поиск минимального «параметра» окажется в критической точке.

Задумываясь, как найти наименьшие или «самые крупные» параметры выражения на графике, можно также рассмотреть третий рисунок. Здесь функция принадлежала промежутку [-3;2]. Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы.

Открытый интервал

Если промежуток задан конкретным числом, определить экстремумы будет не так сложно. Иначе происходит, если интервал открыт.

Здесь:

Функция будет принимать максимум/минимум по значению в стационарных точках на открытом интервале от -6 до 6. Ответ – на 4 рисунке.
Если взять отрезок [1;6), минимум будет достигнут в стационарной точке. А вот максимум – неизвестен. Связано это с тем, что 6 не принадлежит к заданному интервалу. Если бы «шестерка» относилась к соответствующему промежутку, ответ на вопрос относительно определения максимума оказался понятным. Максимальный параметр был бы в точке с абсциссой 6.
На рисунке 6, задумываясь, как найти наименьшие «параметры», нужно обратить внимание на заданный интервал. Он равен (-3;2]. Минимум будет достигнут в правой границе. А вот максимум – не определен.

Найти значения на графиках обычно проще, чем «в чистых формулах». Соответствующие задания можно отыскать тут.

Бесконечность

Иногда значения функций нужно найти на бесконечном промежутке. Графически возможны такие ситуации:

На 7 рисунке функция достигает максимума в стационарной точке с абсциссой 1. Минимум окажется на границе интервала справа. На минус бесконечности значения приближаются к y=3 асимптотически.

Если взять интервал от 2-х до «плюс бесконечности», заданная функция не будет иметь ни максимумов, ни минимумов. Значения здесь стремятся к бесконечности. Связано это с тем, что x=2 является вертикальной асимптотой. Если абсцисса стремится к плюс бесконечности, значения будут асимптотически подходить к y=3. Соответствующий пример показан на рисунке 8.

Чтобы не приходилось долго разбираться с тем, как найти наименьшее у заданной функции, не путаться с тем, какие знаки производной использовать, а также легко строить графики, можно воспользоваться специальными онлайн калькуляторами. А еще – закончить тематические дистанционные онлайн курсы.

Источник

12. Исследование функций с помощью производной

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Поиск наибольшего/наименьшего значения у сложных функций

(blacktriangleright) Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке ([a,b]), необходимо схематично изобразить график функции на этом отрезке.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).

(blacktriangleright) Не стоит забывать, что наибольшее/наименьшее значение функция может принимать не только во внутренних точках отрезка ([a,b]), а также на его концах.

(blacktriangleright) Наибольшее/наименьшее значение функции — это значение координаты (y=f(x)).

(blacktriangleright) Производная сложной функции (f(t(x))) ищется по правилу: [{Large{f'(x)=f'(t)cdot t'(x)}}]
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]

Задание
1

#2357

Уровень задания: Равен ЕГЭ

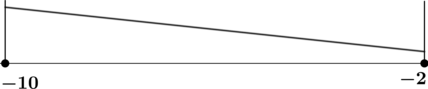
Найдите наименьшее значение функции (y = e^{x^2 — 4}) на отрезке ([-10; -2]).

ОДЗ: (x) – произвольный.

1) [y’ = 2xcdot e^{x^2 — 4}]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2xcdot e^{x^2 — 4} = 0qquadLeftrightarrowqquad x = 0,.] Таким образом, (y’ = 0) при (x = 0). Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-10; -2]):

4) Эскиз графика на отрезке ([-10; -2]):

Таким образом, наименьшего на ([-10; -2]) значения функция достигает в (x = -2).

[y(-2) = e^{4 — 4} = 1,.] Итого: (1) – наименьшее значение функции (y) на ([-10; -2]).

Ответ: 1

Задание
2

#2355

Уровень задания: Равен ЕГЭ

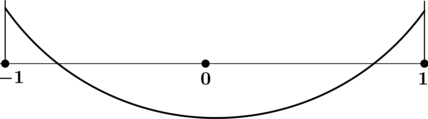
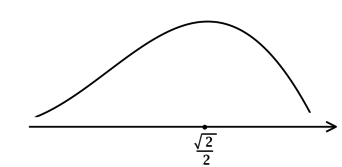
Найдите наибольшее значение функции (y = sqrt{2}cdotsqrt{x^2 + 1}) на отрезке ([-1; 1]).

ОДЗ: (x) – произвольный.

1) [y’ = sqrt{2}cdotdfrac{2x}{2sqrt{x^2 + 1}} = sqrt{2}cdotdfrac{x}{sqrt{x^2 + 1}}]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [sqrt{2}cdotdfrac{x}{sqrt{x^2 + 1}} = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-1; 1]):

4) Эскиз графика на отрезке ([-1; 1]):

Таким образом, наибольшего на ([-1; 1]) значения функция достигает в (x = -1) или в (x = 1). Сравним значения функции в этих точках.

[y(-1) = sqrt{2}cdotsqrt{1 + 1} = sqrt{2}cdotsqrt{2} = 2qquad y(1) = sqrt{2}cdotsqrt{1 + 1} = sqrt{2}cdotsqrt{2} = 2,.] Итого: (2) – наибольшее значение функции (y) на ([-1; 1]).

Ответ: 2

Задание
3

#2356

Уровень задания: Равен ЕГЭ

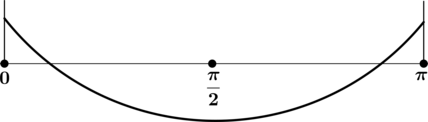
Найдите наименьшее значение функции (y = cos 2x) на отрезке ([0; pi]).

ОДЗ: (x) – произвольный.

1) [y’ = -2cdot sin 2x]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-2cdot sin 2x = 0qquadLeftrightarrowqquad 2x = pi n, ninmathbb{Z}qquadLeftrightarrowqquad x = dfrac{pi n}{2}, ninmathbb{Z},.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

(здесь бесконечное число промежутков, в которых чередуются знаки производной).

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([0; pi]):

4) Эскиз графика на отрезке ([0; pi]):

Таким образом, наименьшего на ([0; pi]) значения функция достигает в (x = dfrac{pi}{2}).

[yleft(dfrac{pi}{2}right) = cos pi = -1,.] Итого: (-1) – наименьшее значение функции (y) на ([0; pi]).

Ответ: -1

Задание
4

#915

Уровень задания: Равен ЕГЭ

Найдите наибольшее значение функции

(y = -log_{17}(2x^2 — 2sqrt{2}x + 2)).

ОДЗ: (2x^2 — 2sqrt{2}x + 2 > 0). Решим на ОДЗ:

1) Обозначим (2x^2-2sqrt{2}x+2=t(x)), тогда (y(t)=-log_{17}t).

[y’ = y’_tcdot t’_x = (-log_{17}t)’cdot(2x^2-2sqrt{2}x+2)’ = -dfrac{1}{ln 17}cdotdfrac{1}{t}cdot(4x-2sqrt{2}) = -dfrac{1}{ln 17}~cdot~dfrac{4x-2sqrt{2}}{2x^2-2sqrt{2}x+2}.]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-dfrac{1}{ln 17}cdotdfrac{4x-2sqrt{2}}{2x^2-2sqrt{2}x+2} = 0qquadLeftrightarrowqquad 4x-2sqrt{2} = 0] – на ОДЗ, откуда находим корень (x = dfrac{sqrt{2}}{2}). Производная функции (y) не существует при (2x^2-2sqrt{2}x+2 = 0), но у данного уравнения отрицательный дискриминант, следовательно, у него нет решений. Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:

Таким образом, наибольшее значение функция достигает в (x = dfrac{sqrt{2}}{2}):

(yleft(dfrac{sqrt{2}}{2}right) = -log_{17}1 = 0),

Итого: (0) – наибольшее значение функции (y).

Ответ: 0

Задание
5

#2344

Уровень задания: Равен ЕГЭ

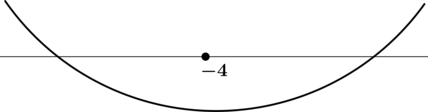
Найдите наименьшее значение функции

(y = log_{3}(x^2 + 8x + 19)).

ОДЗ: (x^2 + 8x + 19 > 0). Решим на ОДЗ:

1) Обозначим (x^2 + 8x + 19=t(x)), тогда (y(t)=log_{3}t).

[y’ = y’_tcdot t’_x = (log_{3}t)’cdot(x^2 + 8x + 19)’ = dfrac{1}{ln 3}cdotdfrac{1}{t}cdot(2x+8) = dfrac{1}{ln 3}~cdot~dfrac{2x+8}{x^2 + 8x + 19}.]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1}{ln 3}cdotdfrac{2x+8}{x^2 + 8x + 19} = 0qquadLeftrightarrowqquad 2x+8 = 0] – на ОДЗ, откуда находим корень (x = -4). Производная функции (y) не существует при (x^2 + 8x + 19 = 0), но у данного уравнения отрицательный дискриминант, следовательно, у него нет решений. Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:

Таким образом, (x = -4) – точка минимума функции (y) и наименьшее значение достигается в ней:

(y(-4) = log_{3}3 = 1).

Итого: (1) – наименьшее значение функции (y).

Ответ: 1

Задание
6

#917

Уровень задания: Сложнее ЕГЭ

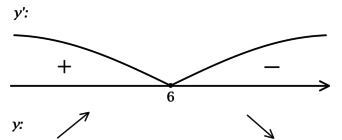
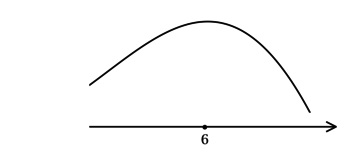
Найдите наибольшее значение функции

(y = -e^{(x^2 — 12x + 36 + 2ln 2)}).

1) Обозначим (x^2 — 12x + 36 + 2ln 2=t(x)), тогда (y(t)=-e^{t}).

[y’ = y’_tcdot t’_x = (-e^{t})’cdot(x^2 — 12x + 36 + 2ln 2)’ = -e^{t}cdot(2x-12) = -e^{x^2 — 12x + 36 + 2ln 2}cdot(2x-12).]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-e^{x^2 — 12x + 36 + 2ln 2}cdot(2x-12) = 0qquadLeftrightarrowqquad 2x-12 = 0] (так как (e^{x^2 — 12x + 36 + 2ln 2} = e^{t}), но (e^{t} > 0) при любом (t)), откуда находим корень (x = 6). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:

Таким образом, (x = 6) – точка максимума функции (y) и наибольшее значение достигается в ней:

(y(6) = -e^{(2ln 2)}=-e^{ln 4} = -4).

Итого: (-4) – наибольшее значение функции (y).

Ответ: -4

Задание
7

#918

Уровень задания: Сложнее ЕГЭ

Найдите наибольшее значение функции

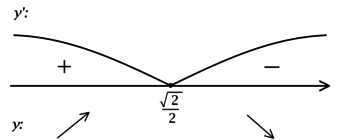
(y = e^{cos x + sin x — sqrt{2}}).

1) Обозначим (cos x + sin x — sqrt{2}=t(x)), тогда (y(t)=e^{t}). [y’ = y’_tcdot t’_x = (e^{t})’cdot(cos x + sin x — sqrt{2})’ = e^{t}cdot(-sin x + cos x) = e^{cos x + sin x — sqrt{2}}cdot(-sin x + cos x).]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [e^{cos x + sin x — sqrt{2}}cdot(-sin x + cos x) = 0qquadLeftrightarrowqquad -sin x + cos x = 0] (так как (e^{cos x + sin x — sqrt{2}} = e^{t}), но (e^{t} > 0) при любом (t)), что равносильно (mathrm{tg}, x = 1) при (cos x neq 0), откуда находим корни (x = dfrac{pi}{4} + pi k, k in -mathbb{Z}). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’): (их бесконечно много, но они чередуются)

3) Эскиз графика:

Таким образом, (x = dfrac{pi}{4} + 2pi k, k in mathbb{Z}) – точки локальных максимумов функции (y) и наибольшее значение достигается в одной из них:

(yleft(dfrac{pi}{4} + 2pi kright) = e^{cosleft(frac{pi}{4} + 2pi kright) + sinleft(frac{pi}{4} + 2pi kright) — sqrt{2}} = e^{frac{sqrt{2}}{2} + frac{sqrt{2}}{2} — sqrt{2}} = e^{0} = 1).

Итого: (1) – наибольшее значение функции (y).

Ответ: 1

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

26 мая

Как заработать +20–30 баллов на ЕГЭ благодаря разборам ЕГЭ с Дальнего Востока

24 мая

Обновлённая панель инструментов

22 мая

Беседы Решу ЕГЭ по подготовке к ЕГЭ

11 мая

Решение досрочных ЕГЭ по всем предметам

5 мая

Обновленный поиск заданий по ключевым словам

1 мая

Новый сервис: можно исправить ошибки!

29 апреля

Разместили актуальные шкалы ЕГЭ  — 2023

24 апреля

Учителю: обновленный классный журнал

7 апреля

Новый сервис: ссылка, чтобы записаться к учителю

30 марта

Решения досрочных ЕГЭ по математике

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Функции, зависящие от параметра

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 17 № 513258

Найдите все значения a, при каждом из которых наибольшее значение функции не меньше 1.

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

Решение

Критерии

1 комментарий

Видеокурс

Помощь

Тип 17 № 485938

Найдите все значения a, при каждом из которых наименьшее значение функции

больше, чем

Аналоги к заданию № 485938: 485946 503150 511452 … Все

Решение

Критерии

4 комментария

Видеокурс

Помощь

Тип 17 № 500016

Найдите все значения а, при каждом из которых наименьшее значение функции

на множестве не менее 6.

Аналоги к заданию № 500016: 500022 500451 500471 … Все

Решение

Критерии

2 комментария

Видеокурс

Помощь

Тип 17 № 484644

Найти все значения a, при каждом из которых функция

имеет более двух точек экстремума.

Аналоги к заданию № 484644: 507185 507186 507187 … Все

Решение

Критерии

2 комментария

Видеокурс

Помощь

Тип 17 № 507624

Найдите все значения параметра a, при каждом из которых неравенство

имеет единственное целое решение.

Решение

Критерии

4 комментария

Видеокурс

Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке x = 17 производная меняет знак с «плюса» на «минус». Значит, x= 17 — точка максимума функции y(x).

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке x = 1 производная меняет знак с «минуса» на «плюс». Значит, x= 1 — точка минимума функции y(x).

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция y=2^t монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же x_0 , что и точка максимума функции А ее найти легко.

$t^{$

$t^{$ при x=-4 . В точке x = -4 производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, x= - 4 — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: — 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке x = - 2 производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции y(x) . Поскольку при функция y(x) убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка x_1=1 — точка минимума функции . Точка $x_2=frac{1}{4}$ не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при x=1. Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции y(x) . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции y(x).

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

если e^x=4. Тогда x=ln4.

При x=ln4 знак производной меняется с «минуса» на «плюс». Значит, x=ln4 — точка минимума функции y(x).

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции y(x) . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при x=0.

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник