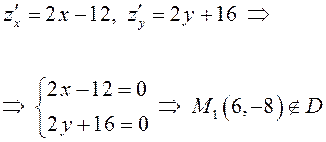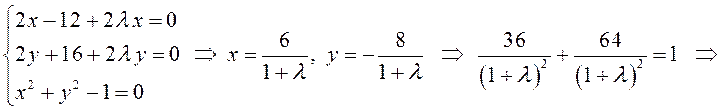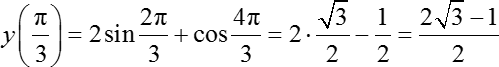Как найти наибольшее значение функции в круге

Экстремумы функции

Необходимое условие экстремума функции одной переменной

Достаточное условие экстремума функции одной переменной

Если в точке x * выполняется условие:

Пример №1 . Найти наибольшее и наименьшее значения функции: на отрезке [1; 3].
Решение.

Критическая точка одна x₁ = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 /₂, f(3)=3 8 /₈₁
Ответ: f_min= 5 /₂ при x=2; f_max=9 при x=1

Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π /₃+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π /₃+2πk, k∈Z – точки минимума функции; , значит x=- π /₃+2πk, k∈Z – точки максимума функции.

Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x₀ или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.

Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x — x 2

Наибольшее и наименьшее значение функции

На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.

Обычно мы определяем эти значения в рамках некоторого интервала x , который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [ a ; b ] , так и открытый интервал ( a ; b ) , ( a ; b ] , [ a ; b ) , бесконечный интервал ( a ; b ) , ( a ; b ] , [ a ; b ) либо бесконечный промежуток — ∞ ; a , ( — ∞ ; a ] , [ a ; + ∞ ) , ( — ∞ ; + ∞ ) .

В этом материале мы расскажем, как вычисляется наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x) y = f ( x ) .

Основные определения

Начнем, как всегда, с формулировки основных определений.

Наибольшее значение функции y = f ( x ) на некотором промежутке x – это значение m a x y = f ( x 0 ) x ∈ X , которое при любом значении x x ∈ X , x ≠ x 0 делает справедливым неравенство f ( x ) ≤ f ( x 0 ) .

Наименьшее значение функции y = f ( x ) на некотором промежутке x – это значение m i n x ∈ X y = f ( x 0 ) , которое при любом значении x ∈ X , x ≠ x 0 делает справедливым неравенство f(X f ( x ) ≥ f ( x 0 ) .

Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее самое большое значение на известном интервале при абсциссе x 0 , а наименьшее – это самое маленькое принимаемое значение на том же интервале при x 0 .

Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0 .

Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.

Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.

Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.

Более понятными эти моменты станут после изображения на графиках:

Наибольшее и наименьшее значение функции на отрезке

Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения ( m a x y и m i n y ) в стационарных точках, расположенных на отрезке [ — 6 ; 6 ] .

Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.

На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [ — 3 ; 2 ] . Они соответствуют наибольшему и наименьшему значению заданной функции.

Наибольшее и наименьшее значение функции на открытом интервале

Теперь посмотрим на четвертый рисунок. В нем функция принимает m a x y (наибольшее значение) и m i n y (наименьшее значение) в стационарных точках на открытом интервале ( — 6 ; 6 ) .

Если мы возьмем интервал [ 1 ; 6 ) , то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x , равном 6 , если бы x = 6 принадлежала интервалу. Именно этот случай нарисован на графике 5 .

На графике 6 наименьшее значение данная функция приобретает в правой границе интервала ( — 3 ; 2 ] , а о наибольшем значении мы не можем сделать определенных выводов.

Наибольшее и наименьшее значение функции на бесконечности

На рисунке 7 мы видим, что функция будет иметь m a x y в стационарной точке, имеющей абсциссу, равную 1 . Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y = 3 .

Если мы возьмем интервал x ∈ 2 ; + ∞ , то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2 , то значения функции будут стремиться к минус бесконечности, поскольку прямая x = 2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y = 3 . Именно этот случай изображен на рисунке 8 .

Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке

В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.

1. Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
2. Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
3. Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
4. Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x = a и x = b .
5. 5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.

Посмотрим, как правильно применить этот алгоритм при решении задач.

Условие: задана функция y = x 3 + 4 x 2 . Определите ее наибольшее и наименьшее значение на отрезках [ 1 ; 4 ] и [ — 4 ; — 1 ] .

Решение:

Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0 . Иными словами, D ( y ) : x ∈ ( — ∞ ; 0 ) ∪ 0 ; + ∞ . Оба отрезка, заданных в условии, будут находиться внутри области определения.

Теперь вычисляем производную функции согласно правилу дифференцирования дроби:

y ‘ = x 3 + 4 x 2 ‘ = x 3 + 4 ‘ · x 2 — x 3 + 4 · x 2 ‘ x 4 = = 3 x 2 · x 2 — ( x 3 — 4 ) · 2 x x 4 = x 3 — 8 x 3

Мы узнали, что производная функции будет существовать во всех точках отрезков [ 1 ; 4 ] и [ — 4 ; — 1 ] .

Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x 3 — 8 x 3 = 0 . У него есть только один действительный корень, равный 2 . Он будет стационарной точкой функции и попадет в первый отрезок [ 1 ; 4 ] .

Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x = 1 , x = 2 и x = 4 :

y ( 1 ) = 1 3 + 4 1 2 = 5 y ( 2 ) = 2 3 + 4 2 2 = 3 y ( 4 ) = 4 3 + 4 4 2 = 4 1 4

Мы получили, что наибольшее значение функции m a x y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 будет достигнуто при x = 1 , а наименьшее m i n y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 – при x = 2 .

Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:

y ( — 1 ) = ( — 1 ) 3 + 4 ( — 1 ) 2 = 3

Значит, m a x y x ∈ [ — 4 ; — 1 ] = y ( — 1 ) = 3 , m i n y x ∈ [ — 4 ; — 1 ] = y ( — 4 ) = — 3 3 4 .

Ответ: Для отрезка [ 1 ; 4 ] — m a x y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 , m i n y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 , для отрезка [ — 4 ; — 1 ] — m a x y x ∈ [ — 4 ; — 1 ] = y ( — 1 ) = 3 , m i n y x ∈ [ — 4 ; — 1 ] = y ( — 4 ) = — 3 3 4 .

Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале

Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.

1. Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
2. Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
3. Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0 , решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.

• Если интервал имеет вид [ a ; b ) , то нам надо вычислить значение функции в точке x = a и односторонний предел lim x → b — 0 f ( x ) .
• Если интервал имеет вид ( a ; b ] , то нам надо вычислить значение функции в точке x = b и односторонний предел lim x → a + 0 f ( x ) .
• Если интервал имеет вид ( a ; b ) , то нам надо вычислить односторонние пределы lim x → b — 0 f ( x ) , lim x → a + 0 f ( x ) .
• Если интервал имеет вид [ a ; + ∞ ) , то надо вычислить значение в точке x = a и предел на плюс бесконечности lim x → + ∞ f ( x ) .
• Если интервал выглядит как ( — ∞ ; b ] , вычисляем значение в точке x = b и предел на минус бесконечности lim x → — ∞ f ( x ) .
• Если — ∞ ; b , то считаем односторонний предел lim x → b — 0 f ( x ) и предел на минус бесконечности lim x → — ∞ f ( x )
• Если же — ∞ ; + ∞ , то считаем пределы на минус и плюс бесконечности lim x → + ∞ f ( x ) , lim x → — ∞ f ( x ) .

1. В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.

Пример 2

Условие: дана функция y = 3 e 1 x 2 + x — 6 — 4 . Вычислите ее наибольшее и наименьшее значение в интервалах — ∞ ; — 4 , — ∞ ; — 3 , ( — 3 ; 1 ] , ( — 3 ; 2 ) , [ 1 ; 2 ) , 2 ; + ∞ , [ 4 ; + ∞ ) .

Решение

Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0 :

x 2 + x — 6 = 0 D = 1 2 — 4 · 1 · ( — 6 ) = 25 x 1 = — 1 — 5 2 = — 3 x 2 = — 1 + 5 2 = 2 ⇒ D ( y ) : x ∈ ( — ∞ ; — 3 ) ∪ ( — 3 ; 2 ) ∪ ( 2 ; + ∞ )

Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.

Теперь выполним дифференцирование функции и получим:

y ‘ = 3 e 1 x 2 + x — 6 — 4 ‘ = 3 · e 1 x 2 + x — 6 ‘ = 3 · e 1 x 2 + x — 6 · 1 x 2 + x — 6 ‘ = = 3 · e 1 x 2 + x — 6 · 1 ‘ · x 2 + x — 6 — 1 · x 2 + x — 6 ‘ ( x 2 + x — 6 ) 2 = — 3 · ( 2 x + 1 ) · e 1 x 2 + x — 6 x 2 + x — 6 2

Следовательно, производные функции существуют на всей области ее определения.

Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x = — 1 2 . Это стационарная точка, которая находится в интервалах ( — 3 ; 1 ] и ( — 3 ; 2 ) .

Вычислим значение функции при x = — 4 для промежутка ( — ∞ ; — 4 ] , а также предел на минус бесконечности:

y ( — 4 ) = 3 e 1 ( — 4 ) 2 + ( — 4 ) — 6 — 4 = 3 e 1 6 — 4 ≈ — 0 . 456 lim x → — ∞ 3 e 1 x 2 + x — 6 = 3 e 0 — 4 = — 1

Поскольку 3 e 1 6 — 4 > — 1 , значит, m a x y x ∈ ( — ∞ ; — 4 ] = y ( — 4 ) = 3 e 1 6 — 4 . Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение — 1 , поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.

Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к — 3 с левой стороны, мы получим только интервал значений:

lim x → — 3 — 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 — 0 3 e 1 ( x + 3 ) ( x — 3 ) — 4 = 3 e 1 ( — 3 — 0 + 3 ) ( — 3 — 0 — 2 ) — 4 = = 3 e 1 ( + 0 ) — 4 = 3 e + ∞ — 4 = + ∞ lim x → — ∞ 3 e 1 x 2 + x — 6 — 4 = 3 e 0 — 4 = — 1

Значит, значения функции будут расположены в интервале — 1 ; + ∞

Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x = — 1 2 , если x = 1 . Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к — 3 с правой стороны:

y — 1 2 = 3 e 1 — 1 2 2 + — 1 2 — 6 — 4 = 3 e 4 25 — 4 ≈ — 1 . 444 y ( 1 ) = 3 e 1 1 2 + 1 — 6 — 4 ≈ — 1 . 644 lim x → — 3 + 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 ( x + 3 ) ( x — 2 ) — 4 = 3 e 1 — 3 + 0 + 3 ( — 3 + 0 — 2 ) — 4 = = 3 e 1 ( — 0 ) — 4 = 3 e — ∞ — 4 = 3 · 0 — 4 = — 4

У нас получилось, что наибольшее значение функция примет в стационарной точке m a x y x ∈ ( 3 ; 1 ] = y — 1 2 = 3 e — 4 25 — 4 . Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до — 4 .

Для интервала ( — 3 ; 2 ) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:

y — 1 2 = 3 e 1 — 1 2 2 + — 1 2 — 6 — 4 = 3 e — 4 25 — 4 ≈ — 1 . 444 lim x → — 3 + 0 3 e 1 x 2 + x — 6 — 4 = — 4 lim x → 2 — 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 ( x + 3 ) ( x — 2 ) — 4 = 3 e 1 ( 2 — 0 + 3 ) ( 2 — 0 — 2 ) — 4 = = 3 e 1 — 0 — 4 = 3 e — ∞ — 4 = 3 · 0 — 4 = — 4

Значит, m a x y x ∈ ( — 3 ; 2 ) = y — 1 2 = 3 e — 4 25 — 4 , а наименьшее значение определить невозможно, и значения функции ограничены снизу числом — 4 .

Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [ 1 ; 2 ) наибольшее значение функция примет при x = 1 , а найти наименьшее невозможно.

На промежутке ( 2 ; + ∞ ) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка — 1 ; + ∞ .

lim x → 2 + 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 ( x + 3 ) ( x — 2 ) — 4 = 3 e 1 ( 2 + 0 + 3 ) ( 2 + 0 — 2 ) — 4 = = 3 e 1 ( + 0 ) — 4 = 3 e + ∞ — 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x — 6 — 4 = 3 e 0 — 4 = — 1

Вычислив, чему будет равно значение функции при x = 4 , выясним, что m a x y x ∈ [ 4 ; + ∞ ) = y ( 4 ) = 3 e 1 14 — 4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y = — 1 .

Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.

Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.

4.2.3. Нахождение наибольших и наименьших значений

Пусть функция U = F (X1 , X2 ,…, Xn) определена и непрерывна в некотором ограниченном и замкнутом множестве D и имеет на этом множестве конечные частные производные (за исключением, быть может, отдельных точек). Тогда эта функция достигает на D своего наибольшего и наименьшего значения (см. свойства непрерывных функций). Если это значение достигается во внутренней точке множества, то, очевидно, эта точка должна быть стационарной; кроме того, наибольшее и наименьшее значение может достигаться на границе множества D. Поэтому для определения наибольшего и наименьшего значений функции на множестве D требуется:

1) найти стационарные точки функции, принадлежащие D, и вычислить значения функции в этих точках;

2) найти наибольшее и наименьшее значение, принимаемое функцией на границе множества D;

3) выбрать наименьшее и наибольшее из полученных чисел, которые и будут являться наименьшим и наибольшим значениями функции на всем множестве D.

1. Найдем наибольшее значение функции Z = Sin X + sin Y – sin (X + Y) в треугольнике со сторонами Х = 0, у = 0, Х + у = 2π. Стационарные точки определяются из решения системы

Единственной внутренней точкой данного треугольника, являющейся решением полученной системы, будет

Это значение оказывается наибольшим и на всем рассматриваемом множестве, так как на его границе Z = 0.

2. Найдем наибольшее и наименьшее значения функции Z = X² + Y² — 12X + 16Y в области X² + Y² ≤ 25.

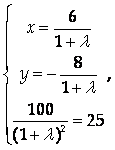
Откуда Х =6, У = -8 – точка, не лежащая в заданном круге. Следовательно, наибольшее и наименьшее значения данная функция принимает на границе области, то есть на окружности X² + Y² = 25. Составим функцию Лагранжа

Ее стационарные точки найдем из системы

Откуда L1 =1, L2 = -3. Следовательно, стационарными точками являются

(3, -4) и (-3, 4). В первой из них Z = -75, во второй Z = 125. Эти числа являются наименьшим и наибольшим значениями Z в заданной области.

Определение
4.2.1. Пусть функция

определена на некоторой области

.
Будем говорить, что в точке

функция

имеет глобальный максимум (минимум),
если для всех точек

выполняется неравенство

.

По
второй теореме Вейерштрасса, непрерывная
функция на ограниченном замкнутом
множестве всегда достигает минимального
и максимального значений, то есть имеет
оба глобальных экстремума.

Очевидно,
что глобальные экстремумы непрерывных
функций могут достигаться либо на
границе области

,
либо в точках локальных экстремумов,
лежащих внутри области

.
Так как локальные экстремумы могут
находиться только критических точках,
то для нахождения глобальных экстремумов
достаточно:

1)
найти критические точки функции

,
лежащие внутри области

;

2)
вычислить значения функции

в этих точках;

3)
найти минимальное и максимальное
значения функции

на границе области

;

4)
выбрать из значений, найденных в пунктах
2) и 3), наименьшее и наибольшее.

Задача.
Найти глобальные экстремумы функции

в круге

.

Решение.

1.
Найдем критические точки функции

,
лежащие внутри круга

.

,

.

Полученные
частные производные первого порядка
существуют всюду на

.
Найдем стационарные точки, решив систему

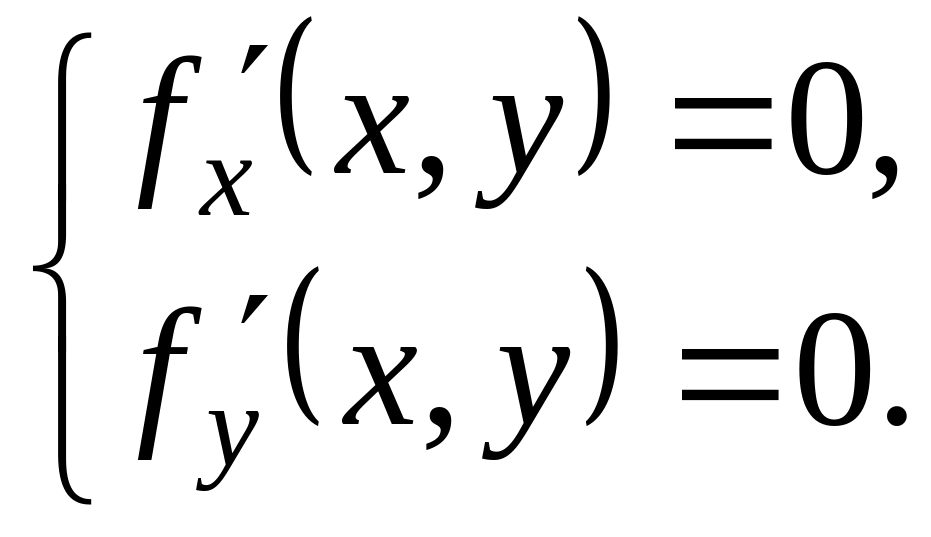
Очевидно,
что

‑ единственная стационарная точка
функции

.
Она принадлежит кругу

.

2.
Найдем значение функции

в стационарной точке

.

.

3.
Найдем минимальное и максимальное
значения функции

на границе круга

,
то есть на окружности

.

Зададим
окружность

в параметрической форме. Получим:

,
где

.

Подставив
выражения для

и

в функцию

,
будем иметь функцию одной переменной

.

Из
свойств функции

получаем, что минимальное значение
функции

на отрезке

будет равно

и оно будет достигаться при

(точка

)
и при

(точка

),
а максимальное значение будет равно

и оно будет достигаться в точках

(точка

),

(точка

),

(точка

).

4.
Выбрав из значений, полученных в пунктах
2 и 3, минимальное и максимальное значения,
получим глобальные экстремумы.

1)

,
минимальное значение функции достигается
в точках

,

;

2)

,
максимальное значение функции достигается
в точках

,

.

Задача.
Найти глобальные экстремумы функции

в треугольнике

ограниченном прямыми

,

и

.

Решение.

1.
Сделаем чертеж.

Рисунок 30

2.
Найдем критические точки функции

,
лежащие внутри треугольника

.

,

.

Полученные
частные производные первого порядка
существуют всюду на

.
Найдем стационарные точки, решив систему

Очевидно,
что

‑ единственная стационарная точка
функции

.
Она принадлежит треугольнику

.

3.
Найдем значение функции

в стационарной точке

.

.

4.
Найдем минимальное и максимальное
значения функции

на границе треугольника

.

Граница
треугольника

состоит из трех отрезков:

,

и

.

Отрезок

:

,

.

.

Отсюда
следует, что минимальное значение
функции

при

достигается при

и равно

.

Найдем
еще значения функции

на концах отрезка

.
Получим

и

.

Получили,
что минимальное значение функции

на отрезке

равно

,
а максимальное значение равно

.

Отрезок

:

,

.

.

Отсюда
следует, что минимальное значение
функции

при

достигается при

и равно

.

Найдем
еще значения функции

на концах отрезка

.
Получим

и

.

Получили,
что минимальное значение функции

на отрезке

равно

,
а максимальное значение равно

.

Отрезок

:

,

.

.

Минимум
этой функции достигается в точке вершины
параболы

,
и он равен

.

Найдем
еще значения функции

на концах отрезка

.
Получим

и

.

Получили,
что минимальное значение функции

на отрезке

равно

,
а максимальное значение равно

.

Таким
образом, на границе треугольника

минимальное значение функции

равно

,
а максимальное значение равно

.

5.
Из пунктов 3-4 имеем, что:

1)

,
минимальное значение функции достигается
в точке

;

2)

,
максимальное значение функции достигается
в точке

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Проверять достаточное  условие здесь нет
необходимости, так как задача имеет ясную геометрическую интерпретацию:
функция   задает плоскость в пространстве, а
уравнение связи   –  цилиндрическую поверхность.
Условные экстремумы – самая высокая и самая низкая точки той части этой
плоскости, которая является сечением цилиндра (рис. 20).

НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ

ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

В ЗАМКНУТОЙ ОГРАНИЧЕННОЙ ОБЛАСТИ

ТЕОРЕМА (Вейерштрасса). Всякая непрерывная в замкнутой ограниченной
области функция достигает в этой области своих наибольшего и наименьшего
значений.

(Без доказательства)

ЗАМЕЧАНИЕ. В случае функции одной переменной теорема Вейерштрасса
была справедлива для функции, непрерывной на отрезке. Таким образом, аналогом
отрезка на плоскости (или в пространстве) является замкнутая ограниченная область.

Рассмотрим непрерывную функцию ,
где  – замкнутая ограниченная область. Тогда по
теореме Вейерштрасса она имеет в этой области наименьшее и наибольшее значения,
которые достигаются либо во внутренних точках области – точках ее экстремума,–
либо на  границе области.

Будем считать, что   дифференцируема
во внутренних точках  . 

Для того, чтобы найти наибольшее и наименьшее
значения, надо

1) найти значения функции в стационарных точках,
принадлежащих ,

2) найти наибольшее и наименьшее значения функции
на границе ,

3) выбрать из найденных значений самое большое и
самое маленькое.

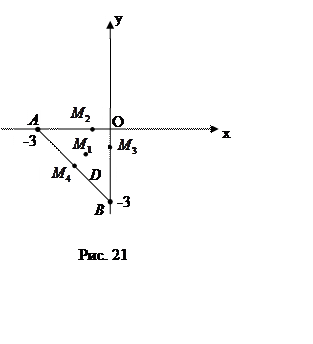
ПРИМЕР.
Найти наибольшее и наименьшее значения функции   в
области    (рис. 21).

1) Найдем стационарные точки функции, принадлежащие области :   . Точка    и   . 2) Исследуем функцию на границе. Граница состоит из трех участков  и  (рис. 21). На каждом из этих участков будем решать задачу на условный экстремум.

На , поэтому  – функция одной переменной, заданная на
отрезке. Здесь уравнение связи  учтено подстановкой в .

Следуя алгоритму поиска наибольшего и наименьшего
значений непрерывной на отрезке функции, найдем

.

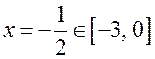
Значит, 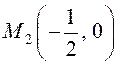 – стационарная точка 
на границе и  .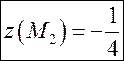

Кроме того,  и .

Аналогично на ,
поэтому

.

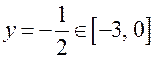
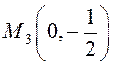
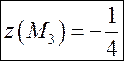
Ещё одна стационарная точка на границе –  и  ;   .

На  –
уравнение связи для третьей задачи на условный экстремум. Подставим  в :

.

 – стационарная точка
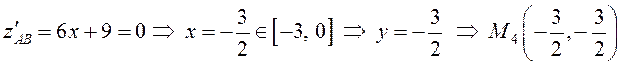
на    и  .

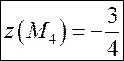
3) Сравним найденные значения функции,
выделенные рамкой. Она достигает наибольшего значения в двух точках на границе:
, , а
наименьшего – во внутренней точке области : .

ПРИМЕР.
Найти наибольшее и наименьшее значения функции   в  круге
   (рис. 22).             

1) Найдем стационарные точки функции, принадлежащие области :   Таким образом, внутри области стационарных точек нет.

2) Исследуем функцию на границе, то
есть решим задачу на условный экстремум функции  при
условии . 

В этом случае будем искать условный экстремум методом
множителей Лагранжа. Функция Лагранжа имеет вид:

.

Составим и решим систему (6.10):

 – стационарные точки
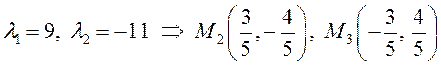
на границе и

.

3) Так как внутри области и на её
границе есть только две стационарные точки, то, очевидно, что  – наименьшее значение, а  – наибольшее значение этой функции в
заданном круге.

Библиографический список

1. Шнейдер В.Е. Краткий курс высшей
математики / В.Е.Шнейдер, А.И. Слуцкий, А.С. Шумов. – М.: Высш. шк. 1978. –
Т.2.

2.
Киркинский А.С. Математический анализ: учебное пособие / А.С.Киркинский. – М.:
Академический Проект, 2006. – 525 с.

3. Мышкис А.Д. Лекции по высшей математике /
Учебное пособие для студентов ВТУЗов. – М.: Наука, 1973. – 640 с.

4. Бутузов В.Ф., Крутицкая Н.Ч.,
Медведев Г.Н., Шишкин А.А. Математический анализ в вопросах и задачах. Функции
нескольких переменных. М.: Высш. шк., 1988. – 288 с.

Для заметок

          Редактор

      Компьютерная верстка

     ИД 06039 от 12.10.01

Подписано в печать                    Формат 60х84 
1/16

Бумага офсетная. Отпечатано на дуплекаторе.

Усл.печ.л.       Уч.-изд.л.

Тираж       экз.        Заказ

 

Издательство ОмГТУ. 644050, Омск, пр-т Мира, 11

Типография ОмГТУ

10 апреля 2014

Сегодня у нас заключительный урок на производные из ЕГЭ по математике. И как всегда по традиции последняя задача будет немножко нестандартной. Итак:

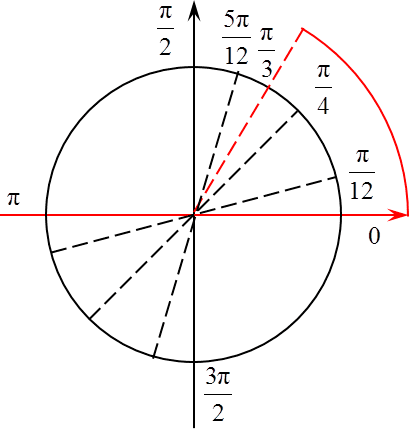
Задача B15. Найдите наибольшее значение функции на отрезке [0; π/3]:

y = 2sin 2x + cos 4x

Общая схема вычисления наибольшего значения функции

Перед тем, как мы начнем решать эту задачу, хотел бы напомнить вам общий универсальный алгоритм поиска наибольшего и наименьшего значения функции на отрезке. Он состоит из 4 шагов:

1. Первый шаг состоит в том, что нужно найти производную нашей функции: y‘ = ?

2. Второй шаг — производную мы приравниваем к нулю в результате решения у нас получится один или несколько корней: x{1}, x{2}, …

3. Затем берем эти корни и оставляем только те из них, которые лежат на отрезке, указанном в условии задачи — в нашем случае речь идет об отрезке [0; π/3]. Другими словами, мы вычеркиваем все корни, которые не лежат на интересующем нас отрезке: x{1}, x{2} ∈ [0; π/3].

4. Наконец, подставляем концы отрезка, а также оставшиеся корни в нашей исходное уравнение. Другими словами, мы находим y(0); y(π/3); y(x₁); y(x₂), т. е. значение функции в нулях производной.

Это стандартная схема, и мы применяли ее уже много раз.

Экстремумы функции на отрезке: пояснение

Естественно, при взгляде на этот алгоритм у многих учеников сразу возникают вопросы. Первый и самый распространенный: «Почему это мы подставляем в нашу функцию концы отрезка? Неужели недостаточно просто посчитать функцию в нулях производной?»

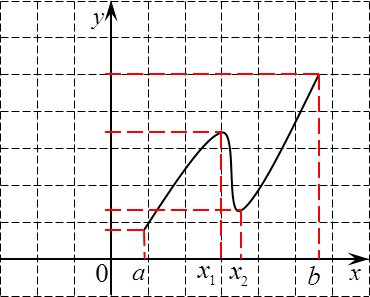
К сожалению, недостаточно. Взгляните вот на такую функцию:

На этом рисунке видно, что наибольшее значение функции достигается именно в правом верхнем конце отрезка — в точке b, а никак не в точке x₁, которая является точкой максимума и, соответственно, возникает при решении уравнения y‘ = 0. То же самое и с наименьшим значением — оно достигается в точке a, но ни в коем случае не в точке x₂, которая также возникнет при решении y‘ = 0.

Локальный и глобальный экстремум функции: в чем разница?

Вспомните определение производной и точки экстремума: в данном случае точка x₁ будет являться точкой локального максимума, т. е. на некотором интервале, достаточно небольшом, именно на этой точке будет приниматься наибольшее значение. То же самое касается и точки x₂. На некотором небольшом интервале, т. е. на определенном отступе от этой точки вправо или влево функция действительно будет принимать наименьшее значение именно в точке x₂.

Однако на глобальном отрезке никто этого не гарантировал. И часто случается так, что настоящее наибольшее или наименьшее значение функции достигается именно на концах рассматриваемого отрезка. Особенно это качается задач B15, которые любят давать на пробниках и разных демонстрационных ЕГЭ по математике.

Наибольшее или наименьшее значение функции совсем не обязательно достигается в нулях производной. Очень часто такие значения возникают на концах отрезка, где производная отлична от нуля.

В общем, чтобы подстраховаться и не допустить обидных ошибок на настоящем экзамене, настоятельно рекомендую вам считать значения функции не только в нулях производной, но и на концах отрезка, т. е. в нашем случае в точках х = 0 и х = π/3.

Решение задачи B15 с тригонометрией

С теорией разобрались, давайте решать нашу задачу. Для начала нам нужно посчитать производную функции:

y = 2sin 2x + cos 4x

Производная тригонометрической функции

Итак, записываем:

y‘ = (2sin 2x + cos 4x)’ = (2sin 2x)’ + (cos 4x)’

И вот тут возникает проблема в данной задаче: дело в том, что внутри синуса и косинуса стоит не переменная х, а выражение 2х и даже 4х.

Как поступать с такими конструкциями? Конечно, можно воспользоваться производной сложной функции, посчитать и в итоге получить правильное значение, но давайте не будем лезть в дебри, а вспомним замечательную формулу, которая рассматривалась не нескольких уроках, посвященным подготовке к ЕГЭ по математике. Формула следующая:

x → kx + b
(f (x))’ → k (f ‘ (kx + b))

Другими словами, замена переменной функции не проходит для всей функции бесследно. В случае, если вместо х мы подставляем линейную функцию, то перед новой производной появляется коэффициент.

Линейная замена переменной приводит лишь к одному дополнительному множителю в производной. Никаких сложных формул при линейной замене применять не нужно!

Это частный случай производной сложной функции. Однако сложные функции в реальном ЕГЭ не встречаются. Поэтому вам достаточно будет знать упрощенную конструкцию, которую мы записали. Ее очень легко применять.

Производная функции при линейной замене

Давайте посчитаем производную sin 2x. Для этого вспомним такое:

(sin x)’ = cos x

Тогда производная от sin 2x будет выглядеть так:

(sin 2x)’ = 2 · cos 2x

Все, производная 2sin 2x найдена. Аналогично давайте разберемся и с производной cos 4x:

(cos 4x)’ = 4 · (−sin 4x) = −4 sin 4x

А теперь собираем это все в одну конструкцию и получаем:

y‘ = 4 cos 2x − 4 sin 4x

Считаем нули производной — точки экстремума

Итак, первый шаг нашего алгоритма выполнен, мы нашли производную. Теперь приравниваем эту производную к нулю и решаем полученное уравнение:

2 cos 2x − 4 sin 4x = 0

Перед нами обычное тригонометрическое уравнение и все, что нам требуется сделать в нем — это свести все тригонометрические функции к одному и тому же аргументу. Как правило, в таких задачах следует стремиться к наименьшему аргументу. Поэтому вспомним формулу двойного угла:

sin 2λ = 2 sin λ cos λ

В нашем случае это будет выглядеть так:

sin 4x = sin 2 · 2x = 2 · sin 2x · cos 2x

Обратите внимание! Мы пишем именно 2х, потому что в исходной формуле, которую мы разложили, вместо переменной λ стоит именно 2х.

Итак, с синусом двойного угла мы разобрались, перепишем наше уравнение с учетом этого факта. Получим:

4 cos 2x − 8 sin 2x cos 2x = 0
4 cos 2x (1 − 2 sin 2x · 1) = 0

Итак, мы разложили наше уравнение на множители. Теперь вспоминаем: произведение равно нулю, когда хотя бы один из множителей равен нулю. Запишем:

cos 2x = 0
1 − 2 sin 2x = 0

Первое уравнение решается элементарно:

2x = π/2 + πn, n ∈ Z

А со вторым уравнением будет немного посложнее:

sin 2x = 1/2
2x = π/6 + 2πn
2x = π − π/6 + 2πn

Напомню, что решение простейших тригонометрических уравнений, которые содержат синус, лучше записывать как совокупность из двух наборов корней.

Однако на этом решение уравнения еще не закончилось. Взгляните, мы нашли только 2х, а нужно найти просто х. Находим:

x = π/3 + πn/2;
x = π/12 + πn;
x = 5π/12 + πn.

Производная тригонометрической функции: отбор корней на отрезке

Уравнение решено. Переходим к третьему шагу: необходимо отобрать корны, которые лежат на отрезке [0; π/3].

Для этого нам сначала потребуется начертить радар, а потом отметить на мне все три набора корней. На этом же отрезке отмечаем концы отрезка. Получим:

На самом деле из всего этого многообразия нас интересуют лишь две точки: π/4 и π/12. Все, третий шаг выполнен. Мы отобрали корни на отрезке.

Вычисление наибольшего значения функции

А теперь возвращаемся к условию задачи и вспоминаем, что нам нужно найти наибольшее значение функции на отрезке. Т. е. нужно взять функцию

y = 2sin 2x + cos 4x

И подставить в нее следующие числа:

1. Оба конца нашего отрезка — числа 0 и π/3
2. А также два корня производной, которую мы нашли: π/4 и π/12

Затем из полученных четырех значений функции надо выбрать наибольшее.

Давайте решать. В первую очередь предлагаю подставить корни нашей производной, т. е. числа π/4 и π/12. Получим:

y(π/4) = 2 · sin 2 · π/4 + cos 4 · π/4 = 2 · sin π/2 + cos π = 2 · 1 − 1 = 1

Итак, y(π/4) = 1

Подставляем второе число — x = π/12:

y(π/12) = 2 · sin 2 · π/12 + cos 4 · π/12 = 2 · sin π/6 + cos π/3 = 2 · 1/2 + 1/2 = 1,5

Все, с корнями из производной мы разобрались, теперь считаем значение функции на концах отрезка:

y(0) = 2 · sin 0 + cos 0 = 2 · 0 + 1 = 1

Вычисление сложных значений тригонометрической функции

Теперь подставляем правый конец отрезка:

y(π/3) = 2 · sin 2 · π/3 + cos 4 · π/3 = 2 · sin 2π/3 + cos 4π/3

Оба аргумента и в синусе, и в косинусе являются нестандартными значениями (их нет в классической таблице значений тригонометрических функций), поэтому давайте отметим их на тригонометрическом круге:

С помощью полученных данных вычисляем значение функции:

Это иррациональное число, которое нельзя записать в ответ. Следовательно, оно не является ответом к задаче.

Итого нам на выбор осталось три числа: y = 1; y = 1,5; y = 1. Требуется найти наибольшее значение. Следовательно, ответом будет являться y = 1,5. Все, задача решена.

Ключевые моменты в задачах B15 на производную функции

В заключение хотел бы еще раз обратить ваше внимание на два ключевых факта в решении этой задачи. В первую очередь, речь идет о производной сложной функции. В реальных задачах из ЕГЭ по математике встречается лишь упрощенная версия формулы, которую мы записали в самом начале решения задачи.

Итак, запомните: если в табличной производной заменить переменную х на линейное выражение kx + b, то и в самой производной нужно везде вместо х подставить выражение kx + b. Кроме того, перед самой производной нужно добавить множитель k — тот саамый, который стоял перед х во время замены.

Это универсальное правило, и оно работает всегда. Давайте посмотрим. Например, у нас есть следующая функция:

y = x¹⁰¹

Возьмем большую степень, чтобы у вас не возникало соблазна раскрывать ее по формулам сокращенного умножения. А теперь мы хотим посчитать производную:

y = (kx + b)¹⁰¹

Как это сделать? Очень просто. Вспоминаем: производная функции y = x¹⁰¹ является табличной и легко считается:

y‘ = 101 · x¹⁰¹

Теперь, если вместо переменной х мы хотим подставить выражение kx + b, например, 5х + 7, то получим, что производная такой функции будет равна:

y‘ = 101 · (5x + 7)¹⁰¹ · 5

Последний множитель «5» появился из-за того, что вместо переменной х мы подставили линейную функцию 5х + 7, т. е. выражение, которое при х содержит множитель 5. Если бы перед их стоял коэффициент k = 10, мы умножили бы производную на 10.

При этом второе слагаемое — число b = 7 — никак не влияет на результат. Т.е. на итоговую производную влияет только коэффициент при х. Запомните это.

Особенности записи корней тригонометрического уравнения

Второй важный момент касается отбора корней и решения тригонометрических уравнений, а конкретно — я бы хотел поговорить про решение тригонометрических уравнений, содержащих синус.

Как обычно нас учат записывать решение таких уравнений? Еще в школьных учебниках можно увидеть формулу:

sin x = a → x = (−1)ⁿ · arcsin a + πn, n ∈ Z

Естественно, многие ученики спросят: почему мы не используем эту формулу? Зачем разбивать эту формулу на какую-то совокупность, что-то там считать, усложняя себе задачу?

На самом деле такая запись имеет одно единственное преимущество — краткость. Во всем остальном работать с этой записью — сплошное мучение:

1. Непонятно, что делать с множителем (−1)ⁿ. Как отмечать постоянно гуляющее то в плюс, то в минус число на тригонометрическом круге?
2. Если вы захотите отбирать корни не с помощью тригонометрического круга, а с помощью двойного неравенства, опять же возникает проблема, потому что слагаемое (−1)ⁿ · arcsin a нужно будет вычитать из обеих частей неравенства. Затем полученную конструкцию нужно будет разделить на π, и вот тут возникает проблема: а что делать с множителем (−1)ⁿ? Он снова будет мешать нам и служить источником многочисленных ошибок для большинства учеников.

Чтобы избежать этих многочисленных проблем, просто записывайте решение синуса в виде совокупности из двух уравнений, так, как мы и сделали сегодня при решении нашей задачи.

Вот и все замечания. Я специально детально рассказывал каждый шаг решения — настолько детально, что сам допустил ошибку при вычислении производной. Но ничего страшного, мы заметили ошибку вовремя, и поэтому итоговый ответ и все выкладки получись правильными.:)

Желаю вам удачи при решении сложных задач на ЕГЭ по математике, тренируйтесь в решении задач, смотрите видеоуроки и сдавайте ЕГЭ на «отлично». А у меня на этом все.

Смотрите также:

1. Сложные задачи B15: комбинация тригонометрии и многочленов
2. Тригонометрические функции
3. Тест к уроку «Что такое числовая дробь» (легкий)
4. Задачи B12, сводящиеся к линейным уравнениям
5. Формулы приведения: ускоряем вычисления в тригонометрии
6. Задача C1: еще одно показательное уравнение
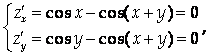
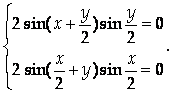
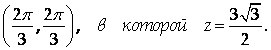
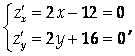
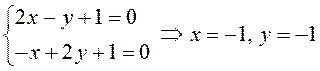