Как найти наибольшее значение с помощью производной - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.

Как найти наибольшее и наименьшее значения функции на отрезке?

Для этого мы следуем известному алгоритму:

1. Находим ОДЗ функции.

2. Находим производную функции

3. Приравниваем производную к нулю

4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:

Если на промежутке I производная функции $f^{prime}(x)>0$ , то функция y=f(x) возрастает на этом промежутке.

Если на промежутке I производная функции $f^{prime}(x)<0$ , то функция y=f(x) убывает на этом промежутке.

5. Находим точки максимума и минимума функции.

В точке максимума функции производная меняет знак с «+» на «-«.

В точке минимума функции производная меняет знак с «-» на «+».

6. Находим значение функции в концах отрезка,

затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции

Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.

Рассмотрим функцию . График этой функции выглядит так:

В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.

1. Рассмотрим функцию на отрезке

Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: f(0) , а наименьшее — в левом: f(-1) .

2. Рассмотрим функцию на отрезке

Очевидно, что наибольшее значение функция принимает в точке максимума f(0) , а наименьшее — в одном из концов отрезка, то есть надо найти значения f(-1) и f(1) и выбрать из них наименьшее.

3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть f(0) и f(2) .

Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть f(4/3) и f(-1) .

Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:

1. ОДЗ функции — множество действительных чисел.

2. $f^{prime}(x)=3x^2-4x$

3. , если x_1=0 или x_2=4/3

Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:

Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике

1. Задание B15 (№ 26695)

Найдите наибольшее значение функции на отрезке .

1. Функция определена при всех действительных значениях х

2. $y^{prime}= 15-3cosx$

cosx=5 Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.

y(0)=5

Ответ: 5.

2. Задание B15 (№ 26702)

Найдите наибольшее значение функции на отрезке [].

1. ОДЗ функции

2. $y^{prime}=3/{cos^2{x}}-3$

Производная равна нулю при , однако, в этих точках она не меняет знак:

$0<cos^2{x}<=1$ , следовательно, $3/{cos^2{x}}>=3$ , значит, $3/{cos^2{x}}-3>=0$ , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, при x=0 .

Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:

$y^{prime}=3/{cos^2{x}}-3={3-3cos^2{x}}/{cos^2{x}}={3sin^2{x}}/{cos^2{x}}=3tg^2{x}>=0$

у(0)=5

Ответ: 5.

3. Задание B15 (№ 26708)

Найдите наименьшее значение функции на отрезке [].

1. ОДЗ функции :

2. $y^{prime}=2/{cos^2{x}}-4$

3. $2/{cos^2{x}}-4=0$

$cos^2{x}=1/2$ ,

Расположим корни этого уравнения на тригонометрической окружности.

Промежутку принадлежат два числа: -{pi}/4 и {pi}/4

Расставим знаки. Для этого определим знак производной в точке х=0: $y^{prime}(0)=2/{cos^2(0)}-4=-2<0$ . При переходе через точки -{pi}/4 и {pi}/4 производная меняет знак.

Изобразим смену знаков производной функции на координатной прямой:

Очевидно, что точка является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции на отрезке , нужно сравнить значения функции в точке минимума и в левом конце отрезка, .

Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а таковым на является, следовательно подставим в уравнение функции

Ответ: -1

Вероятно, Ваш браузер не поддерживается. Попробуйте скачать

Firefox

И.В. Фельдман, репетитор по математике.

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке x = 17 производная меняет знак с «плюса» на «минус». Значит, x= 17 — точка максимума функции y(x).

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке x = 1 производная меняет знак с «минуса» на «плюс». Значит, x= 1 — точка минимума функции y(x).

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция y=2^t монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же x_0 , что и точка максимума функции А ее найти легко.

$t^{$

$t^{$ при x=-4 . В точке x = -4 производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, x= - 4 — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: — 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке x = - 2 производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции y(x) . Поскольку при функция y(x) убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка x_1=1 — точка минимума функции . Точка $x_2=frac{1}{4}$ не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при x=1. Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции y(x) . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции y(x).

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

если e^x=4. Тогда x=ln4.

При x=ln4 знак производной меняется с «минуса» на «плюс». Значит, x=ln4 — точка минимума функции y(x).

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции y(x) . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при x=0.

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Наибольшее и наименьшее значения функции можно найти по графику функции. Иногда это значения удаётся найти, используя свойства функции. В общем случае наибольшее и наименьшее значения функции находятся с помощью производной. Для этого сформулируем некоторые теоремы.

1. Если функция непрерывна на отрезке, то она достигает на нём и своего наибольшего, и своего наименьшего значений (Эта теорема доказывается в курсе высшей математики).

2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.

3. Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.

Как найти наименьшее и наибольшее значения функции на отрезке?

Пусть функция (f(x)) напрерывна на отрезке ([a; b]), тогда:

1) находим производную функции f′(x);

2) приравниваем производную к нулю, определяем точки экстремума функции, отбираем из них те, которые принадлежат отрезку ([a; b]);

3) находим значения функции y=f(x) в отобранных точках, и в конечных точках отрезка (a) и (b); выбираем среди полученных значений наименьшее (yнаим) и наибольшее (yнаиб).

А что делать, если нужно найти наибольшее или наименьшее значения функции, непрерывной на интервале? Один из вариантов — графический метод, который подразумевает построение графика функции и определение наименьшего или наибольшего значения функции по нему. Однако не всегда этот способ удобен, целесообразнее использовать следующую теорему.

Теорема. Пусть функция y=f(x) непрерывна на промежутке (X) и имеет внутри него единственную стационарную или критическую точку x0. Тогда:

а) если x=x0 — точка максимума, то yнаиб=f(xo);

б) если x=x0 — точка минимума, то yнаим=f(xo).

На рисунках продемонстрированы геометрические иллюстрации данной теоремы.

Источник

На этой странице вы узнаете

Кто всегда протянет руку помощи в определении производной?
Что такое сложная функция и зачем тут матрешка?
Как никогда не ошибаться при решении задач с производными?

Теория теорией, а дифференцировать хочется всегда. Эта статья посвящена практике нахождения производных.

Производные основных функций

Должно быть, вы уже слышали о производной и даже пробовали взять её мозговым штурмом. При отрицательном ответе вам обязательно нужно прокатиться на американских горках в нашей статье «Производная». В ней рассмотрели основные понятия производной.

Главный вопрос этой статьи: как ее находить? Для этого существуют свои формулы и правила, которых необходимо придерживаться для правильного решения заданий.

Ниже приведена таблица с формулами для нахождения производных основных функций. Применяя эти формулы, можно найти производную почти любой функции.

Не пугайтесь, если вам покажется, что их много: это основные формулы, с помощью которых можно решить большинство задач.

1	C’ = 0, C = const
2	((x^n)’ = n * x^{n — 1}, x > 0)
3	((a^x)’ = a^x * ln(a), a > 0, a neq 1)
4	((e^x)’ = e^x)
5	((log_{a}x)’ = frac{1}{x * ln(a)}, x > 0, a > 0, a neq 1)
6	((ln(x))’ = frac{1}{x}, x > 0)
7	((sqrt{x})’ = frac{1}{2sqrt{x}}, x > 0)
8	(sin(x))’ = cos(x)
9	(cos(x))’ = -sin(x)
10	((tg(x))’ = frac{1}{cos^{2}x}, x neq frac{pi}{2} + pi n, n in Z)
11	((ctg(x))’ = -frac{1}{sin^{2}x}, x neq pi n, n in Z)

Смотреть на формулы и учить их — это круто, прямо ощущаем себя великими учеными. Что может быть круче этого? Только применять их на практике. Рассмотрим несколько примеров нахождения производной.

Пример 1. Найдите производную функции f(x) = 5.

Решение: 5 — это число, то есть константа. Тогда, пользуясь первой формулой в таблице, получаем:

f'(x) = 5′ = 0.

Ответ: 0

Пример 2. Найдите производную функции (f(x) = x^4)

Решение: В этом случае необходимо воспользоваться второй формулой из таблицы.

(f'(x) = (x^4)’ = 4 * x^{4-1} = 4 * x^3)

Ответ: (4x^3)

Пример 3. Найдите производную функции (f(x) = e^x)

Решение: В этом случае необходимо воспользоваться четвертой формулой из таблицы.

(f'(x) = (e^x)’ = e^x)

Ответ: (e^x)

Правила дифференцирования

С полной уверенностью можем сказать, что вам встречались сложные функции. Даже намного сложнее, чем те, которые приведены в таблицах. Там и сумма, и произведение, и формула в формуле. Одним словом: ужас! Как брать производную, если перед функцией стоит коэффициент, или в функцию включено несколько разных выражений? На этот случай существуют правила дифференцирования.

Кто всегда протянет руку помощи в определении производной?

В сложных функциях невозможно пользоваться только формулами для нахождения производной.

Если функция
— усложнена коэффициентом,
— представлена в виде суммы, произведения или частного
— или является сложной функцией,
то для выбора правильной производной необходимо воспользоваться правилами дифференцирования. Они играют роль супергероев от мира производных. Рассмотрим их внимательнее.

1. Коэффициент можно вынести за знак производной.

(k * f(x))’ = k * (f(x))’

Например, необходимо взять производную у функции f(x) = 6sin(x). Тогда, пользуясь правилом дифференцирования и таблицей, получаем ответ 6cos(x).

2. Производная суммы (разности) равняется сумме (разности) производных.

((f(x) pm g(x))’ = f'(x) pm g'(x))

Найдем производную (f(x) = 4x^5 — sqrt{x} + cos(x)).

(f'(x) = (4x^5 — sqrt{x} + cos(x))’ = (4x^5)’ — (sqrt{x})’ + (cos(x))’ = 4 * 5 * x^{5 — 1} — frac{1}{2sqrt{x}} — sin(x))
(f'(x) = 20x^4 — frac{1}{2sqrt{x}} — sin(x). )

3. Производная произведения.

(f(x) * g(x))’ = f'(x) * g(x) + f(x) * g'(x)

Для примера возьмем производную функции f(x) = x² * ln(x)

f'(x) = (x² * ln(x))’ = (x²)’ * ln(x) + x² * (ln(x))’
(f'(x) = 2x * ln(x) + x^2 * frac{1}{x} = 2x * ln(x) + x)

4. Производная частного.

((frac{f(x)}{g(x)})’ = frac{f'(x) * g(x) — f(x) * g'(x)}{g^{2}(x)})

Возьмем производную функции (f(x) = frac{e^x}{3x})

(f'(x) = frac{(e^x)’ * 3x — ex * (3x)’}{(3x)^2} = frac{e^x * 3x — e^x * 3}{9x^2} = frac{3e^x * (x-1)}{9x^2} = frac{e^x * (x-1)}{3x^2})

5. Производная сложной функции.

Сложная функция — это функция, внутри которой есть другая функция.

Что такое сложная функция и зачем тут матрешка?

Давайте представим матрешку: в одну большую куклу складывается куколка поменьше, а в нее еще меньше и так далее. Точно так же и с функцией: “внутри” одной функции может лежать другая функция.

Например, у нас есть две функции: (sqrt{x}) и cos(x). А теперь попробуем поместить корень в функцию с косинусом, и получим (cos(sqrt{x})). Это и будет сложная функция.

Чтобы найти производную сложной функции, необходимо найти производную “внутренней” функции и умножить ее на производную “внешней” функции.

(f(g(x))’ = g'(x) * f'(g(x))

Найдем производную уже рассмотренной функции (f(x) = cos(sqrt{x})).

(f'(x) = (cos(sqrt{x}))’ = (sqrt{x})’ * (cos(sqrt{x}))’ = frac{1}{2sqrt{x}} * (-sin(sqrt{x})) = -frac{sin(sqrt{x})}{2sqrt{x}})

Исследование функции с помощью производной

В задании нам может быть дана только функция без ее графика. Что делать в таком случае, если нам нужно найти, например, отрезки возрастания, точки экстремума, наибольшее или наименьшее значение функции? Не во всех случаях получится построить график, да и это займет достаточно большое количество времени, которое и без того ограничено на экзамене.

В этом случае мы можем проанализировать поведение функции с помощью производной.

Исследуем функцию f(x) = (x — 4)²(x + 11) + 4.

Cначала возьмем производную от этой функции:

f'(x) = ((x — 4)²(x + 11))‘ + 4′ = ((x — 4)²(x + 11))’ = ((x — 4)²)'(x + 11) + (x — 4)²(x + 11)’
f'(x) = 2(x — 4)(x + 11) + (x — 4)² * 1 = (x — 4)(2(x + 11) + (x — 4)) = (x — 4)(3x + 18)

Любое исследование функции с помощью производной начинается именно с дифференцирования функции.

Теперь рассмотрим алгоритм нахождения точек минимума и максимума:

1 шаг. Нужно найти производную функции.

2 шаг. Найденную производную необходимо приравнять к 0 и решить полученное уравнение.

3 шаг. Расставить корни полученного уравнения на числовой прямой.

4 шаг. Определяем знаки производной на промежутках. Для этого необходимо подставить любое значение с выбранного промежутка в производную функции.

5 шаг. Определить, какие точки будут точками минимума (в них знак меняется с минуса на плюс), а какие — точками максимума (знак меняется с плюса на минус).

Найдем точки минимума и максимума в нашей функции. Поскольку производную мы уже взяли, можно сразу перейти ко второму шагу:

(x — 4)(3x + 18) = 0
x = 4, x = -6.

Полученные значения х расставляем на числовой прямой:

Теперь определим знаки на промежутках слева направо.

1. Возьмем точку -10 и подставим ее в производную функции:
(-10 — 4)(3 * (-10) + 18) = (-14) * (-12) = 168. Производная на этом промежутке будет положительной.

2. Возьмем точку 0 и подставим ее в производную функции:
(0 — 4)(3 * 0 + 18) = (-4) * 18 = -72. Производная на этом промежутке будет отрицательной.

3. Возьмем точку 5 и подставим ее в производную функции:
(5 — 4)(3 * 5 + 18) = 33. Производная на этом промежутке будет положительной.

Расставим полученные знаки на прямой:

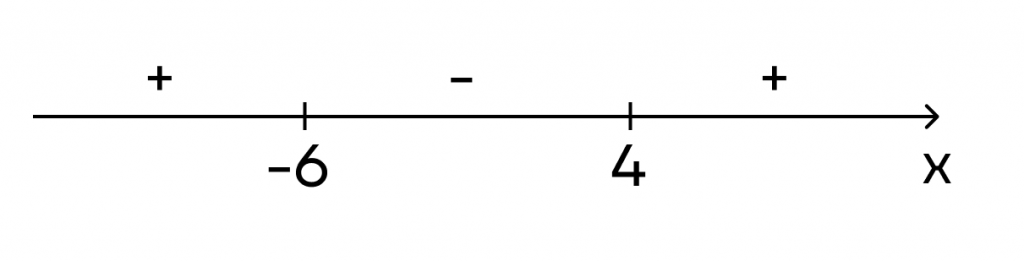
Остался последний пятый шаг. В точке -6 производная меняет знак с плюса на минус, значит, это точка максимума. В точке 4 производная меняет знак с минуса на плюс, значит, это точка минимума.

Важно!
Если в задании встречается формулировка “Найдите точку минимума (максимума) функции”, то необходимо пользоваться именно этим алгоритмом.

Но это не все выводы, которые уже можно сделать о функции. Вспомним, что функция возрастает, когда производная положительна, а убывает, когда производная отрицательна. Поскольку мы уже определили знаки производной, то смело можем сделать вывод, что на промежутках до -6 и после 4 функция будет возрастать, а на промежутке от -6 до 4 — убывать.

Однако могут встретиться задания, в которых необходимо найти наибольшее или наименьшее значение функции на определенном интервале.

Для выполнения таких заданий существует следующий алгоритм нахождения наибольшего и наименьшего значения функции.

Шаг 1. Найти производную функции.

Шаг 2. Найти точки минимума и максимума функции.

Шаг 3. Определить, какие из точек минимума и максимума принадлежат заданному интервалу.

Шаг 4. Найти значение функции в отобранных в предыдущем шаге точках, а также в точках, которые являются границами заданного интервала. Для этого необходимо подставить точки в функцию (не в производную от функции).

Для примера найдем наибольшее значение функции f(x) = (x — 4)²(x + 11) + 4 на отрезке [-10; 0].

Первые два шага мы уже выполнили, когда рассматривали алгоритм нахождения точек минимума и максимума. Из них отрезку [-10; 0] принадлежит х = -6 — точка максимума.

Теперь определим значение функции в трех точках:

f(-10) = (-10 — 4)²(-10 + 11) + 4 = 196 + 4 = 200
f(-6) = (-6 — 4)²(-6 + 11) + 4 = 500 + 4 = 504
f(0) = (0 — 4)²(0 + 11) + 4 = 176 + 4 = 180

Наибольшее из полученных значений — это 504. Это и будет ответ.

Как никогда не ошибаться при решении задач с производными?

Может возникнуть вопрос, почему важно проверять значение функции и на границах отрезка? В заданиях ЕГЭ очень часто встречаются случаи, когда нужно найти наибольшее значение, и в интервале лежит точка максимума, или когда нужно найти наименьшее значение функции и в интервале лежит точка минимума. Логично будет проверить только экстремумы, поскольку в них, скорее всего, достигается наибольшее или наименьшее значение.

Однако стоит вспомнить, что мы не видим график функции и не можем с точностью определить, что в экстремуме достигается нужное нам значение. С помощью экстремумов мы можем описать поведение функции: где она возрастает, а где убывает. Но можно столкнуться с графиком, на котором граничная точка будет лежать выше или ниже точки экстремума. Тогда наибольшее или наименьшее значение будет достигаться именно в ней. Пример на картинке (красными линиями обозначены границы отрезка).

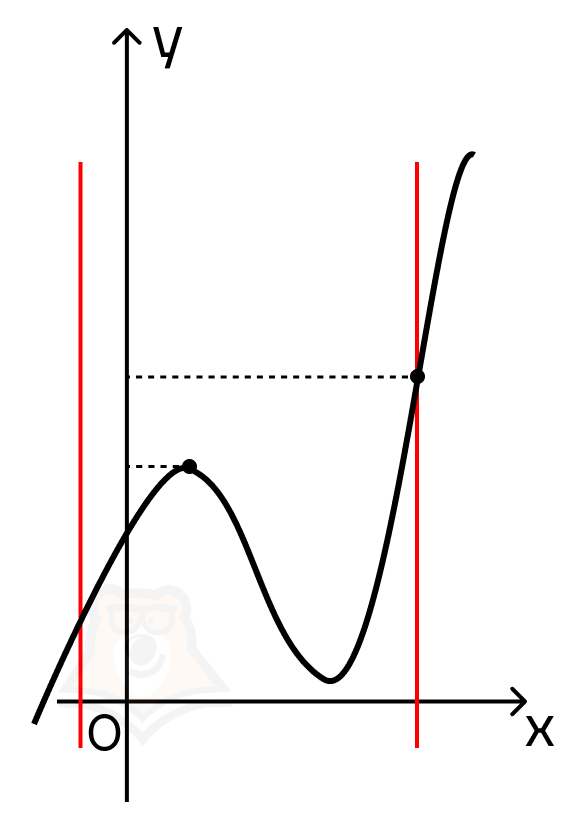
Подведем итог.
Как можно исследовать функцию с помощью производной?
С помощью производной можно с точностью сказать, на каких участках функция будет возрастать и убывать, сколько точек максимума и минимума у нее есть, какое наибольшее или наименьшее значение принимает функция на заданном участке.

Фактчек

Для нахождения производной необходимо пользоваться специальными формулами для производной. С их помощью можно найти производную любой из основных функций.
Если функция усложнена коэффициентом, является сложной или представлена в виде суммы, произведения или частного, то необходимо пользоваться правилами дифференцирования. Они помогут правильно найти производную.
Сложная функция — это функция, внутри которой есть другая функция.
С помощью производной можно исследовать функцию, а именно найти точки минимума и максимума, определить, на каких участках функция возрастает и убывает, найти наибольшее и наименьшее значение функции на заданном отрезке.

Проверь себя

Задание 1.
Чему будет равна производная f(x) = 3?

3;
1;
0;
Производную этой функции невозможно найти.

Задание 2.
Чему будет равна производная f(x) = 5x²?

10x;
10x²;
5x²;
2x.

Задание 3.
Чему будет равна производная f(x) = 13x + 5 + x³?

18 + 3x²;
13 + 3x²;
18;
3x².

Задание 4.
Чему будет равна производная f(x) = ln(x)?

x
(frac{1}{x})
(frac{1}{2sqrt{x}})
e^x

Задание 5.
Чему будет равна производная f(x) = tg(x)?

(frac{1}{cos^{2}(x)})
(-frac{1}{sin^{2}(x)})
(-frac{1}{cos^{2}(x)})
(frac{1}{sin^{2}(x)})

Ответы: 1. — 3 2. — 1 3. — 2 4. — 2 5. — 1

Источник

Алгебра и начала математического анализа, 11 класс

Урок №17. Наибольшее и наименьшее значения функции.

Перечень вопросов, рассматриваемых в теме

1) Нахождение наибольшего и наименьшего значения функции,

2)Определение алгоритма нахождения наибольшего и наименьшего значений функции на отрезке,

3) Рассмотреть прикладные задачи на нахождение наибольшего и наименьшего значений

Глоссарий по теме

Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:

Найти область определения функции D(f).
Найти производную f‘ (x).
Найти стационарные и критические точки функции, принадлежащие интервалу (a; b).
Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b).
Среди полученных значений выбрать наибольшее и наименьшее.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Нахождение наибольшего и наименьшего значений функции на отрезке.

Если функция непрерывна на отрезке, то она достигает на нем своего наибольшего и своего наименьшего значения.
Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
Если наибольшее (наименьшее) значение функции достигается внутри отрезка, то только в стационарной или критической точке.

Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:

Найти производную f‘ (x) стационарные и критические точки функции, принадлежащие интервалу (a; b).
Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b)и среди полученных значений выбрать наибольшее и наименьшее

Примеры и разбор решения заданий тренировочного модуля

№1.Найти наибольшее и наименьшее значения функции f (x) = 2x³ – 9x² + 12x – 2 на отрезке [0; 3]

Решение. Действуем в соответствии с алгоритмом.

1) D(f) = (-∞; +∞).

2) f (x) = 6x² – 18x + 12