Как найти наибольшее значение выражения на отрезке - Исправление недочетов и поиск решений вместе с Examum.ru

Математики и Data Science-специалисты должны хорошо разбираться в функциях. Предлагаем попрактиковаться в решении задач на обнаружение максимальных и минимальных значений у заданных функций.

Максимум

Задумываясь над тем, как найти максимальное значение функции, нужно четко понимать, с чем предстоит иметь дело. Для этого нужно запомнить такое определение:

Наибольшее значение функции y = f(x) на промежутке x – это max y = f(x₀). Оно будет при любом значении x€ X, x≠x₀ делает справедливым неравенство: f(x)≤f(x₀).

Максимальное значение (максимум) – это точка на функции, в которой значение функции больше, чем в соседних «отметках».

Минимум

Наименьшее значение функции находить так же легко, как и наибольшее. Но сначала нужно понимать, что это такое.

Значение функции на отрезке будет считаться минимумом, если оно меньше, чем в соседних «отметках». Здесь действует такое определение:

Наименьшее значение функции y=f(x) на промежутке x – это miny=f(x₀), которое при любом значении x€ X, x≠x₀ делает справедливым неравенство f(x)≥f(x₀).

Соответствующие определения являются достаточными и очевидными. Если говорить простыми словами, то максимум функции – это ее самое большое значение на заданном промежутке (участке) при абсциссе x₀, а минимум – самое маленькое.

Стационарные точки

При решении вопроса о том, как найти наибольшее или наименьшее значение функции, стоит обратить внимание на так называемые «стационарные точки». Это – значения аргумента функции, при которых ее производная будет равняться нулю.

Стационарная точка – это «отметка», в которой расположен экстремум дифференцируемой функции. А именно – локальный минимум или максимум. В одной из таких «отметок» записанное выражение будет достигать своих предельных параметров.

Здесь рекомендуется запомнить следующее:

Экстремум функции – это минимумы и максимумы.
Если определить производную в точках экстремумов, она будет равно 0.
Когда говорят «экстремумы», подразумевается значение функции. Если же речь идет об «отметках» экстремумов, рассматривать стоит x, в которых достигаются соответствующие пределы.

Этого достаточно для того, чтобы разобраться, как найти наибольшее на заданном отрезке у выражения. Для реализации поставленной задачи вовсе не обязательно составлять график. Поэтому сначала воспользуемся записями формул и вычислений.

План действий

Пример – дана функция f(x) на отрезке [a, b]. Наибольшее и наименьшее значение такой непрерывной функции достигаются в определенных местах. Это – критические точки. Там, где производная записанного выражения будет равно нулю.

Для того, чтобы найти наибольшие значения уравнения, потребуется придерживаться следующего алгоритма:

Узнайте, какая перед вами функция. Для этого нужно проверить ее на непрерывность. В расчет обязательно берется заданный отрезок.
Если запись непрерывная – ищем производную.
После того, как найдем производную, приравниваем ее к нулю. Это поможет найти точки экстремумов. В результате получаются корни.
Образовавшиеся корни – это критические точки. Нужно выбрать те «параметры», что относятся к промежутку [a, b].
Вычислить значения функции на концах отрезка [a, b].
Определить значения имеющегося выражения в критических «отметках».

Теперь понятно, как найти наибольшие функции на заданном отрезке. После произведенных подсчетов остается выбрать из результатов M (максимум) и m (минимум).

На отрезке

Разобравшись в тем, как найти наибольшие «параметры» выражения «на бумаге», стоит рассмотреть соответствующий процесс на графиках. Определять максимумы/минимумы в данном случае будет проще.

Первый график указывает на выражение, у которого точка минимума и максимума находятся в стационарных точках на промежутке [-6;6]. Соответствующие «пределы» обозначены жирным.

Второй график указывает на изменение отрезка. Теперь он будет [1;6]. Минимальное значение останется прежним. А вот максимальное – изменится. Оно образуется в правой части в точке с абсциссой. Поиск минимального «параметра» окажется в критической точке.

Задумываясь, как найти наименьшие или «самые крупные» параметры выражения на графике, можно также рассмотреть третий рисунок. Здесь функция принадлежала промежутку [-3;2]. Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы.

Открытый интервал

Если промежуток задан конкретным числом, определить экстремумы будет не так сложно. Иначе происходит, если интервал открыт.

Здесь:

Функция будет принимать максимум/минимум по значению в стационарных точках на открытом интервале от -6 до 6. Ответ – на 4 рисунке.
Если взять отрезок [1;6), минимум будет достигнут в стационарной точке. А вот максимум – неизвестен. Связано это с тем, что 6 не принадлежит к заданному интервалу. Если бы «шестерка» относилась к соответствующему промежутку, ответ на вопрос относительно определения максимума оказался понятным. Максимальный параметр был бы в точке с абсциссой 6.
На рисунке 6, задумываясь, как найти наименьшие «параметры», нужно обратить внимание на заданный интервал. Он равен (-3;2]. Минимум будет достигнут в правой границе. А вот максимум – не определен.

Найти значения на графиках обычно проще, чем «в чистых формулах». Соответствующие задания можно отыскать тут.

Бесконечность

Иногда значения функций нужно найти на бесконечном промежутке. Графически возможны такие ситуации:

На 7 рисунке функция достигает максимума в стационарной точке с абсциссой 1. Минимум окажется на границе интервала справа. На минус бесконечности значения приближаются к y=3 асимптотически.

Если взять интервал от 2-х до «плюс бесконечности», заданная функция не будет иметь ни максимумов, ни минимумов. Значения здесь стремятся к бесконечности. Связано это с тем, что x=2 является вертикальной асимптотой. Если абсцисса стремится к плюс бесконечности, значения будут асимптотически подходить к y=3. Соответствующий пример показан на рисунке 8.

Чтобы не приходилось долго разбираться с тем, как найти наименьшее у заданной функции, не путаться с тем, какие знаки производной использовать, а также легко строить графики, можно воспользоваться специальными онлайн калькуляторами. А еще – закончить тематические дистанционные онлайн курсы.

Источник

Наибольшее и наименьшее значение функции — ключевые понятия

Понятие самого большого и самого малого значения производной функции используется для определения оптимального показателя некоторого параметра.

Допустим, X — это некоторое множество, включенное в область определения функции y=f(x).

Определение

Наибольшее значение функции y=f(x) на заданном интервале x — это такое максимальное значение y=f(x₀) при x∈X, когда неравенство f(x)≤f(x₀) справедливо при всех значениях x, принадлежащих X и не равных нулю.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Определение

Наименьшее значение функции y=f(x) на заданном интервале x — это такое минимальное значение y=f(x₀) при x∈X, когда неравенство f(x)≥f(x₀) верно при всех значениях x, принадлежащих X и не равных нулю.

Если упростить данные определения, то получим следующее: максимальное значение функции представляет собой наибольшее значение на известном промежутке при x₀, а минимальное — это наименьшее значение, которое принимает функция на известном промежутке при x₀.

Определение

При обращении производной функции в ноль значения аргумента именуются стационарными точками.

Согласно теореме Ферма, данное понятие представляет собой такую точку, где расположены локальный минимум и максимум дифференцируемой функции или ее экстремум. Отсюда следует, что наименьшее и наибольшее значения y=f(x) будут достигнуты в одной из стационарных точек.

Самое большое и самое маленькое значение функция может принимать в точках, где функция определена, а первой производной данной функции нет.

Наименьшее и наибольшее значения не всегда можно вычислить. К примеру, это невозможно при совпадении рубежей заданного интервала с рубежами области определения. Также максимальные и минимальные значения не получится определить, когда речь идет о бесконечном промежутке.

Кроме того, функция неизвестном отрезке или на бесконечном интервале будет принимать бесконечно малые либо бесконечно большие значения. Это значит, что наименьшее и наибольшее значения в этом случае невозможно рассчитать.

Как найти для отрезка, алгоритм вычисления

Отрезок представляет собой часть прямой, которая ограничена двумя точками. Возьмем точки a и b за концы заданного отрезка. Тогда необходимо найти max y=f(x₀) и min y=f(x₀) на промежутке [a,b].

Последовательность нахождения:

Проверка заданной функции f(x) на нужном участке [a,b] на прерывность.
При условии, что f(x) непрерывная, определить производную f’(x) и приравнять ее к 0.
Найти точки максимума и минимума, которые вычисляются при решении уравнения f’(x)=0.
Определить критические точки, которые находятся на отрезке [a,b].
Произвести вычисления значений f(x) в этих критических точках и в точках a и b.
Самое большое и самое маленькое число среди вычисленных будет наибольшим и наименьшим значением функции на отрезке [a,b].

Примеры решения задач

Задача 1

Дано: функция, заданная уравнением

f(x)=4x³-5x²-6

Найти max y=f(x₀) и min y=f(x₀) на промежутке [0,4].

Решение

1. Функция представляет собой кубический многочлен. Точки разрыва отсутствуют, следовательно, функция непрерывна на заданном промежутке [0, 4].

2. Найдем производную:

(f'(x)=left(4x^3-5x^2-6right)’=12x^2-10x)

3. Приравниваем найденную производную к нулю:

(12x^2-10x=0)

4. Решим полученное уравнение и определим критические точки:

(12x^2-10x=0)

(2xleft(6x-5right)=0)

(x_1=0,;x_2=frac56)

5. Проверяем, принадлежат ли данные точки отрезку [0,4]:

(x_1inleft[0,4right],;x_2inleft[0,4right])

6. Поскольку обе критические точки находятся на заданном отрезке, то выполним расчет f(x) для этих точек и для границ промежутка [0,4]:

(f(x_1)=fleft(bright)=f(0)=4times0^3-5times0^2-6=-6)

(f(x_2)=fleft(frac56right)=4timesfrac56^3-5timesfrac56^2-6=frac{4times125}{216}-frac{5times25}{36}-6=frac{500}{216}-frac{125}{36}-6=frac{500-750}{216}-6=-frac{250}{216}-frac{1296}{216}=-frac{1546}{216}=-7frac{34}{216}=-7frac{17}{108})

(f(b)=fleft(4right)=4times4^3-5times4^2-6=4times64-5times16-6=256-80-6=170)

Среди найденных чисел наибольшее значение равно 170, наименьшее значение (-7frac{17}{108})

Ответ: (M=170), (m=-7frac{17}{108}).

Задача 2

Вычислить максимальное и минимальное значение функции на интервале [−4,4]. Функция задана уравнением:

(fleft(xright)=frac{2x^2}{6+x^2})

Решение

1. Проверяем функцию на прерывность: f(x) является непрерывной, поскольку при любых x знаменатель не равен нулю.

2. Находим производную:

(f’left(xright)=left(frac{2x^2}{6+x^2}right)’=frac{left(2x^2right)’left(6+x^2right)-left(2x^2right)left(6+x^2right)’}{left(6+x^2right)^2}=frac{4xleft(6+x^2right)-left(2x^2right)left(2xright)}{left(6+x^2right)^2}=frac{24x+4x^3-4x^3}{left(6+x^2right)^2}=frac{24x}{left(6+x^2right)^2})

3. Приравняем образовавшуюся производную к 0 и вычислим крайние точки:

(frac{24x}{left(6+x^2right)^2}=0)

(24x=0;;6+x^2neq0)

(x=0)

4. Единственная критическая точка лежит в пределах [−4,4].

5. Определим значения функции для x=−4, x=0 и x=4:

(f(-4)=frac{2left(-4right)^2}{6+left(-4right)^2}=frac{32}{22}=1frac{10}{22}=1frac5{11})

(f(0)=frac{2times0^2}{6+0^2}=frac06=0)

(f(4)=frac{2times4^2}{6+4^2}=frac{32}{22}=1frac{10}{22}=1frac5{11})

Ответ: (M=1frac5{11}), (m=0).

Источник

Наибольшее и наименьшее значение функции на отрезке

2 февраля 2016

Когда мы только приступаем к изучению производной функции, нам не совсем понятно: а зачем она вообще нужна? Можно, конечно, долго перечислять приложения производной, но сегодня мы рассмотрим важнейшее из них — нахождение наибольшего и наименьшего значения функции на указанном отрезке.

Из видео вы узнаете:

Как производная помогает найти точки экстремума функции;
Почему значения функции в точках экстремума не всегда оказывается наибольшим/наименьшем на отрезке;
Как гарантированно находить правильные максимумы и минимумы даже в сложных задачах.

Готовы? Поехали!

Смотрите также:

Производная сложной функции — основной урок
Простое определение производной функции
Тест к уроку «Сложные выражения с дробями» (легкий)
Метод коэффициентов, часть 1
Задача B5: площадь фигур с вершиной в начале координат
Задача B4: тарифы на сотовую связь

Источник

12. Исследование функций с помощью производной

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Поиск наибольшего/наименьшего значения на отрезке и в интервале

(blacktriangleright) Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке ([a,b]), необходимо схематично изобразить график функции на этом отрезке.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).

(blacktriangleright) Не стоит забывать, что наибольшее/наименьшее значение функция может принимать не только во внутренних точках отрезка ([a,b]), а также на его концах.

(blacktriangleright) Наибольшее/наименьшее значение функции — это значение координаты (y=f(x)).

(blacktriangleright) Если функция задана как частное двух других функций, то [{Large{left(dfrac fgright)’=dfrac{f’cdot
g-fcdot g’}{g^2}}}]
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]

Задание
1

#912

Уровень задания: Равен ЕГЭ

Найдите наибольшее значение функции (y = 13cdotdfrac{x^2 + 3x + 6}{x + 1}) на отрезке ([0; 12]).

ОДЗ: (x neq -1). Решим на ОДЗ:

1) [y’ = 13 dfrac{(2x + 3)(x + 1) — (x^2 + 3x + 6)}{(x + 1)^2} = 13 dfrac{x^2 + 2x — 3}{(x + 1)^2}.]

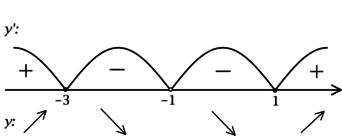
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [13 dfrac{x^2 + 2x — 3}{(x + 1)^2} = 0qquadLeftrightarrowqquad x^2 + 2x — 3 = 0] – на ОДЗ, откуда находим корни (x_1 = 1, x_2 = -3). Производная функции (y) не существует при (x = -1), но (x = -1) не входит в ОДЗ. Таким образом, [y’ = 13dfrac{(x — 1)(x+3)}{(x+1)^2}.] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

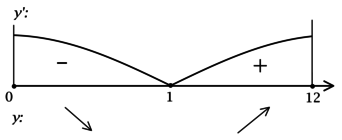
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([0; 12]):

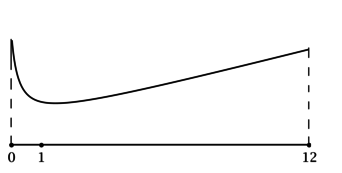
4) Эскиз графика на отрезке ([0; 12]):

Таким образом, наибольшее на ([0; 12]) значение функция достигает в (x = 0) или в (x = 12). Сравним эти значения:

(y(0) = 13cdot dfrac{6}{1} = 78),

(y(12) = 13cdot dfrac{186}{13} = 186).

Итого: (186) – наибольшее значение функции (y) на ([0; 12]).

Ответ: 186

Задание
2

#914

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции (y = x + dfrac{4}{x}) на ([1; 3]).

ОДЗ: (x neq 0). Решим на ОДЗ:

1) [y’ = 1 — dfrac{4}{x^2} = dfrac{x^2 — 4}{x^2}.]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{x^2 — 4}{x^2} = 0qquadLeftrightarrowqquad x^2 — 4 = 0] – на ОДЗ, откуда находим корни (x_1 = -2, x_2 = 2). Производная функции (y) не существует при (x = 0), но (x = 0) не входит в ОДЗ. Таким образом, [y’ = dfrac{(x+2)(x-2)}{x^2}.] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

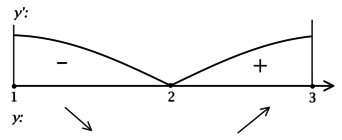
2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([1; 3]):

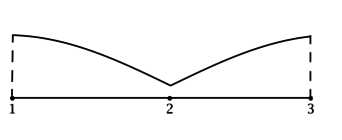
4) Эскиз графика на отрезке ([1; 3]):

Таким образом, (x = 2) – точка минимума функции (y) на ([1; 3]) и наименьшее значение функция достигает в ней.

(y(2) = 4).

Итого: (4) – наименьшее значение функции (y) на ([1; 3]).

Ответ: 4

Задание
3

#913

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции (y = dfrac{x^2 + 324}{x}) на ([2; 25]).

ОДЗ: (x neq 0). Решим на ОДЗ:

1) [y’ = dfrac{2x^2 — (x^2 + 324)}{x^2} = dfrac{x^2 — 324}{x^2}.]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{x^2 — 324}{x^2} = 0qquadLeftrightarrowqquad x^2 — 324 = 0] – на ОДЗ, откуда находим корни (x_1 = -18, x_2 = 18). Производная функции (y) не существует при (x = 0), но (x = 0) не входит в ОДЗ. Таким образом, [y’ = dfrac{(x+18)(x-18)}{x^2}.] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

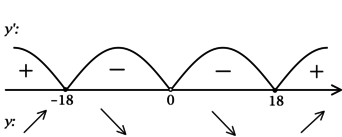
2) Найдём промежутки знакопостоянства (y’):

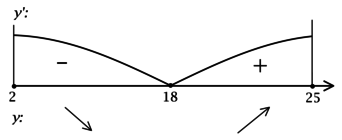
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([2; 25]):

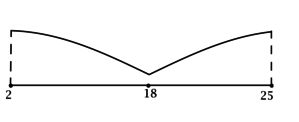
4) Эскиз графика на отрезке ([2; 25]):

Таким образом, (x = 18) – точка минимума функции (y) на ([2; 25]) и наименьшее значение функция достигает в ней.

(y(18) = dfrac{648}{18} = 36).

Итого: (36) – наименьшее значение функции (y) на ([2; 25]).

Ответ: 36

Задание
4

#2350

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции (y = dfrac{x^2 + x + 4}{x + 1}) на отрезке ([0; 3]).

ОДЗ: (x + 1 neq 0).

1) [y’ = dfrac{(2x + 1)(x + 1) — 1cdot (x^2 + x + 4)}{(x + 1)^2} = dfrac{x^2 + 2x — 3}{(x + 1)^2}]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{x^2 + 2x — 3}{(x + 1)^2} = 0qquadLeftrightarrowqquad dfrac{(x + 3)(x — 1)}{(x + 1)^2} = 0,.] Таким образом, (y’ = 0) при (x = 1) и при (x = -3). Производная не существует при (x = -1).

2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([0; 3]):

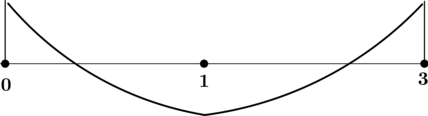
4) Эскиз графика на отрезке ([0; 3]):

Таким образом, наименьшего на ([0; 3]) значения функция достигает в (x = 1).

[y(1) = dfrac{1 + 1 + 4}{1 + 1} = 3,.] Итого: (3) – наименьшее значение функции (y) на ([0; 3]).

Ответ: 3

Задание
5

#2351

Уровень задания: Равен ЕГЭ

Найдите наибольшее значение функции (y = 6cdotdfrac{2x^2 + 0,5x + 1}{x + 2}) на отрезке ([0; 10]).

ОДЗ: (x + 2 neq 0).

1) [y’ = 6cdotdfrac{(4x + 0,5)(x + 2) — 1cdot (2x^2 + 0,5x + 1)}{(x + 2)^2} = 6cdotdfrac{2x^2 + 8x}{(x + 2)^2}]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [6cdotdfrac{2x^2 + 8x}{(x + 2)^2} = 0qquadLeftrightarrowqquad 6cdotdfrac{2x(x + 4)}{(x + 2)^2} = 0,.] Таким образом, (y’ = 0) при (x = 0) и при (x = -4). Производная не существует при (x = -2).

2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([0; 10]):

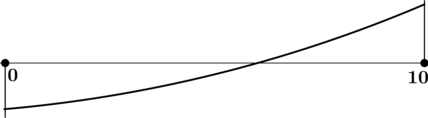
4) Эскиз графика на отрезке ([0; 10]):

Таким образом, наибольшего на ([0; 10]) значения функция достигает в (x = 10).

[y(10) = 6cdotdfrac{200 + 5 + 1}{10 + 2} = 103,.] Итого: (103) – наибольшее значение функции (y) на ([0; 10]).

Ответ: 103

Задание
6

#2352

Уровень задания: Равен ЕГЭ

Найдите наибольшее значение функции (y = dfrac{x^2 + x + 1}{x^2 + 1}) на отрезке ([-10; 1]).

ОДЗ: (x) – произвольный.

1) [y’ = dfrac{(2x + 1)(x^2 + 1) — 2xcdot (x^2 + x + 1)}{(x^2 + 1)^2} = dfrac{-x^2 + 1}{(x^2 + 1)^2}]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{-x^2 + 1}{(x^2 + 1)^2} = 0qquadLeftrightarrowqquad -dfrac{(x — 1)(x + 1)}{(x^2 + 1)^2} = 0,.] Таким образом, (y’ = 0) при (x = -1) и при (x = 1). Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-10; 1]):

4) Эскиз графика на отрезке ([-10; 1]):

Таким образом, наибольшего на ([-10; 1]) значения функция достигает в (x = -10) или в (x = 1). Сравним значения функции в этих точках.

[y(-10) = dfrac{100 — 10 + 1}{100 + 1} = dfrac{91}{101}qquad y(1) = dfrac{1 + 1 + 1}{1 + 1} = 1,5,.] Итого: (1,5) – наибольшее значение функции (y) на ([-10; 1]).

Ответ: 1,5

Задание
7

#2353

Уровень задания: Равен ЕГЭ

Найдите наибольшее значение функции (y = dfrac{x^3 + 2x + 2}{e^x}).

ОДЗ: (x) – произвольный.

1) [y’ = dfrac{(3x^2 + 2)cdot e^x — e^xcdot (x^3 + 2x + 2)}{e^{2x}} = dfrac{-x(x^2 — 3x + 2)}{e^{x}}]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{-x(x^2 — 3x + 2)}{e^{x}} = 0qquadLeftrightarrowqquad -dfrac{x(x — 1)(x — 2)}{e^{x}} = 0,.] Таким образом, (y’ = 0) при (x = 0), (x = 1) и при (x = 2). Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:

Таким образом, наибольшего значения функция достигает в (x = 0) или в (x = 2). Сравним значения функции в этих точках.

[y(0) = dfrac{2}{e^0} = 2qquad y(2) = dfrac{8 + 4 + 2}{e^2} = dfrac{14}{e^2},.] Так как (e > 2,7), то (e^2 > 7,29 > 7), следовательно, (dfrac{14}{e^2} < 2). Итого: (2) – наибольшее значение функции (y).

Ответ: 2

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.

Как найти наибольшее и наименьшее значения функции на отрезке?

Для этого мы следуем известному алгоритму:

1. Находим ОДЗ функции.

2. Находим производную функции

3. Приравниваем производную к нулю

4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:

Если на промежутке I производная функции $f^{prime}(x)>0$ , то функция y=f(x) возрастает на этом промежутке.

Если на промежутке I производная функции $f^{prime}(x)<0$ , то функция y=f(x) убывает на этом промежутке.

5. Находим точки максимума и минимума функции.

В точке максимума функции производная меняет знак с «+» на «-«.

В точке минимума функции производная меняет знак с «-» на «+».

6. Находим значение функции в концах отрезка,

затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции

Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.

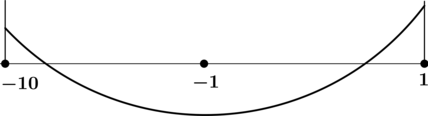
Рассмотрим функцию . График этой функции выглядит так:

В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.

1. Рассмотрим функцию на отрезке

Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: f(0) , а наименьшее — в левом: f(-1) .

2. Рассмотрим функцию на отрезке

Очевидно, что наибольшее значение функция принимает в точке максимума f(0) , а наименьшее — в одном из концов отрезка, то есть надо найти значения f(-1) и f(1) и выбрать из них наименьшее.

3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть f(0) и f(2) .

Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть f(4/3) и f(-1) .

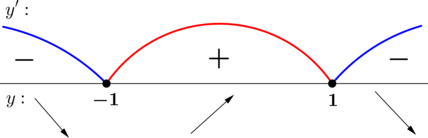
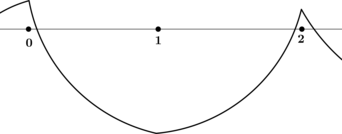
Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:

1. ОДЗ функции — множество действительных чисел.

2. $f^{prime}(x)=3x^2-4x$

3. , если x_1=0 или x_2=4/3

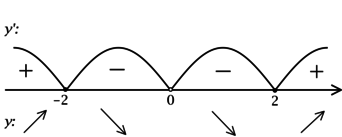
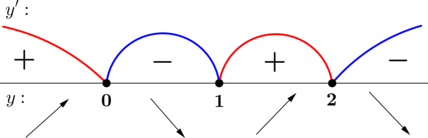
Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:

Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике

1. Задание B15 (№ 26695)

Найдите наибольшее значение функции на отрезке .

1. Функция определена при всех действительных значениях х

2. $y^{prime}= 15-3cosx$

cosx=5 Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.

y(0)=5

Ответ: 5.

2. Задание B15 (№ 26702)

Найдите наибольшее значение функции на отрезке [].

1. ОДЗ функции

2. $y^{prime}=3/{cos^2{x}}-3$

Производная равна нулю при , однако, в этих точках она не меняет знак:

$0<cos^2{x}<=1$ , следовательно, $3/{cos^2{x}}>=3$ , значит, $3/{cos^2{x}}-3>=0$ , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, при x=0 .

Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:

$y^{prime}=3/{cos^2{x}}-3={3-3cos^2{x}}/{cos^2{x}}={3sin^2{x}}/{cos^2{x}}=3tg^2{x}>=0$

у(0)=5

Ответ: 5.

3. Задание B15 (№ 26708)

Найдите наименьшее значение функции на отрезке [].

1. ОДЗ функции :

2. $y^{prime}=2/{cos^2{x}}-4$

3. $2/{cos^2{x}}-4=0$

$cos^2{x}=1/2$ ,

Расположим корни этого уравнения на тригонометрической окружности.

Промежутку принадлежат два числа: -{pi}/4 и {pi}/4

Расставим знаки. Для этого определим знак производной в точке х=0: $y^{prime}(0)=2/{cos^2(0)}-4=-2<0$ . При переходе через точки -{pi}/4 и {pi}/4 производная меняет знак.

Изобразим смену знаков производной функции на координатной прямой:

Очевидно, что точка является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции на отрезке , нужно сравнить значения функции в точке минимума и в левом конце отрезка, .

Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а таковым на является, следовательно подставим в уравнение функции

Ответ: -1

Вероятно, Ваш браузер не поддерживается. Попробуйте скачать

Firefox

И.В. Фельдман, репетитор по математике.

Источник