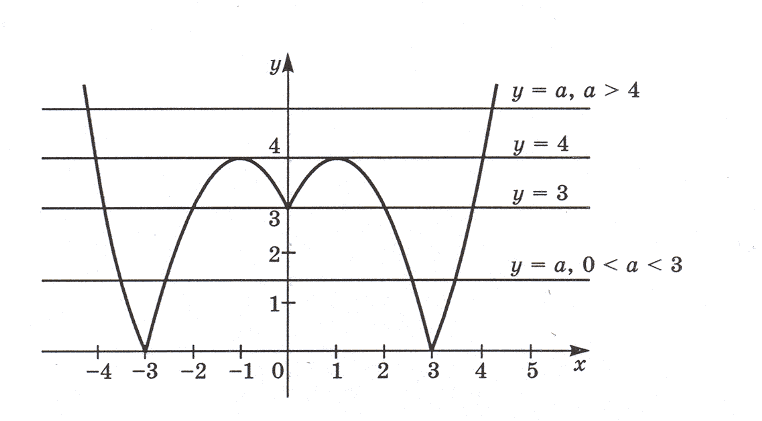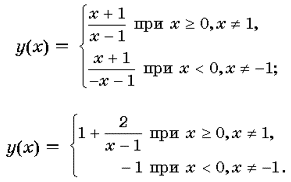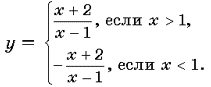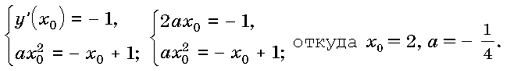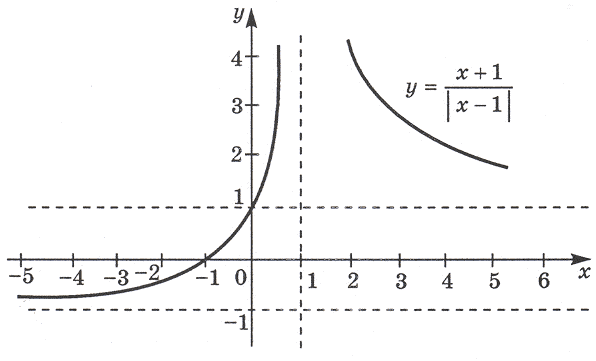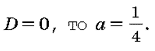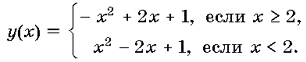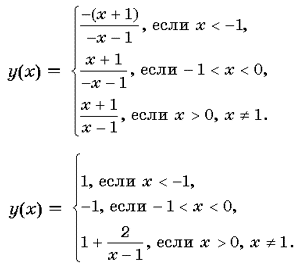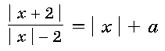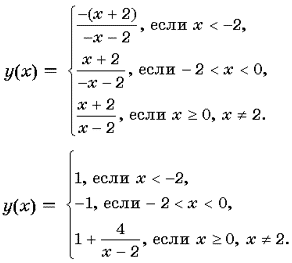Применение производной для решения нелинейных уравнений и неравенств
п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_<1,2>=frac<-2bpmsqrt><6a>). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Пример 1. Сколько корней имеют уравнения:
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения (frac 1x+frac<1>+frac<1>)
б) Найдите число корней уравнения (frac 1x+frac<1>+frac<1>=k)
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac<1>+frac<1> $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft<0;1;3right>)
Все три точки – точки разрыва 2-го рода. begin lim_left(frac1x+frac<1>+frac<1>right)=-infty-1-frac13=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=+infty-1-frac13=+infty\ lim_left(frac1x+frac<1>+frac<1>right)=1-infty-frac12=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=1+infty-frac12=+infty\ lim_left(frac1x+frac<1>+frac<1>right)=frac13+frac12-infty=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=frac13+frac12+infty=+infty end 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin lim_left(frac1x+frac<1>+frac<1>right)=-0-0-0=-0\ lim_left(frac1x+frac<1>+frac<1>right)=+0+0+0=+0\ end Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac<1>-frac<1><(x-1)^2>-frac<1><(x-3)^2>lt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) — три корня
При (k=0) — два корня
При (kgt 0) — три корня
Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt+sqrt<10-2x>=a $$ имеет по крайней мере одно решение.
Исследуем функцию (f(x)=sqrt+sqrt<10-2x>)
ОДЗ: ( begin x-1geq 0\ 10-2xgeq 0 end Rightarrow begin xgeq 1\ xleq 5 end Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt<8>=2sqrt<2>, f(5)=sqrt<4>+0=2)
Первая производная: begin f'(x)=frac<1><2sqrt>+frac<-2><2sqrt<10-2x>>=frac<1><2sqrt>-frac<1><sqrt<10-2x>>\ f'(x)=0 text<при> 2sqrt=sqrt<10-2x>Rightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt<frac73-1>+sqrt<10-2cdot frac73>=sqrt<frac43>+sqrt<frac<16><3>>=frac<6><sqrt<3>>=2sqrt <3>end Промежутки монотонности:
| (x) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| (f'(x)) | ∅ | + | 0 | — | ∅ |
| (f(x)) | (2sqrt<2>) | (nearrow ) | max (2sqrt<3>) |
(searrow ) | 2 |
Можем строить график:
(y=a) — горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:
| $$ alt 2 $$ | нет решений |
| $$ 2leq alt 2sqrt <2>$$ | 1 решение |
| $$ 2sqrt<2>leq alt 2sqrt <3>$$ | 2 решения |
| $$ a=2sqrt <3>$$ | 1 решение |
| $$ agt 2sqrt <3>$$ | нет решений |
По крайней мере одно решение будет в интервале (2leq aleq 2sqrt<3>).
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство (frac<2+log_3 x>gt frac<6><2x-1>)
Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)
Получаем совокупность: begin left[ begin begin xgt 1\ 2+log_3 xgtfrac<6(x-1)> <2x-1>end \ begin 0lt xlt 1\ 2+log_3 xltfrac<6(x-1)> <2x-1>end end right. \ 2+log_3 xgt frac<6(x-1)><2x-1>Rightarrow log_3 xgt frac<6(x-1)-2(2x-1)><2x-1>Rightarrow log_3 xgt frac<2x-4><2x-1>\ left[ begin begin xgt 1\ log_3 xgtfrac<2x-4> <2x-1>end \ begin 0lt xlt 1\ log_3 xltfrac<2x-4> <2x-1>end end right. end Исследуем функцию (f(x)=frac<2x-4><2x-1>=frac<2x-1-3><2x-1>=1-frac<3><2x-1>)
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin lim_left(1-frac<3><2x-1>right)=1-frac<3><-0>=+infty\ lim_left(1-frac<3><2x-1>right)=1-frac<3><+0>=-infty end Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin lim_left(1-frac<3><2x-1>right)=1-frac<3><-infty>=1+0\ lim_left(1-frac<3><2x-1>right)=1-frac<3><+infty>=1-0 end На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-frac<3><2x-1>right)’=frac<3><(2x-1)^2>gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f»(x)=-frac<6> <(2x-1)^3>$$ Одна критическая точка 2-го порядка (x=frac12)
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Построение графиков функций
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
при х ≠ -1.
График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
http://urok.1sept.ru/articles/564361
http://skysmart.ru/articles/mathematic/postroenie-grafikov-funkcij
Решение уравнений с помощью графиков
Решение линейных уравнений
Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.
Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.
Сейчас же я покажу тебе, как это сделать графическим способом.
Итак, у тебя есть уравнение: ( displaystyle 2{x} -10=2)
Как его решить?
Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:
( displaystyle 2x=2+10)
( displaystyle 2x=12)
Обычно дальше мы делим правую часть на левую, и получаем искомый корень, но мы с тобой попробуем построить левую и правую части как две различные функции в одной системе координат.
Иными словами, у нас будет:
( displaystyle {{y}_{1}}=2x)
( displaystyle {{y}_{2}}=12)
А теперь строим. Что у тебя получилось?
Как ты думаешь, что является корнем нашего уравнения? Правильно, координата ( displaystyle x) точки пересечения графиков:
Наш ответ: ( displaystyle x=6)
Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число ( displaystyle 6)!
Вариант 1. Напрямую
Просто строим параболу по данному уравнению: ( displaystyle {{x}^{2}}+2{x} -8=0)
Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:
( displaystyle x=-frac{b}{2a})
( displaystyle y=-frac{{{b}^{2}}-4ac}{4a})
Ты скажешь «Стоп! Формула для ( displaystyle y) очень похожа на формулу нахождения дискриминанта» да, так оно и есть, и это является огромным минусом «прямого» построения параболы, чтобы найти ее корни.
Тем не менее, давай досчитаем до конца, а потом я покажу, как это сделать намного (намного!) проще!
Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:
( displaystyle x=frac{-2}{2}=-1)
( displaystyle y=-frac{{{2}^{2}}-4cdot left( -8 right)}{4}=-frac{4+32}{4}=-9)
Точно такой же ответ? Молодец!
И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, ( displaystyle 3).
Ты знаешь, что парабола симметрична относительно своей вершины, например:
Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:
Возвращаемся к нашей параболе.
Для нашего случая точка ( displaystyle Aleft( -1;-9 right)). Нам необходимо еще две точки, соответственно, ( displaystyle x) можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?
Мне удобней работать с положительными, поэтому я рассчитаю при ( displaystyle x=0) и ( displaystyle x=2).
При ( displaystyle x=0):
( displaystyle y={{0}^{2}}+0-8=-8)
При ( displaystyle x=2):
( displaystyle y={{2}^{2}}+2cdot 2-8=0)
Теперь у нас есть три точки, и мы спокойно можем построить нашу параболу, отразив две последние точки относительно ее вершины:
Как ты думаешь, что является решением уравнения?
Правильно, точки, в которых ( displaystyle y=0), то есть ( displaystyle x=2) и ( displaystyle x=-4). Потому что ( displaystyle {{x}^{2}}+2{x} -8=0).
И если мы говорим, что ( displaystyle y={{x}^{2}}+2{x} -8), то значит, что ( displaystyle y) тоже должен быть равен ( displaystyle 0), или ( displaystyle y={{x}^{2}}+2{x} -8=0).
Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!
Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.
Что у тебя получилось? То же самое?
Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!
Решение смешанных неравенств
Теперь перейдем к более сложным неравенствам!
Как тебе такое:
( displaystyle 4x<{{x}^{3}})?
Жуть, правда? Честно говоря, я понятия не имею, как решить такое алгебраически… Но, оно и не надо. Графически ничего сложного в этом нет! Глаза боятся, а руки делают!
Первое, с чего мы начнем, – это с построения двух графиков:
( displaystyle {{y}_{1}}=4x)
( displaystyle {{y}_{2}}={{x}^{3}})
Я не буду расписывать для каждого таблицу – уверена, ты отлично справишься с этим самостоятельно (еще бы, столько прорешать примеров!).
Расписал? Теперь строй два графика.
Сравним наши рисунки?
У тебя так же? Отлично!
Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть ( displaystyle {{y}_{2}}={{x}^{3}}).
Смотри, что получилось в итоге:
А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график ( displaystyle {{y}_{1}}=4x)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!
На каких промежутках по оси ( displaystyle Ox) у нас ( displaystyle {{y}_{2}}={{x}^{3}}) находится выше, чем ( displaystyle {{y}_{1}}=4x)? Верно, ( displaystyle xin left( -2;0 right)cup left( 2;+infty right)).
Это и есть ответ!
Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!
В. Малинин,
г. Нижний Новгород
Уравнения с
параметрами:графический метод решения
8-9 классы
В статье рассматривается графический метод
решения некоторых уравнений с параметрами,
который весьма эффективен, когда нужно
установить, сколько корней имеет уравнение в
зависимости от параметра a.
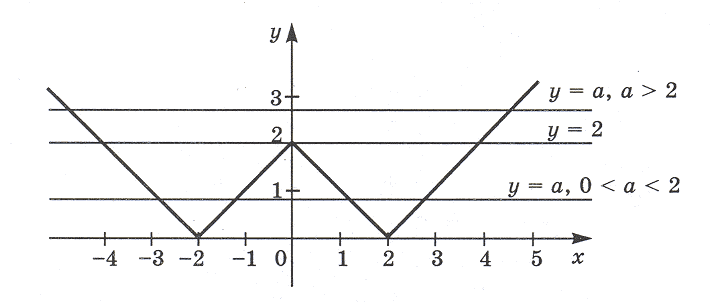
Задача 1. Сколько корней имеет уравнение
| | x | – 2 | = a в зависимости от
параметра a?
Решение. В системе координат (x; y) построим
графики функций y = | | x | – 2 | и y = a.
График функции y = | | x | – 2 | изображен
на рисунке.
Графиком функции y = a является прямая,
параллельная оси Ox или с ней совпадающая (при a
= 0).
Из чертежа видно, что:
Если a = 0, то прямая y = a совпадает с
осью Ox и имеет с графиком функции y = | | x |
– 2 | две общие точки; значит, исходное
уравнение имеет два корня (в данном случае корни
можно найти: x1,2 = д 2).
Если 0 < a < 2, то прямая y = a имеет с графиком
функции y = | | x | – 2 | четыре общие точки
и, следовательно, исходное уравнение имеет
четыре корня.
Если a = 2, то прямая y = 2 имеет с графиком
функции три общие точки. Тогда исходное
уравнение имеет три корня.
Если a > 2, то прямая y = a будет иметь с
графиком исходной функции две точки, то есть
данное уравнение будет иметь два корня.
Ответ:
если a < 0, то корней нет;
если a = 0, a > 2, то два корня;
если a = 2, то три корня;
если 0 < a < 2, то четыре корня.
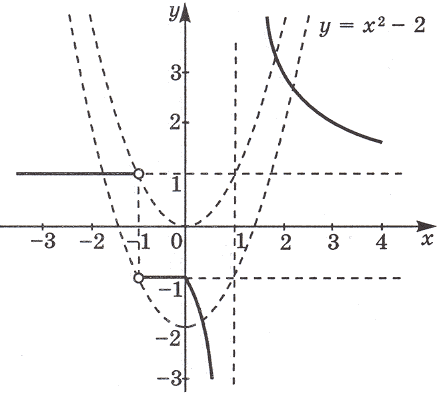
Задача 2. Сколько корней имеет уравнение | x2
– 2| x | – 3 | = a в зависимости от
параметра a?
Решение. В системе координат (x; y) построим
графики функций y = | x2 – 2| x | – 3 |
и y = a.
График функции y = | x2 – 2| x | – 3 |
изображен на рисунке. Графиком функции y = a
является прямая, параллельная Ox или с ней
совпадающая (когда a = 0).
Из чертежа видно:
Если a = 0, то прямая y = a совпадает с
осью Ox и имеет с графиком функции y = | x2 –
2| x | – 3 | две общие точки, а также прямая y =
a будет иметь с графиком функции y = | x2
– 2| x | – 3 | две общие точки при a > 4.
Значит, при a = 0 и a > 4 исходное
уравнение имеет два корня.
Если 0 < a < 3, то прямая y = a имеет с
графиком функции y = | x2 – 2| x | – 3 |
четыре общие точки, а также прямая y=a будет
иметь с графиком построенной функции четыре
общие точки при a = 4. Значит, при 0 < a <
3, a = 4 исходное уравнение имеет четыре корня.
Если a = 3, то прямая y = a пересекает
график функции в пяти точках; следовательно,
уравнение имеет пять корней.
Если 3 < a < 4, прямая y = a пересекает график
построенной функции в шести точках; значит, при
этих значениях параметра исходное уравнение
имеет шесть корней.
Если a < 0, уравнение корней не имеет, так как
прямая y = a не пересекает график функции y = | x2
– 2| x | – 3 |.
Ответ:
если a < 0, то корней нет;
если a = 0, a > 4, то два корня;
если 0 < a < 3, a = 4, то четыре корня;
если a = 3, то пять корней;
если 3 < a < 4, то шесть корней.
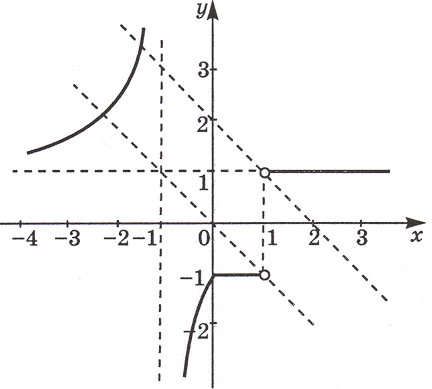
Задача 3. Сколько корней имеет уравнение
в зависимости от параметра a?
Решение. Построим в системе координат (x; y)
график функции
но сначала представим ее в виде:
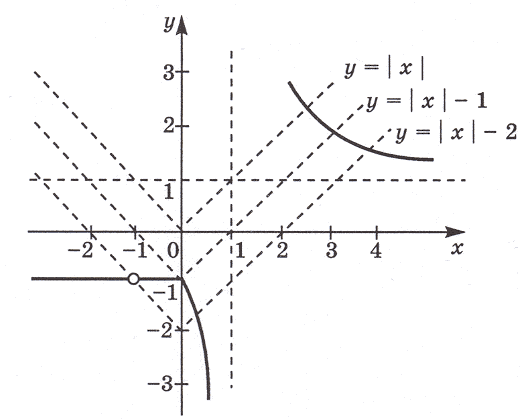
Прямые x = 1, y = 1 являются асимптотами графика
функции. График функции y = | x | + a
получается из графика функции y = | x |
смещением на a единиц по оси Oy.
Графики функций пересекаются в одной точке при a >
– 1; значит, уравнение (1) при этих значениях
параметра имеет одно решение.
При a = – 1, a = – 2 графики
пересекаются в двух точках; значит, при этих
значениях параметра уравнение (1) имеет два корня.
При – 2 < a < – 1, a < – 2
графики пересекаются в трех точках; значит,
уравнение (1) при этих значениях параметра имеет
три решения.
Ответ:
если a > – 1, то одно решение;
если a = – 1, a = – 2, то два решения;
если – 2 < a < – 1, a < – 1, то
три решения.
Замечание. При решении уравнения (1) задачи 3
особо следует обратить внимание на случай, когда a
= – 2, так как точка (– 1; – 1) не принадлежит
графику функции но принадлежит графику функции y = | x |
+ a.
Перейдем к решению другой задачи.
Задача 4. Сколько корней имеет уравнение
x + 2 = a | x – 1 |
(2)
в зависимости от параметра a?
Решение. Заметим, что x = 1 не является корнем
данного уравнения, так как равенство 3 = a·0 не может быть верным ни при
каком значении параметра a. Разделим обе
части уравнения на | x – 1 |(| x – 1 | № 0), тогда уравнение (2) примет вид В системе
координат xOy построим график функции
График этой функции изображен на рисунке.
Графиком функции y = a является прямая,
параллельная оси Ox или с ней совпадающая (при a
= 0).
Далее рассуждая так же, как и в задаче 3,
получаем ответ.
Ответ:
если a Ј – 1, то корней нет;
если – 1 < a Ј 1, то один
корень;
если a > 1, то два корня.
Рассмотрим наиболее сложное уравнение.
Задача 5. При каких значениях параметра a
уравнение
ax2 + | x – 1 | = 0
(3)
имеет три решения?
Решение. 1. Контрольным значением
параметра для данного уравнения будет число a
= 0, при котором уравнение (3) примет вид 0 + | x –
1 | = 0, откуда x = 1. Следовательно, при a = 0
уравнение (3) имеет один корень, что не
удовлетворяет условию задачи.
2. Рассмотрим случай, когда a №
0.
Перепишем уравнение (3) в следующем виде: ax2
= – | x – 1 |. Заметим, что уравнение будет
иметь решения только при a < 0.
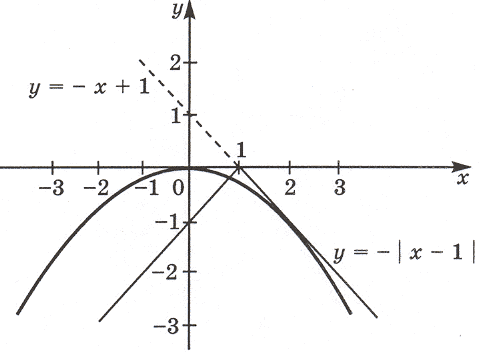
В системе координат xOy построим графики функций
y = | x – 1 | и y = ax2. График функции y =
| x – 1 | изображен на рисунке. Графиком
функции y = ax2 является парабола, ветви
которой направлены вниз, так как a < 0.
Вершина параболы — точка (0; 0).
Уравнение (3) будет иметь три решения только
тогда, когда прямая y = – x + 1 будет касательной
к графику функции y=ax2.
Пусть x0 — абсцисса точки касания
прямой y = – x + 1 с параболой y = ax2.
Уравнение касательной имеет вид
y = y(x0) + y ‘(x0)(x – x0).
Запишем условия касания:
Данное уравнение можно решить без
использования понятия производной.
Рассмотрим другой способ. Воспользуемся тем,
что если прямая y = kx + b имеет единственную общую
точку с параболой y = ax2 + px + q, то
уравнение ax2 + px + q = kx + b должно иметь
единственное решение, то есть его дискриминант
равен нулю. В нашем случае имеем уравнение ax2
= – x + 1 (a№ 0). Дискриминант
уравнения
Ответ:
Задачи для самостоятельного решения
6. Сколько корней имеет уравнение в
зависимости от параметра a?
1) | | x | – 3 | = a;
2) | x + 1 | + | x + 2 | = a;
3) | x2 – 4| x | + 3 | = a;
4) | x2 – 6| x | + 5 | = a.
Ответы:
1) если a<0, то корней нет; если a=0, a>3,
то два корня; если a=3, то три корня; если 0<a<3,
то четыре корня;
2) если a<1, то корней нет; если a=1, то
бесконечное множество решений из отрезка [– 2;
– 1]; если a > 1, то два решения;
3) если a<0, то корней нет; если a=0, a<3,
то четыре корня; если 0<a<1, то восемь
корней; если a=1, то шесть корней; если a=3,
то три решения; если a>3, то два решения;
4) если a<0, то корней нет; если a=0, 4<a<5,
то четыре корня; если 0<a< 4, то восемь
корней; если a=4, то шесть корней; если a=5,
то три корня; если a>5, то два корня.
7. Сколько корней имеет уравнение | x +
1 | = a(x – 1) в зависимости от параметра a?
Указание. Так как x = 1 не является корнем
уравнения, то данное уравнение можно привести к
виду .
Ответ: если aЈ–1, a > 1, a=0,
то один корень; если – 1<a<0, то два
корня; если 0<aЈ1, то корней
нет.
8. Сколько корней имеет уравнение x + 1 = a | x
– 1 |в зависимости от параметра a?
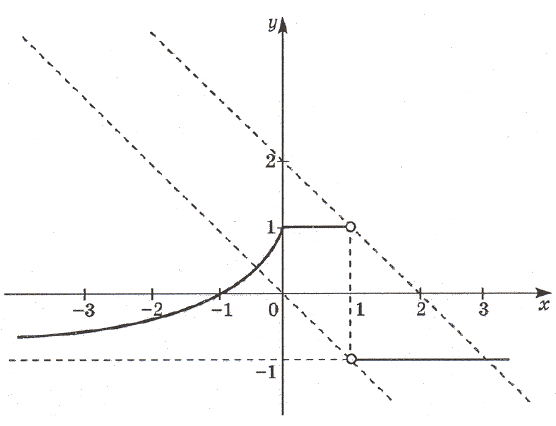
Указание. Привести уравнение к виду Построить график
(см. рисунок).
Ответ: если aЈ–1, то корней
нет; если – 1<aЈ1, то один
корень; если a>1, то два корня.
9. Сколько корней имеет уравнение
2| x | – 1 = a(x – 1)
в зависимости от параметра a?
Указание. Привести уравнение к виду
Ответ: если aЈ–2, a>2, a=1,
то один корень; если –2<a<1, то два корня;
если 1<aЈ2, то корней нет.
10. Сколько корней имеет уравнение
в зависимости от параметра a?
Указание. Построить графики левой и правой
частей данного уравнения.
Ответ: если aЈ0, aі2, то один корень; если 0<a<2, то
два корня.
11. При каких значениях параметра a
уравнение
x2 + a | x – 2 | = 0
имеет три решения?
Указание. Привести уравнение к виду x2 =
– a | x – 2 |.
Ответ: при aЈ–8.
12. При каких значениях параметра a
уравнение
ax2 + | x + 1 | = 0
имеет три решения?
Указание. Воспользоваться задачей 5. Данное
уравнение имеет три решения только в том случае,
когда уравнение ax2 + x + 1 = 0 имеет одно
решение, причем случай a = 0 не удовлетворяет
условию задачи, то есть остается случай, когда
Ответ:
13. Сколько корней имеет уравнение
x | x – 2 | = 1 – a
в зависимости от параметра a?
Указание. Привести уравнение к виду –x |x – 2| +
1 = a. Построить графики функций y =
– x | x – 2 | + 1 и y = a. Отметим, что
Ответ: если a<0, a>1, то один корень;
если a=0, a=1, то два корня; если 0<a<1,
то три корня.
14. Сколько корней имеет уравнение
в зависимости от параметра a?
Указание. Построить графики правой и левой
частей данного уравнения.
Для построения графика функции найдем промежутки
знакопостоянства выражений x + 1 и x:
Ответ: если aі 0, то один
корень; если – 1 < a < 0, то два корня; если
a = – 1, aЈ–2, то три
корня; если – 2<a<–1, то четыре корня.
15. Сколько корней имеет уравнение
в зависимости от параметра a?
Указание. Построить графики левой и правой
частей данного уравнения.
Ответ: если a<0, a>2, то два корня; если
0ЈaЈ2, то один
корень.
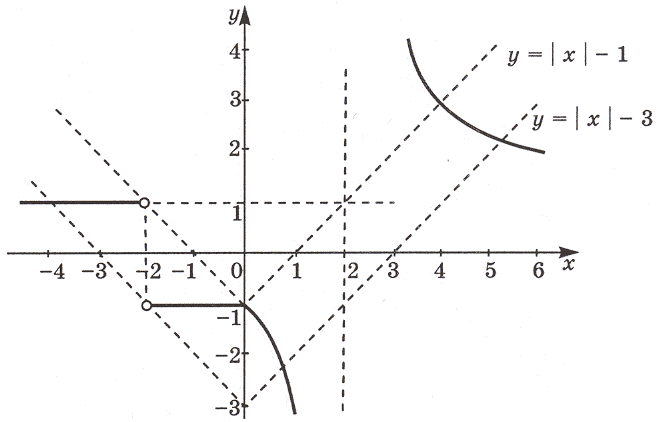
16. Сколько корней имеет уравнение
в зависимости от параметра a?
Указание. Построить графики левой и правой
частей данного уравнения. Для построения графика
функции найдем
промежутки знакопостоянства выражений x + 2 и x:
Ответ: если a>– 1, то одно решение; если a
= – 1, то два решения; если – 3<a<–1, то
четыре решения; если aЈ–3, то
три решения.
.
Применение производной для решения нелинейных уравнений и неравенств
- Количество корней кубического уравнения
- Количество корней произвольного уравнения
- Решение неравенств с построением графиков
п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin{gather*} f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end{gather*} Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_{1,2}=frac{-2bpmsqrt{D}}{6a}). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Уравнение (ax^3+bx^2+cx+d=0)
Имеет три корня, если ( begin{cases} b^2-3acgt 0\ f(x_1)cdot f(x_2)lt 0 end{cases} )
Имеет два корня, если ( begin{cases} b^2-3acgt 0\ f(x_1)cdot f(x_2)= 0 end{cases} )
В противном случае – один корень.
Пример 1. Сколько корней имеют уравнения:
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения (frac 1x+frac{1}{x-1}+frac{1}{x-3})
б) Найдите число корней уравнения (frac 1x+frac{1}{x-1}+frac{1}{x-3}=k)
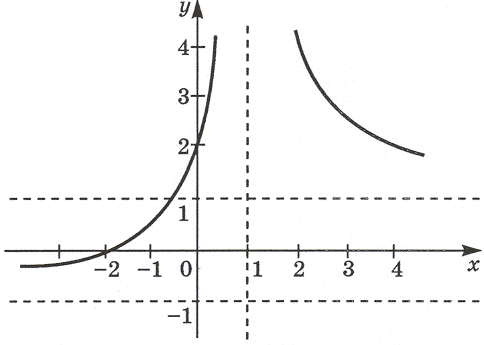
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac{1}{x-1}+frac{1}{x-3} $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft{0;1;3right})
Все три точки – точки разрыва 2-го рода. begin{gather*} lim_{xrightarrow -0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=-infty-1-frac13=-infty\ lim_{xrightarrow +0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=+infty-1-frac13=+infty\ lim_{xrightarrow 1-0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=1-infty-frac12=-infty\ lim_{xrightarrow 1+0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=1+infty-frac12=+infty\ lim_{xrightarrow 3-0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=frac13+frac12-infty=-infty\ lim_{xrightarrow 3+0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=frac13+frac12+infty=+infty end{gather*} 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin{gather*} lim_{xrightarrow -infty}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=-0-0-0=-0\ lim_{xrightarrow +infty}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=+0+0+0=+0\ end{gather*} Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac{1}{x^2}-frac{1}{(x-1)^2}-frac{1}{(x-3)^2}lt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) — три корня
При (k=0) — два корня
При (kgt 0) — три корня
Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt{x-1}+sqrt{10-2x}=a $$ имеет по крайней мере одно решение.
Исследуем функцию (f(x)=sqrt{x-1}+sqrt{10-2x})
ОДЗ: ( begin{cases} x-1geq 0\ 10-2xgeq 0 end{cases} Rightarrow begin{cases} xgeq 1\ xleq 5 end{cases} Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt{8}=2sqrt{2}, f(5)=sqrt{4}+0=2)
Первая производная: begin{gather*} f'(x)=frac{1}{2sqrt{x-1}}+frac{-2}{2sqrt{10-2x}}=frac{1}{2sqrt{x-1}}-frac{1}{sqrt{10-2x}}\ f'(x)=0 text{при} 2sqrt{x-1}=sqrt{10-2x}Rightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt{frac73-1}+sqrt{10-2cdot frac73}=sqrt{frac43}+sqrt{frac{16}{3}}=frac{6}{sqrt{3}}=2sqrt{3} end{gather*} Промежутки монотонности:
| (x) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| (f'(x)) | ∅ | + | 0 | — | ∅ |
| (f(x)) | (2sqrt{2}) | (nearrow ) | max (2sqrt{3}) |
(searrow ) | 2 |
Можем строить график:
(y=a) — горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:
| $$ alt 2 $$ | нет решений |
| $$ 2leq alt 2sqrt{2} $$ | 1 решение |
| $$ 2sqrt{2}leq alt 2sqrt{3} $$ | 2 решения |
| $$ a=2sqrt{3} $$ | 1 решение |
| $$ agt 2sqrt{3} $$ | нет решений |
По крайней мере одно решение будет в интервале (2leq aleq 2sqrt{3}).
Ответ: (ainleft[2;2sqrt{3}right])
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство (frac{2+log_3 x}{x-1}gt frac{6}{2x-1})
Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)
Получаем совокупность: begin{gather*} left[ begin{array}{l} begin{cases} xgt 1\ 2+log_3 xgtfrac{6(x-1)}{2x-1} end{cases} \ begin{cases} 0lt xlt 1\ 2+log_3 xltfrac{6(x-1)}{2x-1} end{cases} end{array} right. \ 2+log_3 xgt frac{6(x-1)}{2x-1}Rightarrow log_3 xgt frac{6(x-1)-2(2x-1)}{2x-1}Rightarrow log_3 xgt frac{2x-4}{2x-1}\ left[ begin{array}{l} begin{cases} xgt 1\ log_3 xgtfrac{2x-4}{2x-1} end{cases} \ begin{cases} 0lt xlt 1\ log_3 xltfrac{2x-4}{2x-1} end{cases} end{array} right. end{gather*} Исследуем функцию (f(x)=frac{2x-4}{2x-1}=frac{2x-1-3}{2x-1}=1-frac{3}{2x-1})
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin{gather*} lim_{xrightarrow frac12 -0}left(1-frac{3}{2x-1}right)=1-frac{3}{-0}=+infty\ lim_{xrightarrow frac12 +0}left(1-frac{3}{2x-1}right)=1-frac{3}{+0}=-infty end{gather*} Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin{gather*} lim_{xrightarrow -infty}left(1-frac{3}{2x-1}right)=1-frac{3}{-infty}=1+0\ lim_{xrightarrow +infty}left(1-frac{3}{2x-1}right)=1-frac{3}{+infty}=1-0 end{gather*} На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-frac{3}{2x-1}right)’=frac{3}{(2x-1)^2}gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f»(x)=-frac{6}{(2x-1)^3} $$ Одна критическая точка 2-го порядка (x=frac12)
| (x) | (left(0;frac12right)) | (frac12) | (left(frac12;+inftyright)) |
| (f»(x)) | >0 | ∅ | <0 |
| (f(x)) | (cup) | ∅ | (cap) |
Пересечения с осью OY: (f(0)=1-frac{3}{0-1}=4), точка (0;4)
Пересечение с осью OX: (1-frac{3}{2x-1}=0Rightarrow 2x-1=3 Rightarrow x=2), точка (2;0)
Строим графики (f(x)=frac{2x-4}{2x-1}) и (g(x)=log_3 x)
Первая система из совокупности ( begin{cases} xgt 1\ log_3 xgt frac{2x-4}{2x-1} end{cases} )
Логарифм при (xgt 1) все время выше, чем правая ветка гиперболы, т.е. система справедлива для всех (xgt 1).
Вторая система из совокупности ( begin{cases} 0lt xlt 1\ log_3 xlt frac{2x-4}{2x-1} end{cases} )
Логарифм попадает под левую ветку гиперболы на интервале (0lt xltfrac12), т.е. $$ begin{cases} 0lt xlt 1\ 0lt xltfrac12 end{cases} Rightarrow 0lt xltfrac12 $$ Решение совокупности – это объединение полученных решений систем: $$ 0lt xltfrac12cup xgt 1 $$ Ответ: (xinleft(0;frac12right)cup (1;+infty))
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y .
Если a < 0 , прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y .
Если a = 0 , функция принимает вид y = b .
Отдельно выделим график уравнения x = a .
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
Парабола
Графиком функции y = a x 2 + b x + c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти x в – координату вершины параболы.
x в = − b 2 a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D > 0 – две точки пересечения.
- Если D = 0 – одна точка пересечения.
- Если D < 0 – нет точек пересечения.



Гипербола
Графиком функции y = k x является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.
Если k < 0, ветви гиперболы проходят через II и IV четверти.
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.
Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Скачать домашнее задание к уроку 5.


















 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):