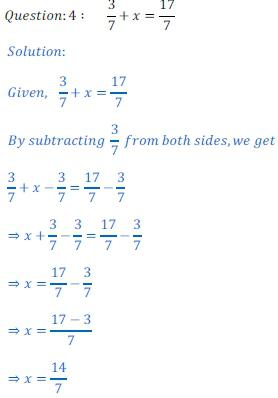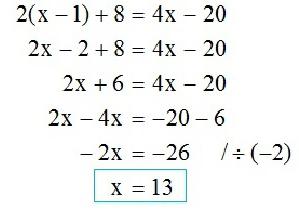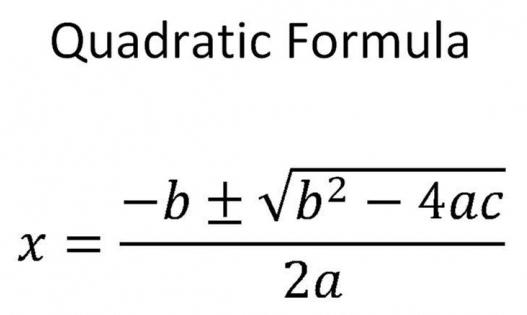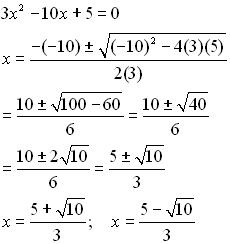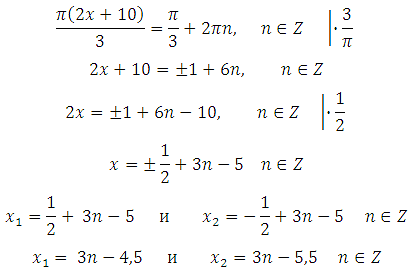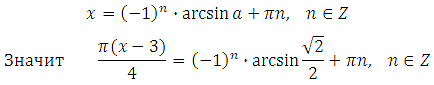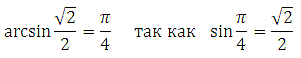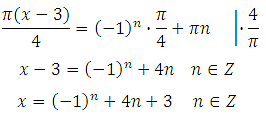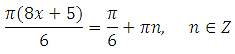Как найти наибольший наименьший корень уравнения

Найти корень уравнения? Это просто!

В математике встречаются разнообразные уравнения. Их всегда нужно решать, то есть искать все числа, которые сделают его верным равенством. Пути поиска решений определяются первоначальным видом уравнения. От него же будет зависеть и количество верных значений переменной, которые обозначаются, как корень уравнения. Это число может варьироваться от нуля до бесконечности.

Что подразумевается под уравнением и его корнем?

Из названия понятно, что оно приравнивает две величины, которые могут быть представлены числовыми или буквенными выражениями. Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.

Видов уравнений большое количество, но понятие корня для них всегда одно и то же. Корень уравнения — это такое значение неизвестного числа, при котором уравнение принимает становится верным равенством. Бывают ситуации, когда таких чисел несколько, тогда неизвестная называется переменной.

В алгебре при решении уравнений можно прийти к такой ситуации, что корней не будет совсем. Тогда говорят о том, что оно неразрешимо. А в ответе такого уравнения нужно записать, что решений нет.

Но иногда бывает и противоположное. То есть в процессе многочисленных преобразований появляются посторонние корни. Они не дадут верного равенства при подстановке. Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.

О линейном уравнении

Оно всегда может быть преобразовано в запись следующего вида: а * х + в = 0. В нем «а» всегда не равно нулю. Чтобы понять сколько корней имеет уравнение, его потребуется решить в общем виде.

• перенести в правую часть равенства слагаемое «в», заменив его знак на противоположный;
• разделить обе части получившегося равенства на коэффициент «а».

х = -в/а.

Из него ясно, что ответом будет одно число. То есть всего один корень.

Квадратное уравнение

Его общий вид: а * х 2 + в * х + с = 0. Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.

Все будет зависеть от значения дискриминанта. Он вычисляется по формуле Д = в 2 — 4 а * с. После расчетов «Д» может получиться больше, меньше или равным нулю. В первом случае корней уравнения будет два, во втором ответом будет «корней нет», а третья ситуация даст только одно значение неизвестной.

Формулы, которые используют для нахождения корней квадратного уравнения, и содержащие дискриминант

В общем случае, когда «Д» положительное число, не равное нулю, нужно использовать такую формулу:

При равенстве «Д» нулю корень уравнения — это единственное число. Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания «Д»:

х = (-в) / (2 * а).

При отрицательном значении дискриминанта извлечь из него квадратный корень не представляется возможным. Поэтому корней у такого уравнения не будет.

Замечание. Это верно для курса школьной программы, в которой не изучаются комплексные числа. Когда они вводятся, то получается, что и в этой ситуации ответов будет два.

Формулы для расчета корней квадратного уравнения, не использующие дискриминант

Речь идет о теореме Виета. Она действительна в случае, когда квадратное уравнение записывается в несколько другом виде:

х 2 + в * х + с = 0.

Тогда формула корней квадратного уравнения сводится к тому, чтобы выполнить решение двух линейных:

Оно решается за счет того, что из первого выводится выражение для одного из корней. И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.

К этому варианту всегда можно прийти от общего вида квадратного уравнения.

Достаточно только разделить все коэффициенты на «а».

Как быть, если нужно узнать наименьшее значение корня?

Решать уравнение и находить все возможные числа, которые подойдут для ответа. А потом выбрать самое малое. Это и будет наименьший корень уравнения.

Чаще всего такие вопросы встречаются в заданиях, которые имеют степень большую, чем 2, или содержат тригонометрические функции. Примером, когда нужно найти наименьший корень, может служить такое равенство:

2 х 5 + 2 х 4 — 3 х 3 — 3 х 2 + х + 1 = 0.

Чтобы найти каждое значение, которое можно назвать «корень уравнения», это равенство нужно преобразовать. Первое действие: сгруппировать его члены попарно: первый со вторым и так далее. Потом из каждой пары вынести общий множитель.

В каждой скобке останется (х + 1). Общим множителем в первой из пар будет 2 х 4 , во второй 3 х 2 . Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка.

После множителя (х + 1) будет стоять (2 х 4 — 3 х 2 + 1). Произведение двух множителей равняется нулю, только если один из них принимает значение, равное нулю.

Первая скобка равна нулю при х = -1. Это будет одним из корней уравнения.

Другие будут получены из уравнения, образованного второй скобкой, приравненной к нулю. Оно биквадратное. Для его решения нужно ввести обозначение: х 2 = у. Тогда уравнение существенно преобразится и примет привычный вид квадратного уравнения.

Его дискриминант равен Д = 1. Он больше нуля, значит корней будет два. Первый корень оказывается равным 1, второй будет 0,5. Но это значения для «у».

Нужно вернуться к введенному обозначению. х_1,2 = ± 1, х_3,4 = ± √0,5. Все корни уравнения: -1; 1; -√0,5; √0,5. Наименьший из них — -1. Это ответ.

В качестве заключения

Напоминание: все уравнения нужно проверять на то, подходит ли корень. Может быть, он посторонний? Стоит выполнить проверку предложенного примера.

Если подставить в изначально данное уравнение вместо «х» единицу, то получается, что 0 = 0. Этот корень верный.

Если х = -1, то получается такой же результат. Корень тоже подходящий.

Аналогично, при значениях «х» равных -√0,5 и √0,5 опять выходит верное равенство. Все корни подходят.

Этот пример не дал посторонних корней. Такое бывает не всегда. Вполне могло оказаться, что самое маленькое значение не подходило бы при проверке. Тогда пришлось бы выбирать из оставшихся.

Вывод: надо помнить о проверке и внимательно подходить к решению.

Тригонометрические уравнения

Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно. Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.

В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.

Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.

Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.

Понимание раздела «Тригонометрия» в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.

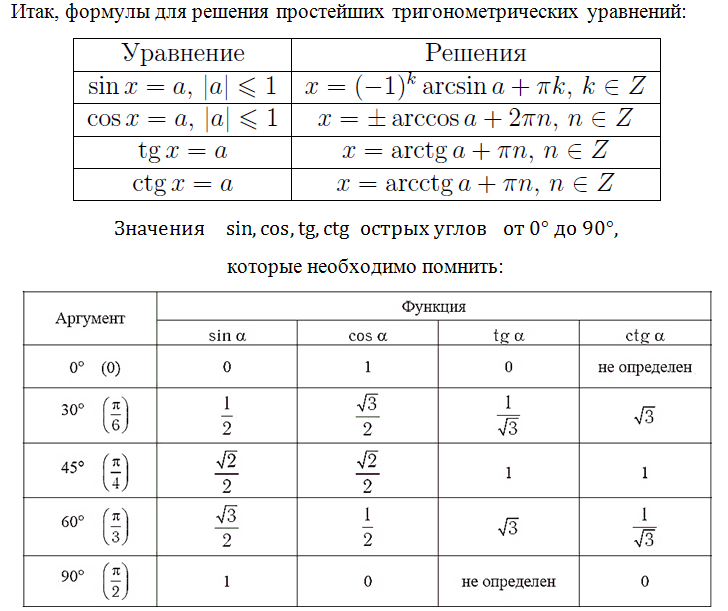
В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:

Знание этих значений необходимо, это «азбука», без которой невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да просто вы именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.

Алгоритм восстановления этих значений прост, он также приведён в теории, полученной вами во втором письме после подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».

Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с использованием угла х для соответствующих уравнений: cosx=a, sinx=a, tgx=a, где х может быть и выражением. В примерах ниже у нас аргумент задан именно выражением.

Итак, рассмотрим следующие задачи:

Найдите корень уравнения:

В ответе запишите наибольший отрицательный корень.

Решением уравнения cos x = a являются два корня:

Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.

Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.

Общая рекомендация для всех подобных задач: для начала берите диапазон n от – 2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: – 3 и 3, – 4 и 4 и так далее.

При n = – 2 х₁= 3 (– 2) – 4,5 = – 10,5 х₂= 3 (– 2) – 5,5 = – 11,5

При n = – 1 х₁= 3 (– 1) – 4,5 = – 7,5 х₂= 3 (– 1) – 5,5 = – 8,5

При n = 0 х₁= 3∙0 – 4,5 = – 4,5 х₂= 3∙0 – 5,5 = – 5,5

При n = 1 х₁= 3∙1 – 4,5 = – 1,5 х₂= 3∙1 – 5,5 = – 2,5

При n = 2 х₁= 3∙2 – 4,5 = 1,5 х₂= 3∙2 – 5,5 = 0,5

Получили, что наибольший отрицательный корень равен –1,5

В ответе напишите наименьший положительный корень.

Решением уравнения sin x = a являются два корня:

Либо (он объединяет оба указанные выше):

Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от – 90 о до 90 о синус которого равен a.

Выразим x (умножим обе части уравнения на 4 и разделим на Пи):

Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n = 0,1,2 …

При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4

При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6

При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12

Проверим при n = –1 х = (–1) –1 + 4∙(–1) + 3 = –2

Значит наименьший положительный корень равен 4.

В ответе напишите наименьший положительный корень.

Решением уравнения tg x = a является корень:

Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90 о до 90 о , тангенс которого равен a.

Выразим x (умножим обе части уравнения на 6 и разделим на Пи):

Найдём наименьший положительный корень. Подставим значения n = 1,2,3. Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:

Таким образом, наименьший положительный корень равен 0,25.

Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.

Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если в ходе решения вы не сможете определить угол, например, для

то данные формулы вам помогут:

Спасибо за внимание, учитесь с удовольствием!

Решение простых линейных уравнений

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = -b : а; если а равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

−4x = 12 | : (−4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Перенести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

1. 4х + 8 = 6 − 7х
2. 4х + 7х = 6 − 8
3. 11х = −2
4. х = −2 : 11
5. х = −2/11

Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.

Пример 5. Решить:

2. 3(3х — 4) = 4 · 7х + 24
3. 9х — 12 = 28х + 24
4. 9х — 28х = 24 + 12
5. -19х = 36
6. х = 36 : (-19)
7. х = — 36/19

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

5х — 15 + 2 = 3х — 2 + 2х — 1

Сгруппировать в левой части неизвестные члены, в правой — свободные члены:

Приведем подобные члены.

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 − 7х.

   Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно.  Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.

В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.  

Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.

Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.

Понимание раздела «Тригонометрия»  в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.

В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:

Знание этих значений необходимо, это «азбука», без которой  невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да  просто вы  именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.

Алгоритм восстановления этих значений прост, он также приведён в теории,  полученной вами во втором письме после  подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».

Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с  использованием угла х для соответствующих  уравнений: cosx=a, sinx=a, tgx=a, где х может быть  и выражением. В примерах ниже у нас аргумент задан именно выражением.

Итак, рассмотрим следующие задачи:

Найдите корень уравнения:

В ответе запишите наибольший отрицательный корень.

Решением уравнения cos x = a  являются два корня:

Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.

Значит

Выразим x:

Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.

Общая рекомендация для всех подобных задач: для начала берите диапазон  n  от   – 2  до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x:  – 3 и 3,  – 4  и 4 и так далее.

Вычисляем:

При  n = – 2     х₁= 3 (– 2) – 4,5 = – 10,5      х₂= 3 (– 2) – 5,5 = – 11,5

При  n = – 1     х₁= 3 (– 1) – 4,5 = – 7,5        х₂= 3 (– 1) – 5,5 = – 8,5

При  n = 0        х₁= 3∙0 – 4,5 = – 4,5            х₂= 3∙0 – 5,5 = – 5,5

При  n = 1        х₁= 3∙1 – 4,5 = – 1,5            х₂= 3∙1 – 5,5 = – 2,5

При  n = 2        х₁= 3∙2 – 4,5 =  1,5              х₂= 3∙2 – 5,5 = 0,5

Получили, что наибольший отрицательный корень равен   –1,5

Ответ:  –1,5

Решите самостоятельно:

Посмотреть решение

Решите уравнение:

В ответе напишите наименьший положительный корень.

Решением уравнения sin x = a  являются два корня:

Либо (он объединяет оба указанные выше):

Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от   – 90^о до 90^о синус которого равен a.

Значит

Выразим x (умножим обе части уравнения на 4 и разделим на Пи):

Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n =  0,1,2 …

При  n = 0     х = (– 1)⁰ + 4∙0 + 3 = 4

При  n = 1     х = (– 1)¹ + 4∙1 + 3 = 6

При  n = 2     х = (– 1)² + 4∙2 + 3 = 12

Проверим при   n = –1     х = (–1)^–1 + 4∙(–1) + 3 = –2

Значит наименьший положительный корень равен 4.

Ответ: 4

Решите самостоятельно:

Посмотреть решение

Решите уравнение:

В ответе напишите наименьший положительный корень.

Решением уравнения tg x = a  является корень:

Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90^о до 90^о,  тангенс которого равен a.

Значит

Выразим x (умножим обе части уравнения на 6 и разделим на  Пи):

Найдём наименьший положительный корень. Подставим значения  n = 1,2,3…    Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:

Таким образом, наименьший положительный корень равен 0,25.

Ответ: 0,25

Решите самостоятельно:

Посмотреть решение

Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.

Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если  в ходе решения вы не сможете определить угол, например, для

то данные формулы вам помогут:

Спасибо за внимание, учитесь с удовольствием!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Как найти наименьший корень

Для решения квадратного уравнения и нахождения его наименьшего корня вычисляется дискриминант. Дискриминант будет равен нулю лишь в том случае, если многочлен имеет кратные корни.

Вам понадобится

• — математический справочник;
• — калькулятор.

Инструкция

Приведите многочлен к квадратному уравнению вида ax2 + bx + c = 0, в котором a, b и c являются произвольными действительными числами, при этом a ни в коем случае не должно равняться 0.

Подставьте значения получившегося квадратного уравнения в формулу для вычисления дискриминанта. Эта формула выглядит следующим образом: D = b2 — 4ac. В том случае, если D больше нуля, квадратное уравнение будет иметь два корня. Если D равняется нулю, оба вычисленных корня будут не только вещественными, но и равными. И третий вариант: если D меньше нуля, корни будут представлять собой комплексные числа. Рассчитайте значение корней: х1 = (-b + sqrt (D)) / 2a и х2 = (-b — sqrt (D)) / 2a.

Для вычисления корней квадратного уравнения использовать можете также следующие формулы: х1 = (-b + sqrt (b2 — 4ac)) / 2a и х2 = (-b — sqrt (b2 — 4ac)) / 2a.

Сравните два вычисленных корня: корень с наименьшим значением и есть искомая вами величина.

Не зная корней квадратного трехчлена, вы с легкостью можете найти их сумму и произведение. Для этого воспользуйтесь теоремой Виета, в соответствии с которой сумма корней квадратного трехчлена, представленного в виде x2 + px + q = 0, равняется второму коэффициенту, то есть p, но с противоположным знаком. члена q. Другими словами, x1 + x2 = – p, а x1x2 = q. К примеру, дано следующее квадратное уравнение: x² – 5x + 6 = 0. Для начала разложите 6 на два множителя, причем таким образом, чтобы сумма этих множителей была равна 5. Если вы подобрали значения правильно, то x1 = 2, x2 = 3. Проверьте себя: 3х2=6, 3+2=5 (как и требуется, 5 с противоположным знаком, то есть «плюсом»).

Обратите внимание

Будьте внимательны: не допустите ошибку, расставляя знаки!

Полезный совет

Число со знаком «минус» всегда меньше положительного. Если же сравниваете два отрицательных значения, то меньшим из них будет то, модуль которого больше.

Источники:

• Решение квадратного уравнения
• как найти равно или меньше

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

    Основными уравнениями школьной алгебры являются линейные и квадратные. Все остальные уравнения путём различных тождественных преобразований или путём соответствующей подстановки сводятся к ним.    

Линейные уравнения

Линейные уравнения ах = b, где а ≠ 0; x=b/a.

Пример 1. Решите уравнение – х + 5,18 = 11,58.
    Решение:
       – х + 5,18 = 11,58;
       – х = – 5,18 + 11,58;
       – х = 6,4;
       х = – 6,4.
    Ответ: – 6,4.

Пример 2. Решите уравнение 3 – 5(х + 1) = 6 – 4х.
    Решение:
       3 – 5(х + 1) = 6 – 4х;
       3 – 5х – 5 = 6 – 4х;
       – 5х + 4х = 5 – 3+6;
       – х = 8;
       х = – 8.
    Ответ: – 8.

Пример 3. Решите уравнение .
    Решение:

       . Домножим обе части равенства на 6. Получим уравнение, равносильное исходному.
       2х + 3(х – 1) = 12; 2х + 3х – 3 =12; 5х = 12 + 3; 5х = 15; х = 3.
    Ответ: 3.

Пример 4. Решите систему  
    Решение:
       Из уравнения 3х – у = 2 найдём у = 3х – 2 и подставим в уравнение 2х + 3у = 5.

Квадратные уравнения

Квадратные уравнения ax² + bx + c = 0, где а ≠ 0.

        D = b² – 4ac;

Помните! Произведение равно нулю, когда хотя бы один из сомножителей равен нулю, но второй при этом имеет смысл.
        y₁ = 0, или  у + 2 = 0;
        у₂ = – 2.
    Ответ: – 2; 0.

Пример 6. Решите уравнение 18 – х² = 14.
    Решение:
        18 – х² = 14 – неполное квадратное уравнение; – х² = 14 – 18;
        – х² = – 4; х² =4; х = ± 2.
    Ответ: ± 2.

Пример 7. Решите уравнение х² + 6х – 3 = 2х³.
    Решение:
        х² + 6х – 3 = 2х³ – уравнение 3-ей степени. Оно решается разложением на множители: х² – 2х³ + 6х – 3 = 0;
        – х²(2х – 1 ) + 3(2х – 1) = 0;
        (2х – 1)(3 – х²) = 0;
        2х – 1 = 0 или 3 – х² =0;
        х₁ = 0,5; х_2,3 =.
    Ответ: 0,5; .

Пример 8. Решите уравнение (х² – 5х)² – 30 (х² – 5х) – 216 = 0.
    Решение:
        (х² – 5х)² – 30 (х² – 5х) – 216 = 0 – биквадратное уравнение. Такое уравнение решается методом подстановки.
    

Рациональные уравнения

Иррациональные уравнения

    Уравнение, содержащее неизвестную под знаком корня n-ой степени, называется иррациональным.
    Иррациональное уравнение чаще всего решается путём возведения в степень, которую имеет корень, содержащий неизвестную, или заменой неизвестной. Не следует забывать, что в степень возводятся обе части уравнения.
    При возведении в нечётную степень обеих частей уравнения, получаем уравнение, равносильное исходному.
    Новое уравнение, получившееся после возведения в чётную степень обеих частей, не всегда равносильно исходному уравнению, поэтому необходимо либо выполнить проверку полученных значений неизвестного путём подстановки в исходное уравнение, либо отбросить корни, не принадлежащие области определения уравнения.

Пример 15. Решить уравнение .
    Решение:
        Область определения: х + 1 ≥ 0.
        x² – 4 = 0 или х + 1 = 0;
        х₁ = – 2 , х₃ = – 1. 
        х₂ = 2,
        х₁ = – 2 не принадлежит области определения.
    Ответ: – 1; 2

Пример 16. Решить уравнение  .
    Решение:
        Данное уравнение решается возведением в квадрат левой и правой частей, и, так как в правой части уравнения содержится переменная, мы получим уравнение не равносильное исходному.
        15 – 3х = х² + 2х + 1;  х² + 5х – 14 = 0;  х₁ = – 7,  х₂ = 2.
        Проверка. При х₁ = – 7,  – не корень.
                        При х₂ = 2,  – корень.
    Ответ: 3.

Пример 17. Решить систему 

    Решение:       

       

Уравнения, содержащие знак модуля

Пример 18. Решите уравнение .
    Решение:
        х + 5 = 3 или х + 5 = – 3. Откуда х₁ = – 2 или х₂ = – 8.
    Ответ: – 2; – 8.

Пример 19. Решите уравнение .
    Решение:

        Данное уравнение будем рассматривать на двух числовых промежутках:.

Пример 20. Решите уравнение .
    Решение:
        Двучлен х – 3 меняет свой знак при переходе через х = 3, а х + 1 – при х = – 1. Данное уравнение будем рассматривать на трёх числовых промежутках: 
        1); имеем-(x-3)-2(x+1)=4; – 3х = 3; х = – 1.
            и не является корнем.
        2) ;-(x-3)-2(x+1)=4; х = – 1.
            , – 1 – корень.
        3) ;(x-3)-2(x+1)=4; 3х = 5; х =5/3.
            , следовательно, корнем не является.
    Ответ: – 1.

Пример 21. Решить систему 

    Решение:

    Ответ: (3; – 1), (1; – 3).

Уравнения с параметром

Пример 22. При каком значении а уравнение х(2 – а) – х = 5 + х не имеет решений?
    Решение:
        Выразим х через а.  2х – ах – х – х = 5; – ах = 5; х = –5/a  .
        При а = 0  х не определён. 
        Подставим а = 0 в исходное уравнение: х(2 – 0) – х = 5 + х; 2х – 2х = 5; 0 ≠ 5, следовательно, при а =0 данное уравнение не имеет решения.
    Ответ: при а = 0.

Пример 23.  Корни х₁ и х₂ уравнения х² + х + а = 0 обладают свойством x₁²+x₂²=5 . Найти а.
    Решение:
        Уравнение х² + х + а = 0 – приведённое квадратное. По теореме Виета х₁ + х₂ = – 1, х₁ ∙ х₂ = а. Т.к. x₁²+x₂²=5, то     х₁ – х₂ = – 5.
        Имеем х₁ = – 3; х₂ = 2, следовательно, а = (– 3)∙2= – 6.
    Ответ: а = – 6.

Пример 24. При каких значениях параметра n уравнение (n-2)x²-2nx+n+3=0  имеет корни разных знаков.
    Решение:
        n – 2 ≠ 0. В противном случае – нет квадратного уравнения.
        Приведём исходное уравнение (путём почленного деления обеих частей равенства на n – 2) к приведённому:

        Чтобы уравнение имело корни разных знаков, необходимо и достаточно выполнение двух условий одновременно: 
        1) D/4 > 0 (по формуле чётного коэффициента);
        2) x₁ ∙ x₂ < 0 (по теореме Виета): 

        

    Ответ: .

Показательные уравнения и системы уравнений

    

Пример 25. Решите уравнение 6^2-x=6^3-2x.
    Решение:
        6^2-x=6^3-2x; 2 – х = 3 – 2х; х = 1.
    Ответ: 1.

Пример 26. Решите уравнение   .
    Решение:
              .
    Ответ: – 2.

Пример 27. Решите уравнение  .
    Решение:
        
    Ответ: 2.

Пример 28. Решите уравнение .
    Решение: 

Логарифмические уравнения

Задачи для самостоятельного решения

Повышенный уровень

Автор проекта:

Шелкова Полина,

Класс: 10

Руководитель:

Злобова Людмила Викторовна,

учитель математики

ВВЕДЕНИЕ

Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον — «тригон» — треугольник и μετρειν — «метрео» — измеряю).

Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.

Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.

Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.

I РАЗДЕЛ (теоретический)

Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?

• Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
• Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
• Тригонометрические уравнения включены в КИМы ЕГЭ по математике.

Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку — это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.

Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.

Задачи:

• познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
• изучить соответствующую литературу;
• научиться решать тригонометрические уравнения;
• найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
• научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
• подготовиться к ЕГЭ по математике.

Приёмы отбора корней тригонометрического уравнения на заданном промежутке.

При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.

Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.

Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.

Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.

Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.

II РАЗДЕЛ (практический)

Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:

sinx=cos2x;

sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos²x−sin²x]

sinx−(cos²x−sin²x)=0;

sinx−(1−sin²x−sin²x)=0;

sinx−(1−2sin²x)=0;

2sin²x+sinx−1=0.

Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим

2t²+t-1=0

D=b²-4ac, т.е. D=9

t₁ = -1, t₂ = ½.

Вернемся к замене:

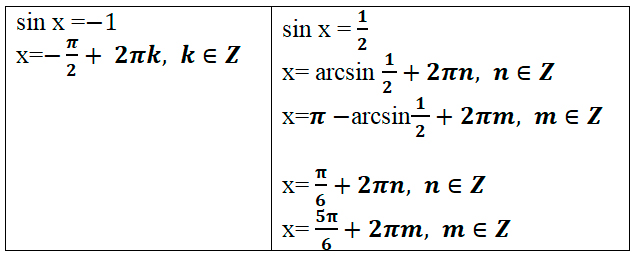
б) Рассмотрим три способа отбора корней, попадающих в отрезок .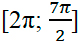

1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:

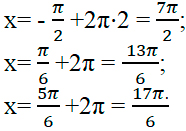
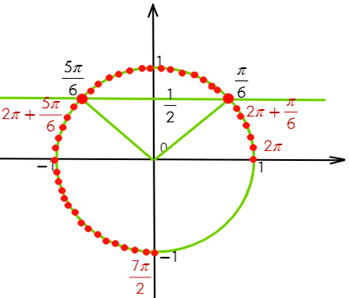
2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни: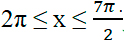

3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.

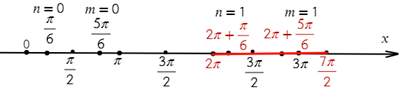
Нам останется только выбрать корни, которые попали в нужный нам отрезок.

Ответ:

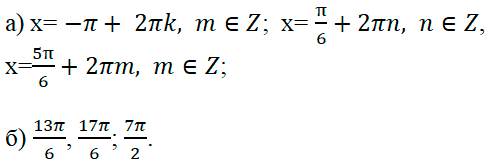
(Более подробный пример в приложении №1)

ЗАКЛЮЧЕНИЕ

При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем — небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.

СПИСОК ЛИТЕРАТУРЫ

1. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
2. Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова — М. Просвещение, 2017.
3. С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных — М: Издательство: «Экзамен», 2005.
4. Корянов А.Г., Прокофьев А.А. — Тригонометрические уравнения: методы решения и отбор корней. — М.: Математика ЕГЭ, 2012.

Электронные ресурсы

1. https://ru.wikipedia.org/wiki/Тригонометрия
2. https://www.yaklass.ru/p/ege/matematika/podgotovka-k-ege-po-matematike-profilnyi-uroven-10744/trigonometricheskie-uravneniia-s-ogranicheniiami-zadacha-13-536475/re-a4b9cc95-fe96-40c2-b70c-f46548b726a0
3. https://mat.1sept.ru/1999/no19.htm

4. Геометрия. Урок 1. Тригонометрия

5. https://math-ege.sdamgia.ru/
6. https://alexlarin.net/ege21.html
7. https://www.academia.edu/10962821/МАТЕМАТИКА_ЕГЭ_2012_Тригонометрические_уравнения_методы_решений_и_отбор_корней_типовые_задания_С1
8. http://teacher-andreeva.ru/wp-content/uploads/2016/03/тригоном-ур-я.pdf
9. https://reshimvse.com/article.php?id=100