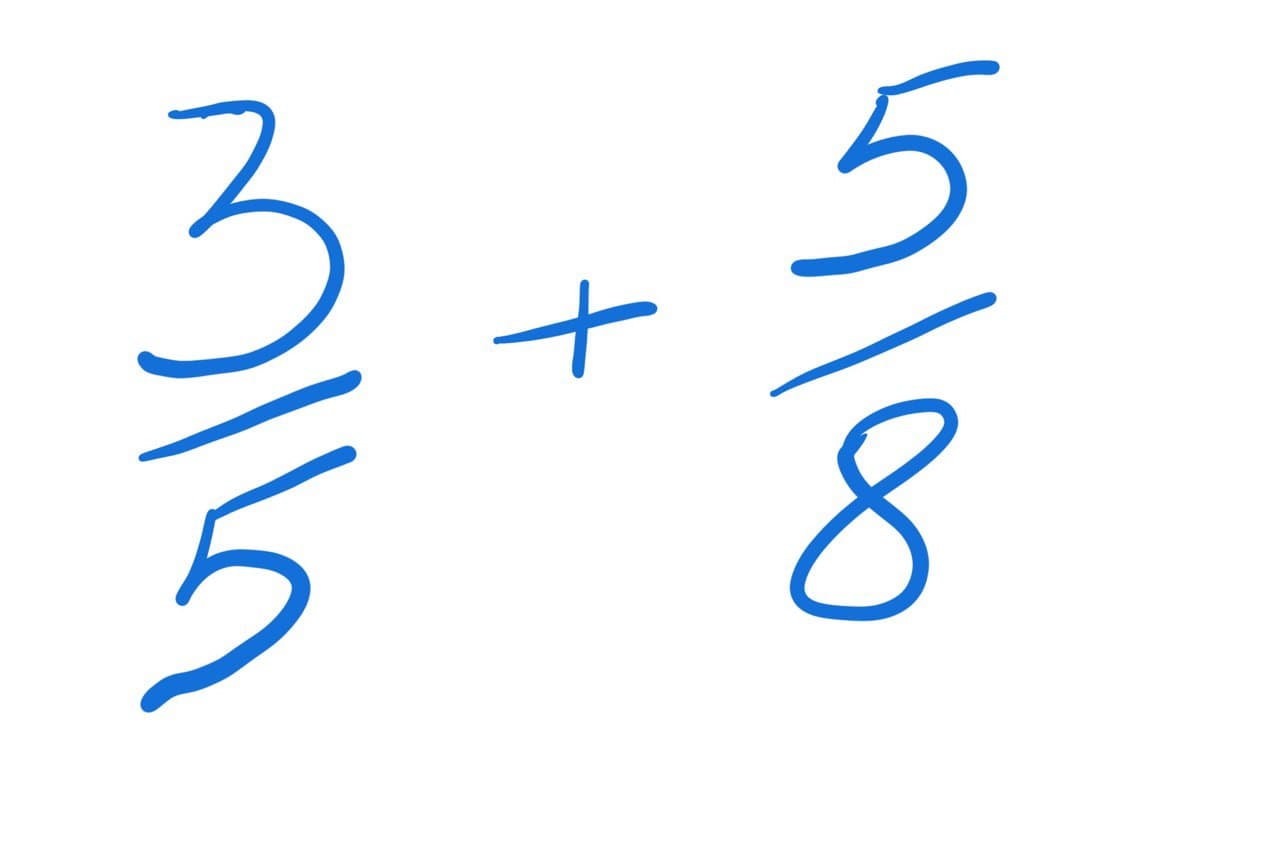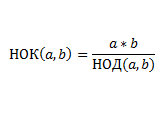I have seen that such a function exists for BigInteger, i.e. BigInteger#gcd. Are there other functions in Java which also work for other types (int, long or Integer)? It seems this would make sense as java.lang.Math.gcd (with all kinds of overloads) but it is not there. Is it somewhere else?
(Don’t confuse this question with «how do I implement this myself», please!)
Oliv
10.1k3 gold badges52 silver badges76 bronze badges
asked Oct 24, 2010 at 16:40
2
As far as I know, there isn’t any built-in method for primitives. But something as simple as this should do the trick:
public int gcd(int a, int b) {
if (b==0) return a;
return gcd(b,a%b);
}
You can also one-line it if you’re into that sort of thing:
public int gcd(int a, int b) { return b==0 ? a : gcd(b, a%b); }
It should be noted that there is absolutely no difference between the two as they compile to the same byte code.
aioobe
411k112 gold badges807 silver badges825 bronze badges
answered Oct 24, 2010 at 16:50
MattMatt
7,0297 gold badges50 silver badges76 bronze badges
12
For int and long, as primitives, not really. For Integer, it is possible someone wrote one.
Given that BigInteger is a (mathematical/functional) superset of int, Integer, long, and Long, if you need to use these types, convert them to a BigInteger, do the GCD, and convert the result back.
private static int gcdThing(int a, int b) {
BigInteger b1 = BigInteger.valueOf(a);
BigInteger b2 = BigInteger.valueOf(b);
BigInteger gcd = b1.gcd(b2);
return gcd.intValue();
}
Ry-♦
217k54 gold badges459 silver badges474 bronze badges
answered Oct 24, 2010 at 16:46
Tony EnnisTony Ennis
11.9k7 gold badges50 silver badges73 bronze badges
5
Or the Euclidean algorithm for calculating the GCD…
public int egcd(int a, int b) {
if (a == 0)
return b;
while (b != 0) {
if (a > b)
a = a - b;
else
b = b - a;
}
return a;
}
answered Oct 24, 2010 at 17:31
XorlevXorlev
8,5313 gold badges34 silver badges36 bronze badges
4
Unless I have Guava, I define like this:
int gcd(int a, int b) {
return a == 0 ? b : gcd(b % a, a);
}
answered Dec 10, 2016 at 11:23
AlexeyAlexey
9,1675 gold badges63 silver badges76 bronze badges
answered Jan 10, 2015 at 14:04
MoradMorad
7345 silver badges14 bronze badges
2
You can use this implementation of Binary GCD algorithm
public class BinaryGCD {
public static int gcd(int p, int q) {
if (q == 0) return p;
if (p == 0) return q;
// p and q even
if ((p & 1) == 0 && (q & 1) == 0) return gcd(p >> 1, q >> 1) << 1;
// p is even, q is odd
else if ((p & 1) == 0) return gcd(p >> 1, q);
// p is odd, q is even
else if ((q & 1) == 0) return gcd(p, q >> 1);
// p and q odd, p >= q
else if (p >= q) return gcd((p-q) >> 1, q);
// p and q odd, p < q
else return gcd(p, (q-p) >> 1);
}
public static void main(String[] args) {
int p = Integer.parseInt(args[0]);
int q = Integer.parseInt(args[1]);
System.out.println("gcd(" + p + ", " + q + ") = " + gcd(p, q));
}
}
From http://introcs.cs.princeton.edu/java/23recursion/BinaryGCD.java.html
answered Jan 3, 2015 at 13:24
linuxjavalinuxjava
1412 silver badges4 bronze badges
1
Some implementations here are not working correctly if both numbers are negative. gcd(-12, -18) is 6, not -6.
So an absolute value should be returned, something like
public static int gcd(int a, int b) {
if (b == 0) {
return Math.abs(a);
}
return gcd(b, a % b);
}
answered Jun 7, 2015 at 12:18
Robot MonkRobot Monk
1071 silver badge7 bronze badges
2
we can use recursive function for find gcd
public class Test
{
static int gcd(int a, int b)
{
// Everything divides 0
if (a == 0 || b == 0)
return 0;
// base case
if (a == b)
return a;
// a is greater
if (a > b)
return gcd(a-b, b);
return gcd(a, b-a);
}
// Driver method
public static void main(String[] args)
{
int a = 98, b = 56;
System.out.println("GCD of " + a +" and " + b + " is " + gcd(a, b));
}
}
Alfabravo
7,4746 gold badges46 silver badges81 bronze badges
answered Mar 15, 2018 at 11:41
Esann Esann
775 bronze badges
public int gcd(int num1, int num2) {
int max = Math.abs(num1);
int min = Math.abs(num2);
while (max > 0) {
if (max < min) {
int x = max;
max = min;
min = x;
}
max %= min;
}
return min;
}
This method uses the Euclid’s algorithm to get the «Greatest Common Divisor» of two integers. It receives two integers and returns the gcd of them. just that easy!
answered Apr 29, 2018 at 8:42
If you are using Java 1.5 or later then this is an iterative binary GCD algorithm which uses Integer.numberOfTrailingZeros() to reduce the number of checks and iterations required.
public class Utils {
public static final int gcd( int a, int b ){
// Deal with the degenerate case where values are Integer.MIN_VALUE
// since -Integer.MIN_VALUE = Integer.MAX_VALUE+1
if ( a == Integer.MIN_VALUE )
{
if ( b == Integer.MIN_VALUE )
throw new IllegalArgumentException( "gcd() is greater than Integer.MAX_VALUE" );
return 1 << Integer.numberOfTrailingZeros( Math.abs(b) );
}
if ( b == Integer.MIN_VALUE )
return 1 << Integer.numberOfTrailingZeros( Math.abs(a) );
a = Math.abs(a);
b = Math.abs(b);
if ( a == 0 ) return b;
if ( b == 0 ) return a;
int factorsOfTwoInA = Integer.numberOfTrailingZeros(a),
factorsOfTwoInB = Integer.numberOfTrailingZeros(b),
commonFactorsOfTwo = Math.min(factorsOfTwoInA,factorsOfTwoInB);
a >>= factorsOfTwoInA;
b >>= factorsOfTwoInB;
while(a != b){
if ( a > b ) {
a = (a - b);
a >>= Integer.numberOfTrailingZeros( a );
} else {
b = (b - a);
b >>= Integer.numberOfTrailingZeros( b );
}
}
return a << commonFactorsOfTwo;
}
}
Unit test:
import java.math.BigInteger;
import org.junit.Test;
import static org.junit.Assert.*;
public class UtilsTest {
@Test
public void gcdUpToOneThousand(){
for ( int x = -1000; x <= 1000; ++x )
for ( int y = -1000; y <= 1000; ++y )
{
int gcd = Utils.gcd(x, y);
int expected = BigInteger.valueOf(x).gcd(BigInteger.valueOf(y)).intValue();
assertEquals( expected, gcd );
}
}
@Test
public void gcdMinValue(){
for ( int x = 0; x < Integer.SIZE-1; x++ ){
int gcd = Utils.gcd(Integer.MIN_VALUE,1<<x);
int expected = BigInteger.valueOf(Integer.MIN_VALUE).gcd(BigInteger.valueOf(1<<x)).intValue();
assertEquals( expected, gcd );
}
}
}
answered Jun 22, 2015 at 1:40
MT0MT0
139k11 gold badges57 silver badges115 bronze badges
1
Is it somewhere else?
Apache! — it has both gcd and lcm, so cool!
However, due to profoundness of their implementation, it’s slower compared to simple hand-written version (if it matters).
answered Jun 27, 2018 at 8:02
/*
import scanner and instantiate scanner class;
declare your method with two parameters
declare a third variable;
set condition;
swap the parameter values if condition is met;
set second conditon based on result of first condition;
divide and assign remainder to the third variable;
swap the result;
in the main method, allow for user input;
Call the method;
*/
public class gcf {
public static void main (String[]args){//start of main method
Scanner input = new Scanner (System.in);//allow for user input
System.out.println("Please enter the first integer: ");//prompt
int a = input.nextInt();//initial user input
System.out.println("Please enter a second interger: ");//prompt
int b = input.nextInt();//second user input
Divide(a,b);//call method
}
public static void Divide(int a, int b) {//start of your method
int temp;
// making a greater than b
if (b > a) {
temp = a;
a = b;
b = temp;
}
while (b !=0) {
// gcd of b and a%b
temp = a%b;
// always make a greater than b
a =b;
b =temp;
}
System.out.println(a);//print to console
}
}
answered Jul 30, 2016 at 2:46
Gitau HarrisonGitau Harrison
3,0791 gold badge18 silver badges22 bronze badges
1
I used this method that I created when I was 14 years old.
public static int gcd (int a, int b) {
int s = 1;
int ia = Math.abs(a);//<-- turns to absolute value
int ib = Math.abs(b);
if (a == b) {
s = a;
}else {
while (ib != ia) {
if (ib > ia) {
s = ib - ia;
ib = s;
}else {
s = ia - ib;
ia = s;
}
}
}
return s;
}
answered Mar 28, 2018 at 14:23
Those GCD functions provided by Commons-Math and Guava have some differences.
- Commons-Math throws an
ArithematicException.classonly forInteger.MIN_VALUEorLong.MIN_VALUE.- Otherwise, handles the value as an absolute value.
- Guava throws an
IllegalArgumentException.classfor any negative values.
answered Jan 13, 2019 at 7:49
Jin KwonJin Kwon
19.8k14 gold badges109 silver badges177 bronze badges
The % going to give us the gcd Between two numbers, it means:-
% or mod of big_number/small_number are =gcd,
and we write it on java like this big_number % small_number.
EX1: for two integers
public static int gcd(int x1,int x2)
{
if(x1>x2)
{
if(x2!=0)
{
if(x1%x2==0)
return x2;
return x1%x2;
}
return x1;
}
else if(x1!=0)
{
if(x2%x1==0)
return x1;
return x2%x1;
}
return x2;
}
EX2: for three integers
public static int gcd(int x1,int x2,int x3)
{
int m,t;
if(x1>x2)
t=x1;
t=x2;
if(t>x3)
m=t;
m=x3;
for(int i=m;i>=1;i--)
{
if(x1%i==0 && x2%i==0 && x3%i==0)
{
return i;
}
}
return 1;
}
answered Nov 17, 2013 at 20:09
1
Алгоритм Евклида
Для начала разберемся, что это и как это работает. Алгоритм Евклида позволяет найти нам наибольший общий делитель чисел. Как это работает:
Пусть a = 18, b = 30.
Цикл: a!=0 and b!=0
Если a > b, то a = a % b, если меньше, то b = b % a, таким образом мы сначала находим остаток деления, а потом повторяем действия. У нас a < b, значит, ищем остаток деления b % a (30 % 18) = 12, присваиваем b = 12, повторяем цикл но теперь у нас уже a > b(b = 12)
значит выполняем a % b (18 % 12) = 6? снова переходим к циклу, теперь снова b > a, значит выполняем b % a (30 % 6), остаток от деления 0, на этом мы прекращаем наш цикл и узнаем, что наибольший общий делитель 18 и 30 = 6. и выводим a + b (b = 0, a = 6).
Python
#!/usr/bin/env python
a = 18
b = 30
while a!=0 and b!=0:
if a > b:
a = a % b
else:
b = b % a
print (a+b)
Perl:
sub nod
{
return $_[0] != 0 ? nod ( ( $_[1] % $_[0] ), $_[0] ) : $_[1];
}
C:
int gcd(int a, int b) {
int c;
while (b) {
c = a % b;
a = b;
b = c;
}
return abs(a);
}
Pascal:
function nod( a, b: longint): longint;
begin
while (a <> 0) and (b <> 0) do
if a >= b then
a:= a mod b
else
b:= b mod a;
nod:= a + b;
end;
Java:
public class GCD {
public static int gcd(int a,int b) {
while (b !=0) {
int tmp = a%b;
a = b;
b = tmp;
}
return a;
}
}
C#:
int gcd(int a, int b)
{
while (b != 0)
b = a % (a = b);
return a;
}
Мы уже не раз складывали два простых числа, две десятичные дроби или даже простое число с десятичной дробью. Однако мир состоит не только из примитивных данных, порой нам приходится работать и с дробями, с обыкновенными дробями.
Обыкновенные дроби
#
сложение дробей
Обыкновенная дробь, как мы знаем из школы, состоит из двух частей: верхней и нижней. Это если не считать чёрточку посередине за часть дроби. Верхнюю часть дроби в математике принято называть числитель, а нижнюю часть знаменатель. В английском соответственно numerator и denominator.
Для того, что бы мы могли проводить математические операции с дробями мы должны привести их к общему знаменателю и научиться сокращать их. Для этого нам нужно вспомнить про НОД и НОК.
НОД — наибольший общий делитель
#
Greatest common divisor — GCD.
НОД´ом для чисел 25 и 15 является 5. Это наибольший общий делитель двух этих чисел.
Для чисел 9 и 15 НОД´ом является 3. Оба числа делятся на 3 без остатка. И три является наибольшим общим делителем.
Математика древняя наука и впервые НОД был описан Евклидом в третьем веке до нашей эры. Алгоритм нахождения назван в его честь — Алгори́тм Евкли́да.
В Java Алгоритм Евклида будет реализован вот так:
public static int euclideanAlgorithm(int a, int b) {
while (a != b) {
if (a > b) {
a = a - b;
} else {
b = b - a;
}
}
return a;
}
Этот алгоритм в цикле занимается вычитанием от одной переменной другой и в итоге находит нод. если задуматься, то “бесконечное” вычитание пока A не сравняется с B это деление с нахождением остатка деления. Сегодня у нас есть оператор модуло и мы можем “усовершенствовать” алгоритм:
public static int gcdAlgorithmModulo(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
Этот же алгоритм мы можем решить с применением рекурсии, мы должны прописать условие выхода и само решение:
public static int gcdRecursionAlgorithm(int a, int b) {
if (b == 0) {
return a;
}
return gcdRecursionAlgorithm(b, a % b);
}
Это не единственные способы решения. Всегда ещё можно решить бинарным поиском. Но думаю на этом мы пока уже можем остановиться и сказать, что НОД мы находить научились и можем попробовать найти НОК.
НОК — Наименьшее общее кратное
#
Least common multiple — LCM
НОК — это произведение наших двух чисел и делении его на НОД. Реализуется это вот так:
public static int leastCommonMultiple(int a, int b) {
return a / gcdRecursionAlgorithm(a, b) * b;
}
Теперь мы попробуем реализовать правильное “поведение” дробей.
public class Fraction {
private int numerator;
private int denominator;
Fraction(int numerator) {
this.numerator = numerator;
this.denominator = 1;
}
public Fraction(int numerator, int denominator) {
this.numerator = numerator;
this.denominator = denominator;
}
public int getNumerator() {
return numerator;
}
public int getDenominator() {
return denominator;
}
public Fraction sum(Fraction fraction) {
Fraction result = sum(fraction, this);
return result;
}
public static Fraction sum(Fraction a, Fraction b) {
// описать сложение;
// выполнить сокращение дробей, если это возможно
// находим нок знаменателей дробей
// подставить полученное значение в знаменатель РЕЗУЛЬТАТА
// Разделить нок на знаменатели данных дробей.
// умножить числитель и знаменатель каждой дроби на дополнительный множитель
int cDenominator = Math.nok(a.denominator, b.denominator);
int cNumerator =
a.numerator * (cDenominator / a.denominator) +
b.numerator * (cDenominator / b.denominator);
Fraction c = new Fraction(cNumerator, cDenominator);
return c;
}
@Override
public String toString() {
return "Fraction(дробь){" +
"numerator(числитель)=" + numerator +
", denominator(знаменатель)=" + denominator +
'}';
}
}
class Math {
static int nok(int a, int b) {
return a * b / nod(a, b);
}
static int nod(int a, int b) {
if (b == 0) {
return a;
}
return nod(b, a % b);
}
}
Дополнительные ссылки
#
- https://docs.oracle.com/javase/8/docs/api/java/lang/Number.html
- https://habr.com/ru/post/205106/
- https://www.baeldung.com/java-least-common-multiple
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| package com.javarush.test.level14.lesson08.bonus02; | |
| /* НОД | |
| Наибольший общий делитель (НОД). | |
| Ввести с клавиатуры 2 целых положительных числа. | |
| Вывести в консоль наибольший общий делитель. | |
| */ | |
| import java.io.BufferedReader; | |
| import java.io.InputStreamReader; | |
| public class Solution | |
| { | |
| public static void main(String[] args) throws Exception | |
| { | |
| BufferedReader reader = new BufferedReader(new InputStreamReader(System.in)); | |
| int a = Integer.parseInt(reader.readLine()); | |
| int b = Integer.parseInt(reader.readLine()); | |
| System.out.println(gcd_3(a, b)); | |
| } | |
| public static int gcd_3(int a, int b) { | |
| while (a != b) { | |
| if (a > b) { | |
| a = a — b; | |
| } else { | |
| b = b — a; | |
| } | |
| } | |
| return a; | |
| } | |
| } |
10 марта, 2014 | Автор:
| Категория:
Java, Алгоритмы |
Нет комментариев »
НОД (Наибольший общий делитель) или gcd (Greatest Common Divisor)
НОД — наибольшее число, которое является делителем одновременно для чисел a и b.
Реализация (Алгоритм Евклида):
long gcd(long a,long b){
return b == 0 ? a : gcd(b,a % b);
}
Применение:
System.out.println(gcd(10,24));//результат: 2 System.out.println(gcd(12,24));//результат: 12 System.out.println(gcd(11,24));//результат: 1
НОК (Наименьшее общее кратное) или lcm (Least Common Multiple)
НОК — наименьшее число, которое делится на a и b без остатка.
НОК можно найти через НОД по следующей формуле:
Реализация:
long lcm(long a,long b){
return a / gcd(a,b) * b;
}
Примечание: a / gcd(a,b) * b более предпочтительно, чем a * b / gcd(a,b), т.к. во втором случае при больших числах переполнение случиться намного раньше.
Применение:
System.out.println(lcm(3, 4));//результат: 12 System.out.println(lcm(3, 9));//результат: 9 System.out.println(lcm(5,12));//результат: 60
| Поделиться данной статьей через: |