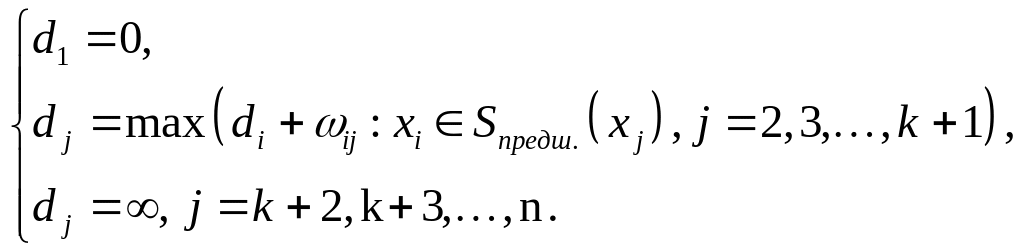Как найти наибольший путь в графе - Исправление недочетов и поиск решений вместе с Examum.ru

Алгоритм Дейкстры. Разбор Задач

Время на прочтение
7 мин

Количество просмотров 36K

Поиск оптимального пути в графе. Такая задача встречается довольно часто и в повседневной жизни, и в мире технологий. Справиться с такими вызовами помогает подход, который должен быть в арсенале каждого программиста — алгоритм Дейкстры.

Если вы хотите найти ответить на вопросы, чем этот алгоритм лучше BFS (поиска в ширину), при каких условиях алгоритм применим, и какие теоретические и практические задачи можно с его помощью решать, читайте далее.

Введение

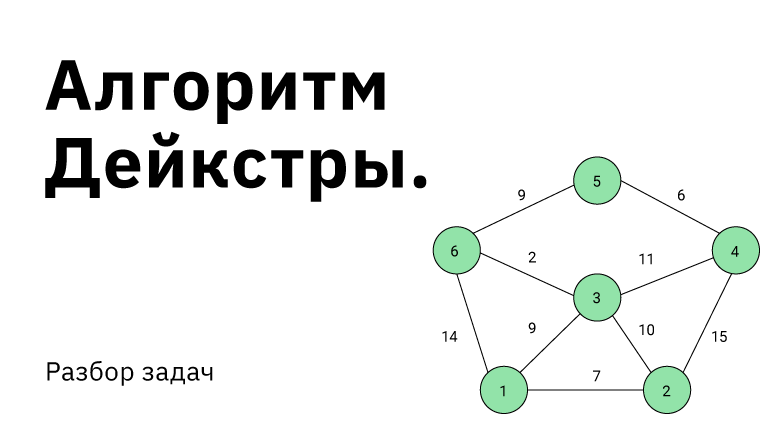
Алгоритм Дейкстры работает на ориентированных (с некоторыми дополнениями и на неориентированных) графах, и призван искать кратчайшие пути между заданной вершиной и всеми остальными вершинами в графе.

Как правило, граф обозначают как набор вершин и рёбер где число рёбер может быть задано , а вершин числом

Для каждого ребра в графе задан неотрицательный вес , а также вершина, из которой осуществляется поиск оптимальных путей.

Алгоритм Дейкстры может найти кратчайший путь между вершинами и в графе, только если существует хотя бы один путь между этими вершинами. Если это условие не выполняется, то алгоритм отработает корректно, вернув значение «бесконечность» для пары несвязанных вершин.

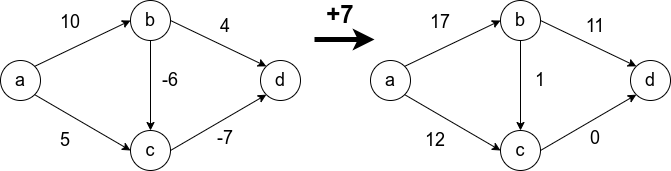
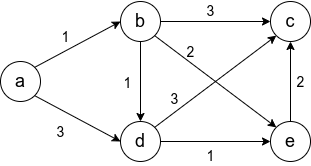
Условие неотрицательности весов рёбер крайне важно и от него нельзя просто избавиться. Не получится свести задачу к решаемой алгоритмом Дейкстры, прибавив наибольший по модулю вес ко всем рёбрам. Это может изменить оптимальный маршрут. На рисунке видно, что в первом случае оптимальный путь между и (сумма рёбер на пути наименьшая) изменяется при такой манипуляции. В оригинале путь проходит через , а после добавления семёрки ко всем рёбрам, оптимальный путь проходит через

Как ведёт себя алгоритм Дейкстры на исходном графе, мы разберём, когда выпишем алгоритм. Но для начала зададимся другим вопросом: «почему не применить поиск в ширину для нашего графа?». Известно, что метод BFS находит оптимальный путь от произвольной вершины в ориентированном графе до любой другой вершины, но это справедливо только для рёбер с единичным весом.

Свести задачу к решаемой BFS можно, но если заменить все рёбра неединичной длины рёбрами длины , то граф очень разрастётся, и это приведёт к огромному числу действий при вычислении оптимального маршрута.

Чтобы этого избежать предлагается использовать алгоритм Дейкстры. Опишем его:

Инициализация:

Основный цикл алгоритма:

Пока все вершины не исследованы (или формально ), повторяем:

В итоге исполнения этого алгоритма, массив будет содержать все оптимальные пути, исходящие из .

Примеры работы

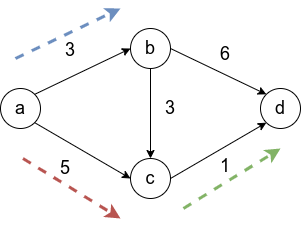
Рассмотрим граф выше, в нём будем искать пути от до всего остального.

Первый шаг алгоритма определит, что кратчайший путь до проходит по направлению синей стрелки и зафиксирует кратчайший путь. Второй шаг рассмотрит, все возможные варианты $inline A[v] + l_{vw}$ и окажется, что оптимальный вариант двигаться вдоль красной стрелки, поскольку меньше, чем и Добавляется длина кратчайшего пути до . И наконец, третьим шагом, когда три вершины уже лежат в , остается рассмотреть только два ребра и выбрать, лежащее вдоль зеленой стрелки.

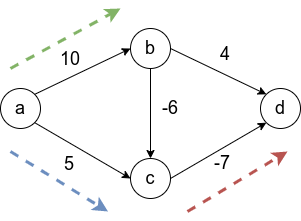
Теперь рассмотрим граф с отрицательными весами, упомянутый выше. Напомню, алгоритм Дейкстры на таком графе может работать некорректно.

Первым шагом отбирается ребро вдоль синей стрелки, поскольку это ребро наименьшего веса из исходной вершины. Затем выбирается ребро Это зафиксирует навсегда неверный путь от к , в то время как оптимальный путь проходит через центр с отрицательным весом. Последним шагом, будет добавлена вершина .

Оценка сложности алгоритма

К этому моменту мы разобрали сам алгоритм, ограничения, накладываемые на его работу и ряд примеров его применения. Давайте упомянем какова вычислительная сложность этого алгоритма, поскольку это пригодится нам для решения задач, ради которых затевалась эта статья.
Базовый подход, основанный на циклах, предполагает проход по всем рёбрам каждого узла, что приводит к сложности .

Эффективная реализация предполагает использование кучи. Об этой структуре данных можно сказать коротко: она позволяет выполнять две операции за логарифмическое время. Первая операция — получение узла в дереве, с наименьшим ключом, и, вторая операция, вставка нового узла в дерево с новым ключом.

Что еще можно сказать о куче:

это сбалансированное бинарное дерево,
ключ текущего узла всегда меньше, либо равен ключей дочерних узлов.

Интересную задачу с использованием куч я разбирал ранее в этом посте.

Используя кучу в алгоритме Дейкстры, где в качестве ключей используются расстояния от вершины в неисследованной части графа (в алгоритме это ), до ближайшей вершины в уже покрытом (это множество вершин ), можно сократить вычислительную сложность до Доказательство справедливости этих оценок я оставляю за пределами этой статьи.

Далее перейдём к разбору задач!

Задача №1

Будем называть узким местом пути в графе ребро максимальной длины в этом пути. Путём с минимальным узким местом назовём такой путь между вершинами и , что не существует другого пути , чьё узкое место меньше по длине. Требуется построить алгоритм, который вычисляет путь с минимальным узким местом для двух данных вершин в графе. Асимптотическая сложность такого алгоритма должна быть

Решение

По условию задачи ребро с большим весом трактуется как узкое место. Вес в этом случае можно воспринимать как цену за проход по ребру. В результате решения задачи хотелось бы получить алгоритм, способный строить маршруты между узлами так, чтобы, если мы захотим провести любой другой путь, он будет содержать более тяжелые рёбра.

В случае классической задачи, поиска пути минимальной длины между двумя вершинами графа, мы поддерживаем в каждой посещенной алгоритмом вершине графа минимальную длину пути до этой вершины. Здесь стоит оговориться, что будем именовать множество посещенными вершинами, а V - X часть графа, для которой еще нужно найти величину пути или узкого места.

В отличии от классического алгоритма, решение этой задачи должно поддерживать величину актуального узкого места пути, приводящего в вершину v in X . А при добавлении новой вершины из V - X , мы должны смотреть не увеличивает ли ребро (v,u_1) величину узкого места пути, которое теперь приводит в u_1 .
Если ребро увеличивает узкое место, то лучше рассмотреть вершину u_2 , ребро до которой легче (v,u_1) . Поиск неувеличивающих узкое место ребёр нужно осуществлять не только среди соседей определенного узла , но и среди всех v in X , поскольку отдавая предпочтение вершине, путь в которую имеет наименьшее узкое место в данный момент, мы гарантируем, что мы не ухудшаем ситуацию для других вершин.

Последнее можно проиллюстрировать примером: если путь, оканчивающийся в вершине имеет узкое место величины , и есть вершина с ребром (p,q) веса , и с ребром (p,r) веса , то предпочтение отдаётся , алгоритм даст верный результат в обоих случая, если существует (q,r) веса или веса .

В результате разбора выше, предлагается руководствоваться следующей формулой при выборе очередной вершины из непосещенных и обновлении величин, которые мы поддерживаем.

$A(u) = min_{v in X}left(max left[A(v), wleft(v,uright)right]right), , u in V - X$

Стоит пояснить, что поиск по v in X осуществляется, только для существующих связей (v,u), а это вес ребра (v,u) .

Задача №2

Предлагается решить более практическую задачу. Пусть городов, между ними существуют пути, заданные массивом edges[i] = [city_a, city_b, distance_ab], а также дано целое число mileage.

Требуется найти такой город из данных, из которого можно добраться до наименьшего числа городов не превысив mileage.

Стоит отметить, что граф неориентированый, т.е. по пути между городами можно двигаться в обе стороны, а длина пути между городами a и c может быть получена как сумма длин путей a -> b и b -> c, если есть маршрут a -> b -> c

Решение

С решением данной проблемы нам поможет алгоритм Дейкстры и описанная выше реализация с помощью кучи. Поставщиком этой структуры данных станет библиотека heapq в Python.

Будем использовать алгоритм Дейкстры для того, чтобы подсчитать количество соседних городов, расстояние до которых меньше mileage, для каждого из городов. Соберем количества соседей в в одном месте и найдем минимум из них.

Поскольку наш граф неориентированный, то из любой его вершины можно добраться до произвольной вершины . Будем использовать алгоритм Дейкстры для того, чтобы для каждого из городов в графе построить кратчайшие пути до всех остальных городов, мы это уже умеем делать в теории. И чтобы, оптимизировать этот процесс, будем в его течении сразу отвергать пути, которые превышают mileage, а не делать постфактум, когда все пути получены.

Давайте опишем функцию решения:

def least_reachable_city(n, edges, mileage):
        """
        входные параметры:
            n --- количество городов,
            edges --- тройки (a, b, distance_ab),
            mileage --- максимально допустимое расстояние между городами 
            для соседства
        """
        # заполняем список смежности (adjacency list), в нашем случае это 
        # словарь, в котором ключи это города, а значения --- пары 
        # (<другой_город>, <расстояние_до_него>)

        graph = {}
        for u, v, w in edges:
            if graph.get(u, None) is None:
                graph[u] = [(v, w)]
            else:
                graph[u].append((v, w))
            if graph.get(v, None) is None:
                graph[v] = [(u, w)]
            else:
                graph[v].append((u, w))
        
        # локально объявим функцию, которая будет считать кратчайшие пути в 
        # графе от вершины, до всех вершин, удовлетворяющих условию
        def num_reachable_neighbors(city):
            # создаем кучу, из одного элемента с парой, задающей нулевую 
            # длину пути до самого исходного города
            heap = [(0, city)]
            # и массив, содержащий города и кратчайшие 
            # расстояния до них от исходного
            distances = {}
            # затем, пока куча не пуста, извлекаем ближайший 
            # от посещенных городов город
            while heap:
                currDist, neighb = heapq.heappop(heap)
                # если кратчайшее ребро ведет к городу, где мы уже знаем 
                # оптимальный маршрут, то завершаем итерацию
                if neighb in distances:
                    continue
                # в остальных случаях, и если сосед не является отправным 
                # городом, мы добавляем новую запись в массив кратчайших расстояний
                if neighb != city:    
                    distances[neighb] = currDist
                # обрабатываем всех смежных городов с соседом, добавляя их в кучу 
                # но только если: а) до них еще не известен кратчайший маршрут и б) путь до них через neighb не выходит за пределы mileage
                for node, d in graph[neighb]:
                    if node in distances:
                        continue
                    if currDist + d <= mileage:
                        heapq.heappush(heap, (currDist + d, node))
            # возвращаем количество городов, прошедших проверку
            return len(distances)
        
        # выполним поиск соседей для каждого из городов
        cities_neighbors = {num_reachable_neighbors(city): city for city in range(n)}
        # вернём номер города, у которого наименьшее число соседей
        # в пределах досигаемости
        return cities_neighbors[min(cities_neighbors)]

В функции выше, в комментариях, подробно описывается, как метод Дейкстры, реализованный на куче позволяет найти расстояния до всех городов, в пределах `mileage`. Основную сложность для понимания предстваляет цикл, работающий с кучей.

Заключение

Алгоритм Дейкстры это мощный инструмент в мире работы с графами, область применения его крайне широка. С его помощью можно оценить даже целесообразность добавления новой ветки метро, новой дороги или маршрута в компьютерной сети. Он прост в исполнении и интуитивно понятен, как другие жадные (greedy) алгоритмы. Вычислительная сложность решений задач с его помощью зачастую не выше . При некоторых условиях может достигать линейной сложности (существует алгоритм линейной сложности, решающий первую задачу, при условии, что граф неориентированный).

Стоит еще раз отметить, что алгоритм не работает, когда в графе существуют отрицательные веса. Для этого существует подход динамического программирования — алгоритм Беллмана – Форда, что может послужить темой другой статьи. Несмотря на это, алгоритм Дейкстры является представителем идеального баланса простоты и мощи, для решения прикладных задач.

Статья подготовлена в преддверии старта курса «Алгоритмы для разработчиков». Узнать о курсе подробнее, а также зарегистрироваться на бесплатный демоурок можно по ссылке.

Информация

[1] Условия задач взяты из книги «Algorithms Illuminated: Part 2: Graph Algorithms and Data Structures» от Tim Roughgarden,
[2] и с сайта leetcode.com.
[3] Решения авторские.

Источник

Алгоритм нахождения максимального пути

Для нахождения максимального пути граф
G (сеть) должен быть
ациклическим, ибо в противном случае
может оказаться, что длины некоторых
путей не ограничены сверху. Если G_n– ациклический граф, то для любых
двух его вершин

выполняется одно из трёх условий:

х_iпредшествует х_j,
х_iследует за х_j,
нет пути
между х_iи х_j.

1-ое и 2-ое условия одновременно не
выполнимы из-за требуемой ацикличности
графа.

Перед вычислением максимального пути
в орграфе необходимо упорядочить вершины
графа по алгоритму Фалкерсона. Сам
алгоритм вычисления максимального пути
чисто перечислительный. Он перебирает
все возможные пути от текущей вершины
до всех последующих, достижимых из
текущей вершины.

Пусть d_j
– длина максимального пути от вершины
х₁до вершины х_j,
тогда удовлетворяет следующим рекуррентным
соотношениям:

(*)

Соотношения
(*) позволяют легко вычислить длины
максимальных путей от S
= х₁ до вершин, достижимых
из вершины S. Сами пути
могут быть построены методом
последовательного возвращения (2-ой
этап в алгоритме Дейкстры).

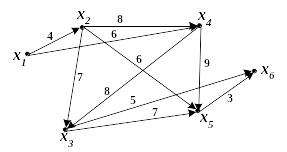
Пример. Граф (сеть,
рис. 34) задан весовой матрицей Ω:

Рис.
36

Найти длину
максимального пути из вершины х₁
в х₆ и сам этот путь.

Решение. Этот граф
ациклический, поэтому возможно
упорядочение его вершин по алгоритму
Фалкерсона. Сделаем это графическим
способом, переобозначив 2 вершины: х₄
назовём

,
а

и применим рекуррентные формулы (*).

Р
ис.
37

Этап 1.

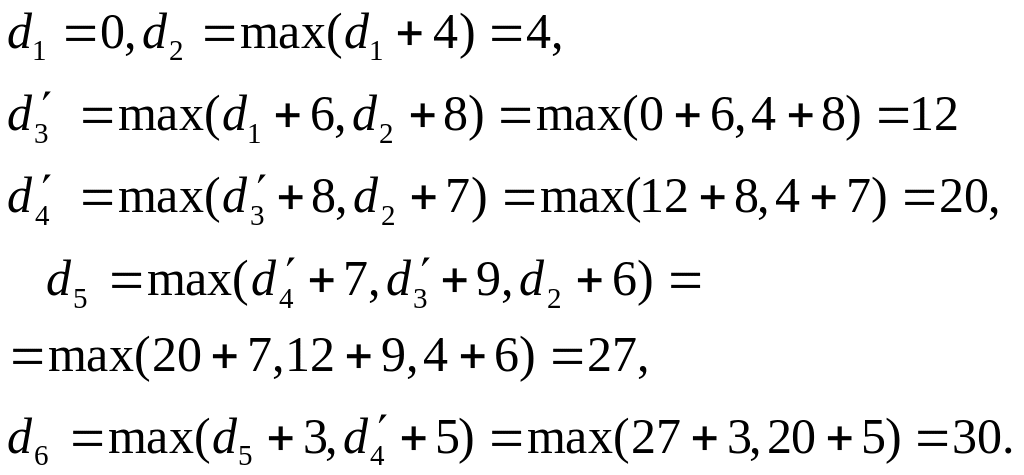
Итак, длина
максимального пути из х₁
в х₆равна 30.

Этап 2.

— включаем дугу
(x₅, x₆)
в максимальный путь,

— включаем дугу
(
,
x₅) в максимальный
путь,

— включаем дугу
(
,

) в максимальный путь,

— включаем дугу
(x₂,

) в максимальный путь,

—
включаем дугу (x₁,
x₂)
в максимальный путь.

Итак,
искомый путь таков:

(x₁,x₂)-
(x₂,

) — (
,

—
(
,x₅)
— (x₅,x₆)
или в первоначальных обозначениях

(x₁,
x₂)
— (x₂,
x₄)
— (x₄,
x₃)
— (x₃,
x₅)
— (x₅,
x₆).

4. Особенности алгоритмов теории графов

Каждый
алгоритм состоит из совокупности
конечного числа правил и предписаний.
Действия над графами (матрицей),
производимые в соответствии с правилами,
должны быть достаточно просты.
Алгоритм
применяется в дискретном времени,
правила алгоритма – по шагам, число
шагов конечно.
Какое из
правил будет применено на данном шаге
или какое действие будет совершено в
соответствии с некоторым правилом,
зависит только от результатов предыдущих
шагов.
Алгоритмы
обладают свойством локальности: действие
в соответствии с правилами или
установление непротиворечивости
некоторого действия правилам алгоритма
происходит на основе анализа дуг,
инцидентных данной вершине, или вершин,
смежных с данной.
Алгоритмы
обладают свойством массовости:
применяются либо для всех, либо для
некоторого бесконечного множества
графов.

Вопросы для повторения.

Нахождение
кратчайших путей с помощью алгоритма
Дейкстры.
Нахождение
кратчайших путей с помощью алгоритма
Беллмана-Мура.
Алгоритм
нахождения максимального пути.
Особенности
алгоритмов теории графов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Алгоритм Дейкстры (англ. Dijkstra’s algorithm) находит кратчайшие пути от заданной вершины $s$ до всех остальных в графе без ребер отрицательного веса.

Существует два основных варианта алгоритма, время работы которых составляет $O(n^2)$ и $O(m log n)$, где $n$ — число вершин, а $m$ — число ребер.

#Основная идея

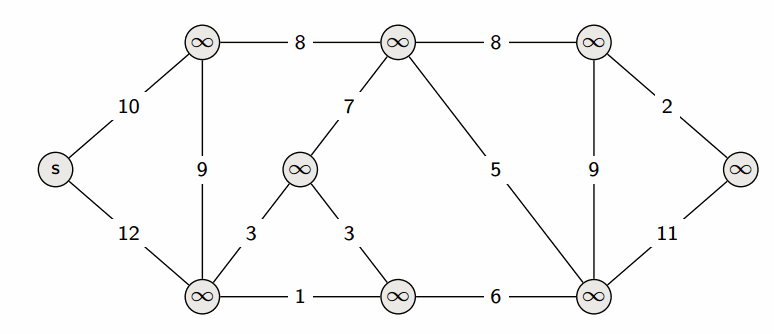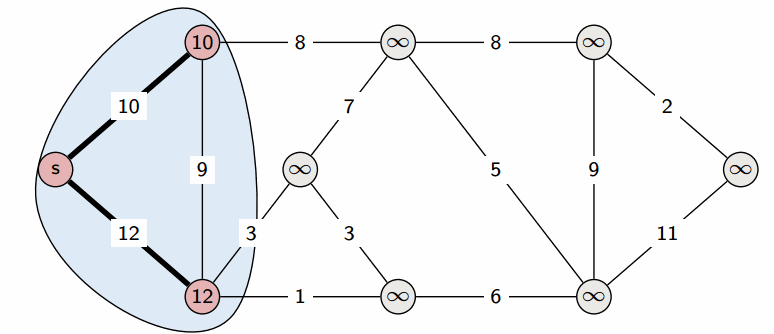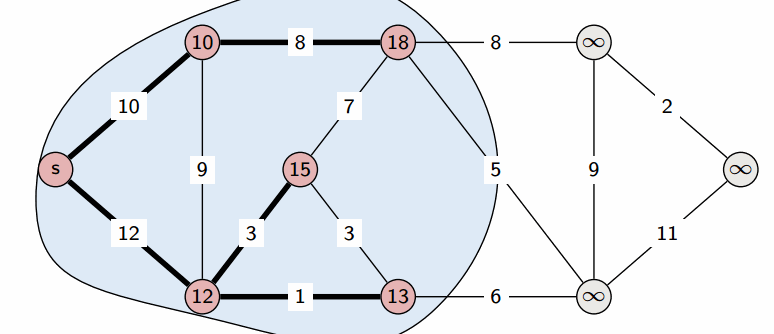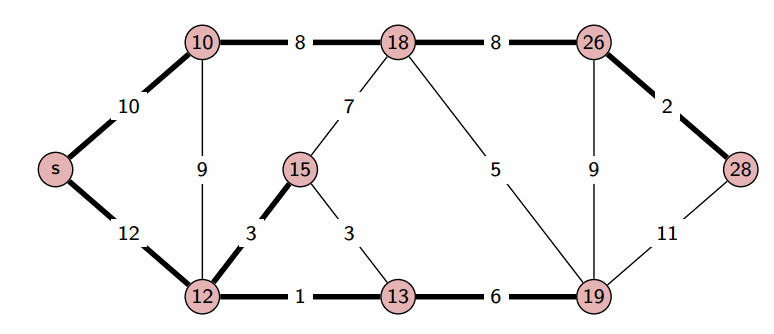
Заведём массив $d$, в котором для каждой вершины $v$ будем хранить текущую длину $d_v$ кратчайшего пути из $s$ в $v$. Изначально $d_s = 0$, а для всех остальных вершин расстояние равно бесконечности (или любому числу, которое заведомо больше максимально возможного расстояния).

Во время работы алгоритма мы будем постепенно обновлять этот массив, находя более оптимальные пути к вершинам и уменьшая расстояние до них. Когда мы узнаем, что найденный путь до какой-то вершины $v$ оптимальный, мы будем помечать эту вершину, поставив единицу ($a_v=1$) в специальном массиве $a$, изначально заполненном нулями.

Сам алгоритм состоит из $n$ итераций, на каждой из которых выбирается вершина $v$ с наименьшей величиной $d_v$ среди ещё не помеченных:

$$
v = argmin_{u | a_u=0} d_u
$$

(Заметим, что на первой итерации выбрана будет стартовая вершина $s$.)

Выбранная вершина отмечается в массиве $a$, после чего из из вершины $v$ производятся релаксации: просматриваем все исходящие рёбра $(v,u)$ и для каждой такой вершины $u$ пытаемся улучшить значение $d_u$, выполнив присвоение

$$
d_u = min (d_u, d_v + w)
$$

где $w$ — длина ребра $(v, u)$.

На этом текущая итерация заканчивается, и алгоритм переходит к следующей: снова выбирается вершина с наименьшей величиной $d$, из неё производятся релаксации, и так далее. После $n$ итераций, все вершины графа станут помеченными, и алгоритм завершает свою работу.

#Корректность

Обозначим за $l_v$ расстояние от вершины $s$ до $v$. Нам нужно показать, что в конце алгоритма $d_v = l_v$ для всех вершин (за исключением недостижимых вершин — для них все расстояния останутся бесконечными).

Для начала отметим, что для любой вершины $v$ всегда выполняется $d_v ge l_v$: алгоритм не может найти путь короче, чем кратчайший из всех существующих (ввиду того, что мы не делали ничего кроме релаксаций).

Доказательство корректности самого алгоритма основывается на следующем утверждении.

Утверждение. После того, как какая-либо вершина $v$ становится помеченной, текущее расстояние до неё $d_v$ уже является кратчайшим, и, соответственно, больше меняться не будет.

Доказательство будем производить по индукции. Для первой итерации его справедливость очевидна — для вершины $s$ имеем $d_s=0$, что и является длиной кратчайшего пути до неё.

Пусть теперь это утверждение выполнено для всех предыдущих итераций — то есть всех уже помеченных вершин. Докажем, что оно не нарушается после выполнения текущей итерации, то есть что для выбранной вершины $v$ длина кратчайшего пути до неё $l_v$ действительно равна $d_v$.

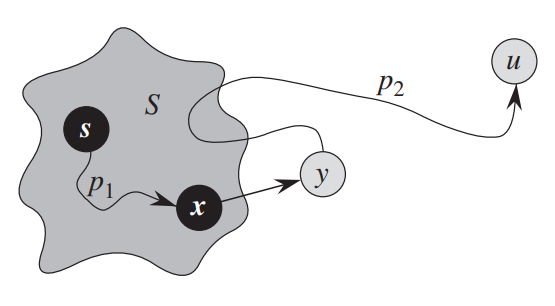
Рассмотрим любой кратчайший путь до вершины $v$. Обозначим первую непомеченную вершину на этом пути за $y$, а предшествующую ей помеченную за $x$ (они будут существовать, потому что вершина $s$ помечена, а вершина $v$ — нет). Обозначим вес ребра $(x, y)$ за $w$.

Так как $x$ помечена, то, по предположению индукции, $d_x = l_x$. Раз $(x,y)$ находится на кратчайшем пути, то $l_y=l_x+w$, что в точности равно $d_y=d_x+w$: мы в какой-то момент проводили релаксацию из уже помеченный вершины $x$.

Теперь, может ли быть такое, что $y ne v$? Нет, потому что мы на каждой итерации выбираем вершину с наименьшим $d_v$, а любой вершины дальше $y$ на пути расстояние от $s$ будет больше. Соответственно, $v = y$, и $d_v = d_y = l_y = l_v$, что и требовалось доказать.

#Время работы и реализация

Единственное вариативное место в алгоритме, от которого зависит его сложность — как конкретно искать $v$ с минимальным $d_v$.

#Для плотных графов

Если $m approx n^2$, то на каждой итерации можно просто пройтись по всему массиву и найти $argmin d_v$.

const int maxn = 1e5, inf = 1e9;
vector< pair<int, int> > g[maxn];
int n;

vector<int> dijkstra(int s) {
    vector<int> d(n, inf), a(n, 0);
    d[s] = 0;
    for (int i = 0; i < n; i++) {
        // находим вершину с минимальным d[v] из ещё не помеченных
        int v = -1;
        for (int u = 0; u < n; u++)
            if (!a[u] && (v == -1 || d[u] < d[v]))
                v = u;
        // помечаем её и проводим релаксации вдоль всех исходящих ребер
        a[v] = true;
        for (auto [u, w] : g[v])
            d[u] = min(d[u], d[v] + w);
    }
    return d;
}

Асимптотика такого алгоритма составит $O(n^2)$: на каждой итерации мы находим аргминимум за $O(n)$ и проводим $O(n)$ релаксаций.

Заметим также, что мы можем делать не $n$ итераций а чуть меньше. Во-первых, последнюю итерацию можно никогда не делать (оттуда ничего уже не прорелаксируешь). Во-вторых, можно сразу завершаться, когда мы доходим до недостижимых вершин ($d_v = infty$).

#Для разреженных графов

Если $m approx n$, то минимум можно искать быстрее. Вместо линейного прохода заведем структуру, в которую можно добавлять элементы и искать минимум — например std::set так умеет.

Будем поддерживать в этой структуре пары $(d_v, v)$, при релаксации удаляя старый $(d_u, u)$ и добавляя новый $(d_v + w, u)$, а при нахождении оптимального $v$ просто беря минимум (первый элемент).

Поддерживать массив $a$ нам теперь не нужно: сама структура для нахождения минимума будет играть роль множества ещё не рассмотренных вершин.

vector<int> dijkstra(int s) {
    vector<int> d(n, inf);
    d[root] = 0;
    set< pair<int, int> > q;
    q.insert({0, s});
    while (!q.empty()) {
        int v = q.begin()->second;
        q.erase(q.begin());
        for (auto [u, w] : g[v]) {
            if (d[u] > d[v] + w) {
                q.erase({d[u], u});
                d[u] = d[v] + w;
                q.insert({d[u], u});
            }
        }
    }
    return d;
}

Для каждого ребра нужно сделать два запроса в двоичное дерево, хранящее $O(n)$ элементов, за $O(log n)$ каждый, поэтому асимптотика такого алгоритма составит $O(m log n)$. Заметим, что в случае полных графов это будет равно $O(n^2 log n)$, так что про предыдущий алгоритм забывать не стоит.

#С кучей

Вместо двоичного дерева «правильнее» использовать более специализированную структуру, которая поддерживает именно добавление элементов и нахождение минимума: кучу. Удалять произвольные элементы в ней немного сложнее, поэтому вместо этого будем просто игнорировать все повторные вершины.

vector<int> dijkstra(int s) {
    vector<int> d(n, inf);
    d[root] = 0;
    // объявим очередь с приоритетами для *минимума* (по умолчанию ищется максимум)
    using pair<int, int> Pair;
    priority_queue<Pair, vector<Pair>, greater<Pair>> q;
    q.push({0, s});
    while (!q.empty()) {
        auto [cur_d, v] = q.top();
        q.pop();
        if (cur_d > d[v])
            continue;
        for (auto [u, w] : g[v]) {
            if (d[u] > d[v] + w) {
                d[u] = d[v] + w;
                q.push({d[u], u});
            }
        }
    }
}

На практике вариант с priority_queue немного быстрее.

Помимо обычной двоичной кучи, можно использовать и другие. С теоретической точки зрения, особенно интересна Фибоначчиева куча: у неё все почти все операции кроме работают за $O(1)$, но удаление элементов — за $O(log n)$. Это позволяет облегчить релаксирование до $O(1)$ за счет увеличения времени извлечения минимума до $O(log n)$, что приводит к асимптотике $O(n log n + m)$ вместо $O(m log n)$.

#Восстановление путей

Часто нужно знать не только длины кратчайших путей, но и получить сами пути.

Для этого можно создать массив $p$, в котором в ячейке $p_v$ будет хранится родитель вершины $v$ — вершина, из которой произошла последняя релаксация по ребру $(p_v, v)$.

Обновлять его можно параллельно с массивом $d$. Например, в последней реализации:

if (d[u] > d[v] + w) {
    d[u] = d[v] + w;
    p[u] = v; // <-- кратчайший путь в u идет через ребро (v, u)
    q.push({d[u], u});
}

Для восстановления пути нужно просто пройтись по предкам вершины $v$:

void print_path(int v) {
    while (v != s) {
        cout << v << endl;
        v = p[v];
    }
    cout << s << endl;
}

Обратим внимание, что код распечатает путь в обратном порядке.

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Given a directed graph G with N vertices and M edges. The task is to find the length of the longest directed path in Graph.
Note: Length of a directed path is the number of edges in it.
Examples:

Input: N = 4, M = 5

Output: 3
The directed path 1->3->2->4
Input: N = 5, M = 8

Output: 3

Simple Approach: A naive approach is to calculate the length of the longest path from every node using DFS.
The time complexity of this approach is O(N²).
Efficient Approach: An efficient approach is to use Dynamic Programming and DFS together to find the longest path in the Graph.
Let dp[i] be the length of the longest path starting from the node i. Initially all positions of dp will be 0. We can call the DFS function from every node and traverse for all its children. The recursive formula will be:

dp[node] = max(dp[node], 1 + max(dp[child1], dp[child2], dp[child3]..))

At the end check for the maximum value in dp[] array, which will be the longest path in the DAG.
Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>

using namespace std;

void dfs(int node, vector<int> adj[], int dp[], bool vis[])

{

vis[node] = true;

for (int i = 0; i < adj[node].size(); i++) {

if (!vis[adj[node][i]])

dfs(adj[node][i], adj, dp, vis);

dp[node] = max(dp[node], 1 + dp[adj[node][i]]);

}

void addEdge(vector<int> adj[], int u, int v)

{

adj[u].push_back(v);

}

int findLongestPath(vector<int> adj[], int n)

{

int dp[n + 1];

memset(dp, 0, sizeof dp);

bool vis[n + 1];

memset(vis, false, sizeof vis);

for (int i = 1; i <= n; i++) {

if (!vis[i])

dfs(i, adj, dp, vis);

}

int ans = 0;

for (int i = 1; i <= n; i++) {

ans = max(ans, dp[i]);

}

return ans;

}

int main()

{

int n = 5;

vector<int> adj[n + 1];

addEdge(adj, 1, 2);

addEdge(adj, 1, 3);

addEdge(adj, 3, 2);

addEdge(adj, 2, 4);

addEdge(adj, 3, 4);

cout << findLongestPath(adj, n);

return 0;

}

Java

import java.util.ArrayList;

class Graph

{

int vertices;

ArrayList<Integer> edge[];

Graph(int vertices)

{

this.vertices = vertices;

edge = new ArrayList[vertices+1];

for (int i = 0; i <= vertices; i++)

{

edge[i] = new ArrayList<>();

}

void addEdge(int a,int b)

{

edge[a].add(b);

}

void dfs(int node, ArrayList<Integer> adj[], int dp[],

boolean visited[])

{

visited[node] = true;

for (int i = 0; i < adj[node].size(); i++)

{

if (!visited[adj[node].get(i)])

dfs(adj[node].get(i), adj, dp, visited);

dp[node] = Math.max(dp[node], 1 + dp[adj[node].get(i)]);

}

int findLongestPath( int n)

{

ArrayList<Integer> adj[] = edge;

int[] dp = new int[n+1];

boolean[] visited = new boolean[n + 1];

for (int i = 1; i <= n; i++)

{

if (!visited[i])

dfs(i, adj, dp, visited);

}

int ans = 0;

for (int i = 1; i <= n; i++)

{

ans = Math.max(ans, dp[i]);

}

return ans;

}

public class Main

{

public static void main(String[] args)

{

int n = 5;

Graph graph = new Graph(n);

graph.addEdge( 1, 2);

graph.addEdge( 1, 3);

graph.addEdge( 3, 2);

graph.addEdge( 2, 4);

graph.addEdge( 3, 4);

graph.findLongestPath(n);

System.out.println( graph.findLongestPath( n));

}

Python3

def dfs(node, adj, dp, vis):

vis[node] = True

for i in range(0, len(adj[node])):

if not vis[adj[node][i]]:

dfs(adj[node][i], adj, dp, vis)

dp[node] = max(dp[node], 1 + dp[adj[node][i]])

def addEdge(adj, u, v):

adj[u].append(v)

def findLongestPath(adj, n):

dp = [0] * (n + 1)

vis = [False] * (n + 1)

for i in range(1, n + 1):

if not vis[i]:

dfs(i, adj, dp, vis)

ans = 0

for i in range(1, n + 1):

ans = max(ans, dp[i])

return ans

if __name__ == "__main__":

n = 5

adj = [[] for i in range(n + 1)]

addEdge(adj, 1, 2)

addEdge(adj, 1, 3)

addEdge(adj, 3, 2)

addEdge(adj, 2, 4)

addEdge(adj, 3, 4)

print(findLongestPath(adj, n))

C#

using System;

using System.Collections.Generic;

class Graph

{

public int vertices;

public List<int> []edge;

public Graph(int vertices)

{

this.vertices = vertices;

edge = new List<int>[vertices + 1];

for (int i = 0; i <= vertices; i++)

{

edge[i] = new List<int>();

}

public void addEdge(int a, int b)

{

edge[a].Add(b);

}

public void dfs(int node, List<int> []adj,

int []dp, Boolean []visited)

{

visited[node] = true;

for (int i = 0; i < adj[node].Count; i++)

{

if (!visited[adj[node][i]])

dfs(adj[node][i], adj, dp, visited);

dp[node] = Math.Max(dp[node], 1 +

dp[adj[node][i]]);

}

public int findLongestPath( int n)

{

List<int> []adj = edge;

int[] dp = new int[n + 1];

Boolean[] visited = new Boolean[n + 1];

for (int i = 1; i <= n; i++)

{

if (!visited[i])

dfs(i, adj, dp, visited);

}

int ans = 0;

for (int i = 1; i <= n; i++)

{

ans = Math.Max(ans, dp[i]);

}

return ans;

}

class GFG

{

public static void Main(String[] args)

{

int n = 5;

Graph graph = new Graph(n);

graph.addEdge( 1, 2);

graph.addEdge( 1, 3);

graph.addEdge( 3, 2);

graph.addEdge( 2, 4);

graph.addEdge( 3, 4);

graph.findLongestPath(n);

Console.WriteLine(graph.findLongestPath(n));

}

Javascript

<script>

function dfs(node, adj, dp, vis)

{

vis[node] = true;

for (var i = 0; i < adj[node].length; i++) {

if (!vis[adj[node][i]])

dfs(adj[node][i], adj, dp, vis);

dp[node] = Math.max(dp[node], 1 + dp[adj[node][i]]);

}

function addEdge(adj, u, v)

{

adj[u].push(v);

}

function findLongestPath(adj, n)

{

var dp = Array(n+1).fill(0);

var vis = Array(n+1).fill(false);

for (var i = 1; i <= n; i++) {

if (!vis[i])

dfs(i, adj, dp, vis);

}

var ans = 0;

for (var i = 1; i <= n; i++) {

ans = Math.max(ans, dp[i]);

}

return ans;

}

var n = 5;

var adj = Array.from(Array(n+1), ()=>Array());

addEdge(adj, 1, 2);

addEdge(adj, 1, 3);

addEdge(adj, 3, 2);

addEdge(adj, 2, 4);

addEdge(adj, 3, 4);

document.write( findLongestPath(adj, n));

</script>

Time Complexity: O(N+M)
Auxiliary Space: O(N)

?list=PLqM7alHXFySEaZgcg7uRYJFBnYMLti-nh

Last Updated :
30 Dec, 2021

Like Article

Save Article

Vote for difficulty

Current difficulty :
Hard

Источник

Strongly connected components

Утверждения:

Если рассматривать любой ациклический граф, то в нем есть сток и исток
Если граф $G$ ациклический, то тогда и только тогда $G^R$ (граф с перевернутыми стрелками) тоже ациклический (и наоборот, если есть цикл в одном графе, то есть и в другом)
$G^R$ можно построить за $O(|V|+|E|)$ по $G$, заданному списком смежности.

Компонента сильной связности — это максимальное подвключение подмножества $V$ такое, что $forall u, v in V$ существует путь $urightarrow v rightarrow u$.

Метаграф — граф, в котором все компоненты сильной связности заменены на единичные вершины (с сохранением ребер между компонентами). Если есть несколько ребер между двумя компонентами, то, в зависимости от задачи, можно либо их склеить в одно ребро, либо оставить все.

Утверждение: — метаграф ациклический.
Доказательство: — если бы в нем был цикл, то несколько компонент сильной связности склеились бы в одну.

Утверждение: — есть две вершины $U$ и $V$ (в метаграфе), которые задают две компоненты сильной связности, $(U rightarrow V) in H$ ($H$ — множество ребер метаграфа).
$maxlimits_{u in U}{post[u]} > maxlimits_{v in V}{post[v]}$ ($post$ — время выхода из вершины при обходе DFS).
Доказательство:

Сначала попали в $U rightarrow$ ОК (у одной из вершин $u$ время выхода будет больше, чем для всех $v$)
Сначала попали в $V rightarrow$ не попали в $U$ (туда попадем только на следующем вызове DFS $rightarrow$ для всех $u$ время выхода больше любого времени $v$).

Утверждение: вершина с максимальным $post$ лежит в компоненте истоке.

Утверждение: если отсортировать вершины по убыванию $post$, то получится топологическая сортировка на метаграфе.

Алгоритм: отсортируем вершины по убыванию $post$ и запустим обычный поиск компонент связности в перевернутом графе.

def scc(g):
    dfs(g)
    g_r = revert(g)
    sort(g_r.v, maxpost, reverse=True)  # сортируем вершины графа g_r
    # можно получить отсортированный массив прямо внутри dfs
    cc(g_r)  # поиск компонент

Время работы $O(|V| + |E|)$ (можно использовать сортировку подсчетом, что сортировать за $O(|V|)$).

Кратчайшие пути

Поиск в ширину

def bfs(g, w):  # w — вершина, откуда запускаем обход
    q = deque()
    dist = [inf for v in g.f]  # массив расстояний
    prev = [0 for v in g.f]    # восстановление пути
    dist[w] = 0
    q.append(v)
    while q:
        v = q.popleft()
        for u in g.v[v].neighbours:
            if dist[u] < inf:
                dist[u] = dist[v] + 1
                prev[u] = v
                q.append(u)
    return dist, prev

Время работы $O(|V| + |E|)$

Утверждение: $forall u: d[u] = text{dist}(w, u)$
База: $u=w Rightarrow d[w] = text{dist}(w, w) = 0$
И.п.: верно на расстояниях $leq k Rightarrow$ верно на расстоянии $k+1$. Все вершины на расстоянии $k+1$ являются соседями вершин на расстоянии $k$ (достаточно очевидно).

Утверждение: пусть $Pi = (v, v_1, v_2, … ,v_k, u)$ — кратчайший путь $v rightarrow u$. Тогда для $forall i, j: i < j: Pi’=(v_i, v_{i+1}, … , v_j)$ — кратчайший путь $v_irightarrow v_j$.

BFS Не работает для поиска кратчайшего пути, если граф взвешенный.

Можно добавить фиктивных вершин (ребро веса 5 — четыре дополнительных вершины веса 1 на это ребро).
Минусы:

требует целых/дробных весов
не работает на иррациональных числах (на это пофиг, т.к. иррациональность не представима на машине Тьюринга)
требует много памяти на ребрах с большим весом

Алгоритм Дейкстры

Работает для графов с неотрицательными ребрами.

Для реализации нужна очередь с приоритетами с операциями:

extract_min()
change_priority(value, key)
insert(value, priority)

def dijkstra(g, s):  # s — стартовая вершина
    dist = [inf for v in g.v]
    prev = [0 for  in g.v]
    dist[s] = 0
    q = priority_queue()
    q.insert(s, 0)
    while q:
        v = q.extract_min()
        for u in g.v[v].neighbours:
            if dist[u] == inf:
                dist[u] = dist[v] + g.w[v]
                prev[u] = v
                q.insert(u, dist[u])
            elif dist[u] > dist[v] + g.w[v]:
                dist[u] = dist[v] + g.w[v]
                prev[u] = v
                q.change_priority(u, dist[u])
            # если запилить такую очередь, что каждое value
            # представлено только 1 раз, и q.insert в случае
            # чего перезапишет старый приоритет, то можно
            # обойтись только одним if'ом
    return dist, prev

Лемма: алгоритм Дейскстры корректен. $forall u: d[u] = text{dist}(w, u)$.
Доказательство:

Для вершин из другой компоненты связности корректность очевидна.
Ведем три множества:
1. $S$ — вершины, которые мы уже обработали (которые вытащили из очереди)
2. $R$ — вершины, которые сейчас в очереди
3. $T$ — вершины, с расстоянием равным $+infty$
  Вершины в $R$ — соседи вершин из $S$.
  Утверждение: если $v$ переходит из $R$ в $S Rightarrow d[v] = text{dist}(s, v)$
  Доказательство: пусть $v$ — вершина в очереди с самым маленьким приоритетом.
  И.п.: для всех вершин в $S$ расстояние вычисленно корректно. Докажем от противного: пусть $Pi = (s, v1, … , v_k, v)$ — более короткий путь $srightarrow v$. Рассмотрим первую вершину этого пути, которая лежит в $R$. Расстояние от нее до $s$ больше, чем предпологаемое расстояние до $v$, которое лежит в очереди. Противоречие.

Сложность алгоритма: $O(|V|) + O(|V|cdot text{insert}) + O(|V|cdot text{extract_min}) + O(|E|cdot text{change_priority})$

Если брать очередь на куче, то сложность $O((V+E)log V)$.
Если брать очередь на массиве, то сложность $O(V^2+E)$ (если граф простой, то $+E$ можно пренебречь).

Для неплотных $left(E = Oleft(frac{V^2}{log V}right)right)$ графов лучше использовать кучу, для плотных ($E thicksim V^2$) — массив.

Tip: можно улучшить, если использовать $d$-ичную кучу. $d approx frac EV$.

(картинкА)

d-ичная куча

Если юзануть $d$-ичную кучу, то выйдет $n * d cdot log_d n$ — при extract_min. При insert’e: $n * log_d n$, а decrease_key: $m * log_d n$. Суммарная сложность: $O((ncdot d + m) log_d n)$.

Утверждается, что если $d approx frac{m}{n}$, то мы получим самое оптимальное решение.

$frac{m}{n} = O(1)$, т.е. $m approx n$, т.е. $d = const Rightarrow O((n+m) log n) = O(n log n)$
Пусть граф полный. $m = Omega(n^2)$, тогда $(d =) frac{m}{n} = n Rightarrow O(m) = O(n^2)$. Это то же что мы получали при реализации на массиве.
$m = Theta(n^{1+eps}), 0 < eps < 1$. Тогда $d = n^{eps}$. Итого $O(ncdot d + m) log_d n) = O((ncdot n^{eps} + m) cdot log_{n^{eps}} n)$, расписав последний логарифм как $frac{log n}{eps cdot log n} = frac{1}{eps}$ получаем $O(n^{1+eps}) = O(m)$.

Кратчайшие пути в графах с отрицательными весами

Дейкстра не работает (был пример),

* --5-->*
       -6
   10----->*

Утверждение. Если в графе есть отрицательный цикл $Rightarrow$ кратчайшие пути не определены.

Это достаточно очевидно утверждение. Мы бы тогда смогли построить путь из $s$ в $t$ отрицательной длины, и каждый раз бы пробовали его уменьшать (до $-infty$).

Напоним про операцию релаксации:

if d[u] + w(u, v) < d[v]:
    d[v] = d[u] + w(u, v)

То есть если пройти по ребру $(u, v)$, то я смогу уменьшить суммарный вес пути. Поэтому до $v$ лучше идти через $u$.

Утверждение. Релаксация только «улучшает» пути (т.е. не увеличивает). Это видно из определения выше.

Утверждение: Релаксация корректна, $d[v] geqslant dist(s, v)$. То есть релаксация не получит путь короче чем существует в графе.

Лемма: Пусть $pi$ — кратчайший путь $(s, v_1, v_2, ldots, v_k, t)$ из $s$ в $t$. Тогда если мы сделаем релаксации для всех рёбер вдоль пути $Rightarrow$ $d[t] = dist(s, t)$.

Рассмотрим перое ребро из $s$: $(s, v_1)$. Если посчитаем релаксацию для этого ребра, то мы правильно посчитаем расстояние до $v_1$. По индукции и по следующему утверждению пути лемма доказана.

Утверждение: Если есть кратчайший путь $pi$, то любой его подпуть тоже кратчайший. (Кстати, это место сломается, если мы ищем кратчайшие пустые пути). Если бы существовал не кратчайший подпуть, то там был бы цикл, т.е. и оригинальный путь не был бы кратчайшим.

Алгоритм Белмана-Форда

Как найти кратчайший путь? Можно просто релаксировать все рёбра случайным образом бесконечно много раз, и найдётся подпоследовательность релаксаций, которая найдёт мне кратчайший путь.

Теперь же хочется делать как можно меньше релаксаций, и чтобы там всё так же осталась подпоследовательность рёбер для нашего кратчайшего путя.

Прорелаксируем все рёбра в том порядке, в котором они пронумерованы: 1, 2, 3, …; потом ещё раз: 1, 2, 3, …; Так нужно делать $|V| — 1$ раз (длина самого длинного простого пути в графе). pi = 7, 5, 4, 13, 21, 2 — на каждой итерации релаксации, мы прорелаксируем сначала 7, потом 5, …, последнюю вершину пути.

for v in V:
  d[v] = inf

d[s] = 0
for i = 1 to |V| - 1:
  for (u, v) in E:
    if d[v] > d[u] + w(u, v):
       d[v] = d[u] + w(u, v)
       prev[v] = u  # для восстановления пути

Утверждение: алгоритм корректный. Нужно доказать, что $forall v: d[v] = dist(s, v)$. Посмотрим на кратчайший путь от $s$ до $v$, в нашей последовательности релаксаций был момент, когда мы релаксировали первое ребро, потом второе, …, последнее, т.е. по предыдущей лемме получаем, что путь будет кратчайшим.

На циклах с отрицательными дугами не работает. Теперь зададимся вопросом: как определить наличие отрицательного цикла? Можно сделать следующее: запустим алгоритм Беллмана-Форда с $V$ итерациями. И на последнем шаге посмотрим, изменится ли значение — по идее, там не должно ничего измениться (релаксация может только улучшить расстояния, а мы уже посчитали все оптимальные расстояния на шаге $|V|-1$). Если всё же изменилось — вот он цикл отрицательной длины.

Утверждение: если отрицательных циклов нет $Rightarrow$ на последней итерации $(= |V|)$, массив $d$ не изменится.

Утверждение: если есть отрицательный цикл, то массив $d$ обязательно (гарантированно) изменится.

Если делать не $V$ итераций а $infty$, то релаксации будут бесконечно долго уменьшать $d$. Если на итерации $k$ ничего не изменилось, тогда ничего не изменится на итерации $k+1$ (стоп). То есть если у нас отрицательный цикл, то на каждой итерации будет что-то уменьшаться (иначе если что-то не изменится, то значит всё зафиксировано, т.е. не бесконечное количество шагов, т.е. нет цикла).

Из этого можно понять, что можно делать не ровно $V$ итераций, а даже меньше, но следить, изменилось ли что-нибудь.

Сложность $O(V cdot E)$ (цикл по $V$ и цикл по $E$). Если выходить раньше, то будет $O(texttt{radius}(G, s) cdot E)$, где $radius(G, s)$ — длина самого длинного кратчайшего пути из $s$ до других вершин.

NB. Если граф ациклический, то можно сделать топологическую сортировку и пройти по ней в порядке топ. сортировки, вычислить за линейное время.

Расстояние от всех вершин до всех других

Хотим считать расстояния от вершины $u$ до $v$ через меньшие подзадачи. Определим $D(u, v, k)$ — кратчайший путь от $u$ до $v$, который проходит через вершины ${ 1, 2, ldots, k}$ (необязательно все, но имеется в виду принадлежность множеству).
$D(u, v, 0) = w(u, v)$, если $(u, v) in E$, иначе $infty$. Если представить куб, то его первый срез — это просто веса рёбер, то есть матрица смежности.

кратчайший путь от $u$ до $v$ проходит через $k$, либо не проходит.
$$D(u, v, k) = min { D(u, v, k-1), D(u, k, k-1) + D(k, v, k-1) }$$
где, вершина $k-1$ находится между $k$ и $v$ во втором случае.

Двигаемся вдоль координаты $k$.

Алгоритм Флойда-Уоршала:

for u = 1 to n:
  for v = 1 to n:
    d[u, v, 0] = w(u, v)  #inf, если ребра нет

for k = 1 to n:
  for u = 1 to n:
    for v = 1 to n:
      d[u, v, k] = d[u, v, k - 1]
      if d[u, v, k] > d[u, v, k-1] + d[k, v, k-1]:
        d[u, v, k] = d[u, v, k-1] + d[k, v, k-1]

Время $O(V^3)$. Память $O(V^3)$, но мы можем хранить только предыдущий слой: $O(V^2)$.

for k = 1 to n:
  for u = 1 to n:
    for v = 1 to n:
      if d[u, v] > d[u, v] + d[k, v]:
        d[u, v]  = d[u, v] + d[k, v]

Можно хранить $prev[u, v]$, которая хранит вершину перед $v$. И при присваивании меняем $prev$.

# init
if (u, w) in E:
  prev[u, v] = u

# loop
if d[u, v] > d[u, v] + d[k, v]:
  d[u, v]  = d[u, v] + d[k, v]
  prev[u, v] = prev[k, v]

Отрицательные рёбра норм, мы нигде не пользовались фактом, что их нет.

Отрицательные циклы можно детектировать, если на диагонали (кроме нулей), появятся отрицательные числа — то есть мы из вершины прошли в саму себя же.

Источник

Алгоритм Дейкстры. Разбор Задач

Введение

Примеры работы

Оценка сложности алгоритма

Задача №1

Решение

Задача №2

Решение

Заключение

Информация

Алгоритм нахождения максимального пути

4. Особенности алгоритмов теории графов

Вопросы для повторения.

#Основная идея

#Корректность

#Время работы и реализация

#Для плотных графов

#Для разреженных графов

#С кучей

#Восстановление путей

C++

Java

Python3

C#

Javascript

Strongly connected components

Кратчайшие пути

Поиск в ширину

Алгоритм Дейкстры

d-ичная куча

Кратчайшие пути в графах с отрицательными весами

Алгоритм Белмана-Форда

Расстояние от всех вершин до всех других