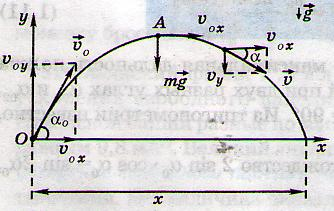
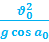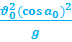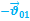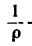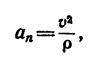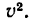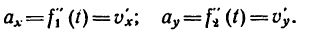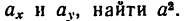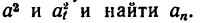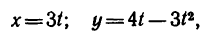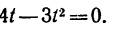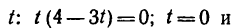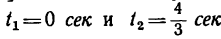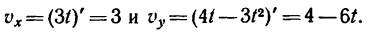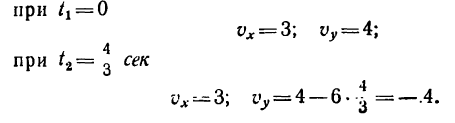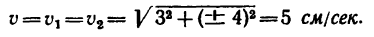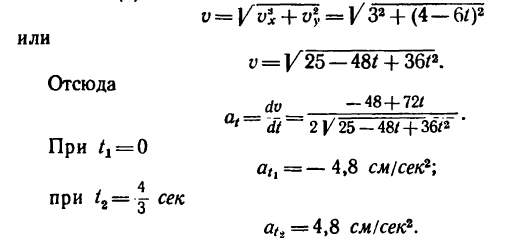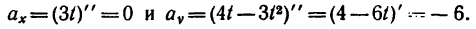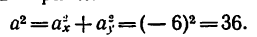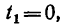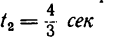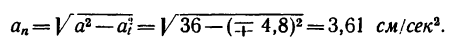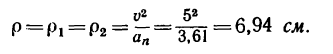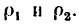Радиус кривизны траектории
В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из задач представляет собой целый набор, поэтому неясностей не должно остаться.
Задача 1.
Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:
Откуда :
То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.
К задаче 1
Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому
Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и
. Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:
Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:
Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :
Определим полную скорость тела в момент времени :
Угол наклона вектора скорости к горизонту в этот момент равен:
А можно было сразу и косинус найти:
Тогда искомый радиус кривизны траектории равен:
Ответ: м,
м,
м.
Задача 2.
Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б)
.
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:
Определим теперь радиус кривизны в вершине:
По условию :
б) Мы уже определили , осталась максимальная высота подъема.
Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:
Приравниваем и
:
Откуда .
Ответ: а) , б)
.
1) найти радиус кривизны траектории в наивысшей точке полета.

2)найти радийс кривизны траектории в начальной точке полета.
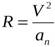
3) найти радиус траектории.
Центр масс твёрдого тела движется так же как двигалась бы материальная точка, масса которой равна массе тела, под действием внешних сил, приложенных к данному телу.
Тело состоит из нескольких элементов. Уравнение i-го элемента массой m записывается так:
Где Fi внешняя сила, а ∑Fik это сумма внутренних сил, действующих на i-ый элемент со стороны всех других элементов.
Сложим все аналогичные уравнения для всех элементов. Т.к. Fik = -Fki третьему закону Ньютона, то их сумма равна нулю.
После сложения получим:
Устойчивое равновесие — это равновесие, при котором, тело, выведенное из положения равновесия, вернётся в то же положение.
Неустойчивое равновесие — если тело, после смещения, не вернётся в это положение.
Скорость точки, движущейся по окружности ,часто называют Линейной скоростью ,чтобы подчеркнуть ее отличие от угловой скорости. Между линейной скоростью точки, обращающейся по окружности, и ее угловой скоростью существует связь. При равномерном движении точки по любой траектории модуль скорости равен s/∆t
Точка A, движущаяся по окружности радиуса R,за время ∆t проходит путь равный дуге A1A2
S=A1A2=∆ϕR .Модуль линейной скорости движения v= s/∆t ==∆ϕR/∆t=ωR
Итак , модуль линейной скорости точки, движущейся по окружности, равен произведению угловой скорости на радиус окружности :
Эта формула справедлива как для равномерного, так и для неравномерного движения точки по окружности.
Модуль ускорения точки, движущейся по окружности, можно выразить через угловую скорость тела и радиус окружности. Так как a=v²/R и v= ωR


















Очевидно, что модуль ускорения при равномерном движении точки по окружности есть постоянная величина, так как U и r не изменяются при движении
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9614 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
1.59. Радиус кривизны траектории в точке бросания: 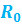
1.60. Радиус кривизны траектории в точке максимальной высоты А :

Замечание1: радиус кривизны 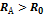
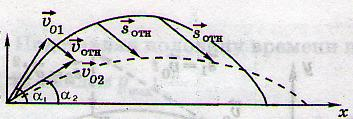
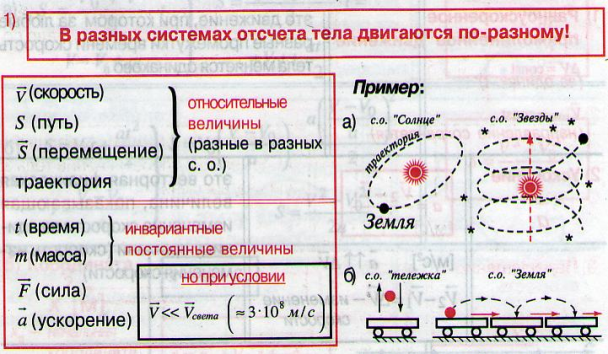
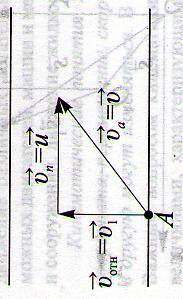
Как будут двигаться относительно друг друга два тела брошенные одновременно под разными углами к горизонту?
1.61.
… —второе тело относительно первого тела будет двигаться равномерно и прямолинейно, и вектор перемещения, соединяющий тела, в любой момент времени будет параллелен вектору относительной скорости:

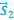
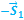

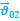
Относительность механического движения
§ 1.6.
1.63. Относительность скорости.
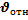
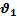
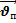
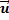
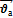
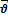


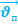
…- формула сложения скоростей



…- формула сложения перемещений.
Замечание: формулы (1) и (2) формулы преобразования Галилея.
Пойдем в обратном порядке.
gh=3/4*(2/3*(g*t)^2);
t=(3*h/*g)^0,5, где g – ускорение свободно падения;
t
0,3 c
А Митин Андрей, по-моему, проврался: в выражении t=2/(h*(8*g*h/5)^0.5) проблемы с размерностью.
2) Аппроксимируем движение точки равномерным движением по окружности.
v=w*R; a=w^2*R; m=p/v=p/(w*R);
F=m*a=(p*w^2*R)/(w*R)=p*w;
F=0,1*0,5*pi Н=0,05*pi Н, где pi – число пи.
1) Тут пока выкладки получаются громоздкие – утомительно писать в подобном окне. Может, потом чего-нибудь попроще придумаю. Но ответ такой: максимальны радиус в крайних точках траектории (начальной и конечной моменты движения), а минимальный – в точке, что делит траекторию пополам и в которой движение горизонтально.
Конечные соотношения:
R(t)=v(t)^3/(g*v(0)*cos(A)), где g – ускорение свободного падения.
Преподаватель который помогает студентам и школьникам в учёбе.
Кинематический способ определения радиуса кривизны траектории в теоретической механике
Кинематический способ определения радиуса кривизны траектории:
При решении многих технических задач возникает необходимость знать радиус кривизны р (или
Таким образом, если закон движения точки задан уравнениями
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
2. Подставив в (б’) выражения 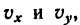
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение 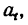
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
5. Подставив в (г) выражения
6. Подставить в (в) значения
7. Подставив в (а) найденные значения 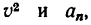
Задача:
Движение точки задано уравнениями
(х, у—в см, t — в сек). Определить радиус кривизны траектории в те моменты, когда она пересекает ось Ох.
Решение.
1. В те моменты, когда траектория пересекает ось Ох, ордината у—0. Поэтому, подставив во второе уравнение движения значение у = 0, получим
Отсюда [решая уравнение относительно 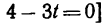
2. Находим выражения проекций скорости:
Как видно, проекция скорости на ось Ох — постоянная величина (не зависит от времени).
3. Определяем значение этих проекций в моменты пересечения траекторией оси Ох:
4. Числовое значение скорости точки в моменты пересечения траекторией оси Ох в данном случае одинаковы
5. Находим касательное ускорение точки. Для этого получим общее выражение (уравнение) скорости, воспользовавшись зависимостью (б):
6. Находим проекции полного ускорения точки:
Следовательно, в данном случае полное ускорение точки — постоянная величина. Причем
7. Определяем нормальное ускорение точки. Как при
так и при
8. Зная, что в моменты пересечения траекторией оси 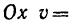
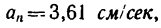
Решение этой задачи рекомендуется самостоятельно иллюстрировать чертежом, изобразив на нем траекторию точки, векторы скорости 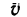
- Равномерное вращательное движение
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки
Радиус кривизны траектории точки окружности
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ
7.1. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.2. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.3. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки:
,
,
.
,
,
Модуль полного ускорения:
.
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.4. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.5. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки по осям :
,
,
Ускорения точки по осям:
,
,
.
Модуль касательного ускорения точки:
, а модуль нормального ускорения .
Нормальное ускорение и радиус кривизны траектории связаны соотношением .
7.6. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки по осям :
,
,
Ускорения точки по осям:
,
,
.
Модуль касательного ускорения точки:
,
а модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением .
7.7. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.8. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
.
,
,
Модуль полного ускорения:
.
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.9. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , , .
Решение: Скорости точки :
,
,
.
,
,
Модуль полного ускорения:
.
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.10. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.11. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.12. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.13. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.14. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Найти: , , .
Решение: Скорости точки по осям :
,
,
,
Ускорения точки по осям:
,
,
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.15. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.16. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.17. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.18. Дан закон движения точки по окружности радиусом r . Определить:
1) скорость и ускорение точки при и ;
2) моменты остановки точки;
3) путь, пройденный точкой за 10секунд.
Дано: , , , .
Найти: , , , , , , П.
Решение: 1. На траектории отметим точку О – начало отсчета координаты s и укажем положительное направление отсчета этой координаты. Отметим положение точки в заданные моменты времени: При :
;
При :
.
Проведем из этих точек естественные оси координат.
Определим проекцию скорости на касательную:
.
При : ;
При : .
Векторы и совпадают со своими проекциями. Определим проекции ускорения на естественнее оси координат :
; , Полное ускорение точки .
При :
,
и
.
При :
,
и
.
2. Чтобы найти время остановки надо найти время, когда скорость точки равна нулю:
, получим и .
3. Поскольку за 10 секунд точка сделала две остановки, пройденный ею путь за 10с можно найти как сумму пути, пройденного от начала до первой остановки, от первой до второй остановки и от второй до момента времени :
,
; ; ; .
Путь пройденный точкой за 10 секунд:
.
7.19. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , (1)
( x и y – в см , t и t 1 – в с).
Найти: 1) вид траектории;
2) для t = t 1 положение точки на траектории;
3) .
Решение: 1) Уравнение движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключаем время t из уравнений (1).
Возводя обе части равенств в квадрат, а затем складывая равенства, получаем , т.е. траекторией точки М является окружность радиуса 2, показанная на рис.1.
2) Определяем положение точки М в заданный момент времени t =1 с :
Вектор скорости точки
. (2)
(3)
Здесь – орты осей и ; – проекции скорости и ускорения точки на оси координат.
Найдем их, дифференцируя по времени уравнения движения (1):
По найденным проекциям определяем модуль скорости:
, (4)
,
,
и модуль ускорения точки:
, (5)
Модуль касательного ускорения точки
, (6)
; (7)
выражает проекцию ускорения точки на направление ее скорости. Знак «+» при означает, что движение точки ускоренное, направление и совпадают; знак «–» – что движение замедленное.
Вычисляем модуль касательного ускорения для заданного момента времени
Модуль нормального ускорения точки
. (8)
Если радиус кривизны траектории в рассматриваемой точке неизвестен, то нормальное ускорение можно определить по формуле
. (9)
При движении точки в плоскости формула (9) принимает вид
.
Модуль нормального ускорения можно определить и следующим образом:
. (10)
Воспользуемся в нашем случае формулой (10)
Радиус кривизны траектории в рассматриваемой точке определим из выражения:
. (11)
Тогда
На рис. 1 показано положение точки М в заданный момент времени. Вектор строим по составляющим и , причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор строим по составляющим и и затем раскладываем на составляющие и . Совпадение величин и , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
7.20. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
( x и y – в см , t и t 1 – в с).
Найти: 1) вид траектории;
2) .
Указания. Задача — относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения. В задаче все искомые величины нужно определить только для момента времени t 1 = 1 с .
1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t :
Отсюда окончательно находим уравнение траектории точки (параболы, см. рисунок):
2. Скорость точки найдем по ее проекциям на координатные оси:
V = и при t 1 = 1 с,
3. Аналогично найдем ускорение точки:
а =
4. Касательное ускорение найдем, дифференцируя по времени равенство:
. (3)
ч исловые значения всех величин, входящих в правую часть выражения (3), определены и даются равенствами (1) и (2).
Подставив в (3) эти числа, найдем сразу, что при t 1 = 1 с
=7,49 см/с 2 .
5. Нормальное ускорение точки:
a n = .
Подставляя сюда найденные числовые значения a 1 и a 1 τ , получим, что при t 1= 1 с
6. Радиус кривизны траектории ρ = V 2 / a n .
Подставляя сюда числовые значения V 1 и a 1 n , найдем, что при t 1 = 1 с
Ответ: V 1= 8 ,54 см/с, а 1 =8 см/с 2 , =7,49 см/с 2 , a 1 n =2,81 см/с 2 , ρ1 =25,95 см.
7.21. Точка движется по дуге окружности радиуса R =1 м по закону ( s – в метрах, t – в секундах), где s = AM (см. рисунок).
Найти: скорость и ускорение точки в момент времени t 1 =1 с .
Определяем скорость точки:
V = ds / dt = .
При t 1 =1 с получим = -1,26 м/ с .
Ускорение находим по его касательной и нормальной составляющим:
,
п ри t 1 = 1 с получим , учтя, что R = 1 м
,
тогда ускорение точки при t 1 =1 с будет:
=1,59 м/с 2 .
Изобразим на рисунке векторы , , учитывая знак V 1 и считая положительным направление от А к М.
7.22. По заданным уравнениям движения точки М установить вид её траектории и для момента времени t = t 1(с) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.
Дано: , , t 1=1 сек ( x и y – в см , t и t 1 – в с).
Найти: 1) вид траектории;
2) .
1) Найдём траекторию движения:
Для этого исключим параметр t .
Возведём во вторую степень, получившиеся уравнения, а затем сложим, таким образом, исключится t . Получим:
Это окружность с центром в точке с координатами (-1;0) и радиусом
2) Найдём положение точки на траектории в момент времени t = t 1:
3) Определим скорость токи:
Для нахождения вектора полной скорости необходимо сложить 2 вектора:
Найдём модуль полной скорости:
для момента времени t 1:
4) Определим ускорение точки:
для момента времени t 1:
для момента времени t 1:
Найдём полное ускорение:
Найдём модуль полного ускорения:
для момента времени t 1:
Определим касательное ускорение :
или,
для момента времени t :
Определим нормальное ускорение an :
для момента времени t 1:
5) Из полученных результатов можно найти радиус кривизны траектории , в момент времени t 1:
Действительно, этот радиус совпадает с радиусом окружности (траектории).
7.23. Точка М движется согласно уравнений ; ; ( x , y — в метрах, t — в секундах). Определить уравнение траектории точки, для момента времени t =1с, найти положение точки, а также скорость, полное, касательное, нормальное ускорения точки и радиус кривизны траектории.
1) Найдем уравнение траектории точки. Для определения уравнения траектории исключим из уравнений движения время . Из первого уравнения движения точки найдем
Из второго уравнения движения найдем
Возведя полученные значения ( правую и левую стороны уравнения ) в квадрат и складывая их находим:
.
Следовательно, траекторией точки является эллипс с центром в точке с координатами (3;1).
Вид траектории показан на рисунке.
2) Найдем положение точки в момент времени t =1с
; .
Положение точки М 1 показано на рисунке.
3) Найдем скорость точки М
,
Где , или в момент времени t1=1c
, или в момент времени t1=1c
4) Найдём ускорение точки.
,
где , или ,
, или
5) Найдем касательное ускорение точки M,
6) Найдём нормальное ускорение точки M ,
7) Найдем радиус кривизны траектории точки М,
,
Направление векторов показано на рисунке.
Ответ: =7.85м/ c ; = 4.93 м/ c 2 ; =0; = 4.93 м/ c 2 ; м
7.24. Пусть точка М движется в плоскости xOy в соответствии с уравнениями . Для момента времени = 0,5 с найти положение точки М на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Решение: Заданный закон движения точки в координатной форме можно рассматривать как параметрические уравнения траектории точки. Исключим время t из уравнений движения и получим уравнение траектории точки в виде:
.
Таким образом, траекторией точки М является эллипс со смещенным центром, изображенный на рис. Отметим на траектории положение точки М 1 ( x 1, y 1) в момент времени t 1 = 0,5 c
;
.
Вектор скорости точки представим в виде:
,
где – орты координатных осей О x и О y ; – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от соответствующих координат по времени
В момент времени t 1 = 0,5 c
Вектор скорости точки строим по двум взаимно перпендикулярным проекциям и в соответствии с выбранным масштабом
.
Полученный вектор должен быть направлен по касательной к траектории точки в сторону движения. Модуль скорости точки определим по уже найденным проекциям
Вектор ускорения точки представим в виде:
,
где – орты координатных осей О x и О y ; – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от проекций вектора скорости или 2-м производным от соответствующих координат по времени:
В момент времени t 1 = 0,5 c
Вектор ускорения точки строим по двум взаимно перпендикулярным проекциям и в соответствии с выбранным масштабом
.
Полученный вектор ускорения точки в общем случае должен отклоняться от вектора скорости в сторону вогнутости траектории, а при движении по эллипсовидной траектории – проходить через центр эллипса. Модуль ускорения точки определим по уже найденным проекциям
Вектор полного ускорения точки можно также представить в виде геометрической суммы его проекций на оси естественной системы отсчета
,
где и – единичные орты касательной и главной нормали; и – соответственно проекции вектора ускорения на касательную и главную нормаль. Касательную М 1 t направляем по касательной к траектории в сторону движения точки движения, а главную нормаль М1 n – перпендикулярно касательной в сторону вогнутости траектории. При вычислении касательного ускорения удобно воспользоваться формулой, устанавливающей связь между координатным и естественным способами задания движения точки
.
В момент времени t 1 = 0,5 c
.
Значение касательного ускорения имеет отрицательный знак, следовательно, в данный момент времени движение точки замедленное и вектор касательного ускорения направлен в противоположную сторону направлению вектора скорости точки .
Нормальное ускорение вычислим по формуле , если известен радиус кривизны траектории. Например, если точка движется по окружности радиусом R, то в любой точке траектории . Если же траекторией движения точки является прямая, то , следовательно, . В данном случае радиус кривизны траектории заранее не известен, поэтому нормальное ускорение определяем по формуле:
.
В момент времени t 1 = 0,5 c
.
Построим векторы и в соответствии с уже выбранным масштабом, а затем сложим их геометрически. В результате получим тот же вектор полного ускорения точки , который ранее уже был получен геометрической суммой составляющих и . Этот факт служит контролем правильности решения.
Радиус кривизны траектории в рассматриваемой точке определим по формуле
.
В момент времени t 1 = 0,5 c
.
Ответ: =8,82 см; =2,59 см; =4,44 см/ c ; =2,22 см/ c ; =4,96 см/с; =6,97 см/с 2 ; =3,49 см/с 2 ; =7,79 см/с 2 ; =4,67 см/с 2 ; =6,23 см/с 2 ; =3,95 см (радиус кривизны траектории в точке ).
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Радиус кривизны плоской кривой
Любая линия является кривой, даже прямая. Поэтому к любой линии применимы такие характеристики как кривизна или радиус кривизны. Как правило кривизна обозначается латинской литерой k, а радиус кривизны греческой литерой ρ.
Между собой эти характеристики кривой связаны следующим образом:
k = 1/ρ (542.1)
Т.е. чем больше радиус кривой, тем меньше ее кривизна.
А теперь рассмотрим несколько частных случаев кривых.
Радиус кривизны окружности
Окружность — это плоская кривая с постоянным радиусом кривизны. Т.е. радиус окружности это и есть радиус кривизны окружности:
Как определить радиус окружности, мы рассмотрим ниже.
Кривизна дуги
Любая дуга — это часть окружности. Соответственно радиус дуги равен радиусу окружности:
Рисунок 542.1. Дуга — часть окружности
На рисунке 542.1 мы видим дугу АВ, показанную оранжевым цветом, являющуюся частью окружности с радиусом R. Кроме того, мы видим, что угол α, образованный радиусами в точках А и В, равен углу между касательными (показаны фиолетовым цветом) к окружности в этих точках.
Эти закономерности позволяют определить радиус дуги и найти центр окружности даже тогда, когда изначально мы окружность не видим, а только имеем дугу.
Понятие кривизны дуги формулируется так:
Кривизна дуги — это отношение угла между касательными, проведенными в начале и конце дуги, к длине дуги
Т.е. зная длину дуги m и угол α между касательными, мы можем определить кривизну дуги:
А так как длина дуги зависит от угла между радиусами или между касательными в концах дуги:
то, подставив значение длины дуги в уравнение (542.3), получим:
Примечание: При измерении угла между касательными не в радианах, а в градусах уравнение длины дуги имеет другой вид:
но сути дела это не меняет. Такая запись по-прежнему означает, что мы рассматриваем часть длины окружности. Так при α = 360° дуга становится окружностью
Более того, сама идея радианов на этой формуле и основана, так прямой угол 90° = П/2, развернутый 180° = П и т.д.
И еще одно интересное свойство дуги: Если соединить точки А и В прямой линией, то угол между этой линией и касательными будет равен α/2, а сама прямая линия — это и есть расстояние между точками А и В. Если дуга расположена в плоскости соответствующим образом, например так, как показано на рисунке 542.2:
Рисунок 542.2. Дуга из точки начала координат.
то расстояние между точками — это проекция l дуги на ось х. А максимальное расстояние между дугой и осью х — это стрела дуги h.
Радиус кривизны прямой линии
Любая прямая линия, даже бесконечно длинная, может рассматриваться как бесконечно малая часть окружности, т.е. как дуга. Соответственно в каких единицах измерять радиус такой окружности даже трудно представить.
Поэтому обычно прямой линией называют кривую с бесконечно большим радиусом:
kп.л = 1/∞ = 0 (542.6)
Про до сих пор неразрешенный парадокс, возникающий при подобных подходах к прямой линии и к окружности, я уже упоминал в статье «Основы геометрии. Определения основных элементов, пятый элемент». Здесь лишь добавлю, что через прямую линию можно провести бесконечное множество плоскостей и в любой из этих плоскостей радиус кривизны прямой линии будет равен бесконечности. При этом через окружность можно провести две взаимно перпендикулярные плоскости, в одной из которых окружность будет окружностью, а в другой — прямой линией конечной длины. Поэтому
все линии, которые в одной из плоскостей имеют бесконечно большой радиус кривизны, считаются плоскими
Ну и на закуску еще несколько парадоксов, на этот раз связанных с определениями кривизны и радиуса:
1. Из уравнения (542.1) можно сделать вывод, что:
kp = 1 (542.7)
Соответственно для прямой линии:
0·∞ = 1 (542.7.2)
Т.е. если бесконечно много раз взять ноль, то на единичку мы наскребем. Впрочем дальше будет еще веселее.
2. Если прямая — это дуга с бесконечно большим радиусом, соответственно касательные, проведенные в концах такой дуги, совпадают с прямой, а угол, образованный касательными, равен нулю.
Это означает, что радиусы проведенные в концах дуги — прямой линии, являются параллельными прямыми и не могут пересекаться. А между тем по определению это радиусы, которые обязательно должны сходиться в некоторой точке — центре окружности.
Получается, что параллельные прямые пересекаться не должны, но где-то в бесконечности все-таки пересекаются.
Разрешить этот парадокс пытались многие математики, однако в пределах евклидовой геометрии при принятом толковании определений данный парадокс не разрешим.
Радиус кривизны точки
Точка — это самый простой и самый сложный элемент геометрии. Одни считают, что точка не имеет размеров, а значит и определить кривизну или радиус кривизны точки не возможно. Другие, в частности Евклид, считают, что точка не имеет частей, а каковы при этом размеры точки — не совсем понятно. Я же считаю, что точка — это начальный, далее не делимый элемент геометрии, размеры которого пренебрежимо малы по сравнению с остальными рассматриваемыми элементами. В этом случае для точки будут справедливыми следующие уравнения кривизны и радиуса кривизны:
kт. = 1/0 = ∞ (542.9)
И хотя нас с первых лет обучения в школе учат, что делить на 0 нельзя и даже встроенный в операционную систему калькулятор пишет, что «деление на ноль невозможно», тем не менее делить на ноль можно, а результатом деления всегда будет бесконечность.
Как и в случае с прямой мы имеем парадоксальный результат, выражаемый формулой (542.5.2). Тем не менее точку также можно отнести к плоской кривой, имеющей постоянный радиус кривизны.
Примечание: На мой взгляд большинство из описанных выше парадоксов возникают из-за неправильного толкования понятия «бесконечность». Бесконечность как некая абсолютная величина не имеет пределов, а значит и никакому измерению не поддается. Кроме того бесконечность — это даже не постоянная, а переменная величина. Например луч — это прямая линия с началом в некоторой точке. Длина луча может быть бесконечно большой. При этом прямая линия тоже может быть бесконечно длинной при этом не иметь ни начала ни конца. Получается, что с одной стороны бесконечно длинный луч вроде бы в 2 раза короче, чем бесконечно длинная прямая. А с другой стороны длины их бесконечны и поэтому равны.
Возможным выходом из этой ситуации является принятие понятия «бесконечность», как относительного. Например, кривизна прямой линии является пренебрежимо малой величиной по отношению к радиусу кривизны. Или радиус кривизны прямой линии несопоставимо больше кривизны. Подобные толкования допускают и наличие кривизны прямой и некое конечное значение радиуса кривизны прямой и многое другое. Я бы назвал такой относительный подход к рассмотрению проблемы реалистичным, а подходы, использующие абсолютные понятия — идеализированными. Впрочем прямого отношения к теме данной статьи это не имеет. Продолжим рассмотрение плоских кривых.
И окружность и прямая линия являются плоскими кривыми с постоянным радиусом кривизны. При этом радиус кривизны прямой линии всегда известен, так как равен бесконечности, а для окружности всегда можно определить радиус, воспользовавшись теоремой Пифагора. Так в частном случае, если центр окружности совпадает с началом координат рассматриваемой плоскости (u = 0; v = 0 — координаты центра окружности), то:
Рисунок 541.4. Радиус окружности, как гипотенуза прямоугольного треугольника.
R 2 = x 2 + y 2 (541.1.2)
А в общем случае, когда координаты центра окружности не совпадают с началом координат:
Рисунок 542.3. Окружность, центр которой не совпадает с началом координат.
R 2 = (x — u) 2 + (y — v) 2 (542.10)
Но в жизни достаточно часто приходится сталкиваться с кривыми, радиус кривизны которых — не постоянная величина. Более того, этот радиус может изменяться в двух плоскостях измерения. Тем не менее так далеко углубляться в геометрию и алгебру мы не будем и далее рассмотрим, как можно определить радиус плоской кривой в некоторой точке.
Плоские кривые с изменяющимся радиусом кривизны
Примеров плоских кривых с изменяющимся радиусом кривизны очень много, это и гиперболы, и параболы, и синусоиды и т.п. Определение радиуса кривизны таких кривых основано на следующих теоретических предпосылках:
1. Любую окружность можно рассматривать как некоторое множество дуг.
2. Если количество дуг, составляющих окружность, стремится к бесконечности, то соответственно длина таких дуг стремится к нулю (m → 0).
3. Если мы обозначим длину такой очень короткой дуги как приращение функции длины окружности (m = Δl), то уравнение кривизны (542.3) примет следующий вид:
(542.3.1)
4. Тогда любую плоскую кривую с изменяющимся радиусом можно рассматривать как стремящееся к бесконечности множество дуг с постоянным радиусом. Другими словами в пределах любой кривой, описываемой параметрическими уравнениями, всегда можно выделить дугу, пусть даже и очень малой длины, стремящейся к точке и определить для нее кривизну и радиус кривизны в рассматриваемой точке.
Это означает, что самый точный способ определения радиуса кривизны в таком случае — это использование дифференциальных исчислений. В общем случае для этого нужно два раза продифференцировать уравнение радиуса окружности (542.10) по аргументу функции х, а затем извлечь квадратный корень из полученного результата. В итоге (полный вывод уравнения здесь не привожу из-за повышенной сложности записи, а для особо заинтересованных есть справочники и другие сайты) мы получим следующую формулу для определения радиуса кривизны:
(542.11)
Соответственно кривизна плоской кривой в рассматриваемой точке будет равна:
(542.12)
В частном случае, когда тангенс угла между касательными — первая производная от функции — является относительно малой величиной, например, tg2° = 0.035 соответственно (tg2°) 2 = 0.0012, то влиянием куба суммы первой производной и единицы на кривизну можно пренебречь (значение знаменателя дроби сводится к единице) и тогда:
k = y» = d 2 y/dx 2 (542.12.2)
Т.е. формально в таких случаях кривизной считается не отношение угла наклона между касательными к длине дуги, а некоторая величина, примерно соответствующая высоте h на рисунке 542.2.
Эта особенность второй производной очень активно используется в частности для упрощения определения прогиба элементов строительных конструкций.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Категории:
- Расчет конструкций . Основы прикладной геометрии
Оценка пользователей:
10.0 (голосов: 1)
Переходов на сайт:
6701
Комментарии:
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Кинематика материальной точки
Основные формулы кинематики материальной точки
Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.
Радиус-вектор материальной точки M в прямоугольной системе координат Oxyz :
,
где – единичные векторы (орты) в направлении осей x, y, z .
Скорость точки:
;
;
;
Единичный вектор в направлении касательной к траектории точки:
.
Вектор можно выбрать двумя способами во взаимно противоположных направлениях. Обычно его выбирают в направлении увеличения дуговой координаты. Тогда, наряду с модулем скорости , вводят алгебраическую величину скорости . При , вектор скорости сонаправлен с . При – имеет противоположное с направление.
Скорость и ускорение точки M
Тангенциальное (касательное) ускорение:
;
;
.
Здесь, как и для скорости, – это алгебраическое касательное ускорение, . Если , то вектор касательного ускорения сонаправлен с . При – имеет противоположное с направление.
Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.
Радиус кривизны траектории:
.
Далее приводится вывод этих формул и изложение теории кинематики материальной точки.
Радиус-вектор и траектория точки
Рассмотрим движение материальной точки M . Выберем неподвижную прямоугольную систему координат Oxyz с центром в некоторой неподвижной точке O . Тогда положение точки M однозначно определяются ее координатами ( x, y, z ) . Эти координаты являются компонентами радиус-вектора материальной точки.
Радиус-вектор точки M – это вектор , проведенный из начала неподвижной системы координат O в точку M .
,
где – единичные векторы в направлении осей x, y, z .
При движении точки, координаты изменяются со временем . То есть они являются функциями от времени . Тогда систему уравнений
(1)
можно рассматривать как уравнение кривой, заданной параметрическими уравнениями. Такая кривая является траекторией точки.
Траектория материальной точки – это линия, вдоль которой происходит движение точки.
Если движение точки происходит в плоскости, то можно выбрать оси и системы координат так, чтобы они лежали в этой плоскости. Тогда траектория определяется двумя уравнениями
В некоторых случаях, из этих уравнений можно исключить время . Тогда уравнение траектории будет иметь зависимость вида:
,
где – некоторая функция. Эта зависимость содержит только переменные и . Она не содержит параметр .
Скорость материальной точки
Согласно определению скорости и определению производной:
Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:
,
где
,
,
– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.
Таким образом
.
Модуль скорости:
.
Касательная к траектории
С математической точки зрения, систему уравнений (1) можно рассматривать как уравнение линии (кривой), заданной параметрическими уравнениями. Время , при таком рассмотрении, играет роль параметра. Из курса математического анализа известно, что направляющий вектор для касательной к этой кривой имеет компоненты:
.
Но это есть компоненты вектора скорости точки. То есть скорость материальной точки направлена по касательной к траектории.
Все это можно продемонстрировать непосредственно. Пусть в момент времени точка находится в положении с радиус-вектором (см. рисунок). А в момент времени – в положении с радиус-вектором . Через точки и проведем прямую . По определению, касательная – это такая прямая , к которой стремится прямая при .
Введем обозначения:
;
;
.
Тогда вектор направлен вдоль прямой .
При стремлении , прямая стремится к касательной , а вектор – к скорости точки в момент времени :
.
Поскольку вектор направлен вдоль прямой , а прямая при , то вектор скорости направлен вдоль касательной .
То есть вектор скорости материальной точки направлен вдоль касательной к траектории.
Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.
Здесь мы направили вектор по направлению к вектору скорости, поскольку это более удобно. Но могут возникнуть случаи, когда точка останавливается и движется по той же траектории в обратном направлении. Чтобы не вводить для одной и той же точки траектории два единичных касательных вектора, нужно охватить случай, когда направлен противоположно скорости. Для этого вводят алгебраическую величину скорости:
.
Если направления векторов и совпадают, то . Если они противоположны, то .
– это проекция скорости на направление единичного вектора . Она равна скалярному произведению этих векторов:
.
Абсолютную величину (модуль) вектора скорости мы обозначаем символом с прямыми скобками, или символом без стрелки:
;
Алгебраическая величина скорости:
.
Тогда вектор скорости точки можно представить в следующем виде:
.
Ускорение материальной точки
Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.
Тангенциальное (касательное) и нормальное ускорения
Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.
Вектор направлен по касательной к траектории. В какую сторону направлена его производная по времени ?
Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают их скалярное произведение. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.
Скорость, касательное и нормальное ускорение точки M
Первую компоненту называют тангенциальным или касательным ускорением:
.
Вторую компоненту называют нормальным ускорением:
.
Тогда полное ускорение:
(2) .
Эта формула представляет собой разложение ускорения на две взаимно перпендикулярные компоненты – касательную к траектории и перпендикулярную к ней.
Тангенциальное (касательное) ускорение
Также как и для скорости, введем алгебраическую величину вектора касательного ускорения :
.
Если , то вектор касательного ускорения сонаправлен с . Если , то эти векторы противоположны. Абсолютную величину касательного ускорения будем обозначать прямыми скобками: . Тогда
.
Умножим обе части уравнения (2) скалярно на :
.
Поскольку , то . Тогда
;
.
Здесь мы положили: .
Отсюда видно, что алгебраическая величина тангенциального ускорения равна проекции полного ускорения на направление касательной к траектории. Она также равна производной по времени алгебраической величины скорости точки: .
Подставив , имеем:
.
Здесь мы учли, что .
Найдем производную по времени модуля скорости . Применяем правила дифференцирования:
;
.
Итак,
.
Отсюда следует, что если между векторами ускорения и скорости острый угол: , то движение ускоренное. Абсолютное значение скорости возрастает. Если между ними тупой угол: , то движение замедленное. Абсолютное значение скорости убывает.
Выразим ускорение через тангенциальное и нормальное: , и учтем, что . Получим:
.
Тогда предыдущую формулировку можно выразить посредством тангенциального ускорения. Если векторы касательного ускорения и скорости направлены в одну сторону, то движение ускоренное. Если их направления противоположны, то движение замедленное.
Радиус кривизны траектории
Теперь исследуем вектор .
Рассмотрим вектор в два момента времени – в момент времени t и в момент t 1 . Введем обозначения: . По определению производной:
.
Пусть в момент времени t , точка находится в положении M , а в момент t 1 – в положении M 1 (см. рисунок).
Рассмотрим случай, когда алгебраическая скорость положительна: . То есть направления векторов и совпадают. Тогда точка M 1 находится справа от M . Через точки и проведем плоскости, перпендикулярные векторам и . Пересечение этих плоскостей образует прямую. Она проходит через точку C перпендикулярно плоскости рисунка. MC – это перпендикуляр, опущенный из точки M на эту прямую.
При , точка стремится к точке , а длина отрезка CM стремится к радиусу кривизны траектории ρ . Поскольку и , то угол между отрезками и равен углу между векторами и . Отложим их для наглядности из одного центра.
Абсолютное значение производной:
.
Здесь мы учли, что .
Вектор , как указывалось выше, перпендикулярен . В данном случае он направлен вдоль единичного вектора главной нормали , направленной к центру кривизны C траектории. Поэтому при имеем:
.
Теперь рассмотрим случай, когда алгебраическое значение скорости отрицательно: . В этом случае, вектор скорости противоположен . Получается тот же рисунок, только точка располагается слева от M . В результате абсолютное значение производной остается прежней:
.
Но ее направление меняется на противоположное:
.
Поскольку , то формула сохраняет прежний вид и в этом случае:
.
Нормальное ускорение
Теперь находим нормальное ускорение:
.
Перепишем результат в следующем виде:
,
где ; – единичный вектор в направлении главной нормали траектории – то есть вектор, направленный к мгновенному центру кривизны перпендикулярно касательной к траектории. Поскольку , то также является модулем нормального ускорения. Для него не нужно вводить алгебраическое значение, как мы это делали для скорости и касательного ускорения.
Нормальное ускорение всегда направлено к центру кривизны траектории.
Из формулы (2) имеем:
(4) .
Из формулы (3) находим модуль нормального ускорения:
.
Умножим обе части уравнения (2) скалярно на :
(2) .
.
Поскольку , то . Тогда
;
.
Отсюда видно, что модуль нормального ускорения равен проекции полного ускорения на направление главной нормали.
Выпишем еще раз следующую формулу:
.
Отсюда видно, что нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.
Радиус кривизны траектории:
.
И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.
Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.
Автор: Олег Одинцов . Опубликовано: 09-02-2016 Изменено: 27-01-2020
http://doctorlom.com/item542.html
http://1cov-edu.ru/mehanika/kinematika/tochki/