Как найти наибольший радиус квадрата - Исправление недочетов и поиск решений вместе с Examum.ru

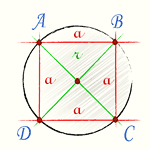
Окружность вписанная в квадрат

Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. У квадрата:

все углы прямые, то есть, равны 90°;
все стороны, как и углы, равны;
диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.

При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD, точку пресечения его диагоналей O. Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ, в котором стороны АО=ОВ, углы ОАВ=АВО=45°, а угол АОВ=90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ полученного равнобедренного треугольника АОВ.

Если предположить, что сторона квадрата равна у, то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:

r={y/2}

Объяснение: в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ. В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.

Для наглядности приведем численный пример нахождения величины радиуса вписанной окружности в квадрат со стороной равной 13 см. В данном случае значение вписанного радиуса будет равно:

Легко решить и обратную задачу. Предположим, что известен радиус вписанной окружности – 9 см, тогда анализируя пример нахождения величины радиуса вписанной окружности в квадрат, можно найти сторону квадрата: 9={y/2}
Находим из этого уравнения неизвестное значение: .

Окружность описанная около квадрата

Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае R описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):

Объяснение: после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA. Рассмотрим один из них. В треугольнике CAD:

угол CDA=90°;
стороны AD=CD. Признак равнобедренного треугольника;
угол DAC равен ACD. Они равны по 45°.

Чтобы найти в этом прямоугольном треугольнике гипотенузу АС, необходимо воспользоваться теоремой Пифагора:
, отсюда $AC=sqrt{ AD^2 + CD^2}$
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:
$AC={ sqrt{AD^2 + CD^2}/ 2}$
Поскольку AD=CD, а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:
$AC={sqrt{2AD^2}/2}={sqrt{2}/2}*AD$

Численный пример нахождения величины радиуса описанной окружности около квадрата будет таким.
Предположим, что диагональ квадрата равна 2/5 , тогда:

Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.

Рассмотрим пример

Задача

: радиус окружности вписанной в квадрат равен . Найти радиус окружности описанной около этого квадрата.

Дано

треугольник ОСЕ – равнобедренный и прямоугольный;
ОЕ=ЕС=;
ОЕС=90°;
ЕОС=ОСЕ=45°;

Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.
$OC={sqrt{2*OE^2} / 2}={ sqrt{2*(10 sqrt{2})^2} /2}=10$

Источник

Как найти радиус окружности

Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.

Выбирайте формулу в зависимости от известных величин.

Через площадь круга

Разделите площадь круга на число пи.
Найдите корень из результата.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
π (пи) — константа, равная 3,14.

Через длину окружности

Умножьте число пи на два.
Разделите длину окружности на результат.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
P — длина окружности (периметр круга).
π (пи) — константа, равная 3,14.

Через диаметр окружности

Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
D — диаметр.

Через диагональ вписанного прямоугольника

Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
a, b — стороны вписанного прямоугольника.

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

Иллюстрация: Лайфхакер

r — искомый радиус окружности.
a — сторона описанного квадрата.

Через стороны и площадь вписанного треугольника

Перемножьте три стороны треугольника.
Разделите результат на четыре площади треугольника.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
a, b, с — стороны вписанного треугольника.
S — площадь треугольника.

Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

Иллюстрация: Лайфхакер

r — искомый радиус окружности.
S — площадь треугольника.
p — полупериметр треугольника (равен половине от суммы всех сторон).

Через площадь сектора и его центральный угол

Умножьте площадь сектора на 360 градусов.
Разделите результат на произведение пи и центрального угла.
Найдите корень из полученного числа.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
S — площадь сектора круга.
α — центральный угол.
π (пи) — константа, равная 3,14.

Через сторону вписанного правильного многоугольника

Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Умножьте результат на два.
Разделите сторону многоугольника на результат всех предыдущих действий.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.

Читайте также 📐✂️📌

Как найти периметр прямоугольника
Как научить ребёнка считать играючи
Как перевести обычную дробь в десятичную
6 способов посчитать проценты от суммы с калькулятором и без
9 логических задач, которые по зубам только настоящим интеллектуалам

Источник

Как найти радиус описанной окружности квадрата?

Namalo
[29.9K]

5 лет назад

Формула радиуса описанной окружности около квадрата?

Ладлен
[266K]

5 лет назад

Эта задача не очень сложная.

Вот конкретный чертеж для данного вопроса.

В данном случае радиус окружности это половина диаметра и половина диагонали заданного квадрата. И получается, что искомый в нашем случае радиус равен.

автор вопроса выбрал этот ответ лучшим

комментировать

в избранное

ссылка

отблагодарить

Roman G
[171K]

5 лет назад

Если у квадрата есть описанная окружность, то диаметр этой окружности — это диагональ квадрата. Диагональ квадрата можно найти как большую сторону треугольника (половина квадрата) по теореме Пифагора: d=sqrt(a^2+a^2)=a*sqrt(2). Чтобы найти радиус окружности, нужно взять половину от диаметра: R=d/2. Совместив 2 указанные формулы, можно получить: R=a*sqrt(2)/2. Здесь a — сторона квадрата, d — диагональ квадрата или диаметр окружности; R — радиус окружности, sqrt — обозначение квадратного корня.

комментировать

в избранное

ссылка

отблагодарить

габбас
[215K]

5 лет назад

Эту формулу можно вывести из общей формулы для описанной окружности вокруг правильного п-угольника при п=4.

При подстановке в формулу для радиуса вписанной окружности получим r = R cos45, оттуда R = 2*r/(sqrt(2)), с учетом r=a/2 (а сторона квадрата), R=a/(sqrt(2)) = а*sqrt(2)/2 .

Можно вывести эту же формулу учитывая, что диагональ квадрата равна диаметру описанной окружности. Диагональ равна а*sqrt(2), радиус равен половине диаметра, то есть получим ту же формулу R= а*sqrt(2)/2 ..

комментировать

в избранное

ссылка

отблагодарить

bezdelnik
[34.1K]

5 лет назад

Радиус R описанной окружности квадрата равен половине диагонали этого квадрата. По теореме Пифагора квадрат диагональ d квадрата равен двум квадратам стороны y квадрата: d^2=2*y^2, d=√2*y, R=(√2)*y/2, то-есть R равен половине стороны квадрата умноженной на корень квадратный из двух или примерно о,7 от стороны квадрата. Например при y = 5 см радиус описанный окружности вокруг этого квадрата будет примерно равен 3,5 см.

комментировать

в избранное

ссылка

отблагодарить

Знаете ответ?

Смотрите также:

Как найти радиус окружности, описанной около прямоугольника (см.рисунок)?

Как найти радиус окружности, описывающей четыре квадрата (см)?

Математика. Как найти радиус окружности вписанной в квадрат со стороной 34?

Радиус окружности, описанной около квадрата, 28√2. Чему равна сторона?

Как найти радиус окружности, если её длина равна 36π?

Как найти радиус окружности, описанной около треугольника АВС (см.)?

Задача. Как определить радиус окружности, зная три размера?

Как изменится радиус окружности, если длину окружности увеличить на 9,42см?

Найдите радиус окружности, вписанной в… Как решить?

Как решить: Радиус окружности, вписанной в равносторонний треугольник, 8√3?

Источник

Квадрат — определение и свойства

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.

Перечислим свойства квадрата:

Все углы квадрата — прямые, все стороны квадрата — равны.

$angle A= angle B=angle C=angle D=90^{circ }.$
Диагонали квадрата равны и пересекаются под прямым углом.
Диагонали квадрата делятся точкой пересечения пополам.
Диагонали квадрата являются биссектрисами его углов (делят его углы пополам).
Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника:

Периметр квадрата P в 4 раза больше его стороны и равен: P=4a.

Площадь квадрата равна квадрату его стороны: S=a^2 .

Теорема 1. Диагональ квадрата равна произведению его стороны на sqrt{2} , то есть
.

Доказательство:

Рассмотрим квадрат ABCD. Проведем диагональ квадрата AC.

Треугольник АВС – прямоугольный с гипотенузой АС. Запишем для треугольника АВС теорему Пифагора:

$AC^{2}=AB^{2}+BC^{2};$

$AC^{2}=a^{2}+a^{2}=2a^{2}, AC=asqrt{2},$ что и требовалось доказать.

Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:

$displaystyle r=frac{1}{2}cdot a$

Доказательство:

Пусть окружность с центром в точке О и радиусом r вписана в квадрат АВСD и касается его сторон в точках
P, M, N, K.

Тогда поскольку AB параллельно CD. Через точку О можно провести только одну прямую, перпендикулярную АВ, поэтому точки Р, О и N лежат на одной прямой. Значит, PN – диаметр окружности. Поскольку АРND – прямоугольник, то PN = AD, то есть

, что и требовалось доказать.

Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:

$R=frac{sqrt{2}}{2}cdot a.$

Доказательство:

Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения пополам. Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой R = d/2 (d=AC=BD). Это и есть описанная около квадрата АВСD окружность.

По теореме

Тогда $R=afrac{sqrt{2}}{2}$ , что и требовалось доказать.

Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:

Четырехугольник является квадратом, если выполняется хотя бы одно из условий:

Все стороны равны и среди внутренних углов есть прямой угол.
Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Задача 1. Найдите сторону квадрата, диагональ которого равна sqrt{8} .

Решение:

Мы знаем, что . Тогда $a=genfrac{}{}{}{0}{displaystyle d}{displaystyle sqrt{2}}= 2$ .

Ответ: 2.

Задача 2. Найдите площадь квадрата, если его диагональ равна 1.

Первый способ решения:

Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:

$displaystyle d=sqrt{2}cdot a Rightarrow a=frac{d}{sqrt{2}}Rightarrow a=frac{1}{sqrt{2}}.$

Тогда по формуле площади квадрата:

$displaystyle S=a^{2}=left (frac{1}{sqrt{2}} right )^{2}=frac{1}{2}=0,5.$

Второй способ решения:

Воспользуемся формулой для площади ромба:

$displaystyle S=frac{1}{2}d_{1}d_{2}=frac{1}{2}d^{2}=0,5.$

Ответ: 0,5

Задача 3. Найдите радиус окружности, описанной около квадрата со стороной, равной sqrt{8} .

Решение:

Радиус описанной окружности равен половине диагонали квадрата, поэтому

$displaystyle R=frac{d}{2}=afrac{sqrt{2}}{2}=sqrt{8}cdot frac{sqrt{2}}{2}=2.$

Ответ: 2.

Задача 4. Найдите сторону квадрата, описанного около окружности радиуса .

Решение:

Диаметр окружности равен стороне квадрата: a=2r=8 .

Ответ: 8.

Задача 5. Радиус вписанной в квадрат окружности равен . Найдите диагональ этого квадрата.

Решение:

Сторона квадрата в два раза больше радиуса вписанной окружности:

Диагональ найдем, зная сторону квадрата:

Ответ: 56.

Задача 6. Радиус вписанной в квадрат окружности равен . Найдите радиус окружности, описанной около этого квадрата.

Решение:

Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:

$displaystyle r=frac{a}{2}; R=frac{d}{2}; d=asqrt{2}.$

Поэтому

Ответ: 22.

Задача 7. Найдите периметр квадрата, если его площадь равна 9.

Решение:

Найдем сторону квадрата:

Периметр квадрата со стороной 3 равен:

Ответ: 12.

Задача 8. Найдите площадь квадрата, в который вписан круг площадью 4pi .

Решение:

Площадь круга $S_{kp}=pi r^{2}=4pi ,$ откуда радиус круга равен 2.

Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.

Ответ: 16.

Задача 9. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными sqrt{2} .

Решение:

Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки. Поскольку длина одной клеточки равна sqrt{2} ., то сторона малого квадрата равна . А сторона квадрата ABCD равна

Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.

Ответ: 2.

Задача 10. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите .

Решение:

Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, AB.

Она равна . Тогда радиус вписанной окружности равен $genfrac{}{}{}{0}{displaystyle sqrt{10}}{displaystyle 2}$ . В ответ запишем .

Ответ: 5.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Квадратu0026nbsp;u0026mdash; определение иu0026nbsp;свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Радиус описанной окружности квадрата, формула

Формула радиуса описанной окружности квадрата выходит из теоремы Пифагора поскольку диагональ квадрата является диаметром описанной окружности.

[R=frac{sqrt{a^2+a^2}}{2}=frac{a}{sqrt{2}}]

(a — сторона квадрата; R — радиус описанной окружности квадрата)

Вычислить, найти радиус описанной окружности квадрата по формуле (1)

a (сторона квадрата)

Вычислить

нажмите кнопку для расчета

Радиус описанной окружности квадрата	стр. 248

Источник