Опираясь на предложенные к заданию объяснения, нам необходимо определить, каков будет радиус карусели.
Однако перед этим разберемся, где на участке расположена сама карусель. Узнать это можно, исходя из пояснений к заданию.
Отсюда следует, что карусель обозначена на плане цифрой 6.
Подсчитаем клеточки, их 3х4.
Также нам известно, что большая клетка имеет сторону — 2 м.
- Далее рассуждаем следующим образом:
- Чтобы получить наибольший радиус карусели, она должна касаться тех сторон, которые больше по размеру — 4 клеточки. Это значит, что радиус карусели должен быть равен половине меньшей стороны данного четырехугольника — 3 клеточки.
Вычисляем 3 кл. * 2м = 6 м — меньшая сторона.
Отсюда радиус:
- 6:2=3 — см.
- Ответ: 3.
Версия для печати и копирования в MS Word
Найдите наибольший возможный радиус карусели (в метрах).
На плане (см. рис.) представлен дизайн‐проект сквера в станице Лужки. Сторона большой клетки равна 2 метра. Участок, отведённый под сквер, имеет квадратную форму. По периметру участка планируется установить забор. С двух сторон сквера будут два входа.
Если зайти в сквер, то справа от входа № 1 будет располагаться карусель, а слева — детский игровой комплекс, отмеченный на плане цифрой 5.
Дом творчества будет находиться слева, если зайти через вход № 2, а зооуголок — справа.
Центр сквера, отмеченный цифрой 4, планируется украсить фонтаном диаметром 2 метра и двумя цветочными клумбами. Рядом с детским игровым комплексом построят кафе, рядом с каруселью — кинотеатр площадью 64 м2.
За кинотеатром будет оборудована тренажёрная площадка, отмеченная цифрой 8.
На территории сквера дорожки шириной 2 м будут выложены тротуарной плиткой размером 1 м × 1 м. Аллея шириной 4 м располагается от входа № 1 до Дома творчества и будет выложена той же плиткой, что и дорожки.
Спрятать решение
Решение.
Сторона одной клетки равна 2 м. Чтобы радиус был наибольшим, карусель должна касаться больших сторон прямоугольника, отмеченного на плане цифрой 6, то есть радиус карусели должен быть равен половине меньшей стороны этого прямоугольника. Значит, поскольку меньшие стороны этого прямоугольника равны 6 м, наибольший возможный радиус карусели равен 3 м.
Ответ: 3.
Источник: Тренировочный вариант № 229, Александр Ларин
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Дом творчества | Кинотеатр | Кафе | Зооуголок |
|---|---|---|---|---|
| Цифры |
Источник: Тренировочный вариант № 229, Александр Ларин
2
Тротуарная плитка продаётся в упаковках по 3 штуки. Сколько упаковок понадобится купить, чтобы выложить аллею от входа № 1 до Дома творчества?
Источник: Тренировочный вариант № 229, Александр Ларин
3
Найдите площадь (в м2) земли, которую занимает Дом творчества.
Источник: Тренировочный вариант № 229, Александр Ларин
4
По периметру участка планируется установить забор. С двух сторон сквера будут два входа. При обсуждении, каким должен быть забор, рассматривалось два варианта: кованый или комбинированный. Цены на доставку оборудования и на установочные работы, а также стоимость изготовления одного погонного метра забора представлены в таблице. На сколько рублей общая стоимость кованного забора меньше общей стоимости комбинированного забора?
| Вариант забора | Стоимость доставки (руб.) |
Стоимость установки (руб.) |
Стоимость изготовления 1 погонного метра забора (руб.) |
|---|---|---|---|
| Кованый | 3500 | 5130 | 1000 |
| Комбинированный | 3000 | 5300 | 1300 |
Примечание. При входах забор не устанавливается.
Источник: Тренировочный вариант № 229, Александр Ларин
Найдите наибольший возможный радиус карусели (в метрах).
На плане (см. рисунок) представлен дизайн‐проект сквера в станице Лужки. Сторона большой клетки равна 2 метра. Участок, отведённый под сквер, имеет квадратную форму. По периметру участка планируется установить забор. С двух сторон сквера будут два входа.
Если зайти в сквер, то справа от входа № 1 будет располагаться карусель, а слева — детский игровой комплекс, отмеченный на плане цифрой 5.
Дом творчества будет находиться слева, если зайти через вход № 2, а зооуголок — справа.
Центр сквера, отмеченный цифрой 4, планируется украсить фонтаном диаметром 2 метра и двумя цветочными клумбами. Рядом с детским игровым комплексом построят кафе, рядом с каруселью — кинотеатр площадью 64 м2.
За кинотеатром будет оборудована тренажёрная площадка, отмеченная цифрой 8.
На территории сквера дорожки шириной 2 м будут выложены тротуарной плиткой размером 1 м × 1 м. Аллея шириной 4 м располагается от входа № 1 до Дома творчества и будет выложена той же плиткой, что и дорожки.
Решение.
Сторона одной клетки равна 2 м. Чтобы радиус был наибольшим, карусель должна касаться больших сторон прямоугольника, отмеченного на плане цифрой 6. Значит, поскольку меньшие стороны этого прямоугольника равны 6 м, наибольший возможный радиус карусели равен 3 м.
Ответ: 3.
Как найти радиус окружности
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Выбирайте формулу в зависимости от известных величин.
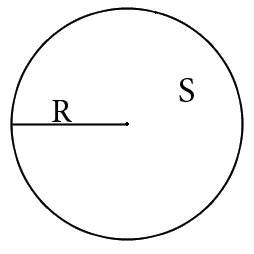
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
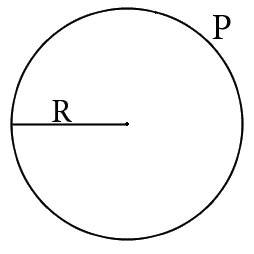
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
При помощи нашего калькулятора вы легко сможете узнать радиус круга или окружности.
Для того что бы вычислить радиус круга необходимо знать его длину или площадь. Если нам известа одна из указаннх величин, для нас не составит труда вычислить радиус круга.
Радиус круга рассчитывается по следующим формулам:
- Если нам известна длина:
Формула для расчета радиуса круга через его длину:
R=P/(2π) - Если нам известна площадь:
Формула для расчета радиус круга через площадь:
R=√
S/π
- Если нам известен диаметр:
Формула для расчета радиус круга через диаметр:
R=D/2
Где R — радиус круга, S – площадь круга, P – длина круга, D — диаметр, π – число Пи которое всегда примерно равно 3,14.