Дата: 2015-07-28
2632
Категория: Производная
Метка: ЕГЭ-№7
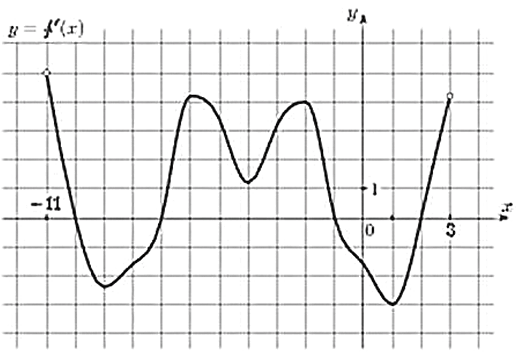
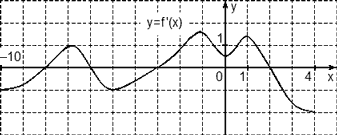
27499. На рисунке изображен график у=f′(x) — производной функции f(x), определенной на интервале (–11;3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Промежутки возрастания функции f(x) соответствуют промежуткам, на которых производная функции положительна. В данной задаче это интервалы (–11;–10), (–7;–1), (2;3).
Наибольшим из них является интервал (–7;–1) его длина равна 6.
Ответ: 6
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
Интервалы возрастания и убывания функции
С помощью данного сервиса можно найти интервалы возрастания и убывания функции в онлайн режиме с оформлением решения в Word.
- Решение онлайн
- Видеоинструкция
Исследование функции с помощью производной
Определение: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)>f(x).
Определение: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)<f(x).
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная f′(x) обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции y=f(x) с помощью первой производной
- Найти производную функции f′(x).
- Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
- Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
- Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
- Вычислить значения функции в точках минимума и максимума.
С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
Пример №1: Найти промежутки монотонности и экстремумы функции: f(x)=x3–3x2.
Решение: Найдем первую производную функции f′(x)=3x2–6x.
Найдем критические точки по первой производной, решив уравнение 3x2–6x=0; 3x(x-2)=0 ;x = 0, x = 2
Исследуем поведение первой производной в критических точках и на промежутках между ними.
| x | (-∞, 0) | 0 | (0, 2) | 2 | (2, +∞) |
| f′(x) | + | 0 | — | 0 | + |
| f(x) | возрастает | max | убывает | min | возрастает |
f(0) = 03 – 3*02 = 0
f(2) = 23 – 3*22 = -4
Ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2);
точка минимума функции (2;-4); точка максимума функции (0;0).
Правило нахождения экстремумов функции y=f(x) с помощью второй производной
- Найти производную f′(x).
- Найти стационарные точки данной функции, т.е. точки, в которых f′(x)=0.
- Найти вторую производную f″(x).
- Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
- Вычислить значения функции в точках экстремума.
Отсюда следует, что дважды дифференцируемая функция f(x) выпукла на отрезке [a, b], если вторая производная f»(x) ≥ 0 при всех х [a, b].
Все вычисления можно проделать в онлайн режиме.
Пример №2. Исследовать на экстремум с помощью второй производной функцию: f(x) = x2 – 2x — 3.
Решение: Находим производную: f′(x) = 2x — 2.
Решая уравнение f′(x) = 0, получим стационарную точку х=1. Найдем теперь вторую производную: f″(x) = 2.
Так как вторая производная в стационарной точке положительна, f″(1) = 2 > 0, то при x = 1 функция имеет минимум: fmin = f(1) = -4.
Ответ: Точка минимума имеет координаты (1; -4).
Версия для печати и копирования в MS Word
1
2
3
На рисунке изображен график производной функции f(x), определенной на интервале (−8; 6). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
4
На рисунке изображён график y = f ’(x) — производной функции f(x), определённой на интервале (−3; 11). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
5
На рисунке изображён график y = f '(x) — производной функции f (x), определённой на интервале (−5; 10). Найдите промежутки возрастания функции f (x). В ответе укажите длину наибольшего из них.
6
На рисунке изображён график функции — производной функции f(x), определённой на интервале (−3; 14). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
7
На рисунке изображён график функции — производной функции f(x), определённой на интервале (−10; 5). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
8
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
9
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
10
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
11
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
12
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
13
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
14
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
15
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
16
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
17
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
18
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
19
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
20
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
21
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
22
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
23
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
24
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
25
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
26
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
27
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
28
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
29
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
30
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
31
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
32
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
33
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
34
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
35
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
36
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
37
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
38
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
39
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
40
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
41
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
42
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
43
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
44
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
45
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
46
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
47
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
48
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
49
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
50
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
51
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
52
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
53
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
54
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
55
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
56
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
57
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
58
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
59
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
60
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
61
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
62
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
63
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
64
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
65
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
66
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
67
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
68
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
69
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
70
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите длину наибольшего из них.
Рассмотрим задания, в которых по данному графику производной функции y=f'(x)нужно найти промежутки возрастания функции y=f(x).
№1
На рисунке изображён график производной функции f(x), определённой на интервале (-12;9). Найти промежутки возрастания функции f(x). В ответе указать длину наибольшего из них.
Решение:
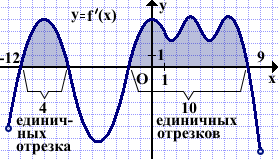
Выделяем промежутки, на которых производная принимает положительные значения (то есть график производной расположен выше оси Ox).
В данном примере таких промежутков два: (-11;-7) и (-2;8). Так как в точках -11, -7, -2 и 8 существует производная f'(x), то функция f(x) непрерывна в этих точках. Поэтому эти точки можно включить в промежутки возрастания и убывания функции. Таким образом, функция f(x) возрастает на промежутках [-11;-7] и [-2;8]. Они имеют длину 4 и 10 единичных отрезков.
Ответ: 10.
№2
Функция f(x) определена на интервале (-10;2). На рисунке изображён график её производной. Найти промежутки возрастания функции f(x). В ответ указать сумму целых точек, входящих в эти промежутки.
Решение:
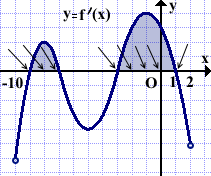
Выделяем промежутки, на которых производная принимает положительные значения. В данном примере таких промежутков два: (-9;-7) и (-3;1). Поскольку в точках -9, -7, -3 и 1 существует производная f'(x), то функция f(x) непрерывна в этих точках, а значит, эти точки можно включить в промежутки возрастания функции f(x).
Итак, функция y=f(x) возрастает на промежутках [-9;-7] и [-2;1].
Ищем сумму целых точек, входящих в эти промежутки:
-9+(-8)+(-7)+(-3)+(-2)+(-1)+0+1=-29.
Ответ: -29.
№3
Функция определена и непрерывна на полуинтервале [-4;6). На рисунке изображён график её производной. Найти промежутки возрастания функции f(x). В ответе указать сумму целых точек, входящих в эти промежутки.
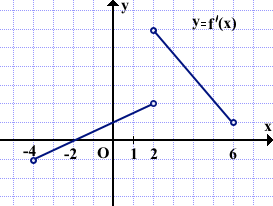
На промежутках возрастания функции y=f(x) её производная f'(x) положительна.
В данном примере производная принимает положительные значения на промежутках (-2;2) и (2;6).
По условию, функция непрерывна на полуинтервале [-4;6). Значит точки -2 и 2, входящие в этот полуинтервал, можно включить в промежутки возрастания. Следовательно, функция y=f(x) возрастает на полуинтервале [-2;6). Ищем сумму целых точек, входящих в промежуток [-2;6):
(-2)+(-1)+0+1+2+3+4+5=12.
Ответ: 12.
15 марта 2011
В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
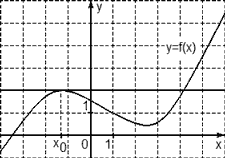
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
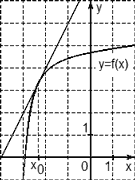
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
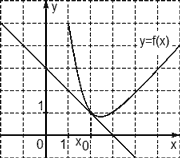
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).
- Точка x0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
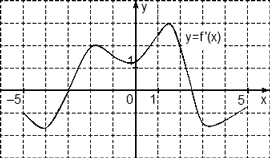
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
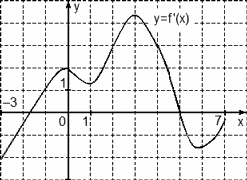
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
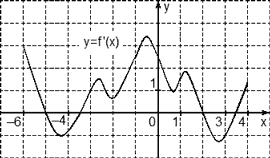
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
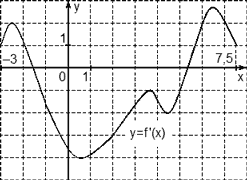
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
Смотрите также:
- ЕГЭ 2022, задание 6. Касательная к графику функции
- ЕГЭ 2022, задание 6. Касательная к графику функции
- Схема Бернулли. Примеры решения задач
- Решение задач B6: №362—377
- Четырехугольная пирамида: как найти координаты вершин
- Нестандартная задача B2: студенты, гонорары и налоги