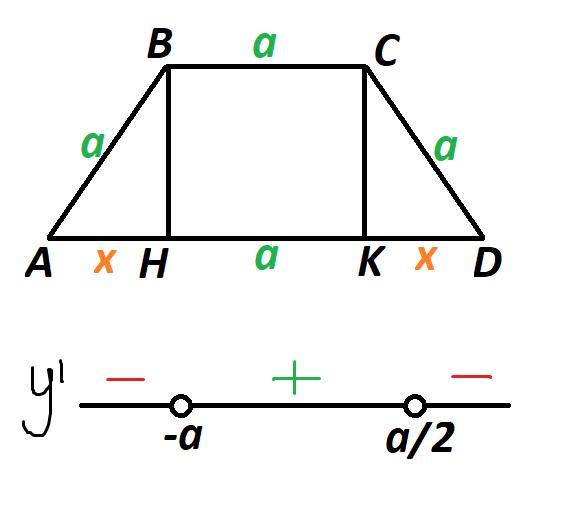
Как найти наибольшую площадь трапеции - Исправление недочетов и поиск решений вместе с Examum.ru

Рассмотрим трапецию ABCD.

Основания трапеции не могут иметь одинаковую длину, так как в противном случае это будет параллелограмм. Значит, одно из оснований BC и две боковые стороны AB и CD равны по а. Заметим, что рассматриваемая трапеция равнобедренная.

Проведем высоты BH и CK. Тогда, HK=а.

Обозначим AH=KD=х.

Высоту трапеции найдем по теореме Пифагора:

$BH=sqrt{a^2-x^2}$

Запишем выражение для площади трапеции:

$S=dfrac{BC+AD}{2}cdot BH$

$S=dfrac{BC+(AH+HK+KD)}{2}cdot BH$

$S=dfrac{a+(x+a+x)}{2}cdot sqrt{a^2-x^2}$

$S=dfrac{2a+2x}{2}cdot sqrt{a^2-x^2}$

$S= (a+x)cdotsqrt{a^2-x^2}$

Исследуем на экстремумы функцию S. Найдем производную:

$S'= (a+x)'cdotsqrt{a^2-x^2}+(a+x)cdot(sqrt{a^2-x^2})'$

$S'=1cdotsqrt{a^2-x^2}+(a+x)cdotdfrac{1}{2sqrt{a^2-x^2}} cdot(a^2-x^2)'$

$S'=sqrt{a^2-x^2}+(a+x)cdotdfrac{-2x}{2sqrt{a^2-x^2}}$

$S'=dfrac{2(a^2-x^2)-2x(a+x)}{2sqrt{a^2-x^2}}$

$S'=dfrac{2a^2-2x^2-2ax-2x^2}{2sqrt{a^2-x^2}}$

$S'=dfrac{-4x^2-2ax+2a^2}{2sqrt{a^2-x^2}}$

Найдем нули производной:

$dfrac{-4x^2-2ax+2a^2}{2sqrt{a^2-x^2}}=0$

$x=dfrac{-a-3a}{2cdot2}=-a$

$x=dfrac{-a+3a}{2cdot2}=dfrac{a}{2}$

При переходе через точку x=-a производная меняет знак с минуса на плюс, значит это точка минимума.

При переходе через точку $x=dfrac{a}{2}$ производная меняет знак с плюса на минус, значит это точка максимума.

Таким образом, наибольшую площадь трапеция имеет при $x=dfrac{a}{2}$ . Эта площадь равна:

$Sleft(dfrac{a}{2}right)= left(a+dfrac{a}{2}right)cdotsqrt{a^2-left(dfrac{a}{2}right)^2}= dfrac{3a}{2}cdotsqrt{a^2-dfrac{a^2}{4}}=dfrac{3a}{2}cdotsqrt{dfrac{3a^2}{4}}=dfrac{3sqrt{3} }{4}a^2$

Ответ: $dfrac{3sqrt{3} }{4}a^2$

Приложения:

Источник

$$S(x)=frac{-20cosx+20}{2}cdot10sinx=100(1-cosx)sinx,xin(pi/2;pi),$$ где $%x$% — угол между боковым ребром и равным ему основанием. Далее $$S^{‘}(x)=100(1-cosx)sinx)^{‘}=100(sin^2x-cos^2x+sinx)=100(2sin^2x+sinx-1);$$
$$S^{‘}(x)=0Leftrightarrow2sin^2x+sinx-1=0Rightarrow sinx=frac{1}{2}; x=frac{5}{6}pi=150^o.$$$$S(pi/2)=100;S(pi)=0;S(frac{5}{6}pi)=5(sqrt{3}+1)10-$$наибольшее значение.

Ответ. при угле между боковым ребром и равным ему основанием $%150^o, S=5(sqrt{3}+1)10.$%

Источник

2 ответа:

0

0

Трапеция равнобокая .

Пусть углы А и D как на рисунке х.

Тогда высота трапеции 8*sin(x)

А площадь

S = 8* 8 * sin(x) + 2 * 8* cos(x) * 8 * sin (x) / 2 = 64 * ( sin(x) + sin(2x)/2 )

S’ = 64 * ( cos(x)+cos(2x))= 64 * (2cos^2(x)+cos(x)-1)

S’=0

2соs^2(x)+cos(x)-1=0

cos(x)= -1 — это минимум

cos(x)=1/2 — это максимум

Синус х при этом равен √3/2

Синус 2x при этом x тоже √3/2

S max = 64 ( √3/2+ √3/4)= 48 √3 см^2

0

0

Основание AD не может быть равен 8, так что AB=BC=CD=8 см.

Обозначим AD=x, тогда $AE=FD=dfrac{AD-BC}{2}=dfrac{x-8}{2}$

Из прямоугольного треугольника CFD, по теореме Пифагора:

$CF=sqrt{64-dfrac{(x-8)^2}{4}}=dfrac{1}{2}sqrt{192+16x-x^2}$

Рассмотрим функцию: $S(x)=dfrac{x+8}{2}cdotdfrac{1}{2}sqrt{192+16x-x^2}=dfrac{x+8}{4}sqrt{192+16x-x^2}$

Производная функции:

$S'(x)=dfrac{1}{4}sqrt{192+16x-x^2}+dfrac{x+8}{4}cdotdfrac{(16-2x)}{2sqrt{192+16x-x^2}}=\ \ =dfrac{192+16x-x^2+64-x^2}{4sqrt{192+16x-x^2}}=dfrac{256+16x-2x^2}{4sqrt{192+16x-x^2}}=0~~Leftrightarrow~~ x=16$

(0)___+___(16)__-___(24)

Производная функции в точке х=16 меняет знак с (+) на (-), следовательно, х=16 — точка максимума.

$S(16)=dfrac{16+8}{4}sqrt{192+16cdot16-16^2}=6sqrt{192}=48sqrt{3}$ см²

Ответ: 48√3 см²

Читайте также

…………………….

2) диагонали ромба точкой пересечения делятся пополам)

Образуются равные треугольники ( равные по первому признаку) треугольник PEM = ТРЕУГ. MDE ( вертикальные углы емр = dmf и равные стороны, так как м середина отрезков) отсюда прямые ре параллельно дф так как соответственные углы равны например секущей еф они являются накрест лежащими отсюда прямые параллельны.
2. рисунок сам(а) сделаешь.
так как угол сде = 68 градусам, а дм биссектриса , то углы сдм=мдн = 34 градусам. так как сд параллельна мн, то углы сдм=дмн = 34 ( как накрест лежащие), а сумма всех углов треугольника равна 180 градусам, значит угол днм = 180 — 34-34 = 112 градусам
ответ 34, 34 112 градусам

Надо использовать свойство:

В параллельных плоскостях линии сечения параллельны.

Для примера приведен один из вариантов.

Остальные есть попроще, в других находить линии пересечения по аналогии с приведенным примером.

Вот так будет это геометрия

Источник

Трапеция равнобокая .

Пусть углы А и D как на рисунке х.

Тогда высота трапеции 8*sin(x)

А площадь

S = 8* 8 * sin(x) + 2 * 8* cos(x) * 8 * sin (x) / 2 = 64 * ( sin(x) + sin(2x)/2 )

S’ = 64 * ( cos(x)+cos(2x))= 64 * (2cos^2(x)+cos(x)-1)

S’=0

2соs^2(x)+cos(x)-1=0

cos(x)= -1 — это минимум

cos(x)=1/2 — это максимум

Синус х при этом равен √3/2

Синус 2x при этом x тоже √3/2

S max = 64 ( √3/2+ √3/4)= 48 √3 см^2

Источник

Сообщения без ответов | Активные темы

Как найти наибольшую площадь трапеции, вписанной в полукруг

Модераторы: Prokop, mad_math

Автор

Сообщение

BarteZzZ

Заголовок сообщения: Как найти наибольшую площадь трапеции, вписанной в полукруг

Добавлено: 11 янв 2012, 22:56

Начинающий

Зарегистрирован:
11 янв 2012, 22:10
Сообщений: 12
Cпасибо сказано: 4
Спасибо получено:
0 раз в 0 сообщении
Очков репутации: 1

Здравствуйте, помогите разобраться вот с такой задачей.

Как найти наибольшую площадь трапеции, вписанной в полукруг так радиуса r так, что нижнее основание трапеции совпадает с диаметром полукруга.

Заранее благодарен.

Вернуться к началу

BarteZzZ

Заголовок сообщения: Re: Вычислить площадь

Добавлено: 12 янв 2012, 21:17

не получается выразить меньшее основание. (оно случаем не будет равно r ?)
т.е площадь выразить через r и h?

Вернуться к началу

BarteZzZ	Заголовок сообщения: Re: Вычислить площадь Добавлено: 12 янв 2012, 23:12
	Shaman писал(а): Ещё раз: сделайте чертёж. Меньшее основание зависит от r и h. Чем больше h, тем меньше основание. Это несложно, по формуле Пифагора. Да, площадь трапеции выразить через r и h. Голова чет не варит совсем( с геометрией напряг. никак это основание не идет(
Вернуться к началу

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Максимальная площадь вписанной трапеции в форуме Геометрия	KOPMOPAH	20	540	20 мар 2020, 17:02
Найти площадь трапеции в форуме Геометрия	oduv	3	1172	18 янв 2014, 18:13
Найти площадь трапеции в форуме Геометрия	ceos	6	643	25 май 2014, 21:27
Планиметрия. Найти площадь трапеции в форуме Геометрия	Flutt1	12	620	27 сен 2017, 21:00
Найти площадь криволинейной трапеции в форуме Интегральное исчисление	Mr_Math_Men	1	222	05 июн 2014, 16:48
Найти периметр и площадь трапеции в форуме Геометрия	Alina321	3	817	11 дек 2013, 13:49
Найти сторону трапеции и площадь четырехугольника в форуме Геометрия	Gudleifr	1	285	30 окт 2016, 16:14
В четырёхугольник вписан полукруг. Найти длину стороны в форуме Геометрия	Wild_man	11	1366	24 май 2021, 00:04
Площадь трапеции в форуме Геометрия	Lord_Adwond	41	1155	01 июл 2017, 20:57
Площадь трапеции в форуме Геометрия	A_5	22	1283	16 июн 2017, 22:39

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group

Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru

Русская поддержка phpBB

Источник