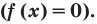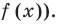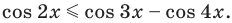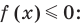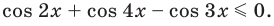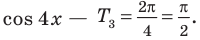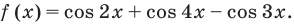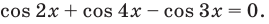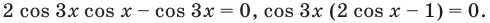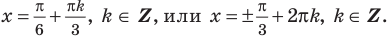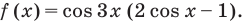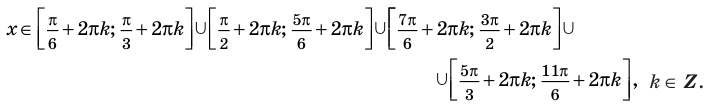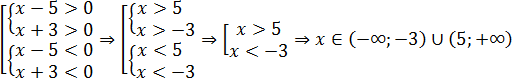Наименьшее решение неравенства
Задания, в которых требуется найти наименьшее решение неравенства, а также наименьшее целое или наименьшее натуральное решение неравенства, в курсе алгебры впервые встречаются при изучении темы «Линейные неравенства». Рассмотрим на примерах решение такого рода задач.
1) Найти наименьшее решение неравенства
Умножим обе части неравенства на наименьший общий знаменатель дробей, равный 12:
При умножении на положительное число знак неравенства не изменяется:
Раскрываем скобки:
Упрощаем:
Неизвестные — в одну сторону, известные — в другую с противоположным знаком:
Обе части неравенства делим на число, стоящее перед иксом:
При делении на положительное число знак неравенства не изменяется:
Наименьшее значение неравенства равно -3,4 (неравенство нестрогое, поэтому -3,4 входит в множество решений). Для большей наглядности решение неравенства можно изобразить на числовой прямой:
Ответ: -3,4.
2) Назвать наименьшее решение неравенства:
Первые скобки раскроем по формуле квадрата суммы. Перед произведением двух скобок стоит знак «минус», поэтому, чтобы не допустить ошибки в знаках, лучше сначала выполнить умножение, а уже потом раскрыть скобки, изменив знак каждого слагаемого на противоположный:
Неизвестные — в одну сторону, известные — в другую с противоположным знаком:
Обе части неравенства делим на число, стоящее перед иксом
При делении на положительное число знак неравенства не изменяется:
Решением данного неравенства является любое число, большее 3:
Но наименьшего решения неравенство не имеет — 3 не входит в решение, так как неравенство строгое, а любое другое число, большее 3, наименьшим решением не является.
Ответ: неравенство наименьшего решения не имеет.
3) Найти наименьшее целое решение неравенства:
Обе части неравенства умножаем на наименьший общий знаменатель 30:
Раскрываем скобки и упрощаем:
Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом. Так как 21 — положительное число, знак неравенства не изменяется:
Наименьшим целым решением данного неравенства является x=2 (так как неравенство нестрогое, 2 входит в множество решений).
Ответ: 2.
4) Найти наименьшее натуральное решение неравенства:
Упрощаем:
Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом:
При делении на отрицательное число знак неравенства изменяется на противоположный:
Наименьшим натуральным решением этого неравенства является x=1.
Ответ: 1.
При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
Напомним свойства числовых неравенств.
1. Если а > b , то b < а; наоборот, если а < b, то b > а.
2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину.
4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.
Замечание.
Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое.
6. Если а > b и m – положительное число, то m а > m b и 
Если же а > b и n – отрицательное число, то n а < n b и 
7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.
8. Если а > b, где а, b > 0, то 

Виды неравенств и способы их решения
1. Линейные неравенства и системы неравенств
Пример 1. Решить неравенство 
Решение:

Ответ: х < – 2.
Пример 2. Решить систему неравенств 
Решение:

Ответ: (– 2; 0].
Пример 3. Найти наименьшее целое решение системы неравенств
Решение:
Ответ:
2. Квадратные неравенства
Пример 4. Решить неравенство х2 > 4.
Решение:
х2 > 4 (х – 2)∙(х + 2) > 0.
Решаем методом интервалов.
Ответ:
3. Неравенства высших степеней
Пример 5. Решить неравенство (х + 3)∙(х2 – 2х + 1) > 0.
Решение:

Ответ: 
Пример 6. Найти середину отрезка, который является решением неравенства 4х2 – 24х + 24 < 4у2, где 
Решение:
Область определения неравенства: 
С учётом области определения 4х2 – 24х + 24 < 4у2 будет равносильно неравенству
Решаем методом интервалов.
Решение неравенства: 
Середина отрезка: 
Ответ: 
4. Рациональные неравенства
Пример 7. Найти все целые решения, удовлетворяющие неравенству 
Решение:

Методом интервалов:
Решение неравенства: 
Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
Ответ: – 6; – 5; – 4; 1.
5. Иррациональные неравенства
Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 8. Решить неравенство 
Решение:
Область определения: 
Так как арифметический корень не может быть отрицательным числом, то 
Ответ: 
Пример 9. Найти все целые решения неравенства 
Решение:
Область определения 



Целыми числами из этого отрезка будут 2; 3; 4.
Ответ: 2; 3; 4.
Пример 10. Решить неравенство 
Решение:
Область определения: 
Преобразуем неравенство: 


Ответ: 
Пример 11. Решить неравенство 
Решение:
Раскрываем знак модуля.
Объединим решения систем 1) и 2): 
Ответ: 
6. Показательные, логарифмические неравенства и системы неравенств
Пример 12. Решите неравенство 
Решение:

Ответ: 
Пример 13. Решите неравенство 
Решение:

Ответ: 
Пример 14. Решите неравенство 
Решение:
Ответ: 
Пример 15. Решите неравенство 
Решение:
Ответ: 
Задания для самостоятельного решения
Базовый уровень
Целые неравенства и системы неравенств
1) Решите неравенство 2х – 5 ≤ 3 + х.
2) Решите неравенство – 5х > 0,25.
3) Решите неравенство 
4) Решите неравенство 2 – 5х ≥ – 3х.
5) Решите неравенство х + 2 < 5x – 2(x – 3).
6) Решите неравенство
.
7) Решите неравенство (х – 3) (х + 2) > 0.


9) Найдите целочисленные решения системы неравенств 
10) Решить систему неравенств 
11) Решить систему неравенств 
12) Найти наименьшее целое решение неравенства 
13) Решите неравенство 
14) Решите неравенство 
15) Решите неравенство 
16) Решите неравенство 
17) Найдите решение неравенства 

18) Решить систему неравенств 
19) Найти все целые решения системы 
Рациональные неравенства и системы неравенств
20) Решите неравенство 
21) Решите неравенство 
22) Определите число целых решений неравенства 
23) Определите число целых решений неравенства 
24) Решите неравенство 
25) Решите неравенство 2x<16 .
26) Решите неравенство 
27) Решите неравенство 
28) Решите неравенство 
29) Найдите сумму целых решений неравенства 
30) Решите неравенство 
31) Решите неравенство 
Иррациональные неравенства
32) Решите неравенство 
33) Решите неравенство
34) Решите неравенство 
Показательные, логарифмические неравенства и системы неравенств
35) Решите неравенство 
36) Решите неравенство 
37) Решите неравенство 
38) Решите неравенство 
39) Решите неравенство 
40) Решите неравенство 49∙7х < 73х + 3.
41) Найдите все целые решения неравенства 
42) Решите неравенство 
43) Решите неравенство 
44) Решите неравенство 7x+1-7x<42 .
45) Решите неравенство log3(2x2+x-1)>log32 .
46) Решите неравенство log0,5(2x+3)>0 .
47) Решите неравенство 
48) Решите неравенство 
49) Решите неравенство 
50) Решите неравенство logx+112>logx+12 .
51) Решите неравенство logx9<2.
52) Решите неравенство 
Повышенный уровень
53) Решите неравенство |x-3|>2x.
54) Решите неравенство 2│х + 1| > х + 4.
55) Найдите наибольшее целое решение неравенства 
56) Решить систему неравенств 
57) Решить систему неравенств 
58) Решите неравенство 
59) Решите неравенство 25•2x-10x+5x>25 .
60) Решите неравенство 
Ответы
1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) 





20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26)
; 29) – 10; 30) (0; + ∞); 31)









.
Содержание:
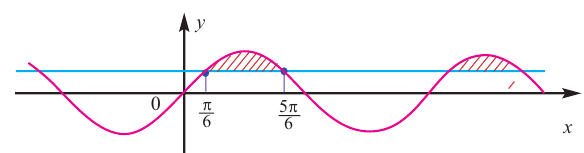
Для решение простейших тригонометрических неравенств можно использовать как единичную окружность, так и графики тригонометрических функций.
Пример 1.
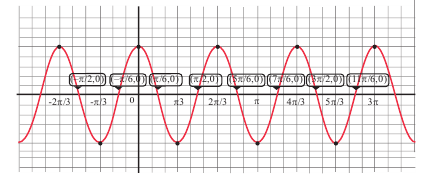
Решим неравенство
Решение:
Запишем решение в общем виде.
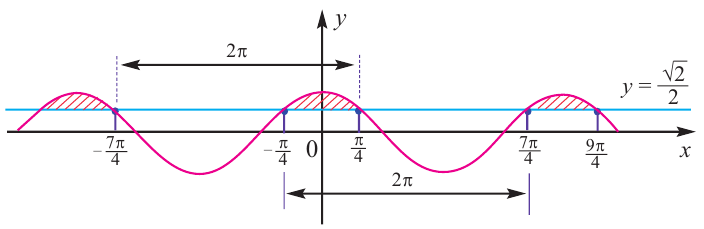
Решить данное неравенство значит, найти абсциссы множества точек графика функции 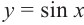
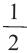
1.Построим график функции 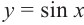
2.В одной системе координат построим график функции 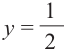
3.Отметим точки пересечения графиков.
4. Как видно, прямая 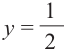
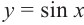
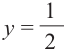
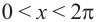
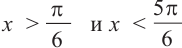
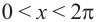
Также решения тригонометрических неравенств можно ясно увидеть на единичной окружности. Все остальные интервалы, удовлетворяющие решению неравенства получаются смещением интервала 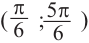
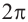
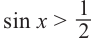
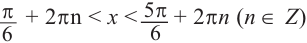
Пример 2.
Решим неравенство
Решение:
Решения уравнения 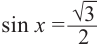
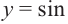
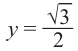
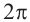
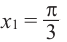
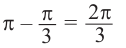
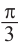
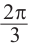
От каждой из них, по обе стороны, отметим ещё две точки — вправо от
точки 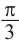
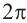
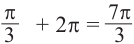
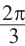
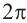
Они также являются абсциссами точек пересечения графиков.
На промежутке (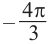
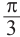
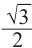
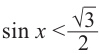
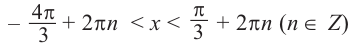
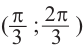
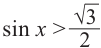
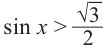
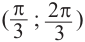
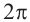
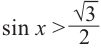
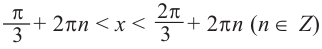
Пример 3.
Решим неравенство
Решение:
Найдём абсциссы точек пересечения графиков функций
и 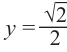
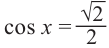
Получим: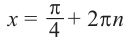
При 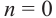
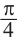
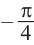
Отметим от точки 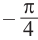
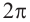
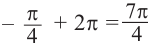
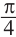
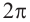
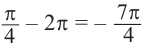
Один из промежутков, удовлетворяющих неравенству, расположен между наименьших но абсолютному значению корней соответствующего уравнения, т.е. между точками 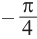
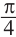
Приняв во внимание периодичность 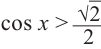
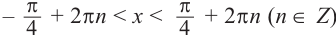
По графику решение неравенства 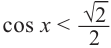
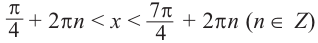
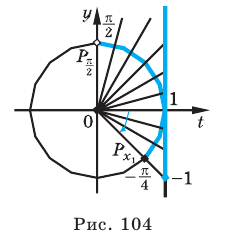
Пример 4.
Решим неравенства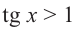
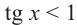
Решение:
В одной системе координат построим графики функций 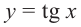
Найдём абсциссу точки пересечения , расположенной в интервале 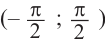
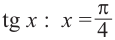
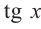
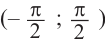
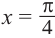
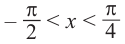
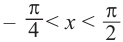
Так как функция 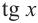
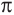
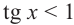
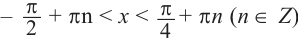
tg х > 1 будет 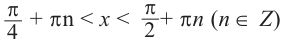
Пример 5.
Решим неравенства 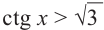
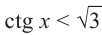
Решение:
На одной координатной плоскости построим графики функций 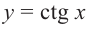
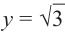
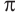
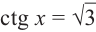
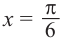
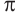
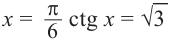
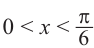
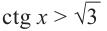
если 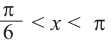
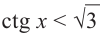
Это говорит о том , что условию неравенства 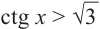
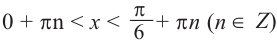
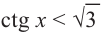
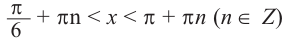
Для решения тригонометрических неравенств:
1) В одной системе координат постройте графики функций из левой и правой частей неравенства;
2) Решите соответствующие уравнения. Найдите абсциссы для нескольких точек пересечения, расположенных близко к началу координат и отметьте их на графике;
3) Определите какой-либо интервал, удовлетворяющий неравенству;
4) Принимая во внимание периодичность функции, запишите все решения.
Пример 6.
Решите неравенство 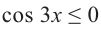
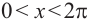
Решение:
1.Построим график функции 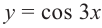
Как видно из графика, значения 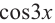
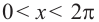
Пример 7.
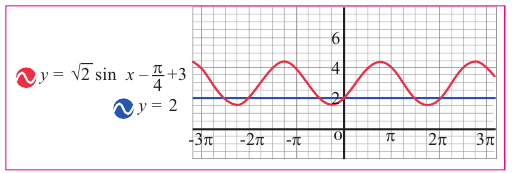
Решим неравенство 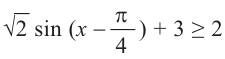
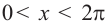
Решение:
1. Построим графики функций 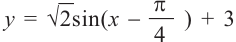
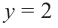
Решением неравенства являются абсциссы всех точек, которые расположены на прямой у = 2 и выше неё. Это точки 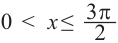
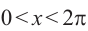
А общее решение неравенства имеет вид 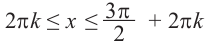
Проверка: На интервале решения для проверки выберем одну точку, напри-л
мер 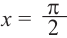
Пример 8.
Решение:
Пусть 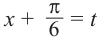
Пример решении задачи:
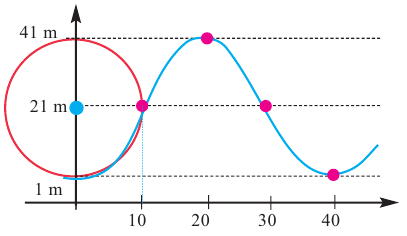
Карусель, радиусом 20 м за каждые 40 секунд совершает один оборот. Самое низкое сиденье находится на высоте 1 м.
а)Изобразите график, соответствующий задаче.
б)Запишите функцию зависимости движения человека, находящегося на сиденье карусели в виде 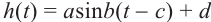
в)В какие секунды за один полный оборот человек на карусели, окажется на высоте выше 21 м?
Решение:
а) Изобразим схематично решение задачи. Отметим на окружности точки, соответствующие каждой четвёртой части оборота при движении карусели. Соединим эти точки и получим график, в виде синусоиды, движения карусели за один оборот (360°).
б)Из графика видно, что с 10 но 30 секунду человек на карусели, будет находится на высоте от 21 ми более.
в)По данным задачи и графику запишем формулу функции.
Зная период, найдём частоту b:
Найдём амплитуду и среднюю линию, зная максимальное и минимальное значения. 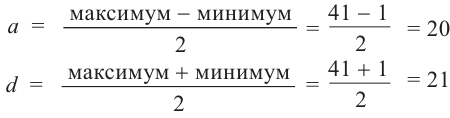
Формула имеет вид 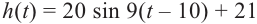
Решение неравенств
Понятия неравенства с одной переменной и его способы решения:
Определение:
Если два выражения с переменной соединить одним из знаков 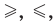
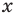
Решением неравенства с переменной называется значение переменной, которое обращает заданное неравенство в верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет.
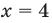
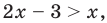
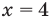
Область допустимых значений (ОДЗ):
Областью допустимых значений (или областью определения) неравенства называется общая область определения для функций 
Для неравенства 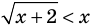
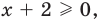
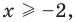
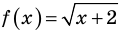
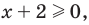
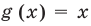
Два неравенства называется равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения, то есть каждое решение первого неравенства является решением второго и наоборот, каждое решение второго неравенства является решением первого.
- Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим неравенство, равносильное заданному (на любом множестве).
- Если обе части неравенства умножить или разделить на одно и то же положительное число (или на одну и ту же функцию, которая определена и положительна на ОДЗ заданного неравенства), не меняя знак неравенства, то получим неравенство, равносильное заданному (на ОДЗ заданного неравенства).
- Если обе части неравенства умножить или разделить на одно и то же отрицательное число (или на одну и ту же функцию, которая определена и отрицательна на ОДЗ заданного неравенства) и изменить знак неравенства на противоположный, то получим неравенство, равносильное задан ному (на ОДЗ заданного неравенства).
- Метод интервалов (решения неравенств вида
Решите неравенство
Пусть
ОДЗ:
Нули функции
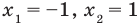
Ответ:
Схема поиска плана решения неравенства
Объяснение и обоснование:
Понятия неравенства с переменной и его решение
Если два выражения с переменной соединить одним из знаков 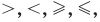
Аналогично уравнению, неравенство с переменной (например, со знаком 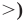
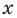
Напомним, что решением неравенства называется значение переменной, которое обращает это неравенство в верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет.
Например, решениями неравенства 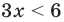
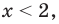

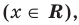
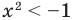
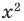
Область допустимых значений (ОДЗ) неравенства
Область допустимых значений (ОДЗ) неравенства определяется аналогично ОДЗ уравнения. Если задано неравенство 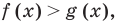
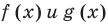
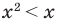
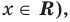
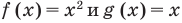
Понятно, что каждое решение заданного неравенства входит как в область определения функции 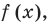
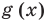
Например, в неравенстве 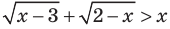
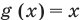
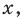
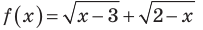
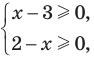
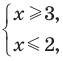
В основном при решении неравенств различных видов приходится применять один из двух методов решения: равносильные преобразования неравенств или так называемый метод интервалов.
Равносильные неравенства
С понятием равносильности неравенств вы знакомы еще из курса алгебры 9 класса. Как и для случая равносильных уравнений, равносильность неравенств мы будем рассматривать на определенном множестве.
Два неравенства называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения, то есть каждое решение первого неравенства является решением второго, и наоборот, каждое решение второго неравенства является решением первого.
Договоримся, что в дальнейшем все равносильные преобразования неравенств будем выполнять на ОДЗ заданного неравенства. Укажем, что в том случае, когда ОДЗ заданного неравенства является множество всех действительных чисел, мы не всегда будем его записывать (как не записывали ОДЗ при решении линейных или квадратных неравенств). И в других случаях главное — не записать ОДЗ при решении неравенства, а действительно учесть ее при выполнении равносильных преобразований заданного неравенства.
Общие ориентиры выполнения равносильных преобразований неравенств аналогичны соответствующим ориентирам выполнения равносильных преобразований уравнений.
Как указывалось выше, выполняя равносильные преобразования неравенств, необходимо учитывать ОДЗ заданного неравенства — это и есть первый ориентир для выполнения равносильных преобразований неравенств.
По определению равносильности неравенств необходимо обеспечить, чтобы каждое решение первого неравенства было решением второго, и наоборот, каждое решение второго неравенства было решением первого. Для этого достаточно обеспечить сохранение верного неравенства на каждом шаге решения не только при прямых, а и при обратных преобразованиях. Это и есть второй ориентир для решения неравенств с помощью равносильных преобразований. Действительно, каждое решение неравенства обращает его в верное числовое неравенство, и если верное неравенство сохраняется, то решение каждого из неравенств будет также и решением другого, таким образом, неравенства будут равносильны (соответствующие ориентиры схематически представлены в пункте 5 табл. 38).
Например, чтобы решить с помощью равносильных преобразований неравенство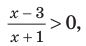
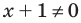
Решение:
Данное неравенство равносильно совокупности двух систем:
Тогда получаем
Таким образом,
Ответ:
Комментарий:
Заметим, что при записи условия положительности дроби — совокупности систем (2) — мы неявно учли ОДЗ неравенства (1). Действительно, если 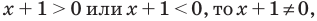
- Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим неравенство, равносильное заданному (на любом множестве).
- Если обе части неравенства умножить или разделить на одно и то же положительное число (или на одну и ту же функцию, которая определена и положительна на ОДЗ заданного неравенства), не изменяя знак неравенства, то получим неравенство, равносильное заданному (на ОДЗ заданного).
- Если обе части неравенства умножить или разделить на одно и то же отрицательное число (или на одну и ту же функцию, которая определена и отрицательна на ОДЗ заданного неравенства) и изменить знак неравенства на противоположный, то получим неравенство, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований заданного неравенства.
Замечание. Для обозначения перехода от заданного неравенства к неравенству, равносильному ему, можно применять специальный значок 
Метод интервалов
Решение неравенств методом интервалов опирается на свойства функций, связанные с изменением знаков функции. Объясним эти свойства, используя графики известных нам функций, например функций 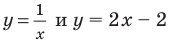
Рассматривая эти графики, замечаем, что функция может изменить свой знак только в двух случаях:
- если график разрывается (как в случае функции
(рис. 100, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);
- если график без разрыва переходит из нижней полуплоскости в верхнюю (или наоборот). Но тогда график пересекает ось
(как в случае функции
(рис. 100,6).
На оси 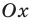
Точки, в которых разрывается график функции 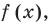
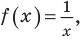
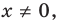
В таблице 39 приведено решение дробно-рационального неравенства 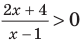
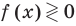
Пример №1
Решение:
1. ОДЗ: 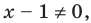
Рассмотрим функцию, стоящую в левой части этого неравенства, и обозначим ее через 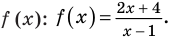
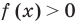
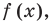
1. Найти ОДЗ неравенства.
2. Нули
тогда
Нас интересуют те промежутки области определения функции 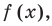
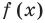
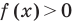
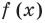
2. Найти нули
Если теперь отметить нули на области определения функции 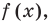
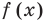
3. Отметить нули на ОДЗ и найти знак функции в каждом промежутке, на которые разбивается ОДЗ.
4 Ответ:
Из рисунка видно, что решением неравенства является объединение промежутков
4. Записать ответ, учитывая знак неравенства.
Приведем пример решения более сложного дробно-рационального неравенства методом интервалов и с помощью равносильных преобразований.
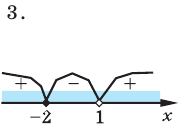
Пример №2
Решите неравенство
1 способ (метод интервалов)
Решение:
Пусть
1 ОДЗ:
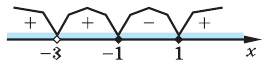
2. Нули
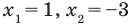
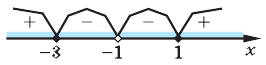
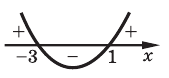
3. Отмечаем нули функции на ОДЗ и находим знак 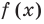
Ответ:
Комментарий:
Данное неравенство имеет вид 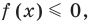
При нахождении нулей 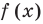
Записывая ответ к нестрогому неравенству, следует учесть, что все нули функции должны войти в ответ (в данном случае — числа -3 и 1).
2 способ (с помощью равносильных преобразований)
Комментарий:
Выберем для решения метод равносильных преобразований неравенства. При выполнении равносильных преобразований мы должны учесть ОДЗ данного неравенства, то есть учесть ограничение
Но если 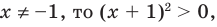
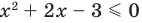
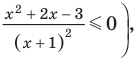
Чтобы решить полученное квадратное неравенство, найдем корни квадратного трехчлена 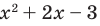
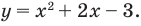
Поскольку все преобразования были равносильными только на ОДЗ, то мы должны выбрать те решения квадратного неравенства, которые удовлетворяют ограничению ОДЗ.
Решение:
ОДЗ:
Тогда 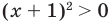
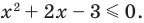
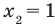
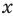
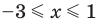
Учитывая ОДЗ, получаем ответ.
Ответ:
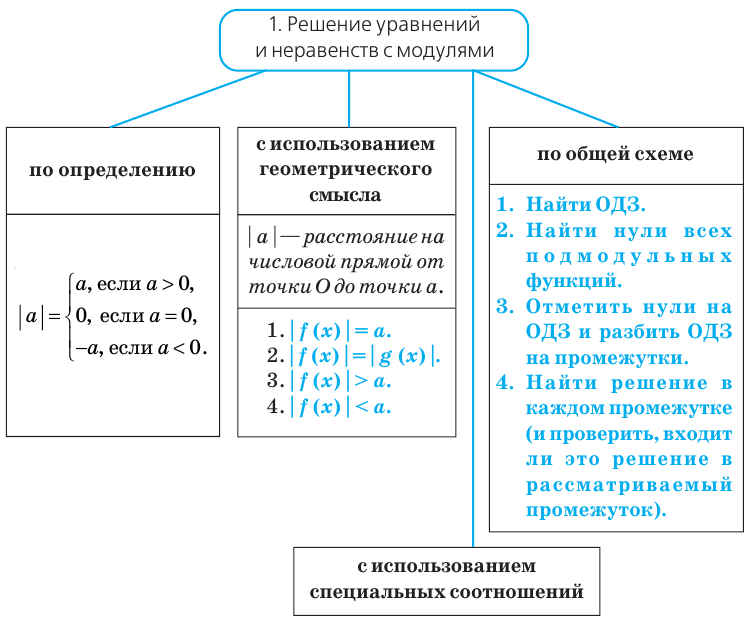
Уравнения и неравенства с модулями
Использование геометрического смысла модуля ( при
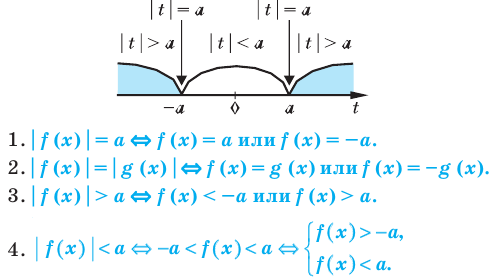
Обобщение:
Использование специальных соотношений:
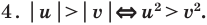
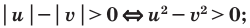
Объяснение и обоснование:
Решение любых уравнений или неравенств с модулем
Решать любое уравнение или неравенство с модулем можно одним из трех основных способов: по определению модуля, исходя из геометрического смысла модуля или по общей схеме. Некоторые уравнения или неравенства с модулем могут быть также решены с использованием специальных соотношений (табл. 40).
В зависимости от выбранного способа решения получаем разные записи решения.
Пример №3
Решите уравнение
1 способ (по определению модуля)
Решение:
- Если
то получаем уравнение
Тогда
что удовлетворяет и условию (1).
- Если
то получаем уравнение
Тогда
что удовлетворяет и условию (2).
Ответ:
Комментарий:
Чтобы раскрыть знак модуля по определению, рассмотрим два случая: 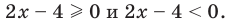
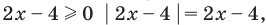
В каждом случае решаем полученное уравнение и выясняем, удовлетворяет ли каждый из найденных корней тому условию, при котором мы его находили.
2 способ (использование геометрического смысла модуля)
Решение:
Ответ: 5; -1.
Комментарий:
С геометрической точки зрения 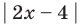
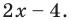
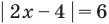
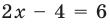
Замечание. При решении уравнения с использованием геометрического смысла модуля знак модуля раскрывается неявно, то есть определение модуля в явном виде не применяется.
Общая схема решения уравнений и неравенств с модулями — это фактически немного измененный метод интервалов. Поясним содержание этой схемы на примере уравнения с двумя модулями вида
Чтобы решить это уравнение, необходимо раскрыть знаки модулей, а для этого необходимо знать, где функции 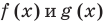
Каждое из этих неравенств мы умеем решать методом интервалов. Перестроим прием решения неравенств методом интервалов таким образом, чтобы он давал возможность одновременно решать каждое из последних неравенств. Как известно, решение неравенства (1) методом интервалов начинается с нахождения его ОДЗ (то есть области определения функции 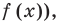
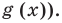
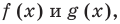
Чтобы продолжить решение неравенств 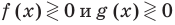
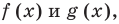
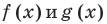
Обоснование возможности применения приведенной схемы к решению неравенств с модулями проводится аналогично.
Примеры решения задач:
Пример №4
Решите уравнение
Решение:
1. ОДЗ:
2. Нули подмодульных функций:
3. Нули 0 и 2 разбивают ОДЗ на четыре промежутка, в которых подмодульные функции имеют знаки*, показанные на рисунке.
4. Находим решения данного уравнения в каждом из промежутков (поскольку знаки подмодульных функций одинаковы на промежутках 1 и 3, удобно для решения объединить эти промежутки).
Промежутки 1 и 3 : 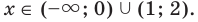
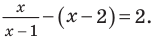
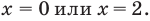
Промежуток 2: 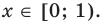
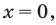
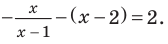
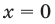
Промежуток 4: 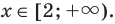
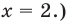
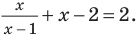
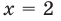
Ответ: 0; 2.
Проиллюстрируем также получение и использование специальных соотношений, приведенных в таблице 40. Обоснуем, например, соотношение
Запишем заданное равенство в виде 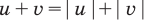
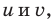
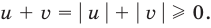
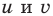
неотрицательные. Наоборот, если 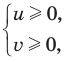
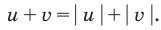
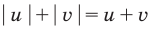
- Заказать решение задач по высшей математике
Пример №5
Решите уравнение
Решение:
Поскольку 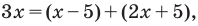
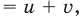
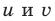
Таким образом,
Ответ:
Комментарий:
Если обозначить 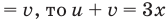
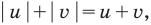
Заметим, что данное уравнение можно решать и по общей схеме, но тогда решение будет более громоздким но системе
При решении неравенств с модулями рассуждения, связанные с раскрытием знаков модулей, полностью аналогичны рассуждениям, которые использовались при решении уравнений с модулями.
Пример №6
Решите неравенство
Решение:
Учитывая геометрический смысл модуля, получаем, что заданное неравенство равносильно неравенству 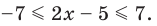
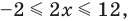
Ответ:
Комментарий:
Неравенство вида 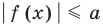
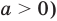
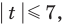
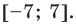
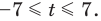
Пример №7
Решите неравенство
Решение:
1. ОДЗ: 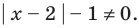
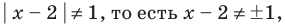
2. Нули подмодульных функций: 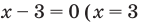
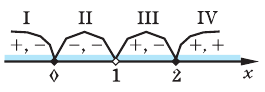
3. Нуль 2 разбивает ОДЗ на четыре промежутка, на которых подмодульные функции имеют знаки, показанные на рисунке (на каждом из промежутков первый знак — это знак функции 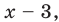
4. Находим решения заданного неравенства в каждом из промежутков (поскольку знаки подмодульных функций являются одинаковыми на промежутках I и II, удобно для решения объединить эти промежутки). Промежутки I и II: 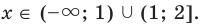
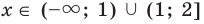
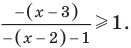
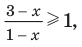
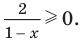
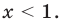
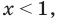
Промежуток III: 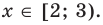
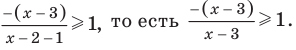
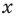
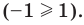
Промежуток IV: 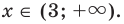
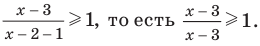
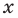
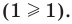
Объединяя все решения, полученные в каждом из промежутков, имеем решение данного неравенства на всей ОДЗ:
Ответ:
Укажем, что для решения некоторых неравенств с модулями удобно применять также специальные соотношения, приведенные в таблице 40.
Пример №8
Решите неравенство
Решение:
Поскольку 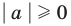
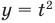
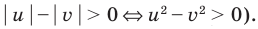
Раскладывая на множители все разности квадратов, имеем:
Далее методом интервалов (см. рисунок)получаем
Ответ:
Общая схема, предложенная в таблице 40, может быть использована не только при решении уравнений или неравенств с модулями, но и при выполнении преобразований выражений с модулями.
Например, для построения графика функции 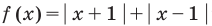
Оформление решения подобного примера может быть таким.
Пример №9
Постройте график функции
Решение:
1. Область определения функции:
2. Нули подмодульных функций:
3. Отмечаем нули на области определения и разбиваем область определения на промежутки (на рисунке также указаны знаки подмодульных функций в каждом из промежутков). 4. Тогда
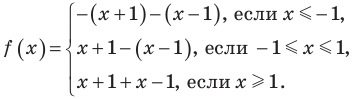
Строим график этой функции (см. рисунок).
Решение тригонометрических неравенств
Примеры решения простейших тригонометрических неравенств:
Способы решения более сложных тригонометрических неравенств:
а) Использование равносильных преобразований и, в частности, сведение тригонометрического неравенства к алгебраичкому неравенству по схеме: 1) к одному аргументу, 2) к одной функции, 3) замена переменной (аналогично схеме решения тригонометрических уравнений, приведенной на с. 170) и последующее решение полученных простейших тригонометрических неравенств.
б) Использование метода интервалов (после сведения неравенства к виду 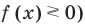
- Найти ОДЗ неравенства.
- Найти общий период (если он существует) для всех функций, входящих в неравенство, то есть период функции
- Найти нули функции:
- Отметить нули функции на ОДЗ на одном периоде и найти знак функции
в каждом из промежутков, на которые разбивается ОДЗ (на одном периоде).
- Записать ответ, учитывая знак заданного неравенства и период функции
Объяснение и обоснование:
Решение простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами считают неравенства вида 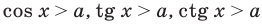
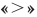
Чтобы рассуждения по нахождению решений этих неравенств были более наглядными, используют единичную окружность или графики соответствующих функций, как это показано в первом пункте таблицы 41.
Пример №10
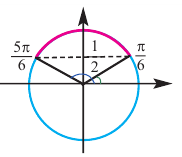
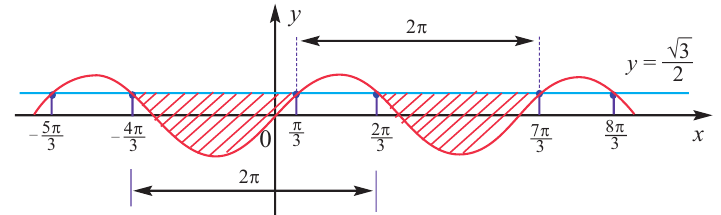
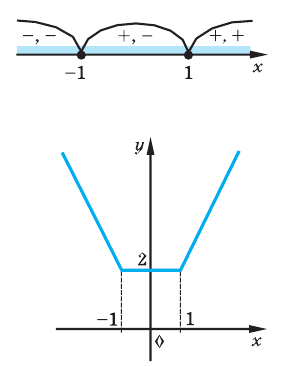
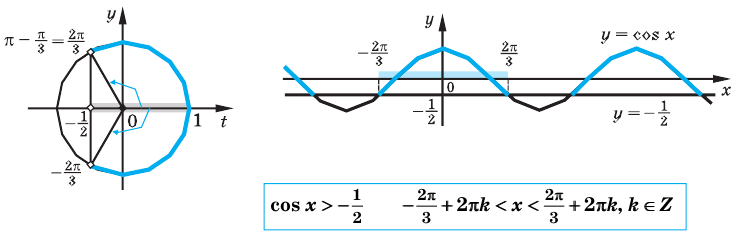
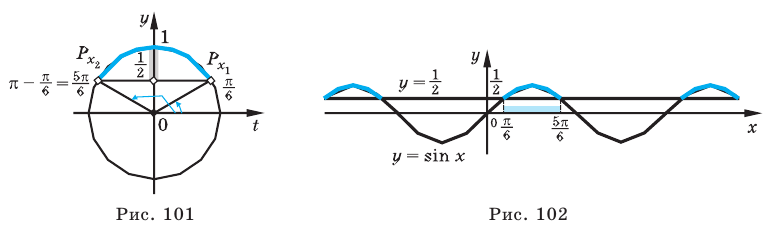
Объясним более детально решение неравенства 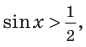
Решение:
Поскольку 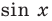
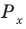
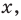
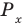
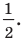
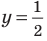
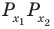
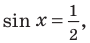
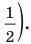
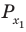
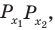
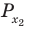
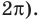
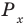
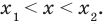
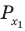
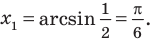
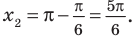
Через период 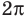
Ответ:
Для решения неравенства 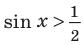
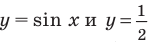
Решениями неравенства 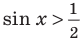
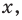
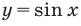
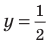
Достаточно решить уравнение 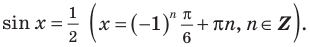
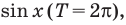
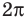
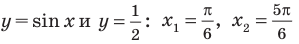
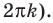
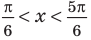
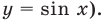
Ответ:
Аналогично можно получить и решения других видов простейших неравенств, приведенных в пункте 1 таблицы 41.
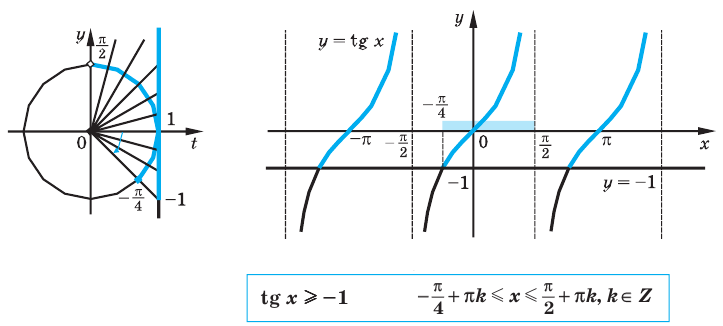
Пример №11
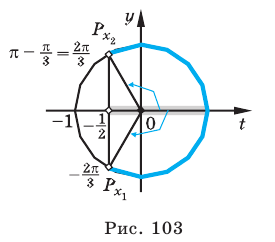
Решите неравенство
Решение:
Поскольку 
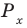
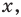
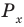
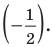
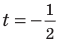
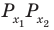
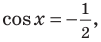
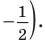
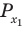
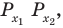
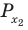
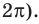
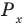
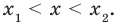
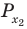
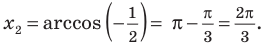
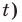
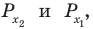
Таким образом, на одном 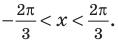
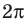
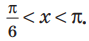
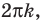
Ответ:
Рассуждения при использовании графической иллюстрации решения неравенства 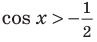
Пример №12
Решите неравенство
Решение:
Период тангенса равен 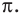
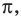
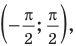
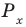
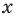
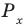
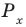
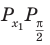
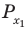
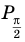
Поскольку точка 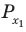
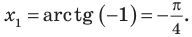
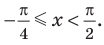
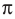
Ответ:
Заметим, что при решении данного неравенства с использованием графиков достаточно, как и в предыдущих случаях, на одном периоде (например, на промежутке 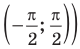
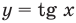
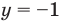
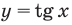
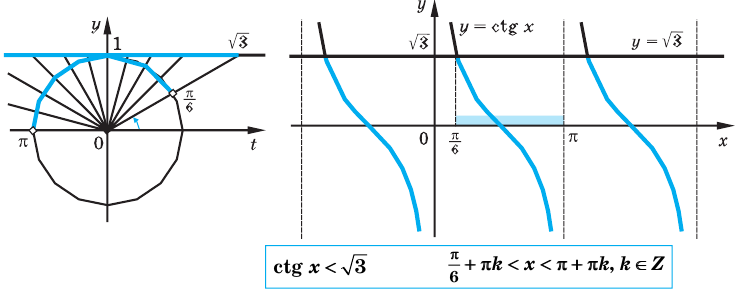
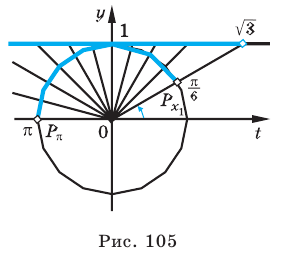
Пример №13
Решите неравенство
Решение:
Период котангенса равен 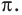
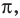
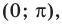
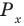
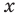
Сначала выделим на линии котангенсов значения котангенсов, меньшие, чем 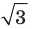
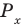
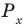
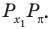
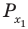
Таким образом, на одном периоде решениями данного неравенства являются
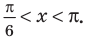
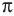
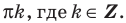
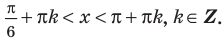
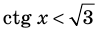
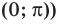
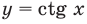
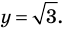
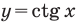
Способы решения более сложных тригонометрических неравенств
Способы решения более сложных тригонометрических неравенств также проиллюстрируем на примерах.
Пример №14
Решите неравенство:
Решение:
Тогда 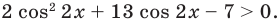
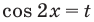
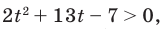
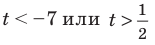
Обратная замена дает: 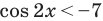
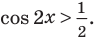
Таким образом,
Комментарий:
Используем равносильные преобразования данного неравенства. Для этого приведем его к алгебраическому по схеме, аналогичной схеме решения
- к одному аргументу
- к одной функции
- проведем замену переменной
После обратной замены решим полученные простейшие тригонометрические неравенства.
Решая более сложные тригонометрические неравенства, можно также применить метод интервалов, немного изменив его. Необходимость коррекции известной схемы решения неравенств 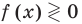
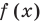
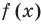
Таким образом, метод интервалов для решения тригонометрических неравенств 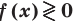
- Найти ОДЗ неравенства.
- Найти период функции
(если он существует).
- Найти нули функции
- Отметить нули на ОДЗ внутри одного периода и найти знак функции в каждом из промежутков, на которые разбивается ОДЗ (внутри одного периода).
- Записать ответ (учитывая знак заданного неравенства и период функции
Пример №15
Решите неравенство
Решение:
Решим данное неравенство методом интервалов. Для этого приведем его к виду
1. ОДЗ: 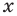
2. Как мы знаем, период функции 
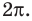
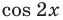
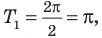
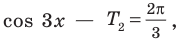
На отрезке длиной 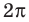
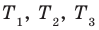
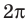
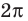
3.Найдем нули этой функции:
Тогда
Отсюда 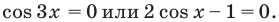
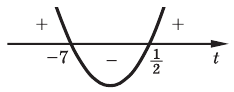
4. Отметим все нули на периоде длиной 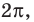
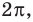
Находим знаки функции 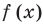
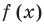
Ответ (записывается с учетом периода):
Замечание. При решении тригонометрических неравенств методом интервалов часто приходится находить знак функции в большом количестве промежутков. Для того чтобы уменьшить объем работы, можно предложить такой способ: следить за тем, через какой нуль мы проходим при переходе от одного интервала к другому и изменяется ли знак заданной функции в этом нуле.
В случае, когда функция 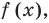
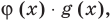
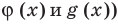
Практически для использования этого свойства в случае, если левая часть неравенства записана как произведение нескольких функций, нули каждого множителя отмечают на промежутке разным цветом (так, как это сделано на рисунке к задаче 6), или, если множителей только два, нули первого множителя обозначают под осью, а нули второго — над осью.
Если у функций-множителей нет одинаковых нулей, то знак функции 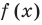
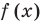
- Формулы приведения
- Синус, косинус, тангенс суммы и разности
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
Метод интервалов
Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.
1. Рассмотрим неравенство:
Метод интервалов позволяет решить его за пару минут.
В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
Метод интервалов основан на следующем свойстве дробно-рациональной функции.
Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .
, где
и
— корни квадратного уравнения
.
Получим:
Рисуем ось X и расставляем точки, в которых числитель и знаменатель обращаются в нуль.
Нули знаменателя и
— выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя).
Напомним, что мы изображаем точку на числовой прямой выколотой (пустой), если соответствующее значение переменной никак не может быть решением неравенства. В нашем примере точки и
выколотые, потому что в них знаменатель обращается в ноль.
Нули числителя и
— закрашены, так как неравенство нестрогое. При
и
наше неравенство выполняется, так как обе его части равны нулю.
Эти точки разбивают ось X на 5 промежутков.
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например,
и проверим знак выражения
в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак
.
Следующий промежуток:
. Проверим знак при
. Получаем, что левая часть поменяла знак на
.
. Возьмем
. При
выражение положительно — следовательно, оно положительно на всем промежутке от
до
.
При
левая часть неравенства отрицательна.
И, наконец,
. Подставим
и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак
.
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Ответ: .
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.
Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
, или
, или
, или
(в левой части — дробно-рациональная функция, в правой — нуль).
Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.
Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.
2. Рассмотрим еще одно неравенство:
Решение:
Снова расставляем точки на оси X. Точки и
— выколотые, поскольку это нули знаменателя. Точка
— тоже выколота, поскольку неравенство строгое, и значение переменной
не может быть решением неравенства.
При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например,
. Левая часть имеет знак
:
При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак
:
При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак
:
Наконец, при все множители положительны, и левая часть имеет знак
:
Ответ: .
Почему нарушилось чередование знаков? Потому что при переходе через точку 2 «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку
знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Решение:
Левая часть та же, что и в предыдущем примере. Та же будет и картина знаков:
Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при
и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.
Ответ: .
В задачах на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:
Решение:
Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения
при всех
одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.
И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех
.
Придём к равносильному неравенству:
Решим неравенство методом интервалов. Действуем по алгоритму: числитель левой части равен нулю при а знаменатель обращается в ноль при
. Отметим эти точки на координатной прямой. Точки выколоты, потому что неравенство строгое. Эти точки разбивают числовую ось на три интервала. Найдем знаки на каждом из интервалов. На крайнем правом знак положителен, а дальше знаки чередуются.
Нам нужен «интервал со знаком минус», то есть такой, где Выпишем ответ.
Ответ:
Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.
5. Рассмотрим еще одно неравенство, на вид совсем простое:
Решение:
Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь
может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.
Мы поступим по-другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:
Применим метод интервалов.
Действуем по алгоритму. Отметим на координатной прямой точки и
. Они выколотые, потому что неравенство строгое. Эти точки разбивают ось Х на три интервала. Расставим знаки на каждом из них.
Ответ:
6. Решите неравенство:
Решение:
Приведем левую часть неравенства к общему знаменателю и преобразуем числитель:
Применим метод интервалов:
Числитель равен нулю при Знаменатель обращается в ноль при
или
. Неравенство строгое, поэтому все эти точки на числовой оси отмечаем как пустые.
Если , то
. Далее знаки чередуются.
Нам нужны «интервалы со знаком минус». Выпишем их и получим ответ.
Ответ:
7. Решите неравенство
Решение:
Приведем неравенство к виду:
Для этого все перенесем в левую часть, приведем к общему знаменателю и разложим числитель и знаменатель на множители. Применяем формулу разности квадратов и формулу разложения квадратного трехчлена на множители
Получим:
Найдем нули числителя и знаменателя и отметим их на числовой оси:
Выпишем интервалы, где неравенство выполняется, и получим ответ.
Ответ:
8. Решите неравенство:
Решение:
Разложим левую часть неравенства на множители.
Для этого вынесем общий множитель за скобки, а затем воспользуемся формулой:
Получим:
Применим метод интервалов.
Левая часть неравенства обращается в ноль, если ,
или
. Нанесем эти точки на координатную прямую. Все точки закрашенные, так как неравенство нестрогое, в нем присутствует знак «меньше или равно».
Ответ:
9. Решите неравенство:
Решение:
Разложим числитель на множители с помощью группировки:
Знаменатель тоже разложим на множители:
Неравенство примет вид:
Мы видим, что числитель равен нулю при
Знаменатель равен нулю при . Множитель
стоит в числителе и в знаменателе, и он не может равняться нулю.
Отметим полученные точки на координатной прямой. Две из них закрашены (это 3 и 1), а две нет (это -1 и -2). Найдем знаки на каждом промежутке.
При переходе через точку знак не меняется, так как множитель
присутствует и в числителе, и в знаменателе.
Выпишем ответ.
Ответ:
10. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Напомним, что выражение мы разложили на множители, решив квадратное уравнение:
Неравенство примет вид:
Воспользуемся методом интервалов.
Числитель дроби в левой части неравенства равен нулю, если Знаменатель обращается в ноль, если
или
. Отметим эти точки на координатной прямой и определим знаки на интервалах.
Ответ:
11. Решите неравенство:
Решение:
Можно сразу применить метод интервалов.
Но лучше, чтобы не запутаться со знаками, умножить обе части неравенства на (-1) и не забыть поменять знак неравенства на противоположный.
Теперь применим метод интервалов.
Отметим на координатной прямой нули числителя и знаменателя и определим знаки на интервалах.
Обратите внимание, что знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени.
Ответ:
12. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Сократим на множитель при условии, что
.
Здесь мы действуем чуть иначе, чем в задаче 9.
Неравенство равносильно системе:
Решаем второе неравенство системы методом интервалов:
Второму неравенству удовлетворяют точки .
Точка в этот промежуток не входит.
Ответ:
13. Решите неравенство:
Решение:
Разложив числитель на множители, получим:
Применим метод интервалов.
Отметим на числовой оси точки, в которых числитель и знаменатель обращаются в ноль. Обратите внимание, что точки -1 и 5 закрашены, а точки 2 и 4 пустые.
Определим знаки на интервалах.
Знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени. При переходе через точку 4 знак меняется, степень соответствующего множителя нечетная.
В ответе запишем интервалы, на которых неравенство выполняется.
Ответ:
14. Решите неравенство:
Разложим числитель и знаменатель на множители, используя формулы сокращенного умножения: суммы и разности кубов, разности квадратов.
Кажется, что неравенство сложное. Попробуем разложить на множители выражения и
Оказывается, что дискриминанты соответствующих квадратных уравнений отрицательны, поэтому и
при всех х.
Разделим обе части неравенства на эти положительные выражения.
Получим:
Неравенство равносильно системе:
Решим первое неравенство системы методом интервалов:
Его решением является промежуток [1;4], причем точка в этот промежуток не входит.
Ответ:
Мы показали на различных примерах, как применяется метод интервалов.
Сделаем вывод:
Метод интервалов помогает решать дробно-рациональные неравенства по алгоритму. Правила просты: приводим неравенство к такому виду, что в его левой части – произведение множителей или дробь, а в правой – ноль. Находим точки, в которых левая часть обращается в ноль или не определена. Отмечаем на числовой оси эти точки. Они разбивают числовую ось (или координатную прямую) на интервалы, на каждом из которых функция в левой части неравенства сохраняет свой знак. Определяем знаки на интервалах, помня о правилах чередования знаков. И записываем ответ.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Метод интервалов» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Метод интервалов: решение простейших строгих неравенств
12 ноября 2017
- Домашнее задание
- Ответы
Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:
(x − 5)(x + 3) > 0
Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:
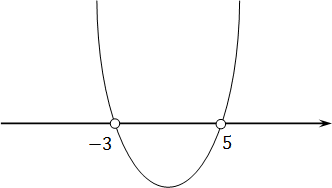
Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:
x2 − 2x − 15 > 0
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:
Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.
Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.
Почему эти методы неэффективны?
Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:
(x − 7)(x − 1)(x + 4)(x + 9) < 0
Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.
Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.
Что такое метод интервалов
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:
- Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
- Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
- Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
- Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.
На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:
Задача. Решите неравенство:
(x − 2)(x + 7) < 0
Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:
(x − 2)(x + 7) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.
Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:
Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:
f (x) = (x − 2)(x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;
Получаем, что f(3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.
Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.
Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:
Вернемся к исходному неравенству, которое имело вид:
(x − 2)(x + 7) < 0
Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.
Задача. Решите неравенство:
(x + 9)(x − 3)(1 − x) < 0
Шаг 1: приравниваем левую часть к нулю:
(x + 9)(x − 3)(1 − x) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.
Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.
Шаг 2: отмечаем все корни на координатной прямой:
Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:
f (x) = (x + 9)(x − 3)(1 − x);
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197 < 0.
Шаг 4: расставляем остальные знаки. Помним, что при переходе через каждый корень знак меняется. В итоге наша картинка будет выглядеть следующим образом:
Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:
(x + 9)(x − 3)(1 − x) < 0
Это неравенство вида f (x) < 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:
x ∈ (−9; 1) ∪ (3; +∞)
Это и есть ответ.
Замечание по поводу знаков функции
Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.
Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:
- Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
- Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.
Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.
Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.
Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a; +∞), где a — самый большой корень уравнения f (x) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:
(x − 1)(2 + x)(7 − x) < 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;
Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.
Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:
Требуется найти знак функции f (x) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.
«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x) = −1 и f (x) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.
На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:
f (x) = (x − 1)(2 + x)(7 − x)
Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.
Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.
Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:
(+) · (+) · (−) = (−)
Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:
Исходное неравенство имело вид:
(x − 1)(2 + x)(7 − x) < 0
Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:
x ∈ (−2; 1) ∪ (7; +∞)
Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:
Задача. Решите неравенство:
x(2x + 8)(x − 3) > 0
Заменяем неравенство уравнением и решаем его:
x(2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.
Отмечаем все три корня на координатной прямой (сразу со знаками):
Справа на координатной оси стоит плюс, т.к. функция имеет вид:
f (x) = x(2x + 8)(x − 3)
А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:
x ∈ (−4; 0) ∪ (3; +∞)
Смотрите также:
- Метод интервалов: случай нестрогих неравенств
- Тест по методу интервалов для строгих неравенств
- Сводный тест по задачам B12 (2 вариант)
- Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной
- Формулы приведения: ускоряем вычисления в тригонометрии
- Задачи B4: перевозка груза тремя фирмами


















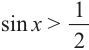
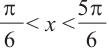
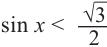
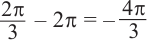
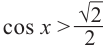
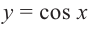
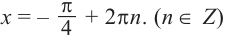
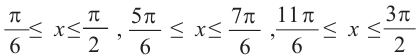
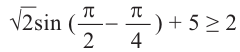
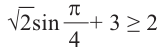
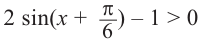
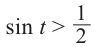
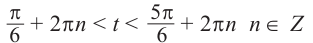
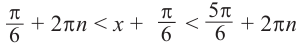
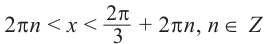


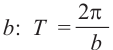
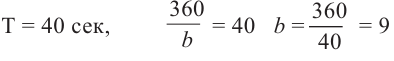
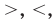
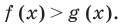
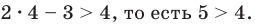
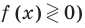
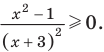
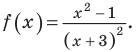
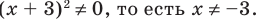
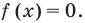
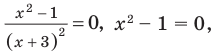
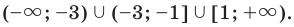

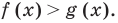
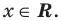
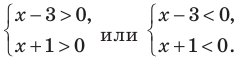
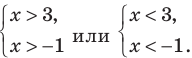
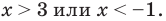
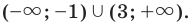
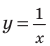 (рис. 100, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);
(рис. 100, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);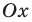 (как в случае функции
(как в случае функции 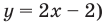 (рис. 100,6).
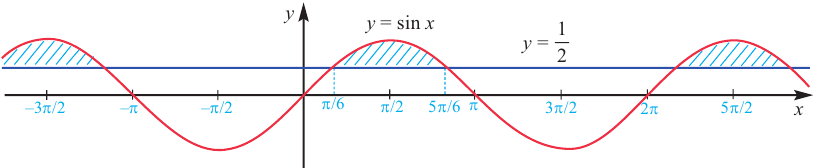
(рис. 100,6).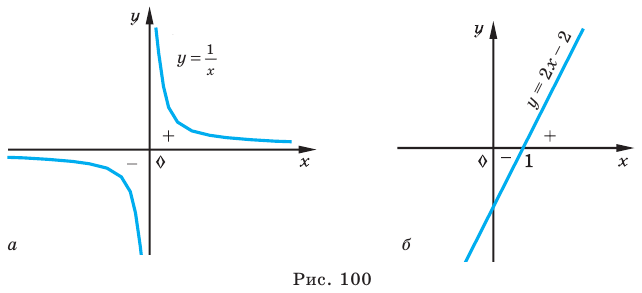
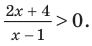
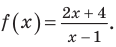
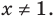
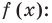
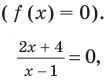
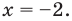
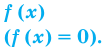
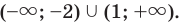

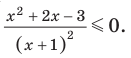
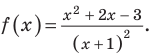
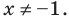
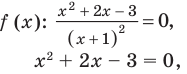
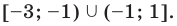
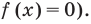
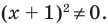
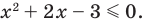
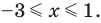
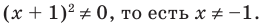
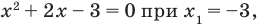
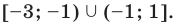
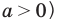
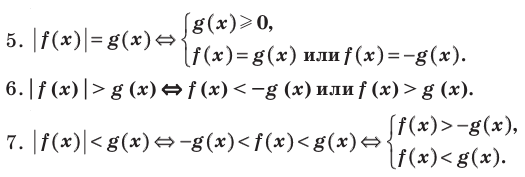
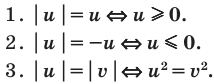
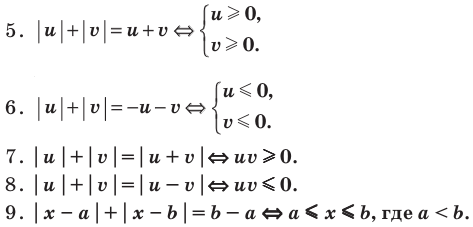
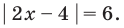
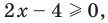 то получаем уравнение
то получаем уравнение 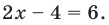 Тогда
Тогда 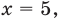 что удовлетворяет и условию (1).
что удовлетворяет и условию (1).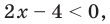 то получаем уравнение
то получаем уравнение 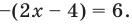 Тогда
Тогда 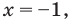 что удовлетворяет и условию (2).
что удовлетворяет и условию (2).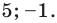
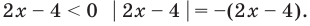
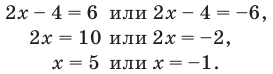
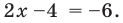
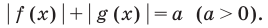
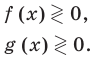
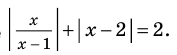
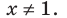
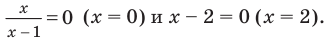
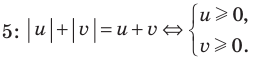
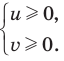
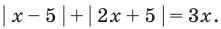
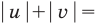
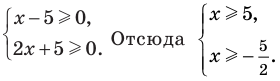
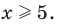
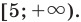
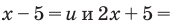
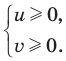
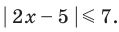
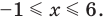
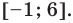
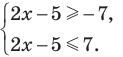
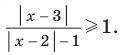
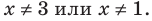
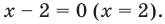
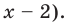
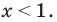
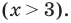
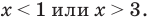
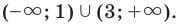
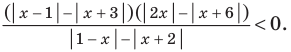
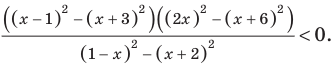
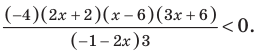
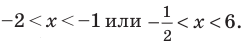
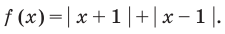
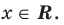
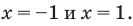

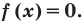
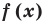 в каждом из промежутков, на которые разбивается ОДЗ (на одном периоде).
в каждом из промежутков, на которые разбивается ОДЗ (на одном периоде).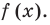
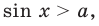

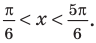
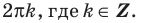
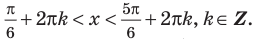
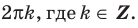
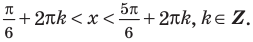
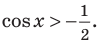
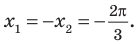
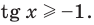
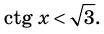
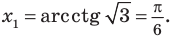
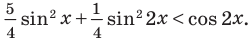
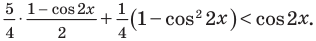
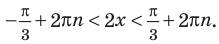
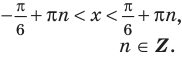
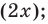
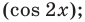
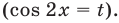 После обратной замены решим полученные простейшие тригонометрические неравенства.
После обратной замены решим полученные простейшие тригонометрические неравенства.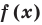 (если он существует).
(если он существует).