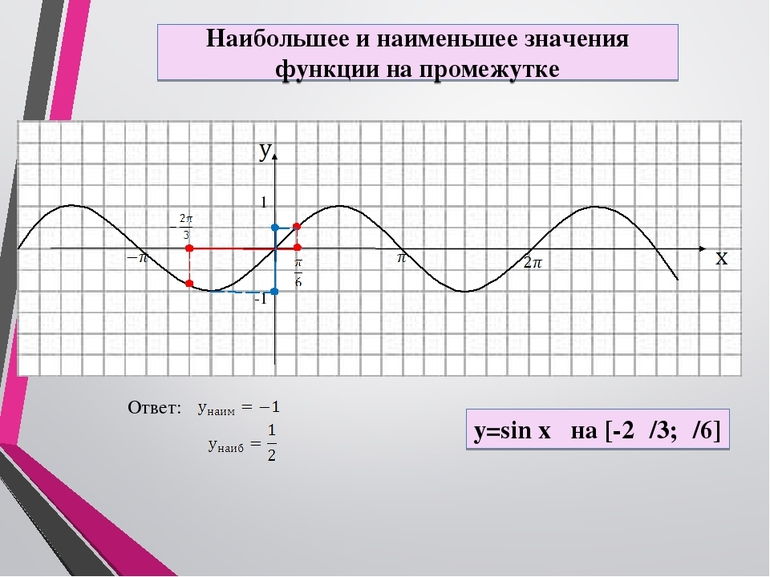
Наибольшее и наименьшее значение функции
Как найти?
Постановка задачи
Найти наибольшее и наименьшее значение функции $ f(x) $ на отрезке $ [a,b] $
План решения
Наибольшее и наименьшее значение непрерывной функции $ f(x) $ на промежутке $ [a,b] $ достигаются в критических точках, то есть в точках в которых производная функции равна нулю $ f'(x) = 0 $, бесконечности $ f'(x) = pm infty $, не существует, либо на концах отрезка $ [a,b] $
- Проверяем на непрерывность функцию $ f(x) $ на заданном отрезке
- Если функция непрерывная, то находим производную $ f'(x) $ и приравниваем её к нулю
- Решая уравнение $ f'(x) = 0 $ получаем корни, являющиеся критическими точками
- Выбираем критические точки, принадлежащие отрезку $ [a,b] $
- Вычисляем значения функции $ f(x) $ в оставшихся критических точках, а так же на концах промежутка $ [a,b] $. Затем выбираем из них наибольшее $ M $ и наименьшее $ m $
Примеры решений
| Пример 1 |
| Найти наибольшее и наименьшее значение функции $ y = 2x^3 — 3x^2 — 4 $ на отрезке $ [0;2] $ |
| Решение |
|
Функция представляет собой кубический многочлен. Точек разрыва нет, значит функция непрерывна на отрезке $ [0;2] $. Находим производную: $$ y’ = (2x^3 — 3x^2 — 4)’ = 6x^2 — 6x $$ Приравниваем производную к нулю. Решаем уравнение и получаем критические точки: $$ 6x^2 — 6x = 0 $$ $$ 6x(x — 1) = 0 $$ $$ x_1 = 0, x_2 = 1 $$ Проверяем принадлежность полученных точек отрезку $ [0;2] $: $$ x_1 in [0;2], x_2 in [0;2] $$ Так как обе точки принадлежат отрезку, то вычисляем в них значение функции $ f(x) $, так же значение этой функции на концах интервала $ [0;2] $: $$ y(x_1) = y(a) = f(0) = 2 cdot 0^3 — 3 cdot 0^2 — 4 = -4 $$ $$ y(x_2) = y(1) = 2 cdot 1^3 — 3 cdot 1^2 — 4 = -5 $$ $$ y(b) = y(2) = 2 cdot 2^3 — 3 cdot 2^2 — 4 = 0 $$ Среди полученных значений наибольшее $ M = 0 $, наименьшее $ m = -5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ M = 0, m = -5 $$ |
| Пример 2 |
| Найти наименьшее и наибольшее значение функции $ y = frac{4x^2}{3+x^2} $ на $ [-1;1] $ |
| Решение |
|
Функция непрерывна на $ x in [-1;1] $ так как знаменатель не обращается в ноль ни при каком $ x $. Выполняем нахождение производной: $$ y’ = (frac{4x^2}{3+x^2})’ = frac{(4x^2)'(3+x^2)-(4x^2)(3+x^2)’}{(3+x^2)^2} = $$ $$ = frac{8x(3+x^2)-(4x^2)(2x)}{(3+x^2)^2} = frac{24x+8x^3-8x^3}{3+x^2)^2} = frac{24x}{(3+x^2)^2} $$ Приравниваем полученную производную к нулю и вычисляем критические точки: $$ frac{24x}{(3+x^2)^2} = 0 $$ $$ 24x = 0, 3+x^2 neq 0 $$ $$ x = 0 $$ Получена единственная критическая точка $ x = 0 $, которая принадлежит $ [-1; 1] $. Вычисляем значение функции $ f(x) $ в критической точке и на концах интервала $ [-1;1] $: $$ y(-1) = frac{4cdot (-1)^2}{3+(-1)^2} = frac{4}{4}=1 $$ $$ y(0) = frac{0}{3} = 0 $$ $$ y(1) = frac{4cdot 1^2}{3+1^2} = frac{4}{4} = 1 $$ Из полученных значений видно, что максимальное значение $ M = 1 $ и минимальное значение $ m = 0 $. |
| Ответ |
| $$ m = 0, M = 1 $$ |
Задания
Версия для печати и копирования в MS Word
Найдите наименьшее значение функции на отрезке
Спрятать решение
Решение.
Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке заданная функция имеет минимум, являющийся её наименьшим значением на данном отрезке. Найдем это наименьшее значение:
Ответ: −137.
Кодификатор ФИПИ/Решу ЕГЭ:
Valeriya M 21.12.2018 16:40
Ответ данного задания противоречит вопросу задания. В задании написано на отрезке [5;8], а на числовой прямой вы не обозначили данный отрезок и получается точка 6 тоже является решением. Хоть это и не влияет на ответ, думаю решение должно все-таки соответствовать вопросу.
Спасибо за внимание.
Александр Иванов
Решение соответствует вопросу, так как точка лежит на данном отрезке.
Общая информация
Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.
Для решения такого типа задач необходим определенный «багаж» знаний, поскольку без него вообще не обойтись. В его состав входят следующие элементы:
- Нахождение области определения функции (ОДФ).
- Понятие дифференциала и основные методы его нахождения.
- Умение решать уравнения.
- Знание графиков простых функций.
- Основные типы функций, полуинтервал и интервал.
Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.
Область определения
Область определения какой-либо функции вида y = f(x) — область значений аргумента, при которых она существует. У каждой функции существует два типа неизвестных: зависимые и независимые. К первым следует отнести переменную y, которая зависит от независимой переменной «х». Необходимо отметить, что бывают функции, в которых нет аргумента. Примером их считается функция вида y = const, где const — константа (любое число).
Область определения обозначается в теории литерой «D». Однако обозначение можно менять, когда исследуются несколько функций. Чтобы не путаться, специалисты рекомендуют следующую запись D(f(x)). Например, для y = x^2 — 27x и y = 12sinx ОДФ записывается таким образом: D(x^2 — 27x) и D(12sinx) соответственно.
Обозначение интервалов
Результатом решения задач на нахождение ОДЗ является определенный интервал. Важно правильно его обозначать, поскольку это существенно влияет на решение. Нужно руководствоваться следующими правилами:
- Жесткая граница обозначается квадратной скобкой «[» или «]». Она обозначает, что число входит включительно в этот интервал. Можно использовать не только одну скобку, но и две одновременно.
- Для обозначения числового значения, которое не входит в промежуток, пользуются круглыми скобками «(» и «)». Их можно применять одновременно.
- Типы границ можно комбинировать.
- Если нужно объединить интервалы, то следует использовать символ «U».
Очень важно правильно читать интервалы. Например, запись (1;4) читается следующим образом: переменная принимает значения, которые находятся в интервале от 1 не включительно до 4 не включительно. Это числа 2 и 3, поскольку 1 и 4 не входят в промежуток. Запись вида [5;10) читается таким образом: некоторое значение принадлежит интервалу от 5 включительно, до 10 не включительно.
Зависимость от типа
Функции различаются между собой. От этого и зависит нахождение их области определения. Они бывают простыми и сложными. Первые состоят из единичных элементов, а сложные включают в себя несколько типов. Их еще называют составными. Простые классифицируются на три вида:
- Алгебраические: рациональные и иррациональные.
- Тригонометрические: sin, cos, tg и ctg.
- Трансцендентные: степенные, показательные и логарифмические.
Рациональные бывают целыми и дробными. Они не включают в себя выражения, содержащие такие элементы: корень, степень, логарифм и тригонометрические функции. D(f) этих функций — все действительные числа (Z). Если она является дробной, то это означает, что в ее числителе и (или) знаменателе находится аргумент, значение которого не должно обращать ее в пустое множество.
Когда под корнем находится выражение, содержащее независимую переменную, то она называется иррациональной. В этом случае D(f) — множество Z, кроме тех, которые превращают выражение под корнем четной степени в отрицательное значение. Функция, представленная степенными выражениями, имеет D(f) = Z, но только тогда, когда значение аргумента не превращает функцию в пустое множество.
Метод нахождения
Для решения любой задачи нужно применять определенные правила. Они называются алгоритмом. Для каждого типа функций существует конкретный вариант решения. Для дробной он является следующим:
- Найти корни уравнения знаменателя, приравнивая его к 0.
- Определить интервал, значения из которого может принимать аргумент.
В случае, когда выражение является иррациональной функцией, корень которой является четным, следует решать не уравнение, а неравенство. Его значение не должно быть меньше 0. Для логарифмического типа выражение натурального логарифма (ln) должно быть всегда больше 0.
Для sin(x) и cos(x) областью определения является множество значений Z. Однако для tg(x) и ctg(x) следует помнить, что аргумент не должен принимать значение x = (Pi / 2) + Pi * k и x = Pi * k соответственно. Следует отметить, что коэффициент k принадлежит множеству чисел Z.
Для примера нужно разобрать задачу, в которой следует найти D(3x / [(x — 1) * (x + 1) * (10 — x)^(1/2)]). Решать ее необходимо по такому алгоритму:
- Знаменатель является сложным. Он состоит из двух выражений: (x — 1) * (x + 1) и (10 — x)^(1/2).
- Первое выражение (решить уравнение): (x — 1) * (x + 1) = 0. Оно имеет два корня: x1 = -1 и x2 = 1. Числовой промежуток: (-бесконечность;-1) U (1;+бесконечность).
- Второе (неравенство): (10 — x) < 0. Интервал: (-бесконечность;10].
- Результат (объединение всех интервалов): (-бесконечность;-1) U (1;10].
Данный пример показывает особенность решения задачи, которая заключается в объединении двух алгоритмов. Это довольно часто практикуется. Результат — объединение трех множеств, при объединении которых получается два интервала.
Сведения о производных
Производная — скоростное изменение какой-либо функции. Эта характеристика присуща не всем, поскольку некоторые из них являются постоянными. Если она имеет производную в некоторой точке, то является дифференцируемой. Дифференцирование применяется не только для исследования функций, но и во многих отраслях науки и техники.
Для нахождения дифференциалов необходима таблица производных. Кроме того, следует освоить все основные правила, поскольку не во всех случаях функция соответствует одному из табличных значений. Для этого нужно воспользоваться некоторыми свойствами. Математики-специалисты рекомендуют применять на начальных стадиях обучения алгоритм нахождения производной, который позволяет существенно сократить время выполнения задания, а также количество ошибок.
Таблица дифференциалов
В некоторых простых задачах возникает необходимость определить производную некоторой элементарной функции. Для этих целей применяется специальная таблица, в которой записаны основные простые выражения.
Данные значения были получены практическим методом — нахождением отношения приращения функции к приращению аргумента. Необходимо учитывать, что последний стремится к нулевому значению.
Однако иногда приходится упрощать выражение, а потом находить его производную. Для этого существует специальный простой алгоритм:
- Выполнить математические преобразования (упростить выражение).
- Найти производную по таблице.
Данный алгоритм справедлив только для простых выражений. Для сложных функций нужно руководствоваться некоторыми свойствами.
Основные свойства
Когда выражение не совпадает с табличным значением или состоит из нескольких элементов, то нужно применять специальные правила. Ими являются следствия из доказательств различных теорем. К ним можно отнести следующие:
- Если константа A (в некоторых источниках «С»), то при дифференцировании ее можно выносить за знак производной: (A * f(x))’ = A(f(x))’.
- Дифференциал суммы или разности 2 и более функций эквивалентен дифференциалу каждой из них: (w(x) + z(x))’ = w'(x) + z'(x) и (w(x) — z(x))’ = w'(x) — z'(x).
- Производная произведения 2 функций соответствует сумме, которая является произведением каждой из них на дифференциал другой: (w(x) * z(x))’ = (w'(x) * z(x) + w(x) * z'(x).
- Если нужно взять производную дробной функции вида w(x) / z(x), то результат действия является дробью, числитель которой равен разности произведений дифференциала числителя на знаменатель, и дифференциала знаменателя, умноженного на числитель. Знаменатель результирующей дроби соответствует знаменателю исходной функции, возведенного в квадрат: (w(x) / z(x))’ = [(w'(x) * z(x) — w(x) * z'(x)] / (z(x))^2.
В некоторых случаях функция является сложной. Для нахождения ее дифференциала нужно разбить ее на составные функции. Затем взять отдельно производную каждого из элементов. Результат — произведение дифференциалов всех элементов. Например, нужно найти дифференциал z = (1/8 * sin (4x^4 — 3x^3 + 6). Алгоритм решения следующий:
- По правилу нужно вынести константу, равную 1/8.
- Состоит из 2 частей: sin и (4x^4 — 3x^3 + 6).
- Производная последней — дифференциал разности (2 свойство): [4x^4 — 3x^3 + 6]’ = ((4 * x^3) / 4) — ((3 * x^2) / 3) + 0 = x^3 — x^2.
- Для второй: (sinx)’ = cosx.
- Итоговый результат: z’ = (1/8) * (x^3 — x^2) * sin (4x^4 — 3x^3 + 6).
Очень важно уметь разбивать выражение на части, поскольку от этого зависит результат решения. В некоторых случаях выражение можно упростить.
Наибольшее и наименьшее значения
Задачи на нахождения максимума и минимума применяются не только в математике, но и в бизнесе, науке, производстве и т. д. Например, вычисление наименьшего значения функции на отрезке (за последний промежуток времени) позволяет узнать минимизацию издержек производства. Кроме того, можно определить максимальную прибыль, найти оптимальную загрузку техники и т. д. Данные значения следует искать на каких-либо интервалах. Они классифицируются следующим образом:
- Отрезок: [a;b].
- Открытый тип: (a;b), (a;b] и [a;b).
- Промежуток бесконечности (в некоторой литературе обозначается «inf»): (-бесконечность;а], (-inf;а), [a;+inf), (a;+inf) и (-inf;+inf).
Следует отметить, что наибольшее и наименьшее значение производной по графику функции можно также найти, однако расчетный метод намного проще.
Универсальный алгоритм
Для данной операции, как и для других математических действий, существуют определенные правила или последовательность действий, которые называются алгоритмом. Специалисты для решения различных задач в любых сферах рекомендуют использовать их. Они позволяют не только существенно экономить время, минимизируя количество вычислений, но и с их помощью можно избежать некоторых ошибок. Суть алгоритма очень проста. Он состоит из определенной последовательности таких шагов:
- Найти D(f(x)).
- Проверить вхождение заданного интервала.
- Взять производную и выполнить поиск всех точек, в которых она не существует (их может и не быть).
- Приравнять к нулю результат, полученный в пункте 4, и найти корни уравнения. Это и будут стационарные точки, но они могут не существовать.
- Подставить в исходную функцию значения границ и стационарные точки.
- Выбрать из них MAX(f(x)) и MIN(f(x)).
Выполнение шестого шага зависит от вида интервала. В некоторых случаях можно просто подставить значение, а в других — найти предел. Если указана скобка «[» или «]», то x равен значению возле этой скобки. Когда указаны круглые скобки, нужно брать предел x = lim (f(x)), где x стремится к числовому значению или бесконечности, которые находятся возле скобки (x->a). Например, (a;+inf): х = lim [f(x)], где x->a и x->+inf.
Для нахождения минимального и максимального значения функции достаточно материала, изложенного выше. Специалисты рекомендуют разобраться с теорией, а затем переходить к практике.
Примеры решений
Дана квадратичная функция y = x^2 + 6x + 9. Необходимо найти наименьшее значение функции квадратного уравнения на отрезке [1;5]. Для этой цели нужно воспользоваться алгоритмом:
- D(y): все множество Z.
- Отрезок входит в D(y).
- Производная: y’ = [x^2 + 6x + 9]’ = 2x + 6 (существует во всех точках).
- Стационарные точки (y’ = 0): 2x + 6 = 0. Отсюда, x = -3.
- Подставить в исходное выражение: y(-3) = (-3)^2 + 6 * (-3) + 9 = 9 — 18 + 9 = 0, y(1) = (1)^2 + 6 * (1) + 9 = 1 + 6 + 9 = 16 и y(5) = (5)^2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.
- Максимум и минимум (с учетом стационарной точки и интервала): MIN(y) = 0 и MAX(y) = 64.
Одним из простейших типов задач является следующая: найдите наибольшее значение линейной функции z = 5x + 10 на отрезке [-3;3]. Для ее решения можно также воспользоваться алгоритмом:
- D(z) — все значения от бесконечно малого до бесконечно большого чисел.
- Промежуток, на котором нужно найти максимум и минимум, полностью входит в D(f).
- Дифференциал: z’ = 5 (существует во всех точках, а стационарных точек нет вообще).
- Минимум и максимум: MIN(z(-3)) = 5 * (-3) + 10 = -5 и MAX(z(3)) = 5 * (3) + 10 = 25.
Последнюю задачу необязательно решать по алгоритму, поскольку она считается простейшей. Математики рекомендуют тренироваться в нахождении MIN и MAX функции, поскольку только практика позволяет быстро решать задачи.
Таким образом, для нахождения максимального и минимального значений заданной функции необходимо пользоваться специальным универсальным алгоритмом. Кроме того, нужно правильно находить дифференциалы, область определения, а также разбираться в интервалах.
Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.
Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.
Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].
Решение
Сначала вычисляем производную исходной функции:
y′=3×2−12xy’=3x^2-12x
Затем приравниваем ее к нулевому значению и решаем уравнение:
3×2−12x=03x^2-12x=0
x(3x−12)=0x(3x-12)=0
x1=0x_1=0
x2=4x_2=4
Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.
Находим значение функции в точке x1x_1:
f(0)=9f(0)=9
Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:
f(−1)=−1−6+9=2f(-1)=-1-6+9=2
f(2)=8−24+9=−7f(2)=8-24+9=-7
Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.
Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.
Решение
Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:
y′=6xy’=6x
Приравниваем производную к нулю:
6x=06x=0
x=0x=0
Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.
Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.
Тест по теме “Наибольшие и наименьшие значения функции”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
12. Исследование функций с помощью производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Поиск наибольшего/наименьшего значения у сложных функций
(blacktriangleright) Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке ([a,b]), необходимо схематично изобразить график функции на этом отрезке.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).
(blacktriangleright) Не стоит забывать, что наибольшее/наименьшее значение функция может принимать не только во внутренних точках отрезка ([a,b]), а также на его концах.
(blacktriangleright) Наибольшее/наименьшее значение функции — это значение координаты (y=f(x)).
(blacktriangleright) Производная сложной функции (f(t(x))) ищется по правилу: [{Large{f'(x)=f'(t)cdot t'(x)}}]
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]
Задание
1
#2357
Уровень задания: Равен ЕГЭ
Найдите наименьшее значение функции (y = e^{x^2 — 4}) на отрезке ([-10; -2]).
ОДЗ: (x) – произвольный.
1) [y’ = 2xcdot e^{x^2 — 4}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2xcdot e^{x^2 — 4} = 0qquadLeftrightarrowqquad x = 0,.] Таким образом, (y’ = 0) при (x = 0). Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-10; -2]):
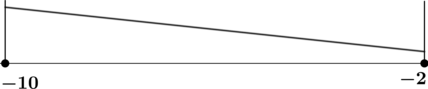
4) Эскиз графика на отрезке ([-10; -2]):
Таким образом, наименьшего на ([-10; -2]) значения функция достигает в (x = -2).
[y(-2) = e^{4 — 4} = 1,.] Итого: (1) – наименьшее значение функции (y) на ([-10; -2]).
Ответ: 1
Задание
2
#2355
Уровень задания: Равен ЕГЭ
Найдите наибольшее значение функции (y = sqrt{2}cdotsqrt{x^2 + 1}) на отрезке ([-1; 1]).
ОДЗ: (x) – произвольный.
1) [y’ = sqrt{2}cdotdfrac{2x}{2sqrt{x^2 + 1}} = sqrt{2}cdotdfrac{x}{sqrt{x^2 + 1}}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [sqrt{2}cdotdfrac{x}{sqrt{x^2 + 1}} = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-1; 1]):
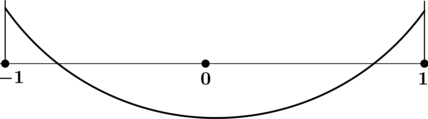
4) Эскиз графика на отрезке ([-1; 1]):
Таким образом, наибольшего на ([-1; 1]) значения функция достигает в (x = -1) или в (x = 1). Сравним значения функции в этих точках.
[y(-1) = sqrt{2}cdotsqrt{1 + 1} = sqrt{2}cdotsqrt{2} = 2qquad y(1) = sqrt{2}cdotsqrt{1 + 1} = sqrt{2}cdotsqrt{2} = 2,.] Итого: (2) – наибольшее значение функции (y) на ([-1; 1]).
Ответ: 2
Задание
3
#2356
Уровень задания: Равен ЕГЭ
Найдите наименьшее значение функции (y = cos 2x) на отрезке ([0; pi]).
ОДЗ: (x) – произвольный.
1) [y’ = -2cdot sin 2x]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-2cdot sin 2x = 0qquadLeftrightarrowqquad 2x = pi n, ninmathbb{Z}qquadLeftrightarrowqquad x = dfrac{pi n}{2}, ninmathbb{Z},.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):
(здесь бесконечное число промежутков, в которых чередуются знаки производной).
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([0; pi]):
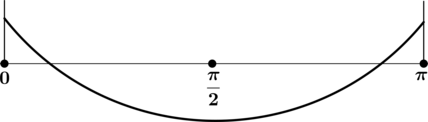
4) Эскиз графика на отрезке ([0; pi]):
Таким образом, наименьшего на ([0; pi]) значения функция достигает в (x = dfrac{pi}{2}).
[yleft(dfrac{pi}{2}right) = cos pi = -1,.] Итого: (-1) – наименьшее значение функции (y) на ([0; pi]).
Ответ: -1
Задание
4
#915
Уровень задания: Равен ЕГЭ
Найдите наибольшее значение функции
(y = -log_{17}(2x^2 — 2sqrt{2}x + 2)).
ОДЗ: (2x^2 — 2sqrt{2}x + 2 > 0). Решим на ОДЗ:
1) Обозначим (2x^2-2sqrt{2}x+2=t(x)), тогда (y(t)=-log_{17}t).
[y’ = y’_tcdot t’_x = (-log_{17}t)’cdot(2x^2-2sqrt{2}x+2)’ = -dfrac{1}{ln 17}cdotdfrac{1}{t}cdot(4x-2sqrt{2}) = -dfrac{1}{ln 17}~cdot~dfrac{4x-2sqrt{2}}{2x^2-2sqrt{2}x+2}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-dfrac{1}{ln 17}cdotdfrac{4x-2sqrt{2}}{2x^2-2sqrt{2}x+2} = 0qquadLeftrightarrowqquad 4x-2sqrt{2} = 0] – на ОДЗ, откуда находим корень (x = dfrac{sqrt{2}}{2}). Производная функции (y) не существует при (2x^2-2sqrt{2}x+2 = 0), но у данного уравнения отрицательный дискриминант, следовательно, у него нет решений. Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
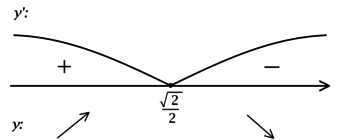
2) Найдём промежутки знакопостоянства (y’):
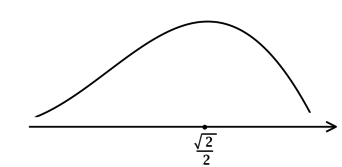
3) Эскиз графика:
Таким образом, наибольшее значение функция достигает в (x = dfrac{sqrt{2}}{2}):
(yleft(dfrac{sqrt{2}}{2}right) = -log_{17}1 = 0),
Итого: (0) – наибольшее значение функции (y).
Ответ: 0
Задание
5
#2344
Уровень задания: Равен ЕГЭ
Найдите наименьшее значение функции
(y = log_{3}(x^2 + 8x + 19)).
ОДЗ: (x^2 + 8x + 19 > 0). Решим на ОДЗ:
1) Обозначим (x^2 + 8x + 19=t(x)), тогда (y(t)=log_{3}t).
[y’ = y’_tcdot t’_x = (log_{3}t)’cdot(x^2 + 8x + 19)’ = dfrac{1}{ln 3}cdotdfrac{1}{t}cdot(2x+8) = dfrac{1}{ln 3}~cdot~dfrac{2x+8}{x^2 + 8x + 19}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1}{ln 3}cdotdfrac{2x+8}{x^2 + 8x + 19} = 0qquadLeftrightarrowqquad 2x+8 = 0] – на ОДЗ, откуда находим корень (x = -4). Производная функции (y) не существует при (x^2 + 8x + 19 = 0), но у данного уравнения отрицательный дискриминант, следовательно, у него нет решений. Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
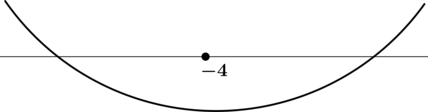
3) Эскиз графика:
Таким образом, (x = -4) – точка минимума функции (y) и наименьшее значение достигается в ней:
(y(-4) = log_{3}3 = 1).
Итого: (1) – наименьшее значение функции (y).
Ответ: 1
Задание
6
#917
Уровень задания: Сложнее ЕГЭ
Найдите наибольшее значение функции
(y = -e^{(x^2 — 12x + 36 + 2ln 2)}).
1) Обозначим (x^2 — 12x + 36 + 2ln 2=t(x)), тогда (y(t)=-e^{t}).
[y’ = y’_tcdot t’_x = (-e^{t})’cdot(x^2 — 12x + 36 + 2ln 2)’ = -e^{t}cdot(2x-12) = -e^{x^2 — 12x + 36 + 2ln 2}cdot(2x-12).]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-e^{x^2 — 12x + 36 + 2ln 2}cdot(2x-12) = 0qquadLeftrightarrowqquad 2x-12 = 0] (так как (e^{x^2 — 12x + 36 + 2ln 2} = e^{t}), но (e^{t} > 0) при любом (t)), откуда находим корень (x = 6). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
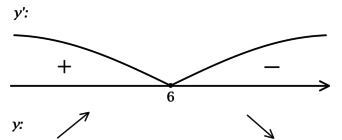
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика:
Таким образом, (x = 6) – точка максимума функции (y) и наибольшее значение достигается в ней:
(y(6) = -e^{(2ln 2)}=-e^{ln 4} = -4).
Итого: (-4) – наибольшее значение функции (y).
Ответ: -4
Задание
7
#918
Уровень задания: Сложнее ЕГЭ
Найдите наибольшее значение функции
(y = e^{cos x + sin x — sqrt{2}}).
1) Обозначим (cos x + sin x — sqrt{2}=t(x)), тогда (y(t)=e^{t}). [y’ = y’_tcdot t’_x = (e^{t})’cdot(cos x + sin x — sqrt{2})’ = e^{t}cdot(-sin x + cos x) = e^{cos x + sin x — sqrt{2}}cdot(-sin x + cos x).]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [e^{cos x + sin x — sqrt{2}}cdot(-sin x + cos x) = 0qquadLeftrightarrowqquad -sin x + cos x = 0] (так как (e^{cos x + sin x — sqrt{2}} = e^{t}), но (e^{t} > 0) при любом (t)), что равносильно (mathrm{tg}, x = 1) при (cos x neq 0), откуда находим корни (x = dfrac{pi}{4} + pi k, k in -mathbb{Z}). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
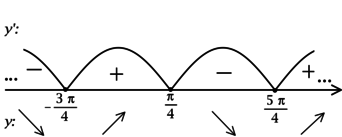
2) Найдём промежутки знакопостоянства (y’): (их бесконечно много, но они чередуются)
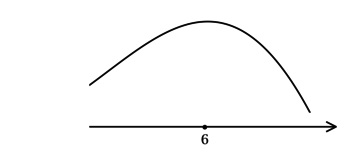
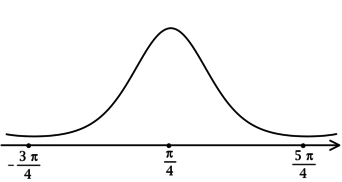
3) Эскиз графика:
Таким образом, (x = dfrac{pi}{4} + 2pi k, k in mathbb{Z}) – точки локальных максимумов функции (y) и наибольшее значение достигается в одной из них:
(yleft(dfrac{pi}{4} + 2pi kright) = e^{cosleft(frac{pi}{4} + 2pi kright) + sinleft(frac{pi}{4} + 2pi kright) — sqrt{2}} = e^{frac{sqrt{2}}{2} + frac{sqrt{2}}{2} — sqrt{2}} = e^{0} = 1).
Итого: (1) – наибольшее значение функции (y).
Ответ: 1

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды