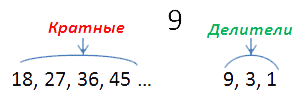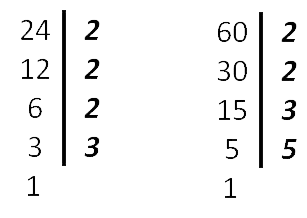Для того, чтобы находить общий знаменатель при сложении и вычитании дробей с разными знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).
Кратное числу « a » — это число, которое само делится на число « a » без остатка.
Числа кратные 8 (то есть, эти числа разделятся на 8 без остатка): это числа 16, 24, 32 …
Кратные 9: 18, 27, 36, 45 …
Чисел, кратных данному числу a бесконечно много, в отличии от делителей этого же числа. Делителей — конечное количество.
Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.
Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.
Как найти НОК
НОК можно найти и записать двумя способами.
Первый способ нахождения НОК
Данный способ обычно применяется для небольших чисел.
- Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
- Кратное числа « a » обозначаем большой буквой «К».
Пример. Найти НОК 6 и 8 .
Второй способ нахождения НОК
Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.
- Разложить данные числа на простые множители. Подробнее правила разложения на простые множители вы можете прочитать в теме как найти наибольший общий делитель (НОД).
- Выписать в строчку множители, входящие в разложение самого большого из чисел, а под ним — разложение остальных чисел.
Количество одинаковых множителей в разложениях чисел может быть разное.
НОК (24, 60) = 2 · 2 · 3 · 5 · 2
Ответ: НОК (24, 60) = 120
Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24) .
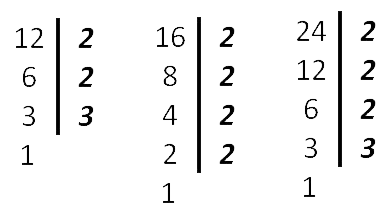
Как видим из разложения чисел, все множители 12 вошли в разложение 24 (самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из разложения числа 16 .
НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48
Ответ: НОК (12, 16, 24) = 48
Особые случаи нахождения НОК
- Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.
Например, НОК (60, 15) = 60
Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее кратное равно произведению этих чисел.
На нашем сайте вы также можете с помощью специального калькулятора найти наименьшее общее кратное онлайн, чтобы проверить свои вычисления.
Рассмотрим три способа нахождения наименьшего общего кратного.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наименьшего общего кратного путём разложения данных чисел на простые множители.
Допустим, нам требуется найти НОК чисел: 99, 30 и 28. Для этого разложим каждое из этих чисел на простые множители:
Чтобы искомое число делилось на 99, на 30 и на 28, необходимо и достаточно, чтобы в него входили все простые множители этих делителей. Для этого нам необходимо взять все простые множители этих чисел в наибольшей встречающейся степени и перемножить их между собой:
2 2 · 3 2 · 5 · 7 · 11 = 13 860
Таким образом, НОК (99, 30, 28) = 13 860. Никакое другое число меньше 13 860 не делится нацело на 99, на 30 и на 28.
Чтобы найти наименьшее общее кратное данных чисел, нужно разложить их на простые множители, затем взять каждый простой множитель с наибольшим показателем степени, с каким он встречается, и перемножить эти множители между собой.
Так как взаимно простые числа не имеют общих простых множителей, то их наименьшее общее кратное равно произведению этих чисел. Например, три числа: 20, 49 и 33 – взаимно простые. Поэтому
НОК (20, 49, 33) = 20 · 49 · 33 = 32 340.
Таким же образом надо поступать, когда отыскивается наименьшее общее кратное различных простых чисел. Например, НОК (3, 7, 11) = 3 · 7 · 11 = 231.
Нахождение путём подбора
Второй способ заключается в нахождении наименьшего общего кратного путём подбора.
Пример 1. Когда наибольшее из данных чисел делится нацело на другие данные числа, то НОК этих чисел равно большему из них. Например, дано четыре числа: 60, 30, 10 и 6. Каждое из них делится нацело на 60, следовательно:
НОК (60, 30, 10, 6) = 60
В остальных случаях, чтобы найти наименьшее общее кратное используется следующий порядок действий:
- Определяем наибольшее число из данных чисел.
- Далее находим числа, кратные наибольшему числу, умножая его на натуральные числа в порядке их возрастания и проверяя делятся ли на полученное произведение остальные данные числа.
Пример 2. Дано три числа 24, 3 и 18. Определяем самое большое из них – это число 24. Далее находим числа кратные 24, проверяя делится ли каждое из них на 18 и на 3:
24 · 1 = 24 – делится на 3, но не делится на 18.
24 · 2 = 48 – делится на 3, но не делится на 18.
24 · 3 = 72 – делится на 3 и на 18.
Таким образом, НОК (24, 3, 18) = 72.
Нахождение путём последовательного нахождения НОК
Третий способ заключается в нахождении наименьшего общего кратного путём последовательного нахождения НОК.
НОК двух данных чисел равно произведению этих чисел, поделённого на их наибольший общий делитель.
Пример 1. Найдём НОК двух данных чисел: 12 и 8. Определяем их наибольший общий делитель: НОД (12, 
Делим произведение на их НОД:
Таким образом, НОК (12, 
Чтобы найти НОК трёх и более чисел используется следующий порядок действий:
- Сначала находят НОК каких-нибудь двух из данных чисел.
- Потом, НОК найденного наименьшего общего кратного и третьего данного числа.
- Затем, НОК полученного наименьшего общего кратного и четвёртого числа и т. д.
- Таким образом поиск НОК продолжается до тех пор, пока есть числа.
Пример 2. Найдём НОК трёх данных чисел: 12, 8 и 9. НОК чисел 12 и 8 мы уже нашли в предыдущем примере (это число 24). Осталось найти наименьшее общее кратное числа 24 и третьего данного числа – 9. Определяем их наибольший общий делитель: НОД (24, 9) = 3. Перемножаем НОК с числом 9:
Содержание статьи
- Как найти наименьшее общее кратное чисел
- Что такое взаимно простые числа
- Как разложить на множители числа
Нахождение наименьшего общего кратного: основные понятия
Чтобы понять, как вычислять НОК, следует определиться в первую очередь со значением термина «кратное».
Кратным числу А называют такое натуральное число, которое без остатка делится на А. Так, числами кратными 5 можно считать 15, 20, 25 и так далее.
Делителей конкретного числа может быть ограниченное количество, а вот кратных бесконечное множество.
Общее кратное натуральных чисел – это такое число, которое делится на них без остатка.
Как найти наименьшее общее кратное чисел
Наименьшее общее кратное (НОК) чисел (двух, трех или больше) – это самое маленькое натурально число, которое делится на все эти числа нацело.
Чтобы найти НОК, можно использовать несколько способов.
Для небольших чисел удобно выписать в строчку все кратные этих чисел до тех пор, пока среди них не найдется общее. Кратные обозначают в записи заглавной буквой К.
Например, кратные числа 4 можно записать так:
Так, можно увидеть, что наименьшим общим кратным чисел 4 и 6 является число 24. Эту запись выполняют следующим образом:
Если числа большие, или нужно найти наименьшее общее кратное трех и более чисел, то лучше использовать другой способ вычисления НОК.
Для выполнения задания необходимо разложить предложенные числа на простые множители.
Сначала нужно выписать в строчку разложение наибольшего из чисел, а под ним – остальных.
В разложении каждого числа может присутствовать различное количество множителей.
Например, разложим на простые множители числа 50 и 20.
В разложении меньшего числа следует подчеркнуть множители, которые отсутствуют в разложении первого самого большого числа, а затем их добавить к нему. В представленном примере не хватает двойки.
Теперь можно вычислить наименьшее общее кратное 20 и 50.
НОК (20, 50) = 2 * 5 * 5 * 2 = 100
Так, произведение простых множителей большего числа и множителей второго числа, которые не вошли в разложение большего, будет наименьшим общим кратным.
Чтобы найти НОК трех чисел и более, следует их все разложить на простые множители, как и в предыдущем случае.
В качестве примера можно найти наименьшее общее кратное чисел 16, 24, 36.
Так, в разложение большего числа на множители не вошли только две двойки из разложения шестнадцати (одна есть в разложении двадцати четырех).
Таким образом, их нужно добавить к разложению большего числа.
НОК (12, 16, 36) = 2 * 2 * 3 * 3 * 2 * 2 = 9
Существуют частные случаи определения наименьшего общего кратного. Так, если одно из чисел можно поделить без остатка на другое, то большее из этих чисел и будет наименьшим общим кратным.
Например, НОК двенадцати и двадцати четырех будет двадцать четыре.
Если необходимо найти наименьшее общее кратное взаимно простых чисел, не имеющих одинаковых делителей, то их НОК будет равняться их произведению.
|
Натуральные числа — это ряд чисел, образуемый при счете предметов или обозначении их количества. Числа эти только положительные и целые (не дробные). Обозначается множество натуральных чисел буквой N. Наименьшее натуральное число — это единица, а не нуль, как некоторые считают. Мы не можем считать предметы или людей, начиная с нуля. Наибольшего натурального числа нет и быть не может. Так как множество натуральных чисел — бесконечно. автор вопроса выбрал этот ответ лучшим Михаил Белодедов 9 лет назад Наименьшее натуральное число — один. А что касается наибольшего, то его, увы, не существует. Доказывается элементарно, от противного. Предположим, оно есть. Раз оно — натуральное число, к нему применимы все действия, применимые к натуральным числам. Прибавляем единицу и сравниваем. Legrana 6 лет назад Наименьшее натуральное число — это единица (один), а вовсе не ноль, как думают некоторые. Ведь натуральные числа используют при подсчете предметов или же для обозначении их количества. А что касается, наибольшего натурального числа — то его не существует, так как ряд натуральных чисел стремится к бесконечности — конечного числа быть не может, к нему всегда можно добавить плюс один. Ксарфакс 4 года назад Числа, которые используются для подсчёта предметов (объектов), называются натуральными. Примеры подобных чисел: 1, 2, 5, 10, 100 и т.д. ** Наименьшее натуральное число Таким числом принято считать 1, а не 0. И это правильно — ведь при подсчёте чего-либо мы увеличиваем общее количество на самое маленькое число, то есть на единицу. Но некоторые математики (например, Н. Бурбаки) всё же включают 0 в множество натуральных чисел. ** Наибольшее натуральное число Его не существует. Если объяснять это простыми словами, то подсчет чего-либо можно вести до бесконечности и увеличивать совокупность каких-то предметов искусственным образом. Например, сейчас на нашей планете проживает более 7,5 миллиарда человек. Но если сюда прибавлять всех домашних животных, которые живут с ними, то это число увеличиться в разы. А затем можно прибавить личный транспорт и т.п. ** Если обобщить, то к натуральным числам будут относиться все целые положительные числа. N = {1, 2, 3…} Galina7v7 5 лет назад Когда говорят о натуральных числах, то любой читающий это понятие должен чётко представить, что это ряд целых и положительных чисел от 1 до любого сколько-нибудь большого, но конечного числа, будь то миллион, миллиард, или ещё какое-то число, но конечное. Естественно, отрицательные числа сюда тоже не входят. О бесконечном числе тоже речь не идёт. Всё это потому, что натуральное число это то число, с помощью которого можно посчитать количество предметов любого качества, а счёт, как правило ведётся с помощью только целых и конечных чисел. И ещё: число 0 в натуральный ряд не входит. И для наглядности нужно запомнить: натуральное число это одно из ряда: 1, 2, 3, 4, 5…И ряд можно продолжить до любого конечного числа. —.—.—.—.— -.—.—.—.—> числовая ось 1 2 3 4 5 ……… 100000…… Божья коровка 8 лет назад Числа, с которых мы и начинаем свой счет, называются натуральными числами. С какого числа мы начинаем что-то считать? С единицы. Она считается наименьшим числом. Например, первый стул, второй стул, третий, четвертый и т.д. Считать можно до бесконечности (если мы, например, будет считать уже звезды). Именно по этой причине наибольшего числа из категории натуральных чисел не существует. Барамбулечка 8 лет назад При ответе на ваш вопрос невольно вспоминаешь теорию относительности Эйнштейна. Ведь то, что наименьшее натуральное число — это единица, никто не спорит, а вот говоря о наибольшем, все говорят, что его нет. Но почему же? Думаю есть, просто мы не имеем ума его сосчитать (например звезды). Это все равно, что для муравья сосчитать деревья в лесу. Но это не значит, что нет этого числа. PanaramWinxx 5 лет назад Числа, которые образуются при подсчете предметов или имея количество, и обозначение их это ряд натуральных чисел. Зачастую это положительные и целые и обозначаются эти множества натуральные числа латинской буквой N. Наименьшее это 1 некоторые 0 считают наименьшим, но это не правильно. Так как мы не можем посчитать сколько людей в комнате 0 это просто для примера. Целесообразно вообще их не считать. Наибольшее это когда натурального числа нет, поскольку натуральных чисел бесконечное количество. Ладлен 6 лет назад Да исходя из практики и теории чисел именно единица считается самым малым числом. А вот самого большого числа мы не знаем и возможно не узнаем, так как всегда можно число увеличить на единицу. Но тем не менее мы оперируем и с большими числами и сейчас применяемым в физике числом которое больше всех частиц во всей вселенной этот гугол, так назвали его физики и это число включает 100 нулей. Kobayashi 5 лет назад Поскольку практика и теория показывает что числа вроде единицы являются самым малым числом. Из этого выходит, что один наименьшее, а утверждать. Что наименьшее ноль это не верно. А наибольшего числа это когда нет натурального числа. Знаете ответ? |
Натуральные числа — одно из старейших
математических понятий.
В далёком прошлом люди не знали чисел и,
когда им требовалось пересчитать предметы
(животных, рыбу и т.д.), они делали это не так, как
мы сейчас.
Количество предметов сравнивали с частями тела, например, с
пальцами на руке и говорили: «У меня столько же орехов, сколько пальцев на руке».
Со временем люди поняли, что пять орехов, пять коз и пять зайцев обладают
общим свойством — их количество равно пяти.
Запомните!
Натуральные числа — это числа, начиная с 1, получаемые
при счете предметов.
1, 2, 3, 4, 5…
Наименьшее натуральное число — 1.
Наибольшего натурального числа не существует.
При счёте число ноль не используется. Поэтому ноль не
считается натуральным числом.
Записывать числа люди научились гораздо позже, чем считать. Раньше
всего они стали изображать единицу одной палочкой, потом
двумя палочками — число 2, тремя — число 3.
| — 1, || — 2, ||| — 3, ||||| — 5 …
Затем появились и особые знаки для обозначения чисел — предшественники современных
цифр. Цифры, которыми мы пользуемся для записи чисел, родились в Индии примерно 1 500
лет назад. В Европу их привезли арабы, поэтому их называют
арабскими цифрами.
Всего цифр десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С помощью этих
цифр можно записать любое натуральное число.
Запомните!
Натуральный ряд — это последовательность всех натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
В натуральном ряду каждое число больше предыдущего на 1.
Натуральный ряд бесконечен, наибольшего натурального числа в нём не существует.
Систему счёта (счисления), который мы пользуемся,
называют десятичной позиционной.
Десятичной потому, что 10 единиц каждого разряда образуют
1 единицу старшего разряда. Позиционной потому, что значение цифры
зависит от её места в записи числа, то есть от
разряда, в котором
она записана.
Важно!
Разряды и классы
(включая класс миллионов) подробно разобраны
на нашем сайте в материалах для начальной школы.
Класс миллиардов
Если взять десять сотен миллионов, то получим новую разрядную единицу —
один миллиард или в записи цифрами.
1 000 миллионов = 1 000 000 000 = 1 млрд
Десять таких единиц — десять миллиардов, десять десятков миллиардов образуют
следующую единицу — сто миллиардов.
Запомните!
Миллиарды, десятки миллиардов и сотни миллиардов образуют четвёртый
класс — класс миллиардов.
Разряды и классы натурального числа
Рассмотрим натуральное число 783 502 197 048
| Название класса |
Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) |
7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
| Название класса |
Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) |
7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
C помощью таблицы разрядов прочитаем это число. Для этого надо слева направо по очереди
называть количество единиц каждого класса и добавлять название класса.
Название класса
единиц не произносят, также не произносят название класса, если все три
цифры в его разрядах — нули.
Теперь прочтем число 783 502 197 048 из таблицы:
783 миллиарда 502 миллиона 197 тысяч
48.
Числа 1, 10, 100, 1000… называются разрядными единицами. С их помощью натуральное число
записывается в виде разрядных слагаемых. Так, например, число 307 898 будет выглядеть
в виде разрядных слагаемых.
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Проверить свои вычисления
вы можете с помощью нашего
калькулятора разложения числа на разряды онлайн.
Следующие за миллиардом классы названы в соответствии с латинскими
наименованиями чисел. Каждая следующая единица содержит тысячу предыдущих.
- 1 000 миллиардов = 1 000 000 000 000 = 1 триллион («три» — по латыни «три»)
- 1 000 триллионов = 1 000 000 000 000 000 = 1 квадриллион («квадра» — по латыни «четыре»)
- 1 000 квадриллионов = 1 000 000 000 000 000 000 = 1 квинтиллион («квинта» — по латыни «пять»)
Все числа пересчитать невозможно, поскольку за каждым числом следует число на единицу большее,
но очень большие числа в повседневной жизни не нужны.
Однако, физики нашли число, которое превосходит количество всех атомов (мельчайших частиц вещества)
во всей Вселенной.
Это число получило специальное название — гугол. Гугол — число, у которого
100 нулей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
7 сентября 2021 в 6:39
Анастасия Орнацкая
Профиль
Благодарили: 0
Сообщений: 1
Анастасия Орнацкая
Профиль
Благодарили: 0
Сообщений: 1
Рассмотрим частное от делений всевозможных двузначных натуральных чисел на суммы их цифр. Какое из частных окажется наибольшим?
0
Спасибо
Ответить
8 сентября 2021 в 3:32
Ответ для Анастасия Орнацкая
Александр Войтов
Профиль
Благодарили: 0
Сообщений: 1
Александр Войтов
Профиль
Благодарили: 0
Сообщений: 1
10
0
Спасибо
Ответить
7 октября 2020 в 10:53
Екатерина Шабан
Профиль
Благодарили: 0
Сообщений: 1
Екатерина Шабан
Профиль
Благодарили: 0
Сообщений: 1
Добрый день. Помогите с заданием: Найти все возможные значения натуральные числа x,y,z, таких, что произведение любых двух увеличеное на 1 будет делится на третье.
0
Спасибо
Ответить
10 октября 2020 в 1:07
Ответ для Екатерина Шабан
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Пусть x ≤ y ≤ z. Тогда xy + 1 = kz ≥ ky.
Откуда y(k — x) ≤ 1.
Тогда x = y = 1; k = 2; z=1;
Или x = y = 1; k = 1; z=2.
0
Спасибо
Ответить
4 декабря 2019 в 19:33
Иван Федянин
Профиль
Благодарили: 0
Сообщений: 1
Иван Федянин
Профиль
Благодарили: 0
Сообщений: 1
Известно, что c и d натуральные числа и 5c+d=33
Каким может быть число c?
Помогите решить и расписать решение.
0
Спасибо
Ответить
18 декабря 2019 в 12:03
Ответ для Иван Федянин
Эмма Аддамс
Профиль
Благодарили: 0
Сообщений: 2
Эмма Аддамс
Профиль
Благодарили: 0
Сообщений: 2
1. Натуральное число может быть только положительным и оно всегда отлично от нуля.
2. Таким образом, если 5с-d=33, то с= и это целое(!) число.
3. Значит, 33-d деится на 5 нацело.
4. Вспоминаем, что на пять делятся числа: 5, 10, 15, 20, 25, 30,…
5.Теперь находим значения d, а потом выражаем через них значения с.
33-d=5, d=28. c==1
33-d=10. d=23. c=2
………………………………….
и так далее до 33-d=30. d=3
Числа больше 35 мы не берем, поскольку тогда мы получим отрицательные значения чисел с и d, а это противоречит условию натуральности этих чисел
6. Ответ: с=1, 2, 3, 4, 5, 6.
Задача решена:)
А вот здесь онлайн занятия по математике
https://www.youtube.com/channel/UChuPWiMp13sUQ6G6oPTjzag
0
Спасибо
Ответить
13 февраля 2019 в 23:06
Mamikon Papikyan
Профиль
Благодарили: 0
Сообщений: 1
Mamikon Papikyan
Профиль
Благодарили: 0
Сообщений: 1
Здравствуйте. Помогите пожалуйста решить этот вопрос!!!как узнать сколько чисел заключенных между 1000 и 9999 содержат цифру 1?
0
Спасибо
Ответить
15 февраля 2019 в 23:26
Ответ для Mamikon Papikyan
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Всего чисел от 1000 до 9999 − 9000.
Чисел без 1 − 8 · 93.
Значит, остальные 9000 − 8 · 93 с единицей.
0
Спасибо
Ответить
15 ноября 2016 в 0:26
Злата Крамаренко
Профиль
Благодарили: 0
Сообщений: 3
Злата Крамаренко
Профиль
Благодарили: 0
Сообщений: 3
Найдите все пары натуральных чисел а и b, таких, что а ? b и выполнено равенство:
+
=
Я привела к дроби левой части к общему знаменателю, сделала правилом пропорции, получила: 10(а+в)=ав. После я предположила, что 10 — это как 5*2, 2*5, 10*1 и 1*10, натуральные числа. но если делать так, то получается, что во всех случаях одно из чисел отрицательное, т.е не натуральное. Пыталась как-то выделить одну переменную через другую, но не пришла ни к чему. И в конце я просто нашла методом подбора и логически это пары (например, 20 и 20, 15 и 30, 14 и 35), но методом подбора это задание решить нельзя, ведь натуральные числа это от 1 и до бесконечности. Что делать? Заранее спасибо.
0
Спасибо
Ответить
18 ноября 2016 в 2:07
Ответ для Злата Крамаренко
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
(11; 110); (12; 60); (14; 35); (15; 30); (20; 20).
b = 10 + .
0
Спасибо
Ответить
26 апреля 2016 в 18:35
Вика Вдовина
Профиль
Благодарили: 0
Сообщений: 1
Вика Вдовина
Профиль
Благодарили: 0
Сообщений: 1
Даны 10 натуральных чисел по порядку, когда убрали одно число, то сумма оставшихся чисел стала 961. Найдите это число?
0
Спасибо
Ответить
1 мая 2016 в 17:16
Ответ для Вика Вдовина
Миха Подписчик
Профиль
Благодарили: 0
Сообщений: 2
Миха Подписчик
Профиль
Благодарили: 0
Сообщений: 2
Пусть х — первое наименьшее число из 10 порядковых натуральных чисел.
Найдем сумму арифметической прогрессии этих чисел:
Сумма чисел без первого числа будет равна:
10х + 45 — х = 9х + 45
Если убрали не первое число, то полученная сумма больше, чем 961.
Составим неравенство и решим его:
9х + 45 > 961
9х > 961 — 45
9х > 916
х > 916: 9
x > 101,777777778
Допустим, что первое наименьшее число х = 102,
тогда сумма всех 10 чисел равна:
1065 — 961 = 104 — число, которое убрали.
Ответ: 104.
Надеюсь помог
0
Спасибо
Ответить
8 июня 2016 в 13:00
Ответ для Вика Вдовина
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Ответ: 104.
Пусть убрали число (k + p).
(k + 1) + (k + 2) +… + (k + 10) = 10k + 55 = 961 + (k + p)
=> p = 9k — 906.
Значит р равно 3 или 6.
p = 3 => k = 101;
p = 6 => 3k = 304, ?.
0
Спасибо
Ответить
11 декабря 2015 в 16:46
Вика Богатырёва
Профиль
Благодарили: 0
Сообщений: 1
Вика Богатырёва
Профиль
Благодарили: 0
Сообщений: 1
верно ли утверждение? а) 3,5 пренадлежит множеству натуральных чисел? б) 7 пренадлежит множеству дествительных чисел? в) 5,4 пренадлежит множеству рациональных чисел?
0
Спасибо
Ответить
14 декабря 2015 в 21:47
Ответ для Вика Богатырёва
Юрий Деченко
Профиль
Благодарили: 0
Сообщений: 4
Юрий Деченко
Профиль
Благодарили: 0
Сообщений: 4
а ложное, б)верно в)тоже верно
0
Спасибо
Ответить
Натуральные числа
Математика начинается с натуральных чисел. Мы оперируем ими ежедневно: складываем, вычитаем, умножаем. Это лишь верхушка айсберга. Мы попросили учителя математики рассказать, что такое натуральные числа и каковы их особенности
Натуральные числа применялись человеком всегда. Даже в древности, используя для счета пальцы или палочки, люди обращались к натуральным числам. Считали, по порядку на единицу увеличивая исходное значение. Ловили рыбу — один карась, второй, третий. Продавали зерно — один мешок, второй, третий. Делали пряжу — один клубок, второй, третий.
Дальше числа оформили графически, а сейчас с их помощью выполняют любые математические действия.
Определение натуральных чисел
Натуральное — это число, которое применяется при счете. С его помощью можно определить количество любых предметов, их осязаемую последовательность. Например, подсчитать, сколько денег в кошельке, ворон на ветке, долек в апельсине, цветов в радуге.
Ряд натуральных чисел открывает единица. А замыкающего у него нет — он бесконечен. При этом в натуральном ряду каждый следующий символ на единицу больше предшественника — 10, 11, 12… Только так и никак иначе.
К натуральным не относятся отрицательные числа, дроби и ноль. С их помощью мы не можем посчитать конкретные, осязаемые предметы.

Натуральными не являются числа, которые не применяются для счета предметов, например отрицательные числа и дроби
Натуральные числа классифицируются по разрядам. Разряд зависит от количества знаков в числе. Как правило, в повседневной жизни используются первые пятнадцать разрядов натуральных чисел: единицы (1, 2, 3), десятки (10, 20, 30), сотни (100, 200, 300) и далее вплоть до сотен триллионов (пятнадцатый разряд).
В каждом разряде натуральные числа различаются по классам, чтобы с помощью них было удобнее считать. Например, в числе 238 672 последние три цифры представляют класс единицы, а первые три — класс тысячи. При этом внутри класса каждое число занимает свое место — сотни, десятки, единицы (238, 672).
Получается, что четкая иерархия и понятная последовательность — главные принципы натуральных чисел. Простота, удобство и универсальность — их основной конек. Поэтому каждый человек в любой точке земного шара, знакомый с десятичной системой исчисления, знает, как прочитать любое число и как с ним работать.
Свойства натуральных чисел
Считать, считать и еще раз считать. Это их прямое и самое важное назначение. С их помощью выполняются самые популярные математические расчеты. Они помогают сложить и умножить числа, вычесть из одного другое, разделить и возвести в степень.
При этом отдельные свойства натуральных чисел упрощают их использование, делая счет простым и понятным. Например, перемена мест слагаемых или множителей при неизменном итоговом результате.
Число ПИ
Что это такое, для чего оно нужно и чему равно
Подробнее
Примеры натуральных чисел
100, 5769, 13, 48221, 487654321 — любое целое положительное число будет натуральным.
Популярные вопросы и ответы
Отвечает Наталия Черняк, учитель математики; профессиональный стаж работы — 11 лет.
Какие числа не являются натуральными?
Натуральными не являются числа, которые не применяются для счета предметов. В математике это отрицательные и нецелые числа. Вот простой пример. Зимой столбик термометра опускается ниже ноля градусов, показывая значения: -3, -10, -25. Эти числа отрицательные. Они натуральными не являются. Что касается нецелых чисел, то здесь приведу такой пример. В корзине лежало пять целых яблок и еще одна половинка. Половинка – это нецелое яблоко, ее нельзя представить целым числом. Ее записывают с помощью дробей: 0,5 или ½. Дроби также не относятся к натуральным числам.
Что такое наименьшее натуральное число?
Применительно к нашей корзинке с яблоками это минимальное количество фруктов, которое может в ней лежать. Наименьшим натуральным числом принято считать единицу. Именно с нее начинается счет предметов.
Относится ли ноль к натуральным числам?
Ноль означает некое отсутствие чего-либо, счет предметов с него не начинается. Соответственно, к натуральным числам он не относится.
В математике существует несколько различных множеств чисел: действительные, комплексные, целые, рациональные, иррациональные, дробные… В нашей повседневной жизни мы чаще всего используем натуральные числа, так как мы сталкиваемся с ними при счете и при поиске, обозначении количества предметов….
Какие числа называются натуральными
Из десяти цифр можно записать абсолютно любую существующую сумму классов и разрядов. Натуральными значениями считаются те, которые используются:
- При счете каких-либо предметов (первый, второй, третий, … пятый, … десятый).
- При обозначении количества предметов (один, два, три…)
N значения всегда целые и положительные. Наибольшего N не существует, так как множество целых значений не ограничено.
Внимание! Натуральные числа получаются при счете предметов или при обозначении их количества.
Абсолютно любое число может быть разложено и представлено в виде разрядных слагаемых, например: 8.346.809=8 миллионов+346 тысяч+809 единиц.
Множество N
Множество N находится в множестве действительных, целых и положительных. На схеме множеств они бы находились друг в друге, так как множество натуральных является их частью.
Множество натуральных чисел обозначается буквой N. Это множество имеет начало, но не имеет конца.
Еще существует расширенное множество N, где включается нуль.
Наименьшее натуральное число
Но в иностранных математических школах, например во французской, нуль считается натуральным. Наличие в ряде нуля облегчает доказательство некоторых теорем.
Ряд значений N, включающий в себя нуль, называется расширенным и обозначается символом N0 (нулевой индекс).
Ряд натуральных чисел
N ряд – это последовательность всех N совокупностей цифр. Эта последовательность не имеет конца.
Особенность натурального ряда заключается в том, что последующее число будет отличаться на единицу от предыдущего, то есть возрастать. Но значения не могут быть отрицательными.
Внимание! Для удобства счета существуют классы и разряды:
- Единицы (1, 2, 3),
- Десятки (10, 20, 30),
- Сотни (100, 200, 300),
- Тысячи (1000, 2000, 3000),
- Десятки тысяч (30.000),
- Сотни тысяч (800.000),
- Миллионы (4000000) и т.д.
Все N
Все N находятся во множестве действительных, целых, неотрицательных значений. Они являются их составной частью.
Эти значения уходят в бесконечность, они могут принадлежать классам миллионов, миллиардов, квинтиллионов и т.д.
Например:
- Пять яблок, три котенка,
- Десять рублей, тридцать карандашей,
- Сто килограммов, триста книг,
- Миллион звезд, три миллиона человек и т.д.
Последовательность в N

от нуля до плюс бесконечности, включая концы, и от единицы до плюс бесконечности, включая концы, то есть все положительные целые ответы.
N совокупности цифр могут быть как четными, так и не четными. Рассмотрим понятие нечетности.
Нечетные (любые нечетные оканчиваются на цифры 1, 3, 5, 7, 9.) при делении на два имеют остаток. Например, 7:2=3,5, 11:2=5,5, 23:2=11,5.
Что значит четные N
Любые четные суммы классов оканчиваются на цифры: 0, 2, 4, 6, 8. При делении четных N на 2, остатка не будет, то есть в результате получается целый ответ. Например, 50:2=25, 100:2=50, 3456:2=1728.
Важно! Числовой ряд из N не может состоять только из четных или нечетных значений, так как они должны чередоваться: за четным всегда идет нечетное, за ним снова четное и т.д.
Свойства N
Как и все другие множества, N обладают своими собственными, особыми свойствами. Рассмотрим свойства N ряда (не расширенного).
- Значение, которое является самым маленьким и которое не следует ни за каким другим – это единица.
- N представляют собой последовательность, то есть одно натуральное значение следует за другим (кроме единицы – оно первое).
- Когда мы производим вычислительные операции над N суммами разрядов и классов (складываем, умножаем), то в ответе всегда получается натуральное значение.
- При вычислениях можно использовать перестановку и сочетание.
- Каждое последующее значение не может быть меньше предыдущего. Также в N ряде будет действовать такой закон: если число А меньше В, то в числовом ряде всегда найдется С, для которого справедливо равенство: А+С=В.
- Если взять два натуральных выражения, например А и В, то для них будет справедливо одно из выражений: А=В, А больше В, А меньше В.
- Если А меньше В, а В меньше С, то отсюда следует, что А меньше С.
- Если А меньше В, то следует, что: если прибавить к ним одно и то же выражение (С), то А+С меньше В+С. Также справедливо, что если эти значения умножить на С, то АС меньше АВ.
- Если В больше А, но меньше С, то справедливо: В-А меньше С-А.
Внимание! Все вышеперечисленные неравенства действительны и в обратном направлении.
Как называются компоненты умножения

Для того, чтобы быстро и правильно умножать и уметь решать обратные задачи, необходимо знать компоненты умножения.
15.10=150. В данном выражении 15 и 10 являются множителями, а 150 – произведением.
Умножение обладает свойствами, которые необходимы при решении задач, уравнений и неравенств:
- От перестановки множителей конечное произведение не изменится.
- Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель (справедливо для всех множителей).
Например: 15.Х=150. Разделим произведение на известный множитель. 150:15=10. Сделаем проверку. 15.10=150. По такому принципу решаются даже сложные линейные уравнения (если упростить их).
Важно! Произведение может состоять не только из двух множителей. Например: 840=2.5.7.3.4
Что такое натуральные числа в математике?
Разряды и классы натуральных чисел
Вывод
Подведем итоги. N используются при счете или обозначении количества предметов. Ряд натуральных совокупностей цифр бесконечен, но он включает в себя только целые и положительные суммы разрядов и классов. Умножение тоже необходимо для того, чтобы считать предметы, а также для решения задач, уравнений и различных неравенств.
Это интересно! Легкие правила округления чисел после запятой