© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены
Задание:
Наименьшее значение первообразной F(x) для функции f(x)=x2-2x-3 на отрезке [0; 6] равно -9. Найдите наибольшее значение первообразной на этом отрезке.
Ответ: 18
Решение:
- 1
- 2
- 3
- 4
- 5
Оценка: 3.8 из 16
Комментарии
Всего комментариев: 0
Нахождение наибольших и наименьших значений.
Пусть функция u
= f (x1
, x2 ,…,
xn)
определена и непрерывна в некотором
ограниченном и замкнутом множестве D
и имеет на этом множестве конечные
частные производные (за исключением,
быть может, отдельных точек). Тогда эта
функция достигает на D
своего наибольшего и наименьшего
значения (см. свойства непрерывных
функций). Если это значение достигается
во внутренней точке множества, то,
очевидно, эта точка должна быть
стационарной; кроме того, наибольшее и
наименьшее значение может достигаться
на границе множества D.
Поэтому для определения наибольшего и
наименьшего значений функции на множестве
D требуется:
-
найти стационарные точки функции,
принадлежащие D, и
вычислить значения функции в этих
точках; -
найти наибольшее и наименьшее значение,
принимаемое функцией на границе
множества D; -
выбрать наименьшее и наибольшее из
полученных чисел, которые и будут
являться наименьшим и наибольшим
значениями функции на всем множестве
D.
Примеры.
-
Найдем наибольшее значение функции
z = sin
x + sin
y – sin
(x + y)
в треугольнике со сторонами х = 0,
у = 0, х + у = 2π. Стационарные точки
определяются из решения системы,
откуда
.
Единственной внутренней точкой данного
треугольника, являющейся решением
полученной системы, будет
,
в которой
.
Это значение оказывается наибольшим
и на всем рассматриваемом множестве,
так как на его границе z
= 0. -
Найдем наибольшее и наименьшее значения
функции z = x²
+ y² — 12x
+ 16y в области x²
+ y² ≤ 25.
,
откуда х =6, у = -8 – точка, не
лежащая в заданном круге. Следовательно,
наибольшее и наименьшее значения
данная функция принимает на границе
области, то есть на окружности x²
+ y² = 25. Составим
функцию Лагранжа
L (x,
y ) = x²
+ y² — 12x
+ 16y + λ (x²
+ y² — 25). Ее стационарные
точки найдем из системы.
Получим
,
откуда λ1 =1, λ2
= -3. Следовательно, стационарными
точками являются (3, -4) и (-3, 4). В первой
из них z = -75, во
второй z = 125. Эти
числа являются наименьшим и наибольшим
значениями z в заданной
области.
Лекция 6.
Первообразная. Неопределенный интеграл и его свойства. Табличные интегралы. Замена переменной и интегрирование по частям в неопределенном интеграле.
Определение 6.1. Функция F(x)
называется первообразной (для)
функции f(x)
на некотором множестве значений х,
если F΄(x)
= f(x)
на этом множестве.
Теорема 6.1. Если функции F(x)
и G(x)
являются первообразными одной и той же
функции f(x)
на некотором множестве, то необходимым
и достаточным условием этого является
то, что G(x)
= F(x)
+ C, где С – любая
постоянная.
Доказательство.
-
Пусть F(x)
— первообразная f(x),
то есть F΄(x)
= f(x).
Тогда для любого числа C
(F(x)
+ C)΄=
F΄(x)
+ C΄= F΄(x)
+ 0 = f(x),
то есть F(x)
+ C — первообразная
f(x). -
Пусть F(x)
и G(x)
– две различные первообразные одной
и той же функции f(x).
Тогда (F(x)
– G(x))΄=
F΄(x)
— G΄(x)
= f(x)
– f(x)
= 0, следовательно, F(x)
– G(x)
= C (по следствию из
теоремы Лагранжа). Теорема доказана.
Таким образом, если функция на данном
множестве имеет одну первообразную, то
она имеет их бесконечно много, причем
все они отличаются друг от друга
постоянными слагаемыми.
Определение 5.2. Совокупность всех
первообразных функции f(x)
на некотором множестве называется ее
неопределенным интегралом.
Обозначение:
.
f(x)
при этом называется подынтегральной
функцией, а f(x)dx
– подынтегральным выражением.
Свойства неопределенного интеграла.
1.
2.
3.
Действительно,
а
.
Но, поскольку С1+С2
– произвольная постоянная, выражения
в левой и правой частях равны.
4.
Замечание. Все перечисленные свойства
формулировались и доказывались в
предположении, что на некотором множестве
существуют первообразные функций f(x)
и g(x),
равные соответственно F(x)
и G(x).
Табличные интегралы.
Из определения первообразной и
неопределенного интеграла следует, что
таблицу основных интегралов можно
получить из таблицы основных производных
(см. лекцию 18 первой части курса), считая
производные табличных функций
подынтегральными функциями, а сами
функции – их первообразными.
1.
2.
3.
3΄)
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
Можно добавить к этой таблице еще
несколько формул, не следующих
непосредственно из таблицы производных,
но удобных для вычисления многих
интегралов, а именно:
14.
15.
Доказательство справедливости этих
формул предлагается провести
самостоятельно.
Примеры.
1.
2.
Соседние файлы в папке Лекции
- #
- #
13.06.20141.98 Mб40Курс лекций — Вычислительная математика.doc
- #
- #
1. Элементарные функции
2. Применение формул производной произведения и частного
| 2.1 | Найдите точку минимума функции y=(3-x)cdot e^{3-x}. | Смотреть видеоразбор |
| 2.2 | Найдите точку максимума функции y=(x^2-10x+10)cdot e^{5-x}. | Смотреть видеоразбор |
| 2.3 | Найдите наименьшее значение функции y=(x-1)e^x на отрезке [-1;1]. | Смотреть видеоразбор |
| 2.4 | Найдите наибольшее значение функции y=(10-x)sqrt{x+2} на отрезке [-1; 7]. | Смотреть видеоразбор |
| 2.5 | Найдите наименьшее значение функции y=2xsqrt{x}-9x+11 на отрезке [2; 9]. | Смотреть видеоразбор |
| 2.6 | Найдите наибольшее значение функции y=(x-2)^2(x-4)+5 на отрезке [1; 3]. | Смотреть видеоразбор |
| 2.7 | Найдите точку максимума функции y=(x+5)e^{5-x}. | Смотреть видеоразбор |
| 2.8 | Найдите точку минимума функции y=(10-x)e^{10-x}. | Смотреть видеоразбор |
| 2.9 | Найдите наименьшее значение функции y=x^2+frac{25+x^2-x^3}{x} на отрезке [1; 10]. | Смотреть видеоразбор |
3. Применение формулы производной сложной функции
4. Тригонометрические функции
| 4.1 | Найдите наибольшее значение функции y=8x-4tg;x-2pi+2 на отрезке [-frac{pi}{3}; frac{pi}{3}]. | Смотреть видеоразбор |
| 4.2 | Найдите наименьшее значение функции y=4sin{x}+3cos{x} на отрезке [0; 7]. | Смотреть видеоразбор |
| 4.3 | Найдите наибольшее значение функции y=2cos{x}-frac{18}{pi}x+4 на отрезке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.4 | Найдите наименьшее значение функции y=5sin{x}+frac{24}{pi}x+6 на отрезке [-frac{5pi}{6}; 0]. | Смотреть видеоразбор |
| 4.5 | Найдите наибольшее значение функции y=3tg{x}-3x+5 на отрезке [-frac{pi}{4}; 0]. | Смотреть видеоразбор |
| 4.6 | Найдите наименьшее значение функции y=3cos{x}-frac{48}{pi}x+19 на отрезке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.7 | Найдите наименьшее значение функции f(x)=sin{x}+sqrt{1+sin^2{x}}. | Смотреть видеоразбор |
| 4.8 | Найдите наибольшее значение функции y=33x-30sin{x}+29 на отрезке [-frac{pi}{2}; 0]. | Смотреть видеоразбор |
| 4.9 | Найдите точку максимума функции y=(2x-3)cos{x}-2sin{x}+5, принадлежащую промежутку (0; frac{pi}{2}). | Смотреть видеоразбор |
| 4.10 | Найдите точку максимума функции y=(2x-1)cos{x}-2sin{x}+5, на промежутке (0; frac{pi}{2}). | Смотреть видеоразбор |
| 4.11 | Найдите наибольшее значение функции y=2sin{x}-frac{36}{pi}x+9 на отрезке [-frac{5pi}{6}; 0]. | Смотреть видеоразбор |
| 4.12 | Найдите наибольшее значение функции y=7sqrt{2}cos{x}+7x-frac{7pi}{4}+4 на отрезке [0; frac{pi}{2}]. | Смотреть видеоразбор |
| 4.13 | Найдите наибольшее значение функции y=12cos{x}+6sqrt{3}x-2sqrt{3}pi+6 на отрезке [0; frac{pi}{2}]. | Смотреть видеоразбор |
| 4.14 | Найдите наибольшее значение функции y=12tg;x -12x+3pi-7 на отрезке [-frac{pi}{4}; frac{pi}{4}]. | Смотреть видеоразбор |
| 4.15 | Найдите наименьшее значение функции y=6cos{x}+frac{24x}{pi}+5 на промежутке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.16 | Найдите наименьшее значение функции y=3+frac{5pi}{4}-5x-5sqrt{2}cos{x} на отрезке [0; frac{pi}{2}]. | Смотреть видеоразбор |
| 4.17 | Найдите наименьшее значение функции y=5cos{x}-6x+4 на отрезке [-frac{3pi}{2}; 0]. | Смотреть видеоразбор |
| 4.18 | Найдите наибольшее значение функции y=15x-3sin{x}+5 на отрезке [-frac{pi}{2}; 0]. | Смотреть видеоразбор |
| 4.19 | Найдите наименьшее значение функции y=9cos{x}+14x+7 на отрезке [0; frac{3pi}{2}]. | Смотреть видеоразбор |
| 4.20 | Найдите наименьшее значение функции y=7sin{x}-8x+9 на отрезке [-frac{3pi}{2}; 0]. | Смотреть видеоразбор |
| 4.21 | Найдите наименьшее значение функции y=6cos{x}+frac{24}{pi}x+5 на отрезке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.22 | Найдите наибольшее значение функции y=10sin{x}-frac{36}{pi}x+7 на отрезке [-frac{5pi}{6}; 0]. | Смотреть видеоразбор |
5. Логарифмическая и показательная функции
| 5.1 | Найдите наименьшее значение функции y=3x-ln(x+3)^3 на отрезке [-2,5; 0]. | Смотреть видеоразбор |
| 5.2 | Найдите наименьшее значение функции y=9x-ln(9x)+3 на отрезке [frac{1}{18}; frac{5}{18}]. | Смотреть видеоразбор |
| 5.3 | Найдите наибольшее значение функции y=2x^2-13x+9cdot ln{x}+8 на отрезке [frac{13}{14}; frac{15}{14}]. | Смотреть видеоразбор |
| 5.4 | Найдите наименьшее значение функции y=5x-ln(x+5)^5 на отрезке [-4,5; 1]. | Смотреть видеоразбор |
| 5.5 | Найдите наименьшее значение функции y=7x-ln(x-2)^7 на отрезке [-1,5; 0]. | Смотреть видеоразбор |
| 5.6 | Найдите точку максимума функции y=ln(x+4)^2+2x+7. | Смотреть видеоразбор |
| 5.7 | Найдите наименьшее значение функции y=log_{sqrt{3}}(x-4sqrt{x-2}+5) на отрезке [5; 10]. | Смотреть видеоразбор |
| 5.8 | Найдите наименьшее значение функции y=4^x-2^{x+4}+100. | Смотреть видеоразбор |
6. Функции, в которых присутствует квадратичная в виде «вложенной»
| 6.1 | Найдите наименьшее значение функции y=2^{x^2+100x+2503} | Смотреть видеоразбор |
| 6.2 | Найдите наибольшее значение функции y=5^{-3x^2+18x-24}. | Смотреть видеоразбор |
| 6.3 | Найдите точку максимума функции y=-sqrt{x^2-8x+17}. | Смотреть видеоразбор |
| 6.4 | Найдите наибольшее значение функции y=3^{-7-6x-x^2}. | Смотреть видеоразбор |
| 6.5 | Найдите наибольшее значение функции y=log_5(4-2x-x^2)+3. | Смотреть видеоразбор |
| 6.6 | Найдите точку максимума функции y=sqrt{4-4x-x^2}. | Смотреть видеоразбор |
7. Задачи на первообразную (не входят в ЕГЭ этого года)
| 7.1 | Найдите первообразную F(x) для функции f(x)=frac{3x+2}{5}, если F(4)=5. В ответе укажите значение F(1). | Смотреть видеоразбор |
| 7.2 | Наименьшее значение первообразной F(x) для функции f(x)=x^2−2x−3 на отрезке [0;6] равно −9. Найдите наибольшее значение первообразной на этом отрезке. | Смотреть видеоразбор |
| 7.3 | Наименьшее значение первообразной F(x) для функции f(x)=x^2-2x-3 на отрезке [0; 6] равно −9. Найдите наибольшее значение первообразной на этом отрезке. | Смотреть видеоразбор |
| 7.4 | Найдите первообразную F(x) для функции f(x)=frac{3x+2}{5}, если F(4)=5. В ответе укажите значение F(1). | Смотреть видеоразбор |
| 7.5 | Один из двух нулей первообразной F(x) для функции f(x)=5x-1 равен -3. Найдите второй нуль. | Смотреть видеоразбор |
Данная тема часто встречается в заданиях ЕГЭ по математике базового уровня, поэтому рассмотрим её более подробно, вспоминая ранее изученные материалы в школьной программе.
Понятие функции в математике является одной из основных тем в математике. Говорят, что математика начинается именно с графиков и функций.
Ведь с помощью производной в ЕГЭ по математике функции находят минимальные и максимальные точки на графике, а также промежутки, на которых функция является убывающей либо возрастающей. Таким образом, получается с большой точностью построить графики. Основное правило, которое следует помнить – производная является скоростью изменения функции.
В данной статье подробно рассмотрены следующие темы:
– Вычисление производных и первообразных функций;
– Исследование функции на монотонность;
– Нахождение наибольшего и наименьшего значения функции.
При решении подобных заданий в ЕГЭ по математике нужно применять графики для наглядности. Тема производной в математике считается одной из наиболее сложных.
На этом рисунке
(рис. 1) изображены три функции. Быстрее других двух функций растёт третья, а это значит, что у неё наибольшая производная. Здесь нужно смотреть какая функция является крутой, то есть стремительно поднимается вверх, как изменяется при этом х. Производную обычно пишут как:
Рассмотрим как найти производную функции на примере графика
(рис. 2).
Представлен график у = а (х ). Отметим на графике точку А, её абсцисса – х0. Проводим через эту точку касательную на графике. Оцениваем, как круто возрастает функция. Для этого находим тангенс наклона касательной. Производная данной функции в х0 равна тангенсу наклона касательной, которая проведена на графике через эту точку.
Следует обратить внимание, что углом наклона касательной считается угол, находящийся меж касательной, также важно найти направление оси ОХ, которое является положительным. Часто выпускников интересует, понятие касательной, проведённой к графику. Нужно помнить, что это прямая, которая имеет только одну точку на графике.
Найдём тангенс а. Имеем в виду, что тангенс угла в прямоугольнике, являющемся прямоугольным, равен отношению катета, лежащего напротив.
Следует, что треугольник AMN: f ( х ) = tg a = AN /MN.
Так мы нашли производную, пользуясь помощью графика. Не применяя приэтот формулу. Такие задания часто можно встретить в заданиях ЕГЭ по математике.
Прямую задают с помощью уравнения: y = kx + b. K в данном уравнении является коэффициентом угла прямой. К равно тангенсу наклона прямой к х. Получается: f ( х0 ) = tg а = k.
Следует запомнить данную формулу, так как она является смыслом производной. Производная в х0 равняется коэффициенту угла касательной, которая проведена через эту точку на графике. Иначе говоря, производная равняется тангенсу наклона касательной к данному углу. У функции в различных точках возможна различная производная. Рассмотрим каким образом функция связана с производной.
Первообразные функции в ЕГЭ по математике
Для функция F ( x ), f ( x ) является производной, она называется первообразной функции y = f ( x ).
Рассмотрим таблицу первообразных. В левой колонке расположены функции, в правой – производные для функций. (Рис. 3).
| Функция f ( x ) | Первообразная F ( x ) |
| 0 | С (константа) |
| 1 | x + C |
| x | ( x^2 / 2 ) + C |
| x^n, n не равняется -1 | ( x^n ) + ( 1 / n ) + C |
| 1 / х | In | x | |
| sin x | – cos x + C |
| cos x | sin x + C |
| e^x | е^x + C |
Первообразная функций в их сумме будет равняться сумме их первообразных.
Первообразная у = kf ( x ), где k – постоянный множитель, равняется произведению k на первообразную f ( x ), то есть kF ( х).
Неопределённым интегралом считают различные первообразные у функции. Это записывают в следующем виде: f ( x ) dx = F ( x ) + C.
Исследование функции на монотонность
В данной теме нужно придерживаться двух основных теорий:
- Если в промежутке х, а именно во всех его точках присутствует f ( х ) больше или равное нулю, то функция у = f ( х ) возрастает на этом промежутке. При этом следует учитывать, что данное равенство подлежит выполнению исключительно в определенных точках графика и не может выполняться ни на одном промежутке, являющемся сплошным.
На данном графике
| Функция f ( x ) | Первообразная F ( x ) |
| 0 | С (константа) |
| 1 | x + C |
| x | ( x^2 / 2 ) + C |
| x^n, n не равняется -1 | ( x^n ) + ( 1 / n ) + C |
| 1 / х | In | x | |
| sin x | – cos x + C |
| cos x | sin x + C |
| e^x | е^x + C |
(рис. 4) детально показана первая теорема.
- Если в промежутке х, а именно во всех его точках можно выполнить неравенство f ( х ) меньше или равно нулю, значит, функция у = f ( х ) будет убывающей в промежутке х. При этом следует учитывать то, что f ( х ) = 0 может выполняться исключительно в некоторых точках и не выполняется ни на одном промежутке, являющимся сплошным.
Рассмотрим пример
(рис. 5). На данном рисунке функция рассмотрена наглядно.
Наибольшее и наименьшее значения функции на отрезке
Рассмотрим более подробно данную тему на примере
(рис. 6).
На первом графике изображена функция, которая имеет наибольшее и наименьшее значения в определённых точках. Данные точки расположены на отрезке от -6 до 6, то есть [−6;6].
На втором графике рассмотрим отрезок от 1 до 6. Здесь наименьшее значение функции принадлежит стационарной точке, а наибольшее – в точке в правой стороне интервала.
Третий рисунок указывает на точки, находящиеся на границе отрезка [−3;2]. Они равны наибольшему и наименьшему значениям.
Сразу же вспомним определение стационарной точки – это определённое значение, при нём будет нулевой.
Итак, для чего нужны стационарные точки? Существует теорема Ферма, согласно которой функция имеет экстремум (то есть минимальное и максимальное значения) в определённой точке. Данная точка будет стационарной.
Наибольшее и наименьшее на интервале
Рассмотрим пример
(рис. 7).
На данном рисунке функция максимального и минимального значения на открытом интервале от -6 до 6, то есть (-6; 6). Эти значения достигаются в стационарных точках.
На втором графике рассмотрена часть от 1 до 6 [1; 6), здесь наибольшее значение невозможно узнать, наименьшее – в стационарной точке.
На последнем графике наименьшее значение достигнуто в интервале (-3; 2], наибольшее значение неизвестно.
Наибольшее и наименьшее значения на бесконечности
Рассмотрим на примере графика
(рис. 8).
Здесь максимальное значение функции достигается в стационарной точке, её абсцисса равна единице. Наименьшее значение достигается в правой стороне графика. Функция приближается к у = 3.
Рассмотрим пример решения подобных задач. В условии задания сказано, что нужно найти наибольшее и наименьшее у функции у = х3 + 4х2 на [ 1; 4 ] и [ −4; − 1].
Сначала находим область определения функции: действительные числа, исключая нуль, то х будет принадлежать промежутку ( -∞; 0 ) и ( 0; +∞ ). Данные отрезки находятся в области определения. Далее находим производную функции в соответствии с дифференцирования дроби: у = ( х^3 + 4х ) / х^2 ) = (( х^3 + 4) * х^2) / x^4 = (3x^2 * x^2 – ( x^3 – 4 ) * 2x ) / x^4 = (x^3 – 8 ) / x^3.
Таким образом, производная есть должна принадлежать отрезку [1;4] и [−4;−1].
Далее определяем стационарные точки, используя уравнение ( х^3 – 8 ) / х3 = 0. Здесь находится один корень равный двум, это и есть стационарная точка, попадающая в отрезок [1;4].
Теперь нужно вычислить значения функции в конце первого отрезка и в стационарной точке, то есть х = 1, х = 2, х = 4:
– y1 = ( 1^3 + 4 ) / 1^2 = 5;
– y2 = (2^3 + 4 ) = 3;
– y3 = (4^3 + 4 ) / 4^2 = 4 ¼.
Наибольшее значение у = 3 будет при х = 1, наименьшее у = 3, при х = 2.
На втором отрезке нет стационарных точек, поэтому вычисляем значения на концах известного отрезка: у ( -1 ) = (( -1^3 )) + 4 / ( -1^2) = 3.
Далее, максимальное значение у ( -1 ) = 3, при этом х принадлежит отрезку [ -4; -1 ], минимальное значение у ( -4 ) = -3 ¾.
Таким образом, тема производной в ЕГЭ по математике базового уровня обычно является одной из наиболее сложных. Изучив данные темы, просмотрев графики и примеры решений, вы сможете решить подобные задания в КИ




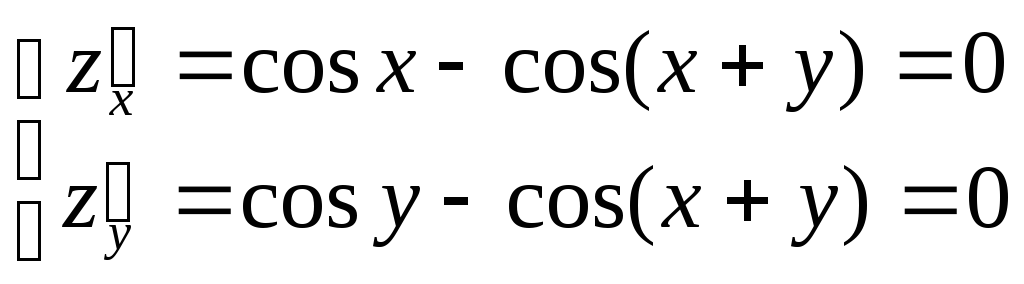 ,
, .
. ,
,
 ,
,





