Как найти наименьшее значение производной на промежутке - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.

Как найти наибольшее и наименьшее значения функции на отрезке?

Для этого мы следуем известному алгоритму:

1. Находим ОДЗ функции.

2. Находим производную функции

3. Приравниваем производную к нулю

4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:

Если на промежутке I производная функции $f^{prime}(x)>0$ , то функция y=f(x) возрастает на этом промежутке.

Если на промежутке I производная функции $f^{prime}(x)<0$ , то функция y=f(x) убывает на этом промежутке.

5. Находим точки максимума и минимума функции.

В точке максимума функции производная меняет знак с «+» на «-«.

В точке минимума функции производная меняет знак с «-» на «+».

6. Находим значение функции в концах отрезка,

затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции

Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.

Рассмотрим функцию . График этой функции выглядит так:

В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.

1. Рассмотрим функцию на отрезке

Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: f(0) , а наименьшее — в левом: f(-1) .

2. Рассмотрим функцию на отрезке

Очевидно, что наибольшее значение функция принимает в точке максимума f(0) , а наименьшее — в одном из концов отрезка, то есть надо найти значения f(-1) и f(1) и выбрать из них наименьшее.

3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть f(0) и f(2) .

Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть f(4/3) и f(-1) .

Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:

1. ОДЗ функции — множество действительных чисел.

2. $f^{prime}(x)=3x^2-4x$

3. , если x_1=0 или x_2=4/3

Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:

Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике

1. Задание B15 (№ 26695)

Найдите наибольшее значение функции на отрезке .

1. Функция определена при всех действительных значениях х

2. $y^{prime}= 15-3cosx$

cosx=5 Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.

y(0)=5

Ответ: 5.

2. Задание B15 (№ 26702)

Найдите наибольшее значение функции на отрезке [].

1. ОДЗ функции

2. $y^{prime}=3/{cos^2{x}}-3$

Производная равна нулю при , однако, в этих точках она не меняет знак:

$0<cos^2{x}<=1$ , следовательно, $3/{cos^2{x}}>=3$ , значит, $3/{cos^2{x}}-3>=0$ , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, при x=0 .

Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:

$y^{prime}=3/{cos^2{x}}-3={3-3cos^2{x}}/{cos^2{x}}={3sin^2{x}}/{cos^2{x}}=3tg^2{x}>=0$

у(0)=5

Ответ: 5.

3. Задание B15 (№ 26708)

Найдите наименьшее значение функции на отрезке [].

1. ОДЗ функции :

2. $y^{prime}=2/{cos^2{x}}-4$

3. $2/{cos^2{x}}-4=0$

$cos^2{x}=1/2$ ,

Расположим корни этого уравнения на тригонометрической окружности.

Промежутку принадлежат два числа: -{pi}/4 и {pi}/4

Расставим знаки. Для этого определим знак производной в точке х=0: $y^{prime}(0)=2/{cos^2(0)}-4=-2<0$ . При переходе через точки -{pi}/4 и {pi}/4 производная меняет знак.

Изобразим смену знаков производной функции на координатной прямой:

Очевидно, что точка является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции на отрезке , нужно сравнить значения функции в точке минимума и в левом конце отрезка, .

Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а таковым на является, следовательно подставим в уравнение функции

Ответ: -1

Вероятно, Ваш браузер не поддерживается. Попробуйте скачать

Firefox

И.В. Фельдман, репетитор по математике.

Источник

Рассмотрим примеры, в которых дан график производной и требуется определить, в какой точке данного отрезка функция принимает наименьшее значение.

№1

На рисунке изображён график производной функции f(x), определённой на интервале (-10;8). В какой точке отрезка [-8;-1] функция f(x) принимает наименьшее значение?

Решение:

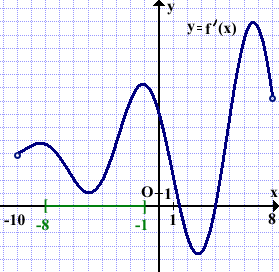
Выделяем отрезок [-8;-1].

На этом отрезке производная f'(x) принимает положительные значения.

Значит, на [-8;-1] функция f(x) возрастает, то есть бо́льшему значению аргумента соответствует бо́льшее значение функции:

x₁,x₂ ∈[-8;-1], x₂>x₁, ⇒ f(x₂)>f(x₁).

Следовательно, наименьшее значение f(x) принимает при наименьшем значении аргумента, то есть на левом конце отрезка, при x=-8.

Ответ: -8.

№2

На рисунке изображён график производной функции f(x), определённой на интервале (-6;8). В какой точке отрезка [-3;6] функция f(x) принимает наименьшее значение?

Решение:

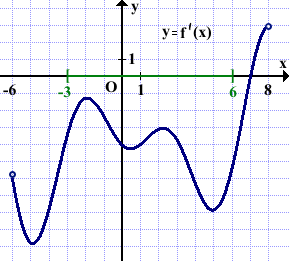
Выделяем отрезок [-3;6].

На этом отрезке f'(x)<0, поэтому f(x) убывает, то есть бо́льшему значению аргумента соответствует меньшее значение функции:

x₁,x₂ ∈[-3;6], x₂>x₁, ⇒ f(x₂)<f(x₁).

Поэтому наименьшее значение функция f(x) в этом случае принимает при наибольшем значении аргумента, то есть на правом конце отрезка, при x=6.

Ответ: 6.

№3

Функция y=f(x) определена на промежутке (-9;6). На рисунке изображён график её производной. Найти абсциссу точки, в которой функция y=f(x) принимает наименьшее значение.

Решение:

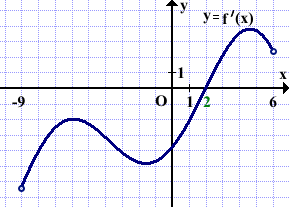
В точке с абсциссой x=2 производная меняет знак с минуса на плюс.

Значит, x=2 — точка минимума.

Производная f'(x) существует на всём интервале (-9;6), следовательно, функция f(x) на (-9;6) непрерывна.

Если непрерывная функция f(x) имеет на заданном интервале (a;b) только одну точку экстремума x_o и это точка минимума, то на (a;b) функция принимает своё наименьшее значение в точке x_o.

Таким образом, наименьшее значение функция f(x) принимает в точке с абсциссой x=2.

Ответ: 2.

№4

Функция y=f(x) определена и непрерывна на отрезке [-4;9]. На рисунке изображён график её производной. Найти точку x_o, в которой функция принимает наименьшее значение, если f(9)≤f(-4).

Решение:

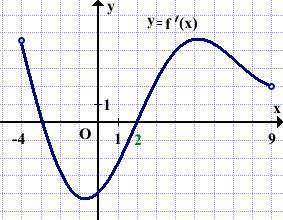
На промежутках (-4;-3) и (2;9) производная f'(x) принимает положительные значения, поэтому функция f(x) на этих промежутках возрастает.

На промежутке (-3;2) производная f'(x)<0, поэтому функция f(x) убывает.

Так как функция определена и непрерывна на отрезке [-4;9], то точки -4, -3, 2 и 9 можно включить в промежутки монотонности.

Следовательно, функция f(x) возрастает на промежутках [-4;-3] и [2;9] и убывает на [-3;2].

На промежутках возрастания своё наименьшее значение функция принимает на левом конце отрезка. На отрезке [2;9] наименьшее значение f(x) принимает в точке x=2 (точке минимума), на [-4;-3] — в точке x=-4.

Так как на [2;9] функция f(x) возрастает, то f(2)<f(9).

По условию, f(9)≤f(-4). Значит, f(2)<f(-4).

Таким образом, наименьшее значение функция f(x) принимает в точке x=2.

Ответ: 2.

Источник

Наибольшее и наименьшее значения функции можно найти по графику функции. Иногда это значения удаётся найти, используя свойства функции. В общем случае наибольшее и наименьшее значения функции находятся с помощью производной. Для этого сформулируем некоторые теоремы.

1. Если функция непрерывна на отрезке, то она достигает на нём и своего наибольшего, и своего наименьшего значений (Эта теорема доказывается в курсе высшей математики).

2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.

3. Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.

Как найти наименьшее и наибольшее значения функции на отрезке?

Пусть функция (f(x)) напрерывна на отрезке ([a; b]), тогда:

1) находим производную функции f′(x);

2) приравниваем производную к нулю, определяем точки экстремума функции, отбираем из них те, которые принадлежат отрезку ([a; b]);

3) находим значения функции y=f(x) в отобранных точках, и в конечных точках отрезка (a) и (b); выбираем среди полученных значений наименьшее (yнаим) и наибольшее (yнаиб).

А что делать, если нужно найти наибольшее или наименьшее значения функции, непрерывной на интервале? Один из вариантов — графический метод, который подразумевает построение графика функции и определение наименьшего или наибольшего значения функции по нему. Однако не всегда этот способ удобен, целесообразнее использовать следующую теорему.

Теорема. Пусть функция y=f(x) непрерывна на промежутке (X) и имеет внутри него единственную стационарную или критическую точку x0. Тогда:

а) если x=x0 — точка максимума, то yнаиб=f(xo);

б) если x=x0 — точка минимума, то yнаим=f(xo).

На рисунках продемонстрированы геометрические иллюстрации данной теоремы.

Источник

Заказать задачи по любым предметам можно здесь от 10 минут

Наибольшее и наименьшее значение функции

Как найти?

Постановка задачи

Найти наибольшее и наименьшее значение функции $ f(x) $ на отрезке $ [a,b] $

План решения

Наибольшее и наименьшее значение непрерывной функции $ f(x) $ на промежутке $ [a,b] $ достигаются в критических точках, то есть в точках в которых производная функции равна нулю $ f'(x) = 0 $, бесконечности $ f'(x) = pm infty $, не существует, либо на концах отрезка $ [a,b] $

Проверяем на непрерывность функцию $ f(x) $ на заданном отрезке
Если функция непрерывная, то находим производную $ f'(x) $ и приравниваем её к нулю
Решая уравнение $ f'(x) = 0 $ получаем корни, являющиеся критическими точками
Выбираем критические точки, принадлежащие отрезку $ [a,b] $
Вычисляем значения функции $ f(x) $ в оставшихся критических точках, а так же на концах промежутка $ [a,b] $. Затем выбираем из них наибольшее $ M $ и наименьшее $ m $

Примеры решений

Пример 1

Найти наибольшее и наименьшее значение функции $ y = 2x^3 — 3x^2 — 4 $ на отрезке $ [0;2] $

Решение

Функция представляет собой кубический многочлен. Точек разрыва нет, значит функция непрерывна на отрезке $ [0;2] $.

Находим производную: $$ y’ = (2x^3 — 3x^2 — 4)’ = 6x^2 — 6x $$

Приравниваем производную к нулю. Решаем уравнение и получаем критические точки:

$$ 6x^2 — 6x = 0 $$ $$ 6x(x — 1) = 0 $$ $$ x_1 = 0, x_2 = 1 $$

Проверяем принадлежность полученных точек отрезку $ [0;2] $:

$$ x_1 in [0;2], x_2 in [0;2] $$

Так как обе точки принадлежат отрезку, то вычисляем в них значение функции $ f(x) $, так же значение этой функции на концах интервала $ [0;2] $:

$$ y(x_1) = y(a) = f(0) = 2 cdot 0^3 — 3 cdot 0^2 — 4 = -4 $$

$$ y(x_2) = y(1) = 2 cdot 1^3 — 3 cdot 1^2 — 4 = -5 $$

$$ y(b) = y(2) = 2 cdot 2^3 — 3 cdot 2^2 — 4 = 0 $$

Среди полученных значений наибольшее $ M = 0 $, наименьшее $ m = -5 $

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ M = 0, m = -5 $$

Пример 2

Найти наименьшее и наибольшее значение функции $ y = frac{4x^2}{3+x^2} $ на $ [-1;1] $

Решение

Функция непрерывна на $ x in [-1;1] $ так как знаменатель не обращается в ноль ни при каком $ x $.

Выполняем нахождение производной:

$$ y’ = (frac{4x^2}{3+x^2})’ = frac{(4x^2)'(3+x^2)-(4x^2)(3+x^2)’}{(3+x^2)^2} = $$

$$ = frac{8x(3+x^2)-(4x^2)(2x)}{(3+x^2)^2} = frac{24x+8x^3-8x^3}{3+x^2)^2} = frac{24x}{(3+x^2)^2} $$

Приравниваем полученную производную к нулю и вычисляем критические точки:

$$ frac{24x}{(3+x^2)^2} = 0 $$ $$ 24x = 0, 3+x^2 neq 0 $$ $$ x = 0 $$

Получена единственная критическая точка $ x = 0 $, которая принадлежит $ [-1; 1] $.

Вычисляем значение функции $ f(x) $ в критической точке и на концах интервала $ [-1;1] $:

$$ y(-1) = frac{4cdot (-1)^2}{3+(-1)^2} = frac{4}{4}=1 $$

$$ y(0) = frac{0}{3} = 0 $$

$$ y(1) = frac{4cdot 1^2}{3+1^2} = frac{4}{4} = 1 $$

Из полученных значений видно, что максимальное значение $ M = 1 $ и минимальное значение $ m = 0 $.

Ответ

$$ m = 0, M = 1 $$

Источник

Аналогичные рассуждения, если функция убывает: значение функции в следующей точке будет меньше, чем в предыдущей, значит производная будет отрицательной.

Итак, если производная положительна на промежутке, то это значит, что функция на этом промежутке возрастает. На рисунке 1 такие участки показаны зеленым. А если производная отрицательна, то функция убывает, на рисунке 1 участки показаны синим:

$$f^{/}(x)>0 leftrightarrow f(x) Uparrow ;$$
$$f^{/}(x)<0 leftrightarrow f(x) Downarrow ;$$

Кроме этого, производная от функции может быть равна нулю. Функция в той точке, где производная равна нулю, будет принимать наибольшее или наименьшее значение в окрестности этой точки. На графике нашей функции (Рис. 1) эти точки выглядят как «холмы» и «впадины».

Обратите внимание, что «холмов» и «впадин» на графике может быть бесконечно много, какие-то из этих «холмов» будут выше, какие-то ниже. Производная равна нулю во всех таких точках. И значения функции во всех таких точках я называю наибольшими и наименьшими, хотя на самом деле это локальные наибольшие и наименьшие значения.

Кстати, ТОЧКАМИ минимума или максимума называют координаты «холмов» и «впадин» по оси (x). Еще их называют точками экстремума функции: это общее название для минимумов и максимумов. Поэтому, когда вас просят найти точки экстремума, это значит найти координаты по оси (x) и минимумов, и максимумов.

В точке (x=-2) будет минимум функции. Точка (x=-3) из знаменателя, поэтому на рисунке она выколотая: ее мы не рассматриваем.

Чтобы определить наименьшее значение, подставим в исходную функцию найденную точку минимума и концы отрезка (xin[-2,5;0]):
$$y(-2)=3x—ln(x+3)^3=3*(-2)-ln(-2+3)^3=-6-0=-6;$$
$$y(-2,5)=3x—ln(x+3)^3=3*(-2,5)-ln(-2,5+3)^3=-7,5-ln(0,5)^3;$$
$$y(0)=3x—ln(x+3)^3=3*0-ln(0+3)^3=ln(3)^3;$$

Обратите внимание, что значение функции в точках ((-2,5)) и ((0)) получились «плохие»: мы не можем посчитать значения таких логарифмов без калькулятора. Поэтому, если возникает такая ситуация, то мы просто отбрасываем эти значения, ведь в заданиях ЕГЭ в первой части не может быть иррациональных значений. Такая маленькая хитрость. Но будьте внимательны, может быть, иррациональные значения у вас получаются, потому что где-то ошибка.

Кстати, подставлять в этом примере границы отрезка необязательно еще и по другой причине: на промежутке ([-2,5;-2)) функция убывает, а на промежутке ((-2;0]] возрастает. Минимальное значение на указанном промежутке может быть только в точке минимума.

Ответ: (-6.)

Пример 21
Найдите наименьшее значение функции (y=x*sqrt{x}-9x+25) на интервале ([1;50].)

Производную от данной функции можно посчитать, воспользовавшись формулой производной от произведения ((f(x)*g(x))^{/}=(f(x))^{/}*g(x)+f(x)*(g(x))^{/}:)
$$y^{/}=(x*sqrt{x}-9x+25)^{/}=(xsqrt{x})^{/}-(9x)^{/}+25^{/}=x^{/}*sqrt{x}+x*(sqrt{x})^{/}-9=$$
$$=1*sqrt{x}+x*frac{1}{2sqrt{x}}-9=sqrt{x}+frac{sqrt{x}*sqrt{x}}{2sqrt{x}}-9=sqrt{x}+frac{1}{2}*sqrt{x}-9=frac{3}{2}*sqrt{x}-9;$$
Есть другой вариант взятия производной, на мой взгляд, он легче. Для это мы представим квадратный корень в виде степени:
$$sqrt{x}=x^{frac{1}{2}};$$
$$y^{/}=(x*sqrt{x}-9x+25)^{/}=(x*x^{frac{1}{2}}-9x+25)^{/}=(x^{frac{3}{2}-9x+25)^{/}=frac{3}[2}*x^{frac{1}{2}}-9=frac{3}{2}*sqrt{x}-9;$$

Приравниваем производную к нулю и находим корни уравнения на указанном интервале:
$$frac{3}{2}*sqrt{x}-9=0;$$
$$sqrt{x}=9*frac{2}{3};$$
$$sqrt{x}=6;$$
$$x=36;$$
На числовой прямой определяем знаки производной и промежутки возрастания и убывания функции:

Источник