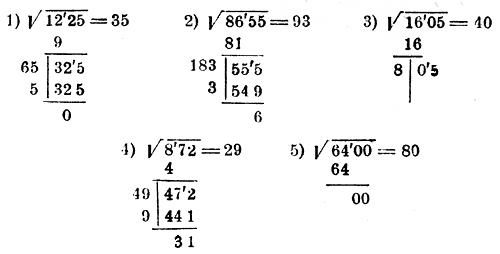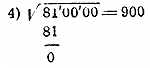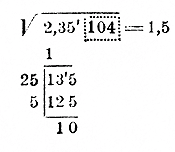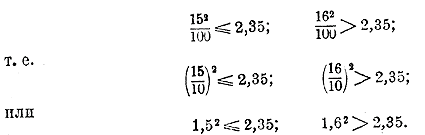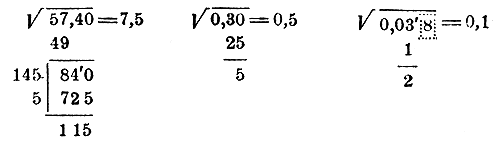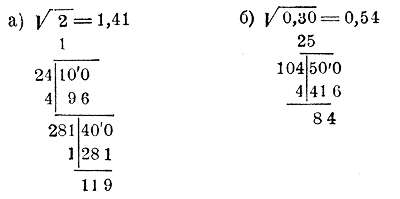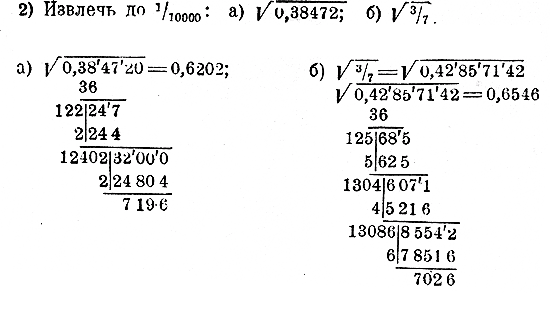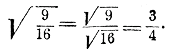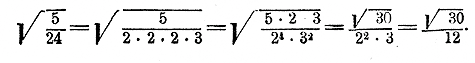Как найти наименьший корень дроби

Дробно-рациональные уравнения

Что такое дробно-рациональные уравнения

Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:

при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.

Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.

9 x 2 — 1 3 x = 0

1 2 x + x x + 1 = 1 2

6 x + 1 = x 2 — 5 x x + 1

Уравнения, которые не являются дробно-рациональными:

Как решаются дробно-рациональные уравнения

В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.

Алгоритм действий при стандартном способе решения:

1. Выписать и определить ОДЗ.
2. Найти общий знаменатель для дробей.
3. Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
4. Записать уравнение со скобками.
5. Раскрыть скобки для приведения подобных слагаемых.
6. Найти корни полученного уравнения.
7. Выполним проверку корней в соответствии с ОДЗ.
8. Записать ответ.

Пример 1

Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:

x x — 2 — 7 x + 2 = 8 x 2 — 4

Начать следует с области допустимых значений:

x 2 — 4 ≠ 0 ⇔ x ≠ ± 2

Воспользуемся правилом сокращенного умножения:

x 2 — 4 = ( x — 2 ) ( x + 2 )

В результате общим знаменателем дробей является:

Выполним умножение каждого из членов выражения на общий знаменатель:

x x — 2 — 7 x + 2 = 8 x 2 — 4

x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )

После сокращения избавимся от скобок и приведем подобные слагаемые:

x ( x + 2 ) — 7 ( x — 2 ) = 8

x 2 + 2 x — 7 x + 14 = 8

Осталось решить квадратное уравнение:

Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:

Примеры задач с ответами для 9 класса

Требуется решить дробно-рациональное уравнение:

x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0

x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0

Определим область допустимых значений:

О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2

x 2 + 7 x + 10 ≠ 0

D = 49 — 4 · 10 = 9

x 1 ≠ — 7 + 3 2 = — 2

x 2 ≠ — 7 — 3 2 = — 5

Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:

a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )

x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0

Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:

x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0

Сократим дроби, избавимся от скобок, приведем подобные слагаемые:

x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —

— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0

x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0

x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0

2 x 2 + 9 x — 5 = 0

Потребуется решить квадратное уравнение:

2 x 2 + 9 x — 5 = 0

Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.

Дано дробно-рациональное уравнение, корни которого требуется найти:

4 x — 2 — 3 x + 4 = 1

В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:

4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0

4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0

4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0

x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0

Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:

— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0

Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:

( x — 2 ) ( x + 4 ) ≠ 0

Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:

— x 2 — x + 30 = 0 _ _ _ · ( — 1 )

Получилось квадратное уравнение, которое можно решить:

Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.

Нужно решить дробно-рациональное уравнение:

x + 2 x 2 — 2 x — x x — 2 = 3 x

На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:

x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0

x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0

x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0

— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0

Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.

— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )

Корни квадратного уравнения:

x 1 = — 4 ; x 2 = 2

Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.

Найти корни уравнения:

x 2 — x — 6 x — 3 = x + 2

Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:

x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0

x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0

x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0

0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0

Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:

Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.

Ответ: х — любое число, за исключением 3.

Требуется вычислить корни дробно-рационального уравнения:

5 x — 2 — 3 x + 2 = 20 x 2 — 4

На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:

5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0

5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0

5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0

2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0

( x — 2 ) ( x + 2 ) ≠ 0

Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.

Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.

Ответ: корни отсутствуют

Нужно найти корни уравнения:

x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )

Начнем с определения ОДЗ:

— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0

При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:

x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )

( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )

( x — 3 ) x + x = x + 5

Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:

x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0

Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:

x 1 · x 2 = — 10 x 1 + x 2 = 3

В этом случае подходящими являются числа: -2 и 5.

Второе значение не соответствует области допустимых значений.

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = −b : а; если а равно нулю, а b не равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
• делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

1. Область допустимых значений: х ≠ −2.
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

Урок по теме «Решение дробных рациональных уравнений». 8-й класс

Разделы: Математика

Класс: 8

Цели урока:

• формирование понятия дробных рационального уравнения;
• рассмотреть различные способы решения дробных рациональных уравнений;
• рассмотреть алгоритм решения дробных рациональных уравнений, включающий условие равенства дроби нулю;
• обучить решению дробных рациональных уравнений по алгоритму;
• проверка уровня усвоения темы путем проведения тестовой работы.

• развитие умения правильно оперировать полученными знаниями, логически мыслить;
• развитие интеллектуальных умений и мыслительных операций — анализ, синтез, сравнение и обобщение;
• развитие инициативы, умения принимать решения, не останавливаться на достигнутом;
• развитие критического мышления;
• развитие навыков исследовательской работы.

• воспитание познавательного интереса к предмету;
• воспитание самостоятельности при решении учебных задач;
• воспитание воли и упорства для достижения конечных результатов.

Тип урока: урок – объяснение нового материала.

Ход урока

1. Организационный момент.

Здравствуйте, ребята! На доске написаны уравнения посмотрите на них внимательно. Все ли из этих уравнений вы сможете решить? Какие нет и почему?

Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Сформулируйте тему урока. Итак, открываем тетради и записываем тему урока «Решение дробных рациональных уравнений».

2. Актуализация знаний. Фронтальный опрос, устная работа с классом.

А сейчас мы повторим основной теоретический материл, который понадобиться нам для изучения новой темы. Ответьте, пожалуйста, на следующие вопросы:

1. Что такое уравнение? (Равенство с переменной или переменными.)
2. Как называется уравнение №1? (Линейное.) Способ решения линейных уравнений. (Все с неизвестным перенести в левую часть уравнения, все числа — в правую. Привести подобные слагаемые. Найти неизвестный множитель).
3. Как называется уравнение №3? (Квадратное.) Способы решения квадратных уравнений. (Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия.)
4. Что такое пропорция? (Равенство двух отношений.) Основное свойство пропорции. (Если пропорция верна, то произведение ее крайних членов равно произведению средних членов.)
5. Какие свойства используются при решении уравнений? (1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному. 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.)
6. Когда дробь равна нулю? (Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.)

3. Объяснение нового материала.

Решить в тетрадях и на доске уравнение №2.

Какое дробно-рациональное уравнение можно попробовать решить, используя основное свойство пропорции? (№5).

х 2 -4х-2х+8 = х 2 +3х+2х+6

х 2 -6х-х 2 -5х = 6-8

Решить в тетрадях и на доске уравнение №4.

Какое дробно-рациональное уравнение можно попробовать решить, умножая обе части уравнения на знаменатель? (№6).

Теперь попытайтесь решить уравнение №7 одним из способов.

В примерах по извлечению квадратного корня из дроби требуется работать с обыкновенными дробями.
Поэтому рекомендуем перед решением примеров освежить знания по действиям с
обыкновенными дробями:

• правильные и неправильные дроби;
• сложение дробей;
• вычитание дробей;
• умножение дробей;
• деление дробей.

Свойство квадратного корня из дроби

Как найти квадратный корень из дроби

По традиции от теории переходим к практике. Разберем пример вычисления квадратного корня из дроби.

Разбор примера

Вычислить:

1)

=

…

Используем правило квадратного корня из дроби. Извлечем квадратный корень отдельно из числителя и знаменателя.

=

=

Разбор примера

Вычислить:

1)

=

=

√9

=

3

Как извлечь квадратный корень из смешанного числа

Разбор примера

Вычислить:

4)

5

= …

Избавимся от целой части дроби и превратим ее в неправильную.

5

=

=

=

=

= …

Используем свойство квадратного корня из дроби.

5

=

=

=

=

=

=

= …

Для завершения примера не забудем выделить целую часть.

5

=

=

=

=

=

=

=
2

Разбор примера

Вычислить:

4)

+

= …

Перед тем как работать с дробями требуется выполнить действие извлечения квадратного корня из дробей.

 

+

=

 

+

= …

Вспомним, что квадратный корень из единицы равен единице (
√1 = 1
) и используем правило сложения дробей.

 
+

=

 
+

=

+

=

=

=
1

Примеры извлечения квадратного корня из дроби

Разбор примера

2)    5

−

3

= …

Вспомним, что в краткой записи между квадратным корнем и числом знак умножения «·» не пишут.
Для наглядности поставим его в пример и вычислим пример по правилу
умножения числа на дробь.

   5

−

3

=

=

  5
 
·

−

3
 
·

=

=

  5
 
·
 

−

3
 
·
 

=

=

  5

·

−

3

·

= …

Вспомним правило умножения дроби на число.

   5

−

3

=

=
  5
  ·

−

3
 
·

=

=

  5
 
·
 

−

3
 
·
 

=

=

  5

·

−

3

·

=

−

=

=
1 − 1 = 0

Разбор примера

Вычислить:

4)
= …

Чтобы вычислить квадратный корень, используем правило умножения дробей
и правило квадратного корня из дроби.

=

·

=

4  

·

=

=

4 · √9 =
4 · 3 = 12

Разбор примера

Вычислить:

2)

5 · 11

= …

Избавимся от целой части
в смешанных числах, чтобы можно было использовать свойство квадратного корня из дроби.

5 · 11

=

=

·

=

=

·

=

·

=

=

·

= …

Вспомним таблицу квадратов, чтобы вычислить
√289.

5 · 11

=

=

·

=

=

·

=

·

=

=

·

=

·

=

=

=

=

…

Выделим целую часть смешанного числа для того, чтобы дать окончательный ответ.

5 · 11

=

=

·

=

=

·

=

·

=

=

·

=

·

=

=

=

=

7

---

Ваши комментарии

Оставить комментарий:

---

ОТДЕЛ  СЕДЬМОЙ.

ИЗВЛЕЧЕНИЕ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЕЛ.

Глава первая. Извлечение из данного целого числа наибольшего целого квадратного корня.
Глава вторая. Извлечение приближенных квадратных корней из целых и дробных чисел
Глава третья. График функции х = √y .

Глава первая.

Извлечение из данного целого числа наибольшего целого квадратного корня.

170. Предварительные замечания.

а) Так как мы будем говорить об извлечении только квадратного корня, то для сокращения речи в этой главе мы вместо „квадратный» корень будем говорить просто „корень».

б) Если   возвысим   в  квадрат   числа   натурального   ряда: 1,2,3,4,5 .  .  . , то получим такую таблицу квадратов: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100,121,144. .,

Очевидно, имеется очень многo целых чисел, которые в этой таблице не находятся; из таких чисел, конечно, нельзя извлечь целый корень. Поэтому, если требуется извлечь корень из какого-нибудь целого числа, напр. требуется найти √4082 , то мы условимся это требование понимать так: извлечь целый корень из 4082, если это возможно; если же нельзя, то мы должны найти наибольшее целое число, квадрат
которого заключается в 4082 (такое
число есть 63, так как 63² = 39б9, а 64² = 4090).

в) Если данное число меньше 100, то корень из него находится по таблице умножения; так, √60  будет 7, так как семью 7 равно  49, что   меньше   60,  а   восемью   8   составляет   64,  что больше 60.

171. Извлечение корня из числа, меньшего  10000, но большего 100. Пусть надо найти √4082 . Так как это число  меньше 10 000, то корень из него меньше √l0 000 = 100. С другой стороны, данное число больше 100; значит, корень из него больше (или равен 10) . (Если бы, напр., требовалось найти √120, то хотя число 120
> 100, однако √120 равен 10, т.к. 11² = 121.) Но всякое число, которое больше 10, но меньше 100,   имеет   2   цифры;   значит,   искомый   корень   есть сумма:

десятки + единицы,

и поэтому квадрат его должен равняться сумме:

(дес.)² + 2 •(дес.) • (ед.) + (ед.)².

Сумма эта должна быть наибольшим квадратом, заключающимся в 4082.

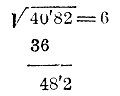Так как (десятки)2 составляют сотни, то квадрат десятков надо искать в сотнях данного числа. Сотен в данном числе 40 (мы находим их число, отделив запятой две цифры справа). Но в 40 заключается несколько целых квадратов: 36,25,16,.. и др.

Возьмем из них наибольший, 36, и допустим,что квадрат десятков корня будет равен именно этому наибольшему квадрату. Тогда число десятков в корне должно быть 6. Проверим теперь, что это всегда должно быть так, т. е. всегда число десятков корня равно наибольшему целому корню из  числа сотен подкоренного  числа.  

Действительно, в нашем примере число десятков корня не может быть больше 6, так как (7 дес.)² = 49 сотен, что превосходит 4082. Но оно не может быть и меньше 6, так как 5 дес. (с единицами) меньше 6 дес, а между тем (6 дес.)² = 36 сотен, что меньше 4082. А так как мы ищем наибольший целый корень, то мы не должны брать для корня 5 дес, когда и 6 десятков оказывается не много.

Итак, мы нашли число десятков корня, именно 6. Пишем эту цифру направо от знака =, запомнив, что она означает
десятки корня. Возвысив ее в квадрат, получим 36 сотен. Вычитаем эти 36 сотен из 40 сотен подкоренного числа и сносим две остальные цифры данного числа. В остатке 482 должны содержаться 2 • (6 дес.) • (ед.) + (ед.)2. Произведение (6 дес.) • (ед.) должно составлять десятки; поэтому удвоенное произведение десятков на единицы надо искать в десятках остатка, т. е. в 48 (мы получим число их, отделив в остатке 48’2 одну цифру справа). Удвоенные десятки корня составляют 12. Значит, если 12 умножим на единицы корня (которые
пока неизвестны), то мы должны получить число, содержащееся в 48. Поэтому мы разделим 48 на 12.

Для этого налево от остатка проводим вертикальную черту и за нею (отступив от черты на одно место влево для цели, которая сейчас обнаружится) напишем удвоенную первую цифру корня, т. е. 12, и на нее разделим 48. В частном получим 4.

Однако, заранее нельзя ручаться, что цифру 4 можно принять за единицы корня,
так как мы сейчас разделили на 12 все число десятков остатка, тогда как некоторая часть из них может и не принадлежать удвоенному произведению десятков на единицы, а входит в состав квадрата единиц.  Поэтому цифра 4 может оказаться велика. Надо ее испытать. Она, очевидно, годится в том   случае, если сумма 2 • (6   дес.) • 4 + 4²   окажется не больше
остатка 482.

Сумму это мы можем вычислить сразу таким простым приемом: за вертикальной чертой к удвоенной цифре корня (к 12) приписываем справа цифру 4 (поэтому-то мы и отступили от черты на одно место) и на нее же умножим полученное число (124 на 4).Действительно, производя это умножение, мы умножаем 4 на 4, значит, находим  квадрат  единиц  корня;  затем  мы  умножаем 12 десятков  на 4,  значит  находим удвоенное произведение десятков корня на единицы.

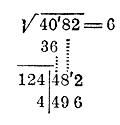В результате
получаем сразу сумму того и другого. Полученное произведение оказалось  496, что больше остатка 482; значит, цифра 4 велика. Тогда испытаем таким же образом следующую меньшую цифру 3. 

Для этого сотрем цифру 4 и произведение 496 и вместо цифры 4 поставим 3 и умножим  123 на 3. Произведение 369 оказалось меньше остатка 492; значит, цифра 3 годится (если бы случилось, что и эта цифра велика, тогда надо было бы испытать следующую меньшую цифру 2). Пишем цифру 3 в корне направо от цифры десятков.Последний   остаток   113   показывает  избыток данного числа над наибольшим целым квадратом, заключающимся в нем.

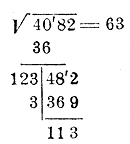Для поверки мы возвысили в квадрат 63 и к результату  приложили 113; так как в сумме получилось данное число 4082, то действие сделано верно.

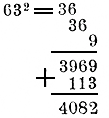Примеры.

В примере 4-м при делении 47 десятков остатка на 4, мы получаем в частном 11. Но так как цифра единиц корня не может быть двузначным числом 11 или 10, то надо прямо испытать цифру 9.

В примере 5-м после вычитания из первой грани квадрата 8 остаток оказывается 0, и следующая грань тоже состоит из нулей. Это показывает, что искомый корень состоит только из 8 десятков, и потому на место единиц надо поставить нуль.

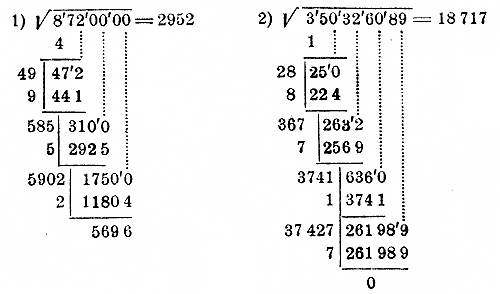
172. Извлечение корня из числа, большего 10000. Пусть требуется найти √35782 . Так как подкоренное число превосходит 10 000, то корень из него больше √10000  = 100 и, следовательно, он состоит из 3 цифр или более. Из скольких бы цифр он ни состоял, мы можем его всегда рассматривать как сумму только десятков и единиц. Если, напр., корень оказался бы 482, то мы можем его считать за
сумму 48 дес. + 2 ед. Тогда квадрат корня будет состоять
из 3 слагаемых:

(дес.)² + 2 • (дес.) (ед.) + (ед.)².

Теперь мы можем рассуждать совершенно так же, как и при нахождении √4082  (в предыдущем параграфе). Разница будет только та, что для нахождения десятков корня из 4082 мы должны были извлечь корень из 40, и это можно было сделать по таблице умножения; теперь же для получения десятков√35782  нам придется извлечь корень из 357, что по таблице умножения нельзя выполнить. Но мы можем найти√357 тем приемом, который был описан в предыдущем параграфе, так как число 357 < 10 000. Наибольший целый корень из 357 оказывается 18. Значит, в √3’57’82  должно быть 18 десятков. Чтобы найти единицы, надо из 3’57’82 вычесть квадрат 18 десятков, для чего достаточно вычесть квадрат 18 из 357 сотен и к остатку снести 2 последние цифры подкоренного числа. Остаток от вычитания квадpaта  18 из   357
  у нас   уже есть: это  33. Значит, для получения остатка от вычитания квадрата 18 дес. из 3’57’82, достаточно к 33 приписать справа цифры 82.

Далее поступаем так, как мы поступали при нахождении √4082 , a именно: налево от остатка 3382 проводим вертикальную черту и за нею пишем (отступив от черты на одно место) удвоенное число найденных десятков корня, т. е. 36 (дважды 18). В остатке отделяем одну цифру справа и делим число десятков остатка, т. е. 338, на 36. В частном получаем 9. Эту цифру испытываем, для чего
ее приписываем к 36 справа и на нее же умножаем. Произведение оказалось 3321, что меньше остатка. Значит, цифра 9 годится, пишем ее в корне.

Вообще, чтобы извлечь квадратный корень из какого угодно целого числа, надо сначала извлечь корень из числа его сотен; если это число более 100, то придется искать корень из числа сотен этих сотен, т. е. из десятков тысяч данного числа; если и это число более 100, придется извлекать корень из числа сотен десятков тысяч, т. е. из миллионов данного числа, и т. д.

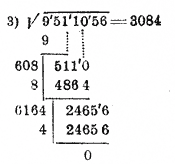
Примеры.

В последнем примере, найдя первую цифру и вычтя квадрат ее, получаем в остатке 0. Сносим следующие 2 цифры 51. Отделив десятки, мы получаем 5 дес, тогда как удвоенная найденная цифра корня есть 6. Значит, от деления 5 на 6 мы получаем 0. Ставим в корне 0 на втором месте и к остатку сносим следующие 2 цифры; получаем 5110. Далее продолжаем как обыкновенно.

В этом примере искомый корень состоит только из 9 сотен, и потому на месте десятков и на месте единиц надо поставить нули.

Правило. Чтобы, извлечь квадратный корень из данною целого числа, разбивают его, от правой руки к левой, на грани, по 2 цифры в каждой, кроме последней, в которой может быть и одна цифра.
    Чтобы найти первую цифру корня, извлекают квадратный корень из первой грани.
    Чтобы найти вторую цифру, из первой грани вычитают квадрат первой цифры корня, к остатку сносят
вторую грань и число десятков получившегося числа делят
на
удвоенную первую цифру корня; полученное целое число подвергают испытанию.
    Испытание это производится так: за вертикальной чертой (налево от остатка) пишут удвоенное ранее найденное число корня и к нему, с правой стороны, приписывают испытуемую цифру, получившееся, после этой приписки число умножают на испытуемую цифру. Если после умножения получится число, большее остатка, то испытуемая цифра не годится и надо испытать следующую меньшую цифру.
   Следующие,
цифры корня находятся по тому же приему.
   Если после снесения грани число десятков получившегося числа окажется меньше делителя, т. е.  меньше удвоенной найденной части корня, то в корне ставят 0, сносят следующую грань и продолжают действие  дальше.

173. Число цифр корня. Из рассмотрения процесса нахождения корня следует, что в корне столько цифр, сколько в подкоренном числе заключается граней по 2 цифры каждая (в левой грани может быть и одна цифра).

Глава вторая.

Извлечение приближенных квадратных корней из целых и дробных чисел.

Извлечение квадратного корня из многочленов см. в дополнениях ко 2-й части § 399 и след.

174. Признаки точного квадратного корня. Точным квадратным корнем из данного числа называется такое число, квадрат которого в точности равняется данному числу. Укажем некоторые признаки, по которым можно судить, извлекается ли из данного числа точный корень, или нет:

а)  Если  из  данного  целого  числа  не  извлекается  точный целый корень (получается при извлечении остаток), то из такого числа нельзя найти и дробный точный корень, так как всякая дробь, не равная целому числу, будучи умножена сама на себя, дает в произведении тоже дробь, а не целое число.

б)  Так  как  корень  из  дроби  равен  корню  из  числителя, деленному на корень из знаменателя, то точный корень из несократимой дроби не может быть найден в том случае,  если его нельзя извлечь из числителя или из знаменателя. Напр, из дробей ⁴/_{5 ,} ⁸/₉ и ¹¹/₁₅ нельзя извлечь точный корень, так как в первой дроби нельзя его извлечь из знаменателя,
 во второй — из числителя и в третьей — ни из числителя, ни из знаменателя.

Из таких чисел, из которых нельзя извлечь точный корень, можно извлекать лишь приближенные корни.

175. Приближенный корень с точностью до 1. Приближенным квадратным корнем с точностью до 1 из данного числа (целого или дробного — все равно) называется такое целое число, которое удовлетворяет следующим двум требованиям:

1) квадрат этого числа не больше данного числа; 2) но квадрат этого числа увеличенного на 1, больше данного числа. Другими словами, приближенным квадратным корнем с точностью до 1 называется наибольший целый квадратный корень из данного числа,
т. е.тот корень, который мы научились находить в предыдущей главе. Корень этот называется приближенным с точностью до 1, потому что для получения точного корня к этому приближенному корню надо было бы добавить еще некоторую дробь, меньшую 1, так что если вместо неизвестного точного корня мы возьмем этот приближенный, то сделаем ошибку, меньшую 1.

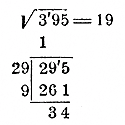Положим, требуется найти приближенный квадратный корень с точностью до 1 из 395,74. Тогда, не обращая внимания на дробь, извлечем корень только из целого числа. Полученный корень 19 будет искомый, так как   192< 395,74,     а   202> 395,74.

Правило. Чтобы извлечь приближенный квадратный корень с точностью до 1, надо извлечь наибольший целый корень из целой части данного числа.

Найденное по этому правилу число есть приближенный корень с  недостатком,  так как в нем недостает до точного корня некоторой дроби (меньшей 1). Если этот корень увеличим на 1, то получим другое число, в котором есть некоторый избыток над точным корнем, и избыток этот меньше 1. Этот увеличенный на 1 корень можно назвать тоже приближенным корнем с точностью до 1, но с избытком. (Названия:
„с недостатком» или „с избытком» в некоторых математических книгах заменены другими равносильными: „по недостатку» или  „по избытку».)

176. Приближенный корень с точностью до ¹/₁₀. Пусть требуется найти √2,35104 с точностью до ¹/₁₀ . Это значит, что требуется найти такую десятичную дробь, которая состояла бы из целых единиц и десятых долей и которая удовлетворяла бы двум следующим требованиям:

1) квадрат этой дроби не превосходит 2,35104, но 2) если увеличим ее на ¹/₁₀ , то квадрат этой увеличенной дроби превосходит 2,35104.

Чтобы найти такую дробь, мы сначала нaйдем приближенный корень с точностью до 1, т. е. извлечем корень только из целого числа 2. Получим 1 (и в остатке 1). Пишем в корне цифру1 и ставим после нее запятую. Теперь будем искать цифру десятых. Для этого сносим к остатку 1 цифры 35, стоящие направо от запятой, и продолжаем извлечениетак, как будто мы извлекали корень из целого числа 235. Полученную цифру 5 пишем в корне на месте десятых. Остальные цифры подкоренного числа (104)
нам не нужны. Что полученное число 1,5 будет действительно приближенный корень с точностью до ¹/₁₀ видно из следующего. Если бы мы находили наибольший целый корень из 235 с точностью до 1, то получили бы 15. Значит:

15²<235, но 16²>235.

Разделив все эти числа на 100, получим:

Значит, число 1,5 есть та десятичная дробь, которую мы назвали приближенным корнем с точностью до ¹/₁₀.

Найдем еще этим приемом следующие приближенные корни с точностью до 0,1:

177. Приближенный квадратный корень с точностью до ¹/₁₀₀  до ¹/₁₀₀₀ и т. д.

Пусть требуется найти с точностью до ¹/₁₀₀  приближенный √248. Это значит: найти такую десятичную дробь, которая состояла бы из целых, десятых и сотых долей и которая удовлетворяла бы двум требованиям:

1) квадрат ее не превосходит 248, но 2) если увеличим эту дробь на ¹/₁₀₀ то квадрат этой увеличенной дроби превосходит 248.

Такую дробь мы найдем в такой последовательности: сначала отыщем целое число, потом цифру десятых, затем и цифру сотых. Корень
из целого числа будет 15 целых. Чтобы получить цифру десятых, надо  как мы видели, снести к остатку 23 еще 2 цифры, стоящие направо от запятой. В нашем примере этих цифр нет вовсе, ставим на их место нули. Приписав их к остатку и продолжая действие так, как будто находим корень из целого числа 24 800, мы найдем цифру десятых 7. Остается найти цифру сотых. Для этого приписываем к остатку 151 еще 2 нуля и продолжаем извлечение, как будто мы находим корень из целого числа 2 480 000. Получаем 15,74. Что это
число   действительно   есть приближенный корень из 248 с точностью до ¹/₁₀₀ видно из следующего. Если бы мы находили наибольший целый квадратный корень из целого числа 2 480 000, то получили бы 1574; значит:

1574²< 2 480 000, но 1575²> 2 480 000.

Разделив все числа на 10 000 ( = 100²), получим:

Значит, 15,74 есть та десятичная дробь, которую мы назвали приближенным корнем с точностью до ¹/₁₀₀ из 248.

Применяя этот прием к нахождению приближенного корня с точностью до ¹/₁₀₀₀ до ¹/₁₀₀₀₀ и т. д.  найдем  следующее.

Правило. Чтобы извлечь из данного целою числа или из данной десятичной дроби приближенный корень с точностью до ¹/₁₀ до ¹/₁₀₀ до ¹/₁₀₀ и т. д., находят сначала приближенный корень с точностью до 1, извлекая корень из целого числа (если его нет, пишут о корне 0 целых).

Потом находят цифру десятых. Для этого к остатку сносят ,2 цифры подкоренного числа, стоящие направо от запятой (если их нет, приписывают к остатку два нуля), и продолжают извлечение так, как это делается при извлечении корня из целого числа. Полученную цифру пишут в корне на месте десятых.

Затем находят цифру сотых. Для этого к остатку сносят снова две цифры, стоящие направо от тех, которые были только что снесены, и т. д.

Таким образом, при извлечении корня из целого числа с десятичной дробью, надо делить на грани по 2 цифры в каждой, начиная от запятой, как влево (в целой части числа), так и вправо, (в дробной части).

Примеры.

1) Найти до ¹/₁₀₀   корни: а) √2 ;   б) √0,3 ;

В последнем примере мы обратили дробь ³/₇ в десятичную, вычислив 8 десятичных знаков, чтобы образовались 4 грани, потребные для нахождения 4 десятичных знаков корня.

178. Описание таблицы квадратных корней. В конце этой книги приложена таблица квадратных корней, вычисленных с четырьмя цифрами. По этой таблице можно быстро находить квадратный корень из целого числа (или десятичной дроби), которое выражено не более, чем четырьмя цифрами. Прежде чем объяснить, как эта таблица устроена, заметим, что первую значащую цифру искомого корня мы всегда можем найти без помощи таблиц по  одному взгляду на подкоренное число; мы легко
также определим, какой десятичный разряд означает первая цифра корня и, следовательно, где в корне, когда найдем его цифры, надо поставить запятую. Приведем несколько примеров:

1)  √5’27,3. Первая цифра будет 2, так как левая грань подкоренного числа  есть  5;  а корень из 5 равен 2. Кроме того, так как в целой части подкоренного числа всех граней только 2, то в целой части искомого корня должно быть 2 цифры и, следовательно, первая его цифра 2 должна означать десятки.

2)  √9,041.   Очевидно,   в   этом  корне   первая   цифра   будет 3 простые  единицы.

3)  √0,00’83’4. Первая значащая цифра есть 9, так как грань, из которой пришлось бы извлекать корень для получения первой значащей цифры, есть 83, а корень из 83 равен 9. Так как в искомом числе не будет ни целых,  ни десятых, то первая цифра 9 должна означать сотые.

4) √0,73’85. Первая значащая цифра есть 8 десятых.

5)  √0,00’00’35’7. Первая значащая цифра будет 5 тысячных.

Сделаем   еще   одно   замечание.   Положим,   что   требуется извлечь корень из такого числа, которое, после отбрасывания в нем занятой, изображается рядом таких цифр: 5681. Корень этот может быть один из слелуюших:

Если возьмем корни, подчеркнутые нами одной чертою, то все они будут выражены одним и тем же рядом цифр, именно теми цифрами, которые получаются при извлечении корня из 5681 (это будут цифры 7, 5, 3, 7). Причина этому та, что грани, на которые приходится разбивать подкоренное число при нахождении цифр корня, будут во всех этих примерах одни и те же, поэтому и цифры для каждого корня окажутся одинаковые (только положение запятой будет, конечно, различное). Точно так же
во всех корнях, подчеркнутых нами двумя чертами, должны получиться одинаковые цифры, именно те, которыми выражается √568,1 (эти цифры будут 2, 3, 8, 3), и по той же причине. Таким образом, цифры корней из чисел, изображаемых (по отбрасывании запятой) одним и тем же рядом цифр 5681, будут двоякого (и только двоякого) рода: либо это ряд 7, 5, 3, 7, либо ряд 2, 3, 8, 3. То же самое, очевидно, может быть сказано о всяком другом ряде цифр. Поэтому, как мы сейчас
увидим,
в таблице каждому ряду цифр подкоренного
числа соответствуют 2 ряда цифр для корней.

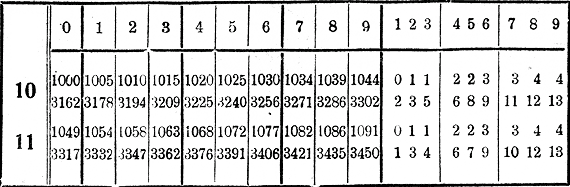
Теперь мы можем объяснить устройство таблицы и способ ее пользования. Для ясности объяснения мы изобразили здесь начало первой страницы таблицы.

Таблица эта расположена на нескольких страницах. На каждой из них в первой слева колонке помещены числа 10, 11, 12… (до 99). Эти числа выражают первые 2 цифры числа, из которого ищется квадратный корень. В верхней горизонтальной строчке (а также и в нижней) размещены числа: 0, 1, 2, 3… 9, представляющие собою 3-ю цифру данного числа, а затем далее направо   помещены цифры 1,  2,   3 . . . 9, представляющие собою4-ю цифру данного числа. Во всех
других горизонтальных строчках помещены по 2 четырехзначных числа, выражающие квадратные корни из соответствующих чисел.

Пусть требуется найти квадратный корень из какого-нибудь числа,  целого  или  выраженного  десятичною дробью. Прежде всего находим  без помощи таблиц первую цифру корня и ее разряд. Затем отбросим в данном числе запятую, если она есть. Положим   сначала,  что после отбрасывания запятой останутся только 3 цифры, напр.  114. Находим  в таблицах в левой крайней колонке первые 2 цифры, т. е. 11, и продвигаемся от   них
направо  по горизонтальной строке до тех пор, пока не дойдем до вертикальной колонки, наверху  (и внизу) которой стоит 3-я цифра числа, т. е. 4. В этом месте мы находим два четырехзначных числа:  1068 и 3376.   Которое из этих двух чисел надо взять и где поставить в нем запятую, это определяется первою цифрою корня и ее разрядом, которые мы нашли раньше. Так, если надо найти √0,11’4, то первая цифра корня есть 3 десятых, и потому мы должны
взять для корня 0,3376. Если бы требовалось
найти √1,14, то первая цифра корня была бы 1, и мы взяли бы тогда 1,068.

Таким образом мы легко найдем:

√5,30 = 2,302;   √7’18 = 26,80;  √0,91’6 = 0,9571 и т.п.

Положим теперь, что требуется найти корень из числа, выраженного (по отбрасывании запятой) 4 цифрами, напр.√7’45,6. Заметив, что первая цифра корня есть 2 десятка, находим для числа 745 так, как сейчас было объяснено, цифры 2729 (это число только замечаем пальцем, но его не записываем). Потом продвигаемся от этого числа еще направо до тех пор, пока в правой части таблицы (за последнею жирною чертою) не встретим ту вертикальную
колонку, которая отмечена наверху (и внизу)
4-й цифрой данного числа, т. е. цифрой 6, и находим там число 1. Это будет поправка, которую надо приложить (в уме) к ранее найденному числу 2729; получим 2730. Это число записываем и ставим в нем запятую на надлежащем месте: 27,30.

Таким путем найдем, напр:

√44,37 = 6,661;   √4,437 = 2,107;   √0,04’437 =0,2107 и т.д.

Если подкоренное число выражается только одной или двумя цифрами, то мы можем предположить, что после этих цифр стоит один или два нуля, и затем поступать так, как было объяснено для трехзначного числа. Напр.√2,7 =√2,70 =1,643;  √0,13  = √0,13’0 = 0,3606 и т.п..

Наконец, если подкоренное число выражено более, чем 4 цифрами, то из них мы возьмем только первые 4, а остальные отбросим, причем для уменьшения ошибки, если первая из отбрасцваемых цифр есть 5 или более 5, то мы увеличим на l четвертую из удержанных цифр. Так:

√357,8|3 | = 18,91;    √0,49’35|7 | =  0,7025; и т.п.

Замечание. В таблицах указан приближенный квадратный корень иногда с недостатком, иногда же с избытком, а именно тот из этих приближенных корней, который ближе подходит к точному корню.

179. Извлечение квадратных корней из обыкновенных дробей. Точный квадратный корень из несократимой дроби можно извлечь лишь тогда, когда оба члена дроби точные квадраты (§ 174). В этом случае достаточно извлечь корень из числителя и знаменателя отдельно, напр.:

Приближенный квадратный корень из обыкновенной дроби c какою-нибудь десятичною точностью проще всего можно находить, если предварительно обратим обыкновенную дробь в десятичную, вычислив в этой дроби такое число десятичных знаков после запятой, которое было бы вдвое больше числа десятичных знаков в искомом корне.

Пусть, напр., надо найти √23/7  c точностью до 0,01, т. е. с 2 десятичными знаками после запятой. Для этого обратим 23/7 в десятичную дробь c 4 десятичными знаками: 28/7 = 2,4285… и извлечем приближенный корень из 2,4285  c  точностью до  0,01.

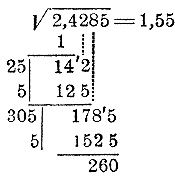Впрочем можно поступать и иначе. Объясним это на следующем примере:

Найти приближенный √ ⁵/₂₄

Сделаем знаменатель точным квадратом. Для этого достаточно было бы умножить оба члена дроби на знаменатель 24; но в этом примере можно поступить иначе. Разложим 24 на простые множители: 24 = 2 • 2 • 2 • 3. Из этого разложения видно, что если 24 умножить на 2 и еще на 3, то тогда в произведении каждый простой множитель будет повторяться четное число раз, и, следовательно, знаменатель сделается квадратом:

Остается вычислить √30 с какой-нибудь точностью и результат разделить на 12. При этом надо иметь в виду, что от деления на 12 уменьшится и дробь, показывающая степень точности. Так, если найдем √30 с точностью до ¹/₁₀ и результат разделим на 12, то получим приближенный корень из дроби ⁵/₂₄ с точностью до ¹/₁₂₀ (а
именно
⁵⁴/₁₂₀ и ⁵⁵/₁₂₀)

Глава третья.

График функции х = √y .

180. Обратная функция. Пусть дано какое-нибудь уравнение, определяющее у как функцию от х, напр, такое: у = х². Мы можем сказать, что оно определяет не только у как функцию от х, но и, обратно, определяет  х как функцию от у, хотя и неявным  образом.  Чтобы сделать эту функцию явной, надо решить данное уравнение относительно х,
принимая у за известное   число;  так,  из  взятого нами  уравнения находим: у = х².

Алгебраическое выражение, полученное для x после решения уравнения, определяющего  у  как функцию  от x, называется функцией,  обратной  той,   которая   определяет у.

Значит, функция , х = √y   обратна функции у = х².  Если, как это принято, независимое переменное обозначим х, а зависимое у, то полученную сейчас   обратную функцию можем выразить так: y = √x .     Таким образом, чтобы получить функцию, обратную данной (прямой), надо из уравнения, определяющего эту данную функцию, вывести х в зависимости от y и в   полученном   выражении заменить y на x, а х на y.

181. График функции y = √x . Функция эта невозможна при отрицательном значении х, но ее возможно вычислить (с любою точностью) при всяком положительном значении x, причем для каждого такого значения функция получает два различных значения с одинаковой абсолютной величиной, но с противоположными знаками. Если знаком √  будем обозначать только арифметическое значение квадратного корня, то эти два значения функции можем выразить так: y = ±√x  Для построения графика этой
функции надо предварительно составить таблицу ее значений. Всего проще эту таблицу составить из таблицы значений прямой функции:

у = х².

x

0

1/2

1

11/2

2

21/2

…

—1/2

—1

—11/2

—2

—21/2

y

0

1/4

1

21/4

4

61/4

…

1/4

1

21/4

4

61/4

если значения у примем за значения х, и наоборот:

y = ±√x

x	0	1/4	1	21/4	4	61/4	…
y	0	± 1/2	± 1	± 11/2	± 2	± 21/2	…

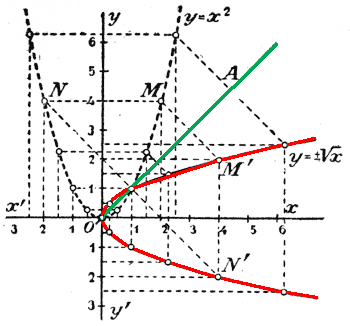
Нанеся  все  эти   значения на чертеже,  получим следующий график .

На том же чертеже мы изобразили (прерывистой линией) и график прямой функции у = х². Сравним эти два графика между собою.

182. Соотношение между графиками прямой и обратной функций. Для составления таблицы значений обратной функции y = ±√x  мы брали для х те числа, которые в таблице прямой функции у = х²  служили значениями для у, а для у брали те числа;   которые  в   этой таблице были значениями для x. Из этого следует, что  оба графика одинаковы, только график прямой функции так расположен относительно оси у — ов,  как график обратной функции расположен относительно   оси   х — ов. Вследствие  этого,   если мы перегнем чертеж вокруг прямой  ОА, делящей пополам прямой угол xОу, так, чтобы часть чертежа, содержащая полуось   Оу,   упала
  на   ту часть, которая содержит полуось Ох, то Оу совместится с Ох, все деления Оу совпадут c делениями Ох, и точки параболы у = х² совместятся с соответствующими точками графика y = ±√x. Напр, точки М и N, у которых ордината 4, а абсциссы 2 и —2, совпадут с точками М’ и N’, у которых абсцисса 4, а ординаты 2 и —2. Если же эти точки совпадут, то это значит, что прямые ММ’ и NN’ перпендикулярны к ОА и делятся этою прямою пополам. То же самое можно сказать о всех других соответствующих точках  обоих графиков.

Таким образом, график обратной функции должен быть такой же, как и грaфик прямой функции, но расположены эти графики различно, а именно симметрично друг с другом относительно биссектрисы угла хОу. Можно сказать, что график обратной функции есть отображение (как в зеркале) графика прямой функции относительно биссектрисы угла хОу.

Корень из десятичных дробей и смешанных чисел извлекается после замены подкоренного выражения обыкновенной дробью.

Пример 1

Извлечь корень из обыкновенной дроби:

Чтобы извлечь кубический корень из дроби воспользуемся свойством корней:

Найдем значения корней в числителе и в знаменателе при помощи таблицы кубов:

Ответ:

Пример 2

Извлечь квадратный корень из 0,16:

Представим десятичную дробь в виде обыкновенной дроби:

Теперь воспользуемся свойством корней:

Извлечем корни из числителя и знаменателя при помощи таблицы квадратов:

Из этой статьи вы узнаете:

• что такое «извлечение корня»;
• в каких случаях он извлекается;
• принципы нахождения значения корня;
• основные способы извлечения корня из натуральных и дробных чисел.

Что такое «извлечение корня»

Для начала введем определение «извлечение корня».

Извлечение корня — процесс нахождения значения корня.

При извлечении корня n -ной степени из числа a, мы находим число b , n -ная степень которого равняется a . Если мы нашли такое число b , можно утверждать, что корень извлечен.

Выражения «извлечение корня» и «нахождение значения корня» равнозначны.

В каких случаях извлекается корень?

Корень n -ной степени можно извлечь из числа a точно в случае, если a можно представить в виде n -ной степени некоторого числа b .

4 = 2 × 2 , следовательно, из числа 4 можно точно извлечь квадратный корень, который равен 2

Когда корень n -ной степени из числа a невозможно представить в виде n -ной степени числа b , то такой корень не извлекается либо извлекается только приближенное значение корня с точностью до любого десятичного разряда.

Принципы нахождения значения корня и способы их извлечения

• Использование таблицы квадратов, таблицы кубов и т.д.
• Разложение подкоренного выражения (числа) на простые множители
• Извлечение корней из дробных чисел
• Извлечение корня из отрицательного числа
• Поразрядное нахождение значения корня

Необходимо понять, по каким принципам находится значение корней, и каким образом они извлекаются.

Главный принцип нахождения значения корней — основываться на свойствах корней, в том числе на равенстве: b n n = b , которое является справедливым для любого неотрицательного числа b .

Начать следует с наиболее простого и очевидного способа: таблицы квадратов, кубов и т.д.

Когда таблицы под руками нет, вам поможет способ разложения подкоренного числа на простые множители (способ незатейливый).

Стоит уделить внимание извлечению корня из отрицательного числа, что является возможным для корней с нечетными показателями.

Изучим, как извлекать корни из дробных чисел, в том числе из смешанных чисел, обыкновенных и десятичных дробей.

И потихоньку рассмотрим способ поразрядного нахождения значения корня — наиболее сложного и многоступенчатого.

Использование таблицы квадратов, кубов и т.д.

Таблица квадратов включает в себя все числа от 0 до 99 и состоит из 2 зон: в первой зоне можно составить любое число до 99 с помощью вертикального столбца с десятками и горизонтальной строки с единицами, во второй зоне содержатся все квадраты образуемых чисел.

Таблица квадратов

Таблица квадратов	единицы
0	1	2	3	4	5	6	7	8	9
десятки	0	0	1	4	9	16	25	36	49	64	81
1	100	121	144	169	196	225	256	289	324	361
2	400	441	484	529	576	625	676	729	784	841
3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2041
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Существуют также таблицы кубов, четвертой степени и т.д., которые созданы по принципу, аналогичному таблице квадратов.

Таблица кубов

Таблица кубов	единицы
0	1	2	3	4	5	6	7	8	9
десятки	0	0	1	8	27	64	125	216	343	512	729
1	1000	1 331	1 728	2 197	2 744	3 375	4 096	4 913	5 832	6 859
2	8000	9 261	10 648	12 167	13 824	15 625	17 576	19 683	21 952	24 389
3	27000	29 791	32 768	35 937	39 304	42 875	46 656	50 653	54 872	59 319
4	64000	68 921	74 088	79 507	85 184	91 125	97 336	103 823	110 592	117 649
5	125000	132 651	140 608	148 877	157 464	166 375	175 616	185 193	195 112	205 379
6	216000	226 981	238 328	250 047	262 144	274 625	287 496	300 763	314 432	328 509
7	343000	357 911	373 248	389 017	405 224	421 875	438 976	456 533	474 552	493 039
8	512000	531 441	551 368	571 787	592 704	614 125	636 056	658 503	681 472	704 969
729000	753 571	778 688	804 357	830 584	857 375	884 736	912 673	941 192	970 299

Принцип функционирования таких таблиц прост, однако их часто нет под рукой, что значительно усложняет процесс извлечение корня, поэтому необходимо владеть минимум несколькими способами извлечения корней.

Разложение подкоренного числа на простые множители

Наиболее удобный способ нахождения значения корня после таблицы квадратов и кубов.

Способ разложения подкоренного числа на простые множители подразумевает под собой представление числа в виде степени с необходимым показателем, что дает нам возможность получить значение корня.

Извлечем квадратный корень из 144 .

Разложим 144 на простые множители:

Таким образом: 144 = 2 × 2 × 2 × 2 × 3 × 3 = ( 2 × 2 ) 2 × 3 2 = ( 2 × 2 × 3 ) 2 = 12 2 . Следовательно, 144 = 12 2 = 12 .

Также при использовании свойств степени и корней можно записать преобразование немного по-другому:

144 = 2 × 2 × 2 × 2 × 3 × 3 = 2 4 × 3 2 = 2 4 × 3 2 = 2 2 × 3 = 12

144 = 12 — окончательный ответ.

Извлечение корней из дробных чисел

Запоминаем: любое дробное число должно быть записано в виде обыкновенной дроби.

Следуя свойству корня из частного, справедливым является следующее равенство:

p q n = p n q n . Исходя из этого равенства, необходимо воспользоваться правилом извлечения корня из дроби: корень из дроби равен от деления корня числителя на корень знаменателя.

Рассмотрим пример извлечения корня из десятичной дроби, поскольку извлечь корень из обыкновенной дроби можно с помощью таблицы.

Необходимо извлечь кубический корень из 474 , 552 . Первым делом, представим десятичную дробь в виде обыкновенной: 474 , 552 = 474552 / 1000 . Из этого следует: 474552 1000 3 = 474552 3 1000 3 . Затем можно приступить к процессу извлечения кубических корней в числителе и знаменателе:

474552 = 2 × 2 × 2 × 3 × 3 × 3 × 13 × 13 × 13 = ( 2 × 3 × 13 ) 3 = 78 3 и 1000 = 10 3 , то

474552 3 = 78 3 3 = 78 и 1000 3 = 10 3 3 = 10 .

Завершаем вычисления: 474552 3 1000 3 = 78 10 = 7 , 8 .

Извлечение корня из отрицательных чисел

Если знаменатель является нечетным числом, то число под знаком корня может оказаться отрицательным. Из этого следует: для отрицательного числа — a и нечетного показателя корня 2 n — 1 справедливо равенство:

— a 2 × n — 1 = — a 2 × n — 1

Правило извлечения нечетной степени из отрицательных чисел: чтобы извлечь корень из отрицательного числа необходимо извлечь корень из противоположного ему положительного числа и поставить перед ним знак минус.

— 12 209 243 5 . Для начала необходимо преобразовать выражение, чтобы под знаком корня оказалось положительно число:

— 12 209 243 5 = 12 209 243 — 5 ​​​​​​

Затем следует заменить смешанное число обыкновенной дробью:

12 209 243 — 5 = 3125 243 — 5

Пользуясь правилом извлечения корней из обыкновенной дроби, извлекаем:

3125 243 — 5 = — 3125 5 243 5

Вычисляем корни в числителе и знаменателе:

— 3125 5 243 5 = — 5 5 5 3 5 5 = — 5 3 = — 1 2 3

Краткая запись решения:

— 12 209 243 5 = 12 209 243 — 5 = 3125 243 — 5 = — 3125 5 243 5 = — 5 5 5 3 5 5 = — 5 3 = — 1 2 3 .

Ответ: — 12 209 243 5 = — 1 2 3 .

Поразрядное нахождение значения корня

Бывают случаи, когда под корнем находится число, которое не получается представить в виде n — ной степени некоторого числа. Но необходимо знать значение корня с точностью до некоторого знака.

В таком случае необходимо воспользоваться алгоритмом поразрядного нахождения значения корня, с помощью которого можно получить достаточное количество значений искомого числа.

Как это происходит, разберем на примере извлечения квадратного корня из 5 .

Сперва необходимо найти значение разряда единиц. Для этого начнем перебирать значения 0 , 1 , 2 , . . . , 9 , вычисляя при этом 0 2 , 1 2 , . . . , 9 2 до необходимого значения, которое больше, чем подкоренное число 5 . Все это удобно представить в виде таблицы:

Возможное значение корня	0	1	2	3
Это значение в степени	0	1	4	9

Значение ряда единиц равняется 2 ( т а к к а к 2 2 5 , а 2 3 > 5 ) . Переходим в разряду десятых — будем возводить в квадрат числа 2 , 0 , 2 , 1 , 2 , 2 , . . . , 2 , 9 , , сравнивая полученные значения с числом 5 .

Возможное значение корня	2,0	2,1	2,2	2,3
Это значение в степени	4	4,41	4,84	5,29

Поскольку 2 , 2 2 5 , а 2 , 3 2 > 5 , то значение десятых равняется 2 . Переходим к нахождению значения сотых:

Возможное значение корня	2.20	2,21	2,22	2,23	2,24
Это значение в степени	4,84	4,8841	4,8294	4,9729	5,0176

Таким образом, найдено значение корня из пяти — 2 , 23 . Можно находить значения корня дальше:

2 , 236 , 2 , 2360 , 2 , 23606 , 2 , 236067 , . . .

Итак, мы изучили несколько наиболее распространенных способов нахождения значения корня, воспользоваться которыми можно в любой ситуации.

1. Квадратный корень из произведения двух неотрицательных множителей равен произведению корней из этих множителей:

1. Квадратний корінь з добутку двох невід’ємних множників дорівнює добутку коренів з цих множників:

2. Квадратный корень из дроби, числитель которой неотрицательный, а знаменатель положительный, равен корню из числителя, разделенному на корень из знаменателя:

2. Квадратний корінь з дробу, чисельник якої ненегативний, а знаменник — позитивний, дорівнює кореню з чисельника, розділеному на корінь із знаменника:

Чтобы извлечь квадратный корень из многочлена, надо вычислить многочлен и из полученного числа извлечь корень.

Внимание! Нельзя извлекать корень из каждого слагаемого (уменьшаемого и вычитаемого) отдельно.

Щоб витягти квадратний корінь з многочлена, треба обчислити багаточлен і з отриманого числа витягти корінь.

Увага! Не можна витягати корінь з кожного додатку (зменшуваного і від’ємного) окремо.

Чтобы извлечь квадратный корень из произведения (частного), можно вычислить корень квадратный из каждого множителя (делимого и делителя), а полученные значения взять произведением (частным).

Щоб витягти квадратний корінь з добутку (частки), можна обчислити корінь квадратний з кожного множника (діленого і дільника), а отримані значення взяти добутком (часткою).

Чтобы извлечь квадратный корень из дроби, надо извлечь квадратный корень из числителя и знаменателя отдельно, а полученные значения оставить дробью или вычислить как частное (если возможно это по условию).

Щоб витягти квадратний корінь з дробу, треба витягти квадратний корінь з чисельника і знаменника окремо, а отримані значення залишити дробом або обчислити як частку (якщо можливо це за умовою).

Из-под знака корня можно вынести множитель и можно внести множитель под знак корня. При вынесении множителя из него извлекается корень, а при внесении — он возводится в соответствующую степень.

З-під знака кореня можна винести множник і можна внести множник під знак кореня. При винесенні множника з нього витягується корінь, а при внесенні — він зводиться у відповідну ступінь.

Если корень в знаменателе дроби, то такую дробь можно заменить тождественной ей дробью, не содержащей радикалов (корней) в знаменателе. Для этого умножают числитель и знаменатель дроби на такое выражение (сопряженное знаменателю), чтобы корень в знаменателе извлекался.

Якщо корінь в знаменнику дробу, то такий дріб можна замінити тотожним йому дробом, що не містить радикалів (коренів) у знаменнику. Для цього множать чисельник і знаменник дробу на такий вираз (поєднане зі знаменником), щоб корінь в знаменнику видалявся.

Примеры. Приклади

1. Избавиться от радикала в знаменателе дроби:

1. Позбутися від радикала в знаменнику дробу:

2. Избавиться от радикала в знаменателе дроби:

2. Позбутися від радикала в знаменнику дробу:

3. Избавиться от радикала в числителе дроби:

3. Позбутися від радикала в чисельнику дробу:

Освобождение дроби от радикалов в числителе (в знаменателе) дроби называется преобразованием алгебраической дроби.

Звільнення дробу від радикалів у чисельнику (в знаменнику) дробу називається перетворенням алгебраїчного дробу. Чтобы преобразовать сумму (разность) квадратных корней, нужно привести подкоренные выражения к одному основанию степени, если это возможно, извлечь корни из степеней и записать их перед знаками корней, а оставшиеся квадратные корни с одинаковыми подкоренными выражениями можно сложить, для чего складываются коэффициенты перед знаком корня и дописывается тот же квадратный корень. Щоб перетворити суму (різницю) квадратних коренів, потрібно привести підкоренні вирази до однієї основи ступеня, якщо це можливо, отримати коріння ступенів і записати їх перед знаками коренів, а решта квадратні корені з однаковими підкореними виразами можна скласти, для чого складаються коефіцієнти перед знаком кореня і дописується той же квадратний корінь. Приведем все подкоренные выражения к основанию 2. Из четной степени корень извлекается полностью, из нечетной степени корень основания в степени 1 оставляем под знаком корня. Приводим подобные целые числа и коэффициенты складываем с одинаковыми корнями. Запишем двучлен как произведение числа и двучлена суммы. Наведемо всі підкорені вирази до основи 2. З парного ступеня корінь витягується повністю, з непарного ступеня корінь основи в ступені 1 залишаємо під знаком кореня. Наводимо подібні цілі числа і коефіцієнти складаємо з однаковим корінням. Запишемо двочлен як добуток числа і двочлена суми. Приводим подкоренные выражения к наименьшему основанию или произведению степеней с наименьшими основаниями. Из четных степеней подкоренных выражений извлекаем корень, остатки в виде основания степени с показателем 1 или произведением таких оснований оставляем под знаком корня. Приводим подобные члены (складываем коэффициенты одинаковых корней). Наводимо підкорені вирази до найменшої основи або добутку ступенів з найменшими основами. З парних ступенів підкорених виразів витягаємо корінь, залишки у вигляді основи ступеня з показником 1 або добутком таких основ залишаємо під знаком кореня. Наводимо подібні члени (складаємо коефіцієнти однакових коренів). Заменим деление дробей на умножение (с заменой второй дроби на обратную). Перемножим отдельно числители и знаменатели дробей. Под каждым знаком корня выделим степени. Сократим одинаковые множители в числителе и знаменателе. Извлечем корни из четных степеней. Замінимо ділення дробів на множення (з заміною другого дробу на зворотний). Перемножимо окремо чисельники і знаменники дробів. Під кожним знаком кореня виділимо ступені. Скоротимо однакові множники в чисельнику і знаменнику. Винесемо коріння з парних ступенів. Чтобы сравнить два квадратных корня, их подкоренные выражения надо привести в степени с одинаковым основанием, тогда чем больше показать степени подкоренного выражения, тем больше значение квадратного корня. В этом примере привести к одному основанию подкоренные выражения нельзя, так как в первом основание 3, а во втором – 3 и 7. Второй способ сравнения состоит в том, чтобы внести коэффициент корня в подкоренное выражение и сравнить числовые значения подкоренных выражений. У квадратного корня чем больше подкоренное выражение, тем больше значение корня. Щоб порівняти два квадратних кореня, їх підкорені вирази треба привести до ступеня з однаковою основою, тоді чим більше показник степеня підкореневого виразу, тим більше значення квадратного кореня. У цьому прикладі привести до одної основи підкорені вирази не можна, так як в першому основа 3, а у другому — 3 і 7. Другий спосіб порівняння полягає в тому, щоб внести коефіцієнт кореня в підкореневий вираз і порівняти числові значення підкорених виразів. У квадратного кореня чим більше підкореневий вираз, тим більше значення кореня. Используя распределительный закон умножения и правило умножения корней с одинаковыми показателями (в нашем случае – квадратных корней), получили сумму двух квадратных корней с произведением под знаком корня. Разложим 91 на простые множители и выносим корень за скобки с общими подкоренными множителями (13*5). Мы получили произведение корня и двучлена, у которого один из одночленов целое число (1). Використовуючи розподільний закон множення і правило множення коренів з однаковими показниками (в нашому випадку — квадратних коренів), отримали суму двох квадратних коренів з добутком під знаком кореня. Розкладемо 91 на прості множники і виносимо корінь за дужки із загальними підкореневими множниками (13*5). Ми отримали добуток кореня і двочлена, у якого один з одночленів ціле число (1). Приклад 9:

В подкоренных выражениях выделим множителями числа, из которых можно извлечь целый квадратный корень. Извлечем квадратные корни из степеней и поставим числа коэффициентами квадратных корней.

У членов данного многочлена есть общий множитель √3, который можно вынести за скобки. Приведем подобные слагаемые.

У підкореневих виразах виділимо множниками числа, з яких можна отримати цілий квадратний корінь. Винесемо квадратні корені із ступенів і поставимо числа коефіцієнтами квадратних коренів.

У членів даного многочлена є спільний множник √3, який можна винести за дужки. Наводимо подібні доданки.

Произведение суммы и разности двух одинаковых оснований (3 и √5) по формуле сокращенного умножения можно записать как разность квадратов оснований.

Корень квадратный в квадрате всегда равен подкоренному выражению, поэтому мы избавимся от радикала (знака корня) в выражении.

Добуток суми і різниці двох однакових основ (3 і √5) з формули скороченого множення можна записати як різницю квадратів основ.

Корінь квадратний у квадраті завжди дорівнює підкореневому виразу, тому ми позбудемося радикала (знака кореня) у виразі.