Как найти наименьший положительный период для функции - Исправление недочетов и поиск решений вместе с Examum.ru

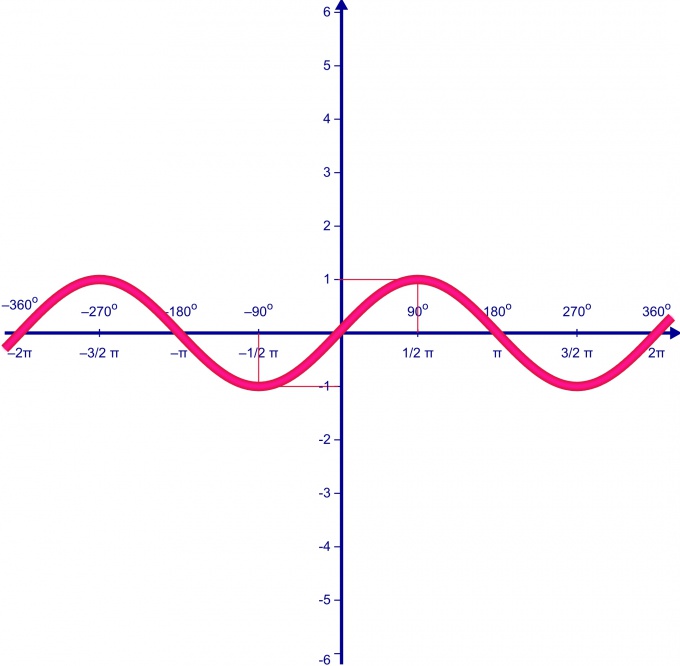
С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.

Дадим определение периодической функции:

Функция y=f(x) называется периодической, если существует такое число , не равное нулю, что для любого из ее области определения

Другими словами, это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого фиксированного ненулевого числа . Число называется периодом функции. Как правило, говоря о периоде, мы имеем в виду наименьший положительный период функции.

Например, — периодические функции.

Для функций и период T = 2pi ,

Для функций tg x и период T = pi.

Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:

1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения

График функции может выглядеть, например, вот так:

Отметим точку М (1; 5), принадлежащую графику функции . Поскольку период функции равен 2, значения функции в точках будут также равны пяти. Здесь k — целое число.

Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.

Значения функции в точках -3 и 7 равны пяти. Мы получим:

2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).

Построим график функции при

Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.

Период функции равен 2. Повторим периодически участок длины 2, который уже построен.

Найдем f(4)

3. Найдите наименьший положительный период функции

Наименьший положительный период функции равен 2pi.

График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).

Значит, у функции частота в 3 раза больше, чем у функции , а наименьший положительный период в 3 раза меньше и равен $frac{{rm 2}pi }{{rm 3}}$ . Значит, на отрезке 2pi укладывается ровно 3 полных волны функции

Рассуждая аналогично, получим, что для функции наименьший положительный период равен $frac{{rm 2}pi }{{rm 5}}.$ На отрезке 2pi укладывается ровно 5 полных волн функции

Числа 3 и 5 — взаимно простые. Поэтому наименьший положительный период функции равен 2pi .

4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции

По условию, период функции равен 12. Это значит, что все значения повторяются через 12, через . Если мы выберем любую точку x_0 на графике функции то через значение функции будет такое же, как и в точке x_0.

Аналогично, все значения функции повторяются через . В этих точках значения будут такие же, как и в точке x_0.

На каком же расстоянии от точки x_0 расположена точка, в которой значение функции такое же, что и в точке x_0 ? Очевидно, на расстоянии Это значит, что число делится и на 12, и на 8, то есть является их наименьшим общим кратным. Значит, T = 24 .

Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Периодические функции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции

$[{T_1} = frac{T}{{left| k right|}}]$

где T — период функции y=f(x). Эта формула позволяет быстро найти период тригонометрических функций такого вида. Для функций y=sin x и y=cos x наименьший положительный период T=2п, для y=tg x и y=ctg x T=п. Рассмотрим на конкретных примерах, как найти период функции, используя данную формулу.

Найти период функции:

1) y=5sin(3x-п/8).

Здесь А=5, k=3, b=-п/8. Для нахождения периода нам нужно только k — число, стоящее перед иксом. Поскольку период синуса T=2п, то период данной функции

$[{T_1} = frac{T}{{left| k right|}} = frac{{2pi }}{{left| 3 right|}} = frac{{2pi }}{3}.]$

$[2)y = frac{2}{7}cos (frac{pi }{5} - frac{x}{{11}})]$

А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то

$[{T_1} = frac{T}{{left| k right|}} = frac{{2pi }}{{left| { - frac{1}{{11}}} right|}} = 2pi cdot 11 = 22pi .]$

$[3)y = 0,3tg(frac{{5x}}{9} - frac{pi }{7})]$

А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции

$[{T_1} = frac{T}{{left| k right|}} = frac{pi }{{left| {frac{5}{9}} right|}} = frac{{9pi }}{5}.]$

А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть

$[{T_1} = frac{T}{{left| k right|}} = frac{pi }{{left| {0,4} right|}} = frac{{10pi }}{4} = frac{{5pi }}{2}.]$

Источник

Как найти наименьший положительный период функции

Наименьший положительный период функции в тригонометрии обозначается f. Он характеризуется наименьшим значением положительного числа T, то есть меньше его значение T уже не будет являться периодом функции.Вам понадобится

Обратите внимание на то, что периодическая функция не всегда имеет наименьший положительный период. Так, к примеру, в качестве периода постоянной функции может быть абсолютно любое число, а значит, у нее может и не быть наименьшего положительного периода. Встречаются также и непостоянные периодические функции, у которых нет наименьшего положительного периода. Однако в большинстве случаев наименьший положительный период у периодических функций все же есть.

Наименьший период синуса равен 2?. Рассмотрите доказательство этого на примере функции y=sin(x). Пусть T будет произвольным периодом синуса, в таком случае sin(a+T)=sin(a) при любом значении a. Если a=?/2, получается, что sin(T+?/2)=sin(?/2)=1. Однако sin(x)=1 лишь в том случае, когда x=?/2+2?n, где n представляет собой целое число. Отсюда следует, что T=2?n, а значит, наименьшим положительным значением 2?n является 2?.

Наименьший положительный период косинуса тоже равен 2?. Рассмотрите доказательство этого на примере функции y=cos(x). Если T будет произвольным периодом косинуса, то cos(a+T)=cos(a). В том случае если a=0, cos(T)=cos(0)=1. Ввиду этого, наименьшим положительным значением T, при котором cos(x)=1, есть 2?.

Учитывая тот факт, что 2? – период синуса и косинуса, это же значение будет и периодом котангенса, а также тангенса, однако не минимальным, поскольку, как известно, наименьший положительный период тангенса и котангенса равен ?. Убедиться в этом сможете, рассмотрев следующий пример: точки, соответствующие числам (х) и (х+?) на тригонометрической окружности, имеют диаметрально противоположное расположение. Расстояние от точки (х) до точки (х+2?) соответствует половине окружности. По определению тангенса и котангенса tg(x+?)=tgx, а ctg(x+?)=ctgx, а значит, наименьший положительный период котангенса и тангенса равен ?.

Источник

Совет 1: Как обнаружить минимальный позитивный период функции

Минимальный позитивный период функции в тригонометрии обозначается f. Он характеризуется наименьшим значением позитивного числа T, то есть поменьше его значение T теснее не будет являться период ом функции .

Вам понадобится

– математический справочник.

Инструкция

1. Обратите внимание на то, что период ическая функция не неизменно имеет минимальный правильный период . Так, к примеру, в качестве период а непрерывной функции может быть безусловно всякое число, а значит, у нее может и не быть наименьшего позитивного период а. Встречаются также и непостоянные период ические функции , у которых нет наименьшего правильного период а. Впрочем в большинстве случаев минимальный правильный период у период ических функций все же есть.

2. Минимальный период синуса равен 2?. Разглядите подтверждение этого на примере функции y=sin(x). Пускай T будет произвольным период ом синуса, в таком случае sin(a+T)=sin(a) при любом значении a. Если a=?/2, получается, что sin(T+?/2)=sin(?/2)=1. Впрочем sin(x)=1 лишь в том случае, когда x=?/2+2?n, где n представляет собой целое число. Отсель следует, что T=2?n, а значит, наименьшим позитивным значением 2?n является 2?.

3. Минимальный правильный период косинуса тоже равен 2?. Разглядите подтверждение этого на примере функции y=cos(x). Если T будет произвольным период ом косинуса, то cos(a+T)=cos(a). В том случае если a=0, cos(T)=cos(0)=1. Ввиду этого, наименьшим позитивным значением T, при котором cos(x)=1, есть 2?.

4. Рассматривая тот факт, что 2? – период синуса и косинуса, это же значение будет и период ом котангенса, а также тангенса, впрочем не минимальным, от того что, как знаменито, минимальный правильный период тангенса и котангенса равен ?. Удостовериться в этом сумеете, разглядев дальнейший пример: точки, соответствующие числам (х) и (х+?) на тригонометрической окружности, имеют диаметрально противоположное расположение. Расстояние от точки (х) до точки (х+2?) соответствует половине окружности. По определению тангенса и котангенса tg(x+?)=tgx, а ctg(x+?)=ctgx, а значит, минимальный правильный период котангенса и тангенса равен ?.

Совет 2: Как находить период функции

Периодической функцией именуется функция, повторяющая свои значения через какой-то ненулевой период. Периодом функции именуется число, при добавление которого к доводу функции значение функции не меняется.

Вам понадобится

Знания по элементарной математике и началам обзора.

Инструкция

1. Обозначим период функции f(x) через число К. Наша задача обнаружить это значение К. Для этого представим, что функция f(x), пользуясь определением периодической функции, приравняем f(x+K)=f(x).

2. Решаем полученное уравнение касательно незнакомой K, так, как словно x – константа. В зависимости от значения К получится несколько вариантов.

3. Если K>0 – то это и есть период вашей функции.Если K=0 – то функция f(x) не является периодической.Если решение уравнения f(x+K)=f(x) не существует ни при каком K не равном нулю, то такая функция именуется апериодической и у неё тоже нет периода.

Видео по теме

Обратите внимание!
Все тригонометрические функции являются периодическими, а все полиномиальные со степенью огромнее 2 – апериодическими.

Полезный совет
Периодом функции, состоящей из 2-х периодический функций, является Наименьшее всеобщее кратное периодов этих функций.

Совет 3: Как обнаружить период функции

Если рассматривать точки на окружности, то точки x, x + 2π, x + 4π и т.д. совпадают друг с ином. Таким образом, тригонометрические функции на прямой периодически повторяют свое значение. Если знаменит период функции , дозволено возвести функцию на этом периоде и повторить ее на других.

Инструкция

1. Период – это число T, такое что f(x) = f(x+T). Дабы обнаружить период, решают соответствующее уравнение, подставляя в качестве довода x и x+T. При этом пользуются теснее вестимыми периодами для функций. Для функций синуса и косинуса период составляет 2π, а для тангенса и котангенса – π.

2. Пускай дана функция f(x) = sin^2(10x). Разглядите выражение sin^2(10x) = sin^2(10(x+T)). Воспользуйтесь формулой для понижения степени: sin^2(x) = (1 – cos 2x)/2. Тогда получите 1 – cos 20x = 1 – cos 20(x+T) либо cos 20x = cos (20x+20T). Зная, что период косинуса равен 2π, 20T = 2&#960. Значит, T = π/10. Т – минимальный правильный период, а функция будет повторяться и через 2Т, и через 3Т, и в иную сторону по оси: -T, -2T и т.д.

Полезный совет
Пользуйтесь формулами для понижения степени функции. Если вам теснее знамениты периоды каких-нибудь функций, пробуйте свести имеющуюся функцию к знаменитым.

Совет 4: Как обнаружить минимальный период функции

Функция, значения которой повторяются через определенное число, именуется периодической . То есть сколько бы периодов вы ни прибавили к значению х, функция будет равна одному и тому же числу. Всякое изыскание периодических функций начинается с поиска наименьшего периода, дабы не исполнять лишнюю работу: довольно исследовать все свойства на отрезке, равном периоду.

Инструкция

1. Воспользуйтесь определением периодической функции . Все значения х в функции замените на (х+Т), где Т – минимальный период функции . Решите полученное уравнение, считая Т незнакомым числом.

2. В итоге вы получите некое тождество, из него испробуйте подобрать наименьший период. Скажем, если получилось равенство sin(2T)=0,5, следственно, 2Т=П/6, то есть Т=П/12.

3. Если равенство получается правильным только при Т=0 либо параметр Т зависит от х (скажем, получилось равенство 2Т=х), делайте итог о том, что функция не периодична.

4. Для того дабы узнать минимальный период функции , содержащей лишь одно тригонометрическое выражение, воспользуйтесь правилом. Если в выражении стоит sin либо cos, периодом для функции будет 2П, а для функций tg, ctg ставьте минимальный период П. Учтите при этом, что функция не должна быть возведена в какую-нибудь степень, а переменная под знаком функции не должна быть умножена на число, хорошее от 1.

5. Если cos либо sin внутри функции построены в четную степень, уменьшите период 2П в два раза. Графически вы можете увидеть это так: график функции , расположенный ниже оси ох, симметрично отразится вверх, следственно функция будет повторяться в два раза почаще.

6. Дабы обнаружить минимальный период функции при том, что угол х умножен на какое либо число, действуете так: определите типовой период этой функции (скажем, для cos это 2П). После этого поделите его на множитель перед переменной. Это и будет желанный минимальный период. Уменьшение периода отменно видно на графике: он сжимается ровно во столько раз, на сколько умножен угол под знаком тригонометрической функции .

7. Обратите внимание, если перед х стоит дробное число поменьше 1, период возрастает, то есть график, наоборот, растягивается.

8. Если в вашем выражении две периодические функции умножены друг на друга, обнаружьте минимальный период для всякой по отдельности. После этого определите минимальный всеобщий множитель для них. Скажем, для периодов П и 2/3П минимальный всеобщий множитель будет 3П (он делится без остатка как на П, так и на 2/3П).

Совет 5: Как обнаружить среднюю зарплату

Расчет размера средней заработной платы работников нужен для начисления пособий по временной нетрудоспособности, оплаты командировок. Средний заработок экспертов исчисляется, исходя из реально отработанного времени, и зависит от оклада, надбавок, премий, указанных в штатном расписании.

Вам понадобится

– штатное расписание;
– калькулятор;
– право;
– производственный календарь;
– табель учета рабочего времени либо акт исполненных работ.

Инструкция

1. Для того дабы сделать расчет средней заработной платы работника, вначале определите период, за тот, что нужно ее исчислить. Как водится, таким периодом выступает 12 календарных месяцев. Но если работник трудится на предприятии менее года, к примеру, 10 месяцев, то вам необходимо обнаружить средний заработок за время, которое эксперт исполняет свою трудовую функцию.

2. Сейчас определите сумму заработной платы, которая была реально начислена ему за расчетный период. Для этого используйте расчетные ведомости, по которым работнику выдавались все положенные ему выплаты. Если немыслимо воспользоваться этими документами, то месячный оклад, премии, надбавки умножьте на 12 (либо то число месяцев, которое работник трудится на предприятии, если он оформлен в компании менее года).

3. Рассчитайте среднедневной заработок. Для этого сумму заработной платы за расчетный период поделите на среднее число дней в месяце (в текущее время оно составляет 29,4). Полученный итог поделите на 12.

4. После этого определите число реально отработанного времени. Для этого используйте табель учета рабочего времени. Данный документ должен заполнять табельщик, кадровый служащий либо другой работник, у которого это прописано в должностных обязанностях.

5. Число реально отработанного времени умножьте на среднедневной заработок. Полученная сумма является средней заработной платой эксперта за год. Итог поделите на 12. Это будет среднемесячным заработком. Такой расчет используется для работников, у которых начисление заработной платы зависит от реально отработанного времени.

6. Когда работнику установлена сдельная оплата труда, то тарифную ставку (указанную в штатном расписании и определенную трудовым договором) умножьте на число произведенных изделий (используйте акт исполненных работ либо иной документ, в котором это фиксируется).

Обратите внимание!
Не путайте функции y=cos(x) и y=sin(x) – имея идентичный период, эти функции изображаются по-различному.

Полезный совет
Для большей наглядности изобразите тригонометрическую функцию, у которой рассчитывается минимальный правильный период.

Источник

Как найти наименьший положительный период функции

Вам понадобится

— математический справочник.

Инструкция

Обратите внимание

Не путайте функции y=cos(x) и y=sin(x) — имея одинаковый период, эти функции изображаются по-разному.

Полезный совет

Для большей наглядности изобразите тригонометрическую функцию, у которой рассчитывается наименьший положительный период.

Источники:

Справочник по математике, школьная математика, высшая математика

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник