ВИДЕО УРОК
Периодические функции.
Функцию у = f(х), х ∈ Х, называют периодической,
если существует такое отличное от нуля число
Т, что для любого х из области определения функции справедливо
равенство:
f(х + Т) = f(х) = f(х – Т).
Число Т называют периодом функции у = f(х).
Из этого
определения сразу следует, что если Т –
период функции
у = f(х), то
2Т, 3Т, 4Т, –Т, –2Т, –3Т,
–4Т
– также периоды
функций. Значит у периодической функции бесконечно много периодов.
Если Т – период функции, то число вида kТ,
где k – любое целое
число, также является периодом функции.
Чаще всего (но не
всегда) среди множества положительных периодов функции можно найти наименьший.
Его называют основным периодом.
График периодической
функции состоит из неограниченно повторяющихся одинаковых фрагментов.
График каждой
периодической функции состоит из одинаковых линий повторяющихся и изолированных
друг от друга, как в рассматриваемом случае, или соединенных в одну общую линию
(синусоида и другие.)
Графики
периодических функций обладают следующей особенностью. Если Т – основной период функции у = f(х), то для построения её графика достаточно построить ветвь
графика на одном из промежутков оси х длиной
Т, а затем осуществить параллельный перенос этой ветви по
оси х на
± Т, ±
2Т, ± 3Т, …
Чаще всего в
качестве такого промежутка длиной Т выбирают промежуток с концами в точках
(–Т/2; 0) и (Т/2; 0) или
(0; 0) и (Т; 0).
ПРИМЕР:
Рассмотрим функцию
у = х – [х], где [х] – целая часть числа. Если к
произвольному значение аргумента этой функции добавить 1, то значение функции от этого не изменится:
f(x + 1) = (x
+1) – [x + 1] = x + 1 – [x] – 1
= x – [x] = f (x).
Следовательно, при любом
значении х
f(x + 1) = f(x).
А это значит, что рассматриваемая функция
периодическая, период которой равен 1. Любое целое число
также является периодом данной функции, но обычно рассматривают только
маленький положительный период функции.
График этой функции
приведен на рисунке. Он состоит из бесконечного множества равных отрезков, которые
повторяются.
Периодичность тригонометрических функций.
Возьмём произвольный угол α и построим
подвижной радиус ОМ единичной окружности такой, что угол,
составленный с осью Ох этим радиусом, равен α.
Если мы к углу прибавим
2π или 360° (то есть полный
оборот), то углу α + 2π или α + 360° будет соответствовать то же положение
подвижного радиуса ОМ, что для угла α.
Так как синус и косинус угла,
составленного с осью Ох подвижным радиусом ОМ единичной
окружности, по сути соответственно ордината
у и
абсцисса х точки М, то
sin (α + 2π) = sin α или
sin (α + 360°) = sin α
и
cos (α + 2π)
= cos α или
cos (α + 360°) = cos α.
Таким образом, функции sin α и cos α от
прибавления к аргументу α одного
полного оборота (2π или 360°) не меняют своих значений.
Точно так же, прибавляя к
углу α любое целое
число полных оборотов, мы не изменим положения подвижного радиуса ОМ, а потому:
sin (α + 2kπ) = sin α или
sin (α + 360°k) = sin α
и
cos (α + 2kπ) = cos α или
cos (α + 360°k) = cos α,
где k – любое целое
число.
Функции, обладающие таким
свойством, что их значения не изменяются от прибавления к любому допустимому
значению аргумента определённого постоянного числа, называются периодическими.
Следовательно, функции sin α и cos α – периодические.
Наименьшее положительное число,
от прибавления которого к любому допустимому значению аргумента не изменяется
значение функции, называется периодом функции.
Периодом функции sin α и cos α
является 2π или 360°.
Функции tg α и сtg α также
периодические и их периодом является число
π или 180°.
В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным
радиусом ОМ единичной окружности.
Построим точку М‘,
симметричную точке М относительно
начала координат. Один из углов, образованных с осью Ох подвижным
радиусом ОМ‘, будет равен α + π.
Если х и у – координаты точки
М, то точки М‘ будут –х и –у. Поэтому
sin α = у, cos α = х,
sin (α + π) = –у,
cos (α + π) = –х.
Отсюда
и, следовательно,
tg (α + π) = tg α,
сtg (α + π)
= сtg α.
отсюда следует, что значения tg α и сtg α не
изменяются, если к углу α прибавить любое число полуоборотов:
tg (α + kπ) = tg α,
сtg (α + kπ) = сtg α.
где k – любое целое
число.
Периоды функций
y = A sin (ωx + φ) и
y = A cos (ωx + φ)
вычисляются по формуле
T = 2π/ω,
а период функции
y = A tg (ωx + φ)
по формуле
T = π/ω.
Если период функции y = f(x) равен T1, а период функции y = g(x) равен T2, то период функций
y = f(x) + g(x) и
y = f(x) – g(x)
равен наименьшему числу, при делении которого
на T1 и T2 получаются целые числа.
ПРИМЕР:
Найти
период функции
y = 3 sin (x – 2) + 7 соs πx.
РЕШЕНИЕ:
Период
функции
y = 3 sin (x – 2)
равен
T1 = 2π/1 = 2π.
Период
функции
y = 7 соs πx
равен
T2 = 2π/π = 2.
Периода
у функции
y = 3 sin (x – 2) + 7 соs πx
не
существует, так как такого числа, при делении которого на 2π и
на 2 получались бы целые числа, нет.
ОТВЕТ:
Периода
не существует.
ПРИМЕР:
Доказать
следующее утверждение:
tg
3850° = tg 250°.
РЕШЕНИЕ:
Так как тангенс – периодическая функция с минимальным
периодом 20 ∙ 180°, то получим:
tg
3850° = tg (20 ∙ 180° + 250°) = tg 250°.
ПРИМЕР:
Доказать
следующее утверждение:
сos (–13π) = –1.
РЕШЕНИЕ:
Так как косинус – чётная и периодическая функция с
минимальным периодом 2π, то получим:
сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.
ПРИМЕР:
Доказать
следующее утверждение:
sin (–7210°) = – sin 10°.
РЕШЕНИЕ:
Так как синус – нечётная и периодическая функция с
минимальным периодом 20 ∙ 360°, то получим:
sin (–7210°) = –sin 7210° = –sin (20 ∙ 360° + 10°) – sin 10°.
ПРИМЕР:
Найти основной период функции
sin 7х.
РЕШЕНИЕ:
Пусть Т основной период функции, тогда:
sin 7х = sin 7(х + t) = sin (7х + 7t)
так как 2πk период синуса, то получим:
sin (7х + 7t) = sin (7х + 2πk),
ОТВЕТ:
ПРИМЕР:
Найти основной период функции
соs 0,3х.
РЕШЕНИЕ:
Пусть Т основной период функции, тогда:
соs 0,3х = соs 0,3(х + t)
= соs (0,3х + 0,3t)
так как 2πk период косинуса, то получим:
соs (0,3х + 0,3t) = соs (0,3х + 2πk),
ОТВЕТ:
ПРИМЕР:
Найти период функции:
y = 5sin 2x + 2ctg 3х.
РЕШЕНИЕ:
Период функции
y = 5sin 2x
равен Т1 = 2𝜋/2 = π,
а период функции
y = 2ctg 3х
равен Т2 = 𝜋/3.
Наименьшее число, при делении которого на
Т1 = π и Т2 = 𝜋/3
– получаются целые числа будет число π.
Следовательно, период заданной функции равен Т = π.
ПРИМЕР:
Найти период функции:
y = 9sin (5x + π/3) – 4cоs (7х + 2).
РЕШЕНИЕ:
Находим периоды слагаемых. Период функции
y = 9sin (5x + π/3)
равен Т1 = 2𝜋/5,
а период функции
y = 4cоs (7х + 2)
равен Т2 = 2𝜋/7.
Очевидно, что период заданной функции равен
Т = 2π.
ПРИМЕР:
Найти период функции:
y = 3sin πx + 8tg (х + 5).
РЕШЕНИЕ:
Период функции
y = 3sin πx
равен Т1 = 2π/π = 2,
а период функции
y = 8tg (х + 5)
равен Т2 = 𝜋/1 = π.
Периода у заданной функции не существует, так как нет
такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.
ПРИМЕР:
Найти период функции:
y = sin 3x + соs 5х.
РЕШЕНИЕ:
Период функции
y = sin 3x
равен Т1 = 2π/3,
а период функции
y = соs 5х
равен Т2 = 2π/5.
Приведём к общему знаменателю периоды:
Т1 = 10π/15, Т2 = 6π/15.
Тогда наименьшее общее кратное (НОК) будет:
НОК (10π; 6π)
= 30π.
Теперь найдём период заданной функции:
Т = 30π/15 = 2π.
Задания к уроку 5
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований
Объяснение и обоснование
Напомним, что . Таким образом, областью определения функции y=будут все значения аргумента, при которых , то есть все значения x, kZ. Получаем
Этот результат можно получить и геометрически. Значения тангенса – это ордината соответствующей точки на линии тангенсов (рис.91). Поскольку точки Aи B единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы не сможем найти значение тангенса дляx, kZ.
Для всех других значений аргумента мы можем найти соответствующую точку на линии тангенсов и ее ординату — тангенс. Следовательно, все
Значенияx входят в область определения функции y=tgx.
Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих т
очек на линии тангенсов принимают
все значения до +, поскольку для любого действительного числа
мы можем указать соответствующую точку на оси ординат, а значит, и соответствующую точку на оси тангенсов. Учитывая, что точка О лежит
внутри окружности, а точка вне ее (или на самой окружности), получаем, что прямая имеет с окружностью хотя бы одну общую точку
(на самом деле их две). Следовательно, для любого действительного числа
найдется аргумент х, такой, что tan x равен данному действительному числу.
Поэтому область значений функции y= tg x — все действительные числа,
то есть R. Это можно записать так: E (=tgx) = R. Отсюда следует, что наибольшего и наименьшего значений функция tan x не имеет.
Как было показано в § 13, тангенс — нечетная функция:tg(-x)=tg x, следовательно, ее график симметричен относительно начала координат.
Тангенс — периодическая функция с наименьшим положительным периодом
Поэтому при построении графика
этой функции достаточно построить график на любом промежутке длиной π,
а потом полученную линию перенести параллельно вправо и влево вдоль оси
Ox на расстоянияkT = πk, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x,
при которых tg x, то есть ордината соответствующей точки линии тангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при x = πk, k ∈ Z.
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции тангенс положительны (то есть ордината соответствующей точкилинии тангенсов положительна) в І и ІІІ четвертях. Следовательно, tgx > 0 при
а также, учитывая период, при всех
Значения функции тангенс отрицательны (то есть ордината соответствующей точки линии тангенсов отрицательна) во ІІ и ІV четвертях. Такимобразом,
Промежутки возрастания и убывания.
Учитывая периодичность функции tgx (период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π,
например на промежутке . Если x (рис. 92), то при увеличении аргумента x (x2>x1) ордината соответствующей точки линии
тангенсов увеличивается (то есть tgx2>tgx1). Таким образом, на этом
промежутке функция tgx возрастает. Учитывая периодичность функции
tgx, делаем вывод, что она возрастает также на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график
функции y = tg x. Учитывая периодичность этой функции (с периодом π),
сначала построим график на любом промежутке длиной π, например на промежутке . Для более точного построения точек графика воспользуемся также тем, что значение тангенса — это ордината соответствующей точки
линии тангенсов. На рисунке 93 показано построение графика функции
y = tg x на промежутке.
Далее, учитывая периодичность тангенса (с периодом π), повторяем вид
графика на каждом промежутке длиной π (то есть параллельно переносим
график вдоль оси Ох на πk, где k — целое число).
Получаем график, приведенный на рисунке 94, который называется тангенсоидой.
14.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК
Объяснение и обоснование
Так как =, то областью определения котангенса будут все значения аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k ∈ Z. Такимобразом,
D (ctg x): x ≠ πk, k ∈ Z.
Тот же результат можно получить, используя геометрическую иллюстрацию. Значение котангенса — это абсцисса соответствующей точки на линии
котангенсов (рис. 95).
Поскольку точки А и В единичной окружности лежат на прямых ОА
и ОВ, параллельных линии котангенсов, мы не можем найти значение котангенса для x = πk, k ∈ Z. Длядругихзначенийаргументамыможемнайтисоответствующуюточкуна линии котангенсов и ее абсциссу — котангенс. Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.
Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все значения от –× до +×, поскольку для любого действительного числа мы можем указать соответствующую точку на оси абсцисс, а значит, и соответствующую точку Qх на оси котангенсов. Учитывая, что точка О лежит внутри окружности, а точка Qх — вне ее (или на самой окружности), получаем, что прямая ОQх имеет с окружностью хотя бы одну общую точку (на самом деле их две). Следовательно, для любого действительного числа найдется аргумент х, такой, что сtg x равен данному действительному числу. Таким образом, область значений функции y = ctg x — все действительные числа, то есть R.
Это можно записать так: E (ctgx) = R.Из приведенных рассуждений также вытекает, что наибольшего и наименьшего значений функция ctgxне имеет.
Как было показано в § 13, котангенс — нечетная функция: ctg (-x) = -ctgx, поэтому ее график симметричен относительно начала координат.
Там же было обосновано, что котангенс — периодическая функция с наименьшим положительным периодом T= : ctg (x+ ) = ctg x, поэтому через промежутки длиной п вид графика функции ctgxповторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oyзначение x= 0. Но ctg0 не существует, значит, график функции y= ctg x не пересекает ось Oy.
На оси Оx значение y= 0. Поэтому необходимо найти такие значения x, при которых ctgx, то есть абсцисса соответствующей точки линии котангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D(рис. 95), то есть при
Промежутки знакопостоянства. Как было обосновано в § 13, значения функции котангенс положительны (то есть абсцисса соответствующей точки линии котангенсов положительна) в I и III четвертях (рис. 96). Тогда ctgx> 0 при всех . Учитывая период, получаем, что ctgx> 0 при всех
Значения функции котангенс отрицательны (то есть абсцисса соответствующей точки линии котангенсов отрицательна) во II и IV четвертях, таким образом, ctgx< 0 при .

Промежутки возрастания и убывания
Учитывая периодичность функции ctg x (наименьший положительный период T = ), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке (0; ). Если (0; ) (рис. 97), то при увеличении аргумента x (x2>x1) абсцисса соответствующей точки линии котангенсов уменьшается (то есть ctgx2<ctgx1), следовательно, на этом промежутке функция ctg x убывает. Учитывая периодичность функции y= ctgx, делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет построить график функции y= ctg x аналогично тому, как был построен график функции y= tg x. Но график функции у = ctg x можно получить также с помощью геометрических преобразований графика функции у = tg х. По формуле, приведенной на с. 172, , то есть Поэтому график функции у = ctg x можно получить из графика функции у = tg х параллельным переносом вдоль оси Ох на (− ) и симметричным отображением полученного графика относительно оси Ох. Получаем график, который называется котангенсоидой (рис. 98).
Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции
где T — период функции y=f(x). Эта формула позволяет быстро найти период тригонометрических функций такого вида. Для функций y=sin x и y=cos x наименьший положительный период T=2п, для y=tg x и y=ctg x T=п. Рассмотрим на конкретных примерах, как найти период функции, используя данную формулу.
Найти период функции:
1) y=5sin(3x-п/8).
Здесь А=5, k=3, b=-п/8. Для нахождения периода нам нужно только k — число, стоящее перед иксом. Поскольку период синуса T=2п, то период данной функции
А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то
А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции
А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть

удовлетворяющих системе неравенств:
sin t > 0,
0 6 t 6 4π.
б) Рассмотрим множество чисел на числовой оси, удовлетворяющих системе неравенств:
sin x 6 0,
0 6 x 6 20π.
Найдите сумму длин отрезков, из которых состоит это множество.
§ 7. Простейшие формулы
В § 3 мы установили для острых углов α такую формулу:
|
sin2 α + cos2 α = 1. |
|||||||
|
Эта же формула |
верна |
и |
в случае, |
||||
|
когда α — любое |
число. В |
самом де- |
|||||
|
ле, пусть M — точка на тригонометри- |
|||||||
|
ческой окружности, соответствующая |
|||||||
|
числу α (рис. 7.1). Тогда |
M имеет ко- |
||||||
|
ординаты x = cos α, y |
= |
sin α. Од- |
|||||
|
нако всякая точка (x; y), лежащая на |
|||||||
|
окружности единичного радиуса с цен- |
|||||||
|
тром в начале координат, удовлетво- |
|||||||
|
Рис. 7.1. |
ряет уравнению x2 + y2 |
= 1, откуда |
|||||
|
cos2 α + sin2 α = 1, что и требовалось. |
Итак, формула cos2 α + sin2 α = 1 вытекает из уравнения окружности. Может показаться, что тем самым для острых углов мы дали новое доказательство этой формулы (по сравнению с указанным в § 3, где мы пользовались теоремой Пифагора). Отличие, однако, чисто внешнее: при выводе уравнения окружности x2 + y2 = 1 используется та же теорема Пифагора.
32
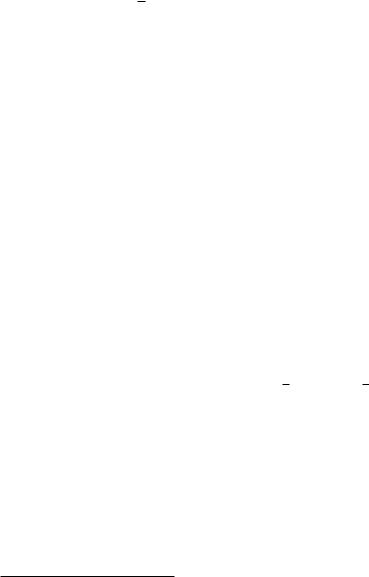
Для острых углов мы получали и другие формулы, напри-
|
мер cos α = 1/ |
1 + tg2 α. Для произвольных углов эта формула |
|
в таком виде |
верна быть не может: согласно общепринятому по- |
|
p |
√
ниманию символа , правая часть всегда неотрицательна, в то время как левая часть вполне может быть и отрицательной. Чтобы формула была верна при всех α, надо ее возвести в квадрат. Получится равенство: cos2 α = 1/(1 + tg2 α). Докажем, что эта формула верна при всех α:1
|
1/(1 + tg2 |
α) = 1 |
1 + |
sin2 α |
= |
cos2 α |
= cos2 α. |
|
|
cos2 α |
sin2 α + cos2 α |
Задача 7.1. Выведите все формулы, приведенные ниже, из определений и формулы sin2 α + cos2 α = 1 (некоторые из них мы уже доказали):
|
sin2 α + cos2 α = 1; |
tg2 α = |
sin α |
; |
ctg α = |
cos α |
; |
||||||||
|
sin α |
||||||||||||||
|
cos α |
||||||||||||||
|
1 |
tg2 α |
|||||||||||||
|
1 |
+ tg2 |
α = |
; |
sin2 α = |
; |
tg α · ctg α = 1; |
||||||||
|
cos2 α |
1 + tg2 α |
|||||||||||||
|
1 |
ctg2 α |
|||||||||||||
|
1 |
+ ctg2 |
α = |
; |
cos2 α = |
. |
|||||||||
|
1 + ctg2 α |
||||||||||||||
|
sin2 |
α |
Эти формулы позволяют, зная значение одной из тригонометрических функций данного числа, почти найти все осталь-
ные. Пусть, например, мы знаем, что sin x = 1/2. Тогда cos2 x =
√ √
= 1−sin2 x = 3/4, так что cos x равен или 3/2, или − 3/2. Чтобы узнать, какому именно из этих двух чисел равен cos x, нужна дополнительная информация.
Задача 7.2. Покажите на примерах, что оба вышеуказанных случая возможны.
Задача 7.3. а) Пусть tg x = −1. Найдите sin x. Сколько ответов у этой задачи?
б) Пусть в дополнение к условиям пункта а) нам известно, что sin x < 0. Сколько теперь ответов у задачи?
1Для которых tg α определен, т. е. cos α 6= 0.
33

Задача 7.4. Пусть sin x = 3/5, x [π/2; 3π/2]. Найдите tg x.
Задача 7.5. Пусть tg x = 3, cos x > sin x. Найдите cos x, sin x.
Задача 7.6. Пусть tg x = 3/5. Найдите sin x + 2 cos x. cos x − 3 sin x
Задача 7.7. Докажите тождества:
|
а) |
tg α + ctg β |
= |
tg α |
; |
б) |
tg α sin α |
= |
tg α − sin α |
; |
|||||
|
ctg α + tg β |
tg β |
tg α + sin α |
tg α sin α |
|||||||||||
|
1 |
1 |
|||||||||||||
|
в) sin α + cos α ctg α + sin α tg α + cos α = |
+ |
. |
||||||||||||
|
sin α |
cos α |
Задача 7.8. Упростите выражения:
а) (sin α + cos α)2 + (sin α − cos α)2; б) (tg α + ctg α)2 + (tg α − ctg α)2;
в) sin α(2 + ctg α)(2 ctg α + 1) − 5 cos α.
§ 8. Периоды тригонометрических функций
Числам x, x+2π, x−2π соответствует одна и та же точка на тригонометрической окружности (если пройти по тригонометрической окружности лишний круг, то придешь туда, где был). Отсюда вытекают такие тождества, о которых уже шла речь в § 5:
sin(x + 2π) = sin(x − 2π) = sin x; cos(x + 2π) = cos(x − 2π) = cos x.
В связи с этими тождествами мы уже употребляли термин «период». Дадим теперь точные определения.
Определение. Число T 6= 0 называют периодом функции f, если для всех x верны равенства f(x − T ) = f(x + T ) = f(x) (подразумевается, что x + T и x − T входят в область определения функции, если в нее входит x). Функцию называют периодической, если она имеет период (хотя бы один).
34

Периодические функции естественно возникают при описании колебательных процессов. Об одном из таких процессов речь уже шла в § 5. Вот еще примеры:
1)Пусть ϕ = ϕ(t) — угол отклонения качающегося маятника часов от вертикали в момент t. Тогда ϕ — периодическая функция от t.
2)Напряжение («разность потенциалов», как сказал бы физик) между двумя гнездами розетки в сети переменного тока, ес-
ли его рассматривать как функцию от времени, является периодической функцией1.
3)Пусть мы слышим музыкальный звук. Тогда давление воздуха в данной точке — периодическая функция от времени.
Если функция имеет период T , то периодами этой функции будут и числа −T , 2T , −2T . . . — одним словом, все числа nT , где n — целое число, не равное нулю. В самом деле, проверим, например, что f(x + 2T ) = f(x):
f(x + 2T ) = f((x + T ) + T ) = f(x + T ) = f(x).
Определение. Наименьшим положительным периодом функции f называется — в соответствии с буквальным смыслом слов — такое положительное число T , что T — период f и ни одно положительное число, меньшее T , периодом f уже не является.
Периодическая функция не обязана иметь наименьший положительный период (например, функция, являющаяся постоянной, имеет периодом вообще любое число и, стало быть, наименьшего положительного периода у нее нет). Можно привести примеры и непостоянных периодических функций, не имеющих наименьшего положительного периода. Тем не менее в большинстве интересных случаев наименьший положительный период у периодических функций существует.
1Когда говорят «напряжение в сети 220 вольт», имеют в виду его «среднеквадратичное значение», о котором мы будем говорить в § 21. Само же напряжение все время меняется.
35
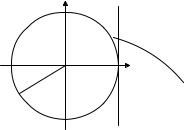

Рис. 8.1. Период тангенса и котангенса.
В частности, наименьший положительный период как синуса, так и косинуса равен 2π. Докажем это, например, для функции y = sin x. Пусть вопреки тому, что мы утверждаем, у синуса есть такой период T , что 0 < T < 2π. При x = π/2 имеем sin x = = 1. Будем теперь увеличивать x. В точке x + T значение синуса должно быть также равно 1. Но в следующий раз синус будет равен 1 только при x = (π/2) + 2π. Поэтому период синуса быть меньше 2π не может. Доказательство для косинуса аналогично.
Наименьший положительный период функции, описывающей колебания (как в наших примерах 1–3), называется просто периодом этих колебаний.
Поскольку число 2π является периодом синуса и косинуса, оно будет также периодом тангенса и котангенса. Однако для этих функций 2π — не наименьший период: наименьшим положительным периодом тангенса и котангенса будет π. В самом деле, точки, соответствующие числам x и x + π на тригонометрической окружности, диаметрально противоположны: от точки x до точки x + 2π надо пройти расстояние π, в точности равное половине окружности. Теперь, если воспользоваться определением тангенса и котангенса с помощью осей тангенсов и котангенсов, равенства tg(x + π) = tg x и ctg(x + π) = ctg x станут очевидными (рис. 8.1). Легко проверить (мы предложим это сделать в задачах), что π — действительно наименьший положительный период тангенса и котангенса.
36
Одно замечание по поводу терминологии. Часто слова «период функции» употребляют в значении «наименьший положительный период». Так что если на экзамене у вас спросят: «Является ли 100π периодом функции синус?», не торопитесь с ответом, а уточните, имеется в виду наименьший положительный период или просто один из периодов.
Тригонометрические функции — типичный пример периодических функций: любую «не очень плохую» периодическую функцию можно в некотором смысле выразить через тригонометрические.
Задача 8.1. Найдите наименьшие положительные периоды функций:
|
а) y = sin 3x; |
б) y = cos |
x |
; |
в) y = cos πx; |
|
2 |
г) y = cos x + cos(1,01x).
Задача 8.2. Зависимость напряжения в сети переменного тока от времени задается формулой U = U0 sin ωt (здесь t — время, U — напряжение, U0 и ω — постоянные величины). Частота переменного тока — 50 Герц (это означает, что напряжение совершает 50 колебаний в секунду).
а) Найдите ω, считая, что t измеряется в секундах;
б) Найдите (наименьший положительный) период U как функции от t.
Задача 8.3. а) Докажите, что наименьший положительный период косинуса равен 2π;
б) Докажите, что наименьший положительный период тангенса равен π.
Задача 8.4. Пусть наименьший положительный период функции f равен T . Докажите, что все остальные ее периоды имеют вид nT для некоторых целых чисел n.
Задача 8.5. Докажите, что следующие функции не являются периодическими:
37
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
















.png)

