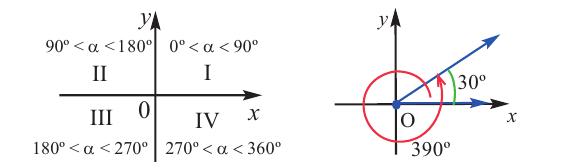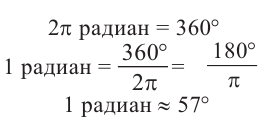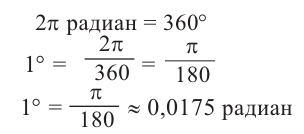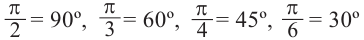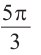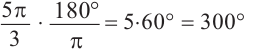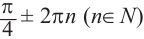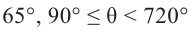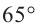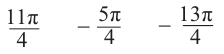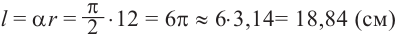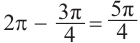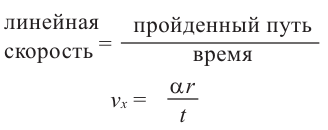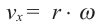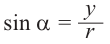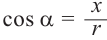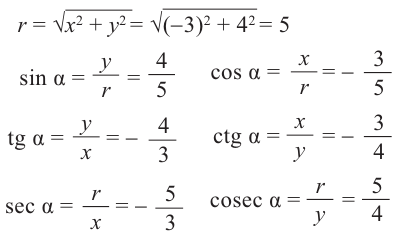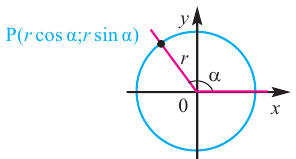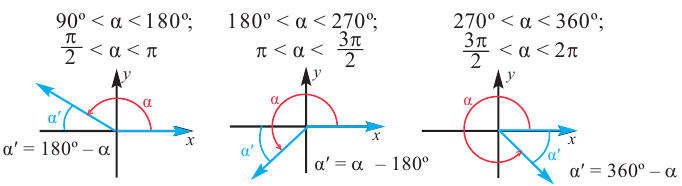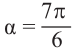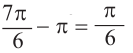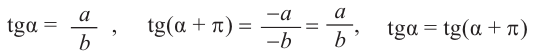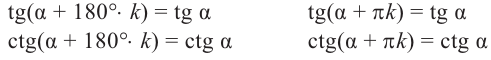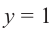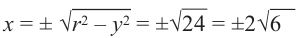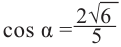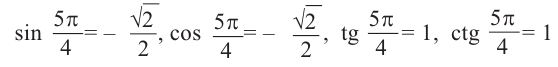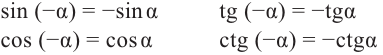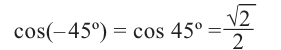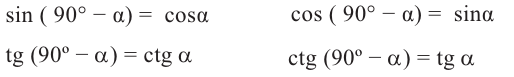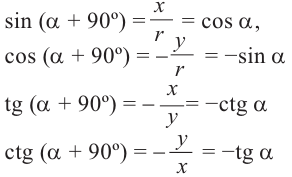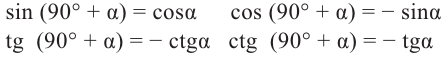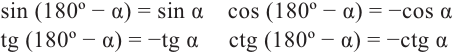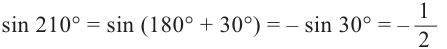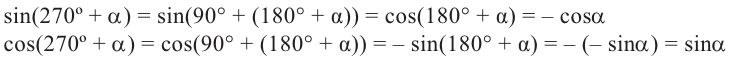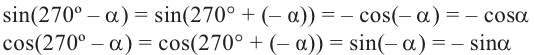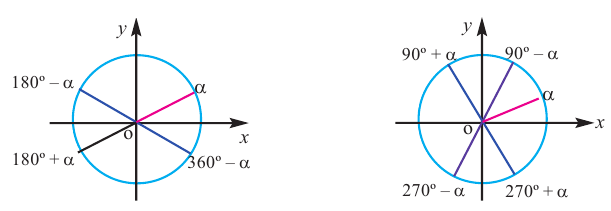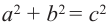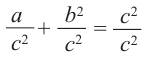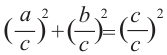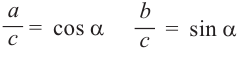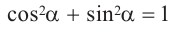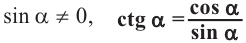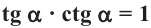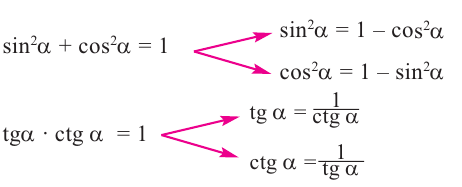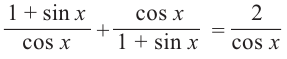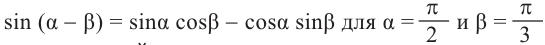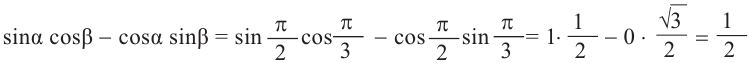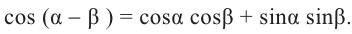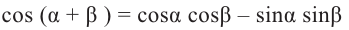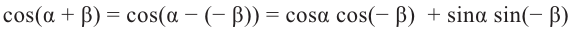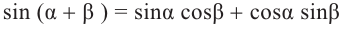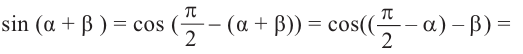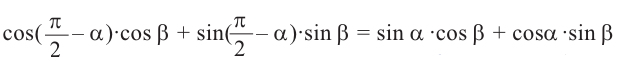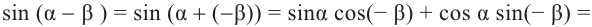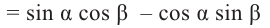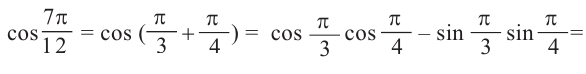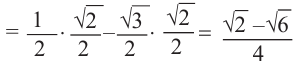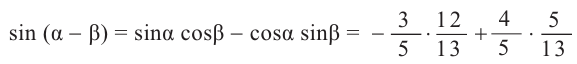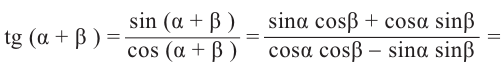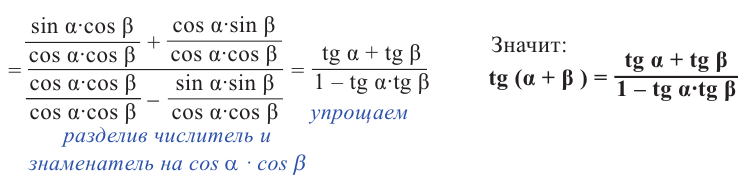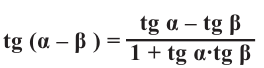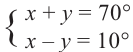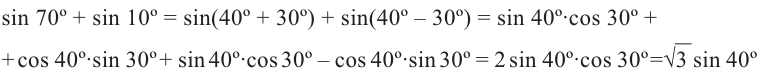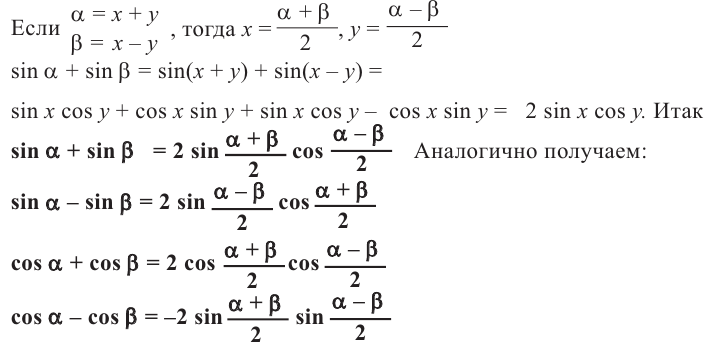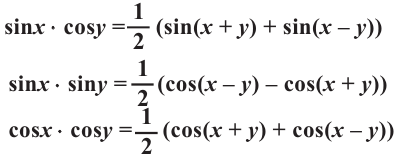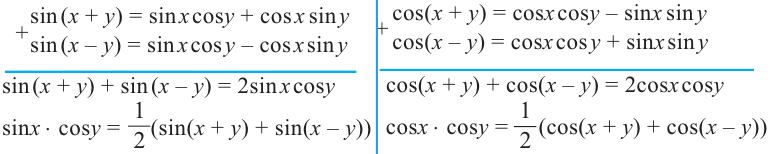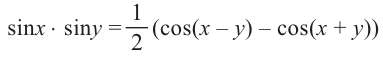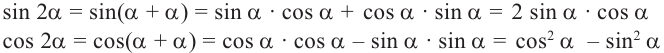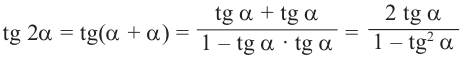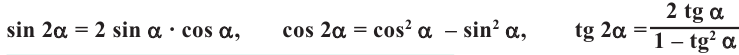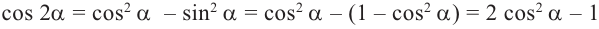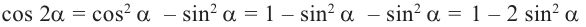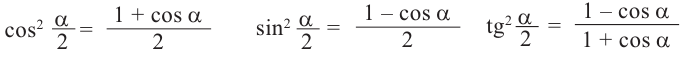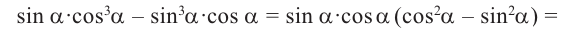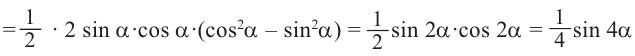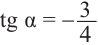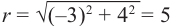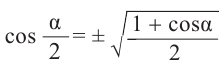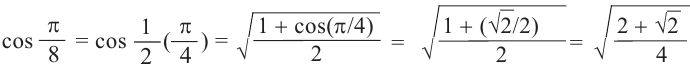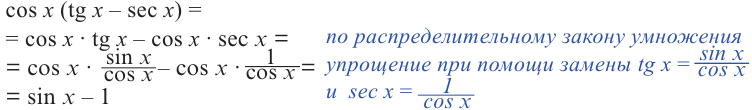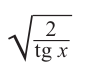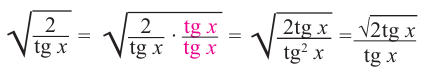Введите целое значение угла
Идет расчет …
Как найти наименьший положительный (отрицательный) угол
Для преобразования угла большего или меньшего 360° градусов, необходимо значение данного угла разделить на 360 с остатком.
В результате деления с остатком – неполное частное будет соответствовать числу полных оборотов, а остаток от деления значению угла.
Приведем примеры:
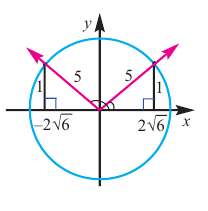
Пример 1. Найдем наименьший положительный угол для угла 1267° градусов.
Разделим 1267 на 360 с остатком:
Следовательно, наименьший положительный угол равен 187° градусов.
Пример 2. Найдем наименьший отрицательный угол для угла -745° градусов.
Разделим 745 на 360 с остатком:
Следовательно, наименьший отрицательный угол равен -25° градусов.
Содержание
- Как найти терминальные углы в градусах
- Как найти терминальные углы в радианах
- Пример 1: Нахождение конерминальных углов и классификация по квадранту
- Пример 10: Котерминальные главные углы
Котерминальные углы — это углы в стандартном положении, которые имеют одинаковые конечные стороны. Каждый угол имеет неограниченное количество концевых углов. Если задано θ в стандартном положении с измерением xn, то угловые меры, которые совпадают с углом, задаются формулой θ = x ° + 360 ° n. Обратите внимание, что n — целое число. Эта теорема утверждает, что меры любых двух котерминальных углов различаются на целое число, кратное 360 °. Например, на приведенном ниже рисунке θ = 430 °. Ниже показан пример угла на одном конце, который показывает θ и два его угла на одном конце, обозначенные цифрами 1 и 2.
1 = 430° + 360° (-1)
1 = 70°
2 = 430° + 360° (-2)
2 = -290°
Если мы сложим положительные кратные от 360 ° до 430 °, мы обнаружим, что углы с размерами 790 °, 1150 °, 1510 ° также совпадают с заданным θ = 430 °.
Запишите эти несколько заметок, чтобы иметь возможность подробно узнать о конерминальных углах. Поверните луч или полулинию вокруг его конечной точки, чтобы определить угол. Начальное положение луча — это начальная сторона угла, а положение после поворота — конечная сторона. Начало координат — это вершина в системе координат, а начальная сторона совпадает с положительной осью абсцисс; такой угол находится в стандартном положении. Также следует помнить, что вращение против часовой стрелки генерирует положительные углы, а вращение по часовой стрелке генерирует отрицательные углы. Наконец, всегда помните, что два угла являются концевыми, если разница в их градусах делится на 360 °.
Давайте посмотрим на концевые углы некоторых основных тригонометрических углов, показанные в таблице вопросов и ответов.
| Часто задаваемые вопросы (FAQ) | Ответы |
|---|---|
|
Что такое угол котерминала 30 °? |
Некоторые из котерминальных углов 30 ° составляют 390 °, 750 °, -330 ° и -690 °. Формула θ = 30 ° + 360 ° n представляет собой концевые углы 30 °, где n — целое число. |
|
Что такое угол котерминала 45 °? |
Некоторые из котерминальных углов 45 ° составляют 405 °, 765 °, -315 ° и -675 °. Формула θ = 45 ° + 360 ° n представляет собой концевые углы 45 °, где n — целое число. |
|
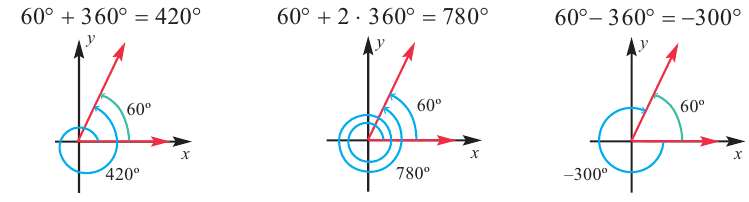
Что такое угол котерминала 60 °? |
Некоторые из котерминальных углов 60 ° составляют 420 °, 780 °, -300 ° и -660 °. Формула θ = 60 ° + 360 ° n представляет собой концевые углы 60 °, где n — целое число. |
|
Что такое угол котерминала 90 °? |
Котерминальные углы 90 ° составляют 450 °, 810 °, -270 ° и -630 °. |
|
Что такое угол котерминала 120 °? |
Котерминальные углы 120 ° составляют 480 °, 840 °, -240 ° и -600 °. |
|
Что такое угол котерминала 112 °? |
Некоторые из котерминальных углов 112 ° составляют 472 °, 832 °, -248 ° и -608 °. |
|
Что такое угол котерминала 220 °? |
Некоторые из котерминальных углов 220 ° составляют 580 °, 940 °, -140 ° и -500 °. |
Как найти терминальные углы в градусах
При нахождении концевых углов обратите внимание на то, что их размеры должны отличаться на целое число, кратное 360 °.
- Случай 1: задан положительный угол и угол больше 360°. Чтобы найти наименьшие положительные концевые углы, вычитайте 360 ° несколько раз, пока результат не станет положительным углом, меньшим или равным 360 °.
- Случай 2: задан неположительный угол. При нахождении концевых углов неположительного угла несколько раз прибавляйте 360 °, пока результат не станет положительным углом, меньшим или равным 360 °.
Как найти терминальные углы в радианах
Два угла являются концевыми, если у них одинаковые начальная и конечная стороны, а другой способ измерения углов — в радианах. Один радиан — это мера центрального угла θ, который пересекает дугу s, равную по длине радиусу r окружности. Это означает, что θ = s / r, где θ в радианах. Поскольку длина окружности равна 2
Тот же принцип применяется к нахождению оконечных углов в радианах. Например, углы 0 и 2
Пример 1: Нахождение конерминальных углов и классификация по квадранту
Предположим, что данные углы находятся в стандартном положении. Определите величину положительного угла величиной менее 360 °, которая совпадает с данным углом. Затем классифицируйте угол по квадранту.
- = 550°
- β = -225°
- = 1105°
Решение
θ = x ° + 360 ° с.
= х ° + 360 ° (п)
1105 ° = х ° + 360 ° (3)
x ° = 1105 ° — 1080 °
х ° = 25 °
Окончательный ответ
- Какой угол между 0 ° и 360 ° имеет ту же конечную сторону, что и θ?
- Какой опорный угол для θ?
Решение
Уменьшите заданное значение θ до минимально возможного угла наклона от 0 ° до 360 °, добавив при необходимости несколько раз 360 °.
928° — 360° = 568°
568° — 360° = 208°
Определим квадрант, в котором находятся концевые углы. Поскольку 928 ° и 208 ° имеют одну и ту же сторону вывода в квадранте III, опорный угол для θ = 928 ° можно определить путем вычитания 180 ° из угла котерминала между 0 ° и 360 °.
208° — 180° = 28°
Окончательный ответ
Угол между 0 ° и 360 ° имеет ту же сторону вывода, что и θ = 928 °, это 208 °, а исходный угол составляет 28 °.

Пример 10: Котерминальные главные углы
Какой главный угол совпадает с углом -743 °?
Решение
Напишите уравнение по общей формуле для концевых углов θ = x ° + 360 ° n, учитывая, что θ = -743.
-743 ° = x ° — 360 ° с.ш.
-743 ° = x ° — 360 ° (3)
-743 ° = х ° — 1080 °
Умножьте обе части уравнения на -1. Обратите внимание, что выбор положительного целого числа для n приводит к углу, который больше, чем угол 743 °, но наиболее близок к нему.
-1 (-743 °) = -1 (x ° — 1080 °)
743 ° = -x ° + 1080 °
x ° = 1080 ° — 743 °
х ° = 337 °
Окончательный ответ
Главный угол на терминале с θ = -743 равен x ° = 337 °.
Содержание:
Тригонометрические функции произвольного угла
Угол поворота
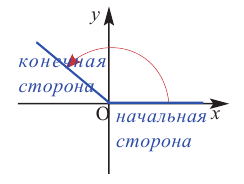
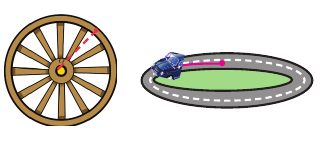
До недавнего времени говоря об угле мы имели в виду угол, полученный между двумя неподвижными сторонами. Угол также можно рассматривать как измерение поворота. Например, радиус колеса, расположенного по горизонтали при вращении вокруг неподвижной оси, через определённое время относительно начального положения образует некоторый угол. К тому же значение угла зависит от направления поворота. Любой угол можно рассматривать как фигуру, полученную вращением луча вокруг начальной точки.
Начальное положение луча соответствует одной стороне угла, конечное положение — другой стороне. При вращении луча на координатной плоскости относительно начала координат в направлении по часовой стрелке или против часовой стрелки, можно получить различные углы.
Начальная сторона угла поворота совпадает с положительным направлением оси абсцисс. Сторону, полученную при вращении относительно начала координат (вершины угла), назовём конечной стороной. Принято считать, что если поворот происходит в направлении против часовой стрелки, то угол имеет положительное значение, при повороте в направлении по часовой стрелке, угол имеет отрицательное значение,
положительный угол отрицательный угол
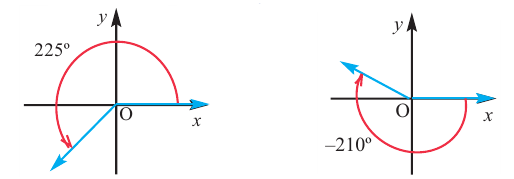
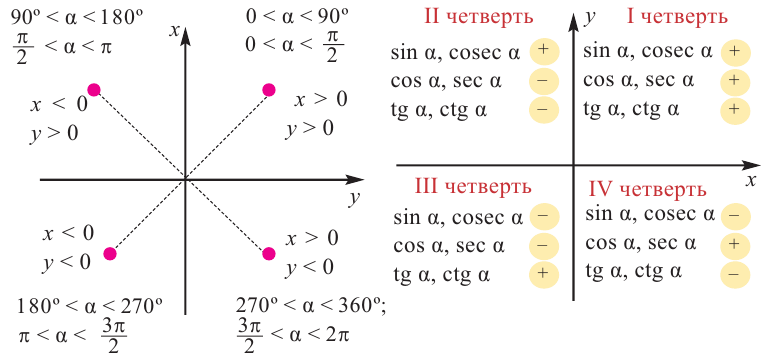
Координатные оси разбивают координатную плоскость на 4 четверти. Значение угла, в зависимости от того, в какой четверти расположена его конечная сторона, меняется в определенном интервале.
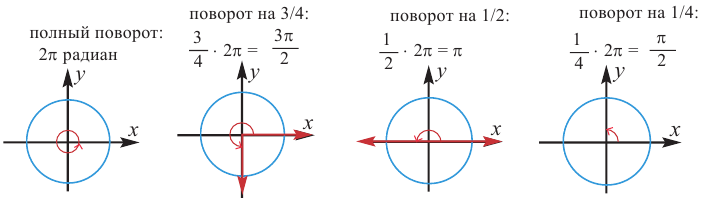
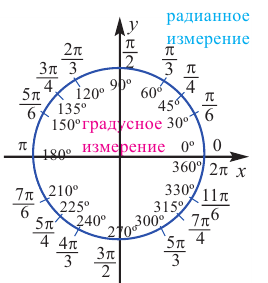
Конечная сторона угла может совершить один или несколько оборотов относительно начала координат. Один полный оборот соответствует углу 360°. Существует бесконечное число углов поворота, у которых начальная и конечная стороны совпадают. Например, конечные стороны углов 30°и 390° совпадают. В общем, для углов поворота 
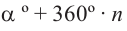
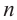
Радианная и градусная мера угла
Пример 1. Нарисуйте угол заданной величины. Определите какой четверти принадлежит конечная сторона угла.
Пример 2. На координатной плоскости покажите и запишите градусные меры двух положительных и одного отрицательного угла поворота, конечные стороны которых совпадают с конечной стороной угла 60°.
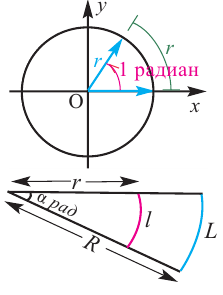
Радианное измерение углов
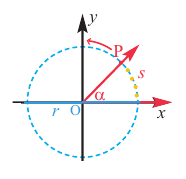
Угол в один радиан-это центральный угол, у которого длина дуги равна радиусу. Радианная мера угла есть отношение длины соответствующей дуги к радиусу окружности: 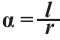
Пример 1. Сколько радиан составляет центральный угол, длина дуги которого равна 12 см, если радиус окружности равен 4 см?
Решение: 1 радиан соответствует длине дуги 4 см. Дуге длиной 12 см будет соответствовать угол 12 : 4 = 3 радиан. Длина окружности 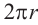
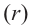
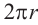
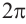
Радианная мера одного целого оборота равна 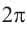
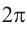
Преобразование градусов в радианы:
Таким образом, 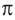
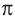
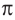
Используя соответствующие радианные и градусные меры углов, расположенных в первой четверти, можно найти увеличенные в разы значения других углов. Например, если 30° =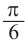
Пример 2. Выразите углы, заданные в градусах радианами, а углы, заданные радианами в градусах, а) 60° ; б)
Решение.
а)60° =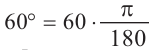
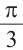

б)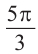
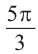
Пример 3. Выразите углы, конечная сторона которых совпадает с углом 45°, в градусах и радианах.
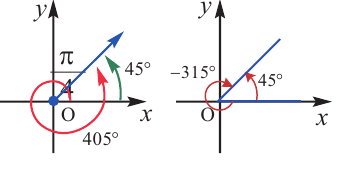
Решение: Конечная сторона угла 45°совпадает с углами 405° и 315°, а также существует бесконечно много углов, конечные стороны которых совпадают с конечной стороной угла 45°: 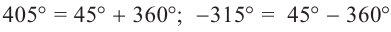
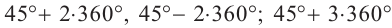
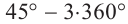
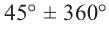
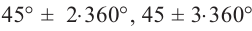
В радианах это можно записать как
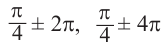
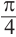
Пример, а)
Все углы поворота, конечные стороны которых совпадают с углом
можно найти но формуле 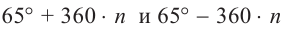
Как видно, в заданном интервале, расположен всего один угол 425°. Пример. д)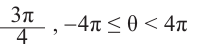
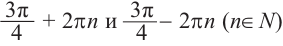
Интервалу 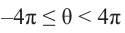
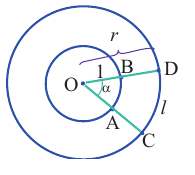
Длина дуги
Запишем формулу нахождения длины дуги, соответствующей центральному углу
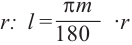
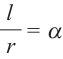
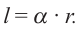
Площадь сектора
Центральному углу 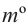
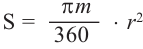
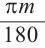
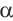
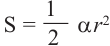
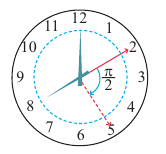
Решение. Секундная стрелка за 60 минут совершают один полный оборот. Это соответствует 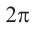
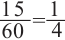
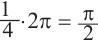
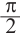
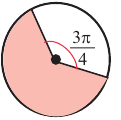
Пример 2. Найдите площадь и периметр закрашенного сектора на рисунке, если радиус круга равен 8 см. Закрашенной части круга соответствует центральный угол:
Площадь сектора равна:
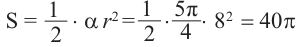
Периметр сектора равен сумме длин двух радиусов и длины дуги: 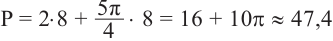
Линейная скорость и угловая скорость
Скорость при движении по окружности, например, скорость движения произвольной точки Р колеса, которое вращается вокруг точки О, может быть вычислена двумя способами.
В первом случае, её можно найти используя расстояние и время. Эта скорость называется линейной скоростью. Во втором случае — используя угол поворота (центральный угол). Эта скорость называется угловой скоростью.
Если тело движется но окружности, то линейная скорость равна отношению пройденного пути (длины дуги окружности) к промежутку времени.
Если тело движется по окружности, то угловая скорость равна отношению угла поворота к промежутку времени.
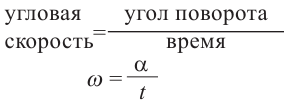
линейная скорость = 
Пример 3. Карусель совершает за минуту 8 полных оборотов.
а)Чему равна угловая скорость карусели за минуту(в радианах)?
б)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 3 м от центра окружности?
в)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 2 м от центра окружности?
Решение:
а) Один целый оборот при вращении соответствует центральному углу 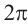
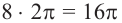
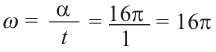
б)Если лошадь находится на расстоянии 3 м от центра, то она движется по окружности радиуса 3 м.
Линейная скорость: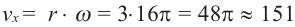
в)Если лошадь находится на расстоянии 2 м от центра, то она движется по окружности радиуса 2 м.
Линейная скорость: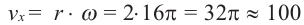
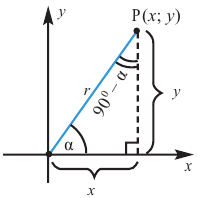
Тригонометрические функции
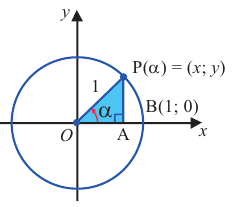
Тригонометрические отношении для угла зависят только от значения угла.
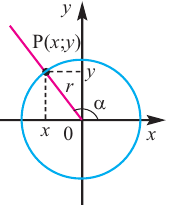
Пусть конечная сторона угла а при повороте пересекается с окружностью радиусом г, центр которой находится в начале координат, в точке Р(х; у).

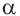

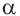

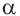
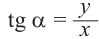
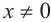

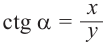
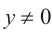

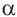
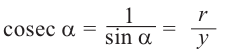
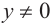

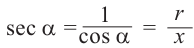
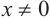
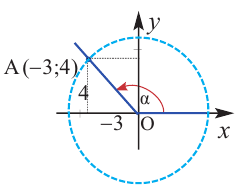
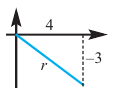
Пример 1. Точка А (- 3; 4) расположена на конечной стороне угла поворота 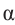
а) Изобразите решение примера.
б) Определите значения тригонометрических отношений для угла поворота 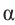
Решение:
а)
б)
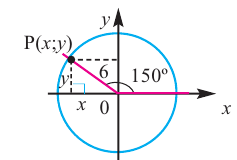
Координаты точки на окружности
Если заданная точка Р окружности находится на конечной стороне угла поворота 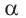
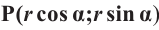
Пример 2. По данным рисунка найдите координаты точки Р.
Точка Р находится во II четверти и косинус отрицательный.
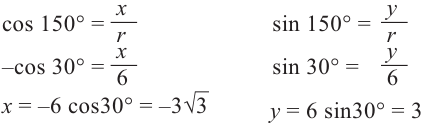
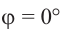
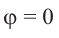
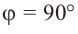
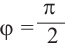
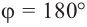
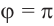
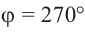
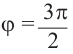
В этом случае координаты х или у равны или нулю, или абсолютному значению длины радиуса.
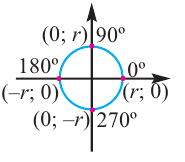
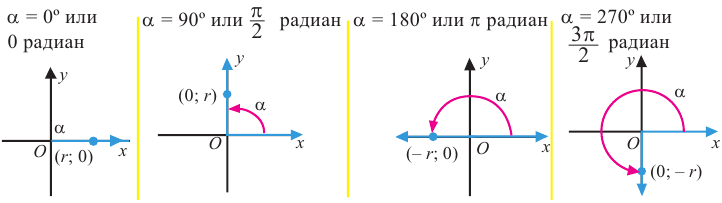
Пример 3. Найдём значения тригонометрических отношений для:
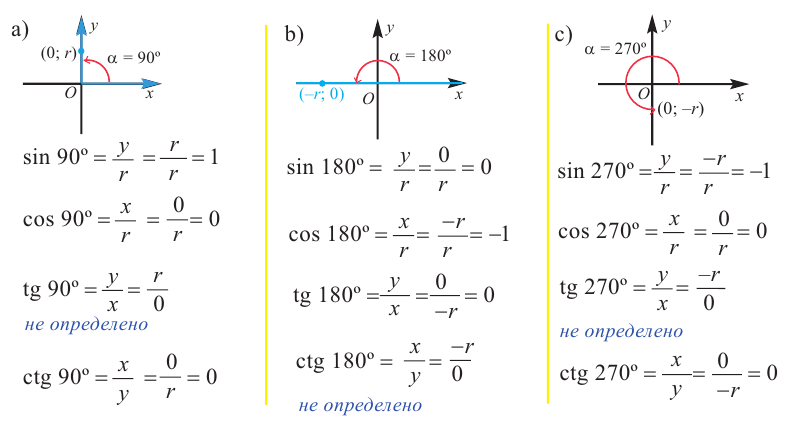
а) а = 90° ; б) а = 180°; в) а = 270° .
При всех допустимых значениях, каждому значению 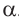
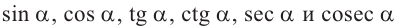
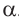
Так как 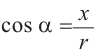
Так как 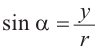
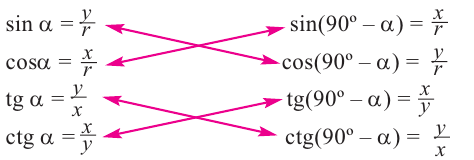
Тригонометрические функции произвольного угла. Нахождение значений тригонометрических функций произвольного угла при помощи острого угла
Чтобы вычислить тригонометрические отношения для углов больше 90°, удобно использовать тригонометрические отношения острого угла.
Для любого угла поворота 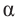
Используя соответствующие острые углы можно определить тригонометрические отношения для любого произвольного угла. Эти значения можно вычислить точно для углов 30°, 45°, 60°, а для остальных острых углов — при помощи калькулятора.
Пример 1. Для следующих углов, определите острые углы:
а)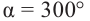
Решение:
а) конечная сторона угла 300° расположена в IV четверти. Соответствующий острый угол равен: 360°- 300° = 60°
б) конечная сторона угла расположена в III четверти. Соответствующий
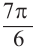
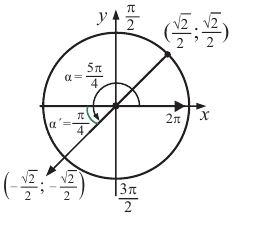
Пример 2. Найдём значение основных тригонометрических функций для угла 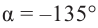
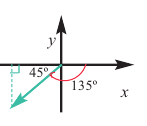
1.Найдём наименьший положительный угол, конечная сторона которого совпадает с заданным углом и дополняет его до 360°: -135° + 360° = 225°
2.Для угла 225° найдём соответствующий острый угол 225° — 180° = 45°.
3.Определим какой четверти принадлежит угол -135° — угол III четверти.
4.Найдём значение тригонометрических функций для угла 45° и учтём знак этих функций в III четверти. Получим:
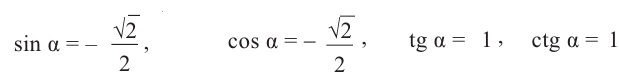
•определяем соответствующий острый угол;
•находим значение тригонометрических функций для этого угла;
•определяем знак значения тригонометрических функций в зависимости от четверти.
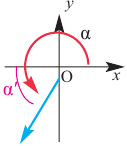
Так как конечные стороны углов 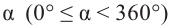
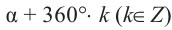
Заметим, что если угол меняется на пол оборота, то значения тангенса и котангенса не изменяются.
На самом деле, если углу поворота 
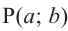
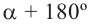

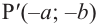
Пример 3. Найдём допустимые значения 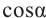
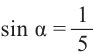
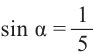
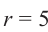
Абсцисса этой точки
Тогда 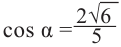
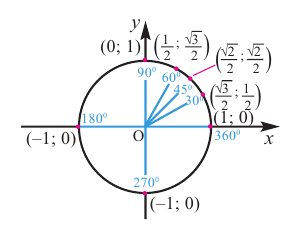
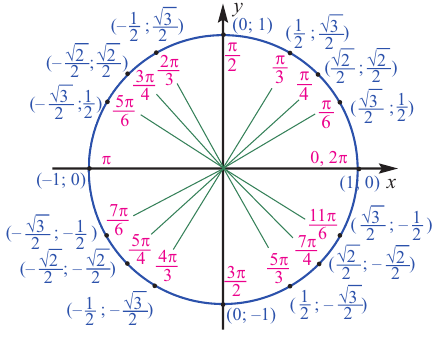
Единичная окружность и тригонометрические функции
Значения тригонометрических функций зависят только от значения угла 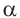
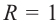
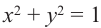
Если точка 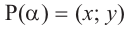
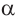
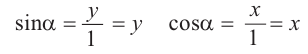
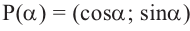
Также по заданным координатам можно найти следующие тригонометрические функции: 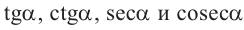
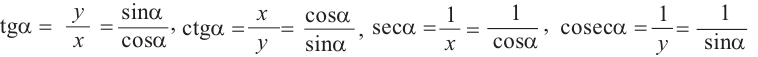
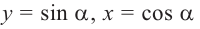
Для этого надо выполнить следующие шаги:
1) На единичной окружности отметим точки, соотвегствующие углу поворота 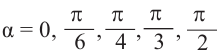
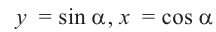
2)Для некоторой точки, принадлежащей единичной окружности, например 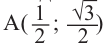
Точка В симметрична точке А относительно оси у, точка С — относительно начала координат, а точка D — относительно оси х. Абсолютные значения координат этих точек равны и отличаются только знаком.
3)Таким образом, можно определить координаты новых точек, зная координаты точки, принадлежащей I четверти. Т.е. получаем единичную окружность, на которой отмечены углы поворота и координаты точек.
- Заказать решение задач по высшей математике
Единичная окружность и тригонометрические функции произвольного угла
Так как координаты точек на единичной окружности удовлетворяют условиям 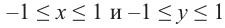
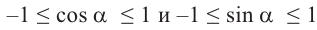
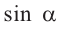
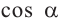
Пример 1. Для угла поворота 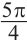
Решение: Конечная сторона угла поворота 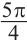
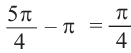
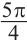
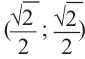
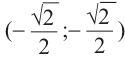
Тогда ,
Пример 2. Точка А, с абсциссой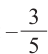
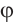
а)Найдём ординату точки А.
б)Изобразим рисунок, соответствующий условию и для угла 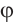
Решение:
а)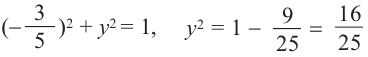
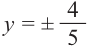
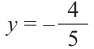
б)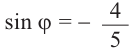
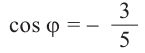
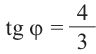
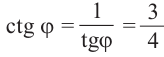
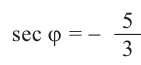
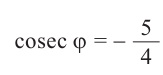
Пример 3. Найдём наибольшее и наименьшее значение выражения 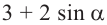
Решение:
Таким образом, для выражения 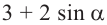
Формулы приведения
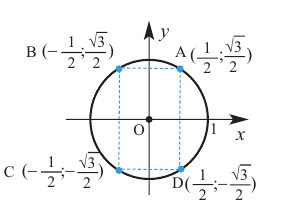
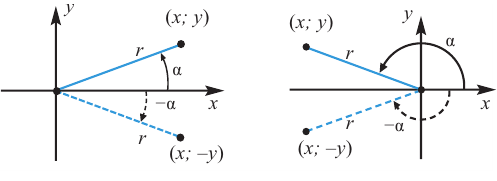
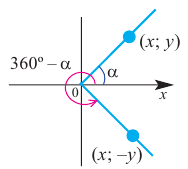
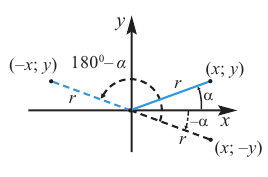
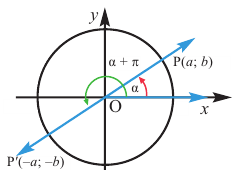
Если объект находится в I четверти, то симметричный ему относительно оси у объект находится во II четверти. Симметричный последнему относительно оси х, объект находится в III четверти, и он совпадает с объектом, симметричным начальному объекту из I относительно начала координат. Обратите внимание, что отображение относительно оси у и отображение, относительно оси х, совпадают с поворотом на 180°.
При отображении относительно оси х, точка расположенная на конечной стороне угла изменяет координаты, как показано на рисунке.
То есть, при этом знак меняет только координата у. Таким образом, так как косинус зависит от х он не меняется, зато меняется знак синуса. Отсюда, для углов 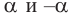
То есть, синус, тангенс и котангенс нечётные функции, косинус-чётная.
Пример 1:
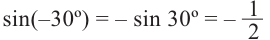
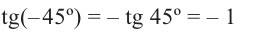
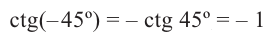

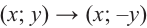
Отсюда получаем:
Запишем для углов 


При попарном сравнении равенств можно увидеть следующую связь-между значениями тригонометрических функций углов 

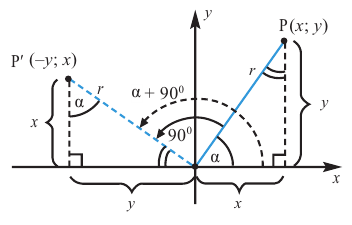
Повернём конечную сторону угла поворота 
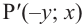
Запишем эти формулы в следующем виде:
Как видно но рисунку отображения относительно оси у и оси х эквивалентны повороту на 180°. Изменение координат, можно записать следующим образом:
Как видно по рисунку, при повороте угла а на 180° конечная сторона расположена в противоположных четвертях, но на одной прямой.
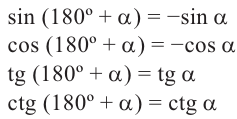
Пример 2.
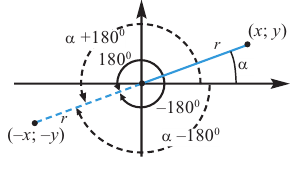
Для получения аналогичных формул тригонометрических функций угла поворота 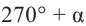
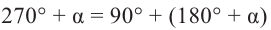
Например:
Теперь запишем соответствующие формулы для угла поворота 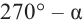
При помощи полученных формул можно найти значения тригонометрических функций произвольного угла, зная значения для соответствующего острого угла. Эти формулы называются формулами приведения. Для формул приведений можно легко увидеть следующую закономерность
1)Если аргумент имеет вид 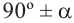
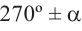
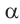
2)Если аргумент имеет вид 180° ± 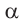
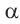
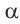
В каждом из обоих случаев, знак полученной в результате преобразования функции имеет одинаковое значение со знаком острого угла 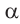
Тригонометрические тождества
Для острого угла 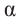
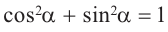
1)Запишите теорему Пифагора:
2)Каждую из сторон равенства разделите на с2:
3)Примените свойство степени:
4) Примите во внимание, что:
Связь между тригонометрическими функциями одного и того же угла
Тождество 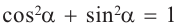
По координатам точки на единичной окружности и по определениям тригонометрических функций имеем:
Для всех значений 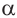
Для всех значений 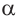
Из данных равенств имеем,что если для угла 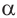
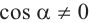
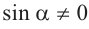
Разделив обе чаете равенства 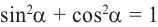
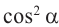
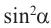
Полученные выше равенства являются тождествами. Их называют основными тригонометрическими тождествами. На основании основных тригонометрических можно написать:
При помощи основных тригонометрических тождеств можно упрощать тригонометрические выражения и вычислять модуль значения всех остальных функций, зная значение одной из них.
Пример 1. Используя основные тригонометрические тождества, докажите,что:
Доказательство:
Пример 2. Зная, что 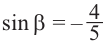
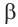
остальные тригонометрические функции.
Из формул 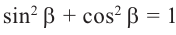
Так как угол 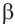
Тогда:
Формулы сложения
Практическая работа .
1)Покажем по шагам, равенство выражения
a)Для значений 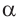
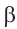
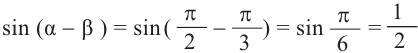
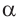
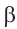
2)Как можно вычислить значение тригонометрических функций для угла 15°, используя разность значений углов 45° и 30°(15° = 45° — 30°)?
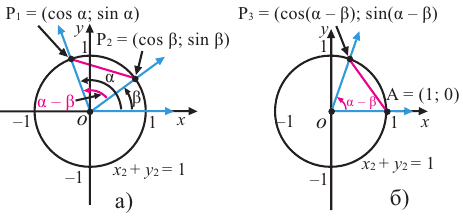
Тригонометрические функции суммы и разности двух углов.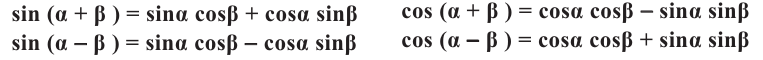

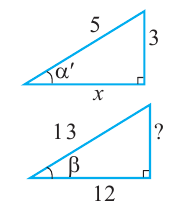
На рисунке
а)для угла 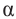
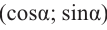
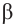
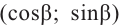
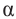
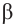
Тогда, для угла 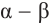
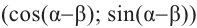
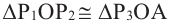
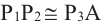

учитывая, что
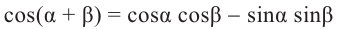

no формулам приведения группируя
no формуле косинуса разности с учётом формул приведения.

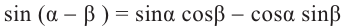
Пример 1. Найдём значение выражения 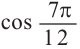
Решение.
Пример 2.
Найдём значение выражения 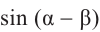
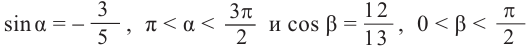
Решение.
Известно что 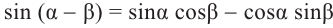
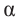
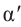
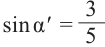
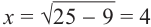
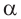
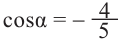
Аналогично, если зная, что 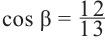
что 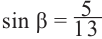
Можно записать формулы сложения для тангенса и котангенса:
no определению no формулам сложения
Аналогичным образом можно показать, что :
Следствия из формул сложения
Практическая работа.
Преобразуйте сумму 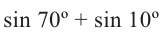
1)
решив систему уравнений найдите такие углы, чтобы их сумма была равна 70°, а разность
2)Запишите следующее 70° = 40° + 30°, 10° = 40° — 30° и упростите
Преобразование суммы(разности) в произведение
Формулы преобразования произведения
Справедливость данных тождеств можно показать при помощи формул сложения:
почленно складываем почленно складываем
Следующее тождество можно доказать аналогичным образом.
Тригонометрические функции двойного аргумента
Формулы сложения позволяют выразить 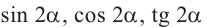
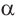
Таким образом, получаем тождества, которые называются формулами двойного аргумента:
Формулы половинного аргумента
Имеем, что
Отсюда: 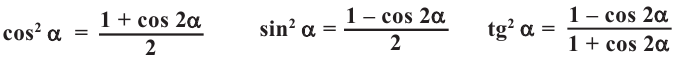
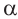
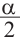
Для половинных аргументов справедливы тождества. 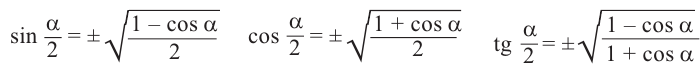
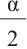
Пример 1. Упростим выражение 
Решение.
Пример 2. He используя калькулятор, вычислим значения 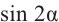
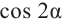

Решение.
Пример 3. Найдём значений 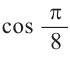
Решение:
Используем формулу половинного аргумента
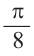
Упрощение тригонометрических выражений
Пример 1. Раскроем скобки и упростим выражение.
Пример 2. Разложим на множители и упростим выражение.
Пример 3. Упростим рациональное выражение, содержащее тригонометрические функции.
Пример 4. Освободим знаменатель от радикала
Здесь 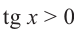
- Теоремы синусов и косинусов
- Система показательных уравнений
- Непрерывные функции и их свойства
- Правило Лопиталя
- Решение уравнений высших степеней
- Системы неравенств
- Квадратные неравенства
- Точка, прямая и плоскость в пространстве
Применим формулу cos(2α)=1-2cos²α к cos(4x): cos(4x)=1-2cos(2x). Тогда уравнение перепишется так: (2cos²(2x)-cos(2x)-1)²=4+cos²(3x)
cos(2x), как и косинус любого другого угла, принимает значения от -1 до 1 включительно. Тогда (2cos²(2x)-cos(2x)-1)² принимает значения от 0 (когда cos2x=1) до 4 (когда cos2x=-1) включительно. Но 4+cos²(3x)≥4,а значит, раз левая часть всегда меньше или равна 4, а правая больше или равна 4, равенство возможно только тогда когда обе части равны 4. Получаем систему:
{4+cos²(3x)=4
{(2cos²(2x)-cos(2x)-1)²=4
Из второго уравнения, с учетом выше написанного, сразу получаем
cos2x=-1. Отсюда
2x=π+2πn
x=π/2+πn, где n — любое целое число. Эта серия корней удовлетворяет и первому уравнению системы, поэтому это и есть решение. Теперь надо отобрать наименьший положительный корень. Это очевидно π/2 или 90°.
А вот и годный сайтик для обучения: http://mathus.ru/math/. Внизу есть раздел «Базовый курс математики», а в нем «Тригонометрия».
Оцени ответ
ВИДЕО УРОК
Изменение
тригонометрических функций с изменением угла от
0° до
90°.
Рассмотрим окружность произвольного радиуса с
центром в точке А.
Пусть радиус
АВ составляет с радиусом АD острый
угол α:
∠ DАВ = α.
Опустим из точки
В
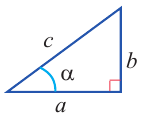
перпендикуляр ВС на АD. Из прямоугольного треугольника АВС имеем:
Будем вращать радиус АВ вокруг центра
А так, чтобы угол изменялся от 0° до 90°. На
чертеже зафиксировано несколько положений подвижного радиуса:
АВ1, АВ2, АВ3, …
Построим соответствующие этим положениям радиуса
прямоугольные треугольники:
∆ АВ1С1, ∆ АВ2С2,
∆ АВ3С3 …
Гипотенузы всех этих треугольников, независимо от
величины угла α, равны радиусу взятой окружности, катеты же с
возрастанием угла α будут
изменяться. Катет, противолежащий углу α, будет увеличиваться с возрастанием угла α, а
катет прилежащий, – уменьшаться. Отсюда заключаем, что синус острого угла α с возрастанием угла α от 0° до
90° возрастает, а косинус – убывает.
Чтобы проследить за изменением тангенса острого
угла, возьмём прямоугольный треугольник АВС
с острым углом
α.
Пусть катет
АС остаётся неизменным, а угол α увеличивается от 0° до
90°. При возрастании угла
α противолежащий ему катет увеличивается
(АВ1 < АВ2 < АВ < АВ3
…),
следовательно, возрастает и tg α так как
катет АС остаётся без изменения.
Значения функции
сtg α являются
числами обратными по отношению к соответствующим значениям функции tg α, и так
как последний с возрастанием угла α от 0° до
90° возрастает, то, следовательно, функция сtg α с возрастанием острого угла убывает.
Построение угла по данному значению его тригонометрической функции с
помощью острого угла.
Из определения sin α и cos α следует, что синус и косинус
острого угла α – положительные числа, меньшие единицы.
0 < sin α <
1,
0 < cos α <
1,
где α – острый угол.
Каково бы ни было положительное число у, меньшее единицы, существует, и притом только один,
острый угол α, синус которого равен у:
sin α = у.
ПРИМЕР:
Построить угол α,
синус которого равен 3/4.
РЕШЕНИЕ:
На произвольной прямой отложим отрезок DЕ = 3.
Через точку Е проводим прямую ЕF ⊥ DЕ. Построим окружность радиуса 4 с центром в точке D.
Пусть К – точка пересечения этой окружности с
прямой ЕF. Тогда угол
ЕКD – искомый угол α, так как синус его
равен
Каково бы ни было положительное число x, меньшее единицы, существует, и притом
только один, острый угол α, косинус которого равен х:
соs α = х.
ПРИМЕР:
Построить угол α,
косинус которого равен 2/5.
РЕШЕНИЕ:
На произвольной прямой отложим отрезок ВС = 2.
Через точку С проводим прямую СМ
⊥ ВС. Построим окружность
радиуса 5 с центром в точке В.
Пусть А – точка пересечения этой окружности с
прямой СМ. Тогда косинус угла АВС равен
Следовательно, угол АВС – искомый угол α.
Каково бы ни было положительное число р, существует, и притом только один, острый угол α, тангенс которого равен
р:
tg α = р.
ПРИМЕР:
Построить угол α,
тангенс которого равен 2/3.
РЕШЕНИЕ:
На одной стороне прямого угла МОN,
например на ОМ,
откладываем от вершины О отрезок ОА
= 3, а на другой стороне – отрезок ОВ
= 2. Соединяем точки А и В.
Тангенс угла ОАВ равен 2/3,
следовательно угол ОАВ
= α.
Каково бы ни было положительное число q, существует, и притом только один, острый
угол α, котангенс которого равен q:
ctg α = q.
ПРИМЕР:
Построить угол α,
котангенс которого равен 3.
РЕШЕНИЕ:
На сторонах прямого угла LKM,
откладываем отрезки КА и КС,
из которых, например, первый (КА) в три раза больше второго (КС).
Соединяем точки А и С.
Котангенс угла КАС равен 3,
следовательно угол КАС
= α.
Выражение тригонометрических функций через одну из них с помощью острого
угла.
ПРИМЕР:
Найдём значение синуса,
косинуса, тангенса и котангенса угла
2π/3.
РЕШЕНИЕ:
Координаты точки
нетрудно найти,
воспользовавшись свойством прямоугольного треугольника с углом 30°.
Поэтому
Аналогично находят значение синуса, косинуса, тангенса и котангенса углов,
обозначенных в верхнем ряду следующей таблицы:
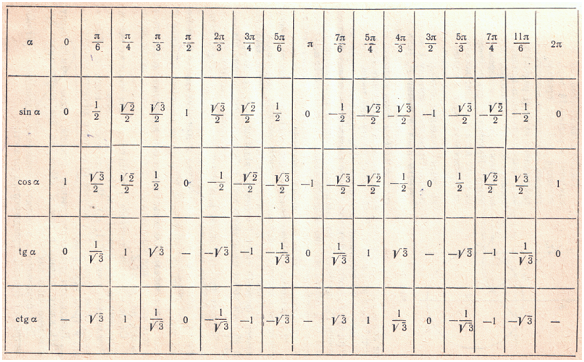
Значения синуса,
косинуса, тангенса та котангенса некоторых углов.
Покажем на примере, как находятся приближённые
численные значения синуса, косинуса, тангенса и котангенса для какого-нибудь
угла.
ПРИМЕР:
Найдите синус, косинус, тангенс и котангенс угла 48°.
РЕШЕНИЕ:
Построим
с помощью линейки и транспортира угол α,
равный 48°. На одной стороне этого угла от его
вершины А
отложим отрезок
АВ, равный, например, 67 мм. Из точки В на другую сторону угла α опустим перпендикуляр ВС. Мы получили прямоугольный треугольник
АВС, у которого ∠ ВАС = 48°.
Измерив катеты ВС и АС, найдём:
ВС ≈ 49 мм,
АС ≈ 45 мм.
Тогда имеем:
sin 48° ≈ 49/67 ≈ 0,73,
cos 48° ≈ 45/67 ≈ 0,67,
tg 48° ≈ 49/45 ≈ 1,09,
ctg 48° ≈ 45/49 ≈ 0,92.
Таким же путём можно найти приближённые значения
синуса, косинуса, тангенса и котангенса любого острого угла.
При этом степень приближения будет зависеть
только от точности наших измерений.
Построение углов по данному значению его тригонометрической функции с
помощью единичной окружности.
ЗАДАЧА:
Построить угол (дугу) α,
синус которого равен m.
РЕШЕНИЕ:
Рассмотрим три случая.
Пусть |m| < 1.
В координатной плоскости хОу строим единичную
окружность. На оси ординат находим точку, соответствующую числу m. Через эту точку проводимо прямую, параллельную
оси абсцисс, и точки пересечения её с единичной окружностью обозначим
через А и В.
Соединив точки А и В с началом координат, получим углы АОх и ВОх,
синусы которых равны m. Эти
углы определяются не однозначно. Обозначим наименьший положительный угол, определяемый
конечной стороной АО,
через ∠
АОх = а1,
а наименьший положительный ∠ ВОх, определяемый
конечной стороной ОВ,
через а2. Тогда искомый угол
α определится равенствами
α = α1 + 2πn и α = α2 +
2πn
где n = 0; ±1; ±2; …
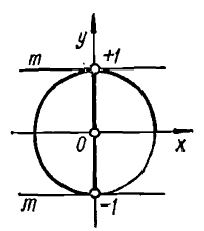
Если |m| = 1.
То
есть m = ±1, тогда
прямые, проведённые через точки (0; 1) и (0; –1) перпендикулярно до оси ординат, касаются единичной
окружности в точках, соответствующих наименьшим положительным углам
а искомый угол
α определяется
формулами
где n = 0; ±1; ±2; …
Если |m| ˃ 1.
То
прямая, проведённая перпендикулярно оси ординат через точку (0; m), не пересекает
единичную окружность.
В этом
случае задача решений не имеет.
ПРИМЕР:
Построить углы α, для
которых соs α = 3/4.
РЕШЕНИЕ:
На положительной оси
Ох откладываем от точки О отрезок, равный 3/4 радиуса единичной окружности.
Для этого делим радиус ОЕ1 на четыре равные части и откладываем на нём
от центра отрезок ОР, равный трём таким частям. Восстановим в точке Р перпендикуляр к оси Ох до пересечения его с единичной
окружностью в точках М и М‘. Искомые углы – это углы, составленные с
осью Ох любым из построенных подвижных
радиусов ОМ или ОМ‘. На чертеже отмечено лишь два угла, косинус каждого из которых равен 3/4.
ПРИМЕР:
Построить углы α, для
которых соs α = –3/4.
РЕШЕНИЕ:
Отрезок, равный 3/4 радиуса единичной окружности, откладываем от
точки О на
отрицательной полуоси Ох, а далее поступаем, как в предыдущем примере. На чертеже
отмечены лишь два угла, косинус каждого из которых равен –3/4.
ПРИМЕР:
Построить углы α, для
которых sin α = –3/5.
РЕШЕНИЕ:
Введём на плоскости прямоугольную систему координат.
Делим радиус
единичной окружности на пять
равных частей, и откладываем на нём от центра отрезок ОК, равный трём таким
частям. Через точку К проводим
прямую, параллельную диаметру
до пересечения с единичной окружностью. Получим точки М и
М‘, ординаты которых равны –3/5.
Соединяя эти точки с началом координат, получим
радиусы ОМ и ОМ‘. Синус любого из углов, составленных с осью Ох любым из радиусов ОМ или ОМ‘, равен –3/5.
На чертеже
отмечены два таких угла.
ПРИМЕР:
Построить углы α, для
которых tg α = 1,5.
РЕШЕНИЕ:
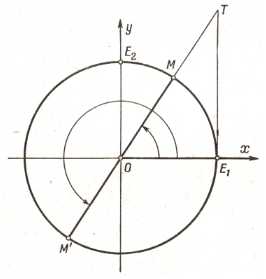
На оси тангенсов от единичной точки Е1 откладываем в положительном направлении
отрезок Е1Т, в 1,5
больший радиуса круга. Если через точку Т и центр круга
О провести прямую, то она пересечёт единичную
окружность в точках М и М‘. Это – концы подвижных радиусов, образующих с
положительным направлением оси Ох углы,
тангенсы которых равны 1,5. На чертеже
отмечены два таких угла.
ПРИМЕР:
Построить углы α, для
которых сtg α = –1/2.
РЕШЕНИЕ:
На оси котангенсов от Е2 откладываем в отрицательном направлении
отрезок Е2К, равный половине
радиуса круга.
Через конец этого
отрезка К и центр
круга О проводим
прямую, пересекающую единичную окружность в точках М и М‘. Это – концы
подвижных радиусов, образующих с положительным направлением оси Ох углы, котангенсы которых равны –1/2.
На чертеже
отмечены два таких угла.
Геометрический вывод значений тригонометрических функций.
Его полезно запомнить, так как часто приходится находить значения sin α и соs α по значению
tg
α.
ПРИМЕР:
tg α =
2/3.
Имеем:
Так же, геометрически, можно найти значения
sin α и
соs α по заданному
значению сtg α, где α – острый угол.
ПРИМЕР:
сtg α
= 3.
Имеем:
Задания к уроку 10
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований