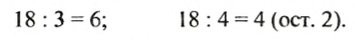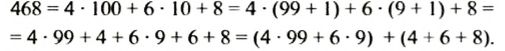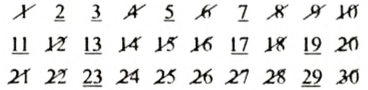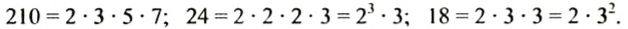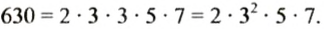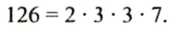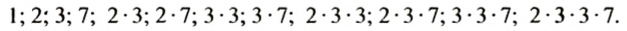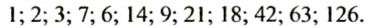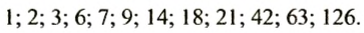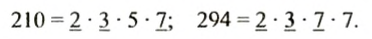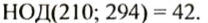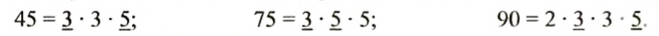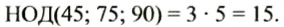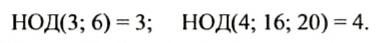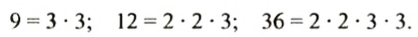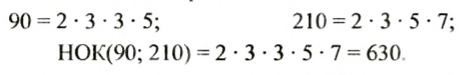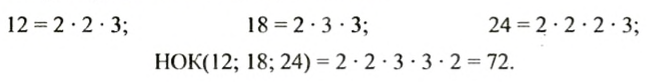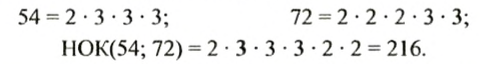Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given a number N, find the smallest prime divisor of N.
Examples:
Input: 25
Output: 5Input: 31
Output: 31
Approach:
- Check if the number is divisible by 2 or not.
- Iterate from i = 3 to sqrt(N) and making a jump of 2.
- If any of the numbers divide N then it is the smallest prime divisor.
- If none of them divide, then N is the answer.
Below is the implementation of the above algorithm:
C++
#include <bits/stdc++.h>
using namespace std;
int smallestDivisor(int n)
{
if (n % 2 == 0)
return 2;
for (int i = 3; i * i <= n; i += 2) {
if (n % i == 0)
return i;
}
return n;
}
int main()
{
int n = 31;
cout << smallestDivisor(n);
return 0;
}
Java
import java.io.*;
class GFG {
static int smallestDivisor(int n)
{
if (n % 2 == 0)
return 2;
for (int i = 3; i * i <= n; i += 2) {
if (n % i == 0)
return i;
}
return n;
}
public static void main (String[] args) {
int n = 31;
System.out.println (smallestDivisor(n));
}
}
Python3
def smallestDivisor(n):
if (n % 2 == 0):
return 2;
i = 3;
while(i * i <= n):
if (n % i == 0):
return i;
i += 2;
return n;
n = 31;
print(smallestDivisor(n));
C#
using System;
class GFG
{
static int smallestDivisor(int n)
{
if (n % 2 == 0)
return 2;
for (int i = 3;
i * i <= n; i += 2)
{
if (n % i == 0)
return i;
}
return n;
}
static public void Main ()
{
int n = 31;
Console.WriteLine(smallestDivisor(n));
}
}
PHP
<?php
function smallestDivisor($n)
{
if ($n % 2 == 0)
return 2;
for ($i = 3; $i * $i <= $n; $i += 2)
{
if ($n % $i == 0)
return $i;
}
return $n;
}
$n = 31;
echo smallestDivisor($n);
?>
Javascript
<script>
function smallestDivisor(n) {
if (n % 2 == 0)
return 2;
for (var i = 3; i * i <= n; i += 2) {
if (n % i == 0)
return i;
}
return n;
}
var n = 31;
document.write(smallestDivisor(n));
</script>
Time Complexity: O(sqrt(N)), as we are using a loop to traverse sqrt (N) times. As the condition is i*i<=N, on application of sqrt function on both the sides we get sqrt (i*i) <= sqrt(N), which is i<= sqrt(N), therefore the loop will traverse for sqrt(N) times.
Auxiliary Space: O(1), as we are not using any extra space.
Last Updated :
13 Jun, 2022
Like Article
Save Article
Только начал изучать Python на платформе Сириус. Смог решить все остальные задачи из темы «while», кроме одной задачи, которая мне не позволяет пройти на следующие темы. Задача «Минимальный простой делитель числа».
Условие: Дано целое число, не меньшее 2. Выведите его наименьший простой делитель. Нельзя использовать дополнительные библиотеки (math и т.п.)!
Входные данные: Вводится целое положительное число N <= 2*10 в 9-ой степени.
Выходные данные: Выведите ответ на задачу.
Пытался решить, написав код с while, но мой ответ не засчитывается, по причине слишком долгого времени работы программы. Рекомендуют организовать цикл, перебирающий делители до корня из числа N: while i*i <= N:, но я не могу понять, как это сделать.
Мой код Python (выдаёт ошибку «Программа выполнялась слишком долго и была прервана» либо «Программа выдаёт ошибку в процессе выполнения»):
N = int(input())
i = 2
while i*i <= N:
if N%i != 0:
i += 1
print(i)
Не могу понять, в чём ошибка?
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Теория чисел
- Простые числа
- Разложение на простые множители
- Решето Эратосфена
- Линейное решето Эратосфена*
- НОД и НОК
- Алгоритм Евклида
- Расширенный алгоритм Евклида*
- Операции по модулю
- Быстрое возведение в степень
- Деление по простому модулю*
Простые числа
Простым называется натуральное число, которое делится только на единицу и на себя. Единица при этом простым числом не считается. Составным числом называют непростое число, которое еще и не единица.
Примеры простых чисел: (2), (3), (5), (179), (10^9+7), (10^9+9).
Примеры составных чисел: (4), (15), (2^{30}).
Еще одно определение простого числа: (N) — простое, если у (N) ровно два делителя. Эти делители при этом равны (1) и (N).
Проверка на простоту за линию
С точки зрения программирования интересно научиться проверять, является ли число (N) простым. Это очень легко сделать за (O(N)) — нужно просто проверить, делится ли оно хотя бы на одно из чисел (2, 3, 4, ldots, N-1) . (N > 1) является простым только в случае, если оно не делится на на одно из этих чисел.
def is_prime(n):
if n == 1:
return False
for i in range(2, n): # начинаем с 2, так как на 1 все делится; n не включается
if n % i == 0:
return False
return True
for i in range(1, 10):
print(i, is_prime(i))(1, False)
(2, True)
(3, True)
(4, False)
(5, True)
(6, False)
(7, True)
(8, False)
(9, False)Проверка на простоту за корень
Алгоритм можно ускорить с (O(N)) до (O(sqrt{N})).
Пусть (N = a times b), причем (a leq b). Тогда заметим, что (a leq sqrt N leq b).
Почему? Потому что если (a leq b < sqrt{N}), то (ab leq b^2 < N), но (ab = N). А если (sqrt{N} < a leq b), то (N < a^2 leq ab), но (ab = N).
Иными словами, если число (N) равно произведению двух других, то одно из них не больше корня из (N), а другое не меньше корня из (N).
Из этого следует, что если число (N) не делится ни на одно из чисел (2, 3, 4, ldots, lfloorsqrt{N}rfloor), то оно не делится и ни на одно из чисел (lceilsqrt{N}rceil + 1, ldots, N-2, N-1), так как если есть делитель больше корня (не равный (N)), то есть делитель и меньше корня (не равный 1). Поэтому в цикле for достаточно проверять числа не до (N), а до корня.
def is_prime(n):
if n == 1:
return False
# Удобно вместо for i in range(2, n ** 0.5) писать так:
i = 2
while i * i <= n:
if n % i == 0:
return False
i += 1
return True
for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
print(i, is_prime(i))(1, False)
(2, True)
(3, True)
(10, False)
(11, True)
(12, False)
(1000000006, False)
(1000000007, True)Разложение на простые множители
Любое натуральное число можно разложить на произведение простых, и с такой записью очень легко работать при решении задач. Разложение на простые множители еще называют факторизацией.
[11 = 11 = 11^1] [100 = 2 times 2 times 5 times 5 = 2^2 times 5^2] [126 = 2 times 3 times 3 times 7 = 2^1 times 3^2 times 7^1]
Рассмотрим, например, такую задачу:
Условие: Нужно разбить (N) людей на группы равного размера. Нам интересно, какие размеры это могут быть.
Решение: По сути нас просят найти число делителей (N). Нужно посмотреть на разложение числа (N) на простые множители, в общем виде оно выглядит так:
[N= p_1^{a_1} times p_2^{a_2} times ldots times p_k^{a_k}]
Теперь подумаем над этим выражением с точки зрения комбинаторики. Чтобы «сгенерировать» какой-нибудь делитель, нужно подставить в степень (i)-го простого число от 0 до (a_i) (то есть (a_i+1) различное значение), и так для каждого. То есть делитель (N) выглядит ровно так: [M= p_1^{b_1} times p_2^{b_2} times ldots times p_k^{b_k}, 0 leq b_i leq a_i] Значит, ответом будет произведение ((a_1+1) times (a_2+1) times ldots times (a_k + 1)).
Алгоритм разложения на простые множители
Применяя алгоритм проверки числа на простоту, мы умеем легко находить минимальный простой делитель числа N. Ясно, что как только мы нашли простой делитель числа (N), мы можем число (N) на него поделить и продолжить искать новый минимальный простой делитель.
Будем перебирать простой делитель от (2) до корня из (N) (как и раньше), но в случае, если (N) делится на этот делитель, будем просто на него делить. Причем, возможно, нам понадобится делить несколько раз ((N) может делиться на большую степень этого простого делителя). Так мы будем набирать простые делители и остановимся в тот момент, когда (N) стало либо (1), либо простым (и мы остановились, так как дошли до корня из него). Во втором случае надо еще само (N) добавить в ответ.
Напишем алгоритм факторизации:
def factorize(n):
factors = []
i = 2
while i * i <= n: # перебираем простой делитель
while n % i == 0: # пока N на него делится
n //= i # делим N на этот делитель
factors.append(i)
i += 1
# возможно, в конце N стало большим простым числом,
# у которого мы дошли до корня и поняли, что оно простое
# его тоже нужно добавить в разложение
if n > 1:
factors.append(n)
return factors
for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
print(i, '=', ' x '.join(str(x) for x in factorize(i)))1 =
2 = 2
3 = 3
10 = 2 x 5
11 = 11
12 = 2 x 2 x 3
1000000006 = 2 x 500000003
1000000007 = 1000000007Задание
За сколько работает этот алгоритм?
.
.
.
.
Решение
За те же самые (O(sqrt{N})). Итераций цикла while с перебором делителя будет не больше, чем (sqrt{N}). Причем ровно (sqrt{N}) операций будет только в том случае, если (N) — простое.
А итераций деления (N) на делители будет столько, сколько всего простых чисел в факторизации числа (N). Понятно, что это не больше, чем (O(log{N})).
Задание
Докажите, что число (N) имеет не больше, чем (O(log{N})) простых множителей в факторизации.
Разные свойства простых чисел*
Вообще, про простые числа известно много свойств, но почти все из них очень трудно доказать. Вот еще некоторые из них:
- Простых чисел, меньших (N), примерно (frac{N}{ln N}).
- N-ое простое число равно примерно (Nln N).
- Простые числа распределены более-менее равномерно. Например, если вам нужно найти какое-то простое число в промежутке, то можно их просто перебрать и проверить — через несколько сотен какое-нибудь найдется.
- Для любого (N ge 2) на интервале ((N, 2N)) всегда найдется простое число (Постулат Бертрана)
- Впрочем, существуют сколь угодно длинные отрезки, на которых простых чисел нет. Самый простой способ такой построить — это начать с (N! + 2).
- Есть алгоритмы, проверяющие число на простоту намного быстрее, чем за корень.
- Максимальное число делителей равно примерно (O(sqrt[3]{n})). Это не математический результат, а чисто эмпирический — не пишите его в асимптотиках.
- Максимальное число делителей у числа на отрезке ([1, 10^5]) — 128
- Максимальное число делителей у числа на отрекзке ([1, 10^9]) — 1344
- Максимальное число делителей у числа на отрезке ([1, 10^{18}]) — 103680
- Наука умеет факторизовать числа за (O(sqrt[4]{n})), но об этом как-нибудь в другой раз.
- Любое число больше трёх можно представить в виде суммы двух простых (гипотеза Гольдбаха), но это не доказано.
Решето Эратосфена
Часто нужно не проверять на простоту одно число, а найти все простые числа до (N). В этом случае наивный алгоритм будет работать за (O(Nsqrt N)), так как нужно проверить на простоту каждое число от 1 до (N).
Но древний грек Эратосфен предложил делать так:
Запишем ряд чисел от 1 до (N) и будем вычеркивать числа: * делящиеся на 2, кроме самого числа 2 * затем деляющиеся на 3, кроме самого числа 3 * затем на 5, затем на 7, и так далее и все остальные простые до n. Таким образом, все незачеркнутые числа будут простыми — «решето» оставит только их.
Красивая визуализация
Задание
Найдите этим способом на бумажке все простые числа до 50, потом проверьте с программой:
N = 50
prime = [1] * (N + 1)
prime[0], prime[1] = 0, 0
for i in range(2, N + 1): # можно и до sqrt(N)
if prime[i]:
for j in range(2 * i, N + 1, i): # идем с шагом i, можно начиная с i * i
prime[j] = 0
for i in range(1, N + 1):
if prime[i]:
print(i)2
3
5
7
11
13
17
19
23
29
31
37
41
43
47У этого алгоритма можно сразу заметить несколько ускорений.
Во-первых, число (i) имеет смысл перебирать только до корня из (N), потому что при зачеркивании составных чисел, делящихся на простое (i > sqrt N), мы ничего не зачеркнем. Почему? Пусть существует составное (M leq N), которое делится на %i%, и мы его не зачеркнули. Но тогда (i > sqrt N geq sqrt M), а значит по ранее нами доказанному утверждению (M) должно делиться и на простое число, которое меньше корня. Но это значит, что мы его уже вычеркнули.
Во-вторых, по этой же самое причине (j) имеет смысл перебирать только начиная с (i^2). Зачем вычеркивать (2i), (3i), (4i), …, ((i-1)i), если они все уже вычеркнуты, так как мы уже вычеркивали всё, что делится на (2), (3), (4), …, ((i-1)).
Асимптотика
Такой код будет работать за (O(N log log N)) по причинам, которые мы пока не хотим объяснять формально.
Гармонический ряд
Научимся оценивать асимптотику величины (1 + frac{1}{2} + ldots + frac{1}{N}), которая нередко встречается в задачах, где фигурирует делимость.
Возьмем (N) равное (2^i — 1) и запишем нашу сумму следующим образом: [left(frac{1}{1}right) + left(frac{1}{2} + frac{1}{3}right) + left(frac{1}{4} + ldots + frac{1}{7}right) + ldots + left(frac{1}{2^{i — 1}} + ldots + frac{1}{2^i — 1}right)]
Каждое из этих слагаемых имеет вид [frac{1}{2^j} + ldots + frac{1}{2^{j + 1} — 1} le frac{1}{2^j} + ldots + frac{1}{2^j} = 2^j frac{1}{2^j} = 1]
Таким образом, наша сумма не превосходит (1 + 1 + ldots + 1 = i le 2log_2(2^i — 1)). Тем самым, взяв любое (N) и дополнив до степени двойки, мы получили асимптотику (O(log N)).
Оценку снизу можно получить аналогичным образом, оценив каждое такое слагаемое снизу значением (frac{1}{2}).
Попытка объяснения асимптотики** (для старших классов)
Мы знаем, что гармонический ряд (1 + frac{1}{2} + frac{1}{3} + ldots + frac{1}{N}) это примерно (log N), а значит [N + frac{N}{2} + frac{N}{3} + ldots + frac{N}{N} sim N log N]
А что такое асимптотика решета Эратосфена? Мы как раз ровно (frac{N}{p}) раз зачеркиваем числа делящиеся на простое число (p). Если бы все числа были простыми, то мы бы как раз получили (N log N) из формули выше. Но у нас будут не все слагаемые оттуда, только с простым (p), поэтому посмотрим чуть более точно.
Известно, что простых чисел до (N) примерно (frac{N}{log N}), а значит допустим, что k-ое простое число примерно равно (k ln k). Тогда
[sum_{substack{2 leq p leq N \ text{p is prime}}} frac{N}{p} sim frac{1}{2} + sum_{k = 2}^{frac{N}{ln N}} frac{N}{k ln k} sim int_{2}^{frac{N}{ln N}} frac{N}{k ln k} dk =N(lnlnfrac{N}{ln N} — lnln 2) sim N(lnln N — lnlnln N) sim N lnln N]
Но вообще-то решето можно сделать и линейным.
Задание
Решите 5 первых задач из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Линейное решето Эратосфена*
Наша цель — для каждого числа до (N) посчитать его минимальный простой делитель. Будем хранить его в массиве min_d. Параллельно будем хранить и список всех найденных простых чисел primes — это ровно те числа (x), у которых (min_d[x] = x).
Основное утверждение такое:
Пусть у числа (M) минимальный делитель равен (a). Тогда, если (M) составное, мы хотим вычеркнуть его ровно один раз при обработке числа (frac{M}{a}).
Мы также перебираем число (i) от (2) до (N). Если (min_d[i]) равно 0 (то есть мы не нашли ни один делитель у этого числа еще), значит оно простое — добавим в primes и сделаем (min_d[i] = i).
Далее мы хотим вычеркнуть все числа (i times k) такие, что (k) — это минимальный простой делитель этого числа. Из этого следует, что необходимо и достаточно перебрать (k) в массиве primes, и только до тех пор, пока (k < min_d[i]). Ну и перестать перебирать, если (i times k > N).
Алгоритм пометит все числа по одному разу, поэтому он корректен и работает за (O(N)).
N = 30
primes = []
min_d = [0] * (N + 1)
for i in range(2, N + 1):
if min_d[i] == 0:
min_d[i] = i
primes.append(i)
for p in primes:
if p > min_d[i] or i * p > N:
break
min_d[i * p] = p
print(i, min_d)
print(min_d)
print(primes)2 [0, 0, 2, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
3 [0, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
4 [0, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
5 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
6 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
7 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
8 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
9 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
10 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
11 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 5, 0, 3, 0, 0, 0]
12 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 0, 3, 0, 0, 0]
13 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 0, 0, 0]
14 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 0]
15 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
16 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
17 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
18 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
19 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
20 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
21 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
22 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
23 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
24 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
25 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
26 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
27 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
28 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
29 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
30 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]Этот алгоритм работает асимптотически быстрее, чем обычное решето. Но на практике, если писать обычное решето Эратсфена с оптимизациями, то оно оказывается быстрее линейнего. Также линейное решето занимает гораздо больше памяти — ведь в обычном решете можно хранить просто (N) бит, а здесь нам нужно (N) чисел и еще массив primes.
Зато один из «побочных эффектов» алгоритма — он неявно вычисляет факторизацию всех чисел от (1) до (N). Ведь зная минимальный простой делитель любого числа от (1) до (N) можно легко поделить на это число, посмотреть на новый минимальный простой делитель и так далее.
НОД и НОК
Введем два определения.
Наибольший общий делитель (НОД) чисел (a_1, a_2, ldots, a_n) — это максимальное такое число (x), что все (a_i) делятся на (x).
Наименьшее общее кратное (НОК) чисел (a_1, a_2, ldots, a_n) — это минимальное такое число (x), что (x) делится на все (a_i).
Например, * НОД(18, 30) = 6 * НОД(60, 180, 315) = 15 * НОД(1, N) = 1 * НОК(12, 30) = 6 * НОК(1, 2, 3, 4) = 12 * НОК(1, (N)) = (N)
Зачем они нужны? Например, они часто возникают в задачах.
Условие: Есть (N) шестеренок, каждая (i)-ая зацеплена с ((i-1))-ой. (i)-ая шестеренка имеет (a_i) зубчиков. Сколько раз нужно повернуть полносьтю первую шестеренку, чтобы все остальные шестеренки тоже вернулись на изначальное место?
Решение: Когда одна шестеренка крутится на 1 зубчик, все остальные тоже крутятся на один зубчик. Нужно найти минимальное такое число зубчиков (x), что при повороте на него все шестеренки вернутся в изначальное положение, то есть (x) делится на все (a_i), то есть это НОК((a_1, a_2, ldots, a_N)). Ответом будет (frac{x}{a_1}).
Еще пример задачи на применение НОД и НОК:
Условие: Город — это прямоугольник (n) на (m), разделенный на квадраты единичного размера. Вертолет летит из нижнего левого угла в верхний правый по прямой. Вертолет будит людей в квартале, когда он пролетает строго над его внутренностью (границы не считаются). Сколько кварталов разбудит вертолёт?
Решение: Вертолет пересечет по вертикали ((m-1)) границу. С этим ничего не поделать — каждое считается как новое посещение какого-то квартала. По горизонтали то же самое — ((n-1)) переход в новую ячейку будет сделан.
Однако еще есть случай, когда он пересекает одновременно обе границы (то есть пролетает над каким-нибудь углом) — ровно тот случай, когда нового посещения квартала не происходит. Сколько таких будет? Ровно столько, сколько есть целых решений уравнения (frac{n}{m} = frac{x}{y}). Мы как бы составили уравнение движения вертолёта и ищем, в скольки целых точках оно выполняется.
Пусть (t = НОД(n, m)), тогда (n = at, m = bt).
Тогда (frac{n}{m} = frac{a}{b} = frac{x}{y}). Любая дробь с натуральными числителем и знаменателем имеет ровно одно представление в виде несократимой дроби, так что (x) должно делиться на (a), а (y) должно делиться на (b). А значит, как ответ подходят ((a, b), (2a, 2b), (3a, 3b), cdots, ((t-1)a, (t-1)b)). Таких ответов ровно (t = НОД(n, m))
Значит, итоговый ответ: ((n-1) + (m-1) — (t-1)).
Кстати, когда (НОД(a, b) = 1), говорят, что (a) и (b) взаимно просты.
Алгоритм Евклида
Осталось придумать, как искать НОД и НОК. Понятно, что их можно искать перебором, но мы хотим хороший быстрый способ.
Давайте для начала научимся искать (НОД(a, b)).
Мы можем воспользоваться следующим равенством: [НОД(a, b) = НОД(a, b — a), b > a]
Оно доказывается очень просто: надо заметить, что множества общих делителей у пар ((a, b)) и ((a, b — a)) совпадают. Почему? Потому что если (a) и (b) делятся на (x), то и (b-a) делится на (x). И наоборот, если (a) и (b-a) делятся на (x), то и (b) делится на (x). Раз множства общих делитей совпадают, то и максимальный делитель совпадает.
Из этого равенства сразу следует следующее равенство: [НОД(a, b) = НОД(a, b operatorname{%} a), b > a]
(так как (НОД(a, b) = НОД(a, b — a) = НОД(a, b — 2a) = НОД(a, b — 3a) = ldots = НОД(a, b operatorname{%} a)))
Это равенство дает идею следующего рекурсивного алгоритма:
[НОД(a, b) = НОД(b operatorname{%} a, a) = НОД(a operatorname{%} , (b operatorname{%} a), b operatorname{%} a) = ldots]
Например: [НОД(93, 36) = ] [= НОД(36, 93spaceoperatorname{%}36) = НОД(36, 21) = ] [= НОД(21, 15) = ] [= НОД(15, 6) = ] [= НОД(6, 3) = ] [= НОД(3, 0) = 3]
Задание:
Примените алгоритм Евклида и найдите НОД чисел: * 1 и 500000 * 10, 20 * 18, 60 * 55, 34 * 100, 250
По-английски наибольший общий делитель — greatest common divisor. Поэтому вместо НОД будем в коде писать gcd.
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)
print(gcd(1, 500000))
print(gcd(10, 20))
print(gcd(18, 60))
print(gcd(55, 34))
print(gcd(100, 250))
print(gcd(2465473782, 12542367456))1
10
6
1
50
6Вообще, в C++ такая функция уже есть в компиляторе g++ — называется __gcd. Если у вас не Visual Studio, то, скорее всего, у вас g++. Вообще, там много всего интересного.
А за сколько оно вообще работает?
Задание
Докажите, что алгоритм Евклида для чисел (N), (M) работает за (O(log(N+M))).
Кстати, интересный факт: самыми плохими входными данными для алгоритма Евклида являются числа Фибоначчи. Именно там и достигается логарифм.
Как выразить НОК через НОД
(НОК(a, b) = frac{ab}{НОД(a, b)})
По этой формуле можно легко найти НОК двух чисел через их произведение и НОД. Почему она верна?
Посмотрим на разложения на простые множители чисел a, b, НОК(a, b), НОД(a, b).
[ a = p_1^{a_1}times p_2^{a_2}timesldotstimes p_n^{a_n} ] [ b = p_1^{b_1}times p_2^{b_2}timesldotstimes p_n^{b_n} ] [ ab = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} ]
Из определений НОД и НОК следует, что их факторизации выглядят так: [ НОД(a, b) = p_1^{min(a_1, b_1)}times p_2^{min(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)} ] [ НОК(a, b) = p_1^{max(a_1, b_1)}times p_2^{max(a_2, b_2)}timesldotstimes p_n^{max(a_n, b_n)} ]
Тогда посчитаем (НОД(a, b) times НОК(a, b)): [ НОД(a, b)НОК(a, b) = p_1^{min(a_1, b_1)+max(a_1, b_1)}times p_2^{min(a_2, b_2)+max(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)+max(a_n, b_n)} =] [ = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} = ab]
Формула доказана.
Как посчитать НОД/НОК от более чем 2 чисел
Для того, чтобы искать НОД или НОК у более чем двух чисел, достаточно считать их по цепочке:
(НОД(a, b, c, d, ldots) = НОД(НОД(a, b), c, d, ldots))
(НОК(a, b, c, d, ldots) = НОК(НОК(a, b), c, d, ldots))
Почему это верно?
Ну просто множество общих делителей (a) и (b) совпадает с множеством делителей (НОД(a, b)). Из этого следует, что и множество общих делителей (a), (b) и еще каких-то чисел совпадает с множеством общих делителей (НОД(a, b)) и этих же чисел. И раз совпадают множества общих делителей, то и наибольший из них совпадает.
С НОК то же самое, только фразу “множество общих делителей” надо заменить на “множество общих кратных”.
Задание
Решите задачи F, G, H, I из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Расширенный алгоритм Евклида*
Очень важным для математики свойством наибольшего общего делителя является следующий факт:
Для любых целых (a, b) найдутся такие целые (x, y), что (ax + by = d), где (d = gcd(a, b)).
Из этого следует, что существует решение в целых числах, например, у таких уравнений: * (8x + 6y = 2) * (4x — 5y = 1) * (116x + 44y = 4) * (3x + 11y = -1)
Мы сейчас не только докажем, что решения у таких уравнений существуют, но и приведем быстрый алгоритм нахождения этих решений. Здесь нам вновь пригодится алгоритм Евклида.
Рассмотрим один шаг алгоритма Евклида, преобразующий пару ((a, b)) в пару ((b, a operatorname{%} b)). Обозначим (r = a operatorname{%} b), то есть запишем деление с остатком в виде (a = bq + r).
Предположим, что у нас есть решение данного уравнения для чисел (b) и (r) (их наибольший общий делитель, как известно, тоже равен (d)): [bx_0 + ry_0 = d]
Теперь сделаем в этом выражении замену (r = a — bq):
[bx_0 + ry_0 = bx_0 + (a — bq)y_0 = ay_0 + b(x_0 — qy_0)]
Tаким образом, можно взять (x = y_0), а (y = (x_0 — qy_0) = (x_0 — (a operatorname{/} b)y_0)) (здесь (/) обозначает целочисленное деление).
В конце алгоритма Евклида мы всегда получаем пару ((d, 0)). Для нее решение требуемого уравнения легко подбирается — (d * 1 + 0 * 0 = d). Теперь, используя вышесказанное, мы можем идти обратно, при вычислении заменяя пару ((x, y)) (решение для чисел (b) и (a operatorname{%} b)) на пару ((y, x — (a / b)y)) (решение для чисел (a) и (b)).
Это удобно реализовывать рекурсивно:
def extended_gcd(a, b):
if b == 0:
return a, 1, 0
d, x, y = extended_gcd(b, a % b)
return d, y, x - (a // b) * y
a, b = 3, 5
res = extended_gcd(a, b)
print("{3} * {1} + {4} * {2} = {0}".format(res[0], res[1], res[2], a, b))3 * 2 + 5 * -1 = 1Но также полезно и посмотреть, как будет работать расширенный алгоритм Евклида и на каком-нибудь конкретном примере. Пусть мы, например, хотим найти целочисленное решение такого уравнения: [116x + 44y = 4] [(2times44+28)x + 44y = 4] [44(2x+y) + 28x = 4] [44x_0 + 28y_0 = 4] Следовательно, [x = y_0, y = x_0 — 2y_0] Будем повторять такой шаг несколько раз, получим такие уравнения: [116x + 44y = 4] [44x_0 + 28y_0 = 4, x = y_0, y = x_0 — 2y_0] [28x_1 + 16y_1 = 4, x_0 = y_1, y_0 = x_1 — y_1] [16x_2 + 12y_2 = 4, x_1 = y_2, y_1 = x_2 — y_2] [12x_3 + 4y_3 = 4, x_2 = y_3, y_2 = x_3 — y_3] [4x_4 + 0y_4 = 4, x_3 = y_4, y_3 = x_4 — 3 y_4] А теперь свернем обратно: [x_4 = 1, y_4 = 0] [x_3 = 0, y_3 =1] [x_2 = 1, y_2 =-1] [x_1 = -1, y_1 =2] [x_0 = 2, y_0 =-3] [x = -3, y =8]
Действительно, (116times(-3) + 44times8 = 4)
Задание
Решите задачу J из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34273
Операции по модулю
Выражение (a equiv b pmod m) означает, что остатки от деления (a) на (m) и (b) на (m) равны. Это выражение читается как «(a) сравнимо (b) по модулю (m)».
Еще это можно опрделить так: (a) сравнимо c (b) по модулю (m), если ((a — b)) делится на (m).
Все целые числа можно разделить на классы эквивалентности — два числа лежат в одном классе, если они сравнимы по модулю (m). Говорят, что мы работаем в «кольце остатков по модулю (m)», и в нем ровно (m) элементов: (0, 1, 2, cdots, m-1).
Сложение, вычитение и умножение по модулю определяются довольно интуитивно — нужно выполнить соответствующую операцию и взять остаток от деления.
С делением намного сложнее — поделить и взять по модулю не работает. Об этом подробнее поговорим чуть дальше.
a = 30
b = 50
mod = 71
print('{} + {} = {} (mod {})'.format(a, b, (a + b) % mod, mod))
print('{} - {} = {} (mod {})'.format(a, b, (a - b) % mod, mod)) # на C++ это может не работать, так как модуль от отрицательного числа берется странно
print('{} - {} = {} (mod {})'.format(a, b, (a - b + mod) % mod, mod)) # на C++ надо писать так, чтобы брать модулю от гарантированно неотрицательного числа
print('{} * {} = {} (mod {})'.format(a, b, (a * b) % mod, mod))
# print((a / b) % mod) # а как писать это, пока неясно30 + 50 = 9 (mod 71)
30 - 50 = 51 (mod 71)
30 - 50 = 51 (mod 71)
30 * 50 = 9 (mod 71)Задание
Посчитайте: * (2 + 3 pmod 5) * (2 * 3 pmod 5) * (2 ^ 3 pmod 5) * (2 — 4 pmod 5) * (5 + 5 pmod 6) * (2 * 3 pmod 6) * (3 * 3 pmod 6)
Для умножения (в C++) нужно ещё учитывать следующий факт: при переполнении типа всё ломается (разве что если вы используете в качестве модуля степень двойки).
intвмещает до (2^{31} — 1 approx 2 cdot 10^9).long longвмещает до (2^{63} — 1 approx 8 cdot 10^{18}).long long longв плюсах нет, при попытке заиспользовать выдает ошибкуlong long long is too long.- Под некоторыми компиляторами и архитектурами доступен
int128, но не везде и не все функции его поддерживают (например, его нельзя вывести обычными методами).
Зачем нужно считать ответ по модулю
Очень часто в задаче нужно научиться считать число, которое в худшем случае гораздо больше, чем (10^{18}). Тогда, чтобы не заставлять вас писать длинную арифметику, автор задачи часто просит найти ответ по модулю большого числа, обычно (10^9 + 7)
Кстати, вместо того, чтобы писать (1000000007) удобно просто написать (1e9 + 7). (1e9) означает (1 times 10^9)
int mod = 1e9 + 7; # В C++
cout << mod;1000000007N = 1e9 + 7 # В питоне такое число становится float
print(N)
print(int(N))1000000007.0
1000000007Быстрое возведение в степень
Задача: > Даны натуральные числа (a, b, c < 10^9). Найдите (a^b) (mod (c)).
Мы хотим научиться возводить число в большую степень быстро, не просто умножая (a) на себя (b) раз. Требование на модуль здесь дано только для того, чтобы иметь возможность проверить правильность алгоритма для чисел, которые не влезают в int и long long.
Сам алгоритм довольно простой и рекурсивный, постарайтесь его придумать, решая вот такие примеры (прямо решать необязательно, но можно придумать, как посчитать значение этих чисел очень быстро):
- (3^2)
- (3^4)
- (3^8)
- (3^{16})
- (3^{32})
- (3^{33})
- (3^{66})
- (3^{132})
- (3^{133})
- (3^{266})
- (3^{532})
- (3^{533})
- (3^{1066})
Да, здесь специально приведена такая последовательность, в которой каждое следующее число легко считается через предыдущее: его либо нужно умножить на (a=3), либо возвести в квадрат. Так и получается рекурсивный алгоритм:
- (a^0 = 1)
- (a^{2k}=(a^{k})^2)
- (a^{2k+1}=a^{2k}times a)
Нужно только после каждой операции делать mod: * (a^0 pmod c = 1) * (a^{2k} pmod c = (a^{k} pmod c)^2 pmod c) * (a^{2k+1} pmod c = ((a^{2k}pmod c) times a) pmod c)
Этот алгоритм называется быстрое возведение в степень. Он имеет много применений: * в криптографии очень часто надо возводить число в большую степень по модулю * используется для деления по простому модулю (см. далее) * можно быстро перемножать не только числа, но еще и матрицы (используется для динамики, например)
Асимптотика этого алгоритма, очевидно, (O(log c)) — за каждые две итерации число уменьшается хотя бы в 2 раза.
Задание
Решите задачу K из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Задание
Решите как можно больше задач из практического контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34273
Деление по модулю*
Давайте все-таки научимся не только умножать, но и делить по простому модулю. Вот только что это значит?
(a / b) = (a times b^{-1}), где (b^{-1}) — это обратный элемент к (b).
Определение: (b^{-1}) — это такое число, что (bb^{-1} = 1)
Утверждение: в кольце остатков по простому модулю (p) у каждого остатка (кроме 0) существует ровно один обратный элемент.
Например, обратный к (2) по модулю (5) это (3) ((2 times 3 = 1 pmod 5)))
Задание
Найдите обратный элемент к: * числу (3) по модулю (5) * числу (3) по модулю (7) * числу (1) по модулю (7) * числу (2) по модулю (3) * числу (9) по модулю (31)
Давайте докажем это утверждение: надо заметить, что если каждый ненулевой остаток (1, 2, ldots, (p-1)) умножить на ненулевой остаток (a), то получатся числа (a, 2a, ldots, (p-1)a) — и они все разные! Они разные, потому что если (xa = ya), то ((x-y)a = 0), а значит ((x — y) a) делится на (p), (a) — ненулевой остаток, а значит (x = y), и это не разные числа. И из того, что все числа получились разными, это все ненулевые, и их столько же, следует, что это ровно тот же набор чисел, просто в другом порядке!
Из этого следует, что среди этих чисел есть (1), причем ровно один раз. А значит существует ровно один обратный элемент (a^{-1}). Доказательство закончено.
Это здорово, но этот обратный элемент еще хочется быстро находить. Быстрее, чем за (O(p)).
Есть несколько способов это сделать.
Через малую теорему Ферма
Малая теорема Ферма: > (a^{p-1} = 1 pmod p), если (p) — простое, (a neq 0 pmod p)).
Доказательство: В предыдущем пункте мы выяснили, что множества чисел (1, 2, ldots, (p-1)) и (a, 2a, ldots, (p-1)a) совпадают. Из этого следует, что их произведения тоже совпадают по модулю: ((p-1)! = a^{p-1} (p-1)! pmod p).
((p-1)!neq 0 pmod p) а значит на него можно поделить (это мы кстати только в предыдущем пункте доказали, поделить на число — значит умножить на обратный к нему, который существует).
А значит, (a^{p — 1} = 1 pmod p).
Как это применить Осталось заметить, что из малой теоремы Ферма сразу следует, что (a^{p-2}) — это обратный элемент к (a), а значит мы свели задачу к возведению (a) в степень (p-2), что благодаря быстрому возведению в степень мы умеем делать за (O(log p)).
Обобщение У малой теоремы Ферма есть обобщение для составных (p):
Теорема Эйлера: > (a^{varphi(p)} = 1 pmod p), (a) — взаимно просто с (p), а (varphi(p)) — это функция Эйлера (количество чисел, меньших (p) и взаимно простых с (p)).
Доказывается теорема очень похоже, только вместо ненулевых остатков (1, 2, ldots, p-1) нужно брать остатки, взаимно простые с (p). Их как раз не (p-1), а (varphi(p)).
Для нахождения обратного по этой теореме достаточно посчитать функцию Эйлера (varphi(p)) и найти (a^{-1} = a^{varphi(p) — 1}).
Но с этим возникают большие проблемы: посчитать функцию Эйлера сложно. Более того, на предполагаемой невозможности быстро ее посчитать построены некоторые криптографические алгоритм типа RSA. Поэтому быстро делить по составному модулю этим способом не получится.
Через расширенный алгоритм Евклида
Этим способом легко получится делить по любому модулю! Рекомендую.
Пусть мы хотим найти (a^{-1} pmod p), (a) и (p) взаимно простые (а иначе обратного и не будет существовать).
Давайте найдем корни уравнения
[ax + py = 1]
Они есть и находятся расширенным алгоритмом Евклида за (O(log p)), так как (НОД(a, p) = 1), ведь они взаимно простые.
Тогда если взять остаток по модулю (p):
[ax = 1 pmod p]
А значит, найденный (x) и будет обратным элементом к (a).
То есть надо просто найти (x) из решения того уравнения по модулю (p). Можно брать по модулю прямо походу решения уравнения, чтобы случайно не переполниться.
2 [0, 0, 2, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 3 [0, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 4 [0, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 5 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0] 6 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0] 7 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0] 8 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0] 9 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0] 10 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0] 11 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 5, 0, 3, 0, 0, 0] 12 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 0, 3, 0, 0, 0] 13 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 0, 0, 0] 14 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 0] 15 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2] 16 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2] 17 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2] 18 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2] 19 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2] 20 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2] 21 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2] 22 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2] 23 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2] 24 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2] 25 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2] 26 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2] 27 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2] 28 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2] 29 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2] 30 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2] [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2] [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
Содержание:
Делимость чисел
Делители натурального числа
18 конфет можно разделить поровну между 3 детьми, дав каждому ребенку по 6. Это же количество конфет, не разрезая их, нельзя разделить поровну между 4 детьми. Если каждому ребенку дать по 4 конфеты, то останется 2. Запишем:
Число 18 делится на число 3 без остатка (еще говорят: 18 делится на 3). Число 3 называют делителем числа 18. Число 18 не делится без остатка на 4 (еще говорят: 18 не делится на 4). Число 4 не является делителем числа 18.
Любое натуральное число, на которое делится данное натуральное число, называют делителем этого числа.
Запишем все натуральные числа, на которые делится число 18 Такими числами являются 1,2,3,6,9, 18. Итак, число 18 имеет 6 делителей: 1,2, 3,6,9 и 18.
Число 1 имеет только один делитель — 1. Любое другое число, например, 23, обязательно имеет по крайней мере два делителя — число 1 и само число (23), причем I — наименьший делитель, само число (23) — наибольший.
Пример:
Найти все делители числа 36.
Решение:
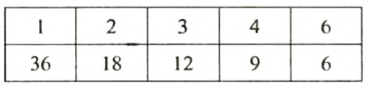
Чтобы найти все делители числа 36, будем делить его на натуральные числа, начиная с 1: 36 : 1 = 36; 36 : 2 = 18; 36 : 3 = 12; 36 : 4 = 9; 36 : 5 = 7 (ост. 1); 36 : 6 = 6; 36 : 7 = 5 (ост. 1); 36 : 8 = 4 (ост. 4) и т. д.
Количество делений можно уменьшить. Найдя один делитель, сразу можем записать еще один, который является частным от деления числа 36 на этот делитель. Делители удобно записать так:
Итак, делителями числа 36 являются: 1, 2, 3,4, 6, 9, 12, 18, 36.
Признаки делимости на 2, 5 и 10
Как известно из изученного в пятом классе, чтобы умножить натуральное число на 10, нужно к записи этого числа дописать справа один нуль, например, 137 • 10 = 1370. Поскольку 10 является делителем числа 1370, то число 1370 делится на 10. В общем, на 10 делятся все числа, запись которых оканчивается цифрой 0.
Число, запись которого не оканчивается цифрой 0, например, 457, на 10 не делится.
Натуральное число, запись которого оканчивается цифрой 0, делится на 10.
Натуральное число, запись которого не оканчивается цифрой 0, не делится на 10.
Это правило называют признаком делимости на 10.
Найдем признак делимости на 5. Для этого разделим на 5 некоторые числа, например, 19, 82, 140, 245, 344, 515, 630, 1027.
Запишем в первый столбик те числа, которые делятся на 5, а во второй — те, которые не делятся на 5.
Какую вы заметили особенность чисел, которые делятся на 5; не делятся на 5?
Натуральное число, запись которого оканчивается цифрой 0 или 5, делится на 5.
Натуральное число, запись которого оканчивается цифрой, отличной от 0 или 5, не делится на 5.
Числа, которые делятся на 2, называют четными, а числа, которые на 2 не делятся, — нечетными. Например, 24 — число четное, поскольку оно делится на 2, а число 25 — нечетное, поскольку оно не делится на 2.
Однозначные числа 0, 2,4, 6, 8 являются четными, а числа 1, 3, 5, 7, 9 — нечетными.
Запись каждого числа, которое делится на 2, оканчивается однозначным четным числом. Если запись числа оканчивается однозначным нечетным числом, то оно не делится на 2.
Натуральное число, запись которого оканчивается однозначным четным числом, делится на 2.
Натуральное число, запись которого оканчивается однозначным нечетным числом, не делится на 2.
Для тех, кто хочет знать больше
Зная последнюю цифру в записи натурального числа, можно установить, делится ли оно на 2, 5 или 10.
Зная две последние цифры в записи натурального числа, можно ответить на вопрос, делится ли число на 4, на 25. А именно:
Натуральное число делится на 4, если число, образованное двумя его последними цифрами, делится на 4.
Натуральное число не делится на 4, если число, образованное двумя его последними цифрами, не делится на 4
Натуральное число делится на 25. если число, образованное двумя его последними цифрами, делится на 25.
Натуральное число не делится на 25, если число, образованное двумя его последними цифрами, не делится на 25.
Например:
- 14 536 делится на 4, поскольку двумя его последними цифрами записано число 36, которое делится на 4;
- 57 375 делится на 25, поскольку 75 делится на 25;
- 28 426 не делится на 4, поскольку 26 не делится на 4;
- 438 635 не делится на 25, поскольку 35 не делится на 25.
Признаки делимости на 9 и на 3
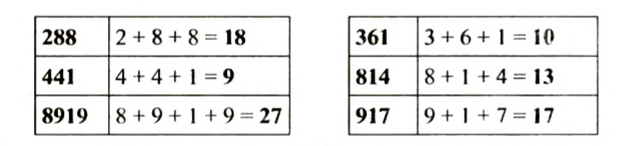
Найдем признак делимости на 9. Для этого разделим на 9 некоторые числа, например, 288, 361,441, 814. 917, 8919.
Запишем в первый столбик те числа, которые делятся на 9, а во второй — те, которые не делятся на 9.
Какую вы заметили особенность чисел которые делятся на 9; не делятся на 9?
Воспользуйтесь такой подсказкой: найдите сумму цифр каждого из этих чисел.
Какое свойство имеет сумма цифр тех чисел, которые делятся на 9?
Какое свойство имеет сумма цифр тех чисел, которые не делятся на 9?
Натуральное число делится на 9, если сумма его цифр делится на 9.
Натуральное число не делится на 9, если сумма его цифр не делится на 9.
Признак делимости на 3 аналогичен признаку делимости на 9.
Натуральное число делится на 3, если сумма его цифр делится на 3.
Натуральное число не делится на 3, если сумма его цифр не делится на 3.
Для тех. кто хочет знать больше
Признак делимости на 9, например, для числа 468, следует из таких преобразований:
Число 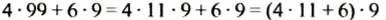
Простые и составные числа
Возьмем несколько натуральных чисел и найдем все их делители.
Мы видим, что числа имеют разное количество делителей. Число 1 имеет только один делитель — само это число. Числа 2, 3, 17 имеют по два делителя: 1 и само себя. Числа 4, 12,21 и 30 имеют больше, чем два делителя.
Натуральное число называют простым, если оно имеет только два разных делителя: единицу и само это число. Число, имеющее более двух делителей, называют составным.
Итак, числа 2, 3, 17 — простые, а числа 4, 12, 21, 30 — составные. Число 1 не является ни простым, ни составным числом.
Если число имеет делитель, отличный от I и самого себя, то это число имеет более двух делителей и поэтому является составным. Число 12 475 — составное, так как имеет среди делителей, например, число 5.
Наименьшим простым числом является число 2. Наибольшего простого числа не существует. Все простые числа, кроме числа 2, являются нечетными.
Таблица простых чисел, которые не превышают 1000, находится на форзаце учебника.
Интересные рассказы
Решето Эратосфена
История математики знает имена ученых, которые приложили немало усилий для составления таблиц простых чисел. Первые такие попытки были сделаны еще в Древней Греции.
Для нахождения простых чисел древнегреческий ученый Эратосфен (ок. 276-ок. 194 г. до н.э.) предложил следующий способ Он выписывал все числа от 1 до некоторого числа 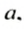
Если «высеять» все простые числа, не превышающие 30, то получим:
2, 3, 5, 7, II, 13, 17, 19, 23, 29 — первые 10 простых чисел.
Эратосфенов метод «высевания» простых чисел называют еще «решетом Эратосфена». Это связано с тем, что древние греки писали на папирусе или табличках, покрытых воском, и числа не вычеркивали, а выкалывали иголкой, после чего папирус или табличка напоминали решето.
В 1603 году итальянский математик Пьетро Катальди опубликовал в Болонье первую известную нам таблицу простых чисел меньше 750. Позже математики продвигались все дальше в глубь натурального ряда чисел, открывая все новые и новые простые числа.
Уже в 1770 голу немецкий математик Иоанн Генрих Ламберт (1728- 1777) опубликовал таблицу наименьших делителей всех чисел меньше 102 000, которые не делятся на 2, 3 и 5. Это была огромная работа. Не зря, призывая ученых продолжить составление таблицы, Ламберт гарантировал бессмертие тому, кто получит таблицу делителей до 1 000 000.
В середине XIX века в прессе появились сообщения, которые казались совершенно невероятными: Венская академия наук получила рукопись пражского математика Якуба Филиппа Кулика, содержащую таблицу деятелей чисел, не делящихся 2, 3 и 5, которую ученый расширил до 100 миллионов.
Редактор таблиц простых чисел Лемер посетил Вену и убедился, что в библиотеке академии хранится семь больших томов рукописных таблиц «Большой канон делителей всех чисел, которые не делятся на 2, 3 и 5, и простых чисел между ними до 100 330 201 Якуба Филиппа Кулика, публичного ординарного профессора высшей математики Пражского университета».
Якуб Филипп Кулик (1793 1863) родился во Львове. Окончив местную гимназию, он изучал философию, право и математику во Львовском университете, ас 1814 гола преподавал математику в лицее. С 1826 года Кулик стал профессором высшей математики Пражского университета. Много сил ученый отдал развитию культуры, науки и образования в родном крае. Он подарил много книг галицким гимназиям и Львовскому университету. Кулик является автором многих научных работ, но в историю математики он вошел как непревзойденный вычислитель и составитель математических таблиц.
Разложение натуральных чисел на простые множители
Составное число 24 можно записать как произведение двух множителей, например, 24 = 6•4. Говорят, что число 24 разложили на два множителя — 6 и 4. Числа 6 и 4 тоже можно разложить на множители: 6 = 3•2; 4 = 2•2. Теперь число 24 можно записать так: 24 = 3 • 2 • 2 • 2. В произведении 3 • 2 • 2 • 2 все множители являются простыми числами. Итак, число 24 разложили на простые множители.
Разложить число на простые множители означает записать его в виде произведения простых чисел. Любое составное число можно разложить на простые множители. Например:
Раскладывая числа на простые множители, надо найти простые делители этого числа. При этом можно использовать признаки делимости чисел. Чтобы разложить на множители большие числа, пользуются специальной схемой.
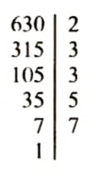
Пусть надо разложить на простые множители число 630.
Записываем это число и проводим справа вертикальную черту Наименьшим простым делителем этого числа является 2; записываем 2 справа or черты. Делим 630 на 2 и записываем частное 315 слева от черты под числом 630. Находим теперь наименьший простой делитель числа 315. Им является число 3, записываем его справа от черты. Делим 315 на 3, частное 105 записываем слева. Делим 105 на 3, получаем 35; 35 делим на 5, получаем 7. Число 7 простое, разделив его на 7, получим I. Разложение закончено.
Итак,
Пример:
Найти все делители числа 126.
Решение:
Разложим число 126 на простые множители:
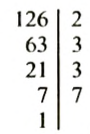
Делителями числа 126 являются: 1, простые числа 2, 3, 7 в полученном разложении и всевозможные произведения чисел 2, 3, 3, 7, то есть:
И так, делителями числа 126 являются:
Запишем все делители в порядке их возрастания:
Интересные рассказы
Расположение простых чисел
Утверждение о том, что каждое отличное от 1 натуральное число можно записать в виде произведения простых множителей и притом единственным способом, если не принимать во внимание порядок расположения сомножителей, является так называемой основной теоремой арифметики — одной из древнейших математических наук (в переводе с греческого «арифметика» — «искусство чисел»).
В соответствии с основной теоремой арифметики простые числа являются как бы кирпичами, из которых «строятся» натуральные числа. Этим и объясняется внимание к простым числам со стороны математиков всех времен. Еще древнегреческий математик Эвклид (ок. 365 ок. 300 г. до н. э.) доказал, что простых чисел есть бесконечно много, поэтому наибольшего простого числа не существует. Но еще до сих пор не изучены закономерности расположения простых чисел в натуральном ряду.
Талантливые математики многих стран стремились найти закон расположения простых чисел.
В решении этого сложного вопроса весомый результат получил русский ученый, академик Пафнутий Львович Чебышев (1821 — 1894). Он доказал, что между любым натуральным числом больше 1 и его удвоением всегда существует хотя бы одно простое число.
О свойствах простых чисел выдвинуто много интересных гипотез. Среди них самой интересной является гипотеза члена Петербургской академии наук Кристиана Гольдбаха (1690 1764), сформулированная так: любое натуральное число больше 5 является суммой трёх простых чисел
Свойства простых чисел можно наглядно представить так:
- а) представим прямолинейный провод, выходящий из комнаты в мировое пространство, проходящий возле Луны и далее за огненный шар Солнца — в бесконечность;
- б) мысленно развесим на нем через каждый метр электрические лампочки и пронумеруем их натуральными числами;
- в) мысленно включим свет с таким расчетом, чтобы загорелись лампочки, номера которых являются простыми числами;
- г) мысленно полетим вдоль этого провода.
Перед нами откроется следующая картина.
- Лампочка под номером 1 не горит, поскольку единица не является простым числом.
- Две следующие лампочки под номерами 2 и 3 горят, поскольку числа 2 и 3 — простые. Больше таких лампочек, которые являются соседними и горят, мы не увидим.
- Будем наблюдать пары лампочек, которые горят, соответствующие числам-близнецам (3 и 5, 5 и 7, 11 и 13 и т. д.). Самой большой из известных пар чисел-близнецов является 10 999 949 и 10 999 951.
- Чем дальше будем лететь, тем будет становиться темнее, потому что реже будут гореть лампочки. А вот наступил большой промежуток темноты. Но мы вспоминаем свойство простых чисел, открытое Эвклидом, и смело движемся вперед, так как знаем, что впереди еще обязательно есть горящие лампочки, и их достаточно много.
- Снова долго летим, а впереди и позади — темнота. Снова вспоминаем свойство простых чисел, доказанное Чебышевым, и следуем далее, уверенные в том, что, пролетев путь не больше того, который уже пролетели, мы обязательно увидим свет.
Наибольший общий делитель
Выпишите все делители чисел 18 и 24 и подчеркните их общие делители
Общими делителями (они подчеркнуты) чисел 18 и 24 являются числа 1, 2, 3, 6, наибольшим из них является 6. Число 6 является наибольшим натуральным числом, на которое делятся и 18, и 24.
Наибольшее натуральное число, на которое делится каждое из данных чисел, называют наибольшим общим делителем этих чисел.
Итак, наибольшим общим делителем чисел 18 и 24 являегся число 6. Сокращенно это записывают так: НОД( 18; 24) 6.
В рассмотренном примере мы легко нашли наибольший общий делитель чисел, записав все делители каждого из них. Если числа большие и имеют много делителей, то нахождение наибольшего общего делителя этим способом является достаточно сложным.
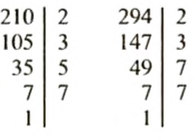
Рассмотрим еще один способ нахождения наибольшего общего делителя, взяв числа 210 и 294. Разложим каждое из этих чисел на простые множители:
Подчеркнем все общие простые множители в разложении данных чисел: 2, 3, 7. Числа 210 и 294 делятся на каждое из чисел 2, 3, 7 и на их произведение: 2•3•7 =42. Число 42 является наибольшим общим делителем чисел 210 и 294:
Назовите последовательность шагов при нахождении НОД двух чисел.
Для нахождения наибольшего общего делителя двух чисел можно разложить эти числа на простые множители и найти произведение их общих множителей.
По такому правилу можно находить наибольший общий делитель трёх и более чисел. Найдем, например, наибольший общий делитель чисел 45, 75 и 90. Разложим эти числа на простые множители и подчеркнем общие для всех чисел множители:
Итак,
Если среди данных чисел есть число, на которое делятся другие из данных чисел, то это число является наибольшим обидим делителем данных чисел. Например:
Два числа, наибольший общий делитель которых равен 1, называют взаимно простыми числами. Например, числа 16 и 27 являются взаимно простыми, так как их наибольшим общим делителем является 1.
Взаимно простые числа вообще имеют только один общий делитель — число 1. Поэтому, если два числа имеют общий делитель, отличный от 1, то они не взаимно простые. Например, числа 18 и 45 не являются взаимно простыми, так как имеют общий делитель 3.
- Заказать решение задач по высшей математике
Пример:
Какое наибольшее количество одинаковых букетов можно составить из 24 васильков и 32 ромашек, использовав все цветы?
Решение:
Из данных цветов можно, например, составить 2 букета. в каждом из которых будет 12 васильков и 16 ромашек. Нельзя составить три букета, так как 32 ромашки нельзя разделить на 3 одинаковые части. Можно составить четыре одинаковых букета, так как и 24 василька, и 32 ромашки можно разделить на 4 одинаковые части. Очевидно, что для решения задачи нужно найти наибольшее число, на которое можно разделить 24 василька и 32 ромашки, то есть найти наибольший общий делитель чисел 24 и 32. Поскольку НОД(24; 32) = 8, то можно составить самое большее 8 одинаковых букетов. Каждый такой букет будет состоять из 24 : 8 = 3 васильков и 32 : 8 = 4 ромашек.
Кратные натурального числа. Наименьшее общее кратное
Числа 36, 72, 180 делятся на 18. Говорят, что числа 36, 72, 180 кратны числу 18.
Любое натуральное число, которое делится на данное натуральное число, называют кратным данного числа.
Все числа, кратные числу 18, можно получить, умножая число 18 последовательно на числа 1,2, 3,4, 5,….
18, 36, 54, 72, 90,… — числа, кратные 18.
Каждое натуральное число имеет бесконечно много чисел, кратных ему, наименьшим из которых является само это число.
Запишите числа, кратные 9. и числа, кратные 12, и подчеркните их общие кратные.
Общими кратными чисел 9 и 12 являются подчеркнутые числа 36, 72, …. Все они делятся на 9 и на 12. Наименьшим общим кратным является число 36
Наименьшим общим кратным двух натуральных чисел называют наименьшее натуральное число, которое делится на каждое изданных чисел.
То, что наименьшим общим кратным чисел 9 и 12 является число 36, сокращенно записывают так: НОК(9; 12) = 36.
Разложим числа 9, 12 и их наименьшее общее кратное 36 на простые множители:
Мы видим, что разложение числа 36 можно получить, если разложение числа 9 умножить на 2 • 2. Числа 2 и 2 — это такие множители из разложения числа 12, которых нет в разложении числа 9
Назовите последовательность шагов при нахождении НОК двух чисел.
Чтобы найти наименьшее общее кратное двух чисел, можно каждое из них разложить на простые множители и разложение одного из чисел умножить на те множители другого числа, которых нет в разложении первого.
Найдем наименьшее общее кратное чисел 90 и 210.
Если одно из чисел делится на другое, то большее из них является наименьшим общим кратным этих чисел. Например, НОК(21; 63) = 63.
Наименьшим общим кратным двух взаимно простых чисел являегся произведение этих чисел. Например, НОК(8; 9) = 72.
Наименьшее общее кратное можно найти не только для двух, но и для трех и более чисел.
Например, для чисел 12, 18, 24 имеем:
Пример:
Найти наименьшее четырехзначное число, кратное 27.
Решение:
1000 — наименьшее четырехзначное число. Разделим его на 27: 1000: 27 = 37 (ост. 1).
27 • 38 = 1026 — наименьшее четырехзначное число, кратное 27.
Пример:
Шаг отца равен 72 см, а шаг сына — 54 см. Найти наименьшее расстояние, которое нужно пройти как отцу, так и сыну, чтобы каждый из них сделал при этом целое число шагов.
Решение:
Искомое расстояние в сантиметрах должно выражаться таким наименьшим числом, которое делится на 72 и на 54. Таким числом являемся наименьшее общее кратное этих чисел. Найдем НОК(54; 72):
Итак, искомое расстояние равно 216 см. На таком расстоянии отец сделает 216 : 72 = 3 шага, а сын — 216 : 54 = 4 шага.
Пример:
Найти наименьшее общее кратное чисел 15 и 12.
Решение:
Находим кратные большего из чисел и проверяем, делятся ли они на меньшее число: 15 не делится на 12; 15 • 2 = 30 — не делится на 12; 15 • 3 = 45 не делится на 12; 15 • 4 = 60 — делится на 12. Итак, НОК( 15; 12) = 60.
Памятка:
- 24 = 6 • 4; 6 и 4 — делители числа 24
- Число 210 делится на 10, так как заканчивается 0.
- Числа 140 и 135 делятся на 5, так как заканчиваются 0 или 5
- Числа 510, 512, 324, 126, 438 делятся на 2, так как заканчиваются однозначным четным числом.
- Число 741 делится на 3; 7 + 4+1 = 12; 12:3 = 4, сумма цифр делится на 3. Число 711 делится на 9; 7+1 + 1=9; 9:9=1, сумма цифр делится на 9.
- Число 17 делится только на 1 и 17; 17 — простое число; делителями являются 1 и само число.
- Число 14 делится не только на I и 14, а и на 2; 14 — составное число; делителей больше двух.
- НОД( 18; 24) = 6; 6 — наибольшее натуральное число, на которое делятся 18 и 24.
- НОК(50; 75) =150; 150 — наименьшее натуральное число, которое делится на 50 и на 75.
- Обыкновенные дроби
- Отношения и пропорции
- Рациональные числа и действия над ними
- Делимость натуральных чисел
- Угол между плоскостями
- Понятие о производной вектор-функции
- Криволинейные интегралы
- Двойные и тройные интегралы