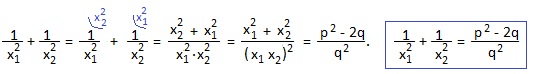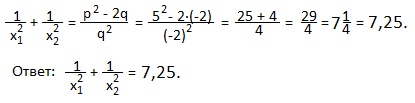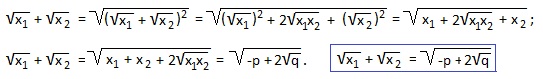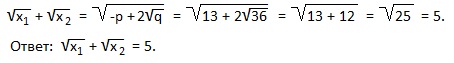Как найти наименьшую сумму квадратов чисел

Задача на число 30 является одной из самых знаменитых задач в математике. Она заключается в следующем: какими числами нужно заменить знаки в выражении 1_2_3_4_5_6_7_8_9_0, чтобы получить число 30?

В этой статье мы рассмотрим математический трюк, который позволяет выбрать числа для наименьшей суммы их квадратов в задаче на число 30.

Шаг 1: Разбиение на группы

Первый шаг заключается в разбиении чисел на группы. Для этого мы разделим числа на две группы: те, которые заканчиваются на 0, и те, которые не заканчиваются на 0.

Шаг 2: Выбор чисел для группы чисел, которые заканчиваются на 0

Для группы чисел, которые заканчиваются на 0, наименьшие возможные числа, которые могут быть подставлены, являются 4 и 6. Это связано с тем, что если заменить любое другое число на 4 или 6, то сумма квадратов чисел будет увеличена.

Шаг 3: Выбор чисел для группы чисел, которые не заканчиваются на 0

Для группы чисел, которые не заканчиваются на 0, наименьшие возможные числа, которые могут быть подставлены, являются 1, 3 и 8. Это связано с тем, что если заменить любое другое число на 1, 3 или 8, то сумма квадратов чисел будет увеличена.

Шаг 4: Сложение чисел

После выбора всех чисел, мы можем приступить к их сложению. В результате получим следующее выражение: 13_14_15_16_17_18_19_2_4_6.

Заменяя знаки «_» на выбранные числа, мы можем получить число 30.

Заключение

В данной статье мы рассмотрели математический трюк, который позволяет выбрать числа для наименьшей суммы их квадратов в задаче на число 30. Этот трюк может быть использован не только для этой задачи, но и для других задач, которые требуют минимизации суммы квадратов чисел.

Нужно найти наименьшое число, которое двумя существенно разными — т.е. не получающимися один из другого перестановкой слагаемых, способами представимо в виде суммы двух квадратов: 1) целых чисел; 2) натуральных чисел.

1) Для целых, наименьшее — два. Можно представить, как 1^2 + 1^2 и (-1)^2 + (-1)^2.

2) Для натуральных (без нуля), такого числа не существует.

Что может быть не так? Может, я неправильно понимаю условие?

I like this question. Fun brain-teaser.

I noticed your sample input was all integers in range(1, 100) with some repetition, so I generated sample lists like so:

>>> import random                                                           
>>> sample_list = [random.choice(range(1, 100)) for i in range(10)]         
>>> sample_list                                                             
[74, 68, 57, 18, 36, 8, 89, 73, 77, 80]

According to the problem statement, these numbers represent data measured at one-minute intervals, and one of our constraints is that our result must represent data gathered at least five minutes apart. Ultimately, that means the indices of the data in the original list must differ by at least five. In other words, for any two inputs v1 and v2:

abs(sample_list.index(v1) - sample_list.index(v2)) >= 5

must be true. We also know that we’re searching for the smallest sum, so it will be helpful to look at the smallest numbers first.

Thus, I started by mapping the values in the sample_list to the indices where they occur, then sorting them:

>>> occurrences = {}                                                        
>>> for index, value in enumerate(sample_list):                             
...   try:                                                                          
...     occurrences[value].append(index)                                        
...   except KeyError:                                                      
...     occurrences[value] = [index]                                        
...                                                                         
>>> occurrences                                                             
{80: [9], 18: [3], 68: [1], 73: [7], 89: [6], 8: [5], 57: [2], 74: [0], 77: [8], 36: [4]}
>>> sorted_occurrences = sorted(occurrences)
>>> sorted_occurrences
[8, 18, 36, 57, 68, 73, 74, 77, 80, 89]

After a whole lot of trial and error, here’s what I finally came up with in function form (including some of the earlier-discussed pieces):

def smallest_sum_of_squares_five_apart(sample):
    occurrences = {}
    for index, value in enumerate(sample):
        try:
            occurrences[value].append(index)
        except KeyError:
            occurrences[value] = [index]
    sorted_occurrences = sorted(occurrences)
    least_sum = 0
    for index, v1 in enumerate(sorted_occurrences):
        if least_sum and v1**2 > least_sum:
            return least_sum
        for v2 in sorted_occurrences[:index+1]:
            if (abs(max(occurrences[v1]) - min(occurrences[v2])) >= 5 or
                    abs(max(occurrences[v2]) - min(occurrences[v1])) >= 5):
                print('Found candidates:', str((v1, v2)))
                sum_of_squares = v1**2 + v2**2
                if not least_sum or sum_of_squares < least_sum:
                    least_sum = sum_of_squares
    return least_sum

The idea here is to:

• Start by looking at the smallest values first.
• Compare them one by one with all the values smaller, up to themselves.
• Check each against our criteria. Notice we do this by checking the extremes of each, where these two numbers occur the farthest away from one another in the original sample.
• Break out when checking becomes pointless.

Unfortunately, it is not sufficient to find the first one. Depending how the list is constructed, it will not always find the smallest pair first this way. In fact, it does not for your own sample input. However, once v1**2 (the square of the larger value) is larger than the sum, we know since all numbers are natural numbers it is pointless to continue looking.

I have included a full runnable implementation of this below. It takes a command line argument (default 10) indicating the number of items you want in the randomly generated sample. It will print the randomly generated sample as well as all candidate pairs it checked, and finally the sum itself. I have checked this on 10-sized inputs several times and it seems to be working in general. However, feedback is welcome if it is not correct. Note also you can uncomment your sample list from the question to see how it works (and that it gets the right answer) for it.

import random
import sys

def smallest_sum_of_squares_five_apart(sample):
    occurrences = {}
    for index, value in enumerate(sample):
        try:
            occurrences[value].append(index)
        except KeyError:
            occurrences[value] = [index]
    sorted_occurrences = sorted(occurrences)
    least_sum = 0
    for index, v1 in enumerate(sorted_occurrences):
        if least_sum and v1**2 > least_sum:
            return least_sum
        for v2 in sorted_occurrences[:index+1]:
            if (abs(max(occurrences[v1]) - min(occurrences[v2])) >= 5 or
                    abs(max(occurrences[v2]) - min(occurrences[v1])) >= 5):
                print('Found candidates:', str((v1, v2)))
                sum_of_squares = v1**2 + v2**2
                if not least_sum or sum_of_squares < least_sum:
                    least_sum = sum_of_squares
    return least_sum


if __name__ == '__main__':
    try:
        r = int(sys.argv[1])
    except IndexError:
        r = 10
    sample_list = [random.choice(range(1, 100)) for i in range(r)]
    #sample_list = [9, 12, 45, 5, 4, 21, 20, 10, 12, 26]
    print(sample_list)
    print(smallest_sum_of_squares_five_apart(sample_list))

Вася Иванов

Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.

8.2.4. Применение теоремы Виета

Часто требуется найти сумму квадратов (x₁ 2 +x₂ 2 ) или сумму кубов (x₁ 3 +x₂ 3 ) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:

Помочь в этом может теорема Виета:

Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Выразим через p и q:

1) сумму квадратов корней уравнения x 2 +px+q=0;

2) сумму кубов корней уравнения x 2 +px+q=0.

Решение.

1) Выражение x₁ 2 +x₂ 2 получится, если взвести в квадрат обе части равенства x₁+x₂=-p;

(x₁+x₂) 2 =(-p) 2 ; раскрываем скобки: x₁ 2 +2x₁x₂+ x₂ 2 =p 2 ; выражаем искомую сумму: x₁ 2 +x₂ 2 =p 2 -2x₁x₂=p 2 -2q. Мы получили полезное равенство: x₁ 2 +x₂ 2 =p 2 -2q.

2) Выражение x₁ 3 +x₂ 3 представим по формуле суммы кубов в виде:

Еще одно полезное равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q).

Примеры.

3) x 2 -3x-4=0. Не решая уравнение, вычислите значение выражения x₁ 2 +x₂ 2 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения

x₁+x₂=-p=3, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 1) равенство:

x₁ 2 +x₂ 2 =p 2 -2q. У нас -p=x₁+x₂=3 → p 2 =3 2 =9; q=x₁x₂=-4. Тогда x₁ 2 +x₂ 2 =9-2·(-4)=9+8=17.

4) x 2 -2x-4=0. Вычислить: x₁ 3 +x₂ 3 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения x₁+x₂=-p=2, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 2) равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q)=2·(2 2 -3·(-4))=2·(4+12)=2·16=32.

Ответ: x₁ 3 +x₂ 3 =32.

Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.

5) 2x 2 -5x-7=0. Не решая, вычислить: x₁ 2 +x₂ 2 .

Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x 2 -2,5x-3,5=0.

По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.

Решаем так же, как пример 3), используя равенство: x₁ 2 +x₂ 2 =p 2 -2q.

x₁ 2 +x₂ 2 =p 2 -2q=2,5 2 -2∙(-3,5)=6,25+7=13,25.

Ответ: x₁ 2 +x₂ 2 =13,25.

6) x 2 -5x-2=0. Найти:

Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x₁ 2 +x₂ 2 =p 2 -2q.

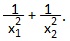
В нашем примере x₁+x₂=-p=5; x₁∙x₂=q=-2. Подставляем эти значения в полученную формулу:

7) x 2 -13x+36=0. Найти:

Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.

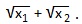
У нас x₁+x₂=-p=13; x₁∙x₂=q=36. Подставляем эти значения в выведенную формулу:

Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!

Квадратные уравнения и квадратичные неравенства с параметрами

Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.

Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.

1. Найдите все значения a, при которых уравнение не имеет действительных корней.

Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при равен нулю, оно станет линейным.

Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.

Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.

Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.

Если и – корни квадратного уравнения
, то по теореме Виета:

Решим первое неравенство системы

Квадратный трехчлен в левой части не имеет корней, так как дискриминант равен -32, то есть отрицателен. Поэтому неравенство будет выполняться для всех действительных значений .

Возведем второе уравнение системы в квадрат:

Из этих двух уравнений выразим сумму квадратов и .

Значит, сумму квадратов корней уравнения можно выразить через параметр

График функции — парабола, ее ветви направлены вверх, минимум будет достигаться в ее вершине. Найдем вершину параболы:

3) Найдите все значения , при каждом из которых все решения уравнения

Как и в первой задаче, уравнение является квадратным, кроме случая, когда . Рассмотрим этот случай отдельно

1) . Получим линейное уравнение

У него единственный корень, причем положительный. Это удовлетворяет условию задачи.

2) При уравнение будет квадратным. Нам надо, чтобы решения существовали, причем были положительными. Раз решения есть, то .

Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:

— Оба корня квадратного уравнения и положительны тогда и только тогда, когда их сумма положительна и произведение положительно.

Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.

— Оба корня квадратного уравнения и отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.

Корни квадратного уравнения и имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим

Второе и третье неравенства имеют одинаковое решение . Решение первого неравенства:
.

С учетом пункта 1 получим ответ

4. При каких значениях параметра a уравнение

имеет единственное решение?

Уравнение является показательным, причем однородным. Мы умеем решать такие уравнения! Разделим обе части на .

Сделаем замену

Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.

1) В случае уравнение будет линейным

Значит, подходит. В этом случае уравнение имеет единственный положительный корень.

2) Если , уравнение будет квадратным.

Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.

Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.

Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.

Объединив все случаи, получим ответ.

И наконец – реальная задача ЕГЭ.

5. При каких значениях a система имеет единственное решение?

Решением квадратного неравенства может быть:

В каких случаях система двух квадратных неравенств имеет единственное решение:

1) единственная общая точка двух лучей-решений ( или интервалов-решений)

2) одно из неравенств имеет решение – точку, которая является решением второго неравенства

Рассмотрим первый случай.

Если является решением 1 и 2 уравнений, то является решением уравнения (вытекает из второго первое) ⇒ или

Если , при этом система примет вид:

Второй корень первого уравнения:

Второй корень второго первого:

Если , при этом система примет вид:

– бесконечно много решений, не подходит.

Рассмотрим второй случай.

– решением является точка, если – является решением второго неравенства.

– решением является точка, если – не является решением первого неравенства.

при каком значение m сумма квадратов корней уравнения x^2 + ( 2- m)*x — m — 3 = 0 наименьшая? помогите плиз. помогите

Дискриминант:
D = (2-m)^2-4(-m-3) = m^2+16
Корни уравнения
Х1 = (-(2-m) + √D)/2
Х2 = (-(2-m) — √D)/2
Сумма корней:
Х1^2 + Х2^2 = (-(2-m) + √D)/2)^2 + ((-(2-m) — √D)/2)^2
Подставим значение дискриминанта и упростим:
Х1^2 + Х2^2 = m^2 — 2m+10
Рассмотрим сумму квадратов как функцию от m. Производная функции по m:
(Х1^2 + Х2^2)’ = (m^2 — 2m+10)’ = 2m-2
2m-2 = 0
m = 1
Можно конечно еще проверить, подставляя значения, но эту радость я оставляю вам
Минимально значение суммы квадратов корней будет при m = 1, и равно оно 9