Как найти наименьшую температуру по графику

22
Дек 2011

Задание 02 (2016)

|
Отзывов нет
| Метки: решение задания В2

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

В этой статье представлено ещё несколько заданий с диаграммами. Речь пойдёт о среднемесячной температуре, вопросы ставятся различные. Задачки эти справедливо можно отнести к самым простым, которые входят в состав экзамена. Но требуется внимательность. Отмечу два момента:

1. Сразу обращайте внимание на цену деления, она не всегда равна единице.
2. Акцентируйте внимание на такие слова в задачах как «наибольшую», «наименьшую», «превышала», «НЕ превышала».

Повторюсь, что ошибиться можно только из-за невнимательности. Рассмотрим задачи:

27511. На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.

Обратите внимание, что цена деления шкалы «температура» равна 2 градусам. Наименьшая среднемесячная температура была в феврале (2-ой месяц) и составила  –14 градусов Цельсия.

Ответ: –14

27512. Показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2003 году. Ответ дайте в градусах Цельсия.

*Цена деления шкалы «температура» равна 2 градусам.

Наибольшая среднемесячная температура была в июле (7-ой месяц) и составила 20  градусов Цельсия.

Ответ: 20

27513. Показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1973 году. Ответ дайте в градусах Цельсия.

Цена деления шкалы «температура» равна 2 градусам.

Наибольшая среднемесячная температура была в июне (6-ой месяц) и составила   18  градусов Цельсия, наименьшая была в январе (1-ый месяц) и составила  –20  градусов Цельсия. Разность составляет 18–(–20) =18+20 = 38 градусов.

Ответ: 38

27516. Показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру во второй половине 1999 года. Ответ дайте в градусах Цельсия.

*Цена деления шкалы «температура» равна 2 градусам. Наименьшую среднемесячную температуру нужно определить с июля до конца года (в условии сказано, что во второй половине года). Указанная температура была в декабре (12-ый месяц) и составила  –2 градуса Цельсия.

Ответ: ­–2

27518. Показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру во второй половине 1973 года. Ответ дайте в градусах Цельсия.

*Цена деления шкалы «температура» равна 2 градусам. Наибольшую среднемесячную температуру нужно определить с июля до конца года (так как в условии сказано, что во второй половине года). Она была в августе (8-ой месяц) и составила 16 градусов  Цельсия.

Ответ: 16

27519. Показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали  — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с положительной среднемесячной температурой.

Необходимо определить количество месяцев с положительной среднемесячной температурой. По графику видно, что положительная температура была с 4-го по 10-ый месяцы, всего это 7 месяцев.

Ответ: 7       

27520. Показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали  — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура была отрицательной.

Необходимо определить количество месяцев с отрицательной среднемесячной температурой. Такая температура была с 1-го по 3-ий месяцы (это январь, февраль, март) и в декабре, всего  4 месяца.

Ответ: 4

27521. Показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура превышала 20 градусов Цельсия.

По графику видно, что среднемесячная температура превышала двадцать градусов Цельсия в 7-ом и 8-ом месяцах (июль и август). То есть всего 2 месяца.

Ответ: 2

27522. Показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура не превышала 4 градусов Цельсия.

Здесь можно ошибиться из-за невнимательности. Обратите внимание на слово «НЕ превышала», частицу не можно и не заметить. Среднемесячная температура не превышала 4 градусов Цельсия в первом, втором, третьем, одиннадцатом и двенадцатом месяцах (это январь, февраль, март, ноябрь, декабрь). Всего их пять.

Ответ: 5

На этом всё. Успеха Вам!

С уважением, Александр Крутицких.

В школе на выпускном подрались физрук и трудовик. Победил трудовик, потому что каратэ — это каратэ, а топор — это топор.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

17 февраля 2011

Пожалуй, самая простая задача из всех, которые встречаются в ЕГЭ. В ней проверяется умение интерпретировать графики, извлекать из них простейшую числовую информацию и делать необходимые выводы.

В задаче B3 используются данные, полученные в результате реальных измерений, наблюдений и опытов. Эти данные представлены в форме графиков, которые условно делятся на два типа:

1. Непрерывные, в которых значение функции определено для каждой точки графика. Как правило, такие графики представляют собой плавные линии, описывающие постоянно меняющееся значение функции. Наиболее типичный пример — график изменения температуры.
2. Дискретные, где функция определена лишь для конечного числа точек. В остальных точках функция не существует. Для наглядности эти точки могут быть соединены или представлены в виде столбцов.

Правильное определение типа графика позволит избежать классических ошибок при решении задания B3. Например, довольно часто на дискретных графиках рассматриваются лишние точки, которые не являются значениями функции.

Задача. Определить тип графиков, представленных на рисунке:

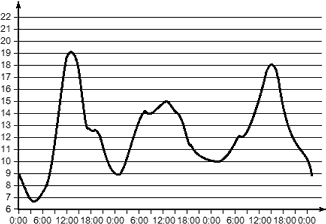
1. Изменение температуры за три дня, начиная с 0:00.
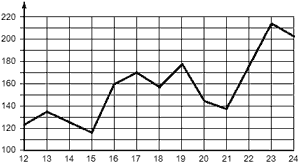
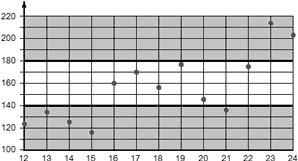
2. Количество изготовленных на станке деталей по дням, с 12 по 24 сентября.

Очевидно, первый график является непрерывным, т.к. в любой момент времени, отмеченный на горизонтальной оси, мы можем определить значение функции. И неважно, что это определение будет довольно приблизительным.

Второй график является дискретным, поскольку количество деталей можно определить лишь для нескольких конкретных дней. Например, 16 сентября было изготовлено 160 деталей, 17 сентября — 170, но любое значение между 16 и 17 сентября не имеет никакого смысла — точки соединены исключительно для наглядности.

Непрерывные графики

Работа с непрерывными графиками, как правило, не вызывает затруднений, поскольку существует эффективный метод решения таких задач: отсечь ненужную информацию.

Например, очень часто встречаются задачи, где требуется определить максимальное или минимальное значение температуры в заданный день. При этом на графике показано изменение температуры в течение сразу нескольких дней.

Чтобы решить подобную задачу, сначала необходимо удалить с графика все, что не относится к рассматриваемому дню. Например, закрыть рукой, линейкой или листом бумаги. Только не зачеркиваете график ручкой — в случае ошибки восстановить его первоначальный вид не получится!

Затем на оставшейся части графика выбираем требуемую точку. Минимальное значение достигается в нижней точке графика, а максимальное — наоборот, в самой высокой.

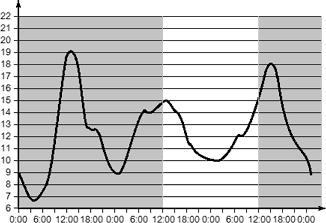
Задача. На графике показано изменение температуры воздуха в течение трех суток, начиная со вторника, 0:00. Определите, до какой наибольшей температуры прогрелся воздух в среду.

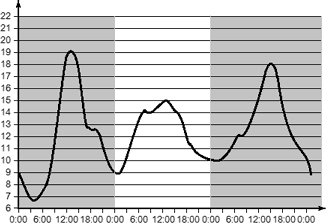
Для начала отсечем всю лишнюю информацию. Нас интересует только среда. Учитывая, что график начинается со вторника, закрасим серым цветом лишние дни:

На оставшейся части графика надо отыскать наибольшую температуру. Очевидно, она равна 15 °C — такое значение достигается ближе к середине дня.

Некоторые преподаватели предлагают довольно эффективный способ поиска максимального и минимального значения на участке графика, который остается после отсечения ненужной информации. Для поиска минимального значения надо приложить горизонтальную полоску бумаги к нижней части картинки и двигать ее вверх до тех пор, пока полоска не пересечет график. Аналогично, для поиска максимального значения надо приложить полоску сверху и двигать вниз.

Дискретные графики

Но как решать задачу B3, если в ней встретился дискретный график? Для начала надо избавиться от соединительных линий, если они есть. Помните: дискретный график — это просто набор точек, остальная информация только мешает решению задачи.

Задача. На дискретном графике показано количество изготовленных на станке деталей в период 12—24 сентября. Очистить этот график от лишней информации.

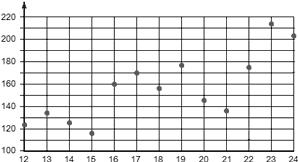
Очевидно, значимой информацией являются только точки, лежащие на вертикальных линиях разметки. Они показывают, сколько деталей было изготовлено в конкретный день. Например, 17 сентября было изготовлено 170 деталей. Уберем отрезки, соединяющие эти точки, и получим следующую картинку:

Обратите внимание на крайние точки графика: в самом начале (12 сентября) и конце (24 сентября). Многие забывают про них, однако на исходном графике эти точки были, и поэтому должны учитываться в решении.

Когда на графике останется только нужная информация, можно решать саму задачу. Здесь применяется уже знакомый метод отсечения, который для дискретных графиков имеет две формы:

1. Вертикальное — указание диапазона точек, которые будут участвовать в решении. Например, если нас интересует только период с 16 до 20 сентября, то все другие точки надо «удалить». Этот прием аналогичен отсечению ненужной информации для непрерывных графиков.
2. Горизонтальное — указание требуемого диапазона значений. Аналога в непрерывных графиках не имеет. Ограничения могут накладываться снизу, сверху или с обеих сторон. Точки, выпадающие из диапазона, не участвуют в дальнейшем решении.

Например, выясним по графику, приведенному выше, сколько раз на станке изготавливалось больше 150 деталей в день. Очевидно, требование «больше 150» — это ограничение снизу. Проведем горизонтальную черту на уровне 150 деталей и удалим все точки, которые оказались ниже. Остальные точки можно легко подсчитать — читателю предлагается сделать это в качестве упражнения.

Задача. На графике показано деталей, изготовленных на станке, в период 12—24 сентября. Определите, сколько раз на станке изготавливалось от 140 до 180 деталей в день.

Уберем отрезки, соединяющие отдельные точки, поскольку это лишняя информация. Затем проведем горизонтальное отсечение, для чего установим границы на уровнях 140 и 180 деталей. Нас интересует только то, что находится между этими границами. Получим следующую картинку:

Все, что выпадает из диапазона, закрашено серым цветом. Осталось лишь подсчитать количество «правильных» точек — очевидно, их шесть.

Дополнительные соображения

Условие задачи B3 с дискретным графиком всегда нужно понимать буквально. Если требуется найти, сколько раз значение функции находилось «в пределах от 2 до 7», то следует учитывать все числа из отрезка [2, 7]. Обратите внимание: границы отрезка, т.е. числа 2 и 7, тоже учитываются! Игнорирование это факта — очень частая ошибка на экзамене.

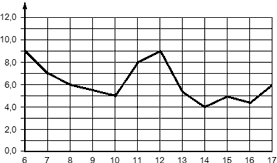
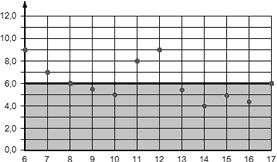
Задача. На рисунке изображен график среднесуточной температуры в Саратове в период с 6 по 17 октября 1969 г. На оси абсцисс откладываются числа, на оси ординат — температура в градусах Цельсия. Определить по графику, сколько дней из указанного периода средняя температура была не ниже 6,0 °C.

Очевидно, это дискретный график. Избавимся от ненужной информации, убрав все соединительные линии. На полученном наборе точек выполним горизонтальное отсечение, проведя черту на уровне 6,0 °C. Все, что ниже этой границы, нас не интересует, поэтому закрашено серым цветом. Имеем:

Подсчитаем точки, попадающие в диапазон — их оказалось шесть. Обратите внимание, что 8 и 17 октября температура равна 6 °C. Эти дни тоже учитываются в итоговом расчете.

Еще раз напомним, что B3 — это самая простая задача ЕГЭ по математике. В ней проверяется умение извлекать из графика и обрабатывать числовую информацию. Требуются именно практические навыки, а не умение работать с формальными теоретическими построениями.

В этих задачах нет сложных и двусмысленных формулировок. Если требуется определить наивысшую точку графика, такая точка будет только одна. А если, например, просят найти минимальную ночную температуру, то по графику будет видно, что самая низкая температура была именно ночью. Не придется размышлять о том, когда именно заканчивается ночь и начинается день.

Задача. На графике показано изменение температуры воздуха на протяжении трех суток, начиная с 0 часов вторника. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах. Определите по графику наименьшую температуру воздуха в ночь со среды на четверг.

Это непрерывный график. Для решения задачи необходимо отбросить всю лишнюю информацию, проведя вертикальные границы. Проблема в том, что фраза «ночь со среды на четверг» не дает четких границ.

Попробуем установить эти границы. Так, 12:00 среды — это точно еще не ночь, а 12:00 четверга — это уже не ночь. Чем ближе мы подходим к указанным моментам, тем выше температура. Очевидно, в этой задаче 12:00 среды и 12:00 четверга могут служить вертикальными границами. Проведем их и получим следующую картинку:

То, что закрашено серым цветом, нас не интересует. На оставшейся части графика минимальная температура равна 10 °C. Это значение достигается как раз ночью — примерно в 0:00 — и поэтому является ответом.

Смотрите также:

1. Введение системы координат
2. Тест к уроку «Десятичные дроби» (2 вариант)
3. Типичные задачи B12 с функциями
4. Координаты вершин правильного тетраэдра