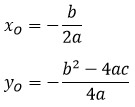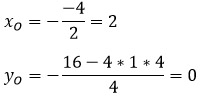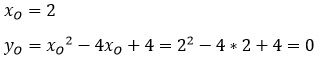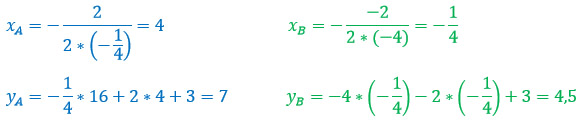|
Какое уравнение наклонит ось параболы?smog2605 7 лет назад
il63 ах2 + bху + cy2 + dx + ey + f = 0. Тогда ось может быть не параллельна осям координат.
Грустный Роджер 6 лет назад Если уравнение «ровной» параболы выглядит как y = x² (поскольку интересует именно наклон параболы, то сдвиг её по обеим осям будем считать нулевым), то для того, чтобы её наклонить, можно взять повёрнутую систему координат, то есть положить x’ = x cosφ — y sinφ, y’ = y cosφ -x sinφ, где φ — произвольный угол. Тогда в координатах x’, y’ парабола будет наклонена, и составить вид уравнения в такой преобразованной системе координат не штука. автор вопроса выбрал этот ответ лучшим комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Download Article
Download Article
If you’ve ever cooked food with a parabolic oven in science class or seen the Death Star’s laser in Star Wars, you have an idea of what the focal point (or focus) of a parabola is. But how do you calculate the focus mathematically? We’ve provided the formulas and equations you need to find the focus of any parabola, and added several helpful sample problems that you might see on your next algebra exam!
Things You Should Know
-
1
Parabola: A parabola can be defined as the graph of a quadratic equation—that is, the curved line you’ll get if you plot the equation on graph paper. Or, if you want to be more technical, it’s a curved line in which all coordinate points
along the line are equidistant from a specific focal point and a specific line called a directrix.[1]
- In practical terms, it’s often easier to recognize parabolas in three dimensions. For example, think of large parabolic satellite dishes, or the clear plastic parabolic microphones you see on the sidelines of football games. Both of these direct waves (radio, sound, etc.) toward a single point—the focal point (or focus).
-
2
Vertex: The vertex is the “turning point” of a parabola—the point along the curve at which it changes direction. So, in a classic “U”-shaped parabola, the vertex is at the very bottom of the “U” shape. You need to know the
coordinates of the vertex in order to find the coordinates of the focus.[2]
Advertisement
-
3
Axis of symmetry: The axis of symmetry is a line that runs through the vertex point and divides the parabola exactly in half. The parabola is a mirror image of itself on either side of the axis of symmetry.[3]
- For our needs, it’s also important that the vertex is always exactly halfway between the focus and the directrix along the axis of symmetry.
-
4
Directrix: The directrix is a straight line that crosses the axis of symmetry and is perpendicular to it. The directrix is always outside of the parabola but closest to the vertex. For example, in a classic “U” parabola, adding the directrix line makes it look like you underlined the «U.»[4]
- The distance between the vertex and the directrix (at the axis of symmetry) is always exactly the same as that between the vertex and the focus.
-
5
Focus: The focus is a point along the axis of symmetry, inside the parabola, that is equal in distance from the vertex as is the directrix. So, if the directrix is 2 units away from the vertex, the focus is also 2 units away (and, as a result, 4 units away from the directrix).[5]
- If you draw a straight line from the focus to any point along the curve of the parabola, and then draw a straight line from that point to intersect at a right angle with the directrix, you’ll find that both of those lines are always equal in length.
Advertisement
-
1
or
. You’ll use one of these “vertex form of a parabola” equations based on the type of parabola you’re dealing with. A “regular” parabola that opens upward or downward (like a right-side up or upside-down “U”) needs to be converted into the form of the first equation, while a “sideways” parabola that opens to the side (like a forwards or backwards “C”) must be converted to the second.[6]
-
2
or
. Once you have determined (or have been given) the coordinates of the parabola’s vertex, you’ll use one of these formulas to determine the coordinates of the focus. Here’s how to know which to use:[7]
Advertisement
-
1
Put the equation into the vertex form of a parabola. Because the
portion of the equation is squared, the correct vertex form is
, meaning this is a “regular” parabola (it opens either up or down).
-
2
-
3
Solve for
to find the focus coordinates.
Advertisement
-
1
-
2
-
3
-
4
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
References
About This Article
Thanks to all authors for creating a page that has been read 3,648 times.
Did this article help you?
Get all the best how-tos!
Sign up for wikiHow’s weekly email newsletter
Subscribe
You’re all set!
Математика для инженеров — Ординаты и углы наклона касательных дуг параболы, окружности, эллипса
Вернуться на страницу «Математика для инженера»
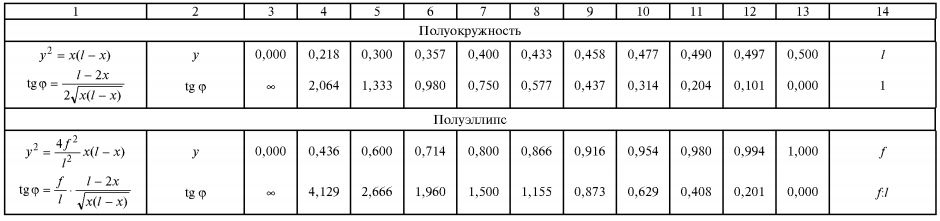
Ординаты и углы наклона касательных дуг параболы, окружности, эллипса
Общие сведения.
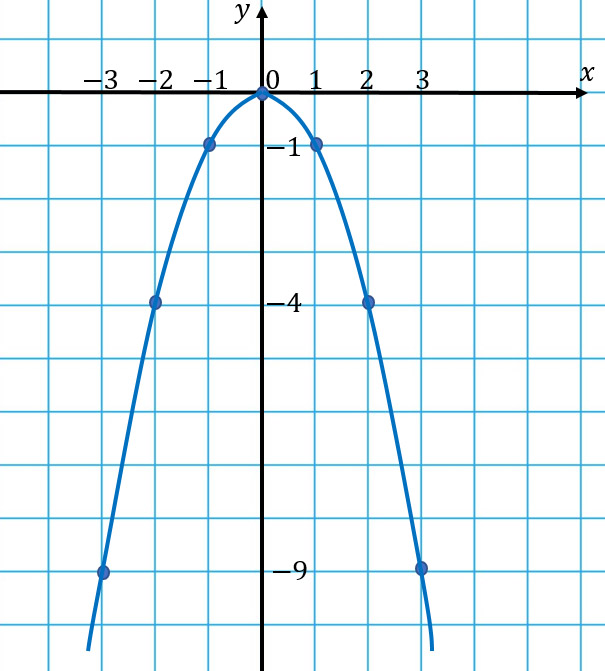
На координатной плоскости отмечаем эти точки и чертим параболу.
Вершина этой параболы находится в точке (0; 0). И не забудь про то, что ветви параболы бесконечно поднимаются ввысь и не ограничены точками с координатами (3; 9) и (3; -9).
Еще одна стандартная парабола задается функцией y = —x2 (в этом случае а = -1). Для этого графика я тоже напишу табличку:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -9 | -4 | -1 | 0 | -1 | -4 | -9 |
Начало координат тоже является вершиной этой параболы, как и в предыдущем случае, но ветви уже будут направлены вниз:
Сразу напрашивается вывод: если перед х2 стоит положительное число, то ветви параболы направлены вверх, если отрицательное — то вниз.
Если у тебя черный пояс по рисованию стандартных парабол, то следующий раздел пройдет у тебя «на ура».
Параболы со смещенной вершиной.
Зачем я начала статью со стандартной параболы? Ответ прост. Графиком любой квадратичной функции y = ±x2 + bx + c (обязательно коэффициент перед х2 должен равняться ±1) является стандартной параболой, только вот вершины этих парабол не будут находится в начале координат.
Чтобы начертить подобные параболы нужно сначала узнать, где находится вершина.
Пусть вершиной параболы будет точка О с координатами (x1; y1). Тогда найти эти координаты можно по формулам:
Кстати, можно найти координаты вершины и другим способом.
Координату хО находим по той же формуле, а координату уО можно найти подстановкой координаты хО в функцию.
Без примера не обойтись)
Пример 1.
Дана функция y = x2 — 4x + 4. Найдите вершину параболы и постройте график.
Найдем сначала вершину параболы двумя способами, чтобы убедится, что оба способа рабочие.
1 способ: по формулам.
2 способ: подстановкой.
Одну координаты мы уже нашли по формуле. Подставляем ее в исходную функцию.
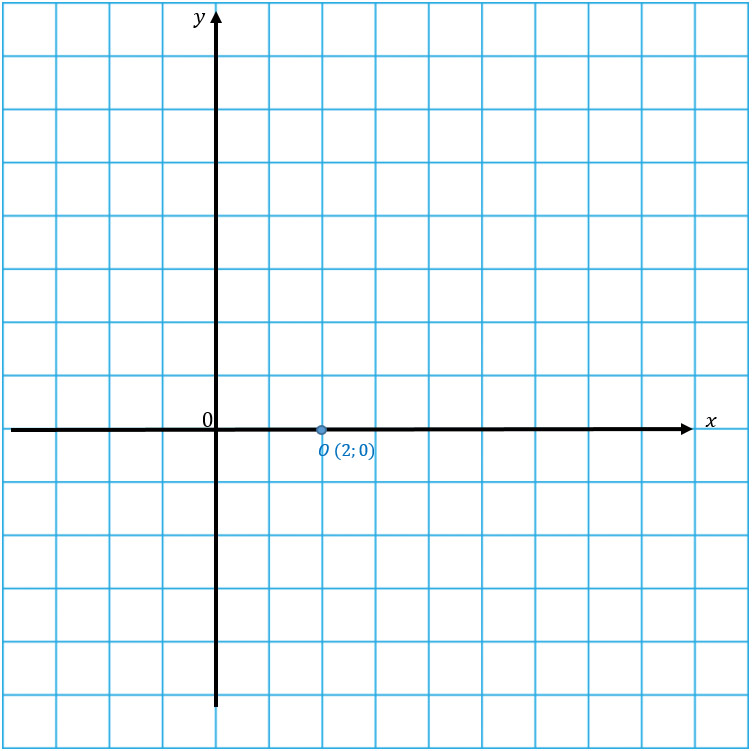
Итак, получили, что О(2; 0) — вершина параболы. Отмечаем ее на координатной плоскости.
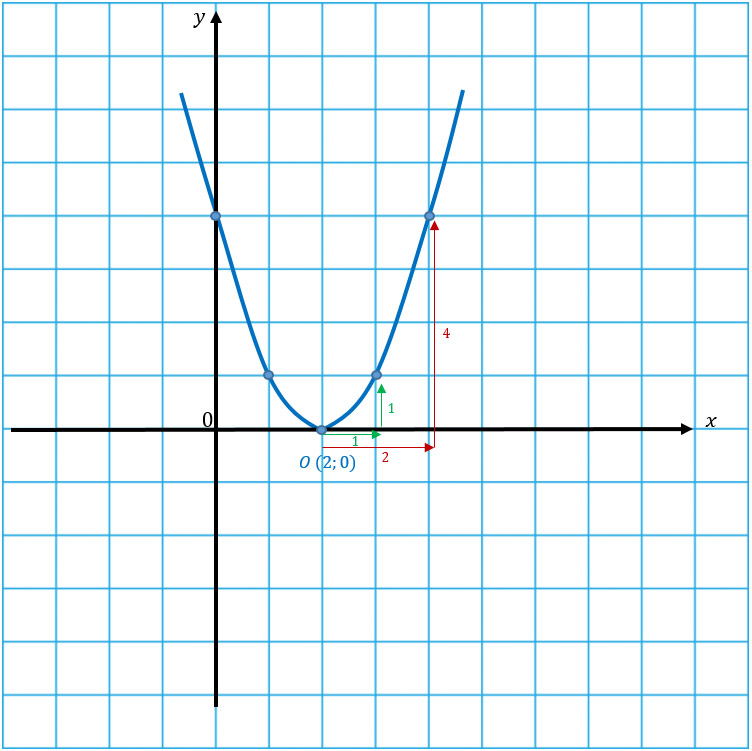
Перед х2 стоит положительное число, значит ветви параболы направлены вверх. Наша задача: нарисовать стандартную параболу, представив, что точка О — начало координат. Если тебе это сложно сделать, то необходимо начертить таблицу значений и уже по ней рисовать параболу.
Параболы-стройняшки и параболы-пухляшки.
Удивительно, но числовой коэффициент перед х2 оказывается влияет на стройность и полноту парабол.
Если числовой коэффициент лежит в промежутке (-1; 0) ∪ (0; 1), то парабола будет более обширно смотреться на координатной плоскости.
А если числовой коэффициент лежит в промежутке (-∞; -1) ∪ (1; +∞), то парабола будет прижиматься к оси Оу и занимать меньше места на плоскости.
Не веришь? Давай проверим! Для примера возьмем две функции:
К сожалению, здесь схитрить не получится: обе параболы нестандартные и для обеих необходимо создать таблицы значений. Но перед эти определимся с их вершинами.
Пусть вершиной первой параболы будет точка А(хА; уА), а вершиной второй параболы — точка B(хB; уB). Вершины буду находить по второму способу (см. выше).
Переходим к таблицам значений.
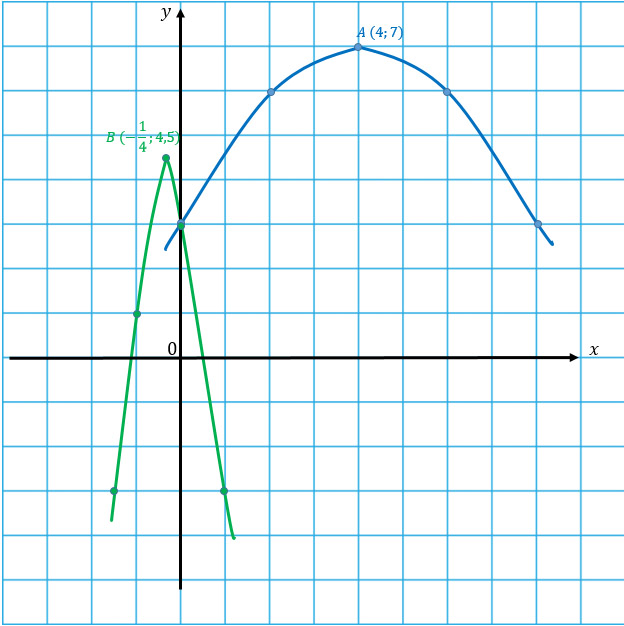
Голубая парабола.
| x | 0 | 2 | 4 | 6 | 8 |
| y | 3 | 6 | 7 | 6 | 3 |
Зеленая парабола.
| x | -1,5 | -1 | -0,25 | 0 | 1 |
| y | -3 | 1 | 4,5 | 3 | -3 |
Чертим обе параболы по получившимся координатам.
Вот о чем я и говорила) Перед тобой парабола-стройняшка и парабола-пухляшка во всей красе.
А ты заметил, что свободный член в уравнении функции — это точка пересечения графика с осью Оу? В обеих функциях свободный член равен 3 и графики пересекают ось Оу в точке с координатами (0; 3).
Практикум по параболам.
Теорию о параболах можно еще писать и дальше, но тебя, скорее всего, интересует практика по графикам.
Поскольку речь идет о параболах, то с параболами мы и будем сейчас возиться.
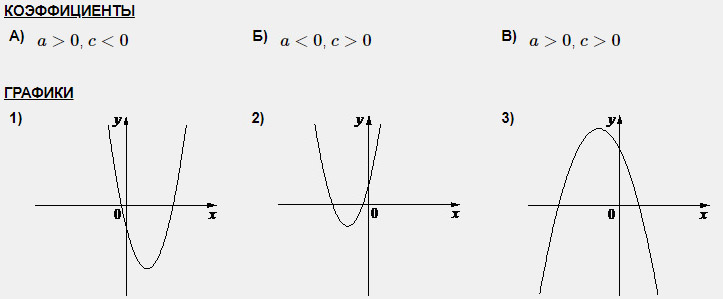
Задание 1. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
Решение. Коэффициент а, стоящий перед х2, отвечает за направление ветвей параболы, а свободный член с — за пересечение графика с осью Оу.
А) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с отрицателен, то график пересекает ось Оу ниже нуля. Подходит график 1.
Б) Если коэффициент а отрицателен, то ветви направлены вниз; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 3.
В) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 2.
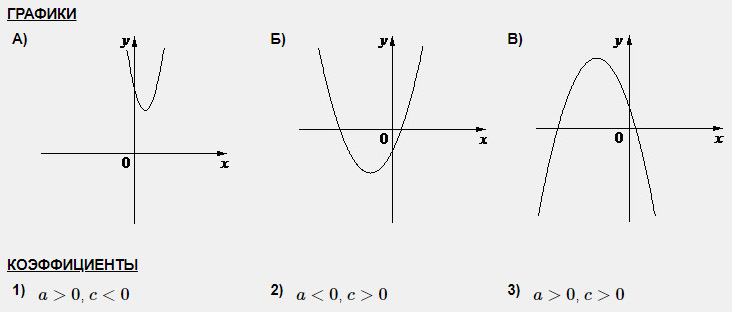
Задание 2 (наоборот). На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Ветви направлены вверх, значит а > 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 3.
Б) Ветви направлены вверх, значит а > 0; график пересекает ось Оу ниже нуля, значит и с < 0. Подходит вариант под номером 1.
В) Ветви направлены вниз, значит а < 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 2.
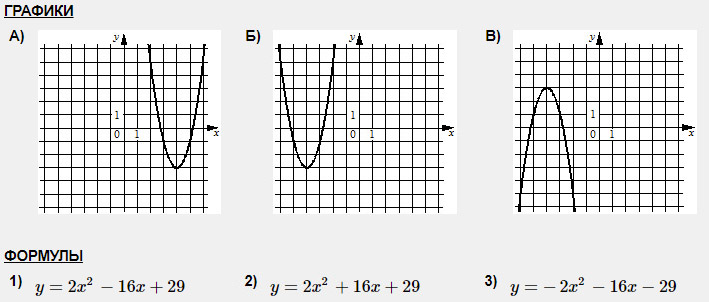
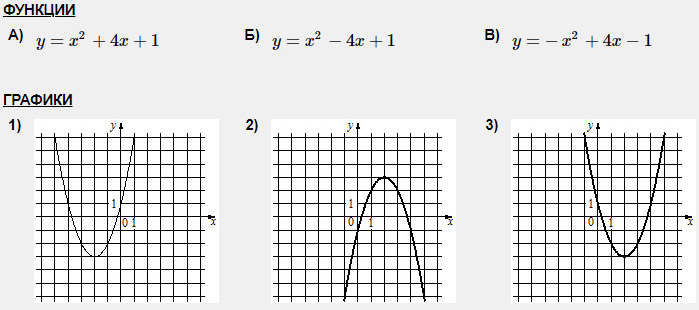
Задание 3. Установите соответствие между графиками и их функциями.
График В отличается от остальных тем, что его ветви направлены вниз. За направление ветвей отвечает коэффициент перед х2 — он отрицательный. Отрицательный коэффициент только в функции под номером 3. Значит В-3.
Дальше рекомендую отработанную годами технику. Она минимизирует твои ошибки, если ты, конечно, умеешь считать)
Итак, рассматриваем график А и выбираем на нем точку с красивыми координатами (красивые значит не дробные). Мне нравится тут вершина. Ее координаты (4; -3). Даже не спрашивайте почему не прорисованы оси; эти задания взяты с сайта ФИПИ)
Теперь эти координаты подставляем в оставшиеся функции: вместо у подставляем -3, а вместо х подставляем 4.
Подставляем в первую функцию: -3 = 2 · 42 — 16 · 4 + 29; -3 = -3 — верно. Значит, А-1.
И остается Б-2.
Задание 4 (наоборот, но принципе тот же). Установите соответствие между функциями и их графиками.
Очевидно, что В-2.
На графике 1 выбираем точку. Вершина снова четкая, но для разнообразия давайте возьмем другую точку, например, точку с координатами (-4; 1). Будь внимателен и смотри, чтобы точно такой же точки не было на третьем графике!
Подставляем в функцию А: 1 = (-4)2 + 4 · (-4) + 1; 1 = 1 — верно. Значит, А-1.
Соответственно, Б-3.
Если ты считаешь, что чего-то не хватает или у тебя есть ещё задания из первой части, связанные с параболами, — напиши мне в VK)
Парабола в математике: уравнение, построение, виды
Содержание:
- Что такое парабола в математике
-
Алгоритм построения параболы
- Примеры решения задач на построение параболы
- Смещение параболы
Что такое парабола в математике
Парабола — график квадратичной функции вида (f(x)=ax^2+bx+c). Состоит данный график из вершины и ветвей.
При этом (aneq0), иначе функция уже будет не квадратичной, а линейной.
Формула параболы может рассказать нам о многом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Коэффициент (a) говорит о направлении ветвей параболы. Если (а>0), то ветви смотрят вверх, если (а<0), вниз.
- От параметра (b) зависит вершина параболы. Она рассчитывается по формуле: (x_в=frac{-b}{2a})
- Свободный член (с) отвечает за пересечение параболы с осью (y).
Алгоритм построения параболы
Построим график функции (f(x)=ax^2+bx+c.)
- Определим куда смотрят ветви параболы.
- Найдем вершину по формуле (x_в=frac{-b}{2a}). Подставим (x_в) в формулу функции и получим значение (y_в). Таким образом мы имеем обе координаты вершины. Нанесем их на систему координат.
- Найдем точку пересечения с осью y по параметру с и нанесем на чертеж точку, симметричную ей, относительно оси симметрии параболы, т.е. прямой (y=frac{-b}{2a}.)
- Далее решаем уравнение (ax^2+bx+c=0). Получаем корни — они являются точками пересечения параболы с осью (x). Если они рациональны, наносим их на чертеж, в обратном случае, они не пригодятся.
- Затем считаем значения функции в дополнительных симметричных точках и соединяем все найденные точки.
Примеры решения задач на построение параболы
Смещение параболы
Свободный член с смещает параболу по оси y. Например, если c=2, то парабола f(x)=ax^2+bx сместится вверх на 2 единичных отрезка, а если с=-2, то график сместится вниз так же на 2 единичных отрезка.
В случае, когда к аргументу x прибавляется или вычитается какое-либо число, график смещается по оси x. Например, для построения графика функции (y={(x+4)}^2) достаточно сместить график (y=x^2 )на 4 единичных отрезка влево, а для построения графика (y={(x-3)}^2) нужно сместить график (y=x^2) на 3 единичных отрезка вправо.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так