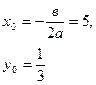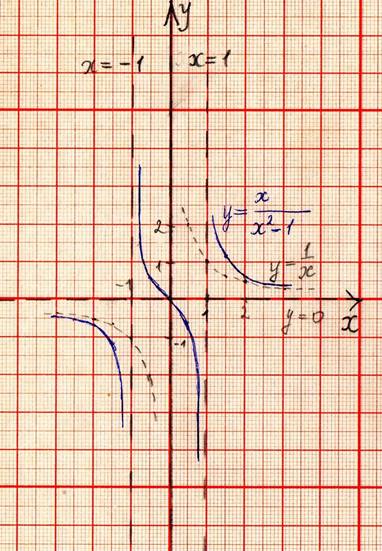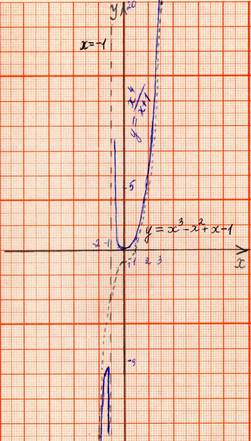Содержание:
Понятие асимптоты:
Асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
Вертикальные асимптоты

Вертикальная асимптота 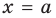
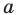
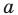
Примеры вертикальных асимптот графиков функций
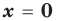
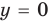
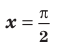
Наклонные и горизонтальные асимптоты
I. Если 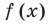
Примеры:
При 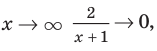
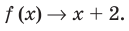
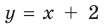
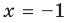
При 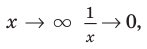
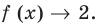
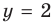
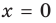
II. В общем случае уравнения наклонных и горизонтальных асимптот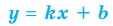
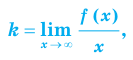
Понятие асимптоты
Если кривая 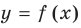
Асимптоты могут быть вертикальными, горизонтальными или наклонными.
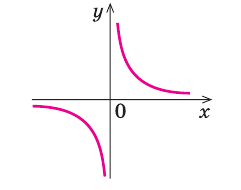
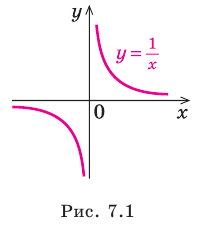
Например, для графика функции 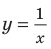
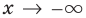
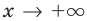
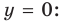
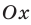
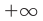
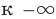
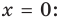
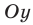
Если рассмотреть функцию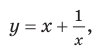
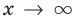
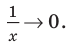
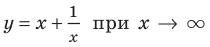
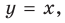
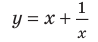
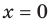
Следует отметить, что не любая кривая имеет асимптоту, поэтому не у каждого графика функции будет асимптота. Но исследование функции на наличие у ее графика асимптот позволяет уточнить свойства функции и поведение ее графика.
Вертикальные асимптоты
Если прямая 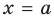
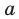

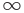
Например, у функции 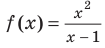
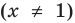

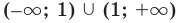

Аналогично
Таким образом, прямая 

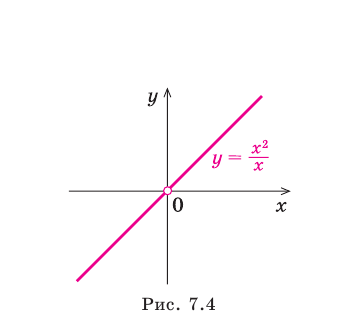
Отметим, что не всегда в точке разрыва области определения функция будет иметь вертикальную асимптоту. Например, функция 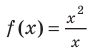
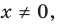
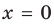
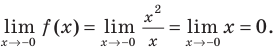
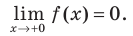
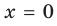
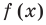
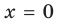
Наклонные и горизонтальные асимптоты
Наклонные и горизонтальные асимптоты довольно просто находятся для графиков дробно-рациональных функций, у которых степень числителя на единицу больше степени знаменателя (или равна степени знаменателя). Для этого достаточно выделить целую часть заданной дроби и использовать определение асимптоты.
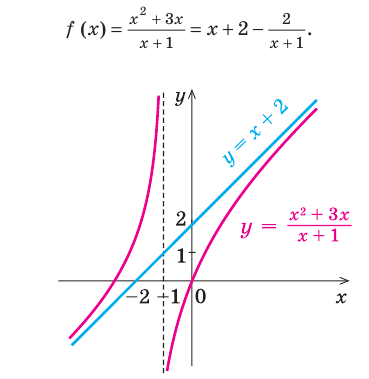
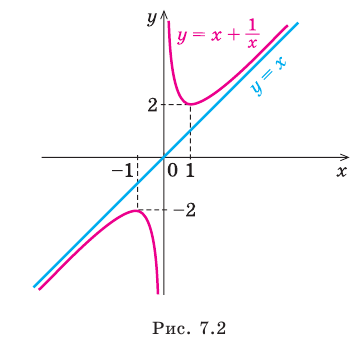
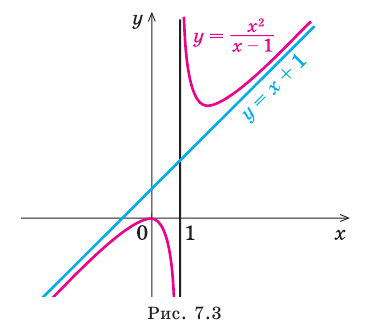
Например, еще раз рассмотрим функцию 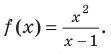
При 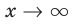
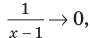
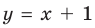
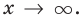
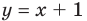
Рассмотрим, как находятся наклонные и горизонтальные асимптоты в общем случае.
Пусть наклонной (или горизонтальной) асимптотой графика функции 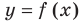

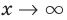
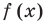
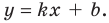
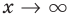
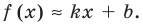
Эта равенство не нарушится, если обе его части разделить на 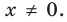
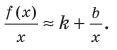
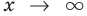
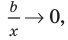
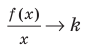
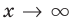
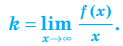
Возвращаясь к формуле (1), получаем, что при 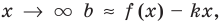
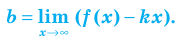
Формулы (2) и (3) дают возможность находить наклонные и горизонтальные асимптоты для графика любой функции 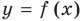
Отметим, что если у графика функции 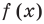
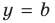
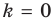
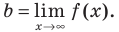
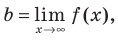
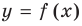
- Заказать решение задач по высшей математике
Пример:
Пользуясь общими формулами, найдите наклонную асимптоту графика функции
Решение:
Будем искать наклонную асимптоту в виде 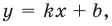
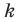
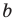
Асимптотой графика данной функции будет прямая 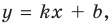
Пример:
Найдите асимптоты графика функции
Решение:
Область определения функции: 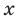
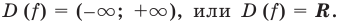
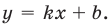
Таким образом, заданная функция имеет только горизонтальную асимптоту 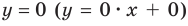
Иногда график функции 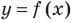
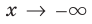
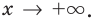
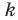
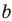
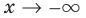
Как найти асимптоты графика функции
При исследовании поведения функции на бесконечности или вблизи точек разрыва часто оказывается, что расстояние между точками графика функции и точками некоторой прямой стремится к нулю при неограниченном удалении точек графика от начала координат. Прямая, к которой стремится кривая в бесконечно удаленной точке, называется асимптотой графика. Различают вертикальные и наклонные асимптоты. Прямая 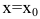
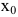
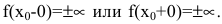
Внимание! Непрерывные на множестве действительных чисел функции вертикальных асимптот на имеют.
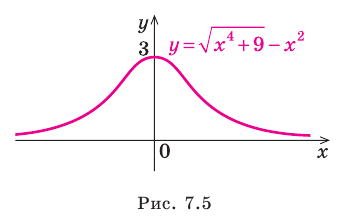
Для того чтобы график функции y=f(x) имел наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы
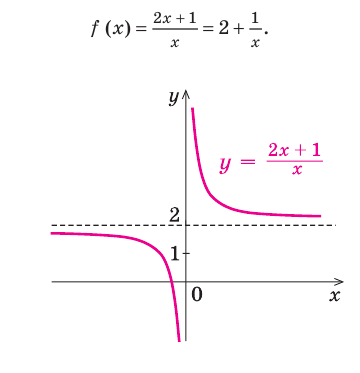
Частным случаем наклонной асимптоты (k=0) является горизонтальная асимптота.
Пример:
Найти асимптоты графика функции
Решение:
Функция 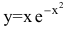
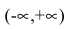
Получаем горизонтальную асимптоту y=0.
Общее исследование функции и построение графика
С помощью производной функции можно провести ее полное исследование и построить график этой функции. При этом рекомендуется использовать следующую схему.
- Найти область определения функции D(f).
- Исследовать функцию на четность
нечетность
периодичность
- Исследовать функцию на непрерывность, найти точки разрыва.
- Найти асимптоты графика функции.
- Исследовать функцию на монотонность, найти точки экстремума.
- Найти интервалы выпуклости и вогнутости, точки перегиба функции.
- Используя результаты проведенного исследования, построить график функции (можно вычислить координаты точек пересечения с осями координат).
Пример:
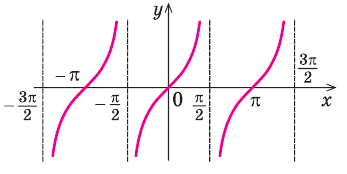
Провести полное исследование функции 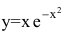
Решение:
Область определения функции — вся числовая прямая:
Функция непериодическая. Она нечетная, т.к. область определения симметрична относительно начала координат и
Следовательно, график функции симметричен относительно начала координат и достаточно исследовать функцию для
Функция непрерывна в области определения как композиция основных элементарных функций. Поскольку 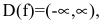
Строим график функции, используя результаты исследования.
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
- Иррациональные уравнения
- Иррациональные неравенства
- Производная в математике
- Как найти производную функции
-
Нахождение асимптоты функции.
Аси́мпто́та (от греч. ασϋμπτωτος —
несовпадающий, не
касающийся) кривой с бесконечной ветвью
— прямая,
обладающая тем свойством, что расстояние
от точки кривой до этой прямой стремится
к нулю при удалении точки вдоль ветви
в бесконечность[2].
Термин впервые появился у Аполлония
Пергского,
хотя асимптоты гиперболы
исследовал
ещё Архимед
Порядок нахождения асимптот
-
Нахождение
вертикальных асимптот. -
Нахождение
двух пределов -
Нахождение
двух пределов
:
если
в
п. 2.), то
,
и предел
ищется
по формуле горизонтальной асимптоты,
.
Наклонная асимптота — выделение целой части
Также
наклонную асимптоту можно найти, выделив
целую часть. Например:
Дана функция
.
Разделив
нацело числитель на знаменатель, получим:
.
При
,
,
то есть:
,
и
является
искомым уравнением асимптоты.
-
Производная и дифференциал.
Произво́дная (функции
в точке) — основное понятие дифференциального
исчисления,
характеризующее скорость изменения
функции (в данной точке). Определяется
как предел отношения
приращения функции к приращению
ее аргумента при
стремлении приращения аргумента к нулю,
если такой предел существует. Функцию,
имеющую конечную производную (в некоторой
точке), называют дифференцируемой (в
данной точке). Процесс вычисления
производной называется дифференци́рованием.
Обратный процесс —интегрирование.
Дифференциа́л (от лат. differentia —
разность, различие) — линейная
часть приращения
функции.
(Δxf(Δx)
= f(x +
Δx)
− f(x).);
малое
изменение величины в математическом
выражении вследствие такого же
незначительного изменения переменной
Для функции:
Дифференциал
функции
в
точке
может
быть определён как линейная функция
где f‘(x0) обозначает производную f в
точке x0.
Таким
образом df есть
функция двух аргументов
.
Дифференциал
может быть определён напрямую, т.е., без
привлечения определения производной
как функция
линейно
зависящая от h и
для которой верно следующее соотношение
-
Основные теоремы о дифференцируемых функциях.
http://termech.mpei.ac.ru/kir/PDF/Lecmatem7.html
у меня не получается
скопировать…ворд съезжает…..сволочь
Остальные
сайты на нобелевскую премию идут))) и
ставят одни формулы
-
Выпуклость функции.
Выпуклая
функция — функция,
у которой надграфик является
выпуклым множеством
Вещественнозначная
функция, определённая на некотором интервале (в
общем случае на выпуклом
подмножестве некотороговекторного
пространства)
выпукла, если для любых двух значений
аргумента x, y и
для любого числа
выполняется
неравенство
Йенсена:
Если
это неравенство является строгим для
всех
,
функция называется строго
выпуклой;
если выполняется обратное неравенство,
функция называется вогнутой,
или выпуклой
вверх.

NB! Иногда
выпуклая функция определяется как
вогнутая и наоборот
Свойства(нужно
тебе или нет, не знаю, но выглядят эти
свойства очень умно)))
-
Функция f,
выпуклая на интервале
, непрерывна на
всём
, дифференцируема на
всём
за
исключением не более чем счётного
множества точек
и дважды дифференцируема почти везде. -
Непрерывная
функция f выпукла
на
тогда
и только тогда, когда для всех
точек
выполняется
неравенство
-
Непрерывно
дифференцируемая функция одной
переменной выпукла на интервале тогда
и только тогда, когда её график лежит
не ниже касательной,
проведённой к этому графику в любой
точке промежутка выпуклости. -
Дважды
дифференцируемая функция одной
переменной выпукла на интервале тогда
и только тогда, когда её
вторая производная неотрицательна
на этом интервале. Если вторая производная
дважды дифференцируемой функции строго
положительна, такая функция является
строго выпуклой, однако обратное неверно
(например, функция f(x)
=x4 строго
выпукла на [
− 1,1],
но её вторая производная в точке x =
0 равна
нулю). -
Если
функции f, g выпуклы,
то любая их линейная
комбинация af + bg с
положительными коэффициентами a, b также
выпукла. -
Локальный
минимум выпуклой
функции является также глобальным
минимумом (соответственно,
для выпуклых вверх функций локальный
максимум является глобальным максимумом). -
Любая стационарная
точка выпуклой
функции будет глобальным экстремумом. -
Для
выпуклых функций выполняется неравенство
Йенсена:
где X — случайная
величина со
значениями в области
определения функции f, E — математическое
ожидание.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для гиперболы 
Аси́мпто́та[1] (от др.-греч. ἀσύμπτωτος — несовпадающий, не касающийся кривой с бесконечной ветвью) — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность[2]. Термин впервые появился у Аполлония Пергского, хотя асимптоты гиперболы исследовал ещё Архимед[3].
Затухающие колебания. 
Пример асимптоты для кривой в пространстве. Спираль бесконечно приближается к прямой
Содержание
- 1 Виды асимптот графиков
- 1.1 Вертикальная
- 1.2 Горизонтальная и наклонная
- 2 Нахождение асимптот
- 2.1 Порядок нахождения асимптот
- 2.2 Наклонная асимптота — выделение целой части
- 3 Свойства
- 4 См. также
- 5 Примечания
- 6 Литература
- 7 Ссылки
Виды асимптот графиков
Вертикальная
Прямая вида 
.
Вертикальных асимптот может быть любое количество.
Прямая не может быть вертикальной асимптотой, если функция непрерывна в точке 
Горизонтальная и наклонная
На графике функции x+1/x, ось y (x = 0) и линия y=x являются асимптотами.
Наклонная асимптота — прямая вида 
.
При этом, если выполняется первое условие, то говорят, что эта прямая является асимптотой при 

Если 
Замечание 1: Число наклонных асимптот у функции не может быть больше двух: одна при 

Замечание 2: Некоторые источники включают требование, чтобы кривая не пересекала эту прямую в окрестности бесконечности[5].
Замечание 3: В некоторых случаях, таких как алгебраическая геометрия, асимптота определена, как прямая, которая является «касательной» к кривой на бесконечности[5].
Функция y=arctgx с двумя горизонтальными асимптотами
Нахождение асимптот
Порядок нахождения асимптот
- Нахождение точек разрыва, выбор точек, в которых есть вертикальная асимптота (прямой проверкой, что предел в этой точке есть бесконечность).
- Проверка, не являются ли конечными пределы
и
. Если да, то существует горизонтальная асимптота
при
и
соответственно.
- Нахождение двух пределов
- Нахождение двух пределов
, если хотя бы один из пределов в пункте 3 или 4 не существует (или равен
), то наклонной асимптоты при
(или
) не существует.
Наклонная асимптота — выделение целой части
Также наклонную асимптоту можно найти, выделив целую часть. Например:
Дана функция 
Разделив нацело числитель на знаменатель, получим: 
При 

и 
Свойства
- Среди конических сечений асимптоты имеют только гиперболы. Асимптоты гиперболы как конического сечения параллельны образующим конуса, лежащим в плоскости, проходящей через вершину конуса параллельно секущей плоскости[6]. Максимальный угол между асимптотами гиперболы для данного конуса равен углу раствора конуса и достигается при секущей плоскости, параллельной оси конуса.
См. также
- Асимптотическая кривая
Примечания
- ↑ Двойное ударение поставлено согласно Советскому энциклопедическому словарю. В словарях XIX и первой половины XX века (например, в кн.: Словарь иностранных слов / Под ред. И. В. Лёхина и проф. Ф. Н. Петрова. — М.: Гос. изд-во иностр. и нац. словарей, 1955. — С. 77. — 856 с.) указывался единственный вариант ударения «асимпто́та».
- ↑ Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1.
- ↑ Математический энциклопедический словарь — М.: Советская энциклопедия, 1988. — 847 с.
- ↑ Кудрявцев Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003. — Т. 1. — С. 374-375. — 704 с. — ISBN 5-7107-4119-1.
- ↑ 1 2 «Asymptotes» by Louis A. Talman
- ↑ Taylor C. Geometrical Conics; Including Anharmonic Ratio and Projection, With Numerous Examples. — Cambridge: Macmillan, 1863. — С. 170.
Литература
- Рашевский П. К. Курс дифференциальной геометрии, 4-е изд. М., 1956.
- Графики функций: Справочник / Вирченко Н. А., Ляшко И. И., Швецов К. И. — Киев: Наук. думка, 1979, — 320 с.
Ссылки
| Портал «Математика» | |
| Асимптота на Викискладе |
- Асимптота // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Асимптота / Э. Г. Позняк // Ангола — Барзас. — М. : Советская энциклопедия, 1970. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 2).
Материал из Википедии — свободной энциклопедии
Данная версия страницы не проверялась участниками с соответствующими правами.
Вы можете прочитать последнюю стабильную версию, проверенную 30 мая 2010, однако она может значительно отличаться от текущей версии.
Проверки требует 1 правка.
Перейти к: навигация,
поиск
- Аси́мптота (от греч. ασϋμπτωτος — несовпадающий, не касающийся) кривой с бесконечной ветвью — прямая, к которой эта ветвь неограниченно приближается.[1][2]
- Асимптота — некоторая прямая, к которой данная кривая неограниченно приближается.[источник не указан 73 дня]
В математическом анализе используются следующие определения асимптоты:
- Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, то есть точка графика функции при своём стремлении в бесконечность должна неограниченно приближаться к асимптоте.[3]
- Асимптота [asymptote] — прямая, к которой стремится (никогда не достигая её) имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент приближается к некоторому заданному значению, неограниченно возрастает или уменьшается.[4]
Некоторые определения несколько не совпадают с приведёнными выше:
- Асимптота (геометр.) — прямая черта, вечно близящаяся к кривой (гиперболе), но никогда с нею не сходящаяся.[5]
- Асимптота — прямая или кривая линия, которая, будучи продолжена, приближается к другой кривой, но никогда не пересекает её, так что расстояние между ними делается бесконечно малой величиной.[6]
Нетрудно заметить, что последние два определения исключают случаи, когда кривая пересекает асимптоту (см., например, рис. 2)
Термин (применительно к гиперболе) приписывают Аполлонию Пергскому (3 век до н. э.).[2]
Содержание
- 1 Виды асимптот графиков
- 1.1 Вертикальная
- 1.2 Горизонтальная
- 1.3 Наклонная
- 2 Нахождение асимптот
- 2.1 Порядок нахождения асимптот
- 2.2 Наклонная асимптота — выделение целой части
- 3 Свойства
- 4 См. также
- 5 Примечания
- 6 Ссылки
[править] Виды асимптот графиков
[править] Вертикальная
Вертикальная асимптота — прямая вида 

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
Замечание: обратите внимание на знаки бесконечностей в этих равенствах.
[править] Горизонтальная
Горизонтальная асимптота — прямая вида 
.
[править] Наклонная
Наклонная асимптота — прямая вида 
Пример наклонной асимптоты
Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!
Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен 


Связь между наклонной и горизонтальной асимптотами
Если при вычислении предела
, то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?
Дело в том, что горизонтальная асимптота является частным случаем наклонной при
, и из выше указанных замечаний следует, что
- Функция имеет или только одну наклонную асимптоту, или одну горизонтальную асимптоту, или одну наклонную и одну горизонтальную, или две наклонных, или две горизонтальных, либо же вовсе не имеет асимптот.
- Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.
График функции с двумя горизонтальными асимптотами
[править] Нахождение асимптот
[править] Порядок нахождения асимптот
- Нахождение вертикальных асимптот.
- Нахождение двух пределов
- Нахождение двух пределов
:
если 



[править] Наклонная асимптота — выделение целой части
Также наклонную асимптоту можно найти, выделив целую часть. Например:
Дана функция 
Разделив нацело числитель на знаменатель, получим:
.
При 

,
и 
[править] Свойства
- Среди конических сечений асимптоты имеют только гиперболы.
[править] См. также
- Асимптотическая кривая
[править] Примечания
- ↑ http://slovari.yandex.ru/dict/bse/article/00004/77000.htm БСЭ
- ↑ 1 2 Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков и др. — М.: Советская энциклопедия, 1988. — 847 с.
- ↑ См., например: Выгодский М. Я. Справочник по высшей математике. М.: Физсатгиз, 1961, 784 с.
- ↑ http://slovari.yandex.ru/dict/lopatnikov/article/lop/lop-0079.htm Экономико-математический словарь
- ↑ http://slovari.yandex.ru/dict/dal/article/dal/03000/56800.htm Толковый словарь живого великорусского языка Владимира Даля
- ↑ http://slovari.yandex.ru/dict/brokminor/article/3/3376.html Малый энциклопедический словарь Брокгауза и Ефрона
[править] Ссылки
- http://mirslovarei.com/content_psy/ASIMPTOTA-21459.html
- Графики функций: Справочник / Вирченко Н. А., Ляшко И. И., Швецов К. И. — Киев: Наук. думка, 1979, — 320 с.
«Асимптоты дробно-рациональных функций»
Секция: математика
Автор:
Мантрова Марина
Николаевна,
учитель математики
МБУ «Школа № 11»
г.о. Тольятти
Самарской обл.
Тольятти
2022
СОДЕРЖАНИЕ.
Введение……………………………………………………………………………3
Раздел 1. Теоретические
сведения об асимптотах…………………………………5
1. Понятие
асимптоты………………………………………….……………..5
2. Виды
асимптот графиков………………………………………………….5
3. Связь
между наклонной и горизонтальной асимптотами……………….6
4. Правила
нахождения асимптот……………………………………………….7
Раздел 2. Образцы
дробно-рациональных функций, при построении графиков которых асимптотами
являются параболы и гиперболы………………….…..10
1. Задача
№ 1405, Берман……………………………………………………10
2. Задача
№ 1215, Минорский………………………………………………11
3. Задача
№ 1217, Минорский………………………………………………13
4. Задача
№1400, Берман……………………………………………………15
5. Задача
№5…………………………………………………………………17
Выводы……………………………………………………………………………20
Литература……………………………………………………………………….21
ВВЕДЕНИЕ.
Графики
функций являются неотъемлемой частью школьного курса математики. От точности их
построения зависит, насколько правильно будут определены свойства тех или иных
функций. Для более точного построения графиков необходимо выявить наличие у них
асимптот.
Цель
работы — выяснить, могут ли графики дробно-рациональных функций асимптотически
приближаться к кривым: параболам и гиперболам.
Для достижения
цели исследования поставлены конкретные задачи:
1.
Изучить
состояние вопроса по источникам информации.
2. Выдвинуть
гипотезу о том, что в качестве асимптот могут выступать параболы и гиперболы.
3. Экспериментально
проверить свою гипотезу в процессе построения графиков.
При решении
сформулированных задач были использованы следующие методы: изучение и
анализ литературы по проблеме исследования, наблюдение, синтез, индукция.
Объектом
исследования являются графики дробно-рациональных функций.
Предмет
исследования: асимптоты.
РАЗДЕЛ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ОБ АСИМПТОТАХ.
1.
Понятие асимптоты.
Асимптотой
кривой называется прямая, расстояние до которой от точки, лежащей на кривой,
стремится к нулю при неограниченном удалении этой точки по кривой от начала
координат или, что то же, когда расстояние точки от начала координат
неограниченно растет. [1,
с 238]
2.
Виды асимптот графиков.
Вертикальная
Вертикальная
асимптота — прямая вида при условии
существования предела .
Как правило, при
определении вертикальной асимптоты ищут не один предел, а два односторонних
(левый и правый). Это делается с целью определить, как функция ведёт себя по
мере приближения к вертикальной асимптоте с разных сторон. Итак, для того,
чтобы ветвь кривой у=f(х) имела вертикальную асимптоту х=а,
необходимо и достаточно, чтобы выполнялось одно из соотношений:
. [2,c.391]
Горизонтальная
Горизонтальная
асимптота — прямая вида при условии
существования предела
.
Наклонная
Наклонная
асимптота — асимптота, не перпендикулярная оси Ох. Уравнение этой
асимптоты должно иметь вид . [2, с.392]
Если существуют
конечные пределы
,
,
то кривая у=f(х) имеет
асимптоту . [1, с. 239]
Замечание: функция может
иметь не более двух наклонных (горизонтальных) асимптот!
Замечание: Если хотя бы
один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при
(или
) не
существует!
3.
Связь
между наклонной и горизонтальной асимптотами
Если при
вычислении предела , то очевидно, что
наклонная асимптота совпадает с горизонтальной. Какова же связь между этими
двумя видами асимптот?
Дело в том, что
горизонтальная асимптота является частным случаем наклонной при , и из выше указанных
замечаний следует, что
А. Функция
имеет или только одну наклонную асимптоту, или одну горизонтальную асимптоту,
или одну наклонную и одну горизонтальную, или две наклонных, или две
горизонтальных, либо же вовсе не имеет асимптот.
Б. Существование
указанных в п. А. асимптот напрямую связано с существованием соответствующих
пределов.
4. Правила
нахождения асимптот.
Алгоритм
нахождения асимптот через пределы:
1. Нахождение
вертикальных асимптот.
2. Нахождение
двух пределов
3. Нахождение
двух пределов
если в п. 2., то
, и предел
ищется по формуле
горизонтальной асимптоты,
Наклонная асимптота может быть получена также путем выделения
целой части из рациональной дроби [3, с.240]. Для кривой у=Р(х)/G(х) существует
наклонная асимптота при условии, что степень многочлена Р(х) на единицу больше
степени многочлена G(х) [3, с.240].
Рассмотрим конкретный пример: Задача №1409, Берман[4,]
Построить график функции у=.
Преобразуем функцию к виду у= и выделим из неё целую
часть
=
, где целая часть
и есть наклонная
асимптота.
Можно было её найти и через пределы.
У=кх+b,
у= — наклонная асимптота.
Проведём полное исследование функции для построения её
графика.
D(у)=, следовательно х=-1
вертикальная асимптота.
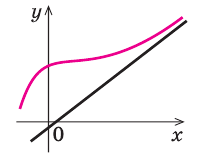
,
при
х=0, х=-1, х=-3.
|
х |
|
-3 |
|
-1 |
|
0 |
|
|
У |
|
|
|
Не |
|
0 |
|
|
|
+ |
0 |
— |
не |
+ |
0 |
+ |
|
Точка |
Точка |
Точка |
Дополнительные точки:
|
х |
-2 |
-0,5 |
1 |
2 |
|
у |
-4 |
-0,25 |
|
|
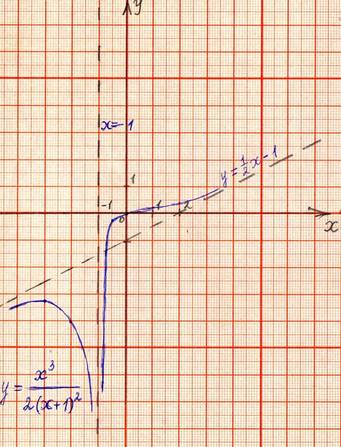
:
Используя исследование функции, строим её график.
Рассмотренный
выше пример показывает, как искать наклонные асимптоты для графиков
дробно-рациональных функций: надо представить, если это возможно, данную
функцию в виде суммы линейной функции и функции, бесконечно малой при
х→∞. Тогда график линейной функции и будет наклонной асимптотой. Из
разобранного примера видно, что наклонная асимптота к графику рациональной
функции существует, если степень числителя на единицу больше степени
знаменателя.[3, c.137 – 138]
Изучая
учебное пособие для углубленного изучения математики Виленкина
Н. Я. « Алгебра и математический анализ для 10 класса» [3], я
нашла задание № 300, в котором говорится найти параболу, к которой
неограниченно приближаются при х→∞ графики следующих: функций: [3]
У
меня возник вопрос, а что будет, если степень числителя на 2 или 3 единицы
больше знаменателя, или на 1,2 единицы меньше степени знаменателя? Ответа на
свой вопрос в книжных источниках и интернете найти не удалось. После анализа
сборников задач по высшей математике [4], [5] я нашла ряд функций,
которые меня заинтересовали. Например,
у=, у=
, у=
, у=
. Более подробно
рассмотрим эти функции в следующем разделе и попробуем к ним применить метод
выделения целой части для нахождения криволинейных асимптот.
РАЗДЕЛ 2. ОБРАЗЦЫ
ДРОБНО-РАЦИОНАЛЬНЫХ ФУНКЦИЙ, ПРИ ПОСТРОЕНИИ ГРАФИКОВ КОТОРЫХ АСИМПТОТАМИ ЯВЛЯЮТСЯ
ПАРАБОЛЫ И ГИПЕРБОЛЫ.
1. Задача
№ 1405, Берман. [4]
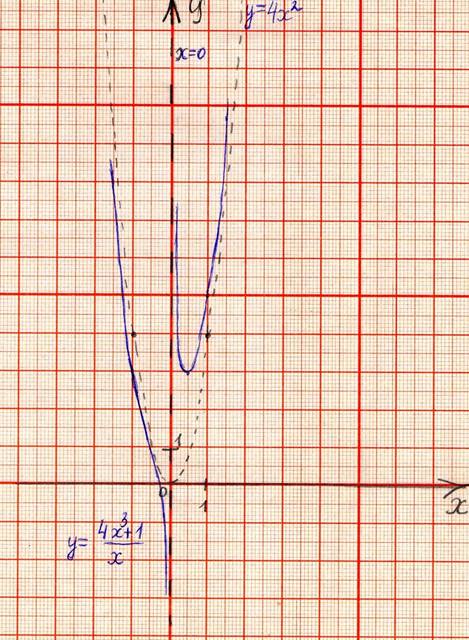
Построить график функции
у= .
По аналогии с рассмотренным
выше примером выделим целую часть из дроби .
Можно
предположить, что —
это асимптота, но явно, что это не линейная функция, а квадратичная. Проверим,
действительно ли это так экспериментальным путём. Построим график функции,
опираясь на её исследование, и график предполагаемой асимптоты.
D(у)= , поэтому х=0 –
вертикальная асимптота.
=
=0, если х=0,5.
=0,
если х=0, х=
.
|
х |
|
|
|
0 |
|
0,5 |
|
|
у |
|
0 |
|
Не сущ. |
|
3 |
|
|
|
— |
|
— |
Не |
— |
0 |
+ |
|
|
+ |
0 |
— |
Не |
+ |
+ |
|
|
Точка |
Точка |
Точка |
Дополнительные точки:
Таблица для асимптоты у=:
|
Х |
-2 |
-1 |
0 |
1 |
2 |
|
у |
16 |
4 |
0 |
4 |
16 |
На основании исследования функции строим её график и
её асимптоты.
Вывод: очевидно, что график функции у= действительно приближается к квадратичной параболе у=4х2
2. Задача
№ 1215, Минорский. [5]
Построить график функции у= .
Преобразуем функцию к виду у= и выделим из дроби целую
часть .
Предположим, что целая часть — это параболическая
асимптота данного графика. Убедимся в этом на практике.
D(у)= , значит х=2 – вертикальная
асимптота.
=0, если х=1 и
х=4.
|
Х |
|
1 |
|
2 |
|
4 |
|
|
У |
|
3 |
|
Не |
|
0 |
|
|
|
— |
0 |
+ |
Не |
+ |
0 |
+ |
|
Точка |
Точка |
Точка |
Дополнительные точки:
|
Х |
0 |
1 |
3 |
4 |
5 |
6 |
|
у |
|
3 |
— |
0 |
|
|
Таблица для параболической асимптоты у= :
Вершина
|
х |
3 |
4 |
5 |
6 |
|
у |
|
|
|
|
Используя результаты исследования функции, строим её
график и асимптоты.
Вывод: убеждаемся, что у= квадратичная парабола является асимптотой для графика функции у=
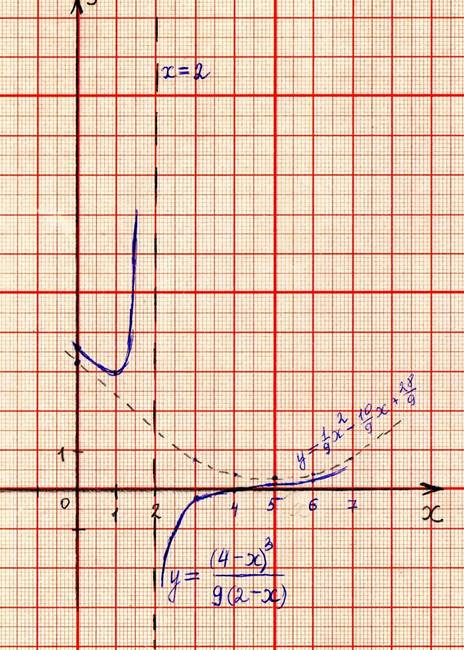
3. Задача
№ 1217, Минорский. [5]
Построить график функции У=.
Преобразуем функцию к
виду у = . Предположим,
что
у= гиперболическая асимптота.
Проверим это, выполнив построения.
D(у)=. Следовательно, х=0 – вертикальная асимптота.
Найдём к=
b=
Значит, у=0 =
горизонтальная асимптота.
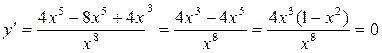
если х=1, х= -1, х=0.
Вычислим
|
х |
|
-1 |
|
0 |
|
1 |
|
|
у |
|
1 |
|
Не |
|
1 |
|
|
|
+ |
0 |
— |
Не |
+ |
0 |
— |
|
Точка |
Точка |
Точка |
Дополнительные точки:
|
Х |
1 |
2 |
3 |
0,5 |
|
у |
1 |
|
|
-8 |
Таблица для асимптоты у=
|
Х |
1 |
2 |
3 |
0,5 |
|
у |
2 |
0,5 |
|
8 |
Вывод: график функции у= имеет
гиперболическую асимптоту у=
4. Задача
№1400, Берман. [4]
Провести полное исследование данной функции и
начертить её график
У= .
Приведём данную функцию к виду у= .
Можно предположить, что у= является
криволинейной асимптотой для данного графика. Проверим это экспериментальным
путём, сделав полное исследование функции, построив её график и асимптоту у= .
D(у)= , следовательно х=1 и х=-1 –
вертикальные асимптоты.
Найдём к=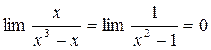
в= 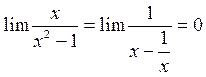
У=0 – горизонтальная асимптота.
Вычислим 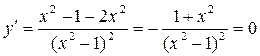
значения х.
|
Х |
|
-1 |
|
1 |
|
|
У |
|
Не |
|
Не |
|
|
|
— |
Не |
— |
Не |
— |
|
Точка |
Точка |
Дополнительные точки для построения данного графика:
|
Х |
0 |
0,5 |
1,5 |
2 |
2,5 |
3 |
|
у |
0 |
— |
1,2 |
|
0,48 |
0,375 |
Таблица для построения асимптоты:
|
Х |
0,5 |
1 |
1,5 |
2 |
|
у |
2 |
1 |
|
0,5 |
Основываясь на исследовании, построим график функции.
Вывод:
кривая у=(гипербола) служит асимптотой для графика
функции у=.
5. Задача 5. Попробую
сама взять дробно – рациональную функцию, у которой степень числителя на 3
единицы больше степени знаменателя .
Найдём асимптоту путём
выделения целой части.. Значит, g(x)=
— асимптота.
Таблица точек для построения асимптоты:
|
Х |
0 |
1 |
2 |
3 |
-1 |
-2 |
|
у |
-1 |
0 |
5 |
20 |
-4 |
-15 |
Проведём исследование функции при помощи аппарата
производной.
при х=0 и х=-
.
|
Х |
|
|
|
-1 |
|
0 |
|
|
|
+ |
0 |
|
Не |
|
0 |
+ |
|
у |
|
-9,5 |
|
Не |
|
0 |
|
|
Точка |
Точка |
Точка |
Дополнительные точки для построения функции :
|
х |
-2 |
-1,5 |
-0,5 |
0,5 |
1 |
2 |
|
у |
-16 |
-10,1 |
-0,125 |
0,04 |
0,5 |
5,3 |
Вывод:
график функции приближается к кубической асимптоте g(x)=
.
ВЫВОДЫ.
Таким образом, на основании проделанной работы мною были сделаны следующие
выводы:
1. Графики
дробно рациональных функций могут иметь не только асимптоты, представленные
линейной функцией, но и кривые линии, к которым они асимптотически приближаются:
квадратичную, кубическую параболы, а также гиперболы.
2. Если
степень многочлена числителя больше степени многочлена знаменателя на 2
единицы, то асимптотой будет квадратичная парабола, если разность степеней
равна 3 единицам, то асимптотой будет кубическая парабола. Логически можно
предположить, что если разница между степенью многочлена числителя больше
степени многочлена знаменателя на четное число единиц, то асимптотой будет
квадратичная парабола, ветви которой ближе к оси ординат; если же эта разность
составляет нечетное число, например 5, 7, 9, то асимптотой будет парабола вида
кубической, ветви которой приближены к оси ординат.
3. Если
степень многочлена числителя меньше степени многочлена знаменателя на 1(также
все нечетные числа) единицу, то асимптотой будет нечётная гипербола, а если
степень знаменателя на 2 (все четные числа) единицы больше степени числителя,
то асимптотой будет чётная гипербола.
4. Знание
криволинейных асимптотических линий необходимо тогда, когда дробная рациональная
функция не имеет прямолинейных асимптот. Криволинейные асимптотические линии
позволяют точнее построить график той или иной функции.
ЛИТЕРАТУРА.
1.
Игнатьева
А. В. и др. Курс высшей математики /А. В. Игнатьева, Т. И. Краснощекова, В. Ф.
Смирнов; Под редакцией П.И.Романовского. – 2-е изд. – М.: «Высшая школа», 1968.
— 670с.
2.
Уваренков
И.М., Малер М.З. Курс математического анализа. — Том 1. — М.: «Просвещение»,
1966. — 640с.
3.
Виленкин
Н. Я. и др. Алгебра и математический анализ для 10 класса: Учеб. пособие для
учащихся школ и классов с углубл. изуч. математики / Н.Я.Виленкин,
О.С.Ивашев–Мусатов, С.И. Шварцбурд. – 4-е изд. — М.: «Просвещение», 1995. —
335с.
4.
Берман
Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для высш.
учеб. заведений. — 17-е изд. – М.: «Наука», 1972. — 412с.
5.
Минорский
В.П. Сборник задач по высшей математике: Учеб. пособие для студ. высш. технич.
учеб. заведений – 12-е изд., стереотип. — М.: «Наука», 1978. — 352с.

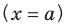
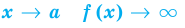
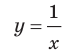
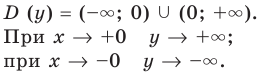
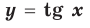
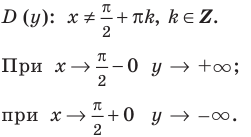
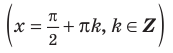
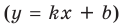
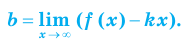
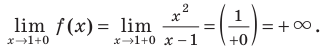
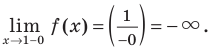
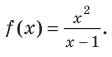
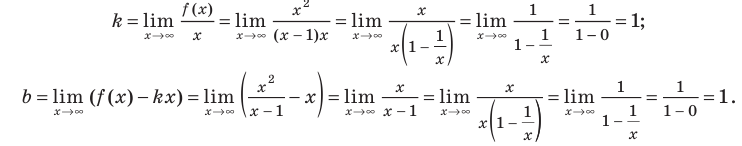
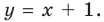
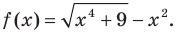
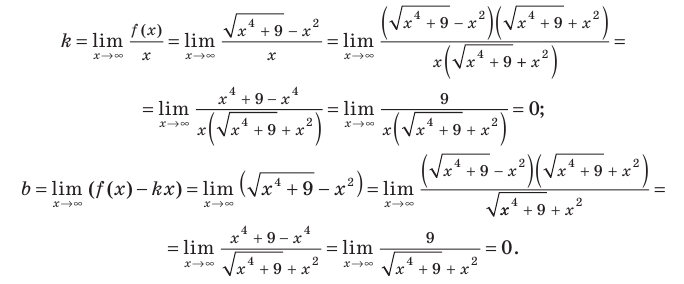
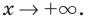
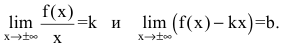
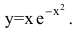
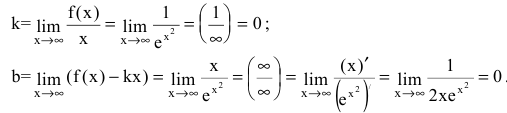
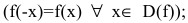 нечетность
нечетность 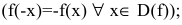 периодичность
периодичность 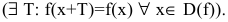
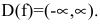
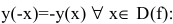
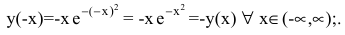
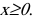
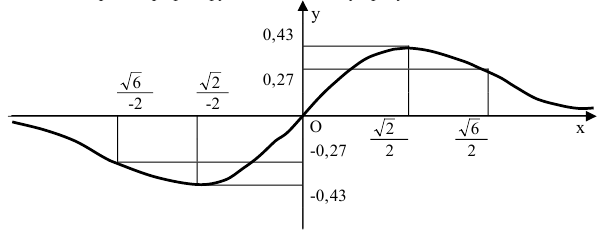























 , то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?
, то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?

 .
. ,
,