Направляющие косинусы вектора.
Навигация по странице:
- Определение направляющих косинусов
- Формулы для направляющих косинусов
- для плоских задач
- для пространственных задач
- Примеры задач с направляющими косинусами вектора
- плоские задачи
- пространственные задачи
Определение направляющих косинусов
Определение. Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.
Направляющие косинусы однозначно задают направление вектора.
Основное соотношение. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.
Соответственно, координаты единичного вектора равны его направляющим косинусам.
Свойство направляющих косинусов. Сумма квадратов направляющих косинусов равна единице.
Формулы вычисления направляющих косинусов вектора
Формула вычисления направляющих косинусов вектора для плоских задач
В случае плоской задачи (рис. 1) направляющие косинусы вектора a = {ax ; ay} можно найти воспользовавшись следующей формулой
| cos α = | ax | ; | cos β = | ay |
| |a| | |a| |
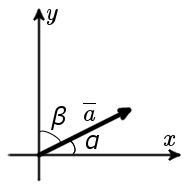 |
| рис. 1 |
Формула вычисления направляющих косинусов вектора для пространственных задач
В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = {ax ; ay ; az} можно найти воспользовавшись следующей формулой
| cos α = | ax | ; | cos β = | ay | ; | cos γ = | az |
| |a| | |a| | |a| |
Свойство:
cos2 α + cos2 β + cos2 γ = 1
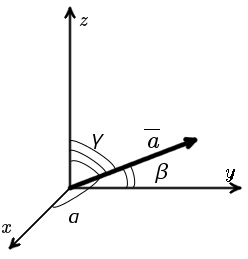 |
| рис. 2 |
Примеры задач с направляющими косинусами вектора
Примеры плоских задач с направляющими косинусами вектора
Пример 1. Найти направляющие косинусы вектора a = {3; 4}.
Решение:
Найдем модуль вектора a:
|a| = √32 + 42 = √9 + 16 = √25 = 5.
Найдем направляющие косинусы вектора a:
| cos α = | ax | = | 3 | = 0.6 |
| |a| | 5 |
| cos β = | ay | = | 4 | = 0.8 |
| |a| | 5 |
Ответ: направляющие косинусы вектора cos α = 0.6, cos β = 0.8.
Пример 2. Найти значение векора a если его длина равна 26, а направляющие косинусы cos α = 5/13, cos β = -12/13.
Решение:
ax = |a| · cos α = 26 ·
513
= 10
ay = |a| · cos β = 26 · (-
1213
) = -24
Ответ: a = {10; -24}.
Примеры пространственных задач с направляющими косинусами вектора
Пример 3. Найти направляющие косинусы вектора a = {2; 4; 4}.
Решение:
Найдем модуль вектора a:
|a| = √22 + 42 + 42 = √4 + 16 + 16 = √36 = 6.
Найдем направляющие косинусы вектора a:
| cos α = | ax | = | 2 | = | 1 |
| |a| | 6 | 3 |
| cos β = | ay | = | 4 | = | 2 |
| |a| | 6 | 3 |
| cos γ = | az | = | 4 | = | 2 |
| |a| | 6 | 3 |
Ответ: направляющие косинусы вектора cos α = 13, cos β = 23, cos γ = 23.
Содержание:
- Формула
- Примеры вычисления направляющих косинусов вектора
Формула
Чтобы найти направляющие косинусы вектора $bar{a}$, заданного на
плоскости своими координатами $bar{a}=left(a_{x} ; a_{y}right)$ нужно воспользоваться формулами:
$$cos alpha=frac{a_{x}}{|bar{a}|}=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}}}, quad cos beta=frac{a_{y}}{|bar{a}|}=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}}}$$
То есть необходимо соответствующую
координату вектора поделить на его
длину.
В случае если вектор задан в пространстве $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$, имеют место
следующие формулы для нахождения направляющих косинусов этого вектора:
$$begin{aligned} cos alpha=frac{a_{x}}{|bar{a}|}=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} &, text { cos } beta=frac{a_{y}}{|bar{a}|}=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} \ cos gamma=frac{a_{z}}{|bar{a}|}=& frac{a_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} end{aligned}$$
Примеры вычисления направляющих косинусов вектора
Пример
Задание. Дан вектор $bar{a}=(1 ;-1)$, найти его направляющие векторы.
Решение. Вектор задан на плоскости. Направляющие косину найдем по формулам:
$$cos alpha=frac{a_{x}}{|bar{a}|}=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}}}, quad cos beta=frac{a_{y}}{|bar{a}|}=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}}}$$
Подставим в них координаты заданного вектора, получим
$$begin{aligned} cos alpha=frac{a_{x}}{|bar{a}|} &=frac{1}{sqrt{1^{2}+(-1)^{2}}}=frac{1}{sqrt{1+1}}=frac{1}{sqrt{2}} \ cos beta=frac{a_{y}}{|bar{a}|} &=frac{-1}{sqrt{1^{2}+(-1)^{2}}}=frac{-1}{sqrt{1+1}}=-frac{1}{sqrt{2}} end{aligned}$$
Ответ. $cos alpha=frac{1}{sqrt{2}}, quad cos beta=-frac{1}{sqrt{2}}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Дан вектор $bar{a}=(2 ;-1 ;-2)$, найти его направляющие
векторы и составить единичный вектор $bar{a}_0$ направлений вектора
$bar{a}$ .
Решение. Вектор задан в пространстве, поэтому для нахождения направляющих векторов воспользуемся формулами
$begin{aligned} cos alpha=frac{a_{x}}{|bar{a}|}=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} &, quad cos beta=frac{a_{y}}{|bar{a}|}=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} \ cos gamma=frac{a_{z}}{|bar{a}|}=& frac{a_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} end{aligned}$
Подставляя в эти формулы координаты заданного вектора, получим
$$begin{aligned} cos alpha=frac{a_{x}}{|bar{a}|}=frac{2}{sqrt{2^{2}+(-1)^{2}+(-2)^{2}}} &=frac{2}{sqrt{4+1+4}}=frac{2}{sqrt{9}}=frac{2}{3} \ cos beta=frac{a_{y}}{|bar{a}|}=frac{-1}{sqrt{2^{2}+(-1)^{2}+(-2)^{2}}} &=frac{-1}{sqrt{4+1+4}}=frac{-1}{sqrt{9}}=-frac{1}{3} \ cos gamma=frac{a_{z}}{|bar{a}|}=frac{-2}{sqrt{2^{2}+(-1)^{2}+(-2)^{2}}} &=frac{-2}{sqrt{4+1+4}}=frac{-2}{sqrt{9}}=-frac{2}{3} end{aligned}$$
Составим единичный вектор $bar{a}_0$ направлений
вектора $bar{a}$ . Он равен
$$bar{a}_{0}=(cos alpha ; cos beta ; cos gamma)=left(frac{2}{3} ;-frac{1}{3} ;-frac{2}{3}right)$$
Ответ. $cos alpha=frac{2}{3}, cos beta=-frac{1}{3}, quad cos gamma=-frac{2}{3}, bar{a}_{0}=left(frac{2}{3} ;-frac{1}{3} ;-frac{2}{3}right)$
Читать дальше: как найти угол между векторами.
Пусть
дан вектор
(
х,
у,
z).
Обозначим
углы наклона этого вектора к осям Ох,
Оу иOz соответственно
буквами
,
и
.Три числа cos
,
cos
и
cosпринято называть направляющими
косинусами вектора
.
Полагая=
(1;0; 0)получаем из (9)
Аналогично
Из
формул (11) — (13) следует:
1)
сos2
+ cos2
+
cos2
= 1,
т.е.
сумма квадратов направляющих
косинусов любого ненулевого вектора
равна единице;
т.е.
направляющие косинусы
этого вектора пропорциональны его
соответствующим проекциям.
Примечание.
Из формул (11)-(13) видно, что проекции
любого единичного вектора
на
оси координат соответственно совпадают
с его направляющими косинусами и,
следовательно,
Пример.
Найти направляющие косинусы вектора
(1;
2; 2). По формулам (11)-(13) имеем
4. Векторное произведение двух векторов и его основные свойства.
Определение.
Векторным произведением двух векторов
и
называется
новый вектор,
модуль которого равен площади
параллелограмма, построенного на
векторахи
,
приведенных к общему началу, и который
перпендикулярен к перемножаемым векторам
(иначе говоря, перпендикулярен к плоскости
построенного на них параллелограмма)
и направлен в такую сторону, чтобы
кратчайший поворот отк
вокруг
полученного векторапредставлялся
происходящим против часовой стрелки,
если смотреть из конца вектора(рис.
40).
Если
векторы
и
коллинеарны,
то их векторное произведение считается
равным нулевому вектору. Из этого
определения следует, что
||
= ||
|| sin
,
где
—
угол между векторамии
(0
).
Векторное произведение векторови
обозначается
символом
х
или
[]
или [,
].
Выясним
физический смысл векторного произведения.
Если вектор
изображает
приложенную в некоторой точкеМ силу,
а векторидет
из некоторой точкиО в точкуМ, то
вектор=[
]
представляет собой момент силыотносительно
точкиО.
Свойства
векторного произведения
1
. При перестановке
сомножителей векторное произведение
меняет знак, т.е.
х
=
-(x
).
2.
()х
=
х(
)=
(
х
),где
—
скаляр.
3.
Векторное произведение
подчиняется распределительному закону,
т.е.
(+
)
x=
x
+
x
.
4.
Если векторное произведение
двух векторов равно нулевому вектору,
то либо равен нулевому вектору хотя бы
один из перемножаемых векторов
(тривиальный случай), либо равен нулю
синус угла между ними, т.е. векторы
коллинеарны.
Обратно,
если два ненулевых вектора
коллинеарны, то их векторное произведение
равно нулевому вектору.
Таким
образом, для того чтобы
два ненулевых вектора
и
были
коллинеарны, необходимо и достаточно,
чтобы их векторное произведение равнялось
нулевому вектору.
Отсюда,
в частности, следует, что векторное
произведение вектора на самого себя
равно нулевому вектору:
х
=0
(х
еще
называют векторным
квадратом вектора
.
5. Смешанное произведение трех векторов и его основные свойства.
Пусть
даны три вектора
,
и
.
Представим себе, что векторумножается
векторно наи
полученный векторх
умножается
скалярно на вектор,
тем самым определяется число (х
)
.
Оно называется илисмешанным
произведениемтрех векторов,
и
.
Для
краткости смешанное произведение (х
)
будем обозначать
или
().
Выясним
геометрический смысл смешанного
произведения
.
Пусть рассматриваемые векторыи
некомпланарны.
Построим параллелепипед на векторах,
и
как
на ребрах.
Векторное
произведение
x
есть
вектор(
=
),
численно равный площади параллелограммаOADB(основание построенного
параллелепипеда), построенного на
векторахи
и
направленный перпендикулярно к плоскости
параллелограмма (рис. 41).
Скалярное
произведение (x
)
=
есть
произведение модуля вектораи
проекции векторана
(см.
п. 1, (2)).
Высота
построенного параллелепипеда есть
абсолютная величина этой проекции.
Следовательно,
произведение |
|
по
абсолютной величине равно произведению
площади основания параллелепипеда на
его высоту, т.е. объему параллелепипеда,
построенного на векторах,
и
.
Рис.42
При
этом важно отметить, что скалярное
произведение
дает
объем параллелепипеда иногда с
положительным, а иногда с отрицательным
знаком. Положительный знак получается,
если угол между векторамии
острый;
отрицательный — если тупой. При остром
угле междуи
вектор
расположен
по ту же сторону плоскостиOADB,
что и вектор и, следовательно, из конца
векторавращение
отк
будет
видно так же, как и из конца вектора,
т.е. в положительном направлении (против
часовой стрелки).
При
тупом угле между
вектор
расположен
по другую сторону плоскостиOADB,
чем вектор,
и, следовательно, из конца векторавращение
отк
будет
видно в отрицательном направлении (по
часовой стрелке). Иными словами,
произведениеположительно,
если векторы,
и
образуют
систему, одноименную с основной Oxyz
(взаимно расположены так же, как оси Ox,
Oy, Oz), и оно отрицательно, если векторы,
образуют
систему, разноименную с основной.
Таким
образом, смешанное
произведение
есть
число,абсолютная
величина которого выражает объем
параллелепипеда,построенного
на векторах
,
как
на ребрах.
Знак
произведения положителен, если векторы
,
,
образуют
систему, одноименную с основной, и
отрицателен в противном .
Отсюда
следует, что абсолютная величина
произведения
=(
х
)
останется той же, в каком бы порядке мы
ни брали сомножители,
,
.
Что касается знака, то он будет в одних
случаях положительным, в других —
отрицательным; это зависит от того,
образуют ли наши три вектора, взятые в
определенном порядке, систему, одноименную
с основной, или нет. Заметим, что у нас
оси координат расположены так, что они
следуют одна за другой против часовой
стрелки, если смотреть во внутреннюю
часть (рис. 42). Порядок следования не
нарушается, если мы начнем обход со
второй оси или с третьей, лишь бы он
совершался в том же направлении, т.е.
против часовой стрелки. При этом множители
переставляются в круговом порядке
(циклически). Таким образом, получаем
следующее свойство:
Смешанное
произведение не меняется при круговой
(циклической) перестановке его
сомножителей. Перестановка двух соседних
сомножителей меняет знак произведения
=
=
=-(
)=-(
)=-(
).
Наконец,
из геометрического смысла смешанного
произведения непосредственно следует
следующее утверждение.
Необходимым
и достаточным условием компланарности
векторов
,
,
является равенство нулю
их смешанного произведения:
=0(14)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
18.04.2015421.31 Кб24бп.rtf
- #
- #
- #
- #
- #
- #
- #
- #
- #
Угол между векторами.
Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70
Ответ: a → , b → ^ = — a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,
b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Как найти косинус угла между векторами
Формула
Чтобы найти косинус угла между векторами нужно, скалярное произведение этих векторов разделить на произведение их длин.
Примеры вычисления косинуса угла между векторами
Задание. Найти косинус угла $phi$ между векторами $bar=(4 ;-3)$ и $bar=(1 ;-2)$
Решение. Так как векторы заданы на плоскости, воспользуемся формулой
Ответ. $cos phi=frac<2 sqrt<5>><5>$
Задание. Найти косинус угла между векторами $bar=(3 ;-4 ; 0)$ и $bar=(4 ;-4 ;-2)$, заданных в пространстве.
Решение. Для нахождения косинуса угла между заданными векторами, воспользуемся формулой
Подставляя координаты векторов $bar$ и $bar$, получим
Ответ. $begin cos phi=frac<14> <15>end$
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/
http://www.webmath.ru/poleznoe/formules_13_9.php
Направление вектора
Направление вектора: основные понятия и определения
Первая точка называется началом вектора, а вторая – его концом.
Расстояние между началом и концом вектора называется длиной или модулем вектора.
Вектор, начало и конец которого совпадают, называется нулевым и обозначается ; его длина считается равной нулю. В противном случае, если длина вектора положительна, то его называют ненулевым.
Замечание. Если длина вектора равна единице, то он называется ортом или единичным вектором и обозначается .
Ненулевой вектор также можно определить как направленный отрезок.
Замечание. Направление нулевого вектора не определено.
Направляющие косинусы вектора
Замечание. Однозначно направление вектора задают его направляющие косинусы.
Чтобы найти направляющие косинусы вектора необходимо вектор нормировать (то есть вектор поделить на его длину):
Замечание. Координаты единичного вектора равны его направляющим косинусам.
| Понравился сайт? Расскажи друзьям! | |