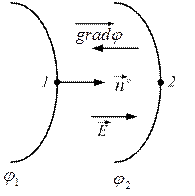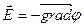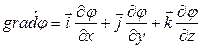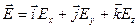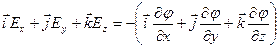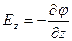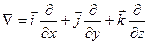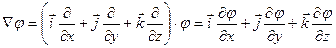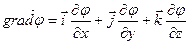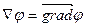Как найти направление градиента потенциала - Исправление недочетов и поиск решений вместе с Examum.ru

Вектор градиента потенциала электростатического поля

§7 Работа силы электростатического поля при перемещении заряда.

Потенциальный характер сил поля.

Циркуляция вектора напряженности

Рассмотрим электростатическое поле, создаваемое зарядом q . Пусть в нем перемещается пробный заряд q ₀ . В любой точке поля на заряд q ₀ действует сила

де — модуль силы, — орт радиус-вектора , определяющего положение заряда q ₀ относительно заряда q . Так как сила меняется от точки к точке, то работу силы электростатического поля запишем как работу переменной силы:

Ввиду того, что рассматривали перемещение заряда из точки 1 в точку 2 по произвольной траектории, можно сделать вывод, что работа по перемещению точечного заряда в электростатическом поле не зависит от формы пути, а определяется лишь начальным и конечным положением заряда. Это свидетельствует о том, что электростатическое поле является потенциальным, а сила Кулона – консервативной силой. Работа по перемещению заряда в таком поле по замкнутому пути всегда рвана нулю.

— проекция на направление контура ?.

Учтем, что работа по замкнутому пути равно нулю

— ЦИРКУЛЯЦИЯ вектора напряженности.

Циркуляция вектора напряженности электростатического поля, взятая по произвольному замкнутому контуру всегда равна нулю.

§7 Потенциал.

Связь между напряженностью и потенциалом.

Градиент потенциала.

Эквипотенциальные поверхности

Поскольку электростатическое поле является потенциальным работа по перемещению заряда в таком поле может быть представлена, как разность потенциальных энергий заряда в начальной и конечной точках пути. (Работа равна уменьшению потенциальной энергии, или изменению потенциальной энергии, взятому со знаком минус.)

Постоянную определяют из условия, что при удалении заряда q ₀ на бесконечность его потенциальная энергия должна быть равна нулю.

Различные пробные заряды q ₀ _i , помещенные в данную точку поля будут обладать в этой точке различными потенциальными энергиями:

…

Отношение W _пот _i к величине пробного заряда q ₀ _i , помещенного в данную точку поля является величиной постоянной для данной точки поля для всех пробных зарядов. Это отношение называется ПОТЕНЦИАЛОМ.

ПОТЕНЦИАЛ – энергетическая характеристика электрического поля. ПОТЕНЦИАЛ численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.

Работу по перемещению заряда можно представить в виде

Потенциал измеряется в Вольтах

ЭКВИПОТЕНЦИАЛЬНЫМИ ПОВЕРХНОСТЯМИ называются поверхности равного потенциала (φ = const ). Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Связь между напряженностью и потенциалом φ можно найти, исходя из того, что работу по перемещению заряда q на элементарном отрезке d ? можно представить как

С другой стороны

— градиент потенциала.

Напряженность поля равна градиенту потенциала, взятому со знаком минус.

Градиент потенциала показывает, как меняется потенциал на единицу длины. Градиент перпендикулярен функции и направлен в сторону возрастания функции. Следовательно, вектор напряженности перпендикулярен эквипотенциальной поверхности и направлен в сторону убывания потенциала.

Рассмотрим поле, создаваемое системой N точечных зарядов q ₁ , q ₂ , … q_N . Расстояния от зарядов до данной точки поля равны r ₁ , r ₂ , … r_N . Работа, совершаемая силами этого поля над зарядом q ₀ , будет равна алгебраической сумме работ сил, каждого заряда в отдельности.

гле

Потенциал поля, создаваемого системой зарядов, определяется как алгебраическая сумма потенциалов, создаваемых в этой же точке каждым зарядом в отдельности.

§9 Вычисление разности потенциалов плоскости, двух плоскостей, сферы, шара, цилиндра

Используя связь между φ и определим разность потенциалов между двумя произвольными точками

Разность потенциалов поля равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ.

2. Разность потенциалов поля двух бесконечных параллельных разноименно заряженных плоскостей с поверхностной плотностью заряда σ.

Если х₁ = 0; х₂ = d , то или

3. Разность потенциалов поля равномерно заряженной сферической поверхности радиуса R .

Внутри сферической поверхности потенциал всюду одинаков и равен

4. Разность потенциалов поля объемно заряженного шара радиуса R с общим зарядом Q.

Вне шара r ₁ , r ₂ > R ,

Внутри шара

5. Разность потенциалов поля равномерно заряженного цилиндра (или бесконечно длинной нити).

r > R :

Градиент потенциала

Градиент потенциала – это скорость возрастания потенциала в направлении кротчайшем между двумя точками.

Между двумя точками имеется некоторая разность потенциалов. Если эту разность разделить на кратчайшее расстояние между взятыми точками, то полученное значение будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками.

Градиент потенциала показывает направление наибольшего возрастания потенциала, численно равен модулю напряженности и отрицательно направлен по отношению к нему.

В определении градиента существенны два положения:

1) Направление, в котором берутся две близлежащие точки, должно быть таким, чтобы скорость изменения была максимальной.

2) Направление таково, что скалярная функция в этом направлении возрастает.

Для декартовой системы координат:

Скорость изменения потенциала в направлении оси Х, Y, Z:

; ;

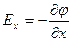
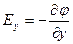
Два вектора равны только тогда, когда равны друг другу их проекции. Проекция вектора напряженности на ось Х равна проекции скорости изменения потенциала вдоль оси Х, взятой с обратным знаком. Аналогично для осей Y и Z.

; ; .

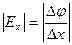
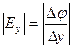
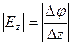
В цилиндрической системе координат выражение градиента потенциала будет иметь следующий вид:

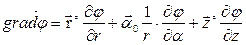
А в сферической системе координат:

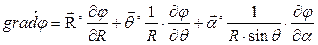
Дифференциальный оператор Гамильтона (оператор Набла)

Для сокращения записи операций над скалярными и векторными величинами употребляют дифференциальный оператор Гамильтона или оператор Набла:

Под дифференциальным оператором Гамильтона понимают сумму частных производных по 3-м координатным осям, умноженных на соответствующие единичные векторы (орты).

Применим оператор Гамильтона к потенциалу:

Правые части одинаковы, значит, будут одинаковы и левые части:

Оператор Гамильтона сочетает в себе как векторные, так и скалярные свойства и может быть применен к скалярным и векторным функциям.

Дата добавления: 2015-07-30 ; просмотров: 19610 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Градиент потенциальных характеристик, как его рассчитать и пример

градиент потенциала является вектором, который представляет отношение изменения электрического потенциала по отношению к расстоянию в каждой оси декартовой системы координат. Таким образом, вектор градиента потенциала указывает направление, в котором скорость изменения электрического потенциала больше, в зависимости от расстояния.

В свою очередь, модуль градиента потенциала отражает скорость изменения электрического потенциала в определенном направлении. Если значение этого известно в каждой точке пространственной области, то электрическое поле может быть получено из градиента потенциала.

Электрическое поле определяется как вектор, с которым оно имеет определенное направление и величину. Определяя направление, в котором электрический потенциал уменьшается быстрее, удаляясь от контрольной точки, и деля это значение на пройденное расстояние, получается величина электрического поля..

1 Характеристики
2 Как рассчитать?
3 Пример
- 3.1 Упражнение
4 Ссылки

черты

Градиент потенциала представляет собой вектор, ограниченный конкретными пространственными координатами, который измеряет отношение изменения между электрическим потенциалом и расстоянием, пройденным этим потенциалом.

Наиболее выдающиеся характеристики градиента электрического потенциала подробно описаны ниже:

1- Потенциальный градиент — это вектор. Следовательно, он имеет определенную величину и направление.

2- Поскольку потенциальный градиент является вектором в пространстве, он имеет величины, адресованные по осям X (ширина), Y (высокая) и Z (глубина), если в качестве эталонной системы координат берется декартова система координат.

3- Этот вектор перпендикулярен эквипотенциальной поверхности в точке, в которой оценивается электрический потенциал.

4- Вектор градиента потенциала направлен в направлении максимального изменения функции электрического потенциала в любой точке..

5- Модуль градиента потенциала равен модулю, полученному из функции электрического потенциала по отношению к расстоянию, пройденному в направлении каждой из осей декартовой системы координат..

6- Потенциальный градиент имеет нулевое значение в стационарных точках (максимальная, минимальная и седловая точки).

7- В международной системе единиц (СИ) единицами измерения градиента потенциала являются вольт / метры.

8. Направление электрического поля такое же, в котором электрический потенциал уменьшает свою величину быстрее. В свою очередь, градиент потенциала указывает в направлении, в котором потенциал увеличивает свое значение по отношению к изменению положения. Тогда электрическое поле имеет то же значение градиента потенциала, но с противоположным знаком.

Как рассчитать?

Разность электрических потенциалов между двумя точками (точка 1 и точка 2) определяется следующим выражением:

V1: электрический потенциал в точке 1.

V2: электрический потенциал в точке 2.

E: величина электрического поля.

Ѳ: угол наклона вектора электрического поля, измеренного относительно системы координат.

Выражая указанную формулу дифференциальным способом, получаем следующее:

Коэффициент E * cos (Ѳ) относится к модулю компонента электрического поля в направлении dl. Пусть L — горизонтальная ось плоскости отсчета, тогда cos (Ѳ) = 1, вот так:

Далее, отношение между изменением электрического потенциала (dV) и изменением пройденного расстояния (ds) является модулем градиента потенциала для упомянутого компонента.

Из этого следует, что величина градиента электрического потенциала равна компоненте электрического поля в направлении исследования, но с противоположным знаком.

Однако, поскольку реальная среда является трехмерной, градиент потенциала в данной точке должен быть выражен как сумма трех пространственных компонентов на осях X, Y и Z декартовой системы..

Разбивая вектор электрического поля на три прямоугольных компонента, мы получаем следующее:

Если в плоскости имеется область, в которой электрический потенциал имеет одинаковое значение, частная производная этого параметра по каждой из декартовых координат будет равна нулю.

Таким образом, в точках, которые находятся на эквипотенциальных поверхностях, напряженность электрического поля будет иметь нулевую величину.

Наконец, вектор градиента потенциала может быть определен как точно такой же вектор электрического поля (по величине) с противоположным знаком. Таким образом, мы имеем следующее:

пример

Из приведенных выше расчетов необходимо:

Теперь, прежде чем определять электрическое поле как функцию градиента потенциала или наоборот, сначала необходимо определить направление, в котором разность электрических потенциалов растет..

После этого определяется коэффициент изменения электрического потенциала и изменения пройденного расстояния..

Таким образом, мы получаем величину соответствующего электрического поля, которая равна величине градиента потенциала в этой координате.

осуществление

Есть две параллельные пластины, как показано на следующем рисунке.

Шаг 1

Направление роста электрического поля на декартовой системе координат определяется.

Электрическое поле растет только в горизонтальном направлении, учитывая расположение параллельных пластин. Следовательно, можно сделать вывод, что компоненты градиента потенциала на оси Y и оси Z равны нулю..

Шаг 2

Данные, представляющие интерес различаются.

— Разность потенциалов: dV = V2 — V1 = 90 В — 0 В => dV = 90 В.

— Разница в расстоянии: дх = 10 сантиметров.

Чтобы обеспечить соответствие единиц измерения, используемых в соответствии с Международной системой единиц, величины, не выраженные в СИ, должны быть соответственно преобразованы. Таким образом, 10 сантиметров равны 0,1 метра, и, наконец, dx = 0,1 м.

Шаг 3

Величина вектора градиента потенциала рассчитывается соответствующим образом.

источники:

http://helpiks.org/4-37431.html

http://ru.thpanorama.com/articles/electrnica/gradiente-de-potencial-caractersticas-cmo-calcularlo-y-ejemplo.html

Источник

Градиент
(потенциала)
– вектор, показывающий направление
наибольшего роста скалярной функции
:

, (9)

где ,

– координатные орты.

Величина
этого вектора равна изменению потенциала

при перемещении на единицу длины в
направлении быстрейшего изменения.

Длина градиента
(потенциала) равна

. (10)

Из механики известно,
что консервативная сила равна градиенту
потенциальной энергии частицы, взятому
с обратным знаком, т.е.

, (11)

где–
символический вектор, называемый
оператором
Гамильтона
или оператором набла.

Для электростатического
поля имеем:

Тогда соотношение
(11) принимает вид

или,
(12)

т.е. напряженность
электрического поля равна градиенту
потенциала с обратным знаком.

Знак
минус в (12) показывает, что вектор
направлен противоположно вектору
градиента потенциала ,
и силовые линии электрического поля
являются линиями, вдоль которых потенциал
изменяется наиболее быстро.

Очевидно,
что проекция вектора
на произвольное направление l
равна со знаком минус частной производной
потенциала по данному направлению:

. (13)

В
случае однородного электрического поля
(поля плоского конденсатора), в любой
точке которого вектор напряженности

постоянен как по величине, так и по
направлению, имеем простое соотношение:

, (14)

где–
разность потенциалов или напряжение
между пластинами конденсатора (или
между двумя эквипотенциальными
поверхностями);

– расстояние между пластинами конденсатора
(или между двумя эквипотенциальными
поверхностями).

Поверхность,
все точки которой имеют одинаковый
потенциал, называется поверхностью
равного потенциала или эквипотенциальной
поверхностью,
для которой

. (15)

Перенос заряда
вдоль эквипотенциальной поверхности
не требует работы (разность потенциалов
двух любых точек этой поверхности равна
нулю). Это означает, что сила, действующая
на переносимый заряд, перпендикулярна
к перемещению.

Следовательно,
вектор
всегда направлен по нормали к
эквипотенциальной поверхности, т.е.
линии напряженности в каждой точке
ортогональны к эквипотенциальной
поверхности.

Итак,
можно сделать важный вывод о том, что
электрическое поле полностью можно
описать векторной величиной –
напряженностью .
Но во многих случаях оказывается, что
для вычисления напряженности
электрического поля удобнее сначала
определить потенциал φ
и затем по формуле

вычислить
напряженность .

Силовые
линии — направленные линии, касательные
к которым в каждой точке совпадают с
направлением вектора напряженности
электрического поля. Отсюда
следует, что напряженность

равна
разности потенциалов U на единицу длины
силовой линии.

Именно
вдоль силовой линии происходит
максимальное изменение потенциала.
Поэтому всегда можно определитьмежду
двумя точками, измеряя U
между ними, причем тем точнее, чем ближе
точки. В однородном электрическом поле
силовые линии – прямые. Поэтому здесь
определить
наиболее
просто:

(3.6.1)

Теперь
дадим определение эквипотенциальной
поверхности.
Воображаемая
поверхность, все точки которой имеют
одинаковый потенциал, называется
эквипотенциальной поверхностью.
Уравнение этой поверхности

(3.6.2)

Графическое
изображение силовых линий и эквипотенциальных
поверхностей показано на рисунке 3.4.

Рис. 3.4

При
перемещении по этой поверхности на dl
потенциал не изменится:

Отсюда
следует, что проекция вектора
на
dlравнанулю,
то есть
Следовательно,

в
каждой точке направлена
по нормали
к эквипотенциальной поверхности.

Эквипотенциальных
поверхностей можно провести сколько
угодно много. По густоте эквипотенциальных
поверхностей можно судить о величине

,
это будет при условии, что разность
потенциалов между двумя соседними
эквипотенциальными поверхностями равна
постоянной величине

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

In physics, chemistry and biology, a potential gradient is the local rate of change of the potential with respect to displacement, i.e. spatial derivative, or gradient. This quantity frequently occurs in equations of physical processes because it leads to some form of flux.

Definition[edit]

One dimension[edit]

The simplest definition for a potential gradient F in one dimension is the following:^[1]

$F={frac {phi _{2}-phi _{1}}{x_{2}-x_{1}}}={frac {Delta phi }{Delta x}},!$

where ϕ(x) is some type of scalar potential and x is displacement (not distance) in the x direction, the subscripts label two different positions x₁, x₂, and potentials at those points, ϕ₁ = ϕ(x₁), ϕ₂ = ϕ(x₂). In the limit of infinitesimal displacements, the ratio of differences becomes a ratio of differentials:

$F={frac {{{rm {d}}}phi }{{{rm {d}}}x}}.,!$

The direction of the electric potential gradient is from $x_{1}$ to $x_{2}$ .

Three dimensions[edit]

In three dimensions, Cartesian coordinates make it clear that the resultant potential gradient is the sum of the potential gradients in each direction:

${mathbf {F}}={mathbf {e}}_{x}{frac {partial phi }{partial x}}+{mathbf {e}}_{y}{frac {partial phi }{partial y}}+{mathbf {e}}_{z}{frac {partial phi }{partial z}},!$

where e_x, e_y, e_z are unit vectors in the x, y, z directions. This can be compactly written in terms of the gradient operator ∇,

although this final form holds in any curvilinear coordinate system, not just Cartesian.

This expression represents a significant feature of any conservative vector field F, namely F has a corresponding potential ϕ.^[2]

Using Stokes’ theorem, this is equivalently stated as

nabla times {mathbf {F}}={boldsymbol {0}},!

meaning the curl, denoted ∇×, of the vector field vanishes.

Physics[edit]

Newtonian gravitation[edit]

In the case of the gravitational field g, which can be shown to be conservative,^[3] it is equal to the gradient in gravitational potential Φ:

There are opposite signs between gravitational field and potential, because the potential gradient and field are opposite in direction: as the potential increases, the gravitational field strength decreases and vice versa.

Electromagnetism[edit]

In electrostatics, the electric field E is independent of time t, so there is no induction of a time-dependent magnetic field B by Faraday’s law of induction:

$nabla times {mathbf {E}}=-{frac {partial {mathbf {B}}}{partial t}}={boldsymbol {0}},,$

which implies E is the gradient of the electric potential V, identical to the classical gravitational field:^[4]

In electrodynamics, the E field is time dependent and induces a time-dependent B field also (again by Faraday’s law), so the curl of E is not zero like before, which implies the electric field is no longer the gradient of electric potential. A time-dependent term must be added:^[5]

$-{mathbf {E}}=nabla V+{frac {partial {mathbf {A}}}{partial t}},!$

where A is the electromagnetic vector potential. This last potential expression in fact reduces Faraday’s law to an identity.

Fluid mechanics[edit]

In fluid mechanics, the velocity field v describes the fluid motion. An irrotational flow means the velocity field is conservative, or equivalently the vorticity pseudovector field ω is zero:

{boldsymbol {omega }}=nabla times {mathbf {v}}={boldsymbol {0}}.

This allows the velocity potential to be defined simply as:

Chemistry[edit]

In an electrochemical half-cell, at the interface between the electrolyte (an ionic solution) and the metal electrode, the standard electric potential difference is:^[6]

${displaystyle Delta phi _{(M,M^{+z})}=Delta phi _{(M,M^{+z})}^{ominus }+{frac {RT}{zeN_{text{A}}}}ln a_{M^{+z}},!}$

where R = gas constant, T = temperature of solution, z = valency of the metal, e = elementary charge, N_A = Avogadro constant, and a_M^+z is the activity of the ions in solution. Quantities with superscript ⊖ denote the measurement is taken under standard conditions. The potential gradient is relatively abrupt, since there is an almost definite boundary between the metal and solution, hence the interface term.^{[clarification needed]}

Biology[edit]

In biology, a potential gradient is the net difference in electric charge across a cell membrane.

Non-uniqueness of potentials[edit]

Since gradients in potentials correspond to physical fields, it makes no difference if a constant is added on (it is erased by the gradient operator ∇ which includes partial differentiation). This means there is no way to tell what the «absolute value» of the potential «is» – the zero value of potential is completely arbitrary and can be chosen anywhere by convenience (even «at infinity»). This idea also applies to vector potentials, and is exploited in classical field theory and also gauge field theory.

Absolute values of potentials are not physically observable, only gradients and path-dependent potential differences are. However, the Aharonov–Bohm effect is a quantum mechanical effect which illustrates that non-zero electromagnetic potentials along a closed loop (even when the E and B fields are zero everywhere in the region) lead to changes in the phase of the wave function of an electrically charged particle in the region, so the potentials appear to have measurable significance.

Potential theory[edit]

Field equations, such as Gauss’s laws for electricity, for magnetism, and for gravity, can be written in the form:

where ρ is the electric charge density, monopole density (should they exist), or mass density and X is a constant (in terms of physical constants G, ε₀, μ₀ and other numerical factors).

Scalar potential gradients lead to Poisson’s equation:

$nabla cdot (nabla phi )=Xrho quad Rightarrow quad nabla ^{2}phi =Xrho$

A general theory of potentials has been developed to solve this equation for the potential. The gradient of that solution gives the physical field, solving the field equation.

References[edit]

^ Essential Principles of Physics, P.M. Whelan, M.J. Hodgeson, 2nd Edition, 1978, John Murray, ISBN 0-7195-3382-1
^ Vector Analysis (2nd Edition), M.R. Spiegel, S. Lipcshutz, D. Spellman, Schaum’s Outlines, McGraw Hill (USA), 2009, ISBN 978-0-07-161545-7
^ Dynamics and Relativity, J.R. Forshaw, A.G. Smith, Wiley, 2009, ISBN 978-0-470-01460-8
^ Electromagnetism (2nd Edition), I.S. Grant, W.R. Phillips, Manchester Physics, John Wiley & Sons, 2008, ISBN 978-0-471-92712-9
^ Introduction to Electrodynamics (3rd Edition), D.J. Griffiths, Pearson Education, Dorling Kindersley, 2007, ISBN 81-7758-293-3
^ Physical chemistry, P.W. Atkins, Oxford University Press, 1978, ISBN 0-19-855148-7

Источник

Беседа 2. Потенциальная энергия

Вы, мой друг, совершенно правильно интересуетесь важнейшей составляющей полной энергии.

Принято считать, что потенциальная энергия является частью общей энергии системы, зависящей от взаимного расположения материальных частиц, составляющих эту систему, и от их положений во внешнем силовом поле (гравитационное, электрическое поле).

Силовым полем мы называем ту часть пространства, в каждой точке которой на помещенную туда материальную частицу действует определённая по величине и направлению сила.

Численно потенциальная энергия системы в данном её положении равна работе, которую произведут действующие на систему силы при её перемещении из этого положения в то, где потенциальная энергия равна нулю.

Коллега, энергией обладает только пробное тело в потенциальном поле или потенциальное поле тоже?

Для ответа на Ваш вопрос открываем БСЭ (Большая Советская Энциклопедия) и в разделе «Поля физические» читаем (дословно):
«Поля физические, особая форма материи; физическая система, обладающая бесконечно большим числом степеней свободы. Примерами полей физических могут служить электромагнитное и гравитационное поля. ».

Отсюда следует, что потенциальное поле является материальной средой. Значит, как и любая материальная среда, это поле обладает энергией (соответственно, и массой). Кстати, это подтверждается, к примеру, наличием в поле электромагнитных волн, которые являются колебаниями этой материальной среды.

Конкретные границы поля определить сложно, поэтому физики давно привыкли оперировать энергией, содержащейся в единице объёма, то есть – объёмной плотностью энергии потенциального поля (измеряется в Дж/м 3 ). Возьмём, к примеру, книгу Зильбермана «Электричество и магнетизм» (Наука, М., 1970) и на стр. 136 читаем (дословно):
«В плоском конденсаторе и вообще в однородном поле плотность энергии, т. е. энергия, содержащаяся в единице объёма, постоянна и равна полной энергии, делённой на объём».

Коллега, раз уж потенциальное поле является материальной средой, то оно должно характеризоваться конкретными параметрами, которые можно вычислить и измерить.

Вы совершенно правы. Мы уже выяснили, что электрическое (потенциальное) поле характеризуется таким параметром, как объёмная плотность энергии (далее – давление, Дж/м 3 или Н/м 2 ). Кроме этого, потенциальное поле характеризуется потенциалом и его градиентом – напряженностью поля. Причем, давление, потенциал и напряженность характеризуют потенциальное поле в данной его точке, независимо от наличия в этой точке пробного тела, ибо поле, как мы уже знаем, само обладает энергией и массой.

Если потенциальную энергию (W_П, Дж) отнести к единичной массе (m, кг) или к единичному электрическому заряду (q, Кл), то получим гравитационный (v 2 = W_П/m, Дж/кг) или электрический (U = W_П/q, Дж/Кл) потенциалы.

Градиентом потенциала в данной его точке является напряженность поля:
— для гравитационного поля: g = – grad v 2 ;
— для электрического: E = – grad U (о знаке речь пойдет ниже).

Градиент (от лат. gradiens, род. падеж gradientis – шагающий), вектор, показывающий направление наискорейшего изменения некоторой величины от одной точки пространства к другой.

С удалением от центра поля изменяется не только потенциал, но и потенциальная энергия. И её градиентом является сила, которую мы называем силой тяготения.

Дополнение: Мы уже договорились, что градиентом гравитационного потенциала является напряженность гравитационного поля g = – grad v 2 . Помножив эти два параметра на массу, мы получим, соответственно, значение силы (F = mg) и потенциальной энергии (W_П = mv 2 ). Следовательно, силу тоже можно считать градиентом энергии в данной точке поля (F = – grad W_П).
Аналогично для электрического поля: напряженность электрического поля E = – grad U, сила F = qE, потенциальная энергия W_П = qU. Значит, и здесь F = – grad W_П.

Уравнение F = – grad W_П показывает, что работа сил вдоль замкнутой траектории в потенциальном поле всегда равна нулю.

Коллега, какие единицы измерения наиболее приемлемы для вышеназванных параметров?

Очень хороший вопрос. СИЛА измеряется в ньютонах (Н = кг*м/с 2 ) или в Дж/м. Второй вариант записи более приемлемый, ибо сразу даёт нам указание на то, что сила является всего лишь ГРАДИЕНТОМ ЭНЕРГИИ (Дж/м). Это важно, ибо упрощает дальнейшее понимание физических процессов. Кстати, это касается не только силы, но и таких параметров, как давление и потенциал.

ДАВЛЕНИЕ измеряется в Н/м 2 или в Дж/м 3 . Здесь тоже более приемлемым является второй вариант записи, ибо сразу указывает нам на ОБЪЁМНУЮ ПЛОТНОСТЬ ЭНЕРГИИ (Дж/м 3 ).

ПОТЕНЦИАЛ измеряется в м 2 /с 2 или в Дж/кг (для гравитационного поля) и в (кг/Кл)*( м 2 /с 2 ) или Дж/Кл (для электрического поля). И здесь более приемлемым является второй вариант записи, ибо сразу указывает на значение потенциальной энергии, отнесенной к единице массы (Дж/кг) для гравитационного поля или отнесенной к единице электрического заряда (Дж/Кл) для электрического поля.

И наконец, коллега, давайте рассмотрим, как определяется значение потенциальной энергии.

Пожалуй, теперь мы готовы решать и эту проблему. Значение потенциальной энергии определяется двумя способами:
— упрощенный (приближенный) – для однородного поля;
— общий (истинный) – для неоднородного поля, которое нас реально и окружает.

Потенциальное поле можно условно считать однородным, если вектор напряженности во всех его точках имеет одно и то же значение и направление. К примеру, для гравитационного поля это правило можно применить только у поверхности Земли на небольшом её участке (скажем, в лабораторном опыте). В этом случае для упрощения расчетов значение потенциальной энергии пробного тела на поверхности Земли условно принимается равной нулю, а её значение в любой другой точке определяется из уравнения:

W_П = mgh, Дж,
где g – напряженность гравитационного поля (Н/кг), а h – вертикальное расстояние (м) от поверхности Земли до пробного тела массой m (кг).

Здесь знак перед значением потенциальной энергии принципиального значения не имеет.

Коллега, но ведь это и есть наиболее распространенный способ определения потенциальной энергии.

К сожалению, многие учебники физики на этом и завершают определение потенциальной энергии. Но не все. Взять, к примеру, Общий курс физики Сивухина (Москва, МФТИ, 2005) или американский курс Физики в переводе под редакцией Ахматова (Москва, Наука, 1974).

Здесь рассматривается:
— уже известный нам способ определения потенциальной энергии пробного тела в однородном поле тяжести у поверхности Земли (том 1, стр. 144-145 первого источника и часть III, стр.152-157 второго источника);
— и общий способ определения потенциальной энергии для неоднородного поля (том 1, стр. 145-146 первого источника и часть III, стр.157-159 второго источника).

Общий способ расчета дает уже отрицательное значение потенциальной энергии:
— уравнение (25.6) W(U) = – GMm/r в первом источнике и
— уравнение W(Ur) = – GMm/r – во втором.

Отрицательное значение потенциальной энергии здесь объясняется следующим образом:
— в первом источнике (цитата): «Максимальной энергией притягивающиеся массы обладают при бесконечном расстоянии между ними. В этом положении потенциальная энергия считается равной нулю. Во всяком другом положении она меньше, т. е. отрицательна»;
— во втором источнике дано доказательство правильности уравнения W(Ur) = – GMm/r.

И действительно, свободно падающее к центру поля тело теряет свою потенциальную энергию, которая переходит в кинетическую. Значит, потенциальная энергия с уменьшением расстояния между центрами масс (M и m) уменьшается и, наоборот, с увеличением расстояния – увеличивается.

Учитывая, что в уже известном нам уравнении W_П = – GMm/r символ радиуса находится в знаменателе, то предельно ясно, что с увеличением расстояния (значение радиуса стремится к бесконечности) потенциальная энергия увеличивается до… нуля. Такое возможно только в том случае, если потенциальная энергия во всяком другом положении отрицательна.

Вывод: потенциальная энергия для всех материальных частиц отрицательна.

Отсюда следует, что значение гравитационного потенциала v 2 = W_П/m = – GM/r тоже отрицательно. И подтверждением этому является уравнение (3) в разделе «Тяготение» (стр. 772) Физического Энциклопедического Словаря или аналогичного раздела Большой Советской Энциклопедии.

Аналогично определяется значение потенциальной энергии и электрического потенциала в электрическом поле. Причем далее мы убедимся в том, что потенциальная энергия и её объёмная плотность (давление) ОДИНАКОВЫ и для гравитационного, и для электрического полей.

Коллега, теперь попробуйте записать Ваше высказывание в виде формулы.

Формулы пишут математики, а физики пользуются уравнениями. Необходимые уравнения здесь уже приводились. Однако попробуем, все же, обойтись пока без них, тем более – без «формул».

Для этого используем бытовые наблюдения, которые подсказывают: чтобы испарить воду, кипящую в чайнике, нужно сжечь некоторое количество дров или газа. Другими словами, нужно совершить работу. С помощью термометра можно убедиться, что температура кипящей воды и температура пара над ней одинаковы. Следовательно, одинакова и средняя энергия движения частиц в кипящей воде и в паре.

Вывод: тепловая энергия, передаваемая кипящей воде от топлива, преобразуется в энергию взаимодействия частиц испаряющейся воды. Значит, энергия связи частиц в кипящей воде меньше, чем в водяном паре. Но в паре эта энергия практически равна нулю, следовательно, энергия взаимодействия частиц в жидкости меньше нуля, т.е. отрицательна.

Коллега, Ваши доводы убедительны и примеры Вы приводите неопровержимые. Однако не все думают так же.

И здесь Вы совершенно правы. Для физиков проблем с пониманием сути и знака потенциальной энергии нет, ибо они гравитационное поле, в том числе и поле тяготения Земли, считают НЕОДНОРОДНЫМ. Для физиков напряженность гравитационного поля изменяется с расстоянием в квадрате: g = Gm/r 2 .

Однако математики так не думают. Для них гравитационное поле является ОДНОРОДНЫМ с неизменной напряженностью гравитационного поля (вроде этот параметр и не зависит от радиуса). Значение потенциальной энергии они определяют по упрощенной формуле W = mgh. Они не связывают h с радиусом поля, а считают его простым отрезком между двумя произвольными точками этого поля. Поэтому для них потенциальная энергия может принимать нулевое значение в любой понравившейся им точке. Нонсенс, но бывает и такое.

Но есть ещё и «физико-математики». Их мнение зависит от того, насколько они физики или математики.

Коллега, почему Вы считаете, что математики «тяготеют» к однородному полю?

В подтверждение этому открываем Краткий курс математического анализа (Бермант, Араманович, 2005) и на стр. 520 в разделе «Теория поля» читаем:
«Векторное поле называется однородным, если А(Р) — постоянный вектор, т.е. Ах, Аy и Az — постоянные величины.
Примером однородного поля может служить, например, поле тяжести».

Теперь Вы и сами видите, что математики гравитационное поле называют «полем тяжести» и «всерьёз» считают его однородным. И это не просто безобидное заблуждение, ибо оно мешает нам осознать Природу гравитации. Однако, об этом мы поговорим немного позже.

Куда и почему направлен градиент потенциала

§7 Работа силы электростатического поля при перемещении заряда.

Потенциальный характер сил поля.

Циркуляция вектора напряженности

— проекция на направление контура ?.

Учтем, что работа по замкнутому пути равно нулю

— ЦИРКУЛЯЦИЯ вектора напряженности.

§7 Потенциал.

Связь между напряженностью и потенциалом.

Градиент потенциала.

Эквипотенциальные поверхности

Различные пробные заряды q ₀_i , помещенные в данную точку поля будут обладать в этой точке различными потенциальными энергиями:

…

Отношение W _пот_i к величине пробного заряда q ₀_i , помещенного в данную точку поля является величиной постоянной для данной точки поля для всех пробных зарядов. Это отношение называется ПОТЕНЦИАЛОМ.

Работу по перемещению заряда можно представить в виде

Потенциал измеряется в Вольтах

С другой стороны

— градиент потенциала.

Напряженность поля равна градиенту потенциала, взятому со знаком минус.

гле

§9 Вычисление разности потенциалов плоскости, двух плоскостей, сферы, шара, цилиндра

Используя связь между φ и определим разность потенциалов между двумя произвольными точками

Если х₁ = 0; х₂ = d , то или

3. Разность потенциалов поля равномерно заряженной сферической поверхности радиуса R .

Внутри сферической поверхности потенциал всюду одинаков и равен

4. Разность потенциалов поля объемно заряженного шара радиуса R с общим зарядом Q.

Вне шара r ₁ , r ₂ > R ,

Внутри шара

5. Разность потенциалов поля равномерно заряженного цилиндра (или бесконечно длинной нити).

r > R :

Градиента потенциала.

В электростатическом поле между двумя близко расположенными точками в общем случае имеется некоторая разность потенциалов. Если эту разность потенциалов разделить на кратчайшее расстояние между взятыми точками, то полученная величина будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками. Эта скорость будет зависеть от направления, вдоль которого взяты точки.

В математике используют понятие градиента скалярной функции, под которым понимают скорость изменения скалярной функции, взятую в направлении ее наибольшего возрастания.

Возьмем две близко расположенные эквипотенциальные линии. Одна из них имеет потенциал φ₁, другая – φ₂, причем φ₁ > φ₂ (рис. 38.3). Тогда градиент изобразится вектором, перпендикулярным к эквипотенциальным линиям и направленным от φ₂ к φ₁ (в сторону увеличения потенциала).

Напряженность электрического поля направлена от более высокого потенциала (φ₁) к менее высокому (φ₂). Если через dn обозначить расстояние по нормали между эквипотенциальными поверхностями, а через вектор, совпадающий с направлением напряженности поля , т.е. ( – единичный вектор, направленный по направлению ), то можно записать выражение

где – приращение потенциала при переходе от точки 1 к точке 2.

Так как векторы и совпадают по направлению, то . Таким образом Отсюда . Вектор напряженности поля . Поэтому

Из определения градиента следует, что

Сопоставляя (19.5) и (19.6), получаем

Физический смысл выражения (38.7) заключается в том, что напряженность поля в какой-либо его точке равна скорости изменения потенциала в этой точке, взятой с обратным знаком.

Нормаль в общем случае может не совпадать с направлением какой-либо координатной оси, и поэтому градиент потенциала в общем случае можно представить в виде суммы трех проекций по координатным осям. Например, в декартовой системе координат

Вектор напряженности поля Таким образом,

Два вектора равны только тогда, когда равны друг другу их соответствующие проекции. Следовательно

Для сокращения записи в математике используют дифференциальный оператор Гамильтона: используя который можно записать

Вопросы для самоконтроля

1. Какова основная отличительная особенность электромагнитного поля как вида материи?

2. Какими двумя сторонами характеризуется электромагнитное поле? Как эти стороны связаны между собой?

3. Охарактеризуйте понятие «электрическое поле».

4. Какими двумя основными величинами характеризуется электрическое поле?

5. Дайте определение потенциала электрического поля.

6. Какие поля называют потенциальными? Почему суммарная работа по переносу электрического заряда по замкнутому контуру в потенциальном поле равна нулю?

Источник

Вектор градиента потенциала электростатического поля

Градиент потенциала

Градиент потенциальных характеристик, как его рассчитать и пример

черты

Как рассчитать?

пример

осуществление

Шаг 1

Шаг 2

Шаг 3

Definition[edit]

One dimension[edit]

Three dimensions[edit]

Physics[edit]

Newtonian gravitation[edit]

Electromagnetism[edit]

Fluid mechanics[edit]

Chemistry[edit]

Biology[edit]

Non-uniqueness of potentials[edit]

Potential theory[edit]

See also[edit]

References[edit]

Беседа 2. Потенциальная энергия

Куда и почему направлен градиент потенциала

Градиента потенциала.