Как найти направление тока самоиндукции - Исправление недочетов и поиск решений вместе с Examum.ru

Явление электромагнитной индукции очень часто наблюдается в электротехнике. Взаимное влияние электрических и магнитных полей иногда приводит к интересным результатам. Самоиндукция – частный случай электромагнитной индукции.

Общеизвестно, что причиной порождения электрического тока является переменное магнитное поле. Именно этот принцип реализован в конструкциях современных генераторов. Природа самоиндукции также связана с электромагнетизмом, но это явление проявляется она по-другому.

Определение

Рассмотрим схему катушки, по обмоткам которой протекает электрический ток (рис. 1). Так как вокруг проводника, который находится под током, всегда существует связанное с ним магнитное поле, то силовые линии этого поля пронизывают плоскости витков. В результате такого взаимодействия соленоиды образуют собственное магнитное поле, магнитные линии которого замыкаются за его пределами.

Рис. 1. Магнитное поле катушки

Частным случаем катушки является замкнутый контур (один виток). В нём, как и в катушке, образуется собственное магнитное поле (см. рис. 2). Если ток постоянный, то в контуре никаких изменений не происходит.

Но при изменении параметров, например, в результате размыкания цепи, изменяется магнитный поток, создаваемый электрическим полем, что является причиной возникновения ЭДС индукции. Аналогичное изменение произойдёт и в случае замыкания цепи.

Изменение параметров магнитного поля вызывает появление вихревого электрического поля, что в свою очередь приводит к возбуждению индуктивной электродвижущей силы. Возникновение ЭДС индукции, в результате изменения ток в замкнутом контуре, называется самоиндукцией.

Магнитный поток, ограниченный поверхностью контура, меняется прямо пропорционально изменению тока, циркулирующего в нём.

Рис. 2. Явление самоиндукции

Направление вектора ЭДС самоиндукции не совпадает с направлением тока в период его возрастания (при замыкании цепи), но он сонаправлен с ним в период убывания (разъединения цепи). Такое действие проявляется в замедлении появления тока в соленоиде при замыкания цепи, или в его задержке на какое-то время после разрыва цепи.

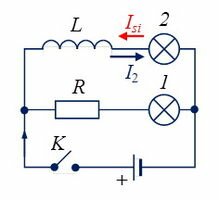
Описанное явление можно наблюдать на опыте с лампочками, одна из которых подключена последовательно с индуктивностью (см. рис. 3).

Рис. 3. Схема опыта с лампочками

Как видно на рисунке слева, ток от источника питания, проходящий через лампочку 2, при замыкании контактов встретит сопротивление вихревых токов, поскольку они противоположно направлены. Поэтому зажигание этой лампочки произойдёт с задержкой.

На время включения лампочки 1 вихревые токи повлияют, но сила тока в её цепи уменьшится после зажигания лампы 2. При отключении цепи от источника питания произойдёт обратный процесс: лампочка в цепи индуктивности некоторое время будет медленно угасать, а вторая лампа потухнет сразу после разъединения контактов.

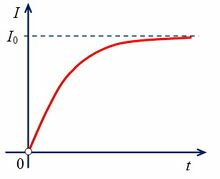
График на рисунке 4 красноречиво объясняет эффект задержки.

Рис. 4. Иллюстрация задержки изменения тока в цепи индуктивности

Обратите внимание на нелинейность изменения силы тока по времени.

Аналогичные процессы происходят в цепи, состоящей из одной катушки. На рисунке 5 изображена такая схема и график изменения силы тока.

Рис. 5. Возникновение самоиндукции

Остаётся добавить, что скорость изменение величины ЭДС зависит от количества витков соленоида. Чем больше витков, тем больше влияние вихревых токов, на параметры цепи.

В случае с переменным током амплитуда ЭДС самоиндукции пропорциональна амплитуде синусоиды питания, её частоте и индуктивности катушки.

Синусоидальный ток, проходя через катушку индуктивности, сдвигается по фазе на величину π/2. Именно этот сдвиг является причиной отставания собственного тока катушки от тока, вырабатываемого источником питания.

Формулы

Собственный магнитный поток контура (Ф) связан прямо пропорциональной зависимостью с индуктивностью (L) этого контура и величиной тока в нём (i). Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.

При этом индуктивность контура пребывает в зависимости от его геометрии, площади плоскости ограниченной витком и магнитной проницаемости окружающей среды. Но этот коэффициент не зависит от силы тока в контуре. Если же форма, линейные размеры и магнитная проницаемость не изменяются, то для определения величины индуктивной ЭДС применяется формула:

где E_{самоинд.} – ЭДС самоиндукции, Δi – изменение силы тока за время Δt.

Индуктивность

Выше мы отметили, что индуктивность контура зависит от его геометрии и размеров, а также от магнитной проницаемости среды. Если речь идёт о катушке, то эти утверждения справедливы и для неё. На индуктивность катушки влияет её диаметр и количество витков. Индуктивность существенно повышается, если в катушку добавить ферромагнитный сердечник.

Магнитные поля отдельных витков катушки складываются. Если витков достаточно много, то ток, протекающий через катушку, образует вокруг неё сильное магнитное поле, реагирующее на изменения электрического поля. Индуктивность является той величиной, которая характеризует то, насколько сильно проводник, из которого состоят витки, противодействует электрическому току.

Чем больше индуктивность катушки и чем выше скорость прерывания её цепи, тем больший всплеск ЭДС произойдёт в цепи. При этом полярность вихревых токов на выводах катушки противоположна направлению тока источника питания.

Индуктивность (то есть коэффициент пропорциональности) является важной характеристикой катушек, дросселей и других контурных элементов. Этот параметр можно сравнить с ёмкостью конденсаторов. Тем более что действие катушки индуктивности и конденсатора в электрических цепях очень похожи. RL и RC цепочки часто используют для сглаживания всплесков напряжений в различных фильтрах.

Единицей измерения индуктивности в международной системе СИ является генри. Величина размеров в 1 Гн – это такая индуктивность, при которой ЭДС составляет 1 В, при скорости изменения тока на 1 А за секунду.

Индуктивность определяет количество энергии, выделяющейся в результате действия собственного магнитного поля при самоиндукции. Эту энергию легко рассчитать по формуле: W_м = LI²/2.

Собственная энергия катушки численно равна работе, которую необходимо выполнить источником питания при преодолении ЭДС самоиндукции.

Важно знать, что в результате резкого разрыва цепи с большой индуктивностью, энергия высвобождается в виде искры или даже с образованием дугового разряда.

Примеры использования на практике

Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.

Работает этот важный узел следующим образом:

На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.
Электрическая цепь резко обрывается специальным прерывателем.
Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
Искровой разряд зажигает топливную смесь, приводя в движение поршень.

В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.

Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.

В блоках питания электронной аппаратуры таким же способом убирают:

шумы:
пульсации;
нежелательные частоты.

Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.

Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред. При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п. С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.

В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.

В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.

Видео в помощь

Источник

Самоиндукция

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: самоиндукция, индуктивность, энергия магнитного поля.

Самоиндукция является частным случаем электромагнитной индукции. Оказывается, что электрический ток в контуре, меняющийся со временем, определённым образом воздействует сам на себя.

Ситуация 1 .Предположим, что сила тока в контуре возрастает. Пусть ток течёт против часовой стрелки; тогда магнитное поле этого тока направлено вверх и увеличивается (рис. 1).

Рис. 1. Вихревое поле препятствует увеличению тока

Таким образом, наш контур оказывается в переменном магнитном поле своего собственного тока. Магнитное поле в данном случае возрастает (вместе с током) и потому порождает вихревое электрическое поле, линии которого направлены по часовой стрелке в соответствии с правилом Ленца.

Как видим, вихревое электрическое поле направлено против тока, препятствуя его возрастанию; оно как бы «тормозит» ток. Поэтому при замыкании любой цепи ток устанавливается не мгновенно — требуется некоторое время, чтобы преодолеть тормозящее действие возникающего вихревого электрического поля.

Ситуация 2 . Предположим теперь, что сила тока в контуре уменьшается. Магнитное поле тока также убывает и порождает вихревое электрическое поле, направленное против часовой стрелки (рис. 2).

Рис. 2. Вихревое поле поддерживает убывающий ток

Теперь вихревое электрическое поле направлено в ту же сторону, что и ток; оно поддерживает ток, препятствуя его убыванию.

Как мы знаем, работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура — это ЭДС индукции. Поэтому мы можем дать такое определение.

Явление самоиндукции состоит в том, что при изменении силы тока в контуре возникает ЭДС индукции в этом же самом контуре.

При возрастании силы тока (в ситуации 1) вихревое электрическое поле совершает отрицательную работу, тормозя свободные заряды. Стало быть, ЭДС индукции в этом случае отрицательна.

При убывании силы тока (в ситуации 2) вихревое электрическое поле совершает положительную работу, «подталкивая» свободные заряды и препятствуя убыванию тока. ЭДС индукции в этом случае также положительна (нетрудно убедиться в том, что знак ЭДС индукции, определённый таким образом, согласуется с правилом выбора знака для ЭДС индукции, сформулированным в листке «Электромагнитная индукция»).

Индуктивность

Мы знаем, что магнитный поток, пронизывающий контур, пропорционален индукции магнитного поля: . Кроме того, опыт показывает, что величина индукции магнитного поля контура с током пропорциональна силе тока: B sim I . Стало быть, магнитный поток через поверхность контура, создаваемый магнитным полем тока в этом самом контуре, пропорционален силе тока: .

Коэффициент пропорциональности обозначается и называется индуктивностью контура:

(1)

Индуктивность зависит от геометрических свойств контура (формы и размеров), а также от магнитных свойств среды, в которую помещён контур (Улавливаете аналогию? Ёмкость конденсатора зависит от его геометрических характеристик, а также от диэлектрической проницаемости среды между обкладками конденсатора). Единицей измерения индуктивности служит генри (Гн).

Допустим, что форма контура, его размеры и магнитные свойства среды остаются постоянными (например, наш контур — это катушка, в которую не вводится сердечник); изменение магнитного потока через контур вызвано только изменением силы тока. Тогда , и закон Фарадея приобретает вид:

$mathcal E_i = -L frac{displaystyle Delta I}{displaystyle Delta t vphantom{1^a}} = -LI.$ (2)

Благодаря знаку «минус» в (2) ЭДС индукции оказывается отрицательной при возрастании тока и положительной при убывании тока, что мы и видели выше.

Рассмотрим два опыта, демонстрирующих явление самоиндукции при замыкании и размыкании цепи.

Рис. 3. Самоиндукция при замыкании цепи

В первом опыте к батарейке подключены параллельно две лампочки, причём вторая — последовательно с катушкой достаточно большой индуктивности (рис. 3).

Ключ вначале разомкнут.

При замыкании ключа лампочка 1 загорается сразу, а лампочка 2 — постепенно. Дело в том, что в катушке возникает ЭДС индукции, препятствующая возрастанию тока. Поэтому максимальное значение тока во второй лампочке устанавливается лишь спустя некоторое заметное время после вспыхивания первой лампочки.

Это время запаздывания тем больше, чем больше индуктивность катушки. Объяснение простое: ведь тогда больше будет напряжённость вихревого электрического поля, возникающего в катушке, и потому батарейке придётся совершить большую работу по преодолению вихревого поля, тормозящего заряженные частицы.

Во втором опыте к батарейке подключены параллельно катушка и лампочка (рис. 4). Сопротивление катушки много меньше сопротивления лампочки.

Рис. 4. Самоиндукция при размыкании цепи

Ключ вначале замкнут. Лампочка не горит — напряжение на ней близко к нулю из-за малости сопротивления катушки. Почти весь ток, идущий в неразветвлённой цепи, проходит через катушку.

При размыкании ключа лампочка ярко вспыхивает! Почему? Ток через катушку начинает резко убывать, и возникает значительная ЭДС индукции, поддерживающая убывающий ток (ведь ЭДС индукции, как видно из (2), пропорциональна скорости изменения тока).

Иными словами, при размыкании ключа в катушке появляется весьма большое вихревое электрическое поле, разгоняющее свободные заряды. Под действием этого вихревого поля через лампочку пробегает импульс тока, и мы видим яркую вспышку. При достаточно большой индуктивности катушки ЭДС индукции может стать существенно больше ЭДС батарейки, и лампочка вовсе перегорит.

Лампочку-то, может, и не жалко, но в промышленности и энергетике данный эффект является серьёзной проблемой. Так как при размыкании цепи ток начинает уменьшаться очень быстро, возникающая в цепи ЭДС индукции может значительно превышать номинальные напряжения и достигать опасно больших величин. Поэтому в агрегатах, потребляющих большой ток, предусмотрены специальные аппаратные меры предосторожности (например, масляные выключатели на электростанциях), препятствующие моментальному размыканию цепи.

Электромеханическая аналогия

Нетрудно заметить определённую аналогию между индуктивностью в электродинамике и массой в механике.

1. Чтобы разогнать тело до заданной скорости, требуется некоторое время — мгновенно изменить скорость тела не получается. При неизменной силе, приложенной к телу, это время тем больше, чем больше масса тела.

Чтобы ток в катушке достиг своего максимального значения, требуется некоторое время; мгновенно ток не устанавливается. Время установления тока тем больше, чем больше индуктивность катушки.

2. Если тело налетает на неподвижную стену, то скорость тела уменьшается очень быстро. Стена принимает на себя удар, и его разрушительное действие тем сильнее, чем больше масса тела.

При размыкании цепи с катушкой ток уменьшается очень быстро. Цепь принимает на себя «удар» в виде вихревого электрического поля, порождаемого убывающим магнитным полем тока, и этот «удар» тем сильнее, чем больше индуктивность катушки. ЭДС индукции может достичь столь больших величин, что пробой воздушного промежутка выведет из строя оборудование.

На самом деле эти электромеханические аналогии простираются довольно далеко; они касаются не только индуктивности и массы, но и других величин, и оказываются весьма полезными на практике. Мы ещё поговорим об этом в листке про электромагнитные колебания.

Энергия магнитного поля

Вспомним второй опыт с лампочкой, которая не горит при замкнутом ключе и ярко вспыхивает при размыкании цепи. Мы непосредственно наблюдаем, что после размыкания ключа в лампочке выделяется энергия. Но откуда эта энергия берётся?

Берётся она, ясное дело, из катушки — больше неоткуда. Но что за энергия была запасена в катушке и как вычислить эту энергию? Чтобы понять это, продолжим нашу электромеханическую аналогию между индуктивностью и массой.

Чтобы разогнать тело массы из состояния покоя до скорости , внешняя сила должна совершить работу . Тело приобретает кинетическую энергию, которая равна затраченной работе: .

Чтобы после замыкания цепи ток в катушке индуктивности достиг величины , источник тока должен совершить работу по преодолению вихревого электрического поля, направленного против тока. Работа источника идёт на создание тока и превращается в энергию магнитного поля созданного тока. Эта энергия запасается в катушке; именно эта энергия и выделяется потом в лампочке после размыкания ключа (во втором опыте).

Индуктивность служит аналогом массы ; сила тока является очевидным аналогом скорости . Поэтому естественно предположить, что для энергии магнитного поля катушки может иметь место формула, аналогичная выражению для кинетической энергии:

$W = frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}}.$ (3)

(тем более, что правая часть данной формулы имеет размерность энергии — проверьте!).

Формула (3) действительно оказывается справедливой. Уметь её выводить пока не обязательно, но если вы знаете, что такое интеграл, то вам не составит труда понять следующие рассуждения.

Пусть в данный момент сила тока через катушку равна . Возьмём малый промежуток времени . В течение этого промежутка приращение силы тока равно ; величина считается настолько малой, что много меньше, чем .

За время по цепи проходит заряд dq=Idt . Вихревое электрическое поле совершает при этом отрицательную работу:

$dA_B = mathcal E_i dq = mathcal E_i Idt = -L frac{displaystyle dI}{displaystyle dt vphantom{1^a}}Idt=-LIdI.$

Источник тока совершает такую же по модулю положительную работу (сопротивлением катушки, напомним, мы пренебрегаем, так что вся работа источника совершается против вихревого поля):

Интегрируя это от нуля до , найдем работу источника , которая затрачивается на создание тока :

$A = int_{0}^{I}LIdI=frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}}.$

Эта работа превращается в энергию магнитного поля созданного тока, и мы приходим к формуле (3).

Разберем задачи ЕГЭ по физике по темам: «Самоиндукция», «Магнитный поток», «Индуктивность», «Электромагнитная индукция».

Задача 1. На катушке сопротивлением 8,2 Ом и индуктивностью 25 мГн поддерживается постоянное напряжение 55 В. Сколько энергии выделится при размыкании цепи? Какая средняя ЭДС самоиндукции появится при этом в катушке, если энергия будет выделяться в течение 12 мс?

Дано:

R = 8,2 Ом;
L= 25 мГн = $25cdot 10^{-3}$ Гн;
t = 12 мс = 12;

Найти:
W_м — ? E_is — ?

Решение:

Решение любой задачи по физике должно начинаться с создания модели, которая поясняет ситуацию, описанную в данной задачи. В качестве модели может выступать чертеж, пояснительный рисунок, электрическая схема.

Для этой задачи необходимо начертить электрическую схему.

На схеме изображены катушка индуктивности, источник тока, поддерживающий на ней постоянное напряжение, ключ.

При замкнутом ключе через катушку протекает постоянный электрический ток, величину которого можно рассчитать, используя закон Ома для участка цепи. Катушка аналогична резистору, подключенному в эту цепь.

$displaystyle I=frac{U}{R}, I=frac{55}{8,2}approx 6,7(A).$

Энергия магнитного поля рассчитывается по формуле:

$displaystyle W_{M}=frac{Li^{2}}{2}, W_{M}=frac{25cdot 10^{-3}cdot 6,7^{2}}{2}approx 0,56$ (Дж).

Стоит обратить внимание, что эта формула аналогична формуле кинетической энергии в механике: $displaystyle E_{K}=frac{mv^{2}}{2}.$

При размыкании ключа, через катушку начинает протекать уже переменный ток. Поэтому магнитный поток, пронизывающий катушку, меняется. В самой катушке возникает ЭДС индукции, так как в ней течёт переменный ток. Тем самым, возникает явление самоиндукции.

Используя закон электромагнитной индукции в виде $displaystyle mathcal E _{is}=-Lfrac{Delta I}{Delta t},$ приходим к расчету второй неизвестной величины этой задачи:

$displaystyle mathcal E _{is}=25cdot 10^{-3}frac{6,7}{12cdot 10^{-3}}approx 14$ (B).

В этих расчетах мы не учитывали знак (-), который указан в законе электромагнитной индукции. Смысл этого знака заключен в учёте правила Ленца, определяющего направление индукционного тока. Но так как о направлении индукционного тока речь в задаче не идет, то в расчетах именно получено значение модуля ЭДС самоиндукции.

Ответ: 0,56 Дж, 14 В.

Задача 2. На рисунке приведён график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 5 до 15 с. Ответ выразите в мкВ.

Решение

Решение любых графических задач необходимо начинать с «чтения» самого графика. В этой задаче рассматривается зависимость силы тока от времени в цепи, содержащей катушку индуктивности. Необходимо обратить внимание на те интервалы времени, в течение которых происходит изменение силы тока. С изменением этой величины связано изменение магнитного потока и, как следствие, возникновение ЭДС самоиндукции. Сила тока меняется в интервале от 0 до 5 с, от 5 до 10 с и от 15 до 20 с. В интервале от 10 до 15 с сила тока постоянна, изменение магнитного потока не происходит, поэтому $mathcal E _{si}=0$ . Для участка от 5 до 10 с надо применить закон электромагнитной индукции $displaystyle mathcal E _{is}=-Lfrac{Delta I}{Delta t}$ .

Для модуля ЭДС самоиндукции, т.е. без учета направления индукционного тока, этот закон будет иметь вид:

$displaystyle |mathcal E _{is}|=left|Lfrac{Delta I}{Delta t} right|$ .

Данные для расчета необходимо взять из графической зависимости, учитывая при этом перевод в систему «СИ».

$displaystyle mathcal E_{is}=left| 1cdot 10^{-3} frac{20cdot 10^{-3}-30cdot 10^{-3}}{10-5}right|=2cdot 10^{-6}(B)=2$ (мкВ).

Ответ: 2 мкВ.

Задача 3. Катушка, обладающая индуктивностью , соединена с источником питания с ЭДС и двумя одинаковыми резисторами . Электрическая схема соединения показана на рис. 1. В начальный момент ключ в цепи разомкнут.

В момент времени t=0 ключ замыкают, что приводит к изменениям силы тока, регистрируемым амперметром, как показано на рис. 2. Основываясь на известных физических законах, объясните почему при замыкании ключа сила тока плавно увеличивается до некоторого нового значения — $I_{1}.$ Определите значение силы тока $I_{1}.$ Внутренним сопротивлением источника тока пренебречь.

Решение

В данной задаче необходимо рассмотреть две ситуации, которые происходят до и после замыкания ключа.

До замыкания ключа в цепи устанавливается постоянная сила тока, которая определяется законом Ома для полной цепи $displaystyle I=frac{mathcal E}{R+r}$ . Так как по условию внутренним сопротивлением источника можно пренебречь, то $displaystyle I=frac{mathcal E}{R}=3$ (A).
После замыкания ключа параллельно к первому резистору подключается второй, имеющий такое же сопротивление. Тогда общее сопротивление цепи можно рассчитать, как $displaystyle frac{1}{R_{ob}}=frac{1}{R}+frac{1}{R}=frac{2}{R}; R_{ob}=frac{R}{2}.$ Таким образом, внешнее сопротивление цепи уменьшается в 2 раза.
Наличие в цепи катушки индуктивности, в которой возникает ЭДС самоиндукции, препятствует мгновенному нарастанию силы тока (по аналогии с механикой – тело большой массы не может быстро изменить свою скорость). Поэтому сила тока плавно увеличивается до некоторого значения $I_{1}.$
Так как ЭДС самоиндукции с течением времени уменьшается до нулевого значения, то ток в цепи будет возрастать в 2 раза, так как общее сопротивление уменьшается также в 2 раза.
$displaystyle I_{1}=frac{mathcal E}{R/2}=frac{2mathcal E}{R}=6$ (A).

Ответ: 6 А.

Задача 4. Катушка Проволочная рамка площадью 60 см² помещена в однородное магнитное поле так, что плоскость рамки перпендикулярна вектору индукции vec{B} . Проекция $B_{n}$ индукции магнитного поля на нормаль к плоскости рамки изменяется во времени t согласно графику на рисунке.

Из приведенного ниже списка выберите все верные утверждения о процессах, происходящих в рамке.

Модуль ЭДС электромагнитной индукции, возникающий в рамке, максимален в интервале от 0 до 1мс.
Ответ. Согласно закону электромагнитной индукции $displaystyle mathcal E=-frac{Delta Phi }{Delta t}=-frac{Delta Bcdot S}{Delta t}.$
Т.е. максимальное значение ЭДС индукции будет наблюдаться на интервале максимального изменения $B_{n}$ с течением времени. В интервале от 0 до 1 мс скорость изменения проекции $B_{n}$ наибольшая.
Утверждение верное.
Магнитный поток через рамку в интервале от 2 до 4 мс равен 12 мВб.
Ответ. Формула для расчета магнитного потока имеет вид $Phi=B_{n}S.$
В данном временном интервале проекция $B_{n}$ постоянна и равна 2 Тл.
$displaystyle Phi=2cdot 60cdot 10^{-4}=12cdot 10^{-3}$ (Вб) = 12 (мВб).
Утверждение верное.
Модуль ЭДС электромагнитной индукции, возникающей в рамке, в интервале от 4 до 6 мс равен 6 В.
Ответ. Согласно закону электромагнитной индукции $displaystyle mathcal E=-frac{Delta Phi }{Delta t}=-frac{Delta Bcdot S}{Delta t}.$
$displaystyle mathcal E=left|frac{(-2-2)cdot 60cdot 10^{-4}}{2cdot 10^{-3}}right|=12$ (B).
Утверждение неверное.
Модуль скорости изменения магнитного потока через рамку минимален в интервале от 0 до 1 мс.
Ответ. В той задаче изменение магнитного потока связано с изменением проекции $B_{n}$ индукции магнитного поля. В интервале от 0 до 1 мс проекция $B_{n}$ меняется быстрее всего, потому и изменение магнитного потока максимальное.
Утверждение неверное.
Модуль ЭДС электромагнитной индукции, возникающей в рамке, равен нулю в интервале времени от 2 до 4 мс.
Ответ. Согласно закону электромагнитной индукции $displaystyle mathcal E=-frac{Delta Phi }{Delta t}=-frac{Delta Bcdot S}{Delta t}.$
В интервале от 2 до 4 мс проекция $B_{n}$ не изменяется, потому и .
Тогда в проволочной рамке ЭДС индукции не возникает.
Утверждение верное.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Самоиндукция» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Содержание

1 Индуктивность
2 Явление самоиндукции
3 Энергия магнитного поля
- 3.1 *Вывод формулы
4 Литература

Индуктивность

Электрический ток, проходящий по контуру, создает вокруг него магнитное поле. Магнитный поток Φ через контур этого проводника (его называют собственным магнитным потоком) пропорционален модулю индукции В магнитного поля внутри контура (left( Phi sim B right)), а индукция магнитного поля в свою очередь пропорциональна силе тока в контуре (left( Bsim I right)).

Таким образом, собственный магнитный поток прямо пропорционален силе тока в контуре (left( Phi sim I right)). Эту зависимость математически можно представить следующим образом:

(Phi = L cdot I,)

где L — коэффициент пропорциональности, который называется индуктивностью контура.

Индуктивность контура — скалярная физическая величина, численно равная отношению собственного магнитного потока, пронизывающего контур, к силе тока в нем:

(~L = dfrac{Phi}{I}.)

В СИ единицей индуктивности является генри (Гн):

1 Гн = 1 Вб/(1 А).

Индуктивность контура равна 1 Гн, если при силе постоянного тока 1 А магнитный поток через контур равен 1 Вб.

Индуктивность контура зависит от размеров и формы контура, от магнитных свойств среды, в которой находится контур, но не зависит от силы тока в проводнике. Так, индуктивность соленоида можно рассчитать по формуле

(~L = mu cdot mu_0 cdot N^2 cdot dfrac{S}{l},)

где μ — магнитная проницаемость сердечника, μ₀ — магнитная постоянная, N — число витков соленоида, S — площадь витка, l — длина соленоида.

При неизменных форме и размерах неподвижного контура собственный магнитный поток через этот контур может изменяться только при изменении силы тока в нем, т.е.

(Delta Phi =L cdot Delta I.) (1)

Явление самоиндукции

Если в контуре проходит постоянный ток, то вокруг контура существует постоянное магнитное поле, и собственный магнитный поток, пронизывающий контур, не изменяется с течением времени.

Если же ток, проходящий в контуре, будет изменяться со временем, то соответственно изменяющийся собственный магнитный поток, и, согласно закону электромагнитной индукции, создает в контуре ЭДС.

Возникновение ЭДС индукции в контуре, которое вызвано изменением силы тока в этом контуре, называют явлением самоиндукции.

Самоиндукция была открыта американским физиком Дж. Генри в 1832 г.

Появляющуюся при этом ЭДС — ЭДС самоиндукции E_si. ЭДС самоиндукции создает в контуре ток самоиндукции I_si.

Направление тока самоиндукции определяется по правилу Ленца: ток самоиндукции всегда направлен так, что он противодействует изменению основного тока. Если основной ток возрастает, то ток самоиндукции направлен против направления основного тока, если уменьшается, то направления основного тока и тока самоиндукции совпадают.

Используя закон электромагнитной индукции для контура индуктивностью L и уравнение (1), получаем выражение для ЭДС самоиндукции:

(E_{si} =-dfrac{Delta Phi }{Delta t}=-Lcdot dfrac{Delta I}{Delta t}.)

ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока в контуре, взятой с противоположным знаком.

Эту формулу можно применять только при равномерном изменении силы тока.

При увеличении тока (ΔI > 0), ЭДС отрицательная (E_si < 0), т.е. индукционный ток направлен в противоположную сторону тока источника.

При уменьшении тока (ΔI < 0), ЭДС положительная (E_si > 0), т.е. индукционный ток направлен в ту же сторону, что и ток источника.

Из полученной формулы следует, что

(L=-E_{si} cdot dfrac{Delta t}{Delta I}.)

Индуктивность – это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

Явление самоиндукции можно наблюдать на простых опытах. На рисунке 1 показана схема параллельного включения двух одинаковых ламп. Одну из них подключают к источнику через резистор R, а другую — последовательно с катушкой L. При замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием. Объясняется это тем, что на участке цепи с лампой 1 нет индуктивности, поэтому тока самоиндукции не будет, и сила тока в этой лампе почти мгновенно достигает максимального значения. На участке с лампой 2 при увеличении тока в цепи (от нуля до максимального) появляется ток самоиндукции I_si, который препятствует быстрому увеличению тока в лампе. На рисунке 2 изображен примерный график изменения тока в лампе 2 при замыкании цепи.

Рис. 1
Рис. 2

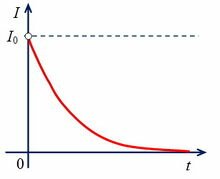
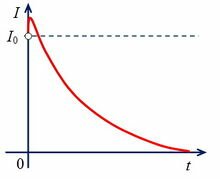
При размыкании ключа ток в лампе 2 также будет затухать медленно (рис. 3, а). Если индуктивность катушки достаточно велика, то сразу после размыкания ключа возможно даже некоторое увеличение тока (лампа 2 вспыхивает сильнее), и только затем ток начинает уменьшаться (рис. 3, б).

Рис. 3

Явление самоиндукции создает искру в том месте, где происходит размыкание цепи. Если в цепи имеются мощные электромагниты, то искра может перейти в дуговой разряд и испортить выключатель. Для размыкания таких цепей на электростанциях пользуются специальными выключателями.

Энергия магнитного поля

Энергия магнитного поля контура индуктивности L с силой тока I

(~W_m = dfrac{L cdot I^2}{2}.)

Так как (~Phi = L cdot I), то энергию магнитного поля тока (катушки) можно рассчитать, зная любые две величины из трех (Φ, L, I):

(~W_m = dfrac{L cdot I^2}{2} = dfrac{Phi cdot I}{2}=dfrac{Phi^2}{2L}.)

Энергию магнитного поля, заключенную в единице объема пространства, занятого полем, называют объемной плотностью энергии магнитного поля:

(omega_m = dfrac{W_m}{V}.)

*Вывод формулы

1 вывод.

Подключим к источнику тока проводящий контур с индуктивностью L. Пусть за малый промежуток времени Δt сила тока равномерно увеличится от нуля до некоторого значения I (ΔI = I). ЭДС самоиндукции будет равна

(E_{si} =-L cdot dfrac{Delta I}{Delta t} = -L cdot dfrac{I}{Delta t}.)

За данный промежуток время Δt через контур переносится заряд

(Delta q = leftlangle I right rangle cdot Delta t,)

где (left langle I right rangle = dfrac{I}{2}) — среднее значение силы тока за время Δt при равномерном его возрастании от нуля до I.

Сила тока в контуре с индуктивностью L достигает своего значения не мгновенно, а в течение некоторого конечного промежутка времени Δt. При этом в цепи возникает ЭДС самоиндукции E_si, препятствующая нарастанию силы тока. Следовательно, источник тока при замыкании совершает работу против ЭДС самоиндукции, т.е.

(A = -E_{si} cdot Delta q.)

Работа, затраченная источником на создание тока в контуре (без учета тепловых потерь), и определяет энергию магнитного поля, запасаемую контуром с током. Поэтому

(W_m = A = L cdot dfrac{I}{Delta t} cdot dfrac{I}{2} cdot Delta t = dfrac{L cdot I^2}{2}.)

2 вывод.

Если магнитное поле создано током, проходящим в соленоиде, то индуктивность и модуль индукции магнитного поля катушки равны

(~L = mu cdot mu_0 cdot dfrac {N^2}{l} cdot S, ,,, ~B = dfrac {mu cdot mu_0 cdot N cdot I}{l})

или

(I = dfrac {B cdot l}{mu cdot mu_0 cdot N}.)

Подставив полученные выражения в формулу для энергии магнитного поля, получим

(~W_m = dfrac {1}{2} cdot mu cdot mu_0 cdot dfrac {N^2}{l} cdot S cdot dfrac {B^2 cdot l^2}{(mu cdot mu_0)^2 cdot N^2} = dfrac {1}{2} cdot dfrac {B^2}{mu cdot mu_0} cdot S cdot l.)

Так как (~S cdot l = V) — объем катушки, плотность энергии магнитного поля равна

(omega_m = dfrac {B^2}{2mu cdot mu_0},)

где В — модуль индукции магнитного поля, μ — магнитная проницаемость среды, μ₀ — магнитная постоянная.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 351-355, 432-434.
Жилко В.В. Физика: учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. Обучения с 12-летним сроком обучения (базовый и повышенный уровни) / В.В. Жилко, Л.Г. Маркович. — Мн.: Нар. асвета, 2008. — С. 183-188.
Мякишев, Г.Я. Физика : Электродинамика. 10-11 кл. : учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. — М.: Дрофа, 2005. — С. 417-424.

Источник

«Я
мог бы расколоть земной шар,

но
никогда не сделаю этого.

Моей
главной целью было указать

на
новые явления и распространить идеи,

которые
и станут отправными

точками
для новых исследований»

Никола
Тесла

В
прошлых темах рассматривались опыты по получению индукционного тока, а также
установили причины его возникновения.

Явление
электромагнитной индукции заключается в том, что при всяком
изменении магнитного потока, пронизывающего контур замкнутого проводника, в
этом проводнике возникает электрический ток, существующий в течение всего
процесса изменения магнитного потока.

Полученный
таким способом ток называется индукционным током.

Значение
индукционного тока не зависит от причины изменения магнитного потока.
Существенное значение имеет лишь скорость изменения магнитного потока.

Как
направлен индукционный ток?

Для
ответа на этот вопрос воспользуемся следующим прибором — это узкая алюминиевая
пластина с алюминиевыми кольцами на концах. Одно кольцо сплошное, а другое
имеет разрез. Пластинка с кольцами помещена на стойку и может свободно
вращаться вокруг вертикальной оси.

Возьмем
полосовой магнит и внесем его в кольцо с разрезом — кольцо остается на месте.
Если же попытаться этот же магнит внести в сплошное кольцо, то ничего не
получится. Сплошное кольцо будет «убегать» от магнита, поворачивая при этом всю
пластинку. Результат будет точно таким же, если магнит повернуть к кольцам не
северным, а южным полюсом.

Объясним
наблюдаемые явления. При приближении к кольцу магнита, поле которого является
неоднородным, проходящий сквозь кольцо магнитный поток увеличивается. При этом в
сплошном кольце возникает индукционный ток, а в кольце с разрезом ток
циркулировать не может.

Отталкивание
сплошного кольца показывает, что индукционный ток в нем имеет такое направление,
что линии индукции магнитного поля, порожденного индукционным током, направлены
противоположно линиям индукции внешнего поля магнита. Т.е., кольцо и магнит
будут обращены друг к другу одноименными полюсами.

При
уменьшении магнитного потока (выдвигание магнита), индукционный ток имеет в нем
такое направление, что линии индукции его магнитного поля совпадают по
направлению с линиями индукции внешнего магнитного поля. Т.е., кольцо и
магнит будут обращены друг к другу разноименными полюсами.

Таким
образом, проследив за взаимодействием между кольцом и магнитом во всех случаях
и сравнив его с направлением движения магнита, можно видеть, что взаимодействие
между полюсами всегда препятствует движению магнита.

В
1833 году Эмилию ХристиановичуЛенцу удалось обобщить эти закономерности и
сформулировать общее правило. Найденную им связь называют правилом Ленца:
электромагнитная индукция создает в контуре индукционный ток такого
направления, что созданное им магнитное поле препятствует изменению магнитного
потока, вызывающего этот ток.

С
помощью правила Ленца всегда можно определить направление индукционного тока.
Для этого необходимо:

1)
Выяснить
причину возникновения индукционного тока (увеличивается или уменьшается
магнитный поток через контур);

2)
Определить
направление вектора магнитной индукции индуцирующего магнитного поля;

3)
Найти
направление индукции магнитного поля индукционного тока (если изменение
магнитного потока больше нуля, то вектора магнитной индукции индуцирующего
магнитного поля и поля созданного индукционным токомпротивоположно направлены; если
изменение магнитного потока меньше нуля, то вектора магнитной индукции
индуцирующего магнитного поля и поля созданного индукционным токомсо направлены);

4)
По
направлению вектора магнитной индукции индукционного тока определить, пользуясь
правилом буравчика, направление индукционного тока.

Теперь
разберем частный случай электромагнитной индукции: возникновение индукционного
тока в проводнике при изменении силы тока в нем.

Для
этого рассмотрим электрическую цепь, состоящую из источника тока, ключа и
проводника, силу тока в котором можно менять с помощью реостата. Как известно,
вокруг проводника с током возникает магнитное поле, которое зависит от силы
тока в цепи. При изменении силы тока произойдет изменение магнитной индукции
этого поля, в результате чего в этом же проводнике возникнет индукционный ток.
Такое явление называется самоиндукцией.

Таким
образом, явление самоиндукции заключается в возникновении индукционного тока
в проводнике при изменении силы тока в нем. При этом возникающий индукционный
ток называется током самоиндукции.

Как
известно, электрический ток, проходящий по контуру, создает вокруг него
магнитное поле. Магнитный поток через контур этого проводника (его также
называют собственным магнитным потоком) пропорционален модулю индукции
магнитного поля внутри контура, а индукция магнитного поля в свою очередь
пропорциональна силе тока в контуре. Следовательно, собственный магнитный
поток через контур прямо пропорционален силе тока в контуре.

Коэффициент
пропорциональности между силой тока в контуре и магнитным потоком, создаваемым
этим током, называется индуктивностью контура. Эта физическая величина
введена для оценивания способности проводника противодействовать изменению силы
тока в нем.

Индуктивность
контура зависит от размеров и формы контура, а также от магнитных свойств
среды, в которой находится контур.

Единицей
индуктивности в СИ является Гн (Генри), названная в честь американского ученого
Джозефа Генри.

Индуктивность
контура равна 1 Гн, если при силе постоянного тока 1 А магнитный
поток через контур равен 1 Вб.

Явление
самоиндукции можно наглядно продемонстрировать на опыте.

Соберем
цепь, состоящую из двух параллельно подключенных к источнику тока одинаковых
ламп. Последовательно с первой лампой включим реостат, а со второй — катушку с
железным сердечником.

При
замыкании цепи первая лампа загорается практически сразу, а вторая с заметным
запаздыванием. Нарастанию тока в части цепи с катушкой препятствует возникающий
ток самоиндукции, который, согласно правилу Ленца, препятствует нарастанию силы
тока при включении цепи и убыванию силы тока в ней при выключении.

Явление
самоиндукции подобно явлению инерции. Так же, как в
механике нельзя мгновенно остановить движущееся тело, так и ток не может
мгновенно приобрести определенное значение за счет явления самоиндукции.

Основные
выводы:

–
Правило Ленца гласит: электромагнитная индукция создает в контуре
индукционный токтакого направления, что созданное им магнитное поле
препятствует изменению магнитного потока, вызывающего этот ток.

–
Явление самоиндукции заключается в возникновении индукционного тока в
проводнике при изменении силы тока в нем.

–
При этом возникающий индукционный ток называется током самоиндукции.

Источник