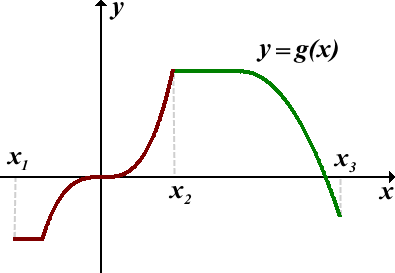Как найти направление убывания - Исправление недочетов и поиск решений вместе с Examum.ru

Что такое возрастание функции

В начале прочитаем определение возрастания функции.

Запомните!

Функция « y(x) » называется возрастающей на некотором промежутке, если

для любых
« x₁ » и « x₂ »
принадлежащих данному промежутку, таких, что « x₂ > x₁ »
выполняется неравенство

« y( x₂ ) > y( x₁ )».

Определение сложно понять без наглядного примера.
Поэтому сразу перейдём к разбору задачи на возрастание функции.

По-другому можно сказать, что, если каждому бóльшему значению « x »
соответствует бóльшее значение « y », значит,
функция « y(x) » возрастает.

x₂ > x₁
y( x₂ ) > y( x₁ )

Обязательное условие возрастания функции

Давайте разберем определение возрастания функции на конкретном примере.

Разбор примера

Возрастающей или убывающей является функция « y = 9x − 4 » ?

Для начала определим
область определения функции
« y = 9x − 4 ».

y = 9x − 4
D(y): x ∈ R ,
то есть « x » —
любое действительное число.

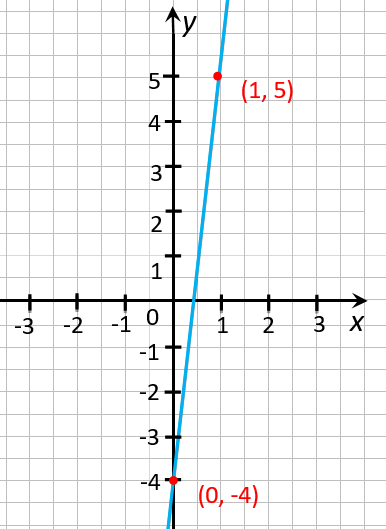
Построим график функции
« y = 9x − 4 ».
Так как функция
« y = 9x − 4 »
линейная, ее график — прямая.

Используем правила построения графика линейной функции. Нам достаточно найти две точки, чтобы построить ее график.

Область определения функции
« y = 9x − 4 » — все действительные числа,
поэтому можно подставить любое число вместо « x » и вычислить « y » по
формуле функции
« y = 9x − 4 ». Например, возьмем
« x = 0 ».

x = 0
y(x) = 9x − 4
y(0) = 9 · 0 − 4 = −4

Для второй точки возьмем « x = 1 ».

x = 1
y(x) = 9x − 4
y(1) = 9 · 1 − 4 = 5

Отметим две полученные
точки «(0; −4)» и «(1; 5)» на

координатной плоскости
и проведем через них прямую.

Докажем, что функция
« y = 9x − 4 » возрастает на всей своей области определения двумя способами: по ее графику и
аналитически
(по ее формуле).

Как определить по графику, что функция возрастает

По определению возрастания функции мы знаем, что
если « x » увеличивается,
то « y » тоже должен увеличиваться.

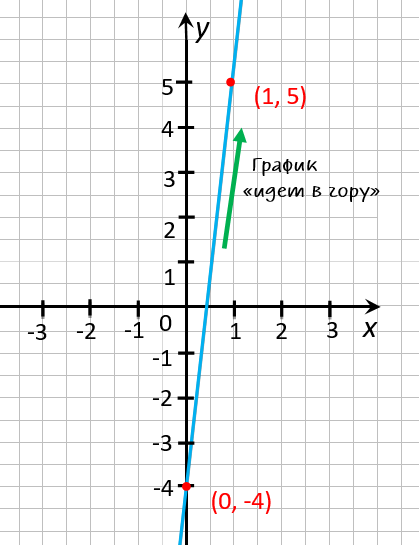
На рисунке ниже видно, что график функции « y = 9x − 4 »
«идет в гору». Другими словами, при увеличении « x »
↑ растет
значение « y » ↑.

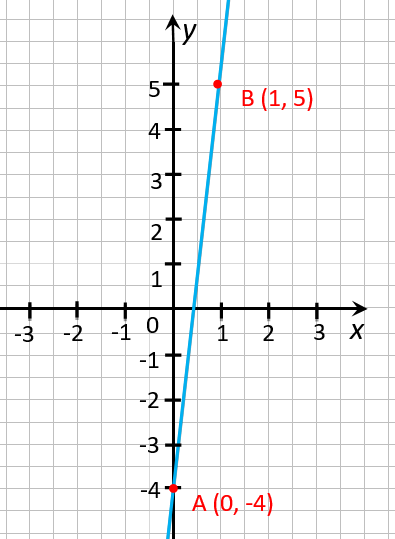
В этом можно убедиться, если взять две любые точки на графике. Например, точки, по
которым мы построили график функции. Назовем эти точки:
« (·)A » и « (·)B ».

У первой точки « (·)A »
координаты:
x₁ = 0 ; y₁ = − 4

У второй точки « (·)B » координаты:
x₂ = 1 ; y₂ = 5

На примере точек « (·)A » и « (·)B » видно, что
при увеличении
« x ↑ ( x₂ > x₁ )»
растет
« y ↑ ( y₂ > y₁ ) ».
Поэтому график зрительно «идет в гору».

Как по формуле доказать, что функция возрастает

Вернёмся к нашей функции
« y = 9x − 4 ».

По графику мы поняли, что
функция « y = 9x − 4 » возрастает,
так как ее график «идет в гору».
Но как доказать по формуле, что функция
возрастает на всей своей области определения?

Запомните!

Функция возрастает на всей области определения, когда при
« x₂ > x₁ »
выполняется условие
« y( x₂ ) > y( x₁ ) ».

Формулировка выше не самая простая для понимания. Давайте разберем ее на практике.

По определению возрастания функции нам нужно доказать, что при
« x₂ > x₁ » увеличивается значение функции
« y( x₂ ) > y( x₁ ) ».

Но как нам найти значения функции
« y( x₁ )» и
«y( x₂ ) »?

Для нахождения « y( x₁ )» и
«y( x₂ ) »

достаточно подставить « x₁ » и
« x₂ » в исходную формулу « y = 9x − 4 ».

y( x₁ ) = 9x₁ − 4
y( x₂ ) = 9x₂ − 4

Теперь запишем обязательное условие возрастания функции.

x₂ > x₁
y( x₂ ) > y( x₁ )

Обязательное условие возрастания функции

Подставим в неравенство
« y( x₂ ) >
y( x₁ ) » полученные формулы

« y( x₁ ) = 9x₁ − 4» и
« y( x₂ ) = 9x₂ − 4 » .

y( x₂ ) > y( x₁ )
9x₂ − 4 > 9x₁ − 4

Упростим полученное
неравенство.

9x₂ − 9x₁ > − 4 + 4
9x₂ − 9x₁ > 0

Вынесем общий множитель
в левой части неравенства.

9(x₂ − x₁) > 0

Разделим левую и правую часть на «9».

При делении нуля на любое число получается ноль.

x₂ − x₁ > 0
x₂ > x₁

Мы доказали, что выполняется исходное условие возрастания функции «x₂ > x₁».
Отсюда следует, что функция
« y = 9x − 4 » возрастает на всей области определения.

В завершении вместо ответа следует написать фразу:
«Что и требовалось доказать».

Посмотрим другой пример, где требуется доказать, что функция возрастает.

Разбор примера

Доказать, что функция возрастает на всей области определения: y = 13x − 1

По аналогии с предыдущим примером составим неравенства, которые доказывают, что функция возрастает.

x₂ > x₁
y( x₂ ) > y( x₁ )

Обязательное условие возрастания функции

Вместо « y( x₁ )» и
«y( x₂ ) » запишем
формулу функции « y = 13x − 1 » и упростим полученное неравенство.

y( x₂ ) > y( x₁ )

13x₂ − 1 > 13x₁ − 1

13x₂ − 13x₁ > 1 − 1

13(x₂ − x₁) > 0 |: 13

x₂ − x₁ > 0

x₂ > x₁

Что и требовалось доказать.

Что такое убывание функции

Запомните!

Функция « y(x) » называется убывающей на некотором промежутке, если для любых
« x₁ » и « x₂ »
принадлежащих данному промежутку, таких,
что « x₂ > x₁ »
выполняется неравенство « y( x₂ ) < y( x₁ )».

x₂ > x₁
y( x₂ ) < y( x₁ )

Обязательное условие убывания функции

Как по графику понять, что функция убывает

Разбор примера

Доказать, что функция убывает на всей области определения: y = 1 − 3x

По определению убывания функции мы знаем, что,
если « x »
↑ растет, то
« y » ↓ должен уменьшаться.

Построим график функции
« y = 1 − 3x ». Ее график — прямая, поэтому нам будет достаточно двух точек.

Область определения функции
« y = 1 − 3x » — все действительные числа,
поэтому можно поставить любое число вместо « x » и вычислить « у » по
формуле функции
« y = 1 − 3x ». Например, возьмем
« x = 0 »
и « x = 1 ».

x = 0
y(x) = 1 − 3x
y(0) = 1 − 3 · 0 = 1

(·) А (0; 1)

x = 1
y(1) = 1 − 3x
y(1) = 1 − 3 · 1 = 1 − 3 = −2

(·) B (1; −2)

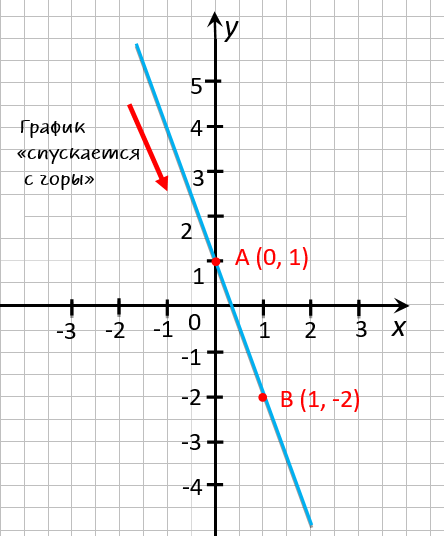
Построим график функции
« y = 1 − 3x » по полученным точкам
« (·)A » и « (·)B ».

На графике функции видно, что зрительно график «спускается с горы», то есть функция убывает. Другими словами, при увеличении
« x »
↑ уменьшается
значение
« y » ↓.

Как по формуле доказать, что функция убывает

Вернёмся к нашей функции
« y = 1 − 3x ».

По ее графику мы поняли, что функция убывает, так как график «спускается с горы». Но как доказать по формуле,
что функция « y = 1 − 3x » убывает на всей области определения?

Запомните!

Чтобы доказать, что функция убывает требуется доказать, что при любых
« x₂ > x₁ » выполняется

« y( x₂ ) < y( x₁ ) ».

Давайте разберем на примере функции
« y = 1 − 3x ». Докажем, что она убывает
на всей своей области определения.

x₂ > x₁
y( x₂ ) < y( x₁ )

Обязательное условие убывания функции

Подставим « y( x₁ )» и
«y( x₂ ) » в
формулу функции « y = 1 − 3x » и упростим полученное неравенство.

y( x₂ ) < y( x₁ )

1 − 3x₂ < 1 − 3x₁

3x₁ − 3x₂ < 1 − 1

3(x₁ − x₂) < 0 | :3

x₁ − x₂ < 0

−x₂ < −x₁

Умножим на « −1 » левую и правую часть неравенства. При
умножении неравенства на отрицательное число знак неравенства поменяется на
противоположный.

−x₂ < −x₁ | · (−1)

x₂ > x₁

Что и требовалось доказать.

Как по графику функции определить
возрастание и убывание

Потренируемся только по графику функции определять промежутки возрастания и убывания функции.

Разбор примера

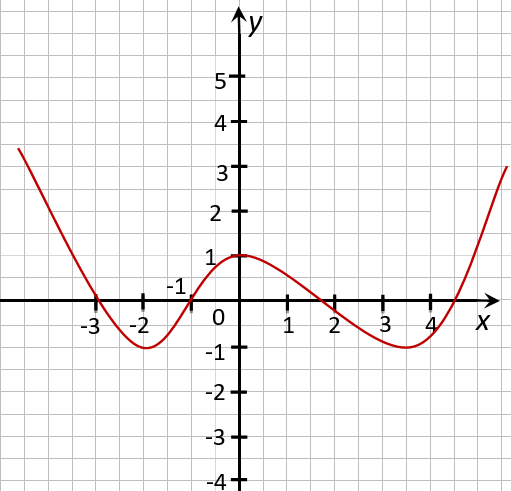
На рисунке ниже изображён график функции, определенной на множестве действительных чисел.
Используя график, найдите промежутки возрастания и промежутки убывания функции.

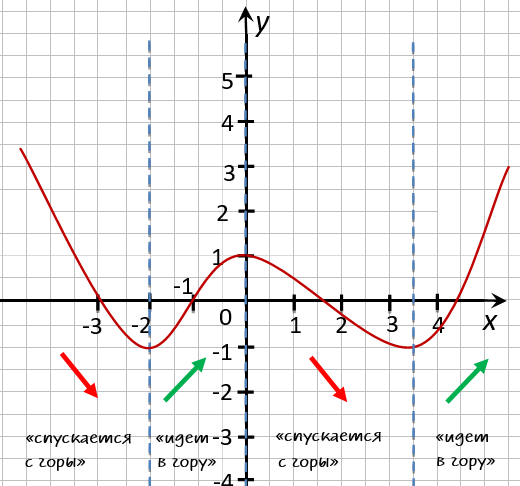
Отметим с помощью штриховых линий промежутки, где график функции убывает
(«спускается с горы») и где он возрастает («идет в гору»).

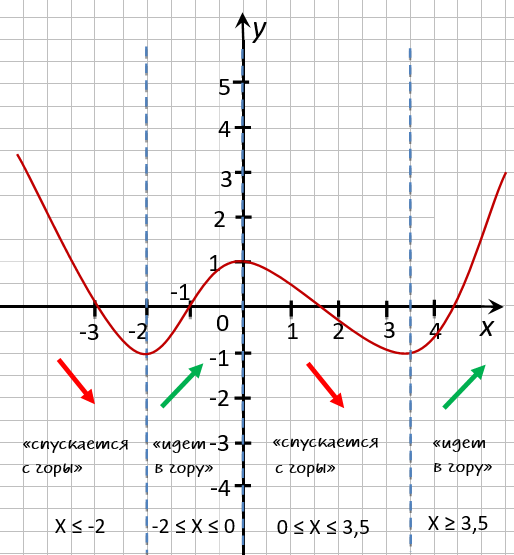
Запишем через знаки неравенств,
какие значения принимает « x » на полученных промежутках.
Обратите внимание, что во всех случаях при указании промежутков, мы указываем, что их
концы входят в промежуток, то есть используем знаки нестрогого неравенства.

Остаётся записать полученные промежутки возрастания и убывания функции в ответ.

Ответ:

функция убывает при
x ≤ −2; 0 ≤ x ≤ 3,5
функция возрастает при
−2 ≤ x ≤ 0 ; x ≥ 3,5

Более грамотно будет записать ответ с помощью специальных
математических символов.

Ответ:

функция убывает на промежутках
x ∈ (−∞ ; −2] ∪ [0; 3,5]
функция возрастает на промежутках x ∈ [−2 ; 0] ∪ [3,5 ; +∞]

При каких значениях
« m »
функция является убывающей или возрастающей

Ещё один тип заданий, в которых требуется определить,
при каких
« m » ( « а, b » или других буквах) функция убывает или возрастает.

Разбор примера

При каких значениях « m » функция

« y = mx − m − 3 + 2x » является убывающей?

Обратимся снова к определению убывания функции. Вспомним, как записать условия убывания функции с точки зрения формул.

x₂ > x₁
y( x₂ ) < y( x₁ )

Обязательное условие убывания функции

Запишем эти условия, используя формулу функции « y = mx − m − 3 + 2x », заданную в
задаче. Вместо
« x »
подставим « x₁ » и « x₂ ».

y( x₂ ) < y( x₁ )

mx₂ − m − 3 + 2x₂ < mx₁ − m − 3 + 2x₁

Упростим полученное неравенство. Перенесем из правой части все члены неравенства в левую часть с противоположными знаками.

mx₂ − m − 3 + 2x₂ − mx₁
+ m
+ 3
− 2x₁
< 0

Упростим полученное выражение. Некоторые члены неравенства взаимоуничтожатся.

mx₂ − mx₁
− m + m − 3 + 3 + 2x₂ − 2x₁

< 0

mx₂ − mx₁ + 2x₂ − 2x₁

< 0

Вынесем общие множители за скобки.

m( x₂ − x₁) + 2(x₂ − x₁)

< 0

Теперь
вынесем общий множитель

« ( x₂ − x₁ ) ».

( x₂ − x₁) (m + 2)

< 0

Вспомним обязательное условие убывания функции.

x₂ > x₁
y( x₂ ) < y( x₁ )

Обязательное условие убывания функции

Преобразуем исходное условие убывания функции « x₂ > x₁ ».
Перенесем все в левую часть.

x₂ > x₁

x₂ − x₁ > 0

По условию убывания функции
« x₂ − x₁ > 0 »,
значит, чтобы
произведение
«( x₂ − x₁) (m + 2)

» было меньше нуля, требуется, чтобы множитель «(m + 2)» был меньше нуля. Так как по
правилу знаков:
плюс на минус даёт минус.

+	·	−	< 0
(x₂ − x₁)	·	(m + 2)	< 0

Решим полученное неравенство.

m + 2 < 0
m < −2

Ответ: при «m < −2» функция
« y = mx − m − 3 + 2x »
является убывающей.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Многие методы минимизации относятся
к числу методов спуска. В методах спуска
направление движения к минимуму на
каждом шаге выбирается из числа
направлений убывания минимизируемой
функции.

Говорят, что вектор h
задает направление убывания функции
f в точке x, если
f(x + h)
< f(x) при всех
достаточно малых 
> 0. Сам вектор h также называют
иногда направлением убывания. Множество
всех направлений убывания функции f
в точке х будем обозначать через
U(х, f).

Таким образом, если любой достаточно
малый сдвиг из х в направлении
вектора h приводит к
уменьшению значения функции f,
то h 
U(x,
f).

Заменив неравенство, фигурирующее в
определении направления убывания, на
противоположное, получим определение
направления возрастания.

В дальнейшем нам понадобятся следующие
достаточный и необходимый признаки
направления убывания.

Лемма 2.1. Пусть функция f
дифференцируема в точке х 
Rⁿ. Если
вектор h удовлетворяет условию

f‘(х),h
< 0, (2.13)

то h
U(х, f). Если h
U(х, f), то

f‘(х),h
 0, (2.14)

Геометрически условие (2.13) означает,
что вектор h составляет тупой угол
с градиентом f’(х).

Метод (2.3) называется методом спуска,
если вектор h^k
задает направление убывания функции f
в точке x^k:

h^k
U(х^k,
f), k = 0, 1, 2, …,

а число _k
положительно и таково, что

f(x^k⁺¹)
< f(x^k),
k = 0, 1, 2,
…

Простейшим примером метода спуска
является градиентный метод, в котором
h^k = –f'(х^k)
(если f‘(х) 
0, то –f’(х) 
U(х, f) в силу леммы 2.1).

2.5. Выбор длины шага из условия минимизации функции вдоль заданного направления

Коэффициенты _k
в методе (2.3) можно определять из
условия

,
(2.15)

где для методов спуска, т. е. при h^k
U(х^k,
f), минимум берется по 
 0. Такой способ
выбора _k
является в некотором смысле наилучшим,
ибо он обеспечивает достижение наименьшего
значения функции вдоль заданного
направления. Однако он требует решения
на каждом шаге одномерной задачи
минимизации. Эти задачи решаются,
как правило, приближенно с помощью
численных методов, что приводит к
значительному объему вычислений.

В простейших случаях величины _k,
удается найти в явном виде.

Адаптивный способ отыскания коэффициентов
_k,
не требующий дополнительных
вычислений характеристик целевой
функции

Ранее рассмотрен способ выбора
коэффициентов _k,
требующий решения вспомогательных
одномерных задач. В процессе их решения
приходится, как правило, производить
дополнительные вычисления характеристик
целевой функции f в точках, отличных
от x⁰, х¹,
…, x^k.

Ниже приводятся явные формулы для _k.
В них используются лишь значения f‘(x^k)
и некоторые константы, характеризующие
глобальные свойства функции f.
Эти формулы выбраны с целью обеспечить
при соответствующих предположениях о
f выполнение неравенства

,
(2.17)

где  
(0, 1), направление h^k
таково, что f‘(x^k),
h^k
< 0 и, стало быть, h^k
U(х^k,
f). Неравенство (2.17) необходимо для
обоснования сходимости многих методов
минимизации. Из него, в частности,
следует, что f(x^k⁺¹)
< f(х^k),
и соответствующий метод минимизации
является, таким образом, методом спуска.

Лемма 2.2. Пусть функция f дифференцируема
на Rⁿ,
а ее градиент удовлетворяет условию
Липшица

||f‘(x)
– f‘(x‘)||
 M||x
– x‘||, x,
x‘ Rⁿ,
(2.18)

где М > 0.

Тогда для произвольных x^k
Rⁿ,


(0, 1) и x^k,
удовлетворяющего неравенству
f‘(x^k),
h^k
< 0, условие (2.17) выполнено при

. (2.19)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Как найти на функции промежутки убывания

Функция представляет собой строгую зависимость одного числа от другого, или значения функции (y) от аргумента (х). Каждый процесс (не только в математике), может быть описан своей функцией, которая будет иметь характерные особенности: промежутки убывания и возрастания, точки минимумов и максимумов и так далее.

Вам понадобится

— бумага;
— ручка.

Инструкция

Функция e=f(x) называется убывающей на интервале (a, b), если любое значение ее аргумента х2 большего х1, принадлежащих интервалу (а,b), приводит к тому, что f(x2) меньше f(x1). Если коротко, то: для любых x2 и x1 таких, что x2 > x1, принадлежащих (a, b) выполнено f(x2)

Известно, что на промежутках убывания производная функции отрицательна, то есть алгоритм поиска промежутков убывания сводится к двум следующим действиям:
1. Определение производной функции y=f(x).
2. Решение неравенства f’(x)

Пример 1.
Найти промежуток убывания функции:
y=2x^3 –15x^2+36x-6.
Производная данной функции будет равна: y’=6x^2-30x+36. Далее необходимо решить неравенство y’

Пример 2.
Найти промежутки убывания f(x)=sinx +x.
Производная данной функции будет равна: f’(x)=cosx+1.
Решая неравенство cosx+1

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Возрастание и убывание функций

Определения

1) Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.

То есть для любых двух значений x₁,x₂ из этого промежутка выполняется условие

2) Функция y=f(x) называется убывающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует меньшее значение функции.

То есть для любых двух значений x₁,x₂ из этого промежутка выполняется условие

Предполагается, что промежуток принадлежит области определения функции y=f(x). Обычно промежуток — это отрезок, интервал или полуинтервал.

График функции на промежутках возрастания «идёт вверх» (чем правее x, тем выше y).

На промежутках убывания график «идёт вниз» (чем правее x, тем ниже y).

Пример 1.

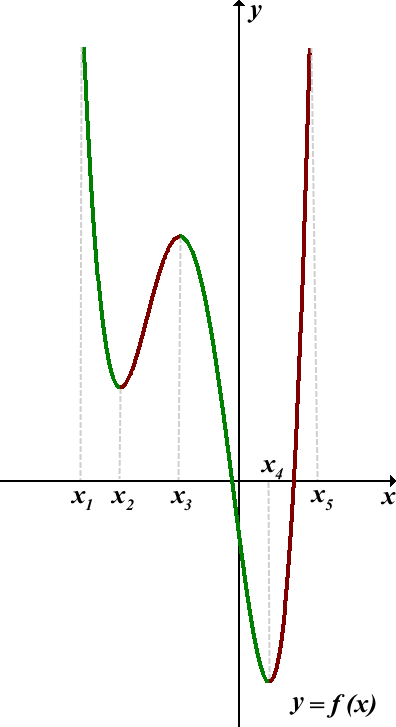
Пользуясь графиком, найти промежутки возрастания и убывания функции y=f(x), определённой на отрезке [x₁;x₅]:

Функция y=f(x) возрастает на промежутках [x₂;x₃] и [x₄;x₅]

Функция y=f(x) убывает на промежутках [x₁;x₂] и [x₃;x₄].

Кратко это записывают так:

$[ f(x) nearrow npu_x in left[ {x_2 ;x_3 } right]uleft[ {x_4 ;x_5 } right], ]$

$[ f(x) searrow npu_x in left[ {x_1 ;x_2 } right]uleft[ {x_3 ;x_4 } right]. ]$

3) Функцию, возрастающую на промежутке либо убывающую на промежутке, называют монотонной функцией на этом промежутке (или строго монотонной).

4) Если функция возрастает на всей своей области определения, то её называют возрастающей.

Если функция убывает на всей своей области определения, то её называют убывающей.

Например, y=√x, y=x³ — возрастающие функции.

Линейная функция y=kx+b возрастающая при k>0 и убывающая при k<0.

5) Если для любых двух значений x₁,x₂ из некоторого промежутка выполняется условие

то функция y=f(x) называется неубывающей на этом промежутке.

6) Если для любых двух значений x₁,x₂ из некоторого промежутка выполняется условие

то функция y=f(x) называется невозрастающей на этом промежутке.

7) Функцию, невозрастающую на промежутке либо неубывающую на промежутке, называют не строго монотонной функцией на этом промежутке.

Пример 2.

Пользуясь графиком, найти промежутки, на которых функции y=g(x), определённая на отрезке [x₁;x₃], является невозрастающей и неубывающей:

Функция y=g(x) является неубывающей на промежутке [x₁;x₂].

Функция y=g(x) является невозрастающей на промежутке [x₂;x₃].

Возрастание и убывание функции можно определять как с помощью графика, так и аналитически.

Как доказать, что функция возрастает или убывает, с помощью задающей эту функцию формулы?

Для этого при условии x₂>x₁ на промежутке надо доказать выполнение одного из неравенств: f(x₂)>f(x₁) либо f(x₂)>f(x₁), то есть определить f(x₂)-f(x₁)>0 или f(x₂)-f(x₁)<0.

Примеры.

1) Доказать, что функция f(x)=x²+4x убывает на промежутке (-∞;-2).

Доказательство:

Функция определена на всей числовой прямой.

Пусть x₂>x₁.

f(x₁)=x₁²+4x₁, f(x₂)=x₂²+4x₂,

f(x₂)-f(x₁)=(x₂²+4x₂)-(x₁²+4x₁)=x₂²+4x₂-x₁²-4x₁=

группирует первое слагаемое с третьим, второе — с четвертым. В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки:

=(x₂²-x₁²)+(4x₂-4x₁)=(x₂-x₁)(x₂+x₁)+4(x₂-x₁)=

Теперь выносим общий множитель (x₂-x₁) за скобки:

=(x₂-x₁)(x₂+x₁+4).

Так как x₂>x₁, то x₂-x₁>0. Следовательно, знак произведения зависит от знака второго множителя.

Для x₁, x₂ ∈(-∞;-2) x₂+x₁+4<0. Значит, (x₂-x₁)(x₂+x₁+4)<0 и f(x₂)<f(x₁). Отсюда следует, что функция функция f(x)=x²+4x убывает на промежутке (-∞;-2).

Что и требовалось доказать.

2) Доказать, что функция

$[ y = frac{4}{{2 - x}} ]$

возрастает на промежутке (2;+∞).

Доказательство:

Функция определена при x∈(-∞;2) и (2;+∞).

Пусть x₂>x₁.

$[ y(x_2 ) - y(x_1 ) = frac{{4^{backslash (2 - x_1 )} }}{{2 - x_2 }} - frac{{4^{backslash (2 - x_2 )} }}{{2 - x_1 }} = ]$

$[ = frac{{4(2 - x_1 ) - 4(2 - x_2 )}}{{(2 - x_1 )(2 - x_2 )}} = frac{{4(x_2 - x_1 )}}{{(2 - x_1 )(2 - x_2 )}}. ]$

Так как x₂>x₁, то x₂-x₁>0.

Для x₁, x₂ ∈ (2;+∞) (2-x₁)(2-x₂)>0. Значит,

$[ frac{{4(x_2 - x_1 )}}{{(2 - x_1 )(2 - x_2 )}} > 0. ]$

Отсюда y(x₂)-y(x₁)>0. Поэтому данная функция возрастает на промежутке (2;+∞).

Что и требовалось доказать.

Исследование функции на монотонность гораздо удобнее проводить с помощью производной (начала математического анализа — производную и её применение — проходят в школьном курсе алгебры в 10-11 классах).

Источник

Краткое описание документа:

«Возрастание и убывание функции»

Цели урока:

1. Научить находить промежутки монотонности.

2. Развитие мыслительных способностей, обеспечивающих анализ ситуации и разработку адекватных способов действия (анализ, синтез, сравнение).

3. Формирование интереса к предмету.

Ход урока

Сегодня мы продолжаем изучать приложение производной и рассмотрим вопрос о её применениик исследованию функций. Фронтальная работа

А теперь дадим некоторые определения свойствам функции “Мозговой штурм”

1. Что называют функцией?

2. Как называется переменная Х?

3. Как называется переменная Y?

4. Что называется областью определения функции?

5. Что называется множеством значения функции?

6. Какая функция называется чётной?

7. Какая функция называется нечётной?

8. Что можно сказать о графике чётной функции?

9. Что можно сказать о графике нечётной функции?

10. Какая функция называется возрастающей?

11. Какая функция называется убывающей?

12. Какая функция называется периодической?

Математика изучает математические модели. Одной из главнейших математических моделей является функция. Существуют разные способы описания функций. Какой самый наглядный?

– Графический.

– Как построить график?

– По точкам.

Этот способ подойдет, если заранее известно, как примерно выглядит график. Например, что является графиком квадратичной функции, линейной функции, обратной пропорциональности, функции y = sinx? (Демонстрируются соответствующие формулы, учащиеся называют кривые, являющиеся графиками.)

А что если требуется построить график функции или еще более сложной? Можно найти несколько точек, но как ведет себя функция между этими точками?

Поставить на доске две точки, попросить учеников показать, как может выглядеть график “между ними”:

Выяснить, как ведет себя функция, помогает ее производная.

Откройте тетради, запишите число, классная работа.

Цель урока: узнать, как связан график функции с графиком ее производной, и научиться решать задачи двух видов:

1. По графику производной находить промежутки возрастания и убывания самой функции, а также точки экстремума функции;

2. По схеме знаков производной на промежутках находить интервалы возрастания и убывания самой функции, а также точки экстремума функции.

Подобные задания отсутствуют в наших учебниках, но встречаются в тестах единого государственного экзамена (часть А и В).

Сегодня на уроке мы рассмотрим небольшой элемент работы второго этапа изучения процесса, исследование одного из свойств функции — определение промежутков монотонности

Для решения поставленной задачи, нам необходимо вспомнить некоторые вопросы, рассмотренные ранее.

Итак, запишем тему сегодняшнего урока: Признаки возрастания и убывания функции.

Признаки возрастания и убывания функции:

Если производная данной функции положительна для всех значений х в интервале (а; в), т.е.f'(x) > 0, то функция в этом интервале возрастает.
Если производная данной функции отрицательна для всех значений х в интервале(а; в), т.е.f'(x) < 0, то функция в этом интервале убывает

Порядок нахождения промежутков монотонности:

Найти область определения функции.

1. Найти первую производную функции.

2. решать самой на доске

Найти критические точки, исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции. Найти промежутки монотонности функций:

а) область определения ,

б) найдем первую производную:,

в)найдем критические точки: ; , и

3. Исследуем знак производной в полученных промежутках, решение представим в виде таблицы.

указать на точки экстремума

Рассмотрим несколько примеровисследования функции на возрастание и убывание.

Достаточное условие существования максимума состоит в смене знака производной при переходе через критическую точку с «+» на «-«, а для минимума с «-» на «+». Если при переходе через критическую точку смены знака производной не происходит, то в данной точке экстремума нет

1. Найти Д(f).

2. Найти f'(x).

3. Найти стационарные точки, т.е. точки, где f'(x) = 0 или f'(x) не существует.
(Производная равна 0 в нулях числителя, производная не существует в нулях знаменателя)

4. Расположить Д(f) и эти точки на координатной прямой.

5. Определить знаки производной на каждом из интервалов

6. Применить признаки.

7. Записать ответ.

. Закрепление нового материала.

Учащиеся работают в парах, решение записывают в тетрадях.

а) у = х³ — 6 х² + 9 х — 9;

б) у = 3 х² — 5х + 4.

Двое работают у доски.

а) у = 2 х³ – 3 х² – 36 х + 40

б) у = х4 — 2 х³

3.Итог урока

Домашнее задание: тест (дифференцированный)

Источник

Что такое возрастание функции

Разбор примера

Как определить по графику, что функция возрастает

Как по формуле доказать, что функция возрастает

Разбор примера

Что такое убывание функции

Как по графику понять, что функция убывает

Разбор примера

Как по формуле доказать, что функция убывает

Как по графику функции определить возрастание и убывание

Разбор примера

При каких значениях « m » функция является убывающей или возрастающей

Разбор примера

Ваши комментарии

2.5. Выбор длины шага из условия минимизации функции вдоль заданного направления

Как найти на функции промежутки убывания

Краткое описание документа:

Как по графику функции определить
возрастание и убывание

При каких значениях
« m »
функция является убывающей или возрастающей