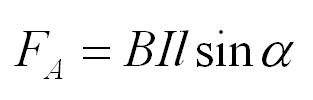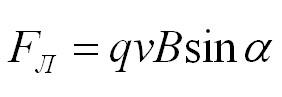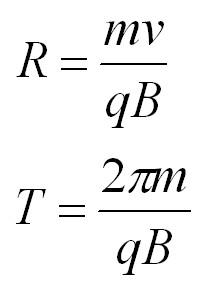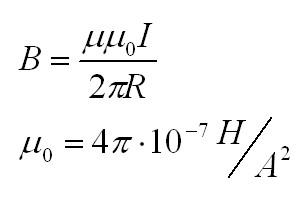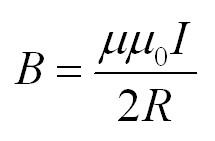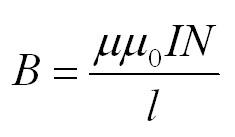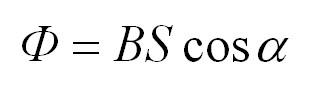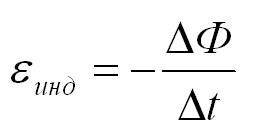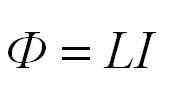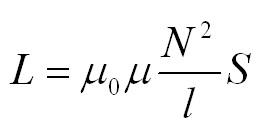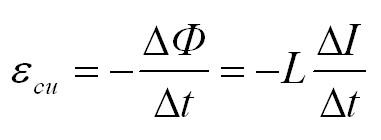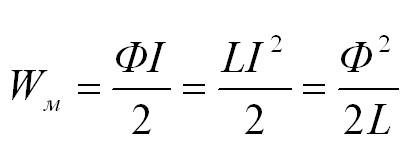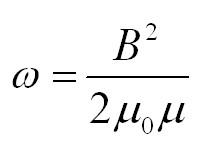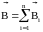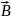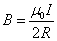Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
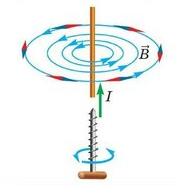
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
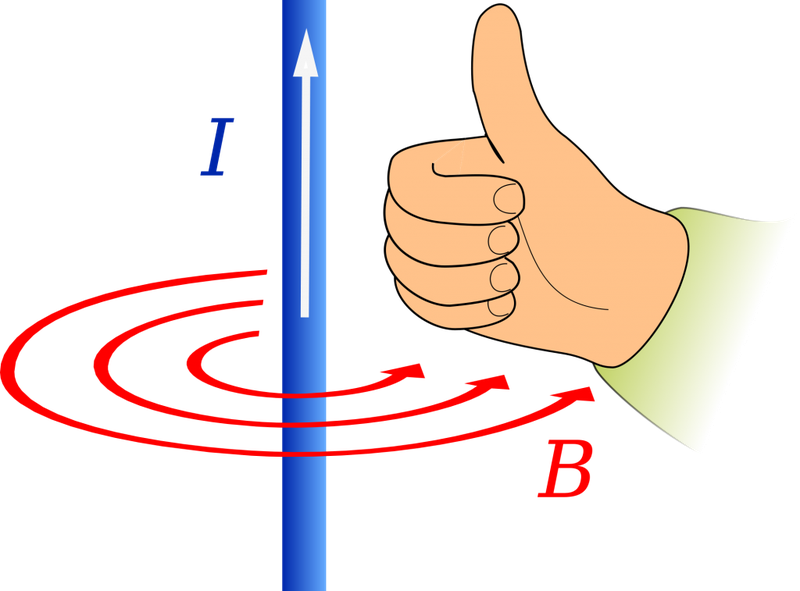
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
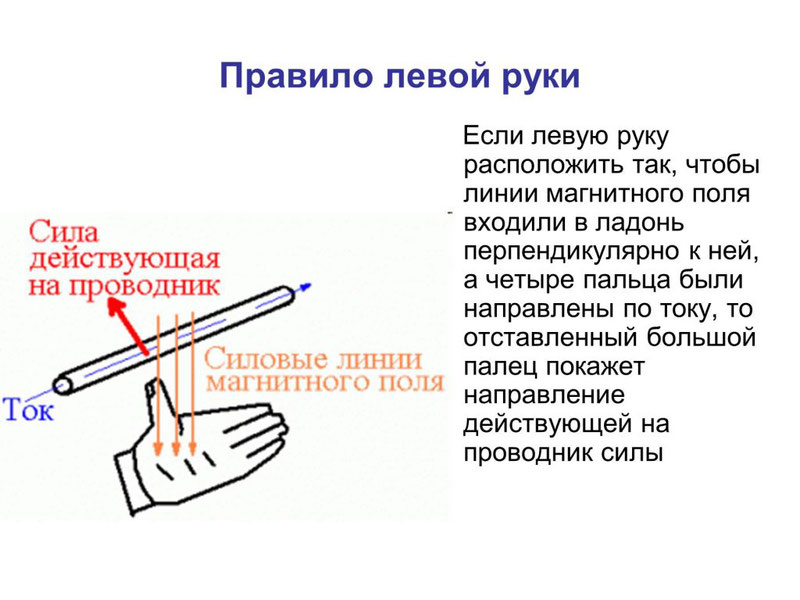
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
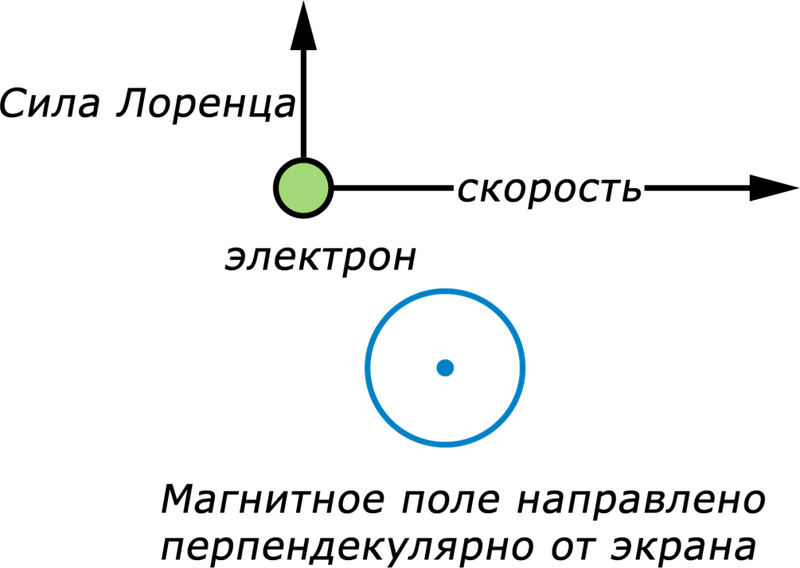
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
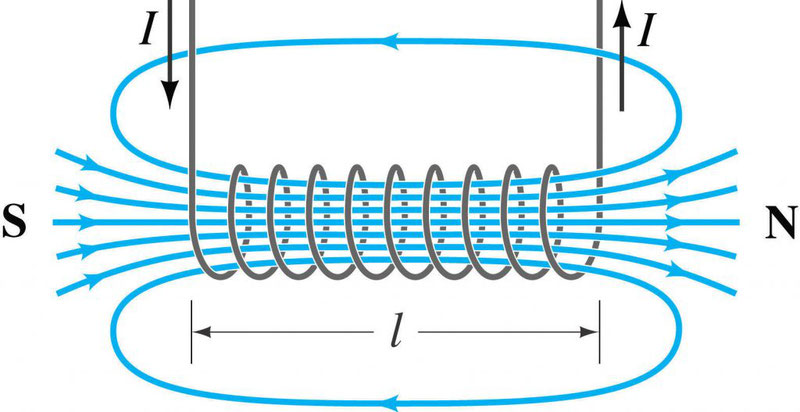
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
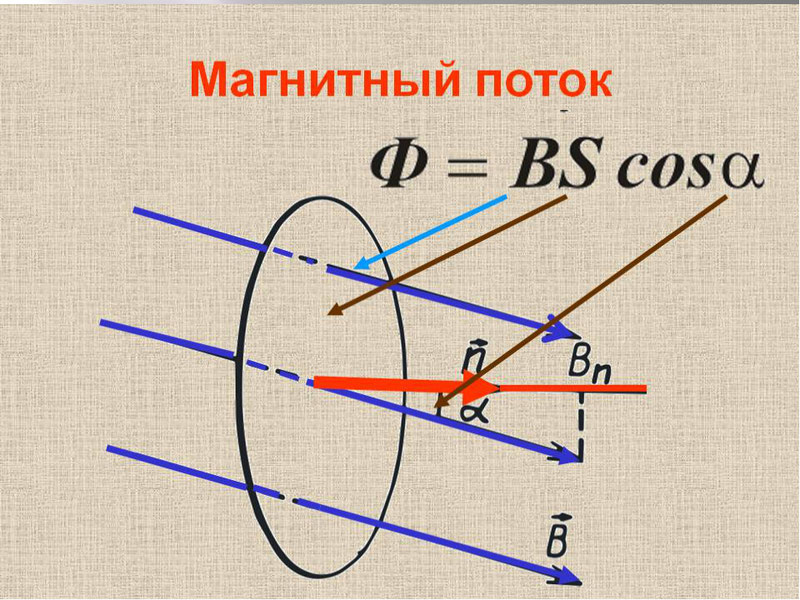
Магнитный поток и ЭДС
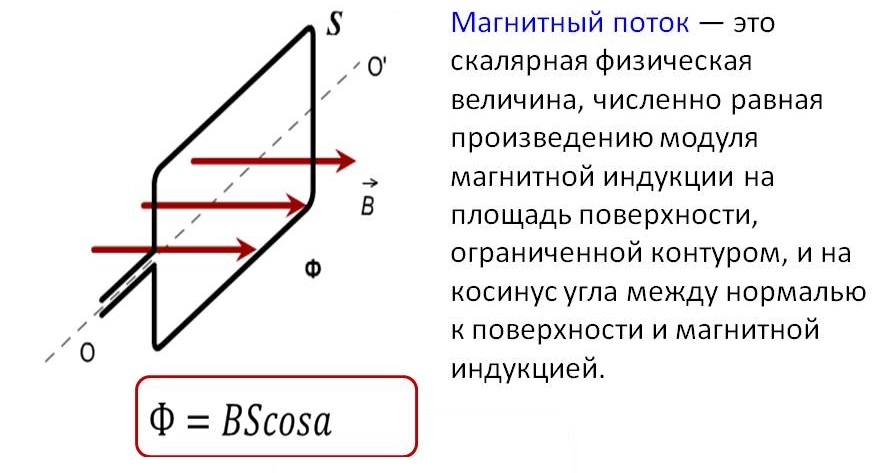
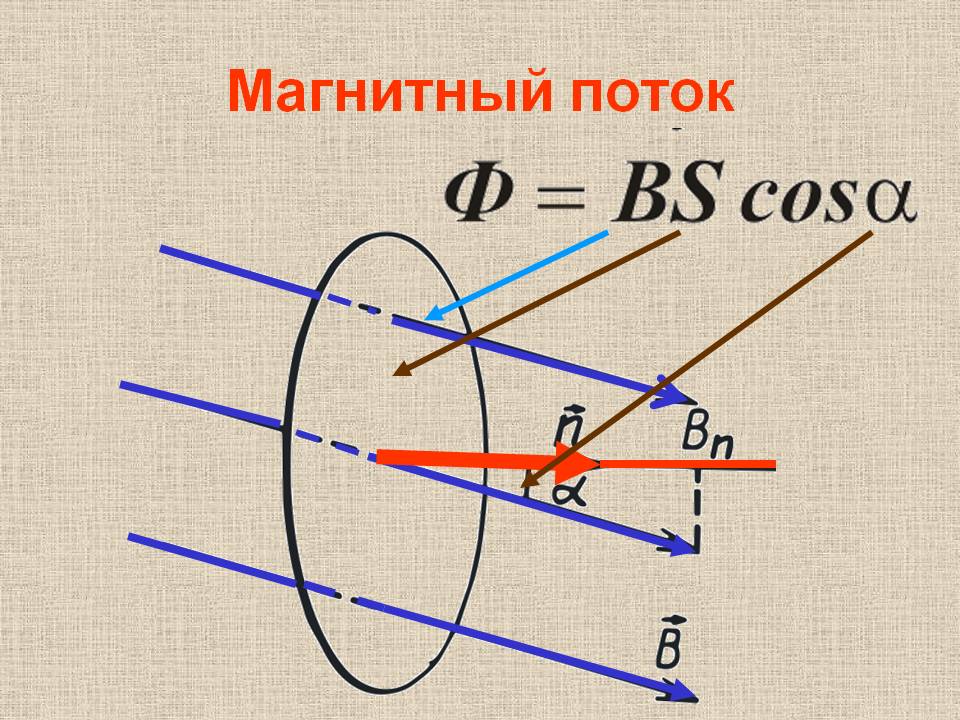
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
Формула для ЭДС самоиндукции:
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
Объемная плотность энергии поля:
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.
Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Модуль вектора индукции поля движущегося заряда
Любой движущийся заряд создает вокруг себя магнитное поле. Будем считать, что скорость движения заряда много меньше скорости света. Найдем формулу для расчета такого магнитной индукции такого поля ($overrightarrow{B}$). Для этого рассмотрим небольшой отрезок проводника (длиной $l$) с током (I). Такой проводник создает в некоторой точке поле, модуль которого можно записать как:
где $r$ — расстояние от данного проводника, до точки, где ищем поле. Силу тока можно записать через плотность тока (j) как:
а плотность тока через концентрацию заряженных частиц:
где $n$ — концентрация частиц, $q$ — заряд частиц, $v$ — модуль скорости их движения. Тогда произведение силы тока на длину проводника можно выразить как:
где $N$ — суммарное число зарядов на отрезке проводника. Подставляя в (1) получим для вектора индукции:
Значит индукция поля, которое создает одна заряженная частица, равна:
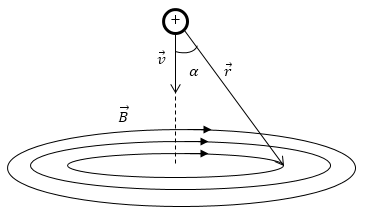
Направление вектора индукции поля движущегося заряда
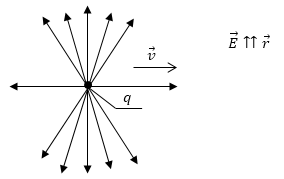
Направление вектора индукции магнитного поля, создаваемого одной частицей перпендикулярно к вектору скорости ($overrightarrow{v}$) частицы и радиус- вектору ($overrightarrow{r}$), который проведен из частицы в рассматриваемую точку и подчиняется правилу правого буравчика. Силовыми линиями поля точечного заряда являются концентрические окружности рис.1.
Значит окончательно, вектор магнитной индукции поля, которое создается движущимся зарядом в системе СИ, можно записать как:
Формула (6) показывает индукцию магнитного поля движущегося положительного заряда. Если мы имеем дело с отрицательным зарядом, то q заменим на —q. Из формулы (6) очевидно, что движущийся заряд эквивалентен элементу тока, то есть:
«Магнитное поле движущегося заряда» 👇
Рис. 1
Влияние магнитного поля на электрическое поле при движении заряда
Необходимо отметить, что появление в формуле для вектора магнитной индукции вектора скорости означает, что в пространстве появляется выделенное направление. Электрическое поле заряда утрачивает свою сферическую симметрию и становится осесимметричным (рис.2). При скорости движения заряда много меньшей чем скорость света в любой момент времени электрическое поле считается не отличающимся от электростатического поля. Но надо помнить, что поле перемещается вместе с зарядом. Поэтому поле изменяется в каждой точке пространства со временем.
При скоростях сравнимых со скоростью света, поле «сплющивается» в направлении движения и сосредоточено около плоскости, которая перпендикулярна вектору скорости ($overrightarrow{v}$) (рис.2).
Рис. 2
Пример 1
Задание: Определите магнитную индукцию (В) поля, которое создает электрон, двигаясь прямолинейно с постоянной скоростью, равной 200 $frac{м}{с}$, в точке на расстоянии r=2$cdot {10}^{-9}м$ от него, лежащей на прямой, которая проходит через мгновенное положение электрона и составляет угол 450 с вектором скорости.
Решение:
Считаем, что электрон находится в вакууме. За основу решения примем формулу:
[overrightarrow{B}=frac{{mu }_0qleft[overrightarrow{v}overrightarrow{r}right] }{4pi r^3}left(1.1right).]
Модуль вектора магнитной индукции при этом имеет вид:
[B=frac{{mu }_0qvsinalpha }{4pi r^2}left(1.2right),]
где $alpha $ — угол между векторами $overrightarrow{v} и overrightarrow{r}.$
Заряд электрона известен $q=1,6cdot {10}^{-19}Кл, {mu }_0=4pi cdot {10}^{-7}frac{Гн}{м}.$ Проведем расчет:
[B=frac{4pi cdot {10}^{-7}1,6cdot {10}^{-19}cdot 200sin(45{}^circ ) }{4pi {(2cdot 10^{-9})}^2}=frac{3,2cdot {10}^{-24}cdot sqrt{2}}{8cdot {10}^{-18}}=0,56cdot {10}^{-6}left(Тлright).]
Ответ: $B=0,56 мк Тл.$
Пример 2
Задание: Найдите индукцию магнитного поля в центре непроводящей сферы, если по ее поверхности равномерно распределен заряд, плотность которого равна $sigma .$ Сфера вращается с постоянной угловой скоростью равной $w$ вокруг своей оси.
Решение:
Выделим произвольный бесконечно тонкий слой сферы высоты dx. Произвольную площадку поверхности сферы обозначим как dS. Тогда заряд, который находится на такой площадке, равен:
[dq=dScdot sigma left(2.1right).]
Этот заряд, двигаясь вместе с поверхностью сферы, создает магнитное поле в ее центре, которое можно записать как:
[dB=frac{{mu }_0}{4pi }frac{dqcdot vcdot R}{R^3}=frac{{mu }_0}{4pi }frac{dScdot sigma cdot wcdot r}{R^2}left(2.2right),]
где $v=wcdot r,$ где $r$ — радиус вращения слоя вокруг оси сферы. Весь слой будет создавать индукцию магнитного поля равную:
[B=int{frac{{mu }_0}{4pi }frac{dScdot sigma cdot wcdot r}{R^2}=}frac{{mu }_0}{4pi }frac{2pi rtriangle xcdot sigma cdot wcdot r}{R^2}left(2.3right),]
где $int{dS}=2pi rtriangle x.$
Сферу можно разделить на бесконечное количество слоев. Каждый слой создает магнитное поле В, которое рассчитывается по формуле (2.3), для нахождения суммарного поля охарактеризуем положение слоя как:
[r=sqrt{R^2-x^2}left(2.4right),]
где x — координата по оси Х считая от начала координат, которое мы поместили в центр сферы. $triangle x=dx$ В таком случае суммарное поле найдется как непрерывная сумма полей слоев, то есть:
[B_S=intlimits^R_{-R}{Bdx}=intlimits^R_{-R}{frac{{mu }_0}{4pi }frac{2pi r^2cdot sigma cdot w}{R^2}dx}=intlimits^R_{-R}{frac{left(R^2-x^2right)}{R^2}dx}=frac{{mu }_0}{2}cdot sigma cdot wcdot frac{4R}{3}=frac{2}{3}{mu }_0cdot sigma cdot wcdot R.]
Ответ: $B_S=frac{2}{3}mu_0•у •w•R.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Физический смысл магнитной индукции
Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.
В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.
При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.
Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.
Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.
Формула магнитной индукции
где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.
Вектор магнитной индукции
Определение
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как →B. Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B=FAmaxIl..
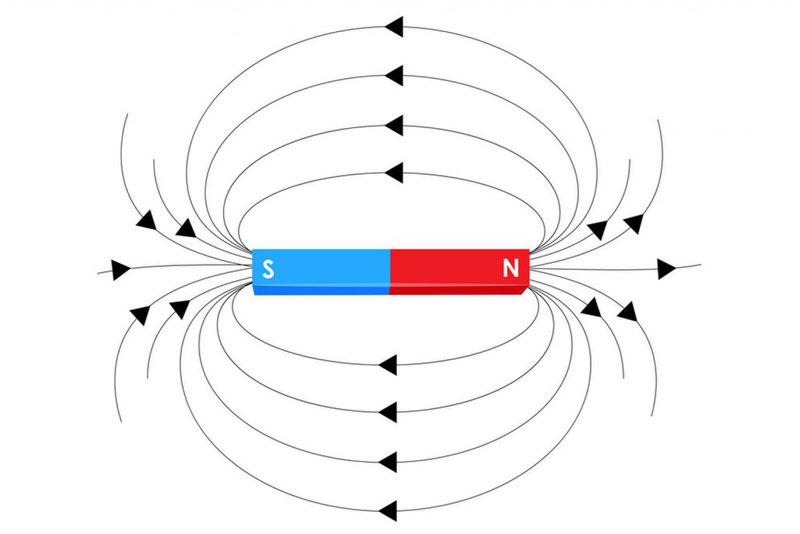
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора →B магнитной индукции.
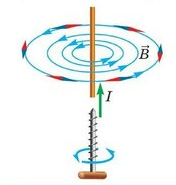
Отсюда следует, что:
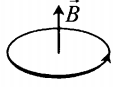
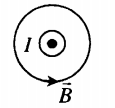
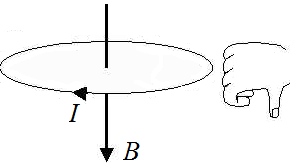
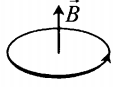
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции →B направлен вверх.
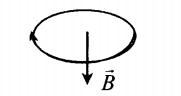
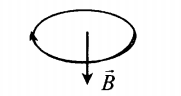
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции →B направлен вниз.
Способы обозначения направлений векторов:
| Вверх | |
| Вниз | |
| Влево | |
| Вправо | |
| На нас перпендикулярно плоскости чертежа |  |
| От нас перпендикулярно плоскости чертежа |  |
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?

Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.
В начале 19 века ученые обнаружили, что магнитное поле создается вокруг проводника с протекающим по нему током. Возникшие силовые линии ведут себя по таким же правилам, как и с природным магнитом. Больше того, взаимодействие электрического поля проводника с током и магнитного поля послужило основой электромагнитной динамики.
Понимание ориентации в пространстве сил во взаимодействующих полях позволяет рассчитать осевые вектора:
- Магнитной индукции;
- Величины и направления индукционного тока;
- Угловой скорости.
Такое понимание было сформулировано в правиле буравчика.
Совместив поступательное движение правостороннего буравчика с направлением тока в проводнике получаем направление линий магнитного поля, на которое указывает вращение рукоятки.
Не являясь законом физики, правило буравчика в электротехнике применяется для определения не только направления силовых линий магнитного поля зависящего от вектора тока в проводнике, но и наоборот, определение направления тока в проводах соленоида в связи с вращением линий магнитной индукции.
Понимание этой взаимосвязи позволило Амперу обосновать закон вращающихся полей, что привело к созданию электрических двигателей различного принципа. Вся втягивающая аппаратура, использующая катушки индуктивности, соблюдает правило буравчика.
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон Био-Савара-Лапласа
Формула ЭДС индукции
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:
dB = µ0 *I*dl*sin α /4*π*r2,
где:
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.
Закон Био-Савара-Лапласа
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
В = µ* µ0*2*I/4*π*r.
Для кругового движения она выглядит так:
В = µ*µ0*I/4*π*r.
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:
B→= B1→+ B2→+ B3→… + Bn→
Принцип суперпозиции
Теорема о циркуляции
Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.
Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.
Другое название теоремы – закон Ампера, описывающий циркуляцию МП.
Математически теорема записывается следующим образом.
Математическая формула теоремы о циркуляции
где:
- B→– вектор магнитной индукции;
- j→ – плотность движения электронов.
Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.
Магнитный поток
Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):
108 Мкс = 1 Вб.
Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.
Формула для расчёта имеет вид:
φ = |B*S| = B*S*cosα,
где:
- В – скалярная величина градиента магнитной индукции;
- S – площадь пересекаемой поверхности;
- α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).
Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900).
Магнитный поток
Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.
Другие формулы, где встречается B
Эти формулы также можно использовать для её расчёта.
Сила Ампера:
Сила Ампера: Fa=IBL sinα
Где:
- Fa — сила Ампера (в Н — ньютон)
- I — сила тока (в А — ампер)
- B — индукция магнитного поля (в Тл)
- L — длина проводника (в м)
- α — угол между вектором В и одним из направлений (силы тока, скорости или др.; измеряется в рад. или град.)
Сила Лоренца:
Сила Лоренца: Fл = qvB sinα
Где:
- Fл — сила Лоренца (в Н — ньютон)
- q — заряд частицы (в Кл — кулон)
- v — скорость (в м/с)
- B — индукция (в Тл)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Магнитный поток:
Магнитный поток: Ф = BS cosα
Где:
- Ф — магнитный поток (в Вб – вебер)
- B — индукция (в Тл)
- S — площадь рамки (в м²)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Электромагнитная индукция и магнитная индукция: какая между ними разница?
Электромагнитная индукция — это производство электродвижущей силы, создаваемой в результате относительного движения между магнитным полем и проводником.
Магнитная индукция может производить постоянный магнит, но может и не производить.
Электромагнитная индукция создаёт ток, но таким образом, что этот созданный ток противодействует изменению магнитного поля.
В электромагнитной индукции используются магниты и электрические цепи, а в магнитной индукции используются только магниты и магнитные материалы.
Предыдущая
РазноеЭлектротехника для чайников. Как научиться разбираться в электрике: уроки для начинающих
Следующая
РазноеАвтоматический выключатель — от чего защищает и как он устроен
Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Основные свойства магнитного поля
- Магнитное поле порождается электрическим током (движущимися зарядами).
- Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
- Магнитное поле существует независимо от нас, от наших знаний о нем.
Вектор магнитной индукции
Определение
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как→B. Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B=FAmaxIl
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Напряженность магнитного поля
Определение
Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как →H. Единица измерения — А/м.
→H=→Bμμ0
μ — магнитная проницаемость среды (у воздуха она равна 1), μ0 — магнитная постоянная, равная 4π·10−7 Гн/м.
Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: →H↑↑→B.
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора →B магнитной индукции.
Отсюда следует, что:
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции →B направлен вверх.
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции →B направлен вниз.
Способы обозначения направлений векторов:
| Вверх | |
| Вниз | |
| Влево | |
| Вправо | |
| На нас перпендикулярно плоскости чертежа |  |
| От нас перпендикулярно плоскости чертежа |  |
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?
Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
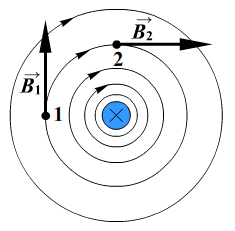
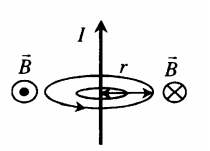
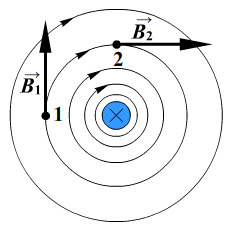
Магнитное поле прямолинейного тока
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.
Вид сверху:
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:
Правило буравчика (правой руки)
Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.
Модуль вектора магнитной индукции на расстоянии r от оси проводника:
B=μμ0I2πr
Модуль напряженности:
H=I2πr
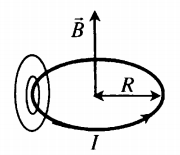
Магнитное поле кругового тока
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.
Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:
Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:
B=μμ0I2R
Модуль напряженности в центре витка:
H=I2R
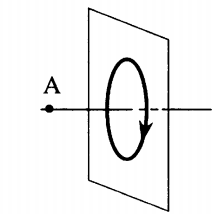
Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.
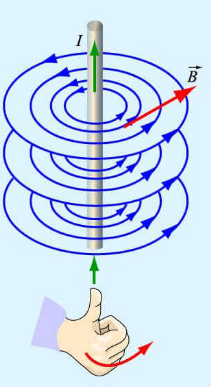
Магнитное поле электромагнита (соленоида)
Определение
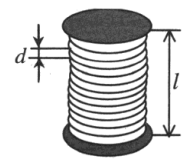
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.
Число витков в соленоиде N определяется формулой:
N=ld
l — длина соленоида, d — диаметр проволоки.
Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции →B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Модуль вектора магнитной индукции в центральной области соленоида:
B=μμ0INl=μμ0Id
Модуль напряженности магнитного поля в центральной части соленоида:
H=INl=Id
Алгоритм определения полярности электромагнита
- Определить полярность источника.
- Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
- Определить направление вектора магнитной индукции.
- Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).
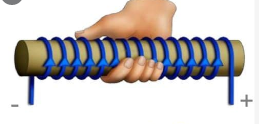
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.
Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.
Задание EF17530
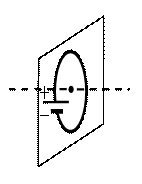
Ответ:
а) вертикально вверх в плоскости витка
б) вертикально вниз в плоскости витка
в) вправо перпендикулярно плоскости витка
г) влево перпендикулярно плоскости витка
Алгоритм решения
1.Определить правило, по которому можно определить направление вектора магнитной индукции в данном случае.
2.Применить выбранное правило и определить направление вектора магнитной индукции относительно рисунка.
Решение
По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора →B магнитной индукции мы будем использовать правило правой руки.
Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.
Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18109
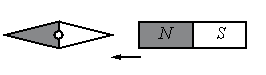
Ответ:
а) повернётся на 180°
б) повернётся на 90° по часовой стрелке
в) повернётся на 90° против часовой стрелки
г) останется в прежнем положении
Алгоритм решения
- Вспомнить, как взаимодействуют магниты.
- Определить исходное положение полюсов.
- Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.
Решение
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
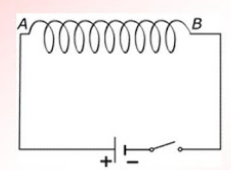
Задание EF18266
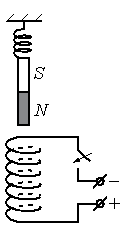
Алгоритм решения
- Определить направление тока в соленоиде.
- Определить полюса соленоида.
- Установить, как будет взаимодействовать соленоид с магнитом.
- Установить, как будет себя вести магнит после замыкания электрической цепи.
Решение
Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.
Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 22.5k
Тема
3.3. Магнитное поле в вакууме. Магнитное
поле–
это особая форма материи.Магнитное поле
– порождается любыми движущимися
зарядами: электрический ток в металле,
в электролите, в газе, пучок электронов,
протонов и т.п.Индукция
магнитного поля-это
силовая характеристика магнитного
поля.
Вектор магнитной индукции направлен
всегда так, как сориентирована свободно
вращающаяся магнитная стрелка в магнитном
поле.Единица измерения магнитной
индукции в системе СИ:

Сила
Лоренца—
сила,
с которой, в рамках классической
(не-квантовой) физики, электромагнитное
поле действует на заряженную частицу
(точечную, в общем случае — движущуюся).Выражение
для силы Ампера можно записать в виде:
|
F = q n S Δl υB sin α. |
Так
как полное число N носителей
свободного заряда в проводнике длиной
Δl и
сечением S равно n S Δl,
то сила, действующая на одну заряженную
частицу, равна
|
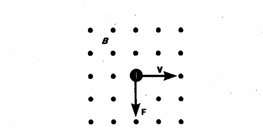
Движение
заряженных частиц в магнитном поле.
Формула
силы Лоренца дает возможность найти
ряд закономерностей движения заряженных
частиц в магнитном поле. Зная направление
силы Лоренца и направление вызываемого
ею отклонения заряженной частицы в
магнитном поле можно найти знак заряда
частиц, которые движутся в магнитных
полях. Для вывода общих закономерностей
будем полагать, что магнитное поле
однородно и на частицы не действуют
электрические поля. Если заряженная
частица в магнитном поле движется со
скоростью v вдоль
линий магнитной индукции, то угол α
между векторами v и Вравен
0 или π. Тогда сила Лоренца равна нулю,
т. е. магнитное поле на частицу не
действует и она движется равномерно и
прямолинейно. В случае, если заряженная
частица движется в магнитном поле со
скоростью v,
которая перпендикулярна вектору В,
то сила ЛоренцаF=Q[vB]
постоянна по модулю и перпендикулярна
к траектории частицы. По второму закону
Ньютона, сила Лоренца создает
центростремительное ускорение. Значит,
что частица будет двигаться по окружности,
радиус r которой находится из условия
QvB=mv2/r
, следовательно
Период
вращения частицы,
т. е. время Т, за которое она совершает
один полный оборот,
т.
е. период вращения частицы в однородном
магнитном поле задается только величиной,
которая обратна удельному заряду (Q/m)
частицы, и магнитной индукцией поля, но
при этом не зависит от ее скорости (при
v<<c). На этом соображении основано
действие циклических ускорителей
заряженных частиц. В случае, если
скорость v заряженной
частицы направлена под углом α к
вектору В (рис.
170), то ее движение можно задать в виде
суперпозиции: 1) прямолинейного
равномерного движения вдоль поля со
скоростью vparall=vcosα
; 2) равномерного движения со скоростью
vperpend=vsinα
по окружности в плоскости, которая
перпендикулярна полю. Радиус окружности
задается формулой (1) (в этом случае надо
вместо v подставить
vperpend=vsinα).
В результате сложения двух данных
движений возникает движение по спирали,
ось которой параллельна магнитному
полю (рис. 1). Шаг винтовой (спиральной)
линии
Направление,
в котором закручивается спираль,
определяется знаком заряда частицы.
Если
скорость v заряженной
частицы составляет угол α с направлением
вектора В неоднородного
магнитного поля,
у которого индукция возрастает в
направлении движения частицы, то r и h
уменьшаются с увеличением В.
На этом основана фокусировка заряженных
частиц в магнитном поле.
Магнитное поле движущегося заряда.
|
|
|
|
Принцип
суперпозиции:магнитное
поле, создаваемое совокупностью
движущихся зарядов, равно векторной
сумме
полей, создаваемых отдельными зарядами
,
где
— магнитная индукция результирующего
поля,
— магнитная индукция полей, создаваемых
отдельными зарядами.
Закон
Био-Савара-Лапласа
для проводника с током I, элемент
dl которого
создает в некоторой точке А (рис. 1)
индукцию поля dB,
равен
где
dl —
вектор, по модулю равный длине dl элемента
проводника и совпадающий по направлению
с током, r —
радиус-вектор, который проведен из
элемента dl проводника
в точку А поля, r — модуль радиуса-вектора r.
Направление dB перпендикулярно
dl и r,
т. е. перпендикулярно плоскости, в которой
они лежат, и совпадает с направлением
касательной к линии магнитной индукции.
Это направление может быть найдено по
правилу правого винта: направление
вращения головки винта дает направление
dB,
если поступательное движение винта
совпадает с направлением тока в
элементе.
Модуль
вектора dB задается
выражением
где
α — угол между векторами dl и r.
Магнитное
поле прямолинейного проводника с током.
Для
получения спектра магнитного поля
прямого проводника с током проводник
пропускают сквозь лист картона. На
картон насыпают тонкий слой железных
опилок, и опилки слегка встряхивают.
Под действием магнитного поля железные
опилки располагаются по концентрическим
окружностям. По касательным к ним
расположатся и магнитные стрелки вокруг
такого проводника с током.Таким образом,
линии магнитной индукции магнитного
поля прямолинейного
тока представляют
собой концентрические
окружности,
расположенные в плоскости, перпендикулярной
к проводнику, с центром на оси проводника.
Направление линий индукции
определяется правилом
правого винта: если
поворачивать головку винта так, чтобы
поступательное движение острия винта
происходило вдоль тока в проводнике,
то направление вращения головки указывает
направление линий магнитной индукции поля
прямого проводника с током.Магнитное
поле кругового тока.Определим
магнитную индукцию на оси проводника
с током на расстоянии х от
плоскости кругового тока.
Векторы
перпендикулярны
плоскостям, проходящим через
соответствующие
и
.
Следовательно, они образуют симметричный
конический веер. Из соображения симметрии
видно, что результирующий вектор
направлен
вдоль оси кругового тока. Каждый из
векторов
вносит
вклад равный
,
а
взаимно
уничтожаются. Но
,
,
а т.к. угол между
и
α
– прямой, то
тогда
получим
|
|
Подставив
в (1.6.1)
и,
проинтегрировав по всему контуру
,
получим выражение для нахождения магнитной
индукции кругового тока:
|
|
(1.6.2) |
При
,
получим магнитную
индукцию в центре кругового тока:
|
|
(1.6.3) |
Заметим,
что в числителе (1.6.2)
–
магнитный момент контура. Тогда, на
большом расстоянии от контура, при
,
магнитную индукцию можно рассчитать
по формуле:
|
|
Теорема
о циркуляции вектора напряженности
(индукции) магнитного поля.
Теорема
о циркуляции вектора В.
Поскольку
магнитное поле создается токами, а
ненулевая циркуляция означает, что
косинус угла между вектором поля и
векторами перемещений преимущественно
не меняет знак (т. е. перемещения происходят
преимущественно вдоль или против силовых
линий), то в этом случае замкнутый контур
обхода пронизывают создающие поле,
направленное вдоль (или против) направления
обхода, токи, алгебраическая сумма
которых не равна нулю. Ток считается
положительным, если его направление
связано с направлением обхода правилом
правого винта:

Циркуляция
вектора индукции магнитного поля
прямопропорциональна алгебраической
сумме пронизывающих контур токов;
коэффициентом пропорциональности
служит магнитная постоянная, умноженная
на магнитную проницаемость
среды,
которая в результате намагничивания
в
раз
изменяет результирующее поле:
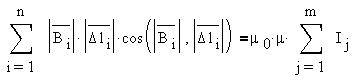
Циркуляцией
вектора В по
заданному замкнутому контуру называется
интеграл
где dl —
вектор элементарной длины контура,
направленной вдоль обхода
контура, Bl=Bcos — составляющая
вектора В в
направлении касательной к контуру (с
учетом выбранного направления обхода), —
угол между векторами В и
dl.
Поле
тороида и соленоида.
Найдем с помощью теоремы о циркуляции,
индукцию магнитного поля внутри соленоида.
Рассмотрим соленоид длиной l,
который имеет N витков, и по которому
течет ток (рис. 1). Будем считать длину
соленоида во много раз больше, чем
диаметр его витков. Экспериментальное
изучение магнитного поля соленоида
(см. главу «магнитное поле и его
характеристики») показывает, что
внутри соленоида поле однородно, вне
соленоида — неоднородно и практически
отсутствует. На
рис. 1 даны линии магнитной индукции
внутри и вне соленоида. Чем соленоид
длиннее, тем магнитная индукция вне его
меньше. Поэтому приближенно можно
полагать, что поле бесконечно длинного
соленоида сосредоточено целиком внутри
него, а поле соленоида можно не
учитывать. Для
вычисления магнитной индукции В выберем
замкнутый прямоугольный контур ABCDA, как
показано на рис. 1. Циркуляция вектора Впо
замкнутому контуру ABCDA, который охватывает
все N витков, используя формулу циркуляции
вектора В,
будет
Интеграл
по ABCDA можно разложить на четыре интеграла:
по АВ, ВС, CD и DA. На участках АВ и CD контур
и линии магнитной индукции перпендикулярны:
Bl=0.
На участке вне соленоида B=0. На участке
DA циркуляция вектора В равна Вl (контур
и линии магнитной индукции совпадают);
значит,
(1)
Из
(1) приходим к формуле магнитной индукции
поля внутри соленоида (в вакууме):
(2)
Мы
видим, что поле внутри соленоида однородно (при
расчетах пренебрегают краевыми эффектами
в областях, прилегающих к торцам
соленоида). Но отметим, что вывод этой
формулы не совсем корректен (поскольку
линии магнитной индукции замкнуты, и
интеграл по внешнему участку магнитного
поля строго нулю не равен). Корректно
найти поле внутри соленоида можно,
используя закон Био — Савара — Лапласа;
в результате получается такая же формула
(2). Важное
практическое значение имеет также
магнитное поле тороида —
кольцевой катушки, у которой витки
намотаны на сердечник, который имеет
форму тора (рис. 2). Магнитное поле, как
известно из опыта, сосредоточено внутри
тороида, а вне его поле равно нулю.
В
данном случае линии магнитной индукции,
как следует из соображений симметрии,
есть окружности, у которых центры
расположены по оси тороида. В качестве
контура возьмем одну такую окружность
радиуса r. Тогда, используя теорему о
циркуляции, B•2πr=μ0NI,
откуда следует, что магнитная индукция
внутри тороида (в вакууме)
где
N — число витков тороида.
Если
контур проходит вне тороида, то токов
он не охватывает и B•2πr = 0. Следовательно,
что поле вне тороида отсутствует (что
показывает и опыт).
Сила
Ампера.
Сила, с которой магнитное поле действует
на помещенный в него проводник с током,
называется силой
Ампера.Величина
этой силы, действующей на элемент
Δl проводника
с током I в
магнитном поле с индукцией
,
определяется законом Ампера:
,
(1)
где α –
угол между направлениями тока и вектора
индукции.Направление силы
Ампера можно найти с помощью правила
левой руки:
если левую руку расположить так, чтобы
линии магнитной индукции входили в
ладонь, а четыре вытянутых пальца
совпадали по направлению с направлением
тока, то отогнутый на 90° большой палец
укажет направление силы, действующей
на элемент проводника.
Взаимодействие
параллельных токов.
Закон
Ампера используется при нахождении
силы взаимодействия двух токов. Рассмотрим
два бесконечных прямолинейных параллельных
тока I1 и
I2;
(направления токов даны на рис. 1),
расстояние между которыми R. Каждый из
проводников создает вокруг себя магнитное
поле, которое действует по закону Ампера
на соседний проводник с током. Найдем,
с какой силой действует магнитное поле
тока I1 на
элемент dl второго
проводника с током I2.
Магнитное поле тока I1 есть
линии магнитной индукции, представляющие
собой концентрические окружности.
Направление вектора B1 задается
правилом правого винта, его модуль по
формуле (5) есть
Направление
силы dF1,
с которой поле B1 действует
на участок dl второго
тока, находится по правилу левой руки
и указано на рисунке. Модуль силы,
используя (2), с учетом того, что угол α
между элементами тока I2 и
вектором B1 прямой,
будет равен
подставляя
значение для В1,
найдем
(3)
Аналогично
рассуждая, можно показать, что сила
dF2 с
которой магнитное поле тока I2 действует
на элемент dl первого
проводника с током I1,
направлена в противоположную сторону
и по модулю равна
(4)
Сопоставление
выражений (3) и (4) дает, что
т.
е. два
параллельных тока одинакового направления
притягиваются друг к другу с
силой, равной
(5)
Если токи
имеют противоположные направления,
то, используя правило левой руки,
определим, что между
ними действует сила отталкивания,
определяемая выражением (5). Магнитный
поток.
—
поток Ф вектора магнитной
индукции В через
к.-л. поверхность S:

Здесь dS
— элемент
площади, п
— единичный
вектор нормали к S. В
СИ М. п. измеряется в веберах (Во), в
гауссовой системе единиц (к-рая применяется
ниже) — в максвеллах (Мкс); 1 Вб=108 Мкс.
Поскольку вектор В является
чисто вихревым
,
М. п. через произвольную замкнутую
поверхность S равен
нулю. Это свойство, установленное
Гауссом, может нарушаться только при
наличии внутри S
магнитных монополей, пока
ещё гипотетических.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #